Introduction

Hybrid nanofluids, such as those composed of copper and aluminium nanoparticles dispersed within a base fluid, represent a novel class of heat transfer fluids with enhanced thermal properties. These fluids have garnered significant interest in recent years due to their potential to address challenges in engineering applications where efficient heat transfer is critical. By combining nanoparticles of different materials, hybrid nanofluids offer tailored thermal conductivity, viscosity, and stability characteristics that can be optimized for specific applications across various industries, ranging from electronics cooling and solar energy systems to automotive engineering and aerospace technology. Their unique thermal properties make them attractive candidates for improving heat transfer efficiency and addressing thermal management challenges in numerous engineering applications. Investigations into the flow and heat transfer characteristics of hybrid nanofluids (HNFs) within rotating systems under the influence of magnetohydrodynamics (MHD) have been conducted by Chamkha et al. [1]. Their findings reveal a notable increase in the Nusselt number with escalating volume percentages of nanoparticles within the HNF. Similarly, Waini et al. [2] have delved into the flow behaviour of nanofluids (NFs) towards a shrinking cylinder composed of Al2O3 nanoparticles. Furthermore, Zafar et al. [3] explored the impact of a magnetic field, mass suction, and heat source on the stagnation region of a ternary HNF comprised of (Cu–Fe3O4–SiO2/polymer) approaching a stretching/shrinking cylinder under convective heating conditions. Their investigation unveiled that the ternary HNF exhibited a notably accelerated heat transfer rate compared to hybrid and conventional NFs. Additionally, a computational analysis by Duguma et al. [4] scrutinized the behaviour of CoFe2O4/TiO2-H2O-Casson nanofluids across a slick surface undergoing stretching/shrinking within a Darcy–Forchheimer porous medium. Their study revealed a direct correlation between the increase in nanoparticle volume fraction and the augmentation of the skin friction (drag force) coefficient. These studies and others related to NFs and HNFs are catalogued in references [5,6,7,8,9,10]. These investigations underscore the growing interest and significance of NFs and HNFs in various engineering applications, offering insights into their dynamic behaviour and potential for enhancing heat transfer efficiency in diverse systems.

A rheological model known as the Maxwell viscoelastic fluid describes materials that display both viscous and elastic behaviour. It comprises a linear combination of a viscous dashpot and an elastic spring. Various fields such as polymer science, geophysics, and biomedical engineering apply this model, emphasizing the crucial understanding of material deformation. Applications range from modelling blood flow in arteries to predicting seismic responses in geology. For instance, in polymer processing, the Maxwell model helps simulate how polymers behave under stress, aiding in the design of manufacturing processes. Examples include modelling the flow of toothpaste or the behaviour of certain types of gels. When magnetic effects are introduced into Maxwell fluids, their rheological properties can be further influenced, leading to intriguing phenomena and potential applications in various fields such as biomedical engineering, intelligent materials, fluid dynamics, and microfluidics. Their ability to respond to external magnetic fields enables novel functionalities and control mechanisms, paving the way for advancements in diverse fields of science and technology. Research investigations into the flow, heat, and mass transfer behaviours of magnetohydrodynamic (MHD) Maxwell nanofluids (NFs) interacting with cylinders featuring constant heat flux (CC) and non-uniform heat sources/sinks were conducted by Raju et al. [11]. Their study revealed a noteworthy decrease in heat transmission rate as the Biot number increased, shedding light on the complex interplay between external heat sources and fluid dynamics in MHD Maxwell NF systems. Bilal et al. [12] also explored the behaviour of Maxwell NFs undergoing stretching with suction/injection action, particularly in the presence of a magnetic field. Their investigation uncovered the generation of a resistive force under the influence of the magnetic field, resulting in a reduction in fluid velocity and an elevation in temperature. Furthermore, Kavya et al. [13] conducted numerical simulations to analyse the flow of Williamson hybrid nanofluids (HNFs) along an expanding cylinder under various conditions, including heat production, suction, MHD effects, and variable thermal conductivity. Their findings indicated a decrease in the heat transfer characteristics of Williamson HNF flow as the Prandtl number values increased, highlighting the intricate relationship between fluid properties and flow dynamics in complex systems. The combined effect of entropy and bilateral reactions on the rotating nanofluid flow model under the impacts of slip and convective boundary conditions is scrutinized by Nisar et al. [14]. Moreover, the study of Maxwell and Maxwell-NF issues with different effects, including exponential or linear stretchable surfaces, has been addressed in references [15,16,17], presenting further intriguing insights into the behaviour of these nanofluids under diverse conditions.

Understanding the complexities of nonlinear convection and heat stratification along inclined stretchable cylinders is important across various practical applications. This research provides valuable insights for optimizing heat transfer processes in engineering systems such as solar collectors, thermal energy storage devices, and cooling systems for electronic devices. Engineers can develop more cost-effective and efficient systems to meet specific heat transfer requirements by investigating the effects of thermal stratification and nonlinear convection. Moreover, this study contributes to advancing technology in climate control, renewable energy, and thermal management by expanding our knowledge of fluid mechanics and thermal sciences, paving the way for innovative solutions. Hayat et al. [18] explored the characteristics of double-stratified mixed convection stagnation point flow induced by an impermeable inclined stretched cylinder. Their findings indicated that lower values of the stratified parameter corresponded to more excellent temperature distribution. Rehman et al. [19] investigated mixed convection tangent hyperbolic fluid flow towards an extending cylindrical surface with thermal stratification in a separate study. They observed that, contrary to the trend of the thermal stratification parameter, the temperature of the tangent hyperbolic fluid increased as the inclination angle increased. Furthermore, Gopal et al. [20] examined the effects of thermal stratification and heat generation/absorption on magnetohydrodynamic (MHD) Carreau nanofluid (NF) flow over a permeable cylinder. Their investigation revealed that, compared to the heat absorption scenario, heat creation imposed a greater limit on temperature. Moreover, Hayat et al. [21] delved into the impacts of thermal radiation and nonlinear convective flow on Maxwell NFs. Additionally, Sehrish et al. [22] studied the effects of nonlinear convection across an inclined sheet, observing that fluid velocity increased with higher thermal Grashof numbers. Because common fluids such as oils, ethylene glycol, and water have low thermal conductivity, technological breakthroughs have enabled creative techniques to improve thermal performance. For instance (Refer to [23]).

Understanding thermal transport phenomena in various industrial and technical processes relies on analysing Cattaneo–Christov (CC) heat flux using hybrid nanofluids (HNFs) over an inclined stretched cylinder. Incorporating the non-Fourier heat conduction mechanism, which elucidates the limited speed of heat propagation, is crucial for predicting more accurate thermal behaviours. This model finds applications in designing and optimizing cooling systems in nuclear reactors, enhancing heat exchangers, and developing efficient thermal management techniques for electronics cooling. Moreover, utilizing HNFs, which combine different types of nanoparticles, can significantly enhance convective heat transfer rates and thermal conductivity, leading to energy-efficient systems. Precise heat management is vital in the manufacturing, automotive, and aerospace sectors, where advancements from this study may occur. Recent research by Hussain et al. [24] investigated the CC model with double stratification, heat source, and thermal relaxation effects, revealing that temperature decreases as the thermal relaxation parameter increases. Christopher et al. [25] examined Darcy–Forchheimer flow on an MHD hybrid stretchable cylinder induced by a magnetic field with CC heat flux, finding that velocity decreases with an increase in the magnetic parameter. Farooq et al. [26] also studied the CC model for Carreau nanofluid flows via a stretched cylinder, revealing the thermal relaxation parameter intensifying with the Nusselt number.

By the conclusion of the project, we aim to address the following research gaps:

  • How nonlinear thermal convection and stratification effects alter the velocity and temperature profiles of Maxwell hybrid nanofluid over a stretching cylinder is paramount.

  • Analysing the influence of different fixed values on skin friction and heat transfer rates.

  • Investigating how streamlines and isotherms are affected by the magnetic field and thermal stratification effects provides valuable insights into the fluid flow and thermal behaviour near the stretching cylinder’s surface.

To enhance heat transfer efficiency in various engineering applications, there is a growing focus on understanding Maxwell hybrid nanofluids’ thermal behaviour under Cattaneo–Christov (CC) heat flow, as discussed in the referenced literature. Utilizing the unique characteristics of CC heat flux and Maxwell HNF fluid holds significant promise for advancing thermal management strategies and offering potential solutions to improve performance and energy efficiency across various technical disciplines. Our study introduces innovative elements, including considerations for thermal stratification, nonlinear thermal convection, heat source effects, and viscous and joule heating. By incorporating these factors, the modified heat flux model with Maxwell HNF flow aims to deliver more effective solutions in engineering domains, resulting in enhanced rates of heat transmission.

Mathematical description of the problem

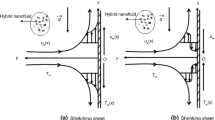
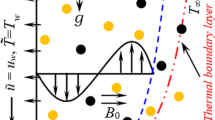
Consider Maxwell hybrid nanofluid’s incompressible stagnation point flow directed towards an inclined cylindrical surface undergoing linear extension. This analysis incorporates the effects of mixed convection and magnetohydrodynamics (MHD). The velocities of stretching/shrinking and free stream are assumed to follow \({U}_{\text{w}}\left(z\right)=\frac{{U}_{0}z}{l}\) and \({w}_{\text{e}}\left(z\right)=\frac{{w}_{\infty }z}{l}\), Fig. 1 schematically depicts the flow model. Additionally, the Cattaneo–Christov (CC) heat flow model enhances heat transfer. Cylindrical coordinates are selected, with the r-axis perpendicular to the cylinder and the z-axis along its axial direction. The governing equations for the flow can be expressed using formulations outlined in previous studies by Narayanaswamy et al. [5], Raju et al. [11], and Sudarmozhi et al. [17].

Fig. 1
figure 1

Coordinate system and physical model

Full size image

Continuity equation

It represents mass conservation within a fluid domain. It states that the rate of change of mass in a control volume equals the net mass flow into or out of the volume. Fluid flow over a stretching cylinder describes mass distribution and conservation, revealing flow patterns and velocities.

$$\frac{\partial u}{{\partial r}} + \frac{u}{r} + \frac{\partial w}{{\partial z}} = 0.$$
(1)

Momentum equation

It describes momentum conservation in fluid flow, considering pressure, viscous, and external forces. In fluid flow over a stretching cylinder, it predicts velocity and flow behaviour and assesses the impact of viscosity and external force.

$$\left.\begin{array}{c}\left(u\frac{\partial w}{\partial r}+w\frac{\partial w}{\partial z}\right)+\tau \left({w}^{2}\frac{{\partial }^{2}w}{\partial {z}^{2}}+{u}^{2}\frac{{\partial }^{2}w}{\partial {r}^{2}}+2uw\frac{{\partial }^{2}w}{\partial r\partial z}\right)={w}_{\text{e}}\frac{\text{d}{w}_{\text{e}}}{\text{d}z}+\frac{{\mu }_{\text{hnf}}}{{\rho }_{\text{hnf}}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial w}{\partial r}\right)-\\ \frac{{\sigma }_{\text{hnf}}{{B}_{0}}^{2}}{{\rho }_{\text{hnf}}}\left(\tau u\frac{\partial w}{\partial r}+w\right)+g\left[{\left({\beta }_{\text{T}}\right)}_{\text{hnf}}\left(T-{T}_{\infty }\right)+{{\left({\beta }_{\text{T}}\right)}^{2}}_{\text{hnf}}{\left(T-{T}_{\infty }\right)}^{2}\right]{\text{cos}}\alpha \end{array}\right\}$$
(2)

Energy equation

It governs energy conservation in fluid flow, considering heat transfer mechanisms like conduction, convection, and radiation. It analyses temperature distribution and heat transfer rates in a fluid flow over a stretching cylinder, assessing the impact of thermal stratification and convection on thermal behaviour (Table 1).

Table 1 The thermophysical properties of both the base fluid (\({H}_{2}O\)) and nanoparticles Cu-Al2O3 (See Refs. [5,6,7])
Full size table
$$\left.\begin{array}{c}\lambda \left({w}^{2}\frac{{\partial }^{2}T}{\partial {z}^{2}}+{u}^{2}\frac{{\partial }^{2}T}{\partial {r}^{2}}+2uw\frac{{\partial }^{2}T}{\partial r\partial z}+w\frac{\partial w}{\partial z}\frac{\partial T}{\partial z}+u\frac{\partial w}{\partial r}\frac{\partial T}{\partial z}+w\frac{\partial u}{\partial z}\frac{\partial T}{\partial r}+u\frac{\partial u}{\partial r}\frac{\partial T}{\partial r}\right)+\\ u\frac{\partial T}{\partial r}+w\frac{\partial T}{\partial z}= \frac{{k}_{\text{hnf}}}{{\left(\rho {c}_{\text{p}}\right)}_{\text{hnf}}}\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial T}{\partial r}\right)+\frac{{\mu }_{\text{hnf}}}{{\left(\rho {c}_{\text{p}}\right)}_{\text{hnf}}}{\left(\frac{\partial w}{\partial r}\right)}^{2}+ \frac{{Q}_{0}}{{\left(\rho {c}_{p}\right)}_{\text{hnf}}}\left(T-{T}_{\infty }\right)+\\ \frac{{\sigma }_{hnf}{B}_{0}^{2}}{{\left(\rho {c}_{p}\right)}_{\text{hnf}}}{w}^{2},\end{array}\right\}$$
(3)

The boundary conditions associated with Eqs. (1) to (3) are regarded following [27]

$$w = U_{{\text{w}}} \left( z \right) + B_{1} \frac{\partial w}{{\partial r}},u = 0,T = T_{{\text{w}}} = T_{0} + \frac{bz}{l}\quad {\text{at}}\quad r = a.$$
(4)
$$w \to w_{{\text{e}}} ,T = { }T_{\infty } = T_{0} + \frac{cz}{l}\quad {\text{as}}\quad r \to \infty .$$
(5)

The stream function, which fulfils the continuity Eq. (1) consistently, can be defined as follows:

$$w = \frac{1}{r}\frac{{\partial {\psi }}}{\partial r}\,{\text{and}}\,u = - \frac{1}{r}\frac{{\partial {\psi }}}{\partial z}.$$
(6)

The similarity variables (\(\eta )\), stream function \((\psi\)) and dimensionless variables are utilised to transform the energy and flow equations into ordinary differential equations (ODEs).

$$\left.\begin{array}{c}\eta =\frac{{r}^{2}-{a}^{2}}{2a}{\left(\frac{{U}_{0}}{{v}_{\text{f}}l}\right)}^\frac{1}{2},\psi ={\left(\frac{{U}_{0}{\upsilon }_{\text{f}}{z}^{2}}{l}\right)}^\frac{1}{2}a f\left(\eta \right) ,w=\frac{{U}_{0}z}{l}{f}^{\prime},u=\frac{-a}{r}{\left(\frac{{U}_{0}{v}_{\text{f}}}{l}\right)}^\frac{1}{2}f\left(\eta \right),\\ \theta \left(\eta \right)=\frac{T-{T}_{\infty }}{{T}_{\text{w}}-{T}_{0}}\end{array}\right\}$$
(7)

By substituting Eq. (7) into Eqs. (2)–(5), the following equations can be obtained.

Momentum equation without dimensions,

$$\left.\begin{array}{c}\frac{{\mu }_{r}}{{\rho }_{r}}\left[\left(1+2\eta \gamma \right){f}^{{\prime\prime\prime}}+{2\gamma f}^{{\prime\prime}}\right]+f{f}^{{\prime\prime}}-{\left({f}{\prime}\right)}^{2}+{\beta }_{1}\left(2f{f}^{\prime}{f}^{{\prime\prime}}-\frac{\gamma }{\left(1+2\eta \gamma \right)}{f}^{2}{f}^{{\prime\prime}}-{f}^{2}{f}^{{\prime\prime\prime}}\right)+\\ {A}^{2}-{M}^{2}\frac{{\sigma }_{\text{r}}}{{\rho }_{r}}\left(-{\beta }_{1}Ref{f}^{{\prime\prime}}+{f}^{\prime}\right)+cos\alpha \left[Gr\frac{{\left(\rho {\beta }_{T}\right)}_{r}}{{\rho }_{r}}\theta +{\left(\frac{{\left(\rho {\beta }_{T}\right)}_{r}}{{\rho }_{r}}\right)}^{2}G{r}_{1}{\theta }^{2}\right]=0,\end{array}\right\}$$
(8)

Energy equation without dimensions,

$$\left.\begin{array}{c}\frac{{k}_{\text{r}}}{{\left(\rho {c}_{p}\right)}_{\text{r}}}\frac{1}{Pr}\left[\left(1+2\eta \gamma \right){\theta }^{{\prime\prime}}+{2\gamma \theta }^{\prime}\right]{-\lambda }_{1}\left[{f}^{2}{\theta }^{{\prime\prime}}-f{f}^{\prime}{\theta }^{\prime}+\left(\delta +\theta \right)\left({f}^{{\prime}2}-f{f}^{{\prime\prime}}\right)\right]+f{\theta }^{\prime}-\\ {\left(\delta +\theta \right)f}^{\prime}+\frac{{\mu }_{r}}{{\left(\rho {c}_{p}\right)}_{\text{r}}}Ec\left(1+2\eta \gamma \right){\left({f}^{{\prime\prime}}\right)}^{2}+{M}^{2}\frac{{\sigma }_{r}}{{\left(\rho {c}_{p}\right)}_{\text{r}}}Ec{\left({f}^{\prime}\right)}^{2}+\frac{1}{{\left(\rho {c}_{p}\right)}_{\text{r}}}Q\theta =0,\end{array}\right\}$$
(9)

The aforementioned boundary conditions (4)–(5) are converted into a dimensionless representation.

$$f = 0, f^{\prime} = 1 + Bf^{\prime\prime}, \theta = 1 - \delta ,\,{\text{at}}\,\eta = 0.$$
(10)
$$f^{\prime} = A, \theta = 0\,{\text{as}}\,\eta \to \infty .$$
(11)

where

$$\left.\begin{array}{c}{\mu }_{\text{r}}={\mu }_{\text{hnf}}/{\mu }_{\text{f}},{\rho }_{\text{r}}={\rho }_{\text{hnf}}/{\rho }_{f},{\sigma }_{r}={\sigma }_{\text{hnf}}/{\sigma }_{\text{f}}, {\left(\rho {\beta }_{\text{T}}\right)}_{\text{r}}=\frac{{\left(\rho {\beta }_{T}\right)}_{\text{hnf}}}{{\left(\rho {\beta }_{\text{T}}\right)}_{\text{f}}},{{k}_{\text{r}}=k}_{\text{hnf}}/{k}_{\text{f}}, \\ {{\left(\rho {c}_{\text{p}}\right)}_{\text{r}}=\left(\rho {c}_{\text{p}}\right)}_{\text{hnf}}/{\left(\rho {c}_{\text{p}}\right)}_{\text{f}},\gamma ={\left(\frac{\upsilon l}{{a}^{2}{U}_{0}}\right)}^\frac{1}{2}{,M}^{2}=\frac{{\sigma }_{f}l{B}_{0}^{2}}{{{\rho }_{f}U}_{0}}, {\beta }_{1}=\frac{\tau {U}_{0}}{l},B={B}_{1}{\left(\frac{{U}_{0}\upsilon }{l}\right)}^\frac{1}{2},\\ A=\frac{{w}_{\infty }}{{U}_{0}},{\lambda }_{1}= \frac{\lambda {U}_{0}}{l},Gr=\frac{g{\beta }_{\text{Tf}}\left({T}_{\text{w}}-{T}_{\infty }\right)}{{U}_{0}{U}_{\text{w}}}, G{r}_{1}=\frac{g{\beta }_{\text{Tf}}^{2}{\left({T}_{\text{w}}-{T}_{\infty }\right)}^{2}}{{U}_{0}{U}_{\text{w}}}, Pr=\frac{{\mu {c}_{p}}_{\text{f}}}{{k}_{\text{f}}}, Ec=\frac{{U}_{0}^{2}\left({T}_{w}-{T}_{0}\right)}{b{\left({c}_{p}\right)}_{\text{f}}},\\ Q=\frac{{Q}_{0}l}{{U}_{0}{\left(\rho {c}_{p}\right)}_{\text{f}}},\delta =\frac{c}{b}. \\ \end{array}\right\}$$
(12)

The formulas presented in Table 2 illustrate the physical parameters of the HNF (Cu-Al2O3/H2O) Where \(\phi\) denotes the volume percentage of the nanoparticles, namely \({\phi }_{1}\)= (\({\phi }_{\text{cu}}\)) signifies the volume fraction of the first nanoparticle copper, and \({\phi }_{2}\)= (\({\phi }_{\text{Al}2\text{O}3}\)) denotes the volume fraction of the second nanoparticle aluminium oxide. Furthermore, the heat capacitance is represented by the symbols \({\left(\rho {C}_{\text{p}}\right)}_{\text{f}}\), \({\left(\rho {C}_{\text{p}}\right)}_{1}\) and \({\left(\rho {C}_{p}\right)}_{2}\). The thermal conductivities are denoted as \({k}_{\text{f}}, {k}_{1}\) and \({k}_{2}\), while the densities are represented as \({\rho }_{\text{f}}\), \({\rho }_{1}\) and \({\rho }_{2}\). The electrical conductivities are denoted as \({\sigma }_{\text{f}}\), \({\sigma }_{1}\) and \({\sigma }_{2}\). Additionally, the thermal expansion coefficients of the pure material and the HNF are denoted \({\left(\rho {\beta }_{\text{T}}\right)}_{\text{f}}\), \({\left(\rho {\beta }_{\text{T}}\right)}_{1}\) and \({\left(\rho {\beta }_{\text{T}}\right)}_{2}\), respectively.

Table 2 Thermal and physical properties of a hybrid nanofluid (Cu-Al2O3/H2O) [6]
Full size table

Physical form quantities of engineering interest

The study of skin friction aids in understanding the behaviour of the boundary layer and the formation of the flow structure along the stretching cylinder. The analysis of the Nusselt number distribution facilitates the evaluation of the efficacy of heat transfer enhancement methods and the identification of areas characterized by higher or lower heat transfer rates throughout the surface of the stretching cylinder. It is described as follows:

$$C_{{\text{f}}} = \frac{{2\tau_{{\text{w}}} }}{{\rho_{{\text{f}}} U_{{\text{w}}}^{2} }}, {\text{Nu}}_{{\text{z}}} = \frac{{zq_{{\text{w}}} }}{{k_{{\text{f}}} \left( {T_{{\text{w}}} - T_{0} } \right)}}.$$
(13)

where

$$\tau_{{\text{w}}} = \mu_{{\text{hnf }}} \left( {\frac{\partial w}{{\partial r}}} \right)_{{\text{r = a}}} \,{\text{and}}\,q_{{\text{w}}} = - k_{{{\text{hnf}}}} \left( {\frac{\partial T}{{\partial r}}} \right)_{{\text{r = a}}} .$$

The expressions of physical quantities in non-dimensional forms are:

$$C_{{\text{f}}} {\text{Re}}_{z}^{0.5} = 2 \mu_{{\text{r}}} f^{{\prime \prime }} \left( 0 \right),\quad {\text{Nu}}_{{\text{z}}} {\text{Re}}_{{\text{z}}}^{ - 0.5} = - k_{{\text{r}}} \theta^{{\prime }} \left( 0 \right).$$
(14)

Numerical procedure

This section outlines our methodology for addressing the system of ordinary differential equations acquired. These equations, characterized by nonlinearity and dimensionless boundary conditions, present a computational challenge. To tackle this, we employ a widely recognized technique known as the shooting method. Specifically, we utilize the bvp4c function, an integral component of MATLAB, popular computational software (See flow chart Fig. 2). Initially, we transform the higher-order ordinary differential equations into a set of first-order equations by introducing supplementary variables. This restructuring facilitates a more tractable approach to the problem, enabling efficient computation and analysis. Equations (8) and (9) of the interconnected nonlinear ODE system are influenced by the boundary conditions (10) and (11) that were solved using this approach. The acceptable value for the convergence conditions was certainly 10−6. Initially, a system of first-order simultaneous equations was simplified by incorporating the equivalent concept.

$$f = y\left( 1 \right),\,f^{{\prime }} = y\left( 2 \right),\,f^{{\prime \prime }} = y(3),\,\theta = y\left( 4 \right),\,\theta^{{\prime }} = y\left( 5 \right)$$
$$y^{\prime}\left( 1 \right) = y\left( 2 \right)$$
$$y^{\prime}\left( 2 \right) = y\left( 3 \right)$$
$$y^{\prime}\left( 3 \right) = \frac{{M^{2} \frac{{\sigma_{{\text{r}}} }}{{\rho_{{\text{r}}} }}\left( {y\left( 2 \right) - \beta_{1} {\text{Re}} y\left( 1 \right)y\left( 3 \right)} \right) + \left( {y\left( 2 \right)} \right)^{2} - \frac{{\mu_{{\text{r}}} }}{{\rho_{{\text{r}}} }}2\gamma y\left( 3 \right) - y\left( 1 \right)y\left( 3 \right) - \beta_{1} \left( {2y\left( 1 \right)y\left( 2 \right)y\left( 3 \right) - \frac{\gamma }{{\left( {1 + 2\eta \gamma } \right)}}\left( {y\left( 1 \right)} \right)^{2} y\left( 3 \right)} \right) - \cos \alpha \left[ {Gr\frac{{\left( {\rho \beta_{{\text{T}}} } \right)_{{\text{r}}} }}{{\rho_{{\text{r}}} }}\theta + \left( {\frac{{\left( {\rho \beta_{{\text{T}}} } \right)_{{\text{r}}} }}{{\rho_{{\text{r}}} }}} \right)^{2} Gr_{1} \theta^{2} } \right]}}{{\left( {\left( {1 + 2\eta \gamma } \right)\frac{{\mu_{{\text{r}}} }}{{\rho_{{\text{r}}} }} - \beta_{1} \left( {y\left( 1 \right)} \right)^{2} } \right)}}$$
$${\text{y}}^{{{\prime}}}\left(4\right)=\text{y}(5)$$
$$y^{\prime}\left( 5 \right) = \frac{{\lambda_{1} \left[ {\left( {\delta + y(4} \right))\left( {(y\left( 2 \right)^{2} - y\left( 1 \right)y\left( 3 \right)} \right) - y\left( 1 \right)y\left( 2 \right)y\left( 5 \right)} \right] - \frac{{k_{{\text{r}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{r}}} }}\frac{1}{\Pr }\left[ {2\gamma y\left( 5 \right)} \right] + \left( {\delta + y\left( 4 \right)} \right)y\left( 1 \right) - y\left( 1 \right)y\left( 5 \right) - \frac{{\mu_{{\text{r}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{r}}} }}{\text{Ec}}\left( {1 + 2\eta \gamma } \right)\left( {y\left( 3 \right)} \right)^{2} - M^{2} \frac{{\sigma_{{\text{r}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{r}}} }}{\text{Ec}}\left( {y\left( 2 \right)} \right)^{2} - \frac{1}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{r}}} }}Qy\left( 4 \right)}}{{\frac{{k_{{\text{r}}} }}{{\left( {\rho c_{{\text{p}}} } \right)_{{\text{r}}} }}\frac{1}{\Pr }\left( {1 + 2\eta \gamma } \right) - \lambda_{1} \left( {y\left( 1 \right)} \right)^{2} }}$$

where the initial conditions

$$y_{{\text{a}}} \left( 1 \right) = 0,\,y_{{\text{a}}} \left( 2 \right) = 1 + Bf^{\prime\prime},\,y_{{\text{b}}} \left( 2 \right) = A $$
$$y_{{\text{a}}} \left( 4 \right) = 1 - \delta , \, \,y_{{\text{b}}} \left( 4 \right) = 0.$$

The present study employs this methodology to investigate the parameter effect, which involves the computation of numerical values for the Nusselt number and skin friction. These results are illustrated in Figs. 3– 13 and presented in Tables 3 and 4.

Fig. 2
figure 2

Flow chart of bvp4c scheme

Full size image
Fig. 3
figure 3

a The impact of magnetic parameter on velocity. b The impact of magnetic parameter on temperature

Full size image
Fig. 4
figure 4

a The Effect of velocity ratio parameter on velocity. b The effect of velocity ratio parameter on temperature

Full size image
Fig. 5
figure 5

a Maxwell parameter’s effects on velocity. b Maxwell parameter’s effects on temperature

Full size image
Fig. 6
figure 6

a The Effect of thermal Grashof number on velocity. b The effect of thermal Grashof number on temperature

Full size image
Fig. 7
figure 7

a Nonlinear thermal Grashof number’s impact on velocity. b Nonlinear thermal Grashof number’s impact on temperature

Full size image
Fig. 8
figure 8

a Temperature profile fluctuation for the Prandtl number. b Temperature profile fluctuation for the thermal relaxation parameter. c Temperature profile fluctuation for the Eckert number. d Temperature profile fluctuation for the Heat source/sink parameter. e Temperature profile fluctuation for the Thermal stratification parameter

Full size image
Fig. 9
figure 9

Skin friction variations versus \({\beta }_{1}\)

Full size image
Fig. 10
figure 10

Skin friction variations versus \(M\)

Full size image
Fig. 11
figure 11

Heat transfer rate in relation to \({\text{Pr}}\)

Full size image
Fig. 12
figure 12

Heat transfer rate in relation to Gr1

Full size image
Fig. 13
figure 13

Rate of heat transmission versus \(\delta\)

Full size image
Table 3 Comparison of \({C}_\text{f}{\left({\text{Re}}_{\text{z}}\right)}^{0.5}\) at various values of A in the scenario where all other parameters are set to zero and \(\text{Pr}=1\)
Full size table
Table 4 Comparison of \({\text{Nu}}_{\mathrm{z}}{\text{Re}}_{\text{z}}^{-0.5}\) at different Pr values for the scenario where \(A=1,\alpha =0, \text{Gr}=1\), and many other parameters are all set to zero
Full size table

Validation

To assess the precision of our numerical computations, Tables 3 and 4 present a comparison between the current outcome and previous published works of [28] and [29]. The numerical results are compared to the findings of [28] and [29] across several values of the \(A\) and \(\text{Pr}\). This comparison illustrates a strong alignment between the current and previous investigations.

Result and discussion

This part aims to investigate the numerical findings using physical explanations. HNF obtains the flow and heat transport characteristics across a stretched/shrinked surface. Table 1 displays the characteristics of the base fluid containing copper nanoparticles and aluminium oxide. The 4th order Runge–Kutta with shooting method was applied effectively to solve equations. To derive the mathematical outcomes, we assigned specific values to various non-dimensional parameters: \(\phi _{1} = 0.02,\,\,\phi _{2} = 0.02,\,\,0 < M < 1.8,\,\,0 < \beta _{1} < 1.8,\,\,1 < Gr < 3,\,\,1 < Gr_{1} < 9,\,\,7 < \Pr < 9,\,\,0.1 < \lambda _{1} < 0.8,\,\,0 < Ec < 0.4,\,\,0.1 < Q < 0.5,\,\,0 < \delta < 0.1.\) A graphical representation of flow profiles (Figs. 3– 8) was generated, illustrating the influence of these non-dimensional parameters using numerical values obtained in our study. Also, numerical outcomes of skin friction and Nusselt number are presented in bar charts (see Figs. 9– 13). Furthermore, to analyse the flow we have plotted streamlines for various physical parameters (see Figs14– 17).

Fig. 14
figure 14

Streamline when \(M=0\)

Full size image
Fig. 15
figure 15

Streamline when \(M=5\)

Full size image
Fig. 16
figure 16

Isothermal when \(\delta =0\)

Full size image
Fig. 17
figure 17

Isothermal when \(\delta =5\)

Full size image

Velocity and temperature profiles

In Fig. 3a, the graph illustrates the impact of parameter \(M\), indicating a proportional decrease in the velocity profile with higher values of \(M\). Raising the values of the magnetic parameters makes the magnetic field surrounding the stretching cylinder stronger. An enhanced magnetic field interacts with the Maxwell hybrid nanofluid, a conducting fluid. The magnetic field interacts with the electrically conducting fluid to produce the Lorentz force, which acts as an opposing force to the fluid’s velocity. Therefore, the fluid’s velocity along the stretching cylinder is reduced due to the Lorentz force’s drag force. The opposing Lorentz force makes it harder for the fluid to flow freely along the inclined surface, which causes the velocity profile of the fluid to collapse. Graphing the influence of parameter \(M\), as shown in Fig. 3b, the \(\theta (\eta )\) consistently increases as \(M\) values increase. Maxwell hybrid nanofluids can have improved thermal conductivity with an increase in the magnetic parameter. Magnetic fields with higher field strength can improve nanoparticle dispersion and alignment in fluids. Because of the enhanced distribution and alignment, the fluid can transmit heat more efficiently. The temperature profile can also rise because the fluid is subject to the Lorentz force, which, through viscous dissipation, can produce heat. Consequently, the temperature profile of the Maxwell hybrid nanofluid flow along the inclined stretched cylinder increases as the values of the magnetic parameters increase. This is due to both the higher thermal conductivity and the heat generation from viscous dissipation.

Figure 4a demonstrates how changes in the velocity ratio parameter (\(A\)) affect the \(f^{\prime}(\eta )\). The parameter A gives a cylinder’s stretching or contracting velocity relative to the free stream velocity. The free stream velocity has a greater impact on the cylinder’s stretching/shrinking velocity as the parameter \(A\) rises. When the velocity ratio parameter is larger than the free stream velocity, it means that the fluid encounters less drag caused by stretching and shrinking. The velocity profile increases as the fluid can flow more freely along the inclined stretching/shrinking cylinder. Because the fluid particles encounter less resistance from the expanding and contracting surface, they can align more closely with the direction of the free stream velocity, leading to this rise. Figure 4b illustrates how alterations in the velocity ratio parameter impact the distribution of temperature. Higher values of the parameter \(A\) promote improved flow mixing, facilitating enhanced heat exchange between the fluid and its surroundings. This increased fluid velocity near the cylinder surface boosts the convective heat transfer coefficient, facilitating greater heat transport from the surface. Consequently, this heightened heat dissipation leads to a diminished temperature gradient near the cylinder surface, resulting in a lowered fluid temperature profile. Additionally, the escalation in velocity ratio parameter values primarily stems from the improved thinning of the thermal boundary layer and flow acceleration, which fosters energy dissipation. These combined effects contribute to a more efficient convective heat transfer away from the cylinder surface.

Figure 5a demonstrates how the \(f^{\prime}(\eta )\) is affected by changes in the \({\beta }_{1}\).The Maxwell fluid parameter is a measure of the relaxation time scale related to the fluid’s reaction to stimulus. The higher the values of the \({\beta }_{1}\), the slower the fluid is to react to external forces. The viscoelastic behaviour of a fluid becomes more apparent and its responsiveness to changes in the external flow field decreases as the \({\beta }_{1}\) increases. As a result, the fluid’s velocity profile along the inclined stretching/shrinking cylinder decreases due to the increasing resistance to flow. The Maxwell fluid’s viscoelastic properties make it difficult for the fluid particles to bend and flow freely in response to external forces, including the cylinder’s expansion and contraction, which causes the volume to decrease. The findings regarding the impact of the \({\beta }_{1}\) on the \(\theta (\eta )\) are presented in Fig. 5b. Increased internal friction inside the fluid is caused by the higher viscosity associated with higher \({\beta }_{1}\) values. The subsequent increase in energy dissipation due to the conversion of kinetic energy into heat is a direct result of the increased internal friction. As a result, the fluid experiences a temperature increase, leading to an enhanced \(\theta (\eta )\). There is an increase in viscosity, a decrease in heat transfer rates, an increase in energy dissipation, and a possibility of shear-thinning behaviour due to the rise in \({\beta }_{1}\) values. All of these things add together to make the fluid’s temperature profile higher than normal.

As depicted in Fig. 6a, there is a notable increase in velocity as the Gr rises. The Gr is a measure of the pressure gradient between the buoyant and viscosity forces acting on a fluid. When the Gr values rise, it means that the buoyancy-driven flow is getting stronger because the density gradients and temperature differences in the fluid are getting larger. Fluids move more efficiently along the inclined stretching/shrinking cylinder when the thermal Grashof number is high because buoyancy forces are stronger than viscous forces. Consequently, the fluid’s velocity profile increases as it undergoes more vertical motion, as determined by the temperature gradient. Because the buoyancy-driven flow overcomes viscous resistance and promotes fluid movement down the inclined surface, it produces larger-scale fluid motion, which causes this increase. Figure 6b illustrates the impact of the Gr on \(\theta (\eta )\).The intensified buoyancy-driven flow resulting from elevated Gr values improves convective heat transfer, facilitating greater heat transport from the cylinder surface. Moreover, the escalation in Gr values is predominantly linked to augmented natural convection and potentially a thicker thermal boundary layer, both of which aid in enhancing convective heat transfer away from the cylinder surface. Consequently, this heightened heat dissipation leads to a diminished temperature gradient near the cylinder surface, culminating in a decrease in the temperature profile of the fluid.

Figure 7a displays the influence of \(\text{Gr}_{1}\) on \(f^{\prime}(\eta )\).The \(\text{Gr}_{1}\) reflects the heightened nonlinear buoyancy effect in fluid flow induced by temperature differences and density gradients. As these values increase, so does the intensity of the buoyancy-driven flow, leading to enhanced fluid motion along the inclined cylinder. This increased fluid motion results in a heightened velocity profile as the stronger nonlinear buoyancy effect overcomes viscous resistance, promoting fluid movement along the inclined surface. Figure 7b demonstrates the temperature distribution variation for different \(\text{Gr}_{1}\) values. The fluid’s temperature profile drops as the \(\text{Gr}_{1}\) rise. Because of the increased buoyancy effects in the fluid flow, this effect occurs. A stronger nonlinear buoyancy effect, resulting in more vigorous fluid motion along the inclined cylinder, is indicated by a rise in the values of the nonlinear thermal Grashof parameters. So, the direction of the temperature gradient determines whether the fluid experiences enhanced velocity upwards or downwards. The fluid’s temperature profile is reduced as a consequence of the greater fluid velocity, which affects the distribution of temperatures.

Figure 8a displays the results of Pr on \(\theta (\eta )\). A rise in the \(\text{Pr}\) values results in a reduction in the \(\theta (\eta )\) of the fluid. This phenomenon arises from the impact of heat diffusivity on the fluid dynamics. A greater \(\text{Pr}\) indicates a lower thermal diffusivity, meaning that the fluid conducts heat less efficiently compared to its momentum. As the \(\text{Pr}\) values increase, the dissipation rate of temperature gradients within the fluid reduces. This leads to a decrease in the temperature distribution, as the fluid holds onto more heat close to the surface of the cylinder instead of effectively releasing it into the surrounding environment. The temperature distribution for different values of \({\lambda }_{1}\) is presented in Fig. 8b. Increasing the \({\lambda }_{1}\) values leads to an increase in the \(\theta (\eta )\) of the fluid. This is because the thermal relaxation affects the fluid’s ability to equilibrate with its surroundings. A higher thermal relaxation parameter means that the fluid can adjust its temperature more easily in response to external changes. As a result, the fluid becomes more responsive to thermal changes, leading to a faster adjustment of its temperature profile. This ultimately results in an overall increase in the fluid’s temperature profile as it reaches thermal equilibrium more efficiently with its surroundings. Figure 8c displays the impact of \(\text{Ec}\) on \(\theta (\eta )\). Higher values of the \(\text{Ec}\) indicate a stronger influence of kinetic energy compared to thermal energy in the fluid flow. This implies that a greater proportion of the fluid’s energy is in the form of kinetic energy in comparison with its thermal energy. As a result, when the values of \(Ec\) increase, the fluid becomes more effective in turning its kinetic energy into heat through convective processes. The increased convective heat transfer leads to a more efficient dispersal of heat from the surface of the cylinder into the surrounding fluid, resulting in an overall rise in the temperature of the fluid. Figure 8d is analysed to determine the effect of \(Q\) on the \(\theta (\eta )\). Increasing the values of the heat source parameter increases the temperature profile of the fluid. This phenomenon can be explained by the direct impact of the heat source on the thermal energy inside the fluid domain. As the values of the heat source parameter increase, a greater amount of thermal energy is added to the system, usually in the form of heating that is concentrated in certain areas. As a result, the extra thermal energy causes the fluid’s total temperature to rise, leading to an elevated temperature profile. The heat source directly transfers heat to the fluid, resulting in an increase in temperature throughout the entire area, which in turn leads to a higher temperature distribution within the fluid. Figure 8e illustrates the temperature θ(η) decreases on increasing the thermal stratification parameter (δ). This leads to more pronounced temperature differences between different layers of the fluid, which prevents the efficiency of heat transfer between these layers. Consequently, the overall temperature profile of the fluid decreases. Higher values of the \(\delta\) result in a more segregated temperature distribution within the fluid, causing the fluid near the cylinder surface to be cooler compared to scenarios with lower values of the \(\delta\). This decrease in temperature profile is directly caused by the hindered heat transfer between different layers of the fluid, which can be attributed to the increased thermal stratification.

A general observation from the velocity and temperature profiles

From the velocity profiles, we noticed that the difference in velocity profiles between the elongating and contracting cylinders can be ascribed to causes such as alterations in surface area caused by stretching, the impact of flow acceleration, and the effects of the boundary layer. These factors together result in a greater velocity profile for the shrinking cylinder in comparison with the expanding cylinder. Stretching a cylinder increases its surface area, which in turn increases the amount of heat that may be transferred from the fluid to its environment. Stretching also improves convective heat transmission by increasing fluid mixing. On the other hand, a lower temperature profile and less heat transfer result from a decreased surface area and restricted fluid velocity caused by a shrinking cylinder. Because of the larger surface area and better convective heat transmission, the temperature profile of the expanding cylinder is higher than that of the shrinking cylinder.

The effect of the \({\beta }_{1}\) on \({C}_{\text{f}}\) is depicted in Fig. 9. As the values of the \({\beta }_{1}\) increase, the viscoelastic behaviour of the fluid becomes more noticeable, resulting in increased skin friction along the surface of the cylinder. This increased viscoelasticity, especially for the stretching vertical cylinder, along with its greater surface area, increases the drag force, leading to noticeably higher skin friction values and total drag force as compared to the shrinking vertical cylinder. For instance, when considering various values of the \({\beta }_{1}\), the stretching vertical cylinder experiences a 33% increase in drag force compared to the shrinking vertical cylinder. The difference between drag force and elongating and contracting vertical cylinders becomes more pronounced as the \({\beta }_{1}\) increases, indicating the increasing influence of the fluid’s viscoelastic properties. Figure 10 illustrates how the M parameter affects the \({\text{C}}_{f}\). When the magnetic field parameter values, denoted as M, increase, the \({C}_{\text{f}}\) of the fluid intensifies. This heightened \({C}_{\text{f}}\) is attributed to the stronger influence of the magnetic field on the fluid flow, which increases resistance along the cylinder surface. The increase in skin friction is further compounded by the larger surface area of the stretching vertical cylinder compared to the shrinking vertical cylinder. This enhanced drag force is particularly pronounced, with a 44% increase compared to the shrinking vertical cylinder, across various values of M. Therefore, as M values rise, the fluid experiences greater skin friction due to the heightened magnetic influence on flow dynamics.

Improvement of heat transfer

In Fig. 12, the influence of the \({\text{Gr}}_{1}\) on the \({\text{Nu}}_{\text{z}}\) is depicted. As \({\text{Gr}}_{1}\) values increase, convective heat transfer intensifies due to heightened buoyancy-driven flow near the cylinder surface. This leads to more efficient heat exchange between the fluid and its surroundings, resulting in a higher Nusselt number. Compared to the shrinking vertical cylinder, a 13% increase in heat transfer is observed for the stretching vertical cylinder across various values of \({\text{Gr}}_{1}\). Figure 11 illustrates how changes in Pr affect the \({\text{Nu}}_{\text{z}}\). This graph allows us to observe how variations in Prandtl number values correspond to changes in the Nusselt number, providing insights into the thermal behaviour of the system. The heat transfer rate increases on increasing the Pr value. It means that a greater ratio of momentum diffusivity to thermal diffusivity in the fluid, there is an enhancement in convective heat transfer efficiency. This is reflected in the Nusselt number, which increases with higher Pr values. Consequently, compared to the shrinking vertical cylinder, an 11% increase in heat transfer has been observed for the stretching vertical cylinder across various Pr values. This augmentation occurs due to improved thermal boundary layer development and enhanced mixing near the surface, resulting in more efficient heat transfer from the cylinder to the surrounding fluid. Figure 13 shows how the \({\text{Nu}}_{\text{z}}\) is affected by changes in the \(\delta\) parameter. By examining this graph, we can better understand how alterations in the \(\delta\) parameter values correspond to shifts in the Nusselt number, providing valuable insights into the system’s thermal behaviour the values of the \(\delta\) increase, the level of stratification within the fluid intensifies. This indicates that the temperature differences between various layers of the fluid become increasingly prominent. As a result, the heat transfer between these layers becomes less effective, causing an increase in the overall Nusselt number of the fluid. The stretching vertical cylinder shows greater Nusselt numbers because of the increased stratification effect than the shrinking vertical cylinder, where an increase in the \(\delta\) values has led to a 21% increase in heat transmission.

Stream lines and isotherms

The streamline and isothermal graphs for the different parameters are depicted in Figs. 14– 17. When the value of \(M\) is zero, it has no impact on the flow characteristics of the Maxwell HNF. The patterns observed in the streamlines would be attributed mainly to several factors, including stretching effects and fluid characteristics. As the value of \(M\) increases to 5, the Lorentz force becomes more prominent, hence impacting the flow of the fluid. In this study, we have noticed that variations in streamline patterns may result in the formation of more structured flow structures or changes in the thicknesses of the boundary layer near the stretching cylinder. Furthermore, it is worth mentioning that a lower value of \(\delta =1\) indicates a diminished impact of thermal stratification. The temperature distribution inside the fluid domain has a reasonably uniform pattern, characterized by low changes in temperature. As the value of \(\delta\) increases to 2, the magnitude of temperature change resulting from density differences becomes more prominent. Enhanced thermal stratification effects are reflected in this instance by more pronounced temperature gradients and clearly defined areas of warmer and colder fluid.

Applications

  • Understanding of nonlinear thermal convection and stratification effects plays a crucial role in enhancing the efficiency of damping performance, particularly in various domains such as automotive suspensions and seismic isolation systems.

  • The application of natural convection in geothermal energy systems facilitates the transmission of heat from the Earth’s interior. Knowledge of nonlinear effects plays an important part in the optimization of good design and fluid circulation, hence improving the efficiency of heat extraction and overall system performance.

  • Aircraft engine cooling systems experience significant temperature variations and aerodynamic obstacles. The comprehension of nonlinear thermal convection effects plays an essential role in the optimization of cooling techniques, as it facilitates the effective evacuation of heat and enhances engine performance.

Tabular values

In this article, we go over the computational results for the local skin friction and Nusselt parameters, as well as the numerical variation in values that results from these physical factors. Table 5 illustrates the impact of several physical characteristics on the local Nusselt number. In the case of stretching and shrinking decelerates from \(M,{\beta }_{1},Ec,Q\) and \(\delta\) and enhance for \(A,\text{Gr},\text{Gr}_{1},Pr\) and \({\lambda }_{1}\), respectively, when the values \({0 < M<1.5, 0<A<0.3, 0<{\beta }_{1}<1, 0.1<Gr<2.5, 0.1<{Gr}_{1}<9, 7<Pr<9, 0<{\lambda }_{1}<0.3, 0<Ec<0.3, 0<Q<0.3, 0<\delta <0.1}\) are restricted. By using the CC heat flux condition, heat transfer in the fluid coming from the cylinder is more effective. Furthermore, a rise in Prandtl number values led to an increase in Nusselt’s count. The reason for this is because a liquid with an excessive Prandtl number will transfer heat more quickly due to its increased heat capacity. Table 6 shows the impact of many relevant factors on the skin friction coefficient. The proportionate reduction for both stretching and shrinking cases is shown in \(A,\text{Gr},\text{Gr}_{1}\), whereas the reverse feature is seen in \(M,{\beta }_{1}\), respectively.

Table 5 Local Nusselt number \({-\theta }^{\prime}\left(0\right)\) numerical data for different parameter values
Full size table
Table 6 Shows the mathematical data for local skin friction \(\left(-{f}^{{\prime\prime}}\left(0\right)\right)\) in relation to different flow parameter values
Full size table

Conclusions

Present applications include enhancing thermal conductivity in sustainable energy systems, optimizing industrial heat management, and perfecting electronics cooling systems. The CC model for Maxwell HNF flows through an inclined stagnated cylinder was considered in this study. Current flow is seen by taking into account the effects of heat sink/source, thermal stratification, viscosity, and Joule dissipations. The MATLAB “bvp4c” solver was used to solve our mathematical model numerically. The results of the findings are summarized as:

  • Compared to the shrinking cylinder, the stretching cylinder has increased heat transfer by 21% as the term \(\delta\) values stimulate internal heating across the flow regime

  • The temperature output demonstrates that the HNF’s temperature increased with the \({\lambda }_{1}\) and Q, leading to an enhanced thermal distribution

  • Raising the M value has increased the stretching cylinder’s drag force by 44% compared to the shrinking cylinder owing to the induced electromagnetic force

  • It was found that the fluid velocity damped when the magnetic parameter increased in both the shrinking and stretching tube scenarios as Lorentz force opposes flow and inspired bonding force.

  • The stretching/shrinking ratio parameter’s value increases the heat transmission rate and decreases the friction factor due to an induced nanoparticle molecular bonding

  • The Nusselt number strengthens the thermal relaxation parameter as heat source terms are encouraged

Future directions include energy technology, sophisticated cooling systems applications, efficiency optimization, and the investigation of novel hybrid nanofluid compositions. The stream dynamics within a stretched/shrieked cylinder have several potential scientific and practical applications. The present study’s conclusions might be helpful for many model studies. The present issue’s discoveries are also fascinating in many fields of science and industry where boundary layers are strained.