A rigorous investigation on the interaction between two three-level $\Lambda$-type atoms and a single-mode cavity field

Abstract

In this paper, we study quantum entanglement and non-classical statistical aspects for a model describing two three-level $\Lambda$ atoms interacting with a single-mode cavity field. The Hamiltonian describes multi-photon processes and includes the Kerr-like medium in the resonance case. The constants of motion are obtained from the Hamiltonian operators under the rotating wave approximation. The exact solution of the wave function for the whole system is obtained under the special initial conditions when the atom is in the ground state and the field in the coherent states. The results are used to perform some studies on the temporal evolution of collapse revival, normal squeezing function, photon antibunching and Q-function to measure the degree of entanglement between subsystems. Entanglement dynamics using von Neumann entropy and Shannon information is used to quantify the entanglement in the quantum subsystems. The numerical results show that the presence of these parameters plays an essential role in developing these aspects. The above optical schemes have many advantages and can be used in various experiments in quantum optics and information, such as trapped ions and quantum electrodynamics resonators.

1 Introduction

The interaction between matter and photons occupies the central position in both quantum optics and information [1]. Jaynes–Cummings (JC) [2] model is the simplest and the most widely used model to study quantum phenomena. It has become the cornerstone of technical progress in treating the interaction between photons and atoms and has enabled major advances in the study of quantum information processing protocols. Moreover, this model leads to the prediction of a wide range of experimentally interesting phenomena. Recently, we have extended this model to the nonlinear time-dependent JC model and the nonlinear JCM model with explicit time dependence [3,4,5]. Moreover, generalisations of this model were obtained, such as the entropy squeezing of a single atom for two atoms with two-level interaction with a binomial field [6], the exact solution of the wave function for atoms with two levels and four levels [7, 8], the interactions of an atom with multiple levels and a field with one or two modes [9, 10], and with a Stark shift term [11, 12], cross-Kerr non-linearity [13] and the squeezing of the deformed JCM [14]. Many non-trivial phenomena have been predicted by the JCM, e.g., the phenomenon of collapse and revival [15, 16], one (two-photon) absorption spectra [17], stimulated emission [18] and nonlinear quantum [19].

On the other hand, the damped interaction between two three-level $\Xi$-type [20] with the Caldirola-Kanai form as well as the collective spontaneous emission of two three-level $\Lambda$ atoms of type $\Lambda$ in a finite Q cavity [21] have been studied using the main equation. In addition, two identical atoms of the three-level $\Lambda$-type [22] were studied, with a photon k surrounded by a down-converting Kerr medium [23]. The exact solution of the wave function for several considered atomic field systems of two identical atoms of three levels of types V, $\Lambda$ and $\Xi$ have been determined using the Laplace transformation technique [24]. Furthermore, the solution for the three-level entangled pair of two atoms in the cascade configuration with and without the effect of atomic motion [25] was presented. Recently, we have studied an atomic system consisting of a three-level atom in the presence of the classical national gravitational field [26, 27].

Quantum entanglement plays an important role in quantum information, such as quantum computing, communication [28, 29], cryptography [30,31,32,33] and teleportation [34]. Entropy is a very useful measure of the purity of quantum state [35] and the Stark shift effect on entropy has been analysed [36, 38]. The second-order correlation function [37] or the Mandel Q-parameter [39] can test the Poisson statistics [40,41,42,43,44]. In addition, the phenomenon of radiation field compression plays an important role in quantum optics and has a number of applications, such as encoding [45, 46]. They have no singularity, they exist for all wave functions, they are bounded and they are greater than or equal to zero [47, 48]. These distributions were not only kept as theoretical tools, but also measured experimentally [49, 50]

The new ingredient in this work is that we have taken into account two atoms which are identical and non-identical and a new algorithm to obtain the exact solution of wave function is found. Also, the Kerr-like medium is applied in the Hamiltonian as a function of photon number operators. The time-dependent Schrödinger equation is employed to obtain the wave function by the Newton interpolation method in the quantum form when the atom and the field are initially prepared in their excited state and coherent state, respectively. The atomic inversion, the Shannon entropy, the second-order coloration function, the normal squeezing and the quasiprobability distribution Q-function properties are calculated. The influence of different parameters and the impact of second atom on the evolution time-dependent non-classical statistical aspects and entanglement are examined. We noticed that the atomic inversion is affected by the presence of these quantities. Furthermore, we observed that the photon statistics distribution changes from sub- to super-Poissonian. Moreover, we remarked that the broadening and splitting of the Q-function occur and the behaviour of the Q-function is changed by the existence of theses parameters.

The article is organised as follows: In the next section, we give a brief description of the quantum model under consideration for the two three-level $\Lambda$-configuration of atoms. Section 2 is devoted to drive the exact solution of the model under consideration and the probability amplitudes are found. We shall use the explicit time evolution of the wave function obtained in §3 to investigate the collapse–revival phenomenon, the Shannon entropy and Von Neumann entanglement of this model in §4–6, respectively. Moreover, we examine the photon counting statistics by using the second-order colouration function $g^2(t)$, in §7. The normal squeezing and the quasiprobability distribution Q-function properties are presented in §8 and 9, respectively. Finally, conclusions are presented in §10.

2 Description of the Hamiltonian of the system

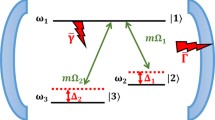
This section is devoted to describe two-(non)-identical three-level $\Lambda$-type atoms (A and B) (i.e., two three-level atoms with three hyperfine levels of $^{87}$Rb: all the pertinent levels are shown in figure 1. In the electric dipole approximation, the transitions $|e_p\rangle \leftrightarrow |i_p\rangle$ and $|e_p\rangle \leftrightarrow |g_p\rangle$ are allowed and the transition $|i_p\rangle \leftrightarrow |g_p\rangle$ is forbidden. The Hamiltonian under the rotating wave approximation (RWA) can be written as ($\hbar =c=1$)

$$\begin{aligned} {\hat{H}}={\hat{H}}_0+{\hat{H}}_I, \end{aligned}$$

(1)

where ${\hat{H}}_0$ is the free Hamiltonian for the atoms and the field, which can given by

$$\begin{aligned} {\hat{H}}_0= & {} \Omega {\hat{a}}^{\dag } {\hat{a}}+\sum _{p} \omega _{1}^p |e_p\rangle \langle e_p|+\omega _{2}^p |i_p\rangle \langle i_p|\nonumber \\{} & {} +\omega _{3}^p |g_p\rangle \langle g_p|, \quad p=A, B, \end{aligned}$$

(2)

Fig. 2

Schematic diagram of two $\Lambda$-type three-level atoms.

where ${\hat{a}}^\dag ({\hat{a}})$ is the creation(annihilation) operator with $\Omega$, which satisfy $[{\hat{a}}, {\hat{a}}^\dag ]={\hat{1}}$ and $[{\hat{a}}, {\hat{a}}]=0$, while the population operators for the pth atom are described by $|e_p\rangle \langle e_p|$, $|i_p\rangle \langle i_p|$ and $|g_p\rangle \langle g_p|$ with $\omega _j^p$ ($\omega _1^p \le \omega _2^p \le \omega _3^p$) ($j = 1, 2, 3$) representing the energy levels. Furthermore, the atoms and the field interaction Hamiltonian (${\hat{H}}_I$) for the whole system is written in the form

$$\begin{aligned} {\hat{H}}_I= & {} \chi ({\hat{a}}^{\dag } {\hat{a}})^{2}+\sum _{p} \left( \lambda _{1}^p \left( {\hat{a}}^{\ell } |e_p\rangle \langle i_p|+{\hat{a}}^{\dag \ell } |i_p\rangle \langle e_p|\right) \right. \nonumber \\{} & {} \left. + \lambda _{2}^p \left( {\hat{a}}^{\ell } |e_p\rangle \langle g_p|+{\hat{a}}^{\dag \ell } |g_p\rangle \langle e_p|\right) \right) , \end{aligned}$$

(3)

where $\chi$ shows a Kerr-like medium, $\lambda _k (k = 1, 2)$ is the coupling constant parameter between the pth atom and the field, $\ell$ is the multiplicity of the photon and $|m_p\rangle \langle n_p|$ ($|n_p\rangle \langle m_p|$) where $m=n=e,i,g$ and $m\ne n$ are the raising and lowering operators, respectively. Also, the atomic operators ($|m_p\rangle \langle n_p|$) in the U(3) group satisfy the relation

$$\begin{aligned}{}[|k_p\rangle \langle l_p|,|m_p\rangle \langle n_p|]=|k_p\rangle \langle n_p| \delta _{lm}^p-|m_p\rangle \langle l_p| \delta _{nk}^p, \end{aligned}$$

(4)

where $\delta _{lm}$ is the Kronecker symbol (equal to unity if $l=m$ and zero otherwise). The field operator relations are

$$\begin{aligned}{}[{\hat{a}}^{\dag } {\hat{a}}, {\hat{a}}^{\dag \ell }] = \ell {\hat{a}}^{\dag \ell }, \quad [{\hat{a}}^{\dag } {\hat{a}}, {\hat{a}}^{\ell }] = -\ell {\hat{a}}^{\ell }. \end{aligned}$$

(5)

These relationships are easily established. The annihilation and creation operators satisfy

$$\begin{aligned} {\hat{a}}^\ell |n\rangle= & {} \sqrt{\frac{n!}{(n-\ell )!}} |n-\ell \rangle , \nonumber \\ {\hat{a}}^{\dag \ell } |n\rangle= & {} \sqrt{\frac{(n+\ell )!}{n!}} |n+\ell \rangle . \end{aligned}$$

(6)

Now, the dynamical operators can be achieved by Heisenberg equations

$$\begin{aligned} \imath \frac{\textrm{d} {\hat{O}}}{\textrm{d} t}= [{\hat{O}},{\hat{H}}]+\imath \frac{\partial {\hat{O}}}{\partial t}. \end{aligned}$$

(7)

With some calculations, we get

$$\begin{aligned} i \frac{\textrm{d} {\hat{a}}^{\dag }{\hat{a}} }{\textrm{d}t}= & {} \ell \left( \sum _{p} \big (\lambda _{1}^p \big (-{\hat{a}}^{\ell } |e_p\rangle \langle i_p|+{\hat{a}}^{\dag \ell } |i_p\rangle \langle e_p|\right) \nonumber \\{} & {} + \lambda _{2}^p \big (-{\hat{a}}^{\ell } |e_p\rangle \langle g_p|+{\hat{a}}^{\dag \ell } |g_p\rangle \langle e_p|\big )\big )\big ), \end{aligned}$$

(8)

$$\begin{aligned} i \frac{\textrm{d} \left( |e_p\rangle \langle e_p|\right) }{\textrm{d}t}= & {} \sum _{p} \big (\lambda _{1}^p \big ({\hat{a}}^{\ell } |e_p\rangle \langle i_p|-{\hat{a}}^{\dag \ell } |i_p\rangle \langle e_p|\big )\nonumber \\{} & {} + \lambda _{2}^p \big ({\hat{a}}^{\ell } |e_p\rangle \langle g_p|-{\hat{a}}^{\dag \ell } |g_p\rangle \langle e_p|\big )\big ), \end{aligned}$$

(9)

$$\begin{aligned} \quad i \frac{\textrm{d} \left( |i_p\rangle \langle i_p|\right) }{\textrm{d}t}= & {} \sum _{p} \big (\lambda _{1}^p \big (-{\hat{a}}^{\ell } |e_p\rangle \nonumber \\{} & {} \quad \times \langle i_p|+{\hat{a}}^{\dag \ell } |i_p\rangle \langle e_p|\big )\big ), \end{aligned}$$

(10)

$$\begin{aligned} i \frac{\textrm{d} \left( |g_p\rangle \langle g_p|\right) }{\textrm{d}t}= & {} \sum _{p} \lambda _{2}^p \big (-{\hat{a}}^{\ell } |e_p\rangle \nonumber \\{} & {} \quad \times \langle g_p|+{\hat{a}}^{\dag \ell } |g_p\rangle \langle e_p|\big ), \end{aligned}$$

(11)

where ${\hat{O}}$ is any operator. According to the Heisenberg equation, the conservation of atomic probability is given by

$$\begin{aligned} \sum _{p}\left( |e_p\rangle \langle e_p|+|i_p\rangle \langle i_p|+ |g_p\rangle \langle g_p|\right) = {\hat{I}} \end{aligned}$$

(12)

and the conservation of excitation numbers is obtained as

$$\begin{aligned} {\hat{a}}^\dag {\hat{a}}-\ell \sum _{p}\left( |i_p\rangle \langle i_p|+|g_p\rangle \langle g_p|\right) = \hat{N.} \end{aligned}$$

(13)

Using these conservations, the effective Hamiltonian (1) is

$$\begin{aligned} {\hat{H}}= & {} \chi ({\hat{a}}^{\dag } {\hat{a}})^{2}+\sum _{p}\left( \Delta _1^p|i_p\rangle \langle i_p|+\Delta _2^p|g_p\rangle \langle g_p|\right) \nonumber \\{} & {} +\sum _{p} \big (\lambda _{1}^p \big ({\hat{a}}^{\ell } |e_p\rangle \langle i_p|+{\hat{a}}^{\dag \ell } |i_p\rangle \langle e_p|\big )\big ) \nonumber \\{} & {} + \sum _{p} \big (\lambda _{2}^p \big ({\hat{a}}^{\ell } |e_p\rangle \langle g_p|+{\hat{a}}^{\dag \ell } |g_p\rangle \langle e_p|\big )\big )\nonumber \\{} & {} + {\hat{I}} \bigg (\sum _p \omega _1p+\Omega {\hat{N}}\bigg ), \end{aligned}$$

(14)

where $\Delta _s^p=\omega _{s+1}^p-\omega _s^p+\Omega$ $(s = 1, 2)$ is the detuning parameter of two different atoms and ${\hat{I}}$ is the identity operator. Obviously, the last two terms of (14) are constants. From now, we will ignore the two constant terms, and the effective Hamiltonian can be written as

$$\begin{aligned} {\hat{H}}_{\textrm{eff}}= \chi ({\hat{a}}^{\dag } {\hat{a}})^{2} {\hat{I}}+{\hat{H}}_{AF} \end{aligned}$$

(15)

where ${\hat{H}}_{AF}$ is given by

$$\begin{aligned} {\hat{H}}_{AF}=\left( \begin{array}{ccccccccc} 0 &{} \lambda _1^A {\hat{a}}^l &{}\lambda _1^A {\hat{a}}^l &{}\lambda _2^B {\hat{a}}^l &{}0 &{}0 &{}\lambda _2^B {\hat{a}}^l&{}0 &{}0 \\ \lambda _1^A {\hat{a}}^{\dag l}&{}\Delta _1^A &{}0 &{}0 &{}\lambda _1^B {\hat{a}}^l &{}0 &{}0 &{}\lambda _2^B {\hat{a}}^l&{} 0 \\ \lambda _1^A {\hat{a}}^{\dag l}&{}0 &{}\Delta _2^A &{}0 &{}0 &{}\lambda _2^B {\hat{a}}^l &{}0 &{}0 &{}\lambda _2^B {\hat{a}}^l\\ \lambda _2^B {\hat{a}}^{\dag l}&{}0 &{}0 &{}\Delta _1^B &{}\lambda _1^A {\hat{a}}^l&{}\lambda _1^A {\hat{a}}^l&{}0 &{}0 &{}0 \\ 0 &{}\lambda _2^B {\hat{a}}^{\dag l} &{}0 &{}\lambda _1^A {\hat{a}}^{\dag l} &{}\Delta _1^A+\Delta _1^B &{}0 &{}0 &{}0 &{}0 \\ 0 &{}0 &{}\lambda _2^B {\hat{a}}^{\dag l}&{}\lambda _1^A {\hat{a}}^{\dag l}&{}0 &{}\Delta _2^A+\Delta _1^B &{}0 &{}0 &{}0 \\ \lambda _2^B {\hat{a}}^{\dag l} &{}0 &{}0 &{}0 &{}0 &{}0 &{}\Delta _2^B &{}\lambda _1^A {\hat{a}}^l &{}\lambda _1^A {\hat{a}}^l\\ 0 &{}\lambda _2^B {\hat{a}}^{\dag l} &{}0 &{}0 &{}0 &{}0 &{}\lambda _1^A {\hat{a}}^{\dag l}&{}\Delta _1^A+\Delta _2^B &{}0 \\ 0 &{}0 &{}\lambda _2^B {\hat{a}}^{\dag l} &{}0 &{}0 &{}0 &{}\lambda _1^A {\hat{a}}^{\dag l} &{}0 &{}\Delta _2^A+\Delta _2^B \\ \end{array} \right) . \end{aligned}$$

(16)

In the next section, we turn our attention to drive the exact solution of the wave function for the considered model when the atom is initially prepared in their excited states.

3 The wave function

It is well-known that to obtain the explicit form of the wave function at any time $t>0$ of the whole system, we solve the Schrödinger equation. We assume that every atom absorbs and emits $\ell$ photons in the cavity $|\Psi \rangle =|\Psi _A\rangle \otimes |\Psi _B\rangle$ where $|\Psi _p\rangle$ $(p = A, B)$ are the wave functions for the atoms and the field, which can be written as

$$\begin{aligned}{} & {} |\Psi _p\rangle =\sum _n Q_n \nonumber \\{} & {} \times \left( \psi _1^p|e_p, n\rangle +\psi _2^p|i_p, n+\ell \rangle +\psi _3^p|g_p, n+\ell \rangle \right) .\nonumber \\ \end{aligned}$$

(17)

The wave function can be written as a linear combination of the basis vectors $|e_A,e_B,n\rangle$, $|e_A,i_B,n+\ell \rangle$, $|e_A,g_B,n+\ell \rangle$, $|i_A,e_B,n+\ell \rangle$, $|i_A,i_B,n+\ell \rangle$, $|i_A,g_B,n+2\ell \rangle$, $|g_A,e_B,n\rangle$, $|g_A,i_B,n+2\ell \rangle$ and $|g_A,g_B,n+2\ell \rangle$. Under theses conditions, the wave function takes the following form:

$$\begin{aligned} |\Psi \rangle= & {} \sum _n q_n\{ \Gamma _1(n,t) |e_A,e_B,n\rangle \nonumber \\{} & {} \quad + \Gamma _2(n+\ell ,t) |e_A,i_B,n+\ell \rangle \nonumber \\{} & {} \quad +\Gamma _3(n+\ell ,t) |e_A,g_B,n+\ell \rangle \nonumber \\{} & {} \quad + \Gamma _4(n+\ell ,t) |i_A,e_B,n+\ell \rangle \nonumber \\{} & {} \quad + \Gamma _5(n+2\ell ,t) |i_A,i_B,n+\ell \rangle \nonumber \\{} & {} \quad +\Gamma _6(n+2\ell ,t) |i_A,g_B,n+2\ell \rangle \nonumber \\{} & {} \quad + \Gamma _7(n+\ell ,t) |g_A,e_B,n+\ell \rangle \nonumber \\{} & {} \quad + \Gamma _8(n+2\ell ,t) |g_A,i_B,n+2\ell \rangle \nonumber \\{} & {} \quad +\Gamma _9(n+2\ell ,t) |g_A,g_B,n+2\ell \rangle \}, \end{aligned}$$

(18)

where $\Gamma _j$ $(j= 1,\ldots ,9)$ are the probability amplitudes and the field is in a coherent state

$$\begin{aligned} |\psi (0)\rangle =|e_A,e_B\rangle \otimes |\alpha \rangle , \end{aligned}$$

(19)

where

$$\begin{aligned} |\alpha \rangle =\sum _{n=0}^{\infty } q_n |n\rangle , \quad q_n=\frac{\alpha ^n}{\sqrt{n!}} \exp \left( -\frac{|\alpha |^2}{2}\right) , \end{aligned}$$

(20)

where $|\alpha |^2$ is the mean photon number. The Schrödinger equation for the probability amplitudes is

$$\begin{aligned} i \frac{\partial }{\partial t}|\Psi (t)\rangle = {\hat{H}}_\textrm{eff}|\Psi (t)\rangle . \end{aligned}$$

(21)

For Schrödinger equation (21), we have the following coupled differential equations for the probability amplitudes:

$$\begin{aligned} \imath {\dot{\Gamma }}_1(n,t)= & {} \Upsilon _1 \Gamma _1(n,t)+f_1 \Gamma _2(n,t) \nonumber \\{} & {} \quad +f_3 \Gamma _3(n,t) +f_5 \Gamma _4(n,t) +f_7 \Gamma _7(n,t), \nonumber \\ \imath {\dot{\Gamma }}_2(n,t)= & {} \Upsilon _2 \Gamma _2(n,t) \nonumber \\{} & {} \quad +f_1 \Gamma _1(n,t) +f_6 \Gamma _5(n,t) +f_8 \Gamma _8(n,t), \nonumber \\ \imath {\dot{\Gamma }}_3(n,t)= & {} \Upsilon _3 \Gamma _3(n,t) \nonumber \\{} & {} \quad +f_3 \Gamma _1(n,t) +f_6 \Gamma _6(n,t) +f_8 \Gamma _9(n,t), \nonumber \\ \imath {\dot{\Gamma }}_4(n,t)= & {} \Upsilon _4 \Gamma _4(n,t) \nonumber \\{} & {} \quad +f_2 \Gamma _5(n,t) +f_4 \Gamma _6(n,t) +f_5 \Gamma _1(n,t), \nonumber \\ \imath {\dot{\Gamma }}_5(n,t)= & {} \Upsilon _5 \Gamma _5(n,t) \nonumber \\{} & {} \quad +f_2 \Gamma _4(n,t) +f_6 \Gamma _2(n,t), \nonumber \\ \imath {\dot{\Gamma }}_6(n,t)= & {} \Upsilon _6 \Gamma _6(n,t) \nonumber \\{} & {} \quad +f_4 \Gamma _4(n,t) +f_6 \Gamma _3(n,t), \nonumber \\ \imath {\dot{\Gamma }}_7(n,t)= & {} \Upsilon _7 \Gamma _7(n,t) \nonumber \\{} & {} \quad +f_2 \Gamma _8(n,t) +f_4 \Gamma _9(n,t) +f_7 \Gamma _1(n,t), \nonumber \\ \imath {\dot{\Gamma }}_8(n,t)= & {} \Upsilon _8 \Gamma _8(n,t) \nonumber \\{} & {} \quad +f_2 \Gamma _7(n,t) +f_8 \Gamma _2(n,t), \nonumber \\ \imath {\dot{\Gamma }}_9(n,t)= & {} \Upsilon _9 \Gamma _9(n,t)+f_4 \Gamma _7(n,t) +f_2 \Gamma _7(n,t) \nonumber \\{} & {} \quad +f_8 \Gamma _3(n,t), \end{aligned}$$

(22)

where

$$\begin{aligned}{} & {} \Upsilon _1= \chi n^2, \nonumber \\{} & {} \Upsilon _2= \chi (n+\ell )^2+\Delta _1^A, \nonumber \\{} & {} \Upsilon _3= \chi (n+\ell )^2+\Delta _2^A, \nonumber \\{} & {} \Upsilon _4= \chi (n+\ell )^2+\Delta _1^B, \nonumber \\{} & {} \Upsilon _5= \chi (n+2\ell )^2+\Delta _1^A +\Delta _1^B, \nonumber \\{} & {} \Upsilon _6= \chi (n+2\ell )^2+\Delta _2^A +\Delta _1^B, \nonumber \\{} & {} \Upsilon _7=\chi (n+\ell )^2 +\Delta _2^A, \nonumber \\{} & {} \Upsilon _8 =\chi (n+2\ell )^2+\Delta _1^A +\Delta _2^A, \nonumber \\{} & {} \Upsilon _9 =\chi (n+2\ell )^2+\Delta _2^A +\Delta _2^B, \end{aligned}$$

(23)

$$\begin{aligned}{} & {} f_1 =\lambda _1^A \sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_2=\lambda _1^A\sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_3 =\lambda _2^A \sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_4= \lambda _2^A\sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_5 = \lambda _1^B \sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_6= \lambda _1^B\sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_7 =\lambda _2^B \sqrt{\dfrac{(n+\ell )!}{n!}}, \nonumber \\{} & {} f_8= \lambda _2^B \sqrt{\dfrac{(n+\ell )!}{n!}}. \end{aligned}$$

(24)

Case 1: Two identical atoms are taken, and the solution for this system in the resonant case is $\Delta _s^p=0.0$, $\chi =0.0$ and $\lambda _s^p=\lambda$. In this case, the probability amplitudes are given as

$$\begin{aligned}{} & {} \Gamma _1(n,t) = \frac{1}{\gamma } \left[ \gamma _+^2+\gamma _-^2 \cos \left( 2\sqrt{\gamma }\tau \right) \right] ,\nonumber \\{} & {} \Gamma _s(n+\ell ,t) = i\gamma \frac{\sin \left( 2\sqrt{\gamma }\tau \right) }{2\sqrt{\gamma }}, \ \ \ \ s=2, 3, 4, 7,\nonumber \\{} & {} \Gamma _h(n+2\ell ,t) = \frac{\gamma _+ \gamma _-}{2\gamma }\left( \cos \left( 2\sqrt{\gamma }\tau \right) -1\right) ,\nonumber \\{} & {} \qquad \qquad \qquad \qquad h=5, 6, 8, 9, \end{aligned}$$

(25)

where

$$\begin{aligned} \gamma =\gamma _+^2+\gamma _-^2, \quad \ \ \tau =\lambda t. \end{aligned}$$

(26)

Case 2: We concentrate on the special case in which the detuning parameters and non-linearity are taken into account. Also, in this stage $\Gamma _2=\Gamma _3=\Gamma _4=\Gamma _7$ and $\Gamma _5=\Gamma _6=\Gamma _8=\Gamma _9$. Thus, system (22) is condensed to three differential equations. According to the method [26], the probability amplitudes are

$$\begin{aligned}{} & {} \Gamma _1(n,t) = \sum _{m=1}^3 C_m \textrm{e}^{i \mu _m t},\nonumber \\{} & {} \Gamma _s(n+\ell ,t) = -\frac{1}{4 f_1} \sum _{m=1}^3 C_m \mu _m \textrm{e}^{i\mu _m t},\nonumber \\{} & {} \qquad s=2, 3, 4, 7\nonumber \\{} & {} \Gamma _h(n+2\ell ,t) = \frac{1}{8 f_1 f_2}\nonumber \\{} & {} \sum _{m=1}^3 C_m \left( \mu _m^2\!+\!\Upsilon _1 \mu _m\!-\!4 f_1^2\right) \textrm{e}^{i\mu _m t}\!, { h\!=\!5, 6, 8, 9,} \end{aligned}$$

(27)

where

$$\begin{aligned} \mu _m= & {} -\frac{1}{3} x_1+\frac{2}{3} \sqrt{x_1^2-3x_2}\nonumber \\{} & {} \quad \times \cos \left( \zeta +\frac{2}{3} (j-1)\pi \right) , \ \ \ j=1,2,3 \nonumber \\ \zeta= & {} \frac{1}{2} \cos \left( \frac{9x_1x_2-2x_1^3-27x_3}{2(x_1^2-3x_2)^{3/2}}\right) \end{aligned}$$

(28)

and

$$\begin{aligned} x_1= & {} \Upsilon _1+\Upsilon _4 \nonumber \\ x_2= & {} \Upsilon _1\Upsilon _4-f_1^2-f_2^2 \nonumber \\ x_3= & {} -\Upsilon _2 f_2^2, \quad C_q=\frac{\mu _q \mu _r+f_1^2}{\mu _{qw} \mu _{qr}}. \end{aligned}$$

(29)

Case 3: We suppose the two atoms are symmetric, the detuning parameters are not taken into account, $\lambda _1^p=\lambda _2^p=\lambda ^p$ and $\lambda ^A \ne \lambda ^B$ and the ratio between the coupling constants is taken $\upsilon =\lambda ^A/\lambda ^B$. The probability amplitudes are

$$\begin{aligned} \Gamma _1(n,t)= & {} \frac{1}{2\zeta }\left[ (\zeta -2 \eta _+\gamma _-^2+\beta _1)\cos (\xi _+t)\right. \nonumber \\{} & {} \left. +(\zeta -2 \eta _-\gamma _-^2-\beta _1)\sin (\xi _- t)\right] , \end{aligned}$$

(30)

$$\begin{aligned}{} & {} \Gamma _2(n+\ell ,t)=\Gamma _3(n+\ell ,t)\nonumber \\{} & {} \qquad \qquad \qquad =\frac{(i \gamma _+ \zeta -2 \eta _-\gamma _-^2+\beta _1)}{\zeta } \nonumber \\{} & {} \qquad \qquad \qquad \quad \times \left( \frac{\sin (\xi _+ t)}{\xi _+}+\frac{\sin (\xi _- t)}{\xi _-}\right) , \end{aligned}$$

(31)

$$\begin{aligned}{} & {} \Gamma _r (n+2\ell ,t) = \frac{\upsilon \gamma _- \gamma _+}{\zeta } (\exp ((\xi _-+\xi _+)t)-1) \end{aligned}$$

(32)

$$\begin{aligned}{} & {} \qquad \qquad \qquad \qquad \times (((\cos (\xi _- t)-\cos (\xi _+ t))\nonumber \\{} & {} \qquad \qquad \qquad \qquad +i(\sin (\xi _- t)-\sin (\xi _+ t)))\nonumber \\{} & {} \qquad \qquad \qquad \qquad \times \exp ((\xi _-+\xi _+)t)),\,r=5,6,8,9 \end{aligned}$$

(33)

$$\begin{aligned}{} & {} \Gamma _4(n+\ell ,t)=\Gamma _7(n+\ell ,t)=-\upsilon \Gamma _2(n+\ell ,t), \end{aligned}$$

(34)

where

$$\begin{aligned} \xi _{\pm }= & {} \frac{\sqrt{\beta _1\pm \zeta }}{\sqrt{2}}, \quad \zeta =\sqrt{\beta _1-4\beta _2}\nonumber \\ \beta _1= & {} \eta _+ \sqrt{\gamma _+^2+\gamma _-^2}, \quad \beta _2=2 \eta _-^2 \gamma _-^2 \gamma _+^2,\nonumber \\ \eta _{\pm }= & {} 2(\upsilon ^2\pm 1). \end{aligned}$$

(35)

Finally, we suppose the general case, where the atoms are non-identical and the detuning parameters and the non-linearity are taken into account. We assume that $A\subset M_n$ is a matrix with eigenvalue $\mu (A)$. Now we define f(A) as follows:

$$\begin{aligned}{} & {} F(A)=\sum _{i=1}^n f[\mu _1, \mu _2,\ldots , \mu _n]\nonumber \\{} & {} \quad \times \coprod _{j=1}^{i-1} \left( \sum _{n,m} A_{nm}|n\rangle \langle m|-\mu _j \sum _n |n\rangle \langle n|\right) , \end{aligned}$$

(36)

where $f[\mu _2,\ldots ,\mu _n]$ is the divided difference at $\mu _2,\ldots ,\mu _n$. If $\mu _2,\ldots ,\mu _n$ are distinct, we compute the divided difference, respectively by

$$\begin{aligned}{} & {} f[\mu _1] = f(\mu _1) \end{aligned}$$

(37)

$$\begin{aligned}{} & {} f[\mu _1,\mu _2] = \frac{f(\mu _2)-\mu _1 }{\mu _2-\mu _1} \end{aligned}$$

(38)

$$\begin{aligned}{} & {} f[\mu _1,\mu _2,....,\mu _n] \nonumber \\{} & {} =\frac{f([\mu _2,\ldots ,\mu _n])-f([\mu _1,\ldots ,\mu _n]) }{\mu _n-\mu _1},n\ge 1 \end{aligned}$$

(39)

$$\begin{aligned}{} & {} |\Psi (t)\rangle = \exp (-\imath {\hat{H}} t)|\Psi (0)\rangle \end{aligned}$$

(40)

and after some minor calculation, this leads to an equation of the ninth order which contains nine eigenfunctions. The general solution for the wave function is obtained as

$$\begin{aligned}{} & {} |\Psi (t)\rangle =\textrm{e}^{-\imath \mu _1 t}\sum _n |n\rangle \langle n| +\sum _{i=1}^9 \exp [\mu _1, \mu _2,\ldots , \mu _i]\nonumber \\{} & {} \quad \times \coprod _{j=1}^{8} \left( \sum _{n,m} A_{nm}|n\rangle \langle m|-\mu _j \sum _n |n\rangle \langle n|\right) |\Psi (0)\rangle , \end{aligned}$$

(41)

where $\mu _n$ is the eigenvalue of matrix A

$$\begin{aligned} A=\left( \begin{array}{ccccccccc} \Upsilon _1 &{} f_1 &{} f_3 &{} f_5 &{} 0 &{} 0 &{} f_7 &{} 0 &{} 0 \\ f_1 &{} \Upsilon _2 &{} 0 &{} 0 &{} f_6 &{} 0 &{} 0 &{} f_8 &{} 0 \\ f_3 &{} 0 &{} \Upsilon _3 &{} 0 &{} 0 &{} f_6 &{} 0 &{} 0 &{} f_8 \\ f_5 &{} 0 &{} 0 &{} \Upsilon _4 &{} f_2 &{} f_4 &{} 0 &{} 0 &{} 0 \\ 0 &{} f_6 &{} 0 &{} f_2 &{} \Upsilon _5 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} f_6 &{} f_4 &{} 0 &{} \Upsilon _6 &{} 0 &{} 0 &{} 0 \\ f_7 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \Upsilon _7 &{} f_2 &{} f_4 \\ 0 &{} f_8 &{} 0 &{} 0 &{} 0 &{} 0 &{} f_2 &{} \Upsilon _8 &{} 0 \\ 0 &{} 0 &{} f_8 &{} 0 &{} 0 &{} 0 &{} f_4 &{} 0 &{} \Upsilon _9 \\ \end{array} \right) , \end{aligned}$$

(42)

where $\mu$ are the roots of the following ninth-order polynomial. Accordingly, the analytical solution of the wave function $|\Psi \rangle$ (41) is obtained. We are in a position to investigate and discuss the interesting and important statistical aspects of the formulated model such as collapse–revival phenomena, Shannon entropy, Von Neumman entropy, the second-order correlation function, the normal squeezing and quasi-probability distribution Q-function. We shall implement our calculations for all the previous cases in the next sections.

4 Collapse–revival phenomenon

It is well-known that the expectation value of any operator ${\hat{O}}$ is $\langle {\hat{O}}\rangle =Tr {\hat{\rho }}_{\textrm{atom}}{\hat{O}}=\langle \Psi (t)|{\hat{O}}|\Psi (t)\rangle$, the behaviour of the collapse and revival phenomenon can be studied by the mean photon number $\langle {\hat{a}}^{\dag }(t) {\hat{a}}(t) \rangle$. From the state vector, we have the following expression for the mean photon number:

$$\begin{aligned} \langle {\hat{a}}(t)^{\dag } {\hat{a}}(t) \rangle= & {} {\bar{n}} \nonumber \\{} & {} \quad + \sum _{n} P_n \left[ \ell \sum _{r=2,3,4,7}|\Gamma _r(n+\ell ,t)|^2\right. \nonumber \\{} & {} \quad \left. +2 \ell \sum _{s=5,6,8,9}|\Gamma _s(n+2 \ell ,t)|^2\right] , \end{aligned}$$

(43)

where $P_n$ is the initial probability distribution of the field mode. Based on the analytical solution in the pervious section, we shall investigate the influence of the setting of the second atom $\upsilon$, the detuning parameters and the Kerr-like medium (nonlinearity) on the evolution of $\langle {\hat{a}}(t)^{\dag } {\hat{a}}(t) \rangle$ for the considered system. For all our plots, we have taken the initial photon number ${\bar{n}}=25$ and $\Delta _s^p=\Delta$.

Fig. 3

Plot of $\langle {\hat{n}}(\tau )\rangle$ vs. scaled time $\tau$ with $|\alpha |=5$, $\Delta =0$ and $\chi =0$ and (a) $\upsilon =0,$ (b) $\upsilon =1$ and (c) $\upsilon =2$.

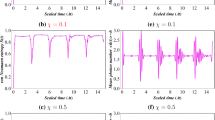
In figures 2a–2c, we have plotted $\langle {\hat{a}}(t)^{\dag } {\hat{a}}(t) \rangle$ as a function of the scaled time $\tau$ for the second atom in the absence of both detuning parameter and Kerr-like medium when $\upsilon =0$, 1 and 2, respectively. We noticed that the collapses and revivals appear clearly and the mean photon number will experience quantum collapses and revivals. Moreover, the collapse time decreases as the rate $\upsilon$ increases which means that the rate of energy interchange between the atoms and the field decreases by increasing $\upsilon$. Also, we noticed that the oscillation of the mean photon number is around 25 and the oscillation in the presence of the second atom is around 0 and this result is the same as in [7] because in this case the two three-level atoms in our system behave similar to the two two-level atoms interacting with a single-mode cavity field.

Fig. 4

Plot of $\langle {\hat{n}}(\tau )\rangle$ vs. scaled time $\tau$ with $|\alpha |=5$, $\upsilon =1$, $\chi =0.0$ and (a) $\Delta =5,$ (b) $\Delta =10$ and (c) $\Delta =15$.

Fig. 5

Plot of $\langle {\hat{n}}(\tau )\rangle$ vs. scaled time $\tau$ with $|\alpha |=5$, $\upsilon =1$, $\Delta =0$ and (a) $\chi =0.2,$ (b) $\chi =0.4$ and (c) $\chi =0.6$.

Figures 3a–3c show the effect of the detuning parameter for two identical atoms when $\chi =0$, when the detuning parameter $\Delta =5$, 10 and 15, respectively. We remarked that as the detuning increases, the collapse time increases. Also, we find that the value of the mean photon number decreases, while the amplitude of the fluctuations increases.

To see the effect of the Kerr medium, we plot W(t) vs. $\tau$ taking $\Delta =0.0$ (the exact resonance case) and $\chi$ = 0.2, 0.4 and 0.6 as shown in figures 4a–4c. We observed that the amplitude of oscillations becomes smaller but with more revivals and periodically when the Kerr medium is present. Also, the maximum value of the mean photon number increases as Kerr parameter increases and the fluctuations are shifted upwards.

Fig. 6

The same as in figure 2 but for Shannon entropy.

Fig. 7

The same as in figure 3 but for Shannon entropy.

In what follows, we shall study the entanglement using the Shannon and Von Neumman entropies.

5 Shannon entropy

It is well known that the Shannon entropy is concerned with the correlations between the states of two atoms and the statistical properties of a system, and any semantic content of those states, is defined as

$$\begin{aligned} S_{H}(t)=-\sum _{n} \ln \left\{ \mathcal {{\hat{P}}}(n,t)^{\mathcal {{\hat{P}}}(n,t)}\right\} \end{aligned}$$

(44)

with

$$\begin{aligned} \mathcal {{\hat{P}}}(n,t)= \langle n | {\hat{\rho }}_F^{AB}| n\rangle , \end{aligned}$$

(45)

where

$$\begin{aligned} S_{H}(t)= & {} \sum _{n} |\Gamma _1(n,t)|^2\ln |\Gamma _1(n,t)|^2 \nonumber \\{} & {} +\sum _{r=2,3,4,7}|\Gamma _r(n+2\ell ,t)|^2\ln |\Gamma _1(n,t)|^2\nonumber \\{} & {} +\sum _{h=5,6,8,9}|\Gamma _h(n+4 \ell ,t)|^2\ln \Gamma _1(n,t)|^2. \end{aligned}$$

(46)

Based on the previous results, we shall investigate $S_{H}(t)$ of the present model. We have plotted the behaviour of $S_{H}(t)$ with various parameters in figures 2–4.

Fig. 8

The same as in figure 4 but for Shannon entropy.

Fig. 9

The same as in figure 3 but for the von Neumann entropy.

In figure 5, the detuning parameter $\Delta =0$ and in the absence of non-linearity, we observed that the maximum value of Shannon entropy is 1.2 and the maximum value increases as $\upsilon$ increases. Also, we noticed that the revival–collapse phenomenon over the envelope is not clear because of the high fluctuations. When the detuning parameters are taken into account in figure 6, the situation is different, $S_{H}(t)$ evolves periodically and the oscillations increase whereas the amplitudes decrease as the scaled time increases. By considering the non-linearity as in figure 7 it is seen that the minima of the curves are slightly shifted above and the fluctuations decrease.

6 Von Neumann entropy

It is well known that the Hilbert space ${\mathbb {H}}$ in which the density operator represented in a Hilbert–Schmidt basis is as follows:

$$\begin{aligned} \tilde{\rho }_{AB}= & {} \frac{1}{d^2} \left[ {\hat{I}} \otimes {\hat{I}}+ \sum _{i=1}^{d^2-1} a_i {\hat{\sigma }}_i \otimes I \right. \nonumber \\{} & {} \left. +\sum _{i=1}^{d^2-1} b_i {\hat{I}} \otimes {\hat{\sigma }}_i +\sum _{i,j}^{d^2-1} R_{ij} {\hat{\sigma }}_i \otimes {\hat{\sigma }}_j \right] , \end{aligned}$$

(47)

where ${\mathbb {I}}$ is the $2 \times 2$ identity operator and ${\{\sigma \}^{3}_n=1}$ are the Pauli matrices. The reduced density matrices are

$$\begin{aligned} {\hat{\rho }}^A= Tr_B\{{\hat{\rho }}^{AB} \} =\sum _j^{N_a} ({\hat{I}}_A \otimes \langle \phi _j|) {\hat{\rho }}^{AB} ({\hat{I}}_A \otimes \langle \phi _j|)^\dag \nonumber \\ \end{aligned}$$

(48)

and

$$\begin{aligned} {\hat{\rho }}^B= Tr_A\{{\hat{\rho }}^{AB} \} =\sum _j^{N_a} (\langle \phi _j| \otimes {\hat{I}}_A) {\hat{\rho }}^{AB} (\langle \phi _j| \otimes {\hat{I}}_A)^\dag . \nonumber \\ \end{aligned}$$

(49)

(A detailed procedure for obtaining the partial reduced density matrix is given in eqs (47) and (48)). The expression $S_f(t)$ is

$$\begin{aligned} S_f(t)=Tr\left\{ {\hat{\rho }}\ln ({\hat{\rho }})\right\} , \end{aligned}$$

(50)

where ${\hat{\rho }}$ is the density operator and the entropy is zero, i.e., satisfy ${\hat{\rho }}={\hat{\rho }}^2$ which means that the entropy is in pure states. The density operator is

$$\begin{aligned} {\hat{\rho }}_f(t)|\psi _f(t)\rangle = \lambda _f^{i} |\psi _f(t)\rangle , \ \ \ i=1,2,3. \end{aligned}$$

(51)

The quantum entropy is

$$\begin{aligned} S^{(p)}_f(t)=-\sum _{i=1}^2 \lambda ^{i(p)}_f(t)\ln (\lambda ^{i(p)}_f(t)), \ \ \ \ p=A,B. \nonumber \\ \end{aligned}$$

(52)

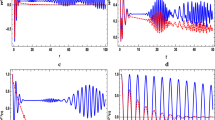
Figure 8 corresponds to the field entropy in the absence of detuning and the Kerr-like medium in the presence of two atoms. In figure 8a, we notice that the entropy is zero which means that the system is in a pure state. By increasing the value of $\upsilon$, we observed that the field entropy evolves periodically and the oscillations increase whereas the amplitude decreases as the scaled time increases.

Fig. 10

The same as in figure 2 but for the von Neumann entropy.

Fig. 11

The same as in figure 4 but for the von Neumann entropy.

The effect of detuning on the entropy of the field in the presence of Kerr nonlinearity can be seen in figure 9. We observe in this figure that the collapse and reactivation take the longest when the amplitude increases and the oscillation decreases. Visualising the effect of the Kerr-like medium in the absence of detuning with the same data from figure 4 as in figure 10 for different values of $\chi$ of the nonlinearity of the Kerr-like medium, we see that the nonlinear weak interaction of the Kerr-like medium with the field mode involves increasing the values of the minimum entropy and the maximum entropy holding time. In this case, the field and the atom are almost strongly entangled, and the field entropy amplitude decreases with increasing $\chi$.

In the next section, we discuss the photon Poissonian statistics. Also, the effect of the existence of the two atoms, the detuning and the nonlinearity on the second-order correlation function will be investigated.

7 The second-order correlation function

In this section, we study the influence of detuning parameter and Kerr-like medium on the photon Poissonian statistics. It will be achieved by using the second-order correlation function $g^2(t)$, which is given by

$$\begin{aligned} g^2(t)=\frac{\langle {\hat{n}}^2(t)\rangle -\langle {\hat{n}}(t)\rangle }{\langle {\hat{n}}(t)\rangle ^2} \end{aligned}$$

(53)

particularly, if $g^2(t)<1$ ($g^2(t)>1$) exhibits sub (super-Poissonian) statistics, respectively. Also, ${\hat{n}}^r(t)$ can be written as

$$\begin{aligned} \langle {\hat{n}}^r\rangle= & {} \sum _n P_n \left[ \left( n+\ell \right) ^r+\left[ n^r-(n+\ell )^r \right] \right. \nonumber \\{} & {} \quad \left. \times |\Gamma _1(n,t)|^2 +\left[ (n+2\ell )^r-(n+\ell )^r\right] \right. \nonumber \\{} & {} \quad \left. \times \sum _{r=5,6,8,9} |\Gamma _r(n+2 \ell ,t)|^2\right] . \end{aligned}$$

(54)

Now let us discuss the affect of the physical parameters at the Poissonian statistics of the present atomic system. For this reason, we have plotted the second-order correlation function of the system as opposed to the scaled time with the identical initial situations taken previously. In figure 11a–c, we notice that the system exhibits sub-Poissonian statistics and also the the system oscillates between super-Poissonian and sub-Poissonian statistics and the second atom increases the sub-Poissonian statistics.

Fig. 12

The same as in figure 2 but for the second-order correlation function.

Fig. 13

The same as in figure 3 but for the second-order correlation function.

Fig. 14

The same as in figure 4 but for the second-order correlation function.

In figure 12, we noticed that the detuning parameters increase the super-Poissonian statistics, which means that the detuning punched the photons. To study the influence of nonlinearity on the Poissonian statistics, we plot $g^2(t)$ as shown in figure 12. We observed that increasing the nonlinearity leads to an increase in the sub-Poissonian statistics,which means that the nonlinearity causes antibunching of the photons. In what follows, we will investigate the evolution of the normal squeezing for the considered atomic system (figure 13).

8 The normal squeezing

To study the normal squeezing phenomenon, we introduced the field operators ${\hat{Y}}_1=({\hat{a}}+{\hat{a}}^\dag )/2$ and ${\hat{Y}}_2=({\hat{a}}-{\hat{a}}^\dag )/ 2 i$. These Hermitian operators satisfy $[{\hat{Y}}_1, {\hat{Y}}_2]=\frac{i}{2}$. This commutation relation implies the uncertainly relation $\left( {\Delta Y_1 } \right) ^{2} < \frac{1}{4}$ and $\left( {\Delta Y_2 } \right) ^{2} < \frac{1}{4}$. We can rewrite theses conditions as follows:

$$\begin{aligned} S_1 =\left( {\Delta Y_1 } \right) ^{2}-\frac{1}{4},\qquad S_2 =\left( {\Delta Y_2 } \right) ^{2}-\frac{1}{4}. \end{aligned}$$

(55)

Fig. 15

The same as in figure 2 but for normal squeezing.

Fig. 16

The same as in figure 3 but for normal squeezing.

Fig. 17

The same as in figure 4 but for normal squeezing.

We can write the variances $\left( {\Delta Y_{1}} \right) ^2$ and $\left( {\Delta Y_{2}} \right) ^2$ in the following forms:

$$\begin{aligned} \left( {\Delta Y_{1}} \right) ^{2}{} & {} = \frac{1}{4}[ \langle {\hat{{a}}^{\dagger 2}} \rangle +\left\langle {\hat{{a}}^{2}} \right\rangle +2\langle {\hat{{a}}^{\dagger }\hat{{a}}} \rangle \nonumber \\{} & {} \quad +1-( {\langle {\hat{{a}}^{\dagger }} \rangle +\left\langle {\hat{{a}}} \right\rangle } ) ^{2} ], \end{aligned}$$

(56)

$$\begin{aligned} \left( {\Delta Y_{2}} \right) ^{2}{} & {} = -\frac{1}{4}[ \langle {\hat{{a}}^{\dagger 2}} \rangle +\langle {\hat{{a}}^{2}} \rangle +2\langle {\hat{{a}}^{\dagger }\hat{{a}}} \rangle \nonumber \\{} & {} \quad +1-( {\langle {\hat{{a}}^{\dagger }} \rangle -\left\langle {\hat{{a}}} \right\rangle } ) ^{2} ]. \end{aligned}$$

(57)

The expectation value of the field operator ${\hat{a}}^{\dag m}$ can be given in the general form

$$\begin{aligned} \langle {\hat{a}}^{\dag m}\rangle = |\alpha |^m{} & {} \sum _{n} P(n) (\Gamma ^*_1(n+m,t) \Gamma _1(n,t)\nonumber \\ +V_1{} & {} \sum _{r=2,3,4,7} \Gamma ^*_r(n+m+1,t) \Gamma _r(n,t) \nonumber \\ +V_2{} & {} \sum _{s=5, 6, 8, 9} \Gamma ^*_s(n+m+2,t) \Gamma _s(n,t)) \end{aligned}$$

(58)

$$\begin{aligned}{} & {} V_1= \sqrt{\frac{n+m+1}{n+1}}, \nonumber \\{} & {} V_2= \sqrt{\frac{(n+m+2)(n+m+1)}{(n+2)(n+1)}}. \end{aligned}$$

(59)

Now, we turn to take a look at the normal squeezing for the considered system in figures 14–16 with the values of the parameters the same as in figures 2–4, respectively. Figures 14–16 show that the impact of the time-dependent coupling is weak at the regular squeezing phenomenon in the absence of detuning parameters as seen in those figures. In figure 12, it is seen that the increase in detuning parameter leads to an increase in the amount of oscillations and squeezing. Furthermore, the non-linearity increases the maximum value of squeezing. In the next section, we shall focus on Q-function. Also, the effect of parameters on the quasiprobability distribution will be given.

Fig. 18

The contour plots of $Q(\beta ,t)$ for the same data as in figure 2 but for $\alpha _0=5$ and $\tau =\pi /2$.

Fig. 19

The contour plots of $Q(\beta ,t)$ for the same data as in figure 3 but for $\alpha _0=5$ and $\tau =\pi /2$.

9 Quasiprobability distribution Q-function

The Q-function (Husimi Q distributions) is one of the quasiprobability distribution in phase space. It is widely used in quantum optics and tomographic purposes and applied to study the quantum effects in superconductors. The Q-function can take the form

$$\begin{aligned} Q(\beta ,t)=\frac{1}{\pi }|\langle \beta |\Psi (t)\rangle |^2= \frac{1}{\pi } \sum _{j=1}^9 |\langle \beta |\Gamma _j(t)\rangle |^2, \end{aligned}$$

(60)

where

$$\begin{aligned} \langle \beta |\Gamma _1(t)\rangle= & {} \sum _n \exp \left[ \frac{-|\beta |^2}{2}\right] \frac{\beta ^n}{\sqrt{n!}} q_n \Gamma _1(n,t), \nonumber \\ \langle \beta |\Gamma _r(t)\rangle= & {} \sum _n \exp \left[ \frac{-|\beta |^2}{2}\right] \frac{\beta ^{n+\ell }}{\sqrt{(n+\ell )!}}\nonumber \\{} & {} \quad \times q_n \Gamma _r(n+\ell ,t), \quad \ r=2, 3, 4, 7, \nonumber \\ \langle \beta |\Gamma _s(t)\rangle= & {} \sum _n \exp \left[ \frac{-|\beta |^2}{2}\right] \frac{\beta ^{n+2 \ell }}{\sqrt{(n+2 \ell )!}} \nonumber \\{} & {} \quad \times q_n \Gamma _s(n+2 \ell ,t), \quad s=5, 6, 8, 9. \end{aligned}$$

(61)

In figures 17–20, we investigated the dynamical behaviour of the Q-function. We sketch the contour plots of this function in complex planes.

Fig. 20

The contour plots of $Q(\beta ,t)$ with the same data as in figure 4 but for $\alpha _0=5$ and $\tau =\pi /2$.

Fig. 21

The contour plots of $Q(\beta ,t)$ but for $\alpha _0=5$, $\upsilon =1.0$, $\Delta =0$ and $\tau =\pi /4$ for different values of non-linearity.

In figures 17a–17c, we plot the contour plots for the same data as in figure 2 with $\alpha _0=5$ and $\tau =\pi /2$. We noticed that the Q-function is represented by one-peak, the shapes of the peak change as the existence via the second atom $\upsilon$. To investigate the influence of detuning parameter on the temporal behaviour of the Q-function, we sketch the contour plots in figure 15 for the same data as in figure 3. We observed that the detuning parameter decreases the peak area, and for large detuning it has a circular shape. On the other hand, the broadening occurs in the distribution of Q-function in figures 16a–16c in the presence of the Kerr-like medium. This broadening increases as the Kerr-like medium parameter increases.

Also, the influence of non-linearity on the dynamical behaviour of the Q-function can be seen in figure 17. We remark that the Q-function has one peak in the absence of Kerr-like medium as in figure 17a. Furthermore, we observed that the peak rotates in the anticlockwise direction when nonlinearity is present. Also, we noticed that as $\chi$ increases the broadening of peak increases as in figure 17g. Moreover, in figure 17i, when $\chi =1.0$, we observe that the plot takes a ring-shape and Q-function has four peaks.

10 Conclusion

In the present work, we have studied the model which describes the interaction between the two three-level $\Lambda$-type atoms and a single-mode cavity field. The system includes the presence of the second atom, the detuning parameter and non-linearity. The exact solution of the wave function is found in Schrödinger picture. The atomic inversion, Shannon entropy, Von Neumman entropy, second-order correlation function, normal squeezing and quasiprobability distribution Q-function have been calculated and investigated. These investigations show that the presence of the second atom, non-linearity and detuning parameters lead to changes in the properties of the mean photon number. Furthermore, these parameters imply useful changes in Shannon entropy, Poissonian statistics and Q-function of the considered system. In the same manner, these investigations can be done in other states. In future, we shall extend this study to two-mode systems.