1 Introduction

The mathematical modelling of fluid flow through a porous medium is of great importance due to its many practical applications in medicine and industry. The torque exerted by slowly rotating a solid particle in an incompressible Newtonian, non-Newtonian or porous medium has applications in chemical, biomedical, environmental engineering and science. Jeffrey [1] solved the problem of slow and steady rotation of spheroids in an unbounded Newtonian fluid. Later, Kanwal [2] studied the slow steady rotation of axisymmetric bodies placed in an incompressible viscous liquid.

In recent years, several investigators studied the effect of slip condition for different fluid flow problems involving solid–liquid, solid–porous interfaces since it is accepted theoretically and experimentally [3,4,5,6,7]. The slip boundary condition was proposed by Navier [8]. According to Navier, fluid slippage exists on the solid boundary. Basset [9] studied translation and rotation problems of a slip sphere and derived the couple and drag expressions exerted by the fluid. The couple exerted on a slip solid sphere of radius a rotating in an unbounded fluid of viscosity \(\mu \) and density \(\rho \) at a vanishing small angular Reynolds number (\(\displaystyle {Re={a^2\Omega \rho }/{\mu }}\)) was first derived by Basset (1888) as

$$\begin{aligned} T_{z}^{\infty }=-8\pi \mu \Omega a^3\left[ \frac{\lambda }{\lambda +3}\right] , \end{aligned}$$
(1)

where \(\displaystyle {\lambda ={\beta a}/{\mu }}\) is the slip parameter (dimensionless), \(\beta \) is the coefficient of sliding friction and \(\Omega \) is the angular velocity of the particle. When the slip parameter \(\lambda \rightarrow \infty \), there is no slip and eq. (1) becomes Stokes result. When \(\lambda =0\), there is a perfect slip, i.e., the particle behaves like an inviscid gas bubble in a liquid and the torque disappears. Hu and Zwanzig [10] calculated the torque generated by the viscous fluid on a prolate or an oblate spheroid using the slipping condition.

Srinivasacharya and Iyengar [11] investigated the rotary oscillations of an approximate sphere in an incompressible micropolar fluid. Tekasakul and Loyalka [12] examined the rotary oscillations of axisymmetric bodies in a viscous flow with slip using the Green’s function technique. They found that slip reduces torque. Ashmawy [13] examined the creeping flow of steady rotational flow of a general axisymmetric particle in a viscous fluid. He observed that the couple acting on the axisymmetric particle depends on the shape and dimensions of the particle. Senchenko and Keh [14] studied the resistance forces for the slow flow around a slightly deformed slip sphere. They found that the drag force is an increasing function of the slip parameter. Chang and Keh [15] studied the Stokes flow rotation of a spheroid about its axis of revolution in a viscous fluid with the slip effect. They observed that for a spheroid with a fixed aspect ratio, torque is monotonically decreasing with an increase in the slip parameter. Sherief et al [16] investigated the axisymmetric rotary and rectilinear oscillations of a spheroid in an unbounded micropolar fluid under the influence of slip. They concluded that the hydrodynamic couple acting on the rotary spheroid is an increasing function of micropolarity and slip parameters. Lee and Keh [17] examined the effect of weak fluid inertia on the slow steady rotation of a slip sphere. They noticed that torque is a decreasing function of the slip parameter and is an increasing function of the Reynolds number. Dehgan et al [18] experimentally investigated the effects of particle size, fluid viscosity, particle density and rotational viscosity, on the terminal velocity of the free-falling rotating and non-rotating spherical particles in a viscous fluid.

Brinkman [19] was the first to model the flow through porous medium of high porosity. The momentum equation has two viscous terms: Darcy viscous term and viscous diffusion term together with the balanced pressure gradient and neglecting the inertial terms. When one wishes to compare the results of the flows in porous medium with that of the clear fluid, the Brinkman equation has a permeability parameter. If the permeability parameter tends to infinity, the momentum equation reduces to Darcy equation. If the permeability parameter approaches zero, the momentum is simply a Stokes equation [20]. Solomentsev and Anderson [21] examined the effect of permeability on the torque exerted on the sphere in a Brinkman fluid. They found that the effect of the Brinkman term is much smaller for rotation than for translation. Feng et al [22] studied the arbitrary motion of a circular disk in a Brinkman’s medium. They found that the effect of dimensionless permeability parameter on the torque of the particle is weaker than for the drag at small values of permeability parameter. Feng et al [23] obtained the solutions for the motion of a spherical particle bounded by a solid wall or a planar free surface in a Brinkman’s medium. They found that the torque on a rotating sphere because of the confining boundary is a lower-order effect than the drag. Seki [24] examined the effect of permeability on the free motion of a sphere in a tube. Cortez et al [25] developed the exact solution for incompressible flow driven by regularised forces. Leiderman and Olson [26] derived a method to compute swimming in 2D Brinkman flow driven by a regularised point force. They observed that a solo swimmer over each beat period had constant efficiency and when they considered two swimmers interacting by the Brinkman flow, they observed the efficiency of two swimmers over each beat period. They found that the solo swimmer has less efficiency than the two swimmers in a Stokesian fluid at baseline stiffness. El-Sapa et al [27, 28] investigated the steady translational motion of two spherical particles in a porous medium without and with the magnetic field. She observed that when the value of permeability parameter increases, the interaction effect between two spherical particles decreases and also normalised drag force decreases. Leshansky [29] developed the theoretical framework of propulsion in heterogeneous viscous medium. He noticed that the optimal velocity of the rotating helix moving through heterogeneous viscous medium increases as scaled resistance increases. Jung [30] investigated the locomotive behaviour of caenorhabditis elegans swimming in a saturated particulate system. After the experiments, he found that caenorhabditis elegans can achieve efficient locomotion in their natural environment by using the nearby porous medium. Nganguia and Pak [31] considered the canonical model swimmer, the squirmer, to study locomotion in a heterogeneous viscous medium by the Brinkman equation. Jeznach and Olson [32] investigated the dynamics of the swimmers. They noticed that when the head radius is increased, the speed of the swimmer decreases regardless of the resistance parameter and because of the large drag on the cell body, beating tails of two swimmers causes the cell body to rotate slightly downward for the bottom swimmer (and upward for the top swimmer). Recently, Chen et al [33] examined the dynamics of the swimmer model in a porous medium. They showed that when scaled resistance increases, scaled swimming speed also increases monotonically in the Brinkman medium. El-Sapa [34] investigated the permeability effect of Brinkman’s porous medium on thermophoretic velocity of a spherical particle in a spherical cavity. She observed that when permeability increases, the normalised thermophoretic mobility of a spherical particle decreases. Faltas et al  [35] investigated the sphere straddling the flat interface of a semi-infinite Brinkman flow region. They found the resistance coefficient for the rotational axisymmetric motion increasing with slip for all finite values of permeability. Prasad et al [36] derived the hydrodynamic drag on the slip spheroid immersed in a porous medium. They analysed that the value of drag force increases as the slip parameter increases. El-Sapa [37] studied the non-concentric rigid sphere interaction in a micropolar fluid with slip effect. She also investigated the translational motion of two spherical particles in a magneto-micropolar fluid [38].

The purpose of the current work is to examine the effects of permeability, deformation and slip parameters on the torque generated by the flow of viscous fluid past a deformed slip sphere immersed in a porous medium. Also, to obtain a correction factor to eq. (1) for the rotation of a deformed slip sphere in the Brinkman’s medium which is not available yet. We have extended the previous work of Solomentsev and Anderson [21] for the rotation of a sphere in the porous medium to the case of rotation of a deformed sphere in the Brinkman’s medium. The slip condition is applied on the spheroid surface. The flow in a porous medium is governed by Brinkman’s equation.

2 Analysis

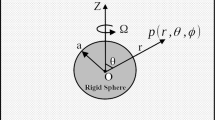
Consider the creeping flow of steady rotational motion of the viscous fluid through a slip which occurs on the surface of the slightly deformed sphere immersed in Brinkman’s medium, as depicted in figure 1. The shape of a deformed sphere varies slightly from that of a sphere.

Let the equation of a deformed sphere surface be \(r=a[1+f(\zeta )]\) [16], where

$$\begin{aligned} \displaystyle {f(\zeta )=\sum _{i=1}^{\infty }\alpha _{i}\,P_{i}(\zeta ).} \end{aligned}$$

Here, \(P_i(\zeta )\) is the Legendre function and \(\zeta =\cos \theta \).

If all the \(\alpha _{i}\) are zero, the deformed sphere reduces to a sphere of radius a. \(\Omega \) is the angular velocity about the z-axis.

Fig. 1
figure 1

Sketch of the problem.

Full size image

The fluid flow is governed by Brinkman’s equation [19, 22]

$$\begin{aligned}{} & {} \nabla \cdot \vec {v}=0 , \end{aligned}$$
(2a)
$$\begin{aligned}{} & {} \nabla p+\mu \,\nabla \times \nabla \times \vec {v}+\frac{\mu }{k}\vec {v}=0,\quad \end{aligned}$$
(2b)

where \(\vec {v}\), p, k are the fluid velocity, dynamic pressure and permeability of the porous medium, respectively.

For axisymmetric slow steady rotational flow, the dynamic pressure is constant and the non-zero velocity vector \(\vec {v}\) is in the form

$$\begin{aligned} \vec {v}= v_\phi (r,\theta )\vec {e}_\phi . \end{aligned}$$
(3)

Substituting eq. (3) in eq. (2) and then inserting the non-dimensional variables \(v_\phi =\Omega \,a\,{\tilde{v}}_\phi \), \(r=a\,{\tilde{r}}\) in the resulting equations, we have the dimensionless equation after dropping the tildes

$$\begin{aligned} (E^2-\alpha ^2)\,r\sqrt{1-\zeta ^2} v_\phi =0, \end{aligned}$$
(4)

where

$$\begin{aligned}{} & {} \displaystyle {E^2=\displaystyle \frac{\partial ^{2}}{\partial r^{2}}+\frac{{1-\zeta ^2}}{r^{2}}\frac{\partial ^{2}}{\partial \zeta ^{2}}},\\{} & {} \displaystyle {\alpha =\frac{a}{\sqrt{k}}}. \end{aligned}$$

We can express the solution of eq. (4) in the form

$$\begin{aligned} v_\phi= & {} a_{1}\,r^{-\frac{1}{2}}\,K_{3/2}(\alpha r)P_{1}^{1}(\zeta )\nonumber \\{} & {} +\sum _{n={2}}^{\infty }A_n r^{-\frac{1}{2}}K_{n+1/2}(\alpha r)\,P_n^{1}(\zeta ), \end{aligned}$$
(5)

where \(P_{n}^{1}(\zeta )\) represents the associated Legendre function of the first kind of order n and degree 1, \(K_{n+1/2}(\alpha r)\) is the modified Bessel’s function of the second kind of order \({n+1/2}\) where n is a positive integer. For \(n\ge 2\), the unknowns \(a_{1}\), \(A_{n}\)  are to be found.

We obtain the solution with respect to the boundary \(r=1+\alpha _{i}\,P_{i}(\zeta )\). Consider that values of \(\alpha _{i}\) are very small and therefore higher powers can be neglected, so that, \(r^\delta \approx {1}+\delta \,\alpha _{i}\,P_{i}(\zeta )\) where \(\delta \) is positive or negative.

On the boundary surface \(r=1+\,\alpha _{i}\,P_{i}(\zeta )\), the normal vector is

$$\begin{aligned} \vec {n}=\vec {e_r}-\alpha _i\,a\,\nabla \,P_{i}(\zeta )=\vec {e_r}+\alpha _i\,P_{i}^{1}(\zeta )\vec {e_\theta }. \end{aligned}$$
(6)

The slip condition on the slightly deformed sphere surface \(r=1+\alpha _{i}\,P_{i}(\zeta )\) [16, 35, 36, 39] is

$$\begin{aligned} \lambda \,(v_\phi -\,r\,\sqrt{1-\zeta ^2})=t_{r\phi }+\alpha _{i}\,t_{\theta \phi }\,P_i^{1}(\zeta ), \end{aligned}$$
(7)

where the sliding friction \(\displaystyle {\lambda ={\beta \,a}/{\mu }}\) is the slip coefficient.

Applying boundary condition eq. (7), we get

$$\begin{aligned}{} & {} [\left( (\lambda +3)\,K_{3/2}(\alpha )+\alpha K_{1/2}(\alpha )\right) \,a_{1}-\lambda ]\,P_{1}^{1}(\zeta )\nonumber \\{} & {} \quad -[((\alpha ^2+2\lambda +9)\,K_{3/2}(\alpha )\nonumber \\{} & {} \quad +\alpha (\lambda +3) K_{1/2}(\alpha ))\,a_{1}+\lambda ]\nonumber \\{} & {} \quad \times \,\alpha _{i}\,P_{i}(\zeta )\,P_{1}^{1}(\zeta )+\sum _{n=2}^{\infty }\,\left[ (\lambda +n+2)\,K_{n+1/2}(\alpha )\right. \nonumber \\{} & {} \quad \left. +\alpha \,K_{n-1/2}(\alpha )\right] A_{n}\,P_n^{1}(\zeta )=0. \end{aligned}$$
(8)

Solving the leading terms of eq. (8), we have

$$\begin{aligned} a_{1}=\frac{\lambda }{(\lambda +3)\,K_{3/2}(\alpha )+\alpha \,K_{1/2}(\alpha )}. \end{aligned}$$
(9)

Using this value in eq. (8), we obtain

$$\begin{aligned}{} & {} \xi _{1}\,\alpha _{i}\,P_{i}(\zeta )\,P_{1}^{1}(\zeta )+\sum _{n=2}^{\infty }\,\left[ (\lambda +n+2)\,K_{n+1/2}(\alpha )\right. \nonumber \\{} & {} \quad \left. +\alpha \,K_{n-1/2}(\alpha )\right] A_{n}P_n^{1}(\zeta )=0, \end{aligned}$$
(10)

where

$$\begin{aligned} \xi _{1}= & {} -[((\alpha ^2+2\lambda +9)\,K_{3/2}(\alpha )\nonumber \\{} & {} + \alpha (\lambda +3) K_{1/2}(\alpha ))\,a_{1}+\lambda ]. \end{aligned}$$
(11)

To solve eq. (10) for \(A_{n}\) (\(n\ge 2\)), we require the following identity [16]:

$$\begin{aligned} P_{1}^{1}(\zeta )\,P_{i}(\zeta )= & {} \frac{1}{2\,i+1}\,P_{i+1}^{1}(\zeta )\nonumber \\{} & {} -\frac{1}{2\,i+1}\,P_{i-1}^{1}(\zeta ). \end{aligned}$$
(12)

Here, we compare the terms in eq. (10) and taking all \(A_{n}\) as zero except when \(n=i-1\) or \(n=i+1\), we get

$$\begin{aligned} \xi _{1}\,{\overline{c}}_{n}+\left[ (\lambda +n+2)\,K_{n+1/2}(\alpha )\right. \nonumber \\{} & {} \quad \left. +\alpha \,K_{n-1/2}(\alpha )\right] A_{n}=0, \end{aligned}$$
(13)

where

$$\begin{aligned} {\overline{c}}_{i-1}=\frac{-\alpha _i}{2\,i+1}\, ,\quad {\overline{c}}_{i+1}=\frac{\alpha _i}{2\,i+1}. \end{aligned}$$
(14)

Solving eq. (13), we get expression \(A_{n}\) for \(n=i-1\) and \(n=i+1.\)

3 Application to an immersed slightly deformed sphere

Consider the slow steady rotation of a solid prolate or a solid oblate spheroid immersed in a porous medium. The equation of the spheroid [16] is described in the Cartesian coordinate system (x, y, z) as

$$\begin{aligned} \frac{x^{2}+y^{2}}{a^{2}\,({1}-\epsilon /{2})^{2}}+\frac{z^{2}}{a^{2}\,({1}+\epsilon )^{2}}={1.} \end{aligned}$$
(15)

Equation (15) is an oblate spheroid if \(\epsilon <0\) and a prolate spheroid if \(0<\epsilon <{1}\). The polar form of eq. (15) is \(r=1+\epsilon \,P_{2}(\zeta )\) to \(O(\epsilon )\). Here, it is necessary to take \(i={2}\), \(\alpha _{2}=\epsilon \). Hence, the velocity component is

$$\begin{aligned} v_\phi= & {} (a_{1}+A_{1})\,r^{-\frac{1}{2}}\,K_{3/2}(\alpha r)\,P_{1}^{1}(\zeta )\nonumber \\{} & {} +A_{3}\,r^{-\frac{1}{2}}\,K_{7/2}(\alpha r)\,P_{3}^{1}(\zeta ). \end{aligned}$$
(16)

4 Torque on the body

The hydrodynamic torque exerted on the rotating spheroid is given by [16]

$$\begin{aligned} T_z= & {} {2}\pi \,a^3\,\int _0^\pi r^3\left( t_{r\phi }+\frac{3}{{2}}\,\epsilon \,t_{\theta \phi }\sin {2}\theta \right) \nonumber \\{} & {} \times \big |_{r={1}+\epsilon \,P_{2}(\zeta )} \sin ^{2} \theta \,\textrm{d}\theta \end{aligned}$$
(17)
$$\begin{aligned} T_2= & {} -\frac{8}{3}\,\pi \,\mu \,\Omega \,a^3\,\Bigg [\alpha \,K_{5/2}(\alpha )\,(a_{1}+A_{1})\nonumber \\{} & {} +\frac{\epsilon }{5}\,\alpha ^2\,K_{3/2}(\alpha )\,a_{1}\Bigg ], \end{aligned}$$
(18)

where

$$\begin{aligned} A_{1}= & {} \frac{\epsilon }{5}\,\xi _{1}\,\left[ (\lambda +3)\,K_{3/2}(\alpha )+\alpha \,K_{1/2}(\alpha )\right] ^{-1} \end{aligned}$$
(19)
$$\begin{aligned} T_z= & {} -\frac{8}{3}\,\pi \,\mu \,\Omega \,a^3\,\lambda \left[ \frac{(\alpha ^2+3\alpha +3)}{\alpha ^2+(\lambda +3)(\alpha +1)}-\frac{\epsilon }{5}\right. \nonumber \\{} & {} \times \left. \frac{(4(\alpha ^2\!+\!3\alpha +3)^2\!+\!\lambda (2\alpha \!+\!3)(2\alpha ^2\!+\!4\alpha +3))}{(\alpha ^2\!+\!(\lambda +3)(\alpha +1))^2}\right] .\nonumber \\ \end{aligned}$$
(20)

5 Special cases

For spheroid \((\epsilon \ne 0)\):

  1. 1.

    When \(\lambda \rightarrow \infty \) in eq. (20), we have the torque acting on the no-slip spheroid embedded in the porous medium

    $$\begin{aligned} T_z^\infty= & {} -\frac{8}{3}\,\pi \,\mu \,\Omega \,a^3\left[ \frac{(\alpha ^2+3\alpha +3)}{(\alpha +1)} \right. \nonumber \\{} & {} -\left. \frac{\epsilon }{5}\frac{(2\alpha +3)(2\alpha ^2+4\alpha +3)}{(\alpha +1)^2}\right] . \end{aligned}$$
    (21)
  2. 2.

    When \(\alpha \rightarrow 0\) in eq. (20), we have the torque exerted by the spheroid in the unbounded medium [14]

    $$\begin{aligned} T_z^\infty =-8\,\pi \,\mu \,\Omega \,a^3\left[ \frac{\lambda }{\lambda +3}-\frac{3\,\epsilon \,\lambda (\lambda +4)}{5(\lambda +3)^2}\right] .\nonumber \\ \end{aligned}$$
    (22)

For perfect sphere \((\epsilon =0)\):

  1. 1.

    The torque acting on a rotating slip sphere embedded in an unbounded porous medium

    $$\begin{aligned} T_z^\infty =-\frac{8}{3}\,\pi \,\mu \,\Omega \,a^3\,\lambda \left[ \frac{(\alpha ^2+3\alpha +3)}{\alpha ^2+(\lambda +3)(\alpha +1)}\right] .\nonumber \\ \end{aligned}$$
    (23)

Exactly half the value of the torque matches with the sphere straddling the interface of a semi-infinite Brinkman flow [35]. For the case of no-slip, the torque agrees with the result obtained by Solomentsev and Anderson [21].

6 Results and discussion

The non-dimensional torque is calculated as

$$\begin{aligned} T=\frac{T_z}{-8\pi \,\mu \,\Omega \,a^{3}}. \end{aligned}$$

Numerical results are computed for the torque coefficient T experienced by the viscous fluid by slow steady rotation of a slip spheroidal particle embedded in a Brinkman’s medium, assuming different values of the permeability parameter \(\displaystyle {k_{1}={1}/{\alpha ^2}}\), the slip coefficient \(\lambda \) and the deformity parameter \(\epsilon \). Figure 2 shows the variation of T with \(k_{1}\) for various values of the slip parameter \(\lambda \) and the deformity parameter \(\epsilon \). The curve \(\lambda \rightarrow \infty \) represents no-slip flow and the curves \(\lambda = 1\) and \(\lambda = 10\) represent the effect of slip flow. The curves \(\epsilon =-0.3\) and \(\epsilon =0.3\) represent an oblate spheroid and a prolate spheroid, respectively. The curve \(\epsilon =0\) indicates that there is no deformation and particle is a sphere. The position of this curve indicates that the torque on the sphere is higher than the torque on an oblate spheroid and lower than the torque on a prolate spheroid. It is observed that the torque coefficient decreases as the permeability parameter \(k_{1}\) increases and increases with the increase in the slip parameter \(\lambda \). The torque exerted by the slip spheroid is less than that of the no-slip spheroid. The torque exerted by the sphere is larger than the torque on a prolate spheroid and smaller than the torque on an oblate spheroid.

Fig. 2
figure 2

The torque coefficient T against permeability \(k_1\) for different values of \(\lambda \) for an oblate spheroid (\(\epsilon =-0.3\)), a sphere (\(\epsilon =0\)) and a prolate spheroid (\(\epsilon =0.3\))

Full size image
Table 1 Numerical values for the torque coefficient T of an oblate spheroid embedded in the porous medium against permeability for varying deformations.
Full size table

The numerical results are presented in tables 1 and 2. It is observed that the torque coefficient generated by the Brinkman fluid on an oblate spheroid, a sphere and a prolate spheroid decreases with an increase in the permeability parameter \(k_{1}\). The torque coefficient increases as the slip parameter increases and it reaches high in the case of a no-slip spheroid. In the case of the perfect slip, the torque vanishes. The Brinkman effect on slow steady rotation of an oblate spheroid, a sphere and a prolate spheroid is weaker than on slow steady translational flow past an oblate spheroid without rotation, sphere and a prolate spheroid, respectively [36] for any value of \(k_{1}\).

Table 2 Numerical values for the torque coefficient T of a prolate spheroid embedded in the porous medium against permeability for varying deformations.
Full size table

7 Conclusions

An analytic solution for the torque acting on a slip-deformed sphere embedded in a porous medium undergoing slow and steady rotation in a viscous fluid is investigated. The torque is a decreasing function of deformation and permeability parameters and is an increasing function of slip parameter. Hence, we have seen that there is a significant effect of the slip parameter on the torque coefficient. The result obtained can be used in helical locomotion in a Brinkman’s medium by considering the head of the swimming bacterium as non-spherical and applying the equilibrium conditions [33].