1 Introduction

Compact stars are fascinating objects of study for various reasons. As they have extremely dense matter inside them, it is very interesting to study the physics of what goes on inside these compact stars. Although they have been studied by various researchers for several decades, their exact nature is yet to be completely understood. Solving Einstein’s field equations by considering various cases, such as isotropic, anisotropic, charged-isotropic and charged-anisotropic fluid distributions, several researchers tried to understand the nature of compact stars. Although isotropic perfect fluids are used quite a lot to portray the construction of various stellar bodies, the existence of anisotropy cannot be discarded while dealing with the nuclear matter at extremely high pressures and densities (for example, see refs [1,2,3,4,5]). In extremely dense conditions, pressure can be split into two components, namely radial, and tangential pressure, which gives pressure anisotropy. As discussed by Herrera [6], we can find that even if initially the matter distribution was isotropic, due to energy dissipation during stellar evolution, the matter will eventually become anisotropic. This energy dissipation happens as a result of the emission of various massless or low-mass particles such as photons or neutrinos and it is one of the important features of the evolution of massive stars. In very high- and very low-density matter distributions, there can be so many factors that can lead to anisotropy. This has been explained in detail by Herrera and Santos [7]. Exotic phase transitions can happen in these extremely dense systems, which can lead to gravitational collapse. One such significant exotic phase transition is the pion condensed state. It effectively softens the equation of state (EoS) by releasing a huge amount of energy. This has a substantial impact on the collapsing configurations. Sawyer and Scalapino [8] pointed out that because of the \(\pi ^-\) modes, the pion condensed phase can, in fact, be the cause of the pressure anisotropy itself. Some researchers [9, 10] argued that the flux lines of a type-II superconductor are related to the anisotropic part of the stress tensor and is associated with the neutron star configuration. The presence of solid core [11, 12], type-P superfluid and boson stars [13, 14] is also associated with the anisotropic factor. Viscosity can be one possible source of local anisotropy. However, when the Fermi energy exceeds the temperature, the matter can be considered isentropic by neglecting the dissipative processes for the relativistic calculation of gravitational collapse. But this approximation does not hold for some particular scenarios of stellar evolution. One such example is neutrino trapping which can happen when the central density reaches the order of \(10^{11}\)–\(10^{12}\) g/cm\(^3\) [15]. Due to the long mean free path, high energy density and small radiative Reynolds number, these trapped neutrinos make the core fluid more viscous [16, 17], eventually leading to local anisotropy. In this regard, Ruderman [18] showed that when the density exceeds \(10^{15} \)g/cm\(^3\), the two components of pressure no longer have the same value and nuclear matter becomes anisotropic. In this connection, a condition of pressure anisotropy (\(P_t-P_r=gq^2r^2\)) was proposed by Herrera and Varela [19], with g being a non-zero constant that comes from the electromagnetic mass model, under a specific case. So it can be said that, for compact stellar objects or more specifically, where matter is extremely densely packed, considering anisotropic matter distribution gives more realistic results. In fact, in this scenario, pressure isotropy can be called an approximation in cases where pressure anisotropy is negligible enough for the key physical aspects of a given model to remain unchanged. Considering anisotropic matter distribution, compact stars have been studied by several researchers [20,21,22,23,24]. On the other hand, Delgaty and Lake [25] listed several exact solutions which have been found over the last century. However, only a few of them satisfy the physical requirements for realistic self-gravitating compact objects in general relativity. In this regard, a well-behaved space–time geometry was proposed by Buchdahl [26] that satisfies all requirements of physical acceptability of the realistic model. A specific form of the Buchdahl metric in the context of embedding of 3-hypersurface as a spheroid in four-dimensional space was studied by Vaidya and Tikekar [27] and Tikekar [28]. This study provides the geometric meaning of the Buchdahl metric. Later on, several pioneering works on the Buchdahl metric have been done by several researchers in different contexts [29,30,31,32,33,34,35,36,37].

On the other hand, obtaining new exact solutions to Einstein’s field equations for different scenarios has always been a challenge for researchers. The situation becomes more complicated when we introduce an extra source, say \(\theta _{\beta \gamma }\), in the original matter distribution (\(T_{\beta \gamma }\)). In this regard, the gravitational decoupling approach is a very efficient approach for solving such complicated systems. This approach allows us to solve this complicated energy–momentum tensor by splitting two comparatively simpler components for \(T_{\beta \gamma }\) and \(\theta _{\beta \gamma }\) individually. After solving both systems separately, the linear combination of those solutions will provide the solution for the initial energy–momentum tensor. In this regard, a direct approach of gravitational decoupling (GD) via minimal geometric deformation (MGD) [38] and its extended version, known as complete geometric deformation (CGD) [39] has been used by several researchers in recent times to investigate various models. This methodology was first developed by Ovalle [40, 41] and it was then applied to Randall–Sundrum brane-world framework to deform Schwarzschild space–time. Using MGD, several well-known solutions of Einstein’s field equations were investigated by several researchers considering several conditions such as isotropic, anisotropic, charged-isotropic matter distributions in different gravities including higher dimensions [42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74]. Technically, MGD transformation is performed over the metric potential by using a decoupler function along with the radial component of the line element. Therefore, a great advantage of MGD is that it simplifies a complex system. However, MGD can also be used to generalise a simple system to more complex ones as well with the addition of an extra source (\(\theta _{\beta \gamma }\)) with the energy–momentum tensor via coupling with a dimensionless parameter. According to Ovalle and his collaborators, one disadvantage of MGD is that considering only radial transformation is inadequate to explain the existence of a stable black hole having a well-defined horizon. To address this issue, the MGD was further extended by deforming both radial and temporal metric functions [39] which introduce two known deformation functions f(r) and g(r). These new degrees of freedom appear in the \(\theta \)-sector. In this regard, several approaches have been taken for solving the system, such as using the mimic approach along with a particular form of f(r) or using the mimic approach along with EoS approach to solve the \(\theta \)-sector [75,76,77]. Moreover, it is worth mentioning that the hydrostatic balance gets affected due to the deformation. So, to check the viability of the solution, the hydrostatic balance is an essential parameter for study. In recent times, gravitational decoupling CGD approaches have been used to investigate the solution in GR and modified gravity theory including higher dimensions [78,79,80,81]. Recently, the gravitational decoupling methodology is applied to see the effect on the complexity of the self-gravitating stellar objects [82,83,84,85,86,87,88]. Another great tool for solving Einstein’s field equations is the embedding Class-I condition. It is a methodology where an n-dimensional pseudo-Riemannian space–time is embedded into an \((n + p)\)-dimensional pseudo-Euclidean space, with p being the class of the embedded manifold. For example, in Class-I condition, the embedding of a four-dimensional pseudo-Riemannian space–time into a five-dimensional pseudo-Euclidean space is performed. The mathematical derivation of this approach was done by Karmarkar [89]. An additional differential equation is obtained from this Class-I condition called the Karmarkar condition, which will be discussed in detail in later sections. It has been proven very potent for generating new exact solutions for relativistic astrophysics and cosmology [90]. Mathematically, by means of the curvature components, the Karmarkar condition takes the following form: \(R_{1212}R_{3030}\) \( + R_{1220}R_{1330}={R_{1010}R_{2323}}\). Pandey and Sharma [91] argued that the above-mentioned condition is inadequate for being a Class-I condition and they suggested that an additional condition \(R_{2323} \ne 0\) is required for being the Class-I condition. These conditions together then lead to a differential equation that relates the two metric potentials W(r) and H(r). So, only one of the metric potential is needed to be defined and the other can be easily obtained from the differential equation obtained from the Class-I condition. Many researchers have used this methodology to find useful solutions to Einstein’s field equations in various scenarios [92,93,94,95,96,97,98,99,100,101,102,103,104,105]. Furthermore, Bhar et al [106] obtained an anisotropic star for the compact star model using the Chaplygin equation of state.

The present article is organised as follows: In §2, the decoupled field equations in CGD are discussed, which are divided into two parts, the system of field equations under CGD and the embedding Class-I condition. In §3, a new CGD solution under the embedding Class-I condition is obtained. Section 4 describes the boundary condition using well-known Israel–Drmois junction conditions. Section 5 describes the detailed physical analysis of the thermodynamical parameters as well as the stability analysis. Section 6 gives the concluding remarks.

2 Decoupled field equations in CGD

Under gravitational decoupling, for the decoupled system, with the addition of extra sources \(\theta _{\alpha \gamma }\) the general equation of motion can be expressed via coupling constant \(\alpha \) as

$$\begin{aligned} G_{\beta \gamma }=-8\pi (T_{\beta \gamma }+\alpha \theta _{\beta \gamma }), \end{aligned}$$
(1)

where the anisotropic matter distribution is denoted by \(T_{\beta \gamma }\) and Einstein’s tensor is expressed as \(G_{\beta \gamma }\). \(T_{\beta \gamma }\) can

$$\begin{aligned}{} & {} G_{\beta \gamma }=R_{\beta \gamma }-\frac{1}{2}g_{\beta \gamma }R \end{aligned}$$
(2)
$$\begin{aligned}{} & {} T_{\beta \gamma }=({\rho }+{p}_t)u_{\beta }u_{\gamma }-{\rho _t}g_{\beta \gamma }+({p_r}-{p_t})\zeta _\beta \zeta _\gamma .\qquad \end{aligned}$$
(3)

Here, the 4-velocity is denoted by the covariant component \(u_\gamma \) which satisfies the condition \(u_\gamma u^\gamma =1\), while \(\zeta _\gamma \), the unit space-like vector satisfies \(\zeta _\gamma \zeta ^\gamma =-1\) and \(u_\gamma \zeta ^\gamma =0\). Here, the radial and tangential pressure components and matter density are described as \({p_r}\), \({p_t}\) and \({\rho }\), respectively.

The following metric form is considered to specify the space–time geometry in MGD for the stellar body,

$$\begin{aligned} \textrm{d}s^2=H(r) \textrm{d}t^2-W(r)\textrm{d}r^2-r^2(\textrm{d}\theta ^2 +\sin ^2\theta \textrm{d}\phi ^2),\nonumber \\ \end{aligned}$$
(4)

where H and W are gravitational potentials that depend solely on the radial component r. So, keeping eqs (2) and (3) in mind, the following set of differential equations are obtained from eq. (1):

$$\begin{aligned}{} & {} 8\pi \epsilon =\frac{1}{W}\Bigg (\frac{W'}{Wr}-\frac{1}{r^2}\Bigg )+\frac{1}{r^2}, \end{aligned}$$
(5)
$$\begin{aligned}{} & {} 8\pi P_r=\frac{1}{W}\Bigg (\frac{H'}{Hr}+\frac{1}{r^2}\Bigg )-\frac{1}{r^2}, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} 8\pi P_\perp =\frac{2WH'-2HW'-H'W'r}{4 H W^2 r}\nonumber \\{} & {} \qquad \qquad \quad +\frac{2H''}{4 W H}-\frac{H'^2}{4 W H^2}, \end{aligned}$$
(7)

where

$$\begin{aligned} \epsilon =({\rho }+\alpha \theta _0^0),~ P_r=({p}_r-\alpha \theta _1^1),~ P_\perp =({p}_t-\alpha \theta _2^2).\nonumber \\ \end{aligned}$$
(8)

As the Bianchi identity is satisfied by \(G_{\beta \gamma }\),

$$\begin{aligned} -\frac{\textrm{d}{P}_r}{\textrm{d}r}-\frac{H'}{2H}({\epsilon }+{P}_r)+\frac{2({P}_t -{P}_r)}{r}=0. \end{aligned}$$
(9)

For anisotropic matter distribution, this is the form of Tolman–Oppenheimer–Volkof (TOV) equation. Moreover, using

$$\begin{aligned} H^{\prime }=H \frac{2m+8\pi P_r r^3}{r(r-2m)}, \end{aligned}$$
(10)

where m(r) is the mass function, which is defined as

$$\begin{aligned} m(r)=\frac{r}{2W} (W-1) ~~\text {or}~~m(r)=4\pi \int ^r_0 x^2\,\epsilon (x)\,\textrm{d}x,\nonumber \\ \end{aligned}$$
(11)

the TOV equation can be written as

$$\begin{aligned} \frac{\textrm{d}{P}_r}{\textrm{d}r}=-\frac{m+4\pi P_r r^3}{r(r-2m)}({\epsilon }+{P}_r)+\frac{2({P}_t -{P}_r)}{r}. \end{aligned}$$
(12)

2.1 System of field equations under CGD

As can be seen, the field equations (5)–(7) contain eight unknowns, such as, \({\rho } ,{p_r},{p_t},H(r),W(r), \theta _0^0,\theta _1^1\) and \(\theta _2^2\) and are significantly non-linear in nature. The gravitational decoupling in the form of the CGD technique will be used to solve these equations, which can be expressed as

$$\begin{aligned}{} & {} \ln H(r)\longrightarrow \ln X (r)+\alpha \, f(r), \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \frac{1}{W(r)} \longrightarrow Y (r)+\alpha \, g(r), \end{aligned}$$
(14)

where the radial and temporal deformation functions are given by f(r) and g(r),  respectively. By using CGD, it enables us to fix \(g(r)\ne 0\) and \(f(r)\ne 0\). After putting these transformations into eqs (5)–(7), the original system bifurcates into two systems such as

$$\begin{aligned}{} & {} 8\pi {\rho }(r)=\frac{1}{r^2}-Y \Bigg (\frac{1}{r^2}+\frac{Y'}{Yr}\Bigg ) \end{aligned}$$
(15)
$$\begin{aligned}{} & {} 8\pi {p}_r(r)=-\frac{1}{r^2}+Y\Bigg (\frac{1}{r^2}+\frac{X'}{X r}\Bigg ) \end{aligned}$$
(16)
$$\begin{aligned}{} & {} 8\pi {p}_t(r)=\frac{Y}{4}\Bigg [2\frac{X''}{X}-\frac{X'^2}{X^2}+\frac{X'Y'}{XY}+\frac{2}{r}\Bigg (\frac{X'}{X}+\frac{Y'}{Y}\Bigg )\Bigg ]\nonumber \\ \end{aligned}$$
(17)

and

$$\begin{aligned}{} & {} 8\pi \theta _0^0=-\frac{g}{r^2}-\frac{g'}{r} \end{aligned}$$
(18)
$$\begin{aligned}{} & {} 8\pi \theta _1^1= -g\Bigg (\frac{1}{r^2}+\frac{X'}{Xr}\Bigg ) -\frac{Yf'}{r} \end{aligned}$$
(19)
$$\begin{aligned}{} & {} 8\pi \theta _2^2=-\frac{g}{4}\Bigg (\frac{2H''}{H}-\frac{H'^2}{H^2}+\frac{2H'}{H\,r}\Bigg )-\frac{g'}{4}\Bigg (\frac{H'}{H}+\frac{2}{r}\Bigg )\nonumber \\{} & {} \quad -\frac{Y}{4}\Big (2f''+\alpha f'^2+\frac{2f'}{r}+2\frac{X'f'}{X}\Big )-\frac{Y'f'}{4}. \end{aligned}$$
(20)

Here, the first system accounts for Einstein’s system in the anisotropic framework and the second one is a quasi-Einstein system. For these systems, the subsequent conservation equations are expressed as

$$\begin{aligned}{} & {} -\frac{\textrm{d}{p}_r}{\textrm{d}r}-\frac{m_{\textrm{GR}}+4\pi p_r r^3}{r(r-2m)} ({\rho }+{p}_r)+\frac{2({p}_t-{p}_r)}{r}=0,\nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \frac{m+4\pi P_r r^3}{r(r-2m)} (\theta _1^1 -\theta _0^0)+\frac{\textrm{d}\theta _1^1}{\textrm{d}r}-\frac{2}{r}(\theta _2^2 -\theta _1^1)\nonumber \\{} & {} \quad =\frac{f^\prime \,(p_r+\rho )}{2}, \end{aligned}$$
(22)

where the mass function of systems (15)–(17) is denoted by \(m_{\textrm{GR}}\). Then,

$$\begin{aligned} m(r)=m_{\textrm{GR}} - \frac{\alpha \,g(r)}{2}. \end{aligned}$$
(23)
Fig. 1
figure 1

Schematic diagram of an extended version of embedding Class-I anisotropic solution via the CGD approach.

Full size image

Now, the main task is to solve both systems of equations. Here, we have ten unknown parameters but only six independent equations. So to solve the system and reduce the number of free variables, the embedding Class-I condition is used. The embedding Class-I condition is very popular among researchers nowadays. It is discussed below.

2.2 Embedding Class-I condition

The four-dimensional space–time can be said to be embedding Class-I condition if it satisfies Karmarkar condition [89] which is given as follows:

$$\begin{aligned} R_{1414}R_{2323}=R_{1212}R_{3434}+R_{1224}R_{1334}. \end{aligned}$$
(24)

It is important to mention that the condition \(R_{2323}\ne 0\) must be satisfied to represent four-dimensional space–time to be a Class-I space–time [107]. For spherically symmetric space–time, the relationship between two metric potentials can be provided by the Karmarkar condition (24), which can be obtained as

$$\begin{aligned} \frac{X'Y'}{(1-Y)X}=\frac{X'^2}{X^2}-\frac{X'Y'}{XY}-2\frac{X''}{X}. \end{aligned}$$
(25)

This condition is basically the embedding of a four-dimensional space–time given by eq. (4) into a five-dimensional pseudo-Euclidean space. Its solution for X(r) can be provided as

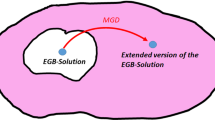
$$\begin{aligned} X=\Bigg (A_1+B_1\int \sqrt{\frac{1-Y}{Y}}\textrm{d}r\bigg )^2, \end{aligned}$$
(26)

where \(A_1\) and \(B_1\) are integration constants. The schematic diagram of the extended version of the embedding Class-I anisotropic solution via CGD approach is shown in figure 1.

3 New CGD solution under embedding Class-I condition

This section is devoted to the solution of the field equations (15) and (20) using CGD techniques. For this purpose, we consider a well-behaved ansatz for the metric function Y(r) as

$$\begin{aligned} Y(r)=\frac{1+a r^2}{1+br^2}, \end{aligned}$$
(27)

where a and b are constants with \(b>a\). This ansatz was originally proposed by Buchdahl [26] which is non-singular for any finite value of r and unity at the centre. Furthermore, the mass function defined by Y(r),

$$\begin{aligned} m_{\textrm{GR}}= \frac{(b-a)r^3}{2(1+br^2)}, \end{aligned}$$
(28)

is monotonically increasing for positive r. Therefore, this metric is suitable for modelling a physically viable self-gravitating system. Substituting the value of Y(r) into Class-I condition given by eq. (24), we have

$$\begin{aligned} X(r)=[A+B\,\sqrt{1+ar^2}]^2, \end{aligned}$$
(29)

where

$$\begin{aligned}{} & {} A=A_1 \quad \textrm{and}\quad B=\frac{B_1 \sqrt{b-a}}{a}. \nonumber \\{} & {} 8\pi {\rho }= -\frac{(a-b) (b r^2+3)}{\left( b r^2+1\right) ^2}, \end{aligned}$$
(30)
$$\begin{aligned}{} & {} 8 \pi {p}_r \nonumber \\{} & {} \ = \frac{a \left( 3 B \sqrt{a r^2+1}+A\right) -b \left( B \sqrt{a r^2+1}+A\right) }{\left( b r^2+1\right) \left( B \sqrt{a r^2+1}+A\right) }, \end{aligned}$$
(31)
$$\begin{aligned}{} & {} 8 \pi {p}_t \nonumber \\{} & {} \ =\frac{{p}_{t1}(r)-b \left( A^2 \sqrt{a r^2+1}+B^2 \sqrt{a r^2+1}+2 A B\right) }{\sqrt{a r^2+1} \left( b r^2+1\right) ^2 \left( B \sqrt{a r^2+1}+A\right) ^2}, \end{aligned}$$
(32)

where

$$\begin{aligned}{} & {} {p}_{t1}(r)=a^2 B r^2 \left( B \sqrt{a r^2+1} (b r^2+3)+A (b r^2+4)\right) \\{} & {} \quad +a \left( A^2 \sqrt{a r^2+1}+3 B^2 \sqrt{a r^2+1}+A B (4-b r^2)\right) . \end{aligned}$$

We already have the complete geometry of the seed system required to get the solution for the quasi-Einstein system (18)–(20). It can be seen that the system predominantly depends on two unknown functions which are deformation functions f(r) and g(r). So two different ways will be adopted to determine these two functions: (i) By mimicking the density constraints, i.e. \({\rho }(r)=\theta _0^0(r)\), the function g(r) will be obtained, while f(r) will be obtained by taking an EoS between \(\theta \)-sectors. These approaches are discussed in the next subsections.

3.1 Mimicking the density constraints \([\rho (r)=\theta _0^0 (r)]\) approach for determining g(r)

Using eqs (15) and (18) we obtain a differential equation of g(r) as

$$\begin{aligned} g^\prime +\frac{1}{r}\,g-\frac{(a-b)\, r\,\left( b r^2+3\right) }{\left( b r^2+1\right) ^2}=0. \end{aligned}$$
(33)

Integrating the above-mentioned differential equation leads to an equation describing the deformation function g(r) as

$$\begin{aligned} g(r)= \frac{r^2 (a-b)}{1+b r^2}+\frac{C}{r}, \end{aligned}$$
(34)

where C is an integration constant. Here, the value of the integration constant is taken to be zero. It is important to mention that mimicking the density constraints has been taken by keeping the following facts in our mind:

  1. (i)

    As the mass of the object depends on the density and when we take \(\rho (r)=\theta ^0_0\), then the gravitationally decoupled mass m(r) will become \((1+\alpha )\) times the seed mass (\(m_{\textrm{GR}}\)). In this way, we can control the mass through the decoupling constant.

  2. (ii)

    This mimicking the density constraints approach will give a first-order linear differential equation in g whose solution can be obtained easily compared to other constraints.

Now using a linear EoS relating the \(\theta \)-components will fetch another deformation function f(r), which is described in the following section.

3.2 Equation of the state (EoS) approach for determining f(r)

The following EoS relating the \(\theta \)-components will be used to obtain f(r) as

$$\begin{aligned} \theta _1^1(r) = \beta \theta _0^0(r) + \gamma , \end{aligned}$$
(35)

where \(\beta \) and \(\gamma \) are constants. (Here we would like to mention that if we involve \(\theta ^2_2\) component in the above EoS, then we will get second-order nonlinear differential equation in f(r) whose exact solution cannot be obtained.) A first-order linear differential equation will be obtained by this EoS and by solving that, the following expression for f(r) can be obtained:

$$\begin{aligned}{} & {} f(r)=\frac{1}{2 a^2 A^2} \bigg [A \Big \{-a^2 \frac{4 B}{\sqrt{a r^2+1}}+a b \Big (\frac{4 B}{\sqrt{a r^2+1}}\nonumber \\{} & {} \quad -A \gamma r^2\Big )-A b \gamma \Big \}+\ln (a r^2+1) \Big [-a (a-b) (A^2\nonumber \\{} & {} \quad +2 B^2)+a A^2 \beta (3 a-b)+A^2 \gamma (b-a)\Big ]-2 a \big [a A^2 \beta \nonumber \\{} & {} \quad \times \ln (a+a b r^2)+2 (a-b) (A-B) (A+B) \nonumber \\{} & {} \quad \times \ln (A+B \sqrt{1+a r^2})\big ]\bigg ]+F, \end{aligned}$$
(36)

where F is an arbitrary constant of integration.

$$\begin{aligned}{} & {} \theta ^0_0 (r)=-\frac{(a-b) (3+b r^2)}{\left( 1+b r^2\right) ^2},\end{aligned}$$
(37)
$$\begin{aligned}{} & {} \theta ^1_1(r)=\frac{(1+a r^2)^{-3/2}\,[\theta _{11}(r)+\theta _{12}(r)]}{ \,(1+b r^2)^2 \left( A \sqrt{a r^2+1}+a B r^2+B\right) }.\nonumber \\ \end{aligned}$$
(38)

Writing the expression of \(\theta ^2_2\) is avoided here because it is too cumbersome.

Fig. 2
figure 2

The behaviour of deformation functions g(r) (left panel) and f(r) (right panel) with respect to r/R for different values of \(\alpha \). We set the numerical values \(~a =0.0001 / \textrm{km}^2,~b = 0.0095/\textrm{km}^2,~R =10.99 \,\textrm{km}\), \(\beta =1.4\) and \(\gamma =-0.001\) for plotting these figures.

Full size image

4 Boundary condition

To determine the constants involved in the anisotropic solution, it is necessary to match the interior (\(r<R\)) and exterior (\(r>R\)) space–time at the pressure-free boundary of the star. In the current scenario, the extended geometric deformed metric represents the interior stellar space–time

$$\begin{aligned} \textrm{d}s^2= & {} - \bigg (1-\frac{2\,{m}(r)}{r}\bigg )^{-1}\textrm{d}r^2\nonumber \\{} & {} -r^2(\textrm{d}\theta ^2+\sin ^2\theta \,\textrm{d}\phi ^2)+X\textrm{e}^{\alpha \,f(r)}\,\textrm{d}t^2, \end{aligned}$$
(39)

where m(r) is the internal mass for original system (1) for anisotropic matter distribution given by eq. (23). The inner metric (39) has to be smoothly matched with the exterior metric, where isotropic fluid is non-existent (both isotropic pressure \(p^{+}\) and density \(\rho ^{+}\) vanish). As some new fields may be present in the exterior space–time (\(r>R\)) due to the \(\theta _{ij}\)-sector, the exterior space–time no longer remains vacuum in the current scenario. The general exterior space–time can be provided as

$$\begin{aligned} \textrm{d}s^2= - W^{+}(r)\textrm{d}r^2-r^2(\textrm{d}\theta ^2+\sin ^2\theta \,\textrm{d}\phi ^2)+H^{+}(r)\,\textrm{d}t^2,\nonumber \\ \end{aligned}$$
(40)

where the exact Schwarzschild solution is used to determine the gravitational potentials \( W^{+}(r)\) and \( H^{+}(r)\). To join the inner and outer geometries smoothly at the boundary \(r=R\), the well-known Israel–Darmois junction conditions [108, 109] are being used. Across the boundary \(\Sigma \), these equations are known as the continuity of the first and second fundamental forms. This is given as

$$\begin{aligned} \big [\textrm{d}s^2\big ]_{\Sigma }=0. \end{aligned}$$
(41)

By writing its explicit form, we have

$$\begin{aligned}{} & {} X(R) \textrm{e}^{\alpha \,h(R)}=H(R), ~~~ \end{aligned}$$
(42)
$$\begin{aligned}{} & {} 1-\frac{2M_{\textrm{GR}}}{R}+\alpha g(R)=\frac{1}{W(r)}, \end{aligned}$$
(43)

where at boundary \(r=R\), where \(M_{\textrm{GR}}=m_{\textrm{GR}}(R)\), f(R) and h(R) are the deformation functions. It is derived from the continuity of the second fundamental which states that the radial pressure vanishes at the boundary, i.e.,

$$\begin{aligned} {[}p_r-\alpha \,\theta ^1_1(r)]_\Sigma =0. \end{aligned}$$
(44)

Expression (40) can be expressed in its final form as

$$\begin{aligned} p_r(R)-\alpha \,(\theta ^1_1)^{-}(R)=-\alpha \,(\theta ^1_1)^{+}(R), \end{aligned}$$
(45)

where \(p_r(R)=p_r^{-}(R)\). Equation (45) is also known as the second fundamental form linked with Einstein’s field equations as referred to in eqs (5)–(7). Now, if the extra contribution is assumed to be confined within the compact object itself, then the corresponding second fundamental form (45) can be expressed as (refer to [77] for more information),

$$\begin{aligned} p_r(R)+\alpha \,\bigg [-\frac{g }{8\pi }\Bigg (\frac{1}{r^2}+\frac{X'}{Xr}\Bigg ) -\frac{Yf'}{r}\bigg ]_{r=R} =0. \end{aligned}$$
(46)

For finding the arbitrary constants involved in the system, conditions (42)–(44) are necessary and sufficient. Using the boundary conditions, we find the expression for the constants

$$\begin{aligned}{} & {} \frac{A}{B}=\frac{A_1(R)+A_2(R)+A_3(R)+A_4(R)}{\left( a R^2+1\right) [A_5(R)+A_6(R)]}, \end{aligned}$$
(47)
$$\begin{aligned}{} & {} B=\frac{(b R^2+1)^{-1/2}\,\sqrt{a (\alpha +1) R^2-b \alpha R^2+1}}{ \sqrt{\left( 2 \text {A1} \sqrt{a R^2+1}+a R^2+\text {A1}^2+1\right) \textrm{e}^{\frac{1}{2} \alpha \,B_1(R) }}},\nonumber \\ \end{aligned}$$
(48)
$$\begin{aligned}{} & {} M=\frac{(1+\alpha ) R^3 (b-a)}{2 b R^2+2}. \end{aligned}$$
(49)

5 Physical analysis

In this section, we discuss the physical analysis of the solution to check the physical viability of the solution. Before starting the analysis, we would like to highlight some other important points for deformation functions and decoupling constant \(\alpha \) [110], which are as follows:

5.1 Case I: For \(\alpha >0\)

  1. 1.

    If \(g(r)\ge 0\), \(f(r)\ge 0\) and for all \(r\in [0,R]\), both are increasing, then the deformed metric functions \(W(r)>0\), \(H(r)>0\) and mass function \(m(r)>0\) also increase if the growth of Y(r) is more than g(r).

  2. 2.

    If \(g(r)\le 0\), \(f(r)\le 0\) and for all \(r\in [0,R]\), both are decreasing, then the deformed metric function \(W(r)>0\), \(H(r)>0\) and mass function \(m(r)>0\) will increase when the growth of X(r) is more than f(r).

  3. 3.

    If \(g(r)\le 0\), \(f(r)\ge 0\) for all \(r\in [0,R]\) then the deformed metric functions \(W(r)>0\), \(H(r)>0\) and mass function \(m(r)>0\) will increase automatically.

  4. 4.

    If \(g(r)\ge 0\), \(f(r)\le 0\) for all \(r\in [0,R]\), then the growth of Y(r) and X(r) must be respectively faster than deformation functions g(r) and f(r), to maintain the increasing behaviour and positiveness of the deformed metric functions W(r), H(r) and the mass function m(r).

Fig. 3
figure 3

Top panels show the energy density [ (\(\epsilon \times 10^{4}\))] and radial pressure (\(P_r\times 10^4\))], while the bottom panels describe tangential pressure (\(P_\perp \times 10^4\)) and anisotropy (\(\Delta \times 10^4\)) with respect to r/R for different values of \(\alpha \). We set the numerical values \(~a =0.0001 /\textrm{km}^2,~b = 0.0095/\textrm{km}^2,~R =10.99 \,\textrm{km}\), \(\beta =1.4\) and \(\gamma =-0.001\) for plotting these figures.

Full size image

5.2 Case II: For \(\alpha <0\)

  1. 1.

    For non-negative and increasing g(r) and f(r), \(\forall \) \(r\in [0,R]\), the deformed metric functions W(r), H(r) and the mass function m(r) will be positive and increasing, when the growth of X(r) is more than f(r).

  2. 2.

    If g(r) and f(r) are non-positive and decreasing for all \(r\in [0,R],\) then growth of Y(r) must be higher than g(r) to preserve the increasing and positive behaviour of W(r), H(r) and the mass function m(r).

  3. 3.

    If \(g(r)\le 0\) and \(f(r)\ge 0\), \(\forall \) \(r\in [0,R]\) then the deformed metric function W(r), H(r) and the mass function m(r) will be positive and increasing, if the growth of Y(r) and X(r) are higher than g(r) and f(r), respectively.

  4. 4.

    If \(g(r)\ge 0\) and \(f(r)\le 0\), \(\forall \) \(r\in [0,R]\), then it yields positive and increasing behaviour of W(r), H(r) and m(r), automatically.

In our case, the deformation function g(r) is negative and f(r) is positive for \(\alpha \ge 0\). Then from the above discussion, the deformed metric functions \(W(r)>0\), \(H(r)>0\) and mass function \(m(r)>0\) will also show a monotonic increasing behaviour automatically for all \(r\in [0,R]\).

5.3 Physical behaviour of energy density, radial pressure, tangential pressure and anisotropic factor

All the physical analyses have been done for the compact star PSR J1416-2230 having \(1.97 \pm 0.04\) \(M_\odot \) mass. From figure 2 (left panel), it can be seen that the deformation function \(g(r)=0\) at the centre and as one moves towards the surface, it becomes negative and its magnitude initially increases slowly and steeply afterwards. Moreover, it can be seen that the curves of g(r) are not affected by \(\alpha \) whatsoever. Figure 2 (right panel) indicates that the deformation function varies very slightly as one moves from the centre towards the surface and has its maximum value at the centre and minimum value as it approaches the surface. Also, it can be seen that the value of \(\alpha \) affects f(r) significantly, as it is inversely proportional to the magnitude of \(\alpha \). Now, while studying the energy density \(\epsilon (r)\), from figure 3 (top left panel), we observe that it is maximum at the centre and then starts to decrease as one moves outwards. Also, it can be seen that the energy density is directly proportional to the value of \(\alpha \). Now, while studying the nature of variation of the radial pressure \(P_r(r)\), we see from figure 3 (top right panel) that it is maximum at the centre and monotonically decreases as one goes outwards. Also, one can see the interesting feature that the radial pressure is directly proportional to \(\alpha \) and the influence of \(\alpha \) is maximum at the centre and all the curves of the radial pressure for different values of \(\alpha \) converge at the surface. While looking into the tangential pressure \(P_\perp \), we can see from figure 3 (bottom left panel) that like the radial pressure, \(P_\perp \) also attains its maximum value at the centre and monotonically decreases towards the surface. Moreover, the tangential pressure is also directly proportional to the value of \(\alpha \) and at the centre, the influence is maximum and near the surface, the curves for different values of \(\alpha \) tend to converge, but unlike the radial pressure, they do not actually converge. The anisotropic factor \(\Delta (r)\) is zero at the centre as we can see from figure 3 (bottom right panel) and it gradually increases as one moves outwards. Moreover, the anisotropy is directly proportional to \(\alpha \) towards the surface and the influence of \(\alpha \) decreases as one moves inwards towards the centre and becomes negligible at the centre as all the curves of the anisotropic factor converge to zero at the centre.

Fig. 4
figure 4

The behaviour of energy conditions \([(\epsilon -P_r)\times 10^4]\), \([(\epsilon -P_t)\times 10^4]\) and \([(\epsilon -P_r-2P_t)\times 10^4]\) with respect to r/R for different values of \(\alpha \). We set the same numerical values for constant parameters as in figure 3.

Full size image

5.4 Energy conditions

The energy conditions with regard to the classical relativistic gravitational field theories are discussed in this subsection. Briefly speaking, these energy conditions are certain relations between matter density and pressure. Several energy conditions have been studied and analysed by various researchers including the censorship theorem [111, 112], positive mass theorem [113], singularity theorems [114] and so on, but the most prominent ones are (i) the null energy condition (NEC), (ii) the weak energy condition (WEC), (iii) the strong energy condition (SEC), (iv) the dominant energy condition (DEC) and (v) the trace energy condition (TEC).

$$\begin{aligned}{} & {} \text {NEC}:~~ \epsilon \ge 0, \end{aligned}$$
(50)
$$\begin{aligned}{} & {} \text {WEC} : ~~\epsilon +P_r \ge 0, ~~~ \epsilon +P_\perp \ge 0,\end{aligned}$$
(51)
$$\begin{aligned}{} & {} \text {SEC}:~~\epsilon +P_r+2\,P_\perp \ge 0,~~~~~ \end{aligned}$$
(52)
$$\begin{aligned}{} & {} \text {DEC}:~~ \epsilon -P_r\ge 0,~~~\epsilon -P_\perp \ge 0,~~~ \end{aligned}$$
(53)
$$\begin{aligned}{} & {} \text {TEC}:~~ \epsilon -P_r-2P_\perp \ge 0. \end{aligned}$$
(54)

It can be clearly seen that \(\epsilon \), \(P_r\), \(P_\perp \) are positive in each point within the model, implying that inequalities (50)–(52) are automatically satisfied. From figure 4 it can be seen that all \(\epsilon -P_r\) , \(\epsilon -P_\perp \), \(\epsilon -P_r-2P_\perp \) remain positive everywhere throughout the model, indicating that inequalities (53) and (54) are also satisfied. So it can be concluded that all the energy conditions are satisfied everywhere within the stellar model.

Fig. 5
figure 5

The behaviour of adiabatic index \(\Gamma _r\) with respect to r/R for different values of \(\alpha \). We set the same numerical values for constant parameters as used in figure 3.

Full size image
Table 1 Numerical values of physical quantities, such as central density, surface density, central pressure, mass-radius ratio (M/R), critical value of adiabatic index (\(\Gamma _{\textrm{crit}}\)), central value of adiabatic index (\(\Gamma _{r0}\)), and surface redshift (\(Z_s\)) for different values of a.
Full size table

5.5 Stability via adiabatic index

To analyse the stability of a system, the radial component of the adiabatic index (\(\Gamma \)) plays an important role, especially when the system becomes anisotropic, as its spherically symmetric form gets changed to avoid gravitational collapse. The condition for the collapse of isotropic and non-relativistic fluid distribution is given as \(\Gamma < 4/3\) [115, 116].

If the relativistic condition is considered, the condition becomes [117, 118],

$$\begin{aligned} \Gamma < \frac{4}{3} + \bigg [\frac{1}{3} \kappa \frac{\rho _0 p_{r0}}{|p^\prime _{r0}|} + \frac{4}{3} \frac{p_{t0}-p_{r0}}{|p^\prime _{r0}| r} \bigg ]_{\textrm{max}}. \end{aligned}$$
(55)

Here, the second term on the right-hand side takes care of the relativistic correction, whereas the third term incorporates anisotropy and both of them vanish if the isotropic, non-relativistic case is considered. Also, the increase in anisotropy slows down the rise in instability [115] and the stability condition is modified to the form of \(\Gamma > 4/3\) by the anisotropic factor (\(\Delta =P_\perp -P_r\)). It must also be noted that considering the relativistic correction for the adiabatic index may also lead to instabilities inside the compact object [119, 120]. To address this, another strict condition was imposed by Moustakidis [121] where the concept of a critical value of the adiabatic index (\(\Gamma _{\textrm{crit}}\)) was introduced, which depends on the Lagrangian displacement amplitude (\(\xi \)) and compactness factor. \(\Gamma _{\textrm{crit}}\) is defined as

$$\begin{aligned} \Gamma _{\textrm{crit}} = \frac{4}{3} + \frac{19 M}{21 R}. \end{aligned}$$
(56)

So, in this context, the condition \(\Gamma \ge \Gamma _{\textrm{crit}}\) must be fulfilled. The adiabatic index can be obtained from the expression

$$\begin{aligned} \Gamma = \frac{\epsilon + P_r}{P_r} \frac{\textrm{d}P_r}{\textrm{d} \epsilon }. \end{aligned}$$
(57)

From figure 5 we see the nature of the adiabatic index \(\Gamma _r\) and it can be seen that it has a non-zero minimum at the centre and as one moves outwards, it tends to increase slowly initially and then towards the surface, it increases sharply. The \(\Gamma _r > 4/3\) condition is maintained everywhere. Moreover, the magnitude of the central values of \(\Gamma _r\) is increasing with \(\alpha \). From table 1, it is seen that the condition \(\Gamma _{\textrm{crit}} > \Gamma _{r0}\) is being satisfied for \(\alpha =0.20\). So, it can be concluded that the current gravitational decoupling approach is more suitable for modelling a stable compact star model than for modelling in a pure GR scenario.

5.6 Causality

The stability with regard to the velocity of sound within the stellar models is discussed in this section. For any stellar model to be physically acceptable, the velocity of sound must not exceed the velocity of light at any point within the stellar model. This basically means that the radial and tangential sound velocity components (\(v^2_r\) and \(v^2_t\)) must lie within [0, 1]. This is known as the causality condition. From figure 6 it is seen that both \(v_r^2\) and \(v_t^2\) lie well within the range \(0 \le v_r^2 \le 1\) and \(0 \le v_t^2 \le 1\) which signifies that the causality condition is satisfied everywhere within the stellar model. Moreover, while studying the nature of the \(v_r^2\) curve, from figure 6 (left panel), it is seen that it initially increases and then attains a maximum value closer to the surface and then slowly decreases. Moreover, the variation in \(v_r^2\) is directly proportional to the variation in \(\alpha \). Looking into the nature of variation of \(v_t^2\), from figure 6 (right panel) it can be seen that the curves slowly increase, but at different rates as one moves from the centre to the surface and the nature of variation is directly proportional to the value of \(\alpha \). Moreover, the curve of \(v_t^2\) for \(\alpha = 0.20\) shows a little different behaviour from the other curves for different values of \(\alpha \).

Fig. 6
figure 6

The radial velocity (\(v^2_r\)) (left panel) and tangential velocity (\(v^2_t\)) (right panel) with respect to r/R for different values of \(\alpha \). We set the numerical values \(a =0.0001/\)km\(^2\), \(b = 0.0095/\)km\(^2\), \(R =\)11.5  km, \(\beta =1.4\) and \(\gamma =-0.001\) for plotting the figures.

Full size image

5.7 Stability via cracking

Now, the stability of the solution will be checked using the criterion given by Herrera [122] and Abreu et al [123]. The concept behind this is to check the stability of the system under cracking instability using the subliminal tangential and radial velocity components of sound. When anisotropy is present in self-gravitating systems, the cracking method becomes a useful way to investigate instability. As Abreu et al described, the cracking concept can be expressed in terms of the perturbation magnitude of density (\(|\delta \epsilon |\)), anisotropy (\(|\delta \Delta |\)) and their ratio \(\left| {\delta \Delta }/{\delta \epsilon }\right| \) as

$$\begin{aligned} \left| \frac{\delta \Delta }{\delta \epsilon }\right|\simeq & {} \left| \frac{\delta \left( P_\perp -P_r \right) }{\delta \epsilon }\right| \simeq \left| \frac{\delta P_\perp }{\delta \epsilon }-\frac{\delta P_r}{\delta \epsilon }\right| \nonumber \\ {}\simeq & {} \left| v^{2}_{t}-v^{2}_r\right| . \end{aligned}$$
(58)

Since it is already shown in the previous subsection that the causality conditions are well satisfied within the model, we have \(0\le v^{2}_{r}\le 1\) and \(0\le v^{2}_{t}\le 1\). But in addition to that, another condition should also be applied, such as the perturbation magnitude of anisotropy must never exceed that of density, i.e. \(|\delta \Delta | \le |\delta \epsilon |\) \(\Longrightarrow \) \(|v^{2}_{t}-v^{2}_{r}|\le 1\). Also, an unstable region is found for \(\left| {\delta {\Delta }}/{\delta {\epsilon }}\right| >0\). So, the stable and unstable regions can be distinguished by the following relation:

$$\begin{aligned} 0\le |v^{2}_{t}-v^{2}_{r}|\le 1 = \left\{ \begin{array}{ll} -1\le v^{2}_{t}-v^{2}_{r}\le 0 \\ 0< v^{2}_{t}-v^{2}_{r}\le 1 \end{array}. \right. ~~~~ \end{aligned}$$
(59)

So, the region \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\) is a stable region and \(0< v^{2}_{t}-v^{2}_{r}\le 1\) provides an unstable region. However, if there is no sign change for \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\), then this also falls in the stable region. From figure 7 it is seen that the quantity \(v^{2}_{r}-v^{2}_{t}\) always lies within the range [0,1]. So it can be said that \(v^{2}_{t}-v^{2}_{r}\) lies within the range [\(-1,0\)]. So the model always stays within the stable region of \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\). Hence, it is inferred that the system is completely stable everywhere. While observing the nature of variation of the \(v_r^2-v_t^2\) curves, it is seen that for \(\alpha =0, 0.05, 0.10\) the magnitude of \(v_r^2-v_t^2\) steadily decreases as one moves from the centre to the surface and after a certain point, the rate of decrease enhances near the surface. However, for \(\alpha = 0.15, 0.20\) it is seen that the curves behave somewhat irregular near the center, as their magnitudes sometimes slightly increase, sometimes decrease, and then attain a peak and after that steadily decrease near the surface. Also, the variation of \(v_r^2-v_t^2\) is directly proportional to the variation of \(\alpha \) barring the \(\alpha =0.20\) curve, where initially, the curve starts off from a much lower value than the expected pattern.

Fig. 7
figure 7

The behaviour of stability factor \((v^2_r-v^2_t)\) with respect to r/R is shown for different values of \(\alpha \). The same numerical values for constant parameters have been used as in figure 3.

Full size image

5.8 Hydrostatic equilibrium via modified TOV equation

The hydrostatic equilibrium through the modified Tolman–Oppenheimer–Volkoff (TOV) equation is a very important aspect to study any stellar model. The general form of the modified TOV equation is given as

$$\begin{aligned}{} & {} -\frac{\textrm{d}{p}_r}{\textrm{d}r}-\frac{m_{\textrm{GR}}+4\pi p_r r^3}{r(r-2m)} ({\rho }+{p}_r)+\frac{2({p}_t-{p}_r)}{r}\nonumber \\{} & {} \quad +\alpha \Big [\frac{m+4\pi P_r r^3}{r(r-2m)} (\theta _1^1 -\theta _0^0)+\frac{\textrm{d}\theta _1^1}{\textrm{d}r}-\frac{2}{r}(\theta _2^2 -\theta _1^1)\nonumber \\{} & {} \quad -\frac{f^\prime \,(p_r+\rho )}{2}\Big ]=0. \end{aligned}$$
(60)

It is noted that if \(\alpha =0,\) i.e. in the absence of gravitational decoupling, the above conservation equation (60) reduces into a standard Tolman–Oppenheimer–Volkoff (TOV) equation in GR for charged matter distribution. To satisfy this conservation equation (60), we spilt this TOV equation into different forces like \(F^{\text {eff}}_{h}\), \(F^{\text {eff}}_{g}\), \(F^{\text {eff}}_{a}\) and \(F^{\text {eff}}_{e}\) such that \(F^{\text {eff}}_{h}+F^{\text {eff}}_{g}+F^{\text {eff}}_{a}=0\), where

$$\begin{aligned}{} & {} F^{\text {eff}}_{h}=- p_r^\prime +\alpha \,({\theta _{1}^{1}})^\prime , \end{aligned}$$
(61)
$$\begin{aligned}{} & {} F^{\text {eff}}_{g}=-\frac{m_{\textrm{GR}}+4\pi p_r r^3}{r(r-2m)}(\rho +p_r)\nonumber \\{} & {} \quad -\alpha \frac{m+4\pi P_r r^3}{r(r-2m)}({\theta _{0}^ {0}}~-{\theta _{1}^{1}})-\frac{\alpha \,h^\prime }{2}(p_r+\rho ),~~~~ \end{aligned}$$
(62)
$$\begin{aligned}{} & {} F^{\text {eff}}_{a} =\frac{2({p}_t-{p}_r)}{r} -\frac{2\alpha }{r}~({\theta _{2}^ {2}}-{\theta _{1}^{1}}). \end{aligned}$$
(63)

When all three forces add up to be zero, then the system is said to be in hydrostatic equilibrium. From figure 8 it is seen that the gravitational force \((F^{\text {eff}}_g\)) is negative, while the anisotropic and hydrostatic forces (\(F^{\text {eff}}_a\) and \(F^{\text {eff}}_g,\) respectively) are positive throughout. All three forces are zero at the centre and their magnitudes increase as one moves outwards and after attaining a peak, they steadily decrease. Also, the magnitudes of the forces are directly proportional to the value of \(\alpha \). Moreover, it must also be noted that the strong, negative (i.e. attractive) gravitational force \((F^{\text {eff}}_g\)) is balanced by the positive (i.e. repulsive) anisotropic force (\(F^{\text {eff}}_a\)) and hydrostatic force (\(F^{\text {eff}}_a\)) to maintain the hydrostatic balance. So, for all values of \(\alpha \), all three forces add up to be zero and thus it can be said that the hydrostatic balance is maintained throughout the model.

Fig. 8
figure 8

The behaviour of different forces \((F_g\) – black curves, \(F_h\) – green curves and \(F_a\) – magenta curves) with respect to r/R for different values of \(\beta \). We set the same numerical values for constant parameters as used in figure 3.

Full size image

5.9 Compactness (mass–radius) relation and surface gravitational red-shift

An essential component for studying any stable self-gravitating compact stellar model is to study the compactness (mass–radius ratio). Moreover, to determine the upper limit of the surface red-shift of the compact stars, the effective mass–radius ratio plays a pivotal role.

  • The following formula can be used to determine the effective mass in GR for perfect fluid or uncharged anisotropic matter distribution,

    $$\begin{aligned}{}[M_{\textrm{GR}}]_{\text {eff}}= & {} 4\pi \int ^{R}_{0}r^{2}\rho (r)\textrm{d}r\nonumber \\ {}= & {} \frac{R}{2}\left[ 1-Y(R) \right] =M_{\textrm{GR}}, \end{aligned}$$
    (64)

where \(M_{\textrm{GR}}\) is the total mass of the compact star having a radius of R with the matter distribution being anisotropic when gravitational decoupling is absent. When gravitational decoupling is present, the total mass \(M_{\textrm{GR}}\) can be expressed as

$$\begin{aligned} M= & {} M_{\textrm{GR}}-\frac{\alpha R}{2}g(R) =4\pi \int ^{R}_{0}r^{2}\epsilon (r)\textrm{d}r\nonumber \\= & {} \frac{R}{2}\left[ 1-\frac{1}{W(R)} \right] . \end{aligned}$$

Then the effective mass under gravitational decoupling can be given as

$$\begin{aligned}{} & {} M_{\text {eff}} =[M_{\textrm{GR}}]_{\text {eff}}-\frac{\alpha \,R}{2}\,g(R). \end{aligned}$$
(65)

In this context, Buchdahl [26] proposed the maximum allowable mass–radius ratio for isotropic uncharged fluid distribution, considering the decreasing density as

$$\begin{aligned} \frac{M_{\textrm{GR}}}{R}\le \frac{4}{9}. \end{aligned}$$

It is worth mentioning that the total mass gets affected by the gravitational decoupling as well. For a fixed radius R, the condition \(M\ge M_{\textrm{GR}}\) will always hold true, as g(r) remains negative throughout the star. The mass–radius ratio for 13 compact star models under the gravitational decoupling is obtained for different values of the decoupling constant \(\alpha \) as mentioned in table 3. As can be seen from this table, the mass–radius ratio increases when \(\alpha \) increases which implies that we get more compact objects when we introduce the gravitational decoupling in the self-gravitating system. On the other hand, the mass–radius ratio for each object did not go beyond the Buchdahl limit. Moreover, the following formula can be used to calculate the surface red-shift \(Z_s\) for compact stars:

$$\begin{aligned} \text {Z}_s=\left( 1-2u\right) ^{-1/2}-1, \end{aligned}$$
(66)

where

$$\begin{aligned} u\equiv \frac{{{M}}_{\text {eff}}}{R}=\frac{{[{M}_{\textrm{GR}}]}_{\text {eff}}}{R}-\frac{\alpha \,R}{2}\,g(R). \end{aligned}$$
Fig. 9
figure 9

The behaviour of gravitational red-shift Z with respect to r/R for different values of \(\alpha \). We set the same numerical values for constant parameters as used in figure 3.

Full size image
Table 2 Predicted radii R for different compact stars.
Full size table
Table 3 Mass–radius ratio (M/R) for different compact stars.
Full size table

6 Concluding remarks

In this paper, a new solution has been obtained for self-gravitating systems having anisotropic matter distribution. Using the complete geometric deformation, i.e., considering both radial and temporal deformation, the highly non-linear field equations could be split into two subsystems, Einstein’s system in the anisotropic framework and the quasi-Einstein’s system containing the deformation functions. Then, the embedding Class-I condition was used to find the relationship between the metric potentials to solve Einstein’s system in the anisotropic framework. To solve the second system or the quasi-Einstein’s system, the density constraints \([{\rho }(r)=\theta _0^0 (r)]\) were mimicked to obtain g(r). Then, a linear equation of state (EoS) relating the \(\theta \) components was used to find a first-order differential equation and it was solved to obtain another deformation function f(r). Thus, the system was solved. Due to the anisotropic distribution, matching the exterior and interior boundaries is important and well-recognised Israel–Darmois junction conditions were used to smoothly join the inner and outer geometries at the boundary \(r=R\). The physical behaviour of various thermodynamic parameters and along with it, energy conditions and stability analysis were studied afterwards to check the viability of the model. The compact star PSR J1416-2230 having \(1.97 \pm 0.04 M_\odot \) mass was considered for the analysis. It was seen in figure  2 (left panel) that the deformation function g(r) remains negative throughout the model and does not get affected by \(\alpha \) at all, whereas, from figure  2 (right panel) it is seen that the deformation function f(r) remains positive throughout and is significantly affected by the variation in \(\alpha \). Both radial (\(P_r\)) and tangential (\(P_\perp \)) pressures have their maxima at the centre which monotonically decrease as one moves outwards, as can be seen from figure 3 and variation in \(\alpha \) affects both the radial and tangential pressure in a directly proportional manner. The anisotropic factor \(\Delta \) is zero at the centre and keeps on increasing as one moves towards the surface as can be seen from figure 3 (bottom right panel). This means that, at the core, the matter distribution is predominantly isotropic and anisotropy grows as one moves outwards. Moreover, \(\alpha \) affects the anisotropy in a directly proportional manner. The study of energy density \(\epsilon (r)\) showed that it has its maximum value at the centre and decreases as one move towards the surface and it varies with \(\alpha \) in a directly proportional manner, as seen in figure 3 (top left panel). While analysing the energy conditions, it was seen that all the energy conditions such as NEC, WEC, SEC, DEC and TEC are satisfied everywhere within the stellar model as can be seen from figure  4. Looking into the stability via the adiabatic index, from figure  5 it was seen that the condition for stability, i.e. \(\Gamma > 4/3,\) is satisfied everywhere and from table 1 it is seen that for \(\alpha =0.20\), the condition \(\Gamma _{\textrm{crit}} > \Gamma _{r0}\) is fulfilled. This shows that the model is stable for higher values of the decoupling constant, implying that the gravitational decoupling approach is a powerful technique to investigate a stable model. Studying the causality condition, it has been found that the velocity of sound never exceeds the speed of light, which can be verified from figure  6. This assures that the causality condition is maintained everywhere in the model. The stability of the solution in terms of the cracking instability was checked and it was found that the model always stays within the stable range of \(-1\le v^{2}_{t}-v^{2}_{r}\le 0\) as can be seen in figure  7. The geometric deformation approach can affect the hydrostatic balance of the system also. Therefore, the hydrostatic equilibrium in terms of the modified TOV equation is also checked and it is seen in figure  8, that the negative or attractive gravitational force \((F^{\text {eff}}_g\)) is balanced by the positive and repulsive anisotropic force (\(F^{\text {eff}}_a\)) and hydrostatic force (\(F^{\text {eff}}_a\)) and thus the hydrostatic equilibrium is maintained and also it can be seen that all three forces combine to cancel each other, i.e. \(F^{\text {eff}}_{h}+F^{\text {eff}}_{g}+F^{\text {eff}}_{a}=0\). The effect of gravitational decoupling on the original mass is also analysed in this paper. For this, the total gravitationally decoupled mass (M) is taken as the combination of two separate mass components, which are the GR mass function (\(M_{\textrm{GR}}\)) and the mass component coming from the gravitational decoupling (\(M_{\textrm{EGD}}\)). Thus, how the original mass (\(M_{\textrm{GR}}\)) is modified due to the extra component of \(M_{\textrm{EGD}}\) can be easily probed. The expression for the total mass after gravitational decoupling is \(M_{\textrm{GR}}-\frac{\alpha R}{2} g(R)\). It can be clearly seen that the factor \(-\frac{\alpha R}{2} g(R)\) will be positive for all values for \(r > 0\) as g(R) is negative. Therefore, it can be concluded that this extra factor will enhance the total mass (M) of the stellar model. In this connection, it is well-known that the massive object warps and curves space–time, while the gravitational field is basically the result of the curving of space–time. This implies that more massive objects create a stronger gravitational field around the objects. Furthermore, gravitational time dilation also happens due to objects with a lot of mass that produce a strong gravitational field (i.e. stronger gravity). Then, it is clear that the introduction of CGD approach in the self-gravitating model may help us to understand the reason for the stronger gravitational field around the black hole, i.e. stronger gravity.

From tables 2 and 3, it is found that with the increase in the value of \(\alpha \), the radius decreases, and subsequently, the mass–radius ratio increases. Moreover, it is also seen that the mass–radius ratio is higher for heavier compact stars. From figure 9 it is seen that the gravitational red-shift has its maximum value at the centre and it decreases as one moves towards the surface and is affected by \(\alpha \) in a directly proportional manner. On the other hand, the expected gravitational red-shift for static spherically symmetric perfect fluid distribution can reach up to 2, i.e. \(z_s\le 2\) [26, 133], while this value can be high as \({\le }3.84\) [134, 135] for the anisotropic case and it can go on up to 5 and 5.211 as studied by Böhmer-Harko [136] and Ivanov [137], respectively. In our study, we found that the gravitational surface red-shift of the star PSR J1614-2230 as mentioned in table 1 for different values of \(\alpha \) is less than 2, i.e. \(Z_s\le 2\) which is physically acceptable.