1 Introduction

The amplitude and phase time-dependent functions of a vibrating object cannot be arbitrarily set: A real potential function leading to an oscillation of the form \(\rho \left( t\right) \cos \left( \varphi \left( t\right) \right) \) is physically attainable, if and only if the product \(\rho ^{2}\left( t\right) \dot{\varphi }\left( t\right) \) is constant [1]. This constant is the orthogonal functions invariant [2], closely related to a family of exact invariants. From this group, the Ermakov invariant is found to be quite useful in various classical and quantum mechanical problems [3,4,5,6,7]. It is also encountered in electromagnetic propagation in stratified media and photonic crystals [8,9,10,11]. The Ermakov invariant has been associated with the corresponding Noether and Lie symmetries [12]. A historical account is given in [13]. The so-called ‘exact’ invariants, such as, the Ermakov invariant [5, 14] have led to a renewed interest in mechanical systems with time-varying parameters [15]. In contrast with the adiabatic theory, where adiabatic invariants only hold in the slowly varying limit, exact invariants are constant even if the variation of the time-dependent parameters is arbitrarily fast compared to the characteristic period of the system. A convincing physical interpretation of the Ermakov invariant has not been put forward. If an auxiliary orthogonal axis is added to the one-dimensional motion, the invariant can be viewed as angular momentum conservation in a higher-dimensional space [16]. If the coordinate variable of the oscillator x is transformed \(x\rightarrow \rho y\), where \(\rho \) is the amplitude function, the energy of the y oscillator becomes the Ermakov–Lewis invariant [17, 18]. These possible interpretations are very interesting and each has its own merits. However, the former interpretation requires an auxiliary dimension while the latter shifts the problem to understand the physical nature of the transformation.

The formulation of complementary variable provides a set of invariants for non-autonomous second-order differential equations. These invariants are bilinear combinations of the complementary variables or their derivatives. Similar invariants have been obtained in several ways, depending on the context and the mathematical tools employed [19,20,21,22,23,24]. The invariants are labelled here as \(Q_{mn}\), where the subindices indicate the order of the derivative in each complementary variable. For example, \(Q_{10}\) implies that v is a first-order derivative of the ODE solution and x a zeroth-order derivative solution. If a former invariant is evaluated in different circumstances when it is no longer constant, the variable is written in lower case Latin letter, i.e. \(q_{10}\). The \(Q_{10}\) invariant has been shown to represent the energy content of a system including the energy stored in the field even if the force acting on the system is time-dependent [23]. For a linear force, in the absence of a time-varying field, \(\frac{1}{2}mQ_{10}\) is identical to the familiar sum of kinetic and potential energies. The zeroth-order \(Q_{00}\) invariant is equal to the Wronskian of two linearly independent solutions. In a coordinate-amplitude representation, the square of \(Q_{00}\) is proportional to the Ermakov–Lewis invariant [25]. A simple derivation of this relationship is presented in §2.

In this communication, the zeroth- and first-order invariants are obtained for an oscillator with friction. Inclusion of damping provides the appropriate scenario to elucidate the nature of the invariants. The physical meaning of the \(Q_{00}\) zeroth-order invariant, according to the present results and interpretation, is a measure of the periodic energy exchange between the two complementary forms of energy. The first-order \(Q_{10}\) invariant will be shown to be the total energy of the system including the dissipation term. This approach gives an alternative route to the evaluation of the oscillator’s energy loss. The structure of the manuscript is the following: In §2, the invariants in the undamped case are recalled. In §3, the \(Q_{00}\) and \(Q_{10}\) invariants are assessed with a damping coefficient linear in the velocity but with arbitrary time dependence. The differences of evaluating the \(Q_{00}\) invariant in the real or complex domain are discussed. In §4, the invariants are evaluated using the analytic solutions of the oscillator with constant damping. The origin of the energy ripples superimposed on the exponential decay is addressed. In §5, the amplitude and phase nonlinear differential equations with damping are derived. The results are discussed in the last section.

2 Time-dependent harmonic oscillator invariants

The time-dependent harmonic oscillator equation is a non-autonomous second-order ordinary differential equation

$$\begin{aligned} \ddot{x}+\Omega ^{2}x=0, \end{aligned}$$
(1)

where \(\Omega ^{2}\left( t\right) \) is the time-dependent parameter and the overdots represent derivatives with respect to time. The zeroth-order invariant to this equation is [26]

$$\begin{aligned} Q_{00}=\left( x_{2}\dot{x}_{1}-\dot{x}_{2}x_{1}\right) , \end{aligned}$$
(2a)

where \(x_{1}\) and \(x_{2}\) are linearly-independent solutions to (1). The above expression may be written as

$$\begin{aligned} Q_{00}=x_{2}^{2}\frac{\textrm{d}}{\textrm{d}t}\left( \frac{x_{1}}{x_{2}}\right) =-x_{1}^{2}\frac{\textrm{d}}{\textrm{d}t}\left( \frac{x_{2}}{x_{1}}\right) . \end{aligned}$$
(2b)

The linear independence of \(x_{1}\) and \(x_{2}\), in order to have a non-vanishing invariant, is clear from these expressions. By convention, the linearly independent solutions are chosen so that \(Q_{00}\) is positive in the undamped case, in particular, for positive constants \(a,\omega \), \(x_{1}=a\sin \left( \omega t\right) \), \(x_{2}=a\cos \left( \omega t\right) \). Recall that these solutions are not linearly independent in the complex domain, since \(x_{1}=ia\textrm{e}^{-i\omega t}=ix_{2}\), for \(x_{2}=a\textrm{e}^{-i\omega t}\). If the differential equation is solved in the complex domain \(\psi \in \mathbb {C}\), the \(Q_{00}\) invariant can be defined in terms of complex conjugate solutions

$$\begin{aligned} Q_{00}^{\mathbb {C}}=\frac{1}{2i}(\psi \dot{\psi }^{*}-\psi ^{*}\dot{\psi })=\rho ^{2}\dot{\varphi }=\rho ^{2}\omega . \end{aligned}$$
(2c)

This result is of course equally obtained if \(x_{1},x_{2}\) are requested to be complex conjugates in (2a). The last equalities in (2c) are written in terms of the amplitude \(\rho \) and phase \(\varphi \), that follow from the polar representation of \(\psi =\rho \textrm{e}^{-i\varphi }\); the angular frequency is defined as the derivative of the phase, \(\dot{\varphi }\equiv \omega \left( t\right) \). From (2c), the phase can be obtained from the amplitude function, since

$$\begin{aligned} \varphi =Q_{00}\int \frac{\textrm{d}t}{\rho ^{2}}. \end{aligned}$$

If and only if \(\Omega ^{2}\) is constant, \(\omega =\Omega \), as will be clear from the frequency differential equation discussed in §5. The Schrödinger convention is followed with the negative sign in the exponential shown explicitly. If \(x_{1}\) and \(x_{2}\) are expressible in terms of trigonometric functions with real arguments, i.e. \(x_{1}\mapsto \rho \sin \varphi \text { and }x_{2}\mapsto \rho \cos \varphi ,\) the \(Q_{00}\) invariant given by (2a) is also equal to \(\rho ^{2}\dot{\varphi }.\)

The Ermakov–Lewis invariant is usually written as

$$\begin{aligned} \mathcal {I}^{\text {Ermakov}}=\frac{1}{2}\left( h\frac{x^{2}}{\rho ^{2}}+\left( x\dot{\rho }-\rho \dot{x}\right) ^{2}\right) \end{aligned}$$

with h usually set equal to one [16, 27]. This is a ‘mixed’ representation in terms of position and amplitude variables [25]. It is readily obtained from (2a), writing the solution \(x_{1}\), in terms of \(x_{2}\) (or vice versa) and the amplitude \(\rho \) from \(x_{1}^{2}+x_{2}^{2}=\rho ^{2}\). The invariant is then

$$\begin{aligned} Q_{00}=\frac{\rho }{\sqrt{\rho ^{2}-x_{2}^{2}}}\left( x_{2}\dot{\rho }-\rho \dot{x}_{2}\right) . \end{aligned}$$

Upon multiplication by the root and squaring of the resulting equation, the usual form of the Ermakov–Lewis invariant is obtained,

$$\begin{aligned} \mathcal {I}^{\text {Ermakov}}=\frac{1}{2}Q_{00}^{2}=\frac{1}{2}\left( Q_{00}^{2}\frac{x^{2}}{\rho ^{2}}+\left( x\dot{\rho }-\rho \dot{x}\right) ^{2}\right) , \end{aligned}$$
(3)

where \(\rho \) satisfies the amplitude equation \(\ddot{\rho }+\Omega ^{2}\rho =Q_{00}^{2}\rho ^{-3}\). This invariant is thus a somewhat disguised form of the squared Wronskian of the functions \(x_{1}\), \(x_{2}\). The \(\mathcal {E}=\frac{1}{2}mQ_{10}\) energy invariant has been shown to be [23],

$$\begin{aligned} \mathcal {E}=\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{df}=\frac{1}{2}m\dot{x}^{2}+\frac{1}{2}\kappa x^{2}-\frac{1}{2}\int \dot{\kappa }x^{2}\textrm{d}t, \end{aligned}$$
(4)

where the first two terms are readily identified as kinetic \(\mathcal {E}_{k}\) and potential \(\mathcal {E}_{p}\) energies, whereas the last term \(\mathcal {E}_{df}\), is the dynamic field energy

$$\begin{aligned} \mathcal {E}_{df}=-\frac{1}{2}\int \dot{\kappa }x^{2}\textrm{d}t. \end{aligned}$$
(5)

\(\mathcal {E}_{df}\) represents the energy that the object gains (or looses) and is equal to the energy that the field looses (or gains) due to a change in the field’s coupling coefficient \(\kappa \), where \(\Omega ^{2}={\kappa }/{m}\). If the restitutive force coefficient \(\kappa \) is constant, this term vanishes and the energy is simply the sum of kinetic plus potential energies \(\mathcal {E}=\mathcal {E}_{\textrm{osc}}=\mathcal {E}_{k}+\mathcal {E}_{p}\).

3 Damped harmonic oscillator

Damping is included via a first-order derivative term,

$$\begin{aligned} \frac{\textrm{d}^{2}x}{\textrm{d}t^{2}}+\gamma \frac{\textrm{d}x}{\textrm{d}t}+\Omega ^{2}x=0, \end{aligned}$$
(6)

where \(\gamma \) is the damping coefficient and \(\Omega ^{2}\) is the restitutive force over mass coefficient. Both coefficients are allowed to be time-dependent. The damping is linear with respect to the velocity.

3.1 Exchange energy

Following the orthogonal functions procedure [23], allow for two linearly independent solutions \(x_{1},\,x_{2}\). These functions are now solutions to the harmonic oscillator equation with damping (6) instead of (1). An equivalent formulation accounts for absorption in wave propagation [8]. The algorithm involves taking product of \(x_{2}\) times eq. (6) evaluated for \(x_{1}\). The equation is also evaluated for \(x=x_{2}\) times \(x_{1}\) and the difference between the two expressions is appraised as

$$\begin{aligned} x_{2}\,\frac{\textrm{d}^{2}x_{1}}{\textrm{d}t^{2}}-x_{1}\,\frac{\textrm{d}^{2}x_{2}}{\textrm{d}t^{2}}+\gamma \left( x_{2}\,\frac{\textrm{d}x_{1}}{\textrm{d}t}-x_{1}\,\frac{\textrm{d}x_{2}}{\textrm{d}t}\right) =0. \end{aligned}$$
(7)

The difference involving the second time derivatives may be written as

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}\left( x_{2}\,\frac{\textrm{d}x_{1}}{\textrm{d}t}-x_{1}\,\frac{\textrm{d}x_{2}}{\textrm{d}t}\right) . \end{aligned}$$

Recalling the form of the invariant for the undamped oscillator system (2a), introduce the exchange energy bracket

$$\begin{aligned} q_{00}\left( t\right) \equiv \left\lfloor x_{2},x_{1}\right\rfloor =x_{2}\,\frac{\textrm{d}x_{1}}{\textrm{d}t}-x_{1}\,\frac{\textrm{d}x_{2}}{\textrm{d}t}. \end{aligned}$$
(8a)

The Wronskian is described in a broader mathematical context as an operator bracket \(\left\lfloor f,g\right\rfloor \) between two functions f, g in Appendix A. Equation (7) is then

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}q_{00}\left( t\right) +\gamma \,q_{00}\left( t\right) =0, \end{aligned}$$

where \(q_{00}\left( t\right) \) is clearly no longer an invariant in this damped case. A lower case Latin letter is used for non-constant quantities. From the solution to this equation

$$\begin{aligned} q_{00}\left( t\right) =Q_{00}^{\left( abs\right) }\textrm{e}^{-\int \gamma \,\textrm{d}t}, \end{aligned}$$

the invariant \(Q_{00}\) when damping is present, is obtained as

$$\begin{aligned} Q_{00}=q_{00}\left( t\right) \textrm{e}^{\int \gamma \,\textrm{d}t}=\left( x_{2}\,\frac{\textrm{d}x_{1}}{\textrm{d}t}-x_{1}\,\frac{\textrm{d}x_{2}}{\textrm{d}t}\right) \textrm{e}^{\int \gamma \,\textrm{d}t}. \end{aligned}$$
(8b)

The capital Latin letter Q is used for invariant quantities. We refer to \(\mathcal {E}_{\omega }^{\textrm{ex}}\) as the exchange energy and \(\mathcal {I}_{\omega }^{\textrm{ex}}\) as the exchange energy invariant in the presence of damping

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}\equiv \frac{1}{2}mq_{00},\quad \mathcal {I}_{\omega }^{\textrm{ex}}\equiv \frac{1}{2}mQ_{00}, \end{aligned}$$
(8c)

where the scaling by \(\frac{1}{2}m\) is introduced to abide with the energies presented in the next subsection. The \(\frac{1}{2}m\) factor is assumed whenever we refer to \(q_{00}\) or \(Q_{00}\) as the energy exchange. In the complex domain, linearly independent solutions are given by complex conjugate solutions. We use \(\psi \) instead of x as the coordinate variable to stress the complex nature of the solution. The polar representation of \(\psi \) is \(\psi =\rho \,\textrm{e}^{-i\varphi }\), where \(\rho ,\varphi \in \mathbb {R}\), are the amplitude and phase variables respectively. From the difference between

$$\begin{aligned} \psi \frac{\textrm{d}^{2}\psi ^{*}}{\textrm{d}t^{2}}+\gamma \psi \frac{\textrm{d}\psi ^{*}}{\textrm{d}t}+\Omega ^{2}\psi \psi ^{*}=0 \end{aligned}$$

and

$$\begin{aligned} \psi ^{*}\frac{\textrm{d}^{2}\psi }{\textrm{d}t^{2}}+\gamma \psi ^{*}\frac{\textrm{d}\psi }{\textrm{d}t}+\Omega ^{2}\psi ^{*}\psi =0, \end{aligned}$$

the exchange energy equation with damping in the complex formalism is

$$\begin{aligned} \frac{\textrm{d}}{\textrm{d}t}q_{00}^{\mathbb {C}}+\gamma \,q_{00}^{\mathbb {C}}=0, \end{aligned}$$
(9a)

where

$$\begin{aligned} q_{00}^{\mathbb {C}}\equiv \frac{1}{2i}(\psi \dot{\psi }^{*}-\psi ^{*}\dot{\psi })=\rho ^{2}\dot{\varphi }=\rho ^{2}\omega . \end{aligned}$$
(9b)

The exchange energy invariant derived from the complex solutions is

$$\begin{aligned} Q_{00}^{\mathbb {C}}=q_{00}^{\mathbb {C}}\textrm{e}^{\int \gamma \,\textrm{d}t}=\rho ^{2}\dot{\varphi }\,\textrm{e}^{\int \gamma \,\textrm{d}t}. \end{aligned}$$
(9c)

Although the real and complex formalisms are quite similar and give the same results in an ample domain (\(\psi \in \mathbb {C}\setminus \mathbb {R}\)), this is not always the case. Notice that if \(\psi \) is real, \(q_{00}^{\mathbb {C}}\) is zero. Nonetheless, \(q_{00}\) evaluated from the real orthogonal functions \(x_{1},\,x_{2}\), does not necessarily vanish. This will be the case under heavy damping, as we shall see.

3.2 Energy and \(Q_{10}\) invariant

Evaluate the derivative of (6),

$$\begin{aligned} \frac{\textrm{d}^{2}v}{\textrm{d}t^{2}}+\gamma \frac{\textrm{d}v}{\textrm{d}t}+\Omega ^{2}v+\frac{\textrm{d}\gamma }{\textrm{d}t}v+\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x=0, \end{aligned}$$
(10)

where \(v=\dot{x}\) represents the velocity. Following the second-order ODEs invariant algorithm [23], take the product of (6) with v,

$$\begin{aligned} v\frac{\textrm{d}^{2}x}{\textrm{d}t^{2}}+\gamma v\frac{\textrm{d}x}{\textrm{d}t}+\Omega ^{2}vx=0 \end{aligned}$$
(11a)

and the product of (10) with x,

$$\begin{aligned} x\frac{\textrm{d}^{2}v}{\textrm{d}t^{2}}+\gamma x\frac{\textrm{d}v}{\textrm{d}t}+\Omega ^{2}xv+\frac{\textrm{d}\gamma }{\textrm{d}t}xv+\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}=0. \end{aligned}$$
(11b)

The difference of eqs (11a) minus (11b) is

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\left( v\frac{\textrm{d}x}{\textrm{d}t}-x\frac{\textrm{d}v}{\textrm{d}t}\right) +\gamma \left( v\frac{\textrm{d}x}{\textrm{d}t}-x\frac{\textrm{d}v}{\textrm{d}t}\right) -\frac{\textrm{d}\gamma }{\textrm{d}t}xv \nonumber \\{} & {} \quad -\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}=0. \end{aligned}$$
(12)

The terms in brackets can be seen as the w-bracket of the position and velocity variables (see Appendix A). The function \(q_{10}\) is then defined as

$$\begin{aligned} q_{10}\equiv \left\lfloor v,x\right\rfloor =v\frac{\textrm{d}x}{\textrm{d}t}-x\frac{\textrm{d}v}{\textrm{d}t}=v^{2}+\Omega ^{2}x^{2}+\gamma xv. \end{aligned}$$
(13)

The invariant (4) suggests that \(q_{10}\) is the quantity that should be associated with the oscillator’s energy in the presence of damping. Multiplying (12) by \(\textrm{e}^{\int \gamma \textrm{d}t}\), we get

$$\begin{aligned}{} & {} \frac{\textrm{d}}{\textrm{d}t}\big [(v^{2}+\Omega ^{2}x^{2}+\gamma xv)\textrm{e}^{\int \gamma \textrm{d}t}\big ]\\{} & {} \quad -\left( \frac{\textrm{d}\gamma }{\textrm{d}t}xv+\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}\right) \textrm{e}^{\int \gamma \textrm{d}t}=0. \end{aligned}$$

The \(Q_{10}\) invariant is then

$$\begin{aligned}{} & {} Q_{10}=(v^{2}+\Omega ^{2}x^{2}+\gamma xv)\textrm{e}^{\int \gamma \textrm{d}t}\\{} & {} \quad -\int \left( \frac{\textrm{d}\gamma }{\textrm{d}t}xv+\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}\right) \textrm{e}^{\int \gamma \textrm{d}t}\textrm{d}t. \end{aligned}$$

Include a \(\frac{1}{2}m\) factor to comply with the usual kinetic \(\mathcal {E}_{k}\) and potential \(\mathcal {E}_{p}\) energy definitions. The total energy of the system, including the energy dissipated and/or transferred by the dissipative and restitutive forces is

$$\begin{aligned} \mathcal {E}= & {} \frac{1}{2}mQ_{10} \nonumber \\= & {} \biggl (\;\underset{\mathcal {E}_{k}}{\underbrace{\frac{1}{2}mv^{2}}}+\underset{\mathcal {E}_{p}}{\underbrace{\frac{1}{2}m\Omega ^{2}x^{2}}}+\underset{\mathcal {E}_{\gamma }}{\underbrace{\frac{1}{2}m\gamma xv}}\biggr )\textrm{e}^{\int \gamma \textrm{d}t}\nonumber \\{} & {} \underset{\mathcal {E}_{df}}{\underbrace{-\frac{1}{2}m\int \left( \frac{\textrm{d} \gamma }{\textrm{d}t}xv+\frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}\right) \textrm{e} ^{\int \gamma \textrm{d}t}\textrm{d}t}}. \end{aligned}$$
(14a)

The third term represents the dissipative modulation energy

$$\begin{aligned} \mathcal {E}_{\gamma }=\frac{1}{2}m\gamma xv. \end{aligned}$$
(14b)

This is a dissipative contribution to the total energy that vanishes if the damping constant \(\gamma \) is zero. It is proportional to the frictional force \(F_{\text {fric}}=-m\gamma \dot{x}\) times distance, since \(\mathcal {E}_{\gamma }=\frac{1}{2}x\left( m\gamma \dot{x}\right) =-\frac{1}{2}xF_{\text {fric}}\), which is consistent with a dissipative force picture. The term \(-\int \dot{\gamma }xv\exp (\int \gamma \textrm{d}t)\textrm{d}t\) in (14a) can be associated with the dissipative modulation or with the dynamic field energy. It is a dissipation term since it is zero if \(\gamma \) is constant or zero. However, it is also a dynamic field property because it is proportional to the time-dependent absorption field. The last term

$$\begin{aligned} \mathcal {E}_{\textrm{d}f}=-\int \frac{\textrm{d}\Omega ^{2}}{\textrm{d}t}x^{2}\textrm{d}t=-\frac{1}{2}\int \dot{\kappa }x^{2}\textrm{d}t, \end{aligned}$$

as mentioned earlier, represents the energy that the time-varying restoring force transfers to or from the object. The time integration exhibits that the dynamic field terms \(\mathcal {E}_{df}\) have memory of the evolution of the oscillator-field system.

Table 1 Energies involved in the description of the damped harmonic oscillator with mass m and frequency \(\omega _{d}=\sqrt{\Omega ^{2}-\gamma ^{2}/4}\). The energy of the system is the total energy including dissipation. \(\mathcal {E}_{t}^{\textrm{ex}}\) and \(\mathcal {E}_{\omega }^{\textrm{ex}}\) measure the energy that is transferred back and forth between the kinetic and potential energies.
Full size table

The total energy \(\mathcal {E}\) of the system, from (14a) is

$$\begin{aligned} \mathcal {E}=(\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma })\exp \left( \int \gamma \textrm{d}t\right) +\mathcal {E}_{df}. \end{aligned}$$
(15)

If the energy of the oscillator is considered to be equal to \(\frac{1}{2}mq_{10}\), from (13),

$$\begin{aligned} \mathcal {E}_{\text {osc}\gamma }\equiv \frac{1}{2}mq_{10}=\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma }=(\mathcal {E}-\mathcal {E}_{df})\textrm{e}^{-\int \gamma \textrm{d}t}. \end{aligned}$$
(16)

The \(\mathcal {E}_{\gamma }\) dissipative modulation energy is then included as part of the oscillator energy \(\mathcal {E}_{\text {osc}\gamma }\), consistent with (13). This choice is quite interesting because, as we shall see in §4.2, it allows for a smooth exponential decay without performing any averaging. However, the energy of the oscillator is usually considered to be only the sum of kinetic plus potential energies \(\mathcal {E}_{\text {osc}}=\mathcal {E}_{k}+\mathcal {E}_{p}\). To discern between these two possibilities, they have been labelled \(\mathcal {E}_{\text {osc}\gamma }\) and \(\mathcal {E}_{\text {osc}}\). Various quantities defined in this paper are abridged in table 1. The oscillator energy is then equal to

$$\begin{aligned} \mathcal {E}_{\text {osc}}=\left( \mathcal {E}-\mathcal {E}_{df}\right) \exp \left( -\int \gamma \,\textrm{d}t\right) -\mathcal {E}_{\gamma }, \end{aligned}$$

which, in terms of position and velocity, is

$$\begin{aligned} \mathcal {E}_{\text {osc}}= & {} \frac{1}{2}m\left( Q_{10}+\int \dot{\gamma }xv\textrm{e}^{\int \gamma \textrm{d}t}\textrm{d}t\right) \textrm{e}^{-\int \gamma \textrm{d}t}\nonumber \\{} & {} -\frac{1}{2}m\gamma x\dot{x}. \end{aligned}$$
(17)

This expression involves three terms: (1) A smooth exponential decay \(\mathcal {E}\exp (-\int \gamma \textrm{d}t)\), (2) a temporally modulated dissipation \(-\mathcal {E}_{\textrm{d}f}\exp (-\int \gamma \textrm{d}t)\) and (3) a dissipative modulation term \(\mathcal {E}_{\gamma }\), associated with the usual exponential decay but modulated at twice the damped frequency.

The present approach has allowed us to write the energy of the oscillator \(\mathcal {E}_{\text {osc}}\) in two ways:

(i) the sum of the kinetic and potential energies,

(ii) the total energy of the system times an exponential decay minus the dissipated energy \(\mathcal {E}_{\gamma }\), as given by eq. (17).

4 Constant damping coefficient, time-independent parameters

To allow for a tractable analytic solution, consider the damping coefficient and the restitutive force parameter to be time-independent. The complex solution to the oscillator equation with constant damping is

$$\begin{aligned} \psi =\rho _{0}\textrm{e}^{\bigl (-\frac{1}{2}\gamma \,t\bigr )}\exp \left( -i\Bigl (\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}}\,t+\phi _{0}\Bigr )\right) , \end{aligned}$$
(18a)

where the multiplicative non-imaginary part is the amplitude variable and the argument of the imaginary exponential excluding the minus sign is the phase,

$$\begin{aligned}{} & {} \rho =\rho _{0}\exp \Bigl (-\frac{1}{2}\gamma \,t\Bigr ),\quad \varphi =\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}}\,t+\phi _{0},\nonumber \\{} & {} \omega _{d}\equiv \dot{\varphi }=\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}}. \end{aligned}$$
(18b)

Due to the amplitude and phase indeterminacy for real fields [28], these variables should be defined in the complex domain, where they are unequivocally characterised.

4.1 Exchange energy with constant damping

The exchange energy function under light damping is the same in the real and complex formalisms (8a), (9a),

$$\begin{aligned} q_{00}=\rho _{0}^{2}\,\omega _{d}\exp \left( -\gamma t\right) ,\quad \gamma \le 2\Omega . \end{aligned}$$
(19a)

The corresponding exchange energy invariant is

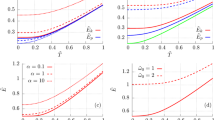
$$\begin{aligned} Q_{00}=\rho ^{2}\dot{\varphi }\,\textrm{e}^{\gamma t}=\rho _{0}^{2}\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}},\quad \gamma \le 2\Omega . \end{aligned}$$
(19b)

This invariant is clearly constant in time for a given damping value \(\gamma \). As a function of \(\gamma \) for constant amplitude \(\rho _{0}\), it decreases from \(\rho _{0}^{2}\Omega \) to zero as depicted in figure 1. The exchange energy \(q_{00}\) has an analogous behaviour but exhibits an exponential time decay.

Fig. 1
figure 1

Energy exchange invariant \(Q_{00}\) as a function of the damping coefficient, given by (19b) if \(\gamma \le 2\Omega \) and (20) in red or (21) in blue, if \(\gamma >2\Omega \).

Full size image

Under heavy damping, \(\gamma ^{2}>4\Omega ^{2}\), the phase is zero and the solution only involves the amplitude function,

$$\begin{aligned} \psi =\underset{\text {amplitude }\rho }{\underbrace{\rho _{0}\exp \biggl (\Bigl (-\frac{1}{2}\gamma \mp \sqrt{\frac{1}{4}\gamma ^{2}-\Omega ^{2}}\Bigr )\,t\biggr )}}\textrm{e}^{i\,\underset{\text {phase }\varphi }{\underbrace{0\,t}}}. \end{aligned}$$

The invariant \(Q_{00}^{\mathbb {C}}\) and the energy exchange \(q_{00}^{\mathbb {C}}\), since \(\dot{\varphi }=0\), are therefore zero,

$$\begin{aligned} q_{00}^{\mathbb {C}}=\rho ^{2}\dot{\varphi }=0,\quad Q_{00}^{\mathbb {C}}=\rho ^{2}\dot{\varphi }\,\textrm{e}^{\gamma t}=0,\quad \text {if }\gamma >2\Omega . \end{aligned}$$
(20)

This result suggests that \(q_{00}\) and \(Q_{00}\) are measures of the energy being periodically exchanged between the two energy forms.

Under heavy damping \(x_{1}\) and \(x_{2}\) \(\in \mathbb {R}\) are no longer expressible in terms of trigonometric functions with real arguments. \(Q_{00}\) then differs from \(Q_{00}^{\mathbb {C}}=0\). The linearly independent real solutions for \(\gamma >2\Omega \) are

$$\begin{aligned} x_{1,2}=\left( \rho _{0}\right) _{1,2}\exp \left[ \left( -\frac{1}{2}\gamma \mp \sqrt{\frac{1}{4}\gamma ^{2}-\Omega ^{2}}\right) t\right] , \end{aligned}$$

where \(\rho _{01}\) and the upper negative sign correspond to \(x_{1}\), whereas \(\rho _{02}\) and the lower sign to \(x_{2}\). \(q_{00}^{\mathbb {R}}\left( t\right) \) evaluated from these linearly independent real solutions for \(\gamma >2\Omega \) is

$$\begin{aligned} q_{00}^{\mathbb {R}}=x_{2}^{2}\frac{\textrm{d}}{\textrm{d}t}\left( \frac{x_{1}}{x_{2}}\right) \!=\!-2\rho _{01}\,\rho _{02}\sqrt{\frac{1}{4}\gamma ^{2}-\Omega ^{2}}\exp \left( -\gamma t\right) \end{aligned}$$

and

$$\begin{aligned} Q_{00}^{\mathbb {R}}=q_{00}\left( t\right) \textrm{e}^{\gamma \,t}\!=\!-2\rho _{01}\,\rho _{02}\sqrt{\frac{1}{4}\gamma ^{2}-\Omega ^{2}},\;\gamma >2\Omega . \end{aligned}$$
(21)

Abiding to the convention that \(Q_{00}\) is positive for the undamped oscillator, if the \(Q_{00}\) invariant is zero (\(Q_{00}^{\mathbb {C}}\)) or negative (\(Q_{00}^{\mathbb {R}}\)) in the damped case, no energy is exchanged back and forth between the kinetic and potential energies. It is advantageous to use \(Q_{00}\) rather than the Ermakov invariant given by (3), that is proportional to the square of this quantity, because \(Q_{00}\le 0\) for the damped case has a clear-cut meaning regarding the lack of a periodic energy exchange.

Let us delve further into the dynamics according to this interpretation. Under light damping, when oscillations take place, the kinetic energy transforms into potential energy as the motion moves away from the equilibrium position. And vice versa, from potential to kinetic energy as the object moves towards the equilibrium position. Under heavy damping, the energy no longer flows back and forth between the potential and kinetic energies. These assertions are illustrated in figure 2.

Fig. 2
figure 2

Energy exchange: Perturbation in the upper row, kinetic (green curve) and potential (magenta curve) energies in the lower row for different damping coefficients. From left to right columns: \(\gamma ={\Omega }/{10}\), \(\gamma =\Omega \) and \(\gamma =3\Omega \).

Full size image

When the damping coefficient is ten times less than the resonant frequency, the kinetic and potential energies are almost out of phase (they are exactly out of phase if there is no damping). If the damping coefficient is larger, for example, when \(\gamma =\Omega \), the kinetic and potential energies are no longer out of phase as seen in the lower middle plot in figure 2. The kinetic energy is largely being dissipated onto the damper and only a small amount is returned to the potential. Beyond \(\gamma =2\Omega \), there is no longer any exchange in both directions between the kinetic and potential energies. The potential energy is slowly transformed into kinetic energy and this in turn is dissipated. No kinetic energy is transformed back into potential energy once the maximum amplitude is reached. This case is illustrated in figure 2 for \(\gamma =3\Omega \). As a consequence, the kinetic and potential energy curves never cross in this regime if the initial velocity is zero (maximum amplitude at initial time). Therefore, if no energy is transferred to and from the kinetic and potential forms, the exchange energy \(q_{00}\) and its corresponding invariant \(Q_{00}\) are zero (for complex solutions, eq. (20)) or negative (for real solutions, eq. (21)).

\(q_{00}\) has units of the perturbation squared over time, as seen from (8a). If the perturbation is a displacement, the exchange energy (8c) is obtained by a \(\frac{1}{2}m\) scaling. For constant light damping, from (19a), the exchange energy is,

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=\frac{1}{2}mq_{00}=\frac{1}{2}m\rho _{0}^{2}\,\omega _{d}\exp \left( -\gamma t\right) ,\quad \gamma \le 2\Omega . \end{aligned}$$
(22)

In SI units,

$$\begin{aligned} \left[ \mathcal {E}_{\omega }^{\textrm{ex}}\right] =\left[ \frac{1}{2}mq_{00}\right] =[\mathrm {kg\,m^{2}\,s^{-1}}]=\left[ \mathrm {J\,s}\right] . \end{aligned}$$

These units, together with the amplitude and phase expression \(\rho ^{2}\dot{\varphi }\), are akin to angular momentum if the amplitude is associated with a radial distance and the phase with an angle in two-dimensional space if an auxiliary axis is introduced. For these reasons, the angular momentum interpretation has been appealing [16]. However, we should recall that the motion is strictly one-dimensional. In contrast, the exchange energy interpretation given here does not invoke an auxiliary dimension. Furthermore, if the oscillatory motion is extended to two or three spatial dimensions, the exchange energy interpretation still holds.

4.2 Energy with constant damping

If the restitutive force and damping coefficient are time- independent, from the \(Q_{10}\) energy invariant (14a),

$$\begin{aligned} \mathcal {E}=(\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma })\textrm{e}^{\gamma t}=\frac{m}{2}(v^{2}+\Omega ^{2}x^{2}+\gamma xv)\textrm{e}^{\gamma t}. \end{aligned}$$
(23)

This constant of motion has been obtained earlier using other methods, such as canonical transformations [29, 30] and Lie groups, leaving the algebraic structure unchanged [31]. In [31], this constant was interpreted as the pseudoenergy. Nonetheless, a physical interpretation as the initial energy of the system for certain initial conditions (\(x=0\), \(\dot{x}=0\)) has been recently put forward in connection with the Bateman Hamiltonian [32]. The present results show that \(\mathcal {E}\) represents the total energy of the system including the kinetic, potential and dissipative energies for arbitrary initial conditions. The inclusion of the \(\mathcal {E}_{\gamma }\) term in (23), allows for \(\gamma xv\ne 0\) at the initial or any later time. The oscillator energy (17) can be written as

$$\begin{aligned} \mathcal {E}_{\text {osc}}=\mathcal {E}\textrm{e}^{-\gamma t}-\mathcal {E}_{\gamma }=\frac{1}{2}mQ_{10}\textrm{e}^{-\gamma t}-\frac{1}{2}m\gamma xv. \end{aligned}$$
(24)

This is a significant result, because in the usual description of the damped oscillator, the energy lost by the system can only be obtained from the sum of the kinetic and potential energies. Several results can be readily obtained from (24). The average energy of the oscillator for light damping is \(\mathcal {E}_{\text {osc}}=\frac{1}{2}mQ_{10}\textrm{e}^{-\gamma t}\), since \(x\dot{x}\) averages to zero. From the time derivative of (24),

$$\begin{aligned} \frac{\textrm{d}\mathcal {E}_{\text {osc}}}{\textrm{d}t}=-m\gamma \dot{x}^{2}, \end{aligned}$$

in accordance with the usual monotonic decay [33, eq. (3.10)].

4.3 Kinetic and potential energy exchange: Kinetic energy splitting

It is possible to separate the energy of the oscillator into a part that is being exchanged between the kinetic and potential energies and another part that is dissipated. To this end, consider the position real trigonometric solution in amplitude and phase variables,

$$\begin{aligned} x=\rho _{0}\,\textrm{e}^{-\frac{1}{2}\gamma t}\cos \left( \omega _{d}\,t+\phi _{0}\right) , \end{aligned}$$
(25a)

where

$$\begin{aligned} \omega _{d}=\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}}. \end{aligned}$$

The amplitude \(\rho _{0}\) and the initial phase \(\phi _{0}\) are specified as usual by the initial conditions. For example, at \(t=0\), if the position is \(x_{0}\) and the velocity is zero,

$$\begin{aligned} \phi _{0}=-\arctan \left( \frac{\gamma }{2\omega _{d}}\right) ,\quad \rho _{0}=x_{0}\frac{\Omega }{\omega _{d}} \end{aligned}$$
(25b)

since

$$\begin{aligned} \cos \left( \arctan \bigl (\frac{\gamma }{2\omega _{d}}\bigr )\right) =\frac{\omega _{d}}{\Omega }. \end{aligned}$$

The potential energy is

$$\begin{aligned} \mathcal {E}_{p}=\frac{1}{2}\kappa x^{2}=\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\Omega ^{2}\cos ^{2}\left( \omega _{d}\,t+\phi _{0}\right) , \end{aligned}$$
(25c)

where \(\kappa =m\Omega ^{2}\). The velocity is

$$\begin{aligned}{} & {} v=-\rho _{0}\textrm{e}^{-\frac{\gamma }{2}t} \nonumber \\{} & {} \quad \times \left( \frac{\gamma }{2}\cos \left( \omega _{d}\,t+\phi _{0}\right) +\omega _{d}\sin \left( \omega _{d}\,t+\phi _{0}\right) \right) . \end{aligned}$$
(25d)

From this velocity, it is straightforward to obtain the kinetic energy,

$$\begin{aligned}{} & {} \mathcal {E}_{k}=\frac{m}{2}\rho _{0}^{2}\textrm{e}^{-\gamma t} \nonumber \\{} & {} \quad \times \left( \frac{\gamma }{2}\cos \left( \omega _{d}\,t+\phi _{0}\right) +\omega _{d}\sin \left( \omega _{d}\,t+\phi _{0}\right) \right) ^{2}.\nonumber \\ \end{aligned}$$
(25e)

The problem is which part of the kinetic energy (25e) is exchanged with the potential energy. The clue is given by the form of the potential energy (25c). The corresponding kinetic term must be equal to the potential energy but temporally displaced \(\frac{\pi }{2}\) out of phase. This contribution comes from the second term squared in the binomial (25e). The kinetic energy contributions can then be separated as \(\mathcal {E}_{k}=\mathcal {E}_{k}^{\text {exchange}}+\mathcal {E}_{k}^{\text {dissipated}}\),

$$\begin{aligned} \mathcal {E}_{k}= & {} \underset{\mathcal {E}_{k}^{\text {exchange}}}{\underbrace{\frac{1}{2}m\rho _{0}^{2}\textrm{e}^{-\gamma t}\;\Omega ^{2}\sin ^{2}\left( \omega _{d}\,t+\phi _{0}\right) }}\nonumber \\{} & {} +\underset{\mathcal {E}_{k}^{\text {dissipated}}}{\underbrace{\frac{1}{4}m\rho _{0}^{2}\textrm{e}^{-\gamma t}\gamma \,\Omega \sin \left( 2\omega _{d}\,t+2\phi _{0}+\gamma _{0}\right) }}, \end{aligned}$$
(25f)

where the square velocity has been rewritten so that the kinetic energy exchanged with the potential energy \(\mathcal {E}_{k}^{\text {exchange}}\leftrightarrow \mathcal {E}_{p}\), is separated from the rest. The phase

$$\begin{aligned} \gamma _{0}=\arctan \bigg (\frac{\gamma }{2\omega _{d}}\bigg ) \end{aligned}$$

arises from the grouping of

$$\begin{aligned} \frac{\gamma ^{2}}{4}\cos \left( 2\omega _{d}\,t+2\phi _{0}\right) +\frac{1}{2}\gamma \omega _{d}\sin \left( 2\omega _{d}\,t+2\phi _{0}\right) \end{aligned}$$

in a single term, as shown in Appendix B. The remaining \(\mathcal {E}_{k}^{\text {dissipated}}\) term in the kinetic energy accounts for the non-conservative part that is lost, as we shall presently confirm. The dissipative modulation energy is

$$\begin{aligned}{} & {} \mathcal {E}_{\gamma }=\frac{m\gamma }{2}x\dot{x}=\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\nonumber \\{} & {} \biggl (\underset{\text {frequency downshift}}{\underbrace{-\frac{\gamma ^{2}}{4}}}-\underset{\text {dissipative modulation}}{\underbrace{\frac{1}{2}\gamma \,\Omega \sin \left( 2\omega _{d}\,t+2\phi _{0}+\gamma _{0}\right) }}\;\biggr ), \nonumber \\ \end{aligned}$$
(26)

where the trigonometric functions product

$$\begin{aligned}{} & {} \cos \left( \omega _{d}\,t+\phi _{0}\right) \\{} & {} \quad \times \left( \frac{\gamma }{2}\cos \left( \omega _{d}\,t+\phi _{0}\right) +\omega _{d}\sin \left( \omega _{d}\,t+\phi _{0}\right) \right) \end{aligned}$$

has been written in terms of the double angle. The last term in (26) is identical to the remaining term in the kinetic energy (25f), but with opposite sign,

$$\begin{aligned} \mathcal {E}_{\gamma }=-\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\frac{\gamma ^{2}}{4}-\mathcal {E}_{k}^{\text {dissipated}}. \end{aligned}$$
(27)

Thus, the non-conservative loss of kinetic energy goes into the dissipative modulation energy \(\mathcal {E}_{k}^{\text {dissipated}}\rightarrow \mathcal {E}_{\gamma }\). The total energy of the system \(\mathcal {E}=\textrm{e}^{\gamma t}\mathcal {E}_{\text {osc}\gamma }\) is

$$\begin{aligned} \mathcal {E}=\textrm{e}^{\gamma t}\Bigl (\underset{\mathcal {E}_{p}+\mathcal {E}_{k}^{\text {exchange}}}{\underbrace{\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\Omega ^{2}}}\quad \underset{\mathcal {E}_{k}^{\text {dissipated}}+\mathcal {E}_{\gamma }}{\underbrace{-\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\frac{\gamma ^{2}}{4}}}\Bigr ), \end{aligned}$$
(28a)

where the first term on the right-hand side comes from the sum of the kinetic energy that is being exchanged with the potential energy. The second term comes from the sum of the kinetic energy that is being dissipated plus the dissipative modulation energy. In this latter term, only the frequency downshift term of the dissipative modulation energy \(\mathcal {E}_{\gamma }\) survives. The energy of the system from (28a), is then

$$\begin{aligned} \mathcal {E}=\frac{1}{2}m\rho _{0}^{2}\left( \Omega ^{2}-\frac{\gamma ^{2}}{4}\right) =\frac{1}{2}m\rho _{0}^{2}\omega _{d}^{2}. \end{aligned}$$
(28b)

The dependence on \(\gamma \) of the total energy, may be somewhat surprising. If at the initial position and time \(\left( x_{0},t_{0}\right) \) all energy is potential,

$$\begin{aligned} \mathcal {E}=\mathcal {E}_{p}=\frac{1}{2}\kappa x_{0}^{2}=\frac{1}{2}m\Omega ^{2}x_{0}^{2}, \end{aligned}$$

and thus independent of the damping coefficient. However, this initial condition requires, from (25b), \(\rho _{0}=x_{0}({\Omega }/{\omega _{d}})\). Substitution of this amplitude in (28b) shows that the total energy is indeed \(\omega _{d}\) independent. In amplitude and phase variables, from the substitution of the coordinate \(x\rightarrow \rho \cos \varphi \) and its derivative in the invariant equation (23), the energy of the system is

$$\begin{aligned} \mathcal {E}=\frac{1}{2}mQ_{10}=\frac{1}{2}m\rho ^{2}\omega ^{2}\textrm{e}^{\gamma t}, \end{aligned}$$
(28c)

reproducing (28b) in a straightforward way. However, the separation of the kinetic energy in conservative and dissipative terms is concealed in the amplitude and phase procedure. The \(\rho ^{2}\omega ^{2}\) dependence of the total energy is preserved in the presence of light damping. The frequency is downshifted from \(\omega =\Omega \) in the undamped case to

$$\begin{aligned} \omega _{d}=\sqrt{\Omega ^{2}-\gamma ^{2}/4} \end{aligned}$$

under light damping. The exponential factor \(\textrm{e}^{\gamma t}\) cancels out the \(\textrm{e}^{-\gamma t}\) decay coming from the square amplitude in order to have a constant total energy. The oscillator energy

$$\begin{aligned} \mathcal {E}_{\text {osc}\gamma }=\frac{1}{2}mq_{10}=\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma } \end{aligned}$$

has a smooth exponential decay. Separating the exchange and dissipated kinetic parts,

$$\begin{aligned} \mathcal {E}_{\text {osc}\gamma }=\mathcal {E}_{k}^{\text {exchange}}+\mathcal {E}_{p}+\mathcal {E}_{k}^{\text {dissipated}}+\mathcal {E}_{\gamma }, \end{aligned}$$

the oscillator energy is

$$\begin{aligned} \mathcal {E}_{\text {osc}\gamma }=\mathcal {E}_{k}^{\text {exchange}}+\mathcal {E}_{p}-\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\frac{\gamma ^{2}}{4}. \end{aligned}$$
(28d)

The oscillator energy \(\mathcal {E}_{\text {osc}\gamma }\) including the dissipative modulation term \(\mathcal {E}_{\gamma }\) thus amounts to adding the potential energy with the kinetic energy that is being exchanged and \(\mathcal {E}_{\gamma }\) cancels out the part of the kinetic energy that is being dissipated. However, \(\mathcal {E}_{\gamma }\) also introduces the downshift coefficient \(-{\gamma ^{2}}/{4}\), that together with \(\Omega ^{2}\) establish the damped frequency of the oscillator. From the amplitude and phase solutions (18b),

$$\begin{aligned} \mathcal {E}_{\text {osc}\gamma }=\frac{1}{2}m\rho ^{2}\omega _{d}^{2}=\frac{1}{2}m\rho _{0}^{2}\,\omega _{d}^{2}\textrm{e}^{-\gamma t}, \end{aligned}$$
(29)

consistent with (28d). The various energies used in this description are summarised in table 1.

4.4 Exchange energy per period

Consider a scaling of \(q_{00}\) by \(\frac{1}{2}\kappa =\frac{1}{2}m\Omega ^{2}\), one half the restitutive force coefficient of the harmonic oscillator. The exchange energy (with subindex t) from (25e),

$$\begin{aligned} \mathcal {E}_{t}^{\textrm{ex}}\equiv \frac{1}{2}\kappa q_{00}=\frac{1}{2}\kappa \left( x_{2}\dot{x}_{1}-\dot{x}_{2}x_{1}\right) , \end{aligned}$$
(30)

then has units of energy over time \([\mathrm {J\,s^{-1}}]\), since \(\left[ \kappa \right] =\left[ \mathrm {{N}/{m}}\right] \). \(I_{t}^{\textrm{ex}}\equiv \frac{1}{2}\kappa Q_{00}\) is the corresponding exchange energy invariant in the presence of damping. \(\mathcal {E}_{t}^{\textrm{ex}}\) has the appropriate units for the physical interpretation of energy exchanged per time interval. If light damping at a constant rate \(\gamma \) takes place, exchange energy \(\mathcal {E}_{t}^{\textrm{ex}}\) decreases exponentially as seen from (29), for \(\gamma \le 2\Omega \),

$$\begin{aligned} \mathcal {E}_{t}^{\textrm{ex}}=\frac{1}{2}\kappa q_{00}=\frac{1}{2}m\Omega ^{2}\rho _{0}^{2}\,\omega _{d}\,\textrm{e}^{-\gamma t},\;\omega _{d}=\sqrt{\Omega ^{2}-\frac{1}{4}\gamma ^{2}}. \end{aligned}$$
(31)

Recall that the out-of-phase oscillations between the kinetic and potential energies evince the energy that is being exchanged between them. The sum of these two terms from (25c) and (25f) is

$$\begin{aligned} \mathcal {E}_{p}+\mathcal {E}_{k}^{\,\text {exchange}}=(\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}=\frac{1}{2}m\rho _{0}^{2}\,\textrm{e}^{-\gamma t}\Omega ^{2}. \end{aligned}$$
(32)

The potential energy can always be tagged with the ‘exchange’ label because all the potential energy is transformed into kinetic energy but not the other way around, if damping is present. Dissipation is velocity-dependent but the potential energy does not involve motion, and thus it cannot contribute to dissipation. Substitution of (32) in the exchange energy expression (31) gives \(\mathcal {E}_{t}^{\textrm{ex}}=(\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}\omega _{d}\). The exchange energy \(\mathcal {E}_{t}^{\textrm{ex}}\) can then be written as

$$\begin{aligned} \mathcal {E}_{t}^{ex}= & {} \frac{(\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}}{\tau _{d}} \nonumber \\= & {} \frac{{ {\mathrm {kinetic \,and \,potential\, energy \,exchange}}}}{\text {one period}}. \end{aligned}$$
(33)

Therefore, \(\mathcal {E}_{t}^{\textrm{ex}}\) represents the total energy that is being exchanged between the kinetic and potential energies per period, more precisely per damped period. This derivation confirms the interpretation that the zeroth-order bracket \(q_{00}\) (8a) is a measure of the energy exchange between the position and velocity vector fields as proposed in §4.1. In the limit of critical damping and beyond, the period tends to infinity and \(\mathcal {E}_{t}^{\textrm{ex}}\) is zero. Then, no energy is exchanged back and forth between the potential and kinetic energies.

Let us now return to the exchange energy \(\mathcal {E}_{\omega }^{\textrm{ex}}=\frac{1}{2}mq_{00}\) (with subindex \(\omega \)) defined in (8c). This quantity can be viewed merely as a scaling of the previous exchange energy, \(\mathcal {E}_{\omega }^{\textrm{ex}}=\Omega ^{-2}\mathcal {E}_{t}^{\textrm{ex}}\). However, if \(\mathcal {E}_{\omega }^{\textrm{ex}}\) is multiplied and divided by \(\omega _{d}\), then

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=(\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}\frac{\omega _{d}^{2}}{\Omega ^{2}}\frac{1}{\omega _{d}}, \end{aligned}$$

that can be written as

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=(\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}\left( 1-\frac{1}{4}\frac{\gamma ^{2}}{\Omega ^{2}}\right) \frac{1}{\omega _{d}}. \end{aligned}$$

But note that

$$\begin{aligned}{} & {} (\mathcal {E}_{p}+\mathcal {E}_{k})^{\text {exchange}}\left( 1-\frac{1}{4}\frac{\gamma ^{2}}{\Omega ^{2}}\right) \\{} & {} \quad =\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma }=\mathcal {E}_{\text {osc}\gamma }. \end{aligned}$$

Thus,

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=\frac{\mathcal {E}_{\text {osc}\gamma }}{\omega _{d}}. \end{aligned}$$

Therefore, \(\mathcal {E}_{\omega }^{\textrm{ex}}\) is the oscillator energy \(\mathcal {E}_{\text {osc}\gamma }\) per damped frequency \(\omega _{d}\).

The \(\mathcal {E}_{\text {osc}\gamma }\) energy loss, from (29) is

$$\begin{aligned} \frac{\textrm{d}\mathcal {E}_{\text {osc}\gamma }}{\textrm{d}t}=-\gamma \mathcal {E}_{\text {osc}\gamma } \end{aligned}$$

and the energy lost in one period is \(({\textrm{d}\mathcal {E}_{\text {osc}\gamma }}/{\textrm{d}t})\tau _{d}\). The well-known quality factor Q for an oscillator with light damping is then

$$\begin{aligned} Q\equiv & {} 2\pi \frac{{ \text {energy stored}}}{{ \left| \text {energy loss in one period}\right| }}\nonumber \\= & {} 2\pi \frac{\mathcal {E}_{\text {osc}\gamma }}{\left| {\textrm{d}\mathcal {E}_{\text {osc}\gamma }}/{\textrm{d}t}\right| \tau _{d}}=\frac{\omega _{d}}{\gamma }. \end{aligned}$$
(34)

Since the energy was evaluated with \(\mathcal {E}_{\text {osc}\gamma }=\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma }\) including the \(\mathcal {E}_{\gamma }\) term, the kinetic energy dissipative oscillations at twice the frequency are cancelled out. Thus, there is neither the need to make the usual assumptions of very light damping (\(\gamma \ll 2\Omega \)) nor averaging of the energy function \(\langle \mathcal {E}_{k}+\mathcal {E}_{p}\rangle \) to obtain this factor. Moreover, this result suggests that the energy stored is \(\mathcal {E}_{\text {osc}\gamma }\), that as we have seen, removes the kinetic energy part that is dissipated.

4.5 Energy ripples

The present description neatly separates the exponential decay from the ripples of the oscillator’s energy as a function of time [34, 35]. The kinetic, potential and dynamic dissipative energies are depicted in figure 3. The ripples in the sum of kinetic and potential energies are clearly seen in the red curve. This modulation of the exponential decay is necessary because the dissipation is velocity-dependent and it must be zero when the kinetic energy is zero. Thus, the sum of kinetic and potential energies must be constant (i.e. with zero slope) when the kinetic energy is zero [36]. This behaviour is clearly seen in figure 3. When the \(\mathcal {E}_{\gamma }\) term is added to \(\mathcal {E}_{k}+\mathcal {E}_{p}\), the energy exhibits a smooth exponential decay. The oscillating part of \(\mathcal {E}_{\gamma }\) cancels out the ripples. For this purpose, it seems advantageous to include the dissipative modulation term with the kinetic and potential energies, \(\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma }\). The \(\left\lfloor v,x\right\rfloor \) w-bracket (13) also suggested this grouping. In contrast, to achieve this even decay in the standard approach, an averaging process is necessary [33]. The averaging needs to be judiciously performed to iron out the wiggles but retain the exponential decay. In the present description, the averaging is completely avoided.

Fig. 3
figure 3

Energy ripples for \(\gamma ={\Omega }/{5}\). \(\mathcal {E}_{k}\) (dot–dashed green curve), \(\mathcal {E}_{k}+\mathcal {E}_{p}\) (red curve) exhibit ripples, \(\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma }\) (dashed blue curve) has a smooth exponential decay and \(\mathcal {E}_{\gamma }\) (brown curve on the abscissa) depicts the dissipative modulation energy that oscillates at \(2\omega _{d}\) with a \(-{\gamma ^{2}}/{4}\) offset.

Full size image

5 Ermakov approach

It is also possible to write from the outset, the damped oscillator differential equation (6) using the complex polar representation, \(x\rightarrow \rho \textrm{e}^{-i\varphi }\). The real part of the differential equation is

$$\begin{aligned} \frac{\ddot{\rho }}{\rho }-\dot{\varphi }^{2}+\gamma \frac{\dot{\rho }}{\rho }+\Omega ^{2}=0, \end{aligned}$$
(35)

whereas the imaginary part \((\ddot{\varphi }+2\dot{\varphi }\dot{\rho }\rho ^{-1})+\gamma \dot{\varphi }=0\), upon multiplication by \(\rho ^{2}\exp (\int \gamma \textrm{d}t)\) can be readily integrated to obtain

$$\begin{aligned} Q_{00}=\rho ^{2}\dot{\varphi }\,\textrm{e}^{\int \gamma \textrm{d}t}. \end{aligned}$$
(36)

This result was obtained in §3.1 using the complex conjugate solutions and the ODEs invariant procedure in (9c). \(Q_{00}\) is denoted in this context as the decoupling constant leading to the amplitude and frequency nonlinear differential equations. The amplitude nonlinear differential equation with time-dependent damping is

$$\begin{aligned} \ddot{\rho }+\gamma \dot{\rho }+\Omega ^{2}\rho =\frac{Q_{00}^{2}\textrm{e}^{-2\int \gamma \textrm{d}t}}{\rho ^{3}}. \end{aligned}$$
(37)

This equation can also be viewed as an anharmonic damped oscillator [37]. The evaluation of the amplitude first and second derivatives from the invariant relationship (36) yield

$$\begin{aligned} \frac{\dot{\rho }}{\rho }=-\frac{1}{2}\left( \frac{\dot{\omega }}{\omega }+\gamma \right) \end{aligned}$$

and

$$\begin{aligned} \frac{\ddot{\rho }}{\rho }=\left( -\frac{1}{2}\frac{\ddot{\omega }}{\omega }+\frac{3}{4}\frac{\dot{\omega }^{2}}{\omega ^{2}}+\frac{1}{4}\gamma ^{2}+\frac{1}{2}\gamma \frac{\dot{\omega }}{\omega }\right) \end{aligned}$$

respectively. Subsequent substitution in (35) gives the frequency nonlinear differential equation in the presence of time-dependent damping,

$$\begin{aligned} \frac{1}{2}\frac{\ddot{\omega }}{\omega }-\frac{3}{4}\frac{\dot{\omega }^{2}}{\omega ^{2}}+\frac{1}{4}\gamma ^{2}+\omega ^{2}-\Omega ^{2}=0. \end{aligned}$$
(38)

This procedure is akin to the Ermakov approach, that originally led to the Ermakov invariant in the undamped case. The usual amplitude and phase solutions for constant \(\gamma \) can be obtained from the amplitude and phase differential equations. The former requires a rescaling of the amplitude by

$$\begin{aligned} \textrm{e}^{-\int \frac{\gamma }{2}dt}=\textrm{e}^{-\frac{\gamma }{2}t}. \end{aligned}$$

The latter is straightforward if a constant \(\omega \) is considered (\(\ddot{\omega }=\dot{\omega }=0\)). The solution to (38) is then

$$\begin{aligned} \omega ^{2}=\Omega ^{2}-\frac{1}{4}\gamma ^{2}=\omega _{d}^{2}. \end{aligned}$$

General solutions with time-dependent amplitude and phase functions can be obtained via the nonlinear superposition principle [38, 39]. Even if \(\gamma \) is constant, the frequency is not necessarily constant since for a phase

$$\begin{aligned} \varphi =\int \omega \, \textrm{d}t=\arctan \left( \eta \tan \left( \omega _{d}t\right) \right) . \end{aligned}$$

The frequency

$$\begin{aligned} \dot{\varphi }=\omega =\frac{\eta }{\cos ^{2}\omega _{d}t+\eta ^{2}\sin ^{2}\omega _{d}t}\omega _{d}, \end{aligned}$$
(39)

with constant \(\eta ={B}/{A}\), is also a solution to the frequency differential equation (38). This assertion can be verified by direct substitution, noticing that

$$\begin{aligned} \dot{\omega }=\frac{\eta (1-\eta ^{2})\sin \left( 2\omega _{d}t\right) }{(\cos ^{2}\omega _{d}t+\eta ^{2}\sin ^{2}\omega _{d}t)^{2}}\omega _{d}^{2} \end{aligned}$$

and

$$\begin{aligned} \ddot{\omega }= & {} \frac{2\eta (1-\eta ^{2})^{2}\sin ^{2}\left( 2\omega _{d}t\right) }{(\cos ^{2}\omega _{d}t+\eta ^{2}\sin ^{2}\omega _{d}t)^{3}}\omega _{d}^{3}\\{} & {} +\frac{2\eta (1-\eta ^{2})\cos \left( 2\omega _{d}t\right) }{(\cos ^{2}\omega _{d}t+\eta ^{2}\sin ^{2}\omega _{d}t)^{2}}\omega _{d}^{3}. \end{aligned}$$

The system’s energy can also be written in amplitude and phase variables via the transformation \(x=\rho \cos \varphi \). The \(\mathcal {E}_{\text {osc}\gamma }=\frac{1}{2}mq_{10}\) energy function (13) is then

$$\begin{aligned}{} & {} \mathcal {E}_{\text {osc}\gamma }=\frac{1}{2}m\rho ^{2}\omega ^{2} \nonumber \\{} & {} \quad \times \left( 1+\frac{1}{2}\frac{\dot{\omega }}{\omega ^{2}}\sin \left( 2\varphi \right) +\frac{1}{2\omega ^{2}}\frac{d}{dt}\left( \frac{\dot{\omega }}{\omega }\right) \cos ^{2}\varphi \right) , \nonumber \\ \end{aligned}$$
(40)

where the expression for the frequency \(\omega \) and its derivative in terms of \(\Omega ^{2}\) and \(\gamma \) is given by the solution to the differential equation (38). If the frequency is constant, the usual \(\frac{1}{2}m\rho ^{2}\omega ^{2}\) dependence is recovered. The transformation \(x\rightarrow ({x}/{\rho )}\) viewed in terms of the bracket expression

$$\begin{aligned} \left\lfloor f,g\right\rfloor =f^{2}\frac{\textrm{d}}{\textrm{d}t}\left( \frac{g}{f}\right) , \end{aligned}$$

derived in the Appendix, explains the \(\rho ^{2}\) time scaling proposed by [17]. The role of the invariant as the energy function in the transformed coordinates has been pointed out before [17, 24, 40]. In the quantum version, this invariant can be used in an equivalent fashion as the Hamiltonian in the time-independent case, i.e., to obtain evolution operators, to cast the equations of motion of different operators in commutative expressions and to produce a phase shift with its exponential form [41].

6 Discussion and conclusions

The complementary or orthogonal functions rationale has been used to derive various conserved quantities. The energy as well as the energy exchange emerge from Wronskian operators, referred here as w-brackets. The general case that was undertaken is a one-dimensional time-dependent harmonic oscillator with damping. The time-dependent restitutive and damping coefficients give rise to dynamic field energies, \(\mathcal {E}_{df}\), in eq. (14a), that keep memory of the system’s evolution.

The damped harmonic oscillator problem provides a clear-cut scenario to give a physical meaning to the zeroth-order w-bracket \(q_{00}\). The exchange energy

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=\frac{1}{2}mq_{00}=\frac{\mathcal {E}_{\text {osc}\gamma }}{\omega _{d}} \end{aligned}$$

represents the periodic transfer between two energy forms per unit frequency, the kinetic and potential energies in this case. If the exchange energy \(q_{00}\) is scaled by \(\kappa =m\Omega ^{2}\), as proposed in eq. (30), the physical interpretation of \(\mathcal {E}_{t}^{\textrm{ex}}\) is the energy exchanged between the kinetic and potential energies per period. In either case, if \(q_{00}\) is zero or negative, that is, at critical or heavy damping, there is no periodic exchange between the two forms of energy but, at most, only a non-periodic transfer between them.

In the absence of damping, the total energy of the system \(\mathcal {E}\), the energy of the oscillator

$$\begin{aligned} \mathcal {E}_{\text {osc}}=\mathcal {E}_{\text {osc}\gamma }=\frac{1}{2}m\rho _{0}^{2}\,\Omega ^{2} \end{aligned}$$

and the energy exchanged between the kinetic and potential energies

$$\begin{aligned} \mathcal {E}_{\omega }^{\textrm{ex}}=\frac{1}{2}m\rho _{0}^{2}\,\Omega \end{aligned}$$

are the same, except for the constant factor \(\Omega \). This degeneracy is lifted when damping is present, allowing for a clear distinction and physical interpretation of these quantities.

A scheme of the energies involved and their interaction for a damped oscillator with time-independent parameters, is summarised in figure 4. The energy of the system is composed of three parts: kinetic, potential and dissipation modulation energies. Recall that contrary to our approach, dissipation is often described via open systems, where the dissipated energy is no longer part of the system. The total energy in the present conceptualisation, is given by the sum of these three contributions times an exponential function, and is measured by the first-order invariant \(\mathcal {E}=\frac{1}{2}mQ_{10}\). The transformation of kinetic into potential energy and vice versa is evaluated by the zeroth-order \(q_{00}\) exchange energy. To this end, the kinetic energy \(\mathcal {E}_{k}\) has been separated in two parts, \(\mathcal {E}_{k}^{\text {exchange}}\) is converted into potential energy whereas \(\mathcal {E}_{k}^{\text {dissipated}}\) is lost by dissipation. The dissipative modulation energy \(\mathcal {E}_{\gamma }\) has an oscillating contribution that cancels out the dissipative part of the kinetic energy. The inclusion of this term circumvents the necessity of averaging, an asset that is particularly useful close to critical damping. The remaining frequency offset \({\gamma ^{2}}/{4}\) term, together with \(\Omega ^{2}\) from the potential plus the non-dissipative kinetic energy, add up to \(\omega _{d}^{2}\), the damped frequency squared.

Fig. 4
figure 4

Energy scheme for a harmonic oscillator with constant damping. The exchange energy \(\mathcal {E}_{t}^{\textrm{ex}}\) represents the energy flow between the kinetic and potential forms per period. The invariant \(\mathcal {E}=\frac{1}{2}mQ_{10}=\textrm{e}^{\gamma t}(\mathcal {E}_{k}+\mathcal {E}_{p}+\mathcal {E}_{\gamma })\) evaluates the total energy of the system including the dissipated energy.

Full size image

The Ermakov amplitude and phase equations with damping have been derived. The \(Q_{00}\) decoupling invariant has been obtained in two ways: via the complementary functions and in the more conventional Ermakov approach. To the best of our knowledge, the frequency nonlinear differential equation (38) with time-dependent damping has not been presented before. The position (6), amplitude (37) and frequency (38) differential equations form the so-called Ermakov triplet [23] for the time-dependent damped harmonic oscillator.