Analytical studies on the dynamics of higher-dimensional nonlinear circuit systems

Abstract

Explicit analytical solutions of higher-dimensional chaotic and hyperchaotic systems are areas of research to be much explored. Till now, the dynamics of higher-dimensional systems and the synchronisation dynamics of coupled higher-dimensional systems have not been studied analytically. In the present work, explicit analytical solutions are developed for the dynamical behaviours observed in third-order and fourth-order nonlinear dissipative systems and also for the coupled dynamics of these systems. The Chua’s circuit and the modified canonical Chua’s circuit are studied analytically in the present work. The analytical results explaining the underlying important features of these systems are validated through experimental results.

1 Introduction

The observation of chaos in the Chua’s circuit system [1] has marked the beginning of the era of real-time chaotic systems. The emergence and the chaotic nature of the single-scroll and double-scroll attractors in the Chua’s circuit have been rigorously studied [2, 3]. Different parameter regions for the evolution of chaos and the numerous patterns of chaotic attractors in the Chua’s circuit system has been well studied [4,5,6]. The emergence of synchronisation in coupled Chua’s circuit systems [7,8,9] has been reported following the master–slave concept of chaos synchronisation introduced by Pecora and Carroll [10]. Several types of synchronisation and their mechanism of evolution in coupled chaotic systems have been reported [11]. Several variants of the Chua’s circuit and the chaotic, strange non-chaotic, hyperchaotic dynamics observed in these circuits have been subsequently reported [12,13,14,15]. A detailed analysis of the geometrical structure of the double-scroll chaotic attractor observed in Chua’s circuit has been done in [2]. The chaotic nature of the double-scroll attractor is rigorously established by studying the existence of homoclinic orbits using the analytic expressions derived for the Poincaré return maps [3]. Further, the analytical proofs of the Poincaré maps are used to characterise the birth and death of the double-scroll attractor. Mostly, the analytical expressions rigorously prove the structural stability of the double-scroll attractor through an analysis of the Poincaré return maps obtained analytically. In the case of a second-order electronic circuit system with a negative resistance and diode pair, analytical solution for the Poincaré map is derived as a return map [16]. The construction of the Chua’s diode using operational amplifiers and linear resistors [17] lead to the identification of chaos in several simple second-order, non-autonomous electronic circuits that quite changed the researchers’ perspective on chaotic systems [18,19,20,21]. The identification of chaos and its synchronisation in a second-order circuit system with a memristor element has also been reported [22]. The mathematical simplicity of the circuit equations of second-order chaotic systems has enabled the development of explicit analytical solutions to the normalised state equations of the systems. A standard method for obtaining explicit analytical solutions for the normalised state equations of the simple chaotic systems has been reported [23]. The evolution of chaos through analytical solutions in several simple chaotic systems has been studied through phase portraits using this method [20, 21, 24, 25]. The dynamics of third-order non-autonomous chaotic systems have been studied analytically using phase portraits [26, 27]. The analytical dynamics of simple chaotic systems studied through phase portraits, Poincaré maps and bifurcation diagrams have been reported recently [28]. Further, the strange non-chaotic dynamics observed in quasiperiodically forced simple chaotic systems have been studied analytically [29,30,31]. This analytical method has been further developed to reveal the synchronisation dynamics of coupled second-order chaotic systems [32]. The synchronisation dynamics of unidirectionally coupled chaotic, strange non-chaotic systems, mutually coupled chaotic systems and a linear network of unidirectionally coupled chaotic systems have been studied analytically [33,34,35,36,37]. Further, explicit analytical solutions for the transmission of and recovery of information signals using a simple communication scheme have been developed using this method [38]. The evolution of different attractors pertaining to the second-order piecewise-linear systems could be studied using the aforementioned method which marks the importance of analytical solutions in studying the behaviour of dynamical systems [39]. However, the analytical method has not been well developed to study the dynamics of higher-dimensional autonomous piecewise-linear systems which is the prime objective of this research. The present work is focussed on developing explicit analytical solutions for the state equations of third-order and fourth-order autonomous nonlinear systems exhibiting chaotic and hyperchaotic behaviour in their dynamics.

This article is arranged as follows: In §2, we develop explicit analytical solutions for the third-order Chua’s circuit system [1] and the analytical solutions for the fourth-order modified canonical Chua’s circuit [15] are developed in §3. Finally, summary and conclusions are given in §4.

2 Chua’s circuit

Fig. 1

Schematic diagram of the Chua’s circuit with two capacitors $C_1, C_2$, an inductor L, a linear resistor R and the Chua’s diode ($N_R$).

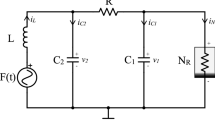
The Chua’s circuit [1] consisting of an inductor, a linear resistor, two capacitors and a Chua’s diode connected parallel to one of the capacitor is shown in figure 1. The op-amp realisation of the Chua’s diode and its corresponding $v-i$ characteristics are shown in figure 2. The normalised state equations of the Chua’s circuit shown in figure 1 is given as

$$\begin{aligned}&C_1 {\mathrm {d}v_1 \over \mathrm {d}t }=\frac{1}{R} (v_2 - v_1) - h(v_1), \end{aligned}$$

(1a)

$$\begin{aligned}&C_2 {\mathrm {d}v_2 \over \mathrm {d}t }=\frac{1}{R} (v_1 - v_2) + i_L, \end{aligned}$$

(1b)

$$\begin{aligned}&L {\mathrm {d}i_L \over \mathrm {d}t }=-v_2, \end{aligned}$$

(1c)

where $h(v_1)$ is the mathematical form of the piecewise-linear resistor given by

$$\begin{aligned} g(v) = {\left\{ \begin{array}{ll} {G_b}v_1+({G_a}-{G_b}) &{} \hbox { if}\ v_1 > 1,\\ {G_a}v_1 &{} \hbox { if}\ |v_1|\le 1,\\ {G_b}v_1-({G_a}-{G_b}) &{} \hbox { if}\ v_1 < -1. \end{array}\right. } \end{aligned}$$

(2)

Fig. 2

(a) Schematic representation of the Chua’s diode and (b) its corresponding $(v-i)$ characteristics.

The state equations in dimensionless form is written as

$$\begin{aligned} \dot{x}= & {} \alpha (y - x - h(x)), \end{aligned}$$

(3a)

$$\begin{aligned} \dot{y}= & {} x - y +z, \end{aligned}$$

(3b)

$$\begin{aligned} \dot{z}= & {} -\beta y \end{aligned}$$

(3c)

and h(x) is given by

$$\begin{aligned} h(x) = {\left\{ \begin{array}{ll} bx+(a-b) &{} \hbox { if}\ x > 1,\\ ax &{} \hbox { if}\ |x|\le 1,\\ bx-(a-b) &{} \hbox { if}\ x < -1, \end{array}\right. } \end{aligned}$$

(4)

where $v_1=x B_P$, $v_2=yB_P$, $i_L=B_Pz/R$, $\alpha = C_2/C_1$, $\beta = C_2 R^2/L$, $a = R G_a$, $b = R G_b$. Considering $\beta$ as the control parameter, the other parameters take the values $a=-1.1516$, $b=-0.818$, $\alpha =10$.

2.1 Analytical dynamics of the Chua’s circuit

In this section, we develop analytical solutions for each of the piecewise-linear regions of eq. (3).

2.1.1 $D_0$ region

In this region, $h(x)=ax$, and the state equations obtained from eq. (3) are written as

$$\begin{aligned} \dot{x}= & {} \alpha (y - x - ax), \end{aligned}$$

(5a)

$$\begin{aligned} \dot{y}= & {} x - y +z, \end{aligned}$$

(5b)

$$\begin{aligned} \dot{z}= & {} -\beta y. \end{aligned}$$

(5c)

Differentiating eq. (5a), we get

$$\begin{aligned} \dddot{x} + A \ddot{x} + B \dot{x} + C x = 0, \end{aligned}$$

(6)

where $A=\alpha (1+a)$, $B=a \alpha + \beta$ and $C=\alpha \beta (1+a)$. In this region, the roots $m_1,m_{2,3} = u \pm iv$ corresponding to eq. (6) are real roots and a pair of complex conjugates for all values of $\beta$. Hence, the general solution to eq. (6) is written as

$$\begin{aligned} x(t) = C_1 \mathrm {e}^{m_1 t} + \mathrm {e}^{ut} (C_2 \cos vt + C_3 \sin vt). \end{aligned}$$

(7)

Differentiating eq. (7) and using it in eqs (5) yields

$$\begin{aligned}&y(t) = \frac{\dot{x}(t)}{\alpha } + (1+a) x(t), \end{aligned}$$

(8)

$$\begin{aligned}&z(t) = \dot{y}(t) - x(t) + y(t). \end{aligned}$$

(9)

The constants $C_1, C_2, C_3$ are given as

$$\begin{aligned} C_3= & {} \frac{(uv-vm_1) A_1 \mathrm {e}^{-ut_0} - v^2 B_1 \mathrm {e}^{-ut_0}}{{((uv-vm_1)}^2+v^4)}, \end{aligned}$$

(10a)

$$\begin{aligned} C_2= & {} \frac{-v^2 A_1 \mathrm {e}^{-ut_0}-(uv-vm_1) B_1 \mathrm {e}^{-ut_0}}{{((uv-vm_1)}^2+v^4)}, \end{aligned}$$

(10b)

$$\begin{aligned} C_1= & {} \mathrm {e}^{-m_1t_0} \{x_0 -\mathrm {e}^{ut_0}(C_2 \mathrm {cos} vt_0 + C_3 \mathrm {sin} vt_0)\}, \end{aligned}$$

(10c)

where

$$\begin{aligned} A_1= & {} ((P_1 - m_1Q_1)-u(Q_1-m_1x_0)) \cos vt_0 \\&+\, v(Q_1-m_1x_0) \sin vt_0, \\ B_1= & {} ((P_1 - m_1Q_1)-u(Q_1-m_1x_0)) \sin vt_0 \\&-\, v(Q_1-m_1x_0) \cos vt_0, \\ P_1= & {} \alpha (x_0-y_0+z_0) - \alpha ^2(1+a) (y_0-x_0-ax_0), \\ Q_1= & {} \alpha (y_0 - (1+a)x_0). \end{aligned}$$

2.1.2 $D_{+1}$ region

In this region, $h(x)=bx+(a-b)$, and the state equations obtained from eq. (3) are

$$\begin{aligned} \dot{x}= & {} \alpha (y - x - bx - (a-b)), \end{aligned}$$

(11a)

$$\begin{aligned} \dot{y}= & {} x - y +z,\end{aligned}$$

(11b)

$$\begin{aligned} \dot{z}= & {} -\beta y. \end{aligned}$$

(11c)

Differentiating eq. (11a) we get

$$\begin{aligned} \dddot{x} + A \ddot{x} + B \dot{x} + C x = \Delta , \end{aligned}$$

(12)

where $A=\alpha (1+b)$, $B=b \alpha + \beta$, $C=\alpha \beta (1+b)$ and $\Delta =-\alpha \beta (a-b)$. The roots $m_4,m_5, m_6$ of eq. (12) are real roots and a pair of complex conjugates for $\beta \le 17.9301$ while the roots are a pair of complex conjugates and a real root for $\beta > 17.9301$. Considering $m_4$ as the real root and $m_{5,6} = u \pm iv$ as the complex conjugates for all the values of $\beta$ under study, the general solution to eq. (12) is written as

$$\begin{aligned} x(t) = C_4 \mathrm {e}^{m_4 t} + \mathrm {e}^{ut} (C_5 \cos vt + C_6 \sin vt) + C_7. \nonumber \\ \end{aligned}$$

(13)

Differentiating eq. (13) and using it in eq. (11) we get

$$\begin{aligned}&y(t) = \frac{\dot{x}(t)}{\alpha } + (1+b) x(t) + (a-b), \end{aligned}$$

(14)

$$\begin{aligned}&z(t) = \dot{y}(t) - x(t) + y(t). \end{aligned}$$

(15)

The constants $C_4, C_5, C_6, C_7$ are given as

$$\begin{aligned} C_7= & {} \frac{\Delta }{C}, \end{aligned}$$

(16a)

$$\begin{aligned} C_6= & {} \frac{(uv-vm_4) A_2 \mathrm {e}^{-ut_0}-v^2 B_2 \mathrm {e}^{-ut_0}}{{((uv-vm_4)}^2+v^4)}, \end{aligned}$$

(16b)

$$\begin{aligned} C_5= & {} \frac{-v^2 A_2 \mathrm {e}^{-ut_0}-(uv-vm_4) B_2 \mathrm {e}^{-ut_0}}{{((uv-vm_4)}^2+v^4)}, \end{aligned}$$

(16c)

$$\begin{aligned} C_4= & {} \mathrm {e}^{-m_4t_0} \{x_0 -\mathrm {e}^{ut_0}(C_5 \cos vt_0 + C_6 \sin vt_0) \nonumber \\&-\, C_7\}, \end{aligned}$$

(16d)

where

$$\begin{aligned} A_2= & {} ((P_2 - m_4Q_2)-u(Q_2-m_4x_0)) \cos vt_0 \\&+\, v(Q_2-m_4x_0) \sin vt_0 \\&+\, vm_4 C_7 \sin vt_0 - um_4 C_7 \cos vt_0, \\ B_2= & {} ((P_2 - m_4Q_2)-u(Q_2-m_4x_0)) \sin vt_0 \\&-\, v(Q_2-m_4x_0) \cos vt_0 \\&-\,um_4 C_7 \sin vt_0 - vm_4 C_7 \cos vt_0, \\ P_2= & {} \alpha (x_0-y_0+z_0) \\&- \alpha ^2(1+b) (y_0-x_0-ax_0-a+b), \\ Q_2= & {} \alpha (y_0 - (1+b)x_0-a+b). \end{aligned}$$

2.1.3 $D_{-1}$ region

In this region, $h(x)=bx-(a-b)$, and the state equations are written as

$$\begin{aligned} \dot{x}= & {} \alpha (y - x - bx + (a-b)), \end{aligned}$$

(17a)

$$\begin{aligned} \dot{y}= & {} x - y +z,\end{aligned}$$

(17b)

$$\begin{aligned} \dot{z}= & {} -\beta y. \end{aligned}$$

(17c)

Differentiating eq. (17a), we get

$$\begin{aligned} \dddot{x} + A \ddot{x} + B \dot{x} + C x = \Delta , \end{aligned}$$

(18)

where $A=\alpha (1+b)$, $B=b \alpha + \beta$, $C=\alpha \beta (1+b)$ and $\Delta =\alpha \beta (a-b)$. The roots of eq. (18) are the same as given in the $D_{+1}$ region and the state variables corresponding to this region are given as

$$\begin{aligned} x(t)= & {} C_4 \mathrm {e}^{m_4 t} + \mathrm {e}^{ut} (C_5 \cos vt + C_6 \sin vt) + C_7, \end{aligned}$$

(19)

$$\begin{aligned} y(t)= & {} \frac{\dot{x}(t)}{\alpha } + (1+b) x(t) - (a-b), \end{aligned}$$

(20)

$$\begin{aligned} z(t)= & {} \dot{y}(t) - x(t) + y(t). \end{aligned}$$

(21)

The constants $C_4, C_5, C_6, C_7$ and $A_2, B_2$ are as given in §2.1.2 except for $P_2$ and $Q_2$ which are given as follows:

$$\begin{aligned} P_2= & {} \alpha (x_0-y_0+z_0) \\&- \alpha ^2(1+b) (y_0-x_0-ax_0+a-b), \\ Q_2= & {} \alpha (y_0 - (1+b)x_0+a-b). \end{aligned}$$

The analytical solutions obtained can be used to generate the trajectories of the state variables in phase space. Starting with an initial condition in the $D_0$ region, the arbitrary constants $C_1$, $C_2$ and $C_3$ given in eq. (7) get fixed and x(t) evolves as given in eq. (7) up to the time $t=T_1$, when $x(T_1)=1$ and ${\dot{x}}(T_1) > 0$ or $t=T'_1$, when $x(T'_1) = -1$ and ${\dot{x}}(T'_1) < 0$. By knowing whether $T_1 < T'_1$ or $T_1 > T'_1$, the next region of operation $(D_{\pm 1})$ can be determined and the arbitrary constants of the solutions of the state variables pertaining to the region can be fixed by matching the solutions. This procedure can be continued for each successive crossing and the explicit solutions are obtained in the regions $D_0$, $D_{\pm 1}$. Further, at each crossing of the break point region, the sensitive dependence on initial conditions is introduced at appropriate parameter regimes during the inverse procedure of finding $T_1, T'_1, T_2, T'_2,...,$ etc., from the solutions.

Fig. 3

(a) One-parameter bifurcation diagram observed analytically indicating the reverse period-doubling route with $\beta$ as the control parameter and (b) largest Lyapunov exponent ($\lambda _L$).

The analytically obtained state variables in each of the piecewise-linear regions can be used to generate chaotic dynamics in Chua’s circuit. The period-doubling sequence to chaos observed in the circuit for the chosen values of the system parameters is shown in the bifurcation diagram given in figure 3. Figure 3a showing the analytically observed bifurcation diagram indicates the reverse period-doubling sequence to chaos as the control parameter $\beta$ is varied. The corresponding largest Lyapunov exponent $\lambda _L$ is shown in figure 3b. The analytically observed phase portraits and Poincaré maps (blue coloured dots) indicating the period-doubling sequence to chaos along with the multistability of the attractors in the (x–y) phase-plane is shown in figure 4. The attractors evolving from two different sets of initial conditions revealing the coexistence of attractors in the left half plane (red) and right half plane (green) are shown in figures 4a–4e. Figures 4a–4e show the period-T limit cycle for $\beta =18.5$, period-2T limit cycle for $\beta =17.6$, period-4T limit cycle for $\beta =17.5$, period-8T limit cycle for $\beta =17.435$ and the single-scroll chaotic attractor for $\beta =16.6$, respectively. Figure 4f shows the double-scroll chaotic attractor obtained for $\beta =16.5$. The experimental results for the period-doubling route to chaos revealing the multistability of the attractors is shown in figure 5. The analytically observed basins of attraction for the single-scroll chaotic attractor in the $(x_0$–$y_0)$ plane is shown in figure 6. The region in red indicates the set of initial conditions leading to the attractor settling down at the left half plane while the green coloured region represents the initial conditions leading to the attractor of the right half plane. Figures 7a and 7b show the analytically observed double-scroll chaotic attractor obtained for $\beta =16.5$ in the x–y–z phase-space and the experimentally observed double-scroll chaotic attractor in the $v_1(\tau )$–$v_2(\tau )$ plane, respectively. The analytical evolution of the double-scroll chaotic attractor of the Chua’s circuit with time in the x–y–z phase-space is shown in the supplementary file. In the next section, the synchronisation dynamics of the Chua’s circuit system studied using explicit analytical solutions is presented.

Fig. 4

Analytical results: Phase portraits and Poincaré maps (blue dots) in the x–y plane indicating period-doubling sequence to chaos and multistability of the attractors in the left half plane (red) and right half plane (green). (a) period-T limit cycle for $\beta =18.5$; (b) period-2T limit cycle for $\beta =17.6$; (c) period-4T limit cycle for $\beta =17.5$; (d) period-8T limit cycle for $\beta =17.435$; (e) single-scroll chaotic attractor for $\beta =16.6$ and (f) double-scroll chaotic attractor for $\beta =16.5$.

Fig. 5

Experimental observation of phase portraits in the $v_1(\tau )$–$v_2(\tau )$ plane confirming the multistability and period-doubling sequence of attractors in the (a) left half plane and (b) right half plane. (i) Period-T limit cycle, (ii) period-2T limit cycle, (iii) period-4T limit cycle and (iv) single-scroll chaotic attractor (vertical scale: 20 mV/div., horizontal scale: 50 mV/div.).

Fig. 6

Analytical results: Basin of attraction of the single-scroll chaotic attractor shown in figure 4e corresponding to the left half plane (red) and right half plane (green) in the $(x_0$–$y_0)$ plane.

Fig. 7

(a) Analytically observed double-scroll chaotic attractor in the x–y–z phase space and (b) experimentally observed double-scroll chaotic attractor in the $v_1(\tau )$–$v_2(\tau )$ plane (vertical scale: 50 mV/div., horizontal scale: 20 mV/div.).

2.2 Analytical study of synchronisation of Chua’s circuit

In this section, analytical solutions are developed for the synchronisation process observed in coupled Chua’s circuit systems. The system discussed in §2.1 acts as the drive, response systems and each system operates with different initial conditions. The schematic diagram of the unidirectionally coupled Chua’s circuit systems is shown in figure 8. The two systems are coupled through the x-variable and their synchronisation process is studied by evaluating the difference system obtained from their state equations. The state equations of the drive system is given in eq. (3) and that of the response system is given as

$$\begin{aligned} \dot{x}'= & {} \alpha (y' - x' - h(x')) + \epsilon (x-x'), \end{aligned}$$

(22a)

$$\begin{aligned} \dot{y}'= & {} x' - y' +z', \end{aligned}$$

(22b)

$$\begin{aligned} \dot{z}'= & {} -\beta y', \end{aligned}$$

(22c)

where $\epsilon$ is the coupling parameter and $h(x')$ is given by

$$\begin{aligned} h(x') = {\left\{ \begin{array}{ll} bx'+(a-b) &{} \hbox { if}\ x' > 1,\\ ax' &{} \hbox { if}\ |x'|\le 1,\\ bx'-(a-b) &{} \hbox { if}\ x' < -1, \end{array}\right. } \end{aligned}$$

(23)

where $x',y',z'$ are the state variables of the response system. The difference system obtained from eqs (3) and (22) is written as

$$\begin{aligned} \dot{x}^{*}= & {} \alpha (y^{*} - x^{*} - h(x^{*})) + \epsilon x^{*}, \end{aligned}$$

(24a)

$$\begin{aligned} \dot{y}^{*}= & {} x^{*} - y^{*} +z^{*},\end{aligned}$$

(24b)

$$\begin{aligned} \dot{z}^{*}= & {} -\beta y^{*}, \end{aligned}$$

(24c)

where $x^{*}=$ $x-x'$, $y^{*}=y-y'$, $z^{*}=z-z'$ and $h(x^{*}) = h(x) - h(x')$. The state variables of the response system are written as

$$\begin{aligned} x'(t)= & {} x(t) - x^{*}(t), \end{aligned}$$

(25a)

$$\begin{aligned} y'(t)= & {} y(t) - y^{*}(t),\end{aligned}$$

(25b)

$$\begin{aligned} z'(t)= & {} z(t) - z^{*}(t). \end{aligned}$$

(25c)

The origin is the equilibrium point in the three regions of the difference system and are given as

$$\begin{aligned} \left. \begin{aligned}&D^{*}_{+1} = \{ (x^{*},y^{*},z^{*})| x^{*} > 1 \}| P^{*}_+ = (0,0,0)\\&D^{*}_0 = \{ (x^{*},y^{*},z^{*})|| x^{*} | \le 1 \}| O^{*} = (0,0,0)\\&D^{*}_{-1} = \{ (x^{*},y^{*},z^{*})|x^{*} < -1 \}| P^{*}_- = (0,0,0)\\ \end{aligned} \right\} .\nonumber \\ \end{aligned}$$

(26)

The stability of the origin given in eq. (26) is observed through stability matrices. In the $D^{*}_0$ region, the stability matrix is

$$\begin{aligned} J^{*}_{0} = \begin{pmatrix} -(\alpha +\alpha a +\epsilon ) &{}&{}&{} \alpha &{}&{}&{} 0 \\ 1 &{}&{}&{} -1 &{}&{}&{} 1 \\ 0 &{}&{}&{} -\beta &{}&{}&{} 0 \\ \end{pmatrix}, \end{aligned}$$

(27)

while in the $D^{*}_{\pm 1}$ regions it is

$$\begin{aligned} J^{*}_{\pm 1} = \begin{pmatrix} -(\alpha +\alpha b +\epsilon ) &{}&{}&{} \alpha &{}&{}&{} 0 \\ 1 &{}&{}&{} -1 &{}&{}&{} 1 \\ 0 &{}&{}&{} -\beta &{}&{}&{} 0 \\ \end{pmatrix}. \end{aligned}$$

(28)

The stability of the origin varies with $\epsilon$ in each region as $\epsilon$ is changed. In the $D^{*}_0$ region, for $\beta =16.5$, the eigenvalues are a pair of complex conjugates and a real root for $\epsilon \le 3.027$ while it is a real root and a pair of complex conjugates for $\epsilon > 3.027$. Similarly, in the $D^{*}_0$ region, for $\beta =16.6$, the eigenvalues are a pair of complex conjugates and a real root for $\epsilon \le 3.049$ while it is a real root and a pair of complex conjugates for $\epsilon > 3.049$. In the $D^{*}_{\pm 1}$ region, the eigenvalues are one real root and a pair of complex conjugates for all values of $\epsilon$. When $\epsilon =0,$ i.e. under the uncoupled state, the dynamics of the systems are determined by the state variables x(t), y(t), z(t) given in §2.1 except that the drive and response systems operate with different initial conditions and hence become unsynchronised. For $\epsilon >0$, the systems are coupled and the dynamics of the response system is controlled by the drive through $\epsilon$. The state variables of the response system $x'(t), y'(t), z'(t)$ could be obtained from eq. (25) by solving eq. (24) for the state variables $[x^{*} (t; t_0, x^{*}_0, y^{*}_0, z^{*}_0),$ $y^{*}(t; t_0, x^{*}_0, y^{*}_0, z^{*}_0),$ $z^{*}(t; t_0, x^{*}_0, y^{*}_0, z^{*}_0)]^T$ with the initial conditions given as $(t, x^{*}, y^{*},z^{*})$ $= (t_0, x^{*}_0, y^{*}_0, z^{*}_0)$ and using the state variables of the drive x(t), y(t), z(t). The solutions of the difference system given in eq. (24) for the three regions is summarised as follows:

Fig. 8

Schematic diagram of the unidirectionally coupled drive and response Chua’s circuit systems.

Fig. 9

Analytical results of the coupled Chua’s circuits operating in single-scroll chaotic attractor state: (a) Unsynchronised and (b) synchronised states for $\epsilon =0$ and $\epsilon =15$, respectively. (i) Drive system attractor in the (x–y) plane; (ii) response system attractor in the $(x'$–$y')$ plane; (iii) dynamical process in the x–$x'$ plane and (iv) time series of the drive system signal x (red) and response system signal $x'$ (blue) indicating the unsynchronised and synchronised states.

2.2.1 Region $D^{*}_0$

In this region, $h(x^{*}) = ax^{*}$ and the state equations obtained from eq. (24) are

$$\begin{aligned} \dot{x}^{*}= & {} \alpha y^{*} - (\alpha +\alpha a +\epsilon ) x^{*}, \end{aligned}$$

(29a)

$$\begin{aligned} \dot{y}^{*}= & {} x^{*} - y^{*} +z^{*},\end{aligned}$$

(29b)

$$\begin{aligned} \dot{z}^{*}= & {} -\beta y^{*}. \end{aligned}$$

(29c)

Differentiating eq. (29a) we get

$$\begin{aligned} \dddot{x}^{*} + A \ddot{x}^{*} + B \dot{x}^{*} + C x^{*} = 0, \end{aligned}$$

(30)

where $A=(1+\alpha (1+a)+\epsilon )$, $B= \alpha a + \beta +\epsilon$ and $C=\beta (\alpha (1+a)+\epsilon )$. The roots of eq. (30) are a pair of complex conjugates and a real root for $\epsilon \le 3.027$ and are a pair of complex conjugates and a real root for $\epsilon > 3.027$. Taking $m_1$ as the real root and $m_{2,3} = u \pm iv$ as the complex conjugate pairs, the general solution to eq. (30) is written as

$$\begin{aligned} x^{*}(t) = C_1 \mathrm {e}^{m_1 t} + \mathrm {e}^{ut} (C_2 \cos vt + C_3 \sin vt). \end{aligned}$$

(31)

Differentiating eq. (31) we get the state variables

$$\begin{aligned} y^{*}(t)= & {} \frac{1}{\alpha } \{\dot{x}^{*}(t) + (\alpha +\alpha a+\epsilon ) x^{*}(t)\}, \end{aligned}$$

(32)

$$\begin{aligned} z^{*}(t)= & {} \dot{y}^{*}(t) - x^{*}(t) + y^{*}(t). \end{aligned}$$

(33)

The constants $C_1, C_2, C_3$ are given as

$$\begin{aligned} C_3= & {} \frac{(uv-vm_1) A_1 \mathrm {e}^{-ut_0}- v^2 B_1 \mathrm {e}^{-ut_0}}{{((uv-vm_1)}^2+v^4)}, \end{aligned}$$

(34a)

$$\begin{aligned} C_2= & {} \frac{-v^2 A_1 \mathrm {e}^{-ut_0}-(uv-vm_1) B_1 \mathrm {e}^{-ut_0}}{{((uv-vm_1)}^2+v^4)}, \end{aligned}$$

(34b)

$$\begin{aligned} C_1= & {} \mathrm {e}^{-m_1t_0} \{x^{*}_0 -\mathrm {e}^{ut_0}(C_2 \cos vt_0 + C_3 \sin vt_0)\},\nonumber \\ \end{aligned}$$

(34c)

where

$$\begin{aligned} A_1= & {} ((P_1 - m_1Q_1)-u(Q_1-m_1x^{*}_0)) \cos vt_0 \\&+\, v(Q_1-m_1x^{*}_0) \sin vt_0, \\ B_1= & {} ((P_1 - m_1Q_1)-u(Q_1-m_1x^{*}_0)) \sin vt_0 \\&-\, v(Q_1-m_1x^{*}_0) \cos vt_0, \\ P_1= & {} \alpha (x^{*}_0-y^{*}_0+z^{*}_0) - \alpha (\alpha +\alpha a+\epsilon ) y^{*}_0 \\&+\, {(\alpha +\alpha a+\epsilon )}^{2} x^{*}_0, \\ Q_1= & {} \alpha y^{*}_0 - (\alpha +\alpha a+\epsilon ) x^{*}_0. \end{aligned}$$

Using the state variables $x^{*}(t),~y^{*}(t),~z^{*}(t)$ from eqs (31)–(33) and x(t),  y(t),  z(t) obtained from eqs (7)–(9), $x{'}(t)$, $y{'}(t)$, $z{'}(t)$ can be obtained from eq. (25).

Fig. 10

Experimentally observed complete synchronisation in Chua’s circuit for coupled single-scroll chaotic attractors. (i) Phase portraits (vertical scale: 10 mV/div., horizontal scale: 10 mV/div.) and (ii) time series of the drive (yellow) and the response (green) signals (vertical scale: 2 V/div., horizontal scale: 500 $\mu$s/div.) indicating the (a) unsynchronised and (b) synchronised states.

2.2.2 Region $D^{*}_{\pm 1}$

In these regions, $h(x^{*}) = bx^{*}$ and the state equations obtained from eq. (24) are

$$\begin{aligned} \dot{x}^{*}= & {} \alpha y^{*} - (\alpha +\alpha b +\epsilon ) x^{*}, \end{aligned}$$

(35a)

$$\begin{aligned} \dot{y}^{*}= & {} x^{*} - y^{*} +z^{*},\end{aligned}$$

(35b)

$$\begin{aligned} \dot{z}^{*}= & {} -\beta y^{*}. \end{aligned}$$

(35c)

Differentiating eq. (35a) we get

$$\begin{aligned} \dddot{x}^{*} + A \ddot{x}^{*} + B \dot{x}^{*} + C x^{*} = 0, \end{aligned}$$

(36)

where $A=1+\alpha (1+b)+\epsilon$, $B= \alpha b + \beta +\epsilon$ and $C=\beta (\alpha (1+b)+\epsilon )$. The roots of eq. (36) are a real root $m_4$, and a pair of complex conjugates $m_{5,6} = u \pm iv$ for all the values of $\epsilon$ and the general solution is

$$\begin{aligned} x^{*}(t)&= C_4 \mathrm {e}^{m_1 t} \nonumber \\&\quad + \mathrm {e}^{ut} (C_5 \cos vt + C_6 \sin vt). \end{aligned}$$

(37)

Differentiating eq. (37) and using it in eq. (29) we get the state variables,

$$\begin{aligned} y^{*}(t)= & {} \frac{1}{\alpha } \{\dot{x}^{*}(t) + (\alpha +\alpha b+\epsilon ) x^{*}(t)\} , \end{aligned}$$

(38)

$$\begin{aligned} z^{*}(t)= & {} \dot{y}^{*}(t) - x^{*}(t) + y^{*}(t). \end{aligned}$$

(39)

The constants $C_4, C_5, C_6$ are given as

$$\begin{aligned} C_6= & {} \frac{(uv-vm_4) A_2 \mathrm {e}^{-ut_0}-v^2 B_2 \mathrm {e}^{-ut_0}}{{((uv-vm_4)}^2+v^4)}, \end{aligned}$$

(40a)

$$\begin{aligned} C_5= & {} \frac{-v^2 A_2 \mathrm {e}^{-ut_0}-(uv-vm_4) B_2 \mathrm {e}^{-ut_0}}{{((uv-vm_4)}^2+v^4)}, \end{aligned}$$

(40b)

$$\begin{aligned} C_4= & {} \mathrm {e}^{-m_4t_0} \{x^{*}_0 -\mathrm {e}^{ut_0}(C_5 \cos vt_0 + C_6 \sin vt_0)\},\nonumber \\ \end{aligned}$$

(40c)

where

$$\begin{aligned} A_2= & {} ((P_2 - m_4Q_2)-u(Q_2-m_4x^{*}_0)) \cos vt_0 \\&+\, v(Q_2-m_4x^{*}_0) \sin vt_0, \\ B_2= & {} ((P_2 - m_4Q_2)-u(Q_2-m_4x^{*}_0)) \sin vt_0 \\&-\, v(Q_2-m_4x^{*}_0) \cos vt_0, \\ P_2= & {} \alpha (x^{*}_0-y^{*}_0+z^{*}_0) - \alpha (\alpha +\alpha b+\epsilon ) y^{*}_0 \\&+\, {(\alpha +\alpha b+\epsilon )}^{2} x^{*}_0, \\ Q_2= & {} \alpha y^{*}_0 - (\alpha +\alpha b+\epsilon ) x^{*}_0. \end{aligned}$$

Fig. 11

Analytical results of the coupled Chua’s circuits operating in double-scroll chaotic attractor state: (a) Unsynchronised and (b) synchronised states for $\epsilon =0$ and $\epsilon =15$, respectively. (i) Drive system attractor in the (x–y) plane; (ii) response system attractor in the $(x'$–$y')$ plane; (iii) dynamical process in the x–$x'$ plane and (iv) time series of the drive system signal x (red) and response system signal $x'$ (blue) indicating the unsynchronised and synchronised states.

Fig. 12

Experimentally observed complete synchronisation in Chua’s circuit for coupled double-scroll chaotic attractors. (i) Phase portraits (vertical scale 50 mV/div., horizontal scale: 50 mV/div.) and (ii) time series of the drive (yellow) and the response (green) signals (vertical scale: 2.5 V/div., horizontal scale: 1 ms/div.) indicating the (a) unsynchronised and (b) synchronised states.

Fig. 13

MSF $(\lambda ^{\perp }_{\mathrm{max}})$ variation with coupling parameter $\epsilon$ for (a) coupled single-scroll attractors and (b) coupled double-scroll attractors.

Using the state variables $x^{*}(t),~y^{*}(t),~z^{*}(t)$ from eqs (37)–(39) and x(t),  y(t),  z(t) from eqs (13)–(15) or eqs (19)–(21), $x'(t)$, $y'(t)$, $z'(t)$ can be obtained from eq. (25) for the corresponding region of operation $D^{*}_{+1}$ or $D^{*}_{-1}$. The procedure presented in §2.1 can be followed to obtain the state variables of the difference system in each of the piecewise-linear region and hence to find the state variables of the response system.

The complete synchronisation of the coupled single-scroll and coupled double-scroll chaotic attractors is studied using the explicit analytical solutions developed above. The synchronisation of the single-scroll attractors emerging from two different regions of the phase planes is first discussed. The unsynchronised and the synchronised state of the coupled Chua’s circuits operating in the single-scroll chaotic state are shown in figures 9a and 9b for the values of coupling parameter $\epsilon =0$ and $\epsilon =15$, respectively. Figures 9a(i) and 9a(ii) show the attractors of the drive and the response systems existing in the left half and right half planes leading to their unsynchronised state as shown in figure 9a(iii). The time series of the signals corresponding to the drive (x) and the response $(x')$ system indicating the unsynchronised nature are shown in figure 9a(iv). The synchronised state of the coupled systems for a greater value of the coupling parameter is presented in figure 9b. Figure 9b(ii) shows the chaotic attractor of the response system settling down the way of the attractor of the drive shown in figure 9b(i). The corresponding synchronised state in the $x-x'$ phase plane and the time series of the drive signal x (red) and response signal $x'$ (blue) indicating the synchronised nature of the attractors are shown in figures 9b(iii) and 9b(iv), respectively. The experimental observations indicating the unsynchronised and the synchronised states of the coupled single-scroll chaotic attractors confirming the analytical results are shown in figure 10. Similar analytical results are presented for the unsynchronised and synchronised states of the coupled double-scroll chaotic attractors as shown in figure 11 and the experimental results to substantiate the analytical results are presented in figure 12. The stability of synchronisation of the coupled Chua’s circuit attractors can be observed through an analysis of the master stability function (MSF) which is the largest transverse Lyapunov exponent $(\lambda ^{\perp }_{\mathrm{max}})$ [40, 41] obtained as a function of the coupling parameter. Figures 13a and 13b show the variation of MSF with $\epsilon$ for coupled single-scroll and double-scroll chaotic attractors. For coupled single-scroll chaotic attractors, the MSF indicates stable synchronisation to larger values of $\epsilon$ for $\epsilon >6.465$ and for coupled double-scroll chaotic attractors, the MSF indicates stable synchronisation for $\epsilon >6.638$. Hence, the x-coupled system gives rise to stable synchronised states even at greater values of coupling strength. In the next section, explicit analytical solutions are developed for studying the dynamics of a fourth-order nonlinear electronic circuit system and its synchronisation.

Fig. 14

Schematic diagram of the modified canonical Chua’s circuit system with two capacitors $C_1, C_2$, two inductors $L_1, L_2$, one linear resistor R, forced negative conductance element $g_N$ and a nonlinear element $N_R$.

Fig. 15

Modified canonical Chua’s circuit: (a) Analytically observed bifurcation diagram in the R–y plane; (b) the three largest Lyapunov exponents as a function of R from eq. (42).

3 Modified canonical Chua’s circuit

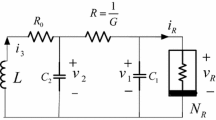
The modified canonical Chua’s circuit consisting of two inductors, two capacitors, a linear resistor, a negative conductance element and a piecewise-linear element is shown in figure 14 [15]. The normalised state equations of the circuit shown in figure 14 is written as

$$\begin{aligned} C_1 {\mathrm {d}v_1 \over \mathrm {d}t }= & {} i_{L_1} - h(v_1), \end{aligned}$$

(41a)

$$\begin{aligned} C_2 {\mathrm {d}v_2 \over \mathrm {d}t }= & {} g_N v_2 - i_{L_1} -i_{L_2}, \end{aligned}$$

(41b)

$$\begin{aligned} L_1 {\mathrm {d}i_{L_1} \over \mathrm {d}t }= & {} v_2 - v_1 - Ri_{L_1}, \end{aligned}$$

(41c)

$$\begin{aligned} L_2 {\mathrm {d}i_{L_2} \over \mathrm {d}t }= & {} v_2, \end{aligned}$$

(41d)

where $v_1,v_2$ and $i_{L_1}, i_{L_2}$ represent the voltage across $C_1, C_2$ and current through $L_1, L_2$, respectively. The term $g_N$ represents the forced negative conductance and $h(v_1)$ representing the nonlinear resistor is given by eq. (2). The state equations of the circuit in dimensionless form is written as

$$\begin{aligned} \dot{x}= & {} \alpha _1 (z - h(x)), \end{aligned}$$

(42a)

$$\begin{aligned} \dot{y}= & {} \alpha _2 y - z - w,\end{aligned}$$

(42b)

$$\begin{aligned} \dot{z}= & {} \beta _1 (y - x - z), \end{aligned}$$

(42c)

$$\begin{aligned} \dot{w}= & {} \beta _2 y, \end{aligned}$$

(42d)

where x, y, z, w represent the normalised state variables and $v_1=x B_P$, $v_2=y B_P$, $i_{L_1}=z B_P$, $i_{L_2}=w B_P$, $\alpha _1 = C_2/C_1$, $\alpha _2 = g_N R$, $\beta _1 = C_2 R^2/L_1$, $\beta _2 = C_2 R^2/L_2$, $a = R G_a$, $b = R G_b$. The mathematical form of h(x) representing the nonlinear resistor is as given by eq. (4) except that the values a and b vary for this circuit. The dynamics of the system has been studied by varying the value of the resistance R. The change in R results in a change in the parameters $\alpha _2, \beta _1, \beta _2, a, b$. Hence, the analytical solution is presented for the set of parameters in which R is varied over a certain range. The analytical solutions for the state variables can be obtained in each of the piecewise-linear region as given in §2.

Fig. 16

Modified canonical Chua’s circuit: Analytical results of period-3 doubling route to hyperchaos in the (i) x–y phase plane along with the Poincaré map (red coloured dots), (ii) y–z phase plane, (iii) z–w phase plane and (iv) x–z phase plane. (a) Period-3 limit cycle for $\alpha _1=2.1429, \alpha _2=0.3263, \beta _1=0.2543,\beta _2=0.0099,a=-0.0761, b=5.0750$; (b) period-6 limit cycle for $\alpha _1=2.1429, \alpha _2=0.3105, \beta _1=0.2304,\beta _2=0.0090,a=-0.0725, b=4.83$; (c) chaotic attractor for $\alpha _1=2.1429, \alpha _2=0.2025, \beta _1=0.0980,\beta _2=0.0038,a=-0.0473, b=3.15$ and (d) hyperchaotic attractor for $\alpha _1=2.1429, \alpha _2=0.1283, \beta _1=0.0393,\beta _2=0.0015,a=-0.0299, b=1.995$.

3.1 Analytical dynamics of the modified canonical Chua’s circuit

In this section, we present the explicit analytical solutions developed for the state equations of the circuit and report the period-3 doubling route to chaos and hyperchaos observed in the circuit.

3.1.1 $D_0$ region

In this region, $h(x)=ax$, and the state equations are written as

$$\begin{aligned} \dot{x}= & {} \alpha _1 (z - ax), \end{aligned}$$

(43a)

$$\begin{aligned} \dot{y}= & {} \alpha _2 y - z - w,\end{aligned}$$

(43b)

$$\begin{aligned} \dot{z}= & {} \beta _1 (y - x - z), \end{aligned}$$

(43c)

$$\begin{aligned} \dot{w}= & {} \beta _2 y. \end{aligned}$$

(43d)

Differentiating eq. (43a) we get

$$\begin{aligned} \ddddot{x} + A \dddot{x} + B \ddot{x} + C \dot{x} + D x = 0, \end{aligned}$$

(44)

where $A=a \alpha _1+\beta _1-\alpha _2$, $B=\beta _1+\beta _2+\alpha _1 \beta _1(1+a)-\alpha _2 \beta _1 - a \alpha _1 \alpha _2$, $C=a \alpha _1(\beta _1+\beta _2)+\beta _1 \beta _2-\alpha _1\alpha _2 \beta _1 (1+a)$ and $D=\alpha _1 \beta _1 \beta _2 (1+a)$. In this region, the roots $m_1,m_2,m_3,m_4$ corresponding to eq. (44) are a pair of complex conjugates and two real roots. Considering $m_1,m_2$ as the real roots and $m_{3,4} = u \pm iv$ as the pair of complex conjugates, the general solution is written as

$$\begin{aligned} x(t) = C_1 \mathrm {e}^{m_1 t} + C_2 \mathrm {e}^{m_2 t} + \mathrm {e}^{ut} (C_3 \cos vt + C_4 \sin vt).\nonumber \\ \end{aligned}$$

(45)

Differentiating eq. (45) we get the state variables

$$\begin{aligned}&y(t) = \frac{\dot{z}(t)}{\beta _1} + x(t) + z(t), \end{aligned}$$

(46)

$$\begin{aligned}&z(t) = \frac{\dot{x}(t)}{\alpha _1} + a x(t), \end{aligned}$$

(47)

$$\begin{aligned}&w(t) = \alpha _2 y(t) - z(t) - \dot{y}(t). \end{aligned}$$

(48)

The constants $C_1, C_2, C_3, C_4$ are given as

$$\begin{aligned} C_4= & {} \frac{F_1 A_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2} + \frac{E_1 B_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2}, \end{aligned}$$

(49a)

$$\begin{aligned} C_3= & {} \frac{E_1 A_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2} - \frac{F_1 B_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2}, \end{aligned}$$

(49b)

$$\begin{aligned} C_2= & {} \frac{\mathrm {e}^{-m_2t_0}}{m_2-m_1} \{(R_1-m_1 x_0) \nonumber \\&-\, u\mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0) \nonumber \\&+\, v\mathrm {e}^{ut_0}(C_3 \sin vt_0 - C_4 \cos vt_0) \nonumber \\&+\, m_1\mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0)\}, \end{aligned}$$

(49c)

$$\begin{aligned} C_1= & {} \mathrm {e}^{-m_1t_0} \{x_0 - C_2 \mathrm {e}^{m_2 t_0} \nonumber \\&-\, \mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0)\}, \end{aligned}$$

(49d)

where

$$\begin{aligned} E_1= & {} v^2(m_1+m_2-2u) \\ F_1= & {} u^2 v -v^3 - (m_1+m_2)uv + m_1 m_2 v \\ A_1= & {} \{((P_1 - m_1Q_1)- m_2(Q_1-m_1R_1)) \\&-\,u((Q_1-m_1R_1)-m_2(R_1-m_1 x_0))\} \cos vt_0 \\&+\, \{v(Q_1-m_1R_1)-m_2(R_1-m_1 x_0)\} \sin vt_0, \\ B_1= & {} \{((P_1 - m_1Q_1)- m_2(Q_1-m_1R_1)) \\&-\,u((Q_1-m_1R_1)-m_2(R_1-m_1 x_0))\} \sin vt_0 \\&-\, \{v(Q_1-m_1R_1)-m_2(R_1-m_1 x_0)\} \cos vt_0,\\ P_1= & {} \alpha _1 \beta _1 (\alpha _2 y_0-z_0-w_0) \\&+\, \alpha _1 (a^2 {\alpha _1}^2 - \alpha _1 \beta _1) (z_0-ax_0) \\&-\, \beta _1(\alpha _1 \beta _1+a {\alpha _1}^2) (y_0 - x_0-z_0), \\ Q_1= & {} \alpha _1 \beta _1 (y_0 - x_0 -z_0) - a {\alpha _1}^2 (z_0 - a x_0), \\ R_1= & {} \alpha _1 z_0 - a \alpha _1 x_0. \end{aligned}$$

3.1.2 $D_{+1}$ region

In this region, $h(x)=bx+(a-b)$, and the state equations are written as

$$\begin{aligned} \dot{x}= & {} \alpha _1 (z - bx - (a-b)), \end{aligned}$$

(50a)

$$\begin{aligned} \dot{y}= & {} \alpha _2 y - z - w, \end{aligned}$$

(50b)

$$\begin{aligned} \dot{z}= & {} \beta _1 (y - x - z), \end{aligned}$$

(50c)

$$\begin{aligned} \dot{w}= & {} \beta _2 y. \end{aligned}$$

(50d)

Differentiating eq. (50a) we get

$$\begin{aligned} \ddddot{x} + A \dddot{x} + B \ddot{x} + C \dot{x} + D x = \Delta , \end{aligned}$$

(51)

where $A=b \alpha _1+\beta _1-\alpha _2$, $B=\beta _1+\beta _2+\alpha _1 \beta _1(1+b)-\alpha _2 \beta _1 - b \alpha _1 \alpha _2$, $C=b \alpha _1(\beta _1+\beta _2)+\beta _1 \beta _2-\alpha _1\alpha _2 \beta _1 (1+b)$, $D=\alpha _1 \beta _1 \beta _2 (1+b)$ and $\Delta = - \alpha _1 \beta _1 \beta _2 (a-b)$. In this region, the roots $m_5,m_7,m_8,m_6$ corresponding to eq. (51) are a real root, a pair of complex conjugates and a real root. Considering $m_5,m_6$ as the real roots and $m_{6,7} = u \pm iv$ as the pair of complex conjugates, the general solution is

$$\begin{aligned} x(t)&= C_5 \mathrm {e}^{m_5 t} + C_6 \mathrm {e}^{m_6 t} \nonumber \\&\quad + \mathrm {e}^{ut} (C_7 \cos vt + C_8 \sin vt) + C_9. \end{aligned}$$

(52)

Differentiating eq. (52) and using it in eq. (50), we get the state variables,

$$\begin{aligned} y(t)= & {} \frac{\dot{z}(t)}{\beta _1} + x(t) + z(t), \end{aligned}$$

(53)

$$\begin{aligned} z(t)= & {} \frac{\dot{x}(t)}{\alpha _1} + b x(t) + (a-b), \end{aligned}$$

(54)

$$\begin{aligned} w(t)= & {} \alpha _2 y(t) - z(t) - \dot{y}(t). \end{aligned}$$

(55)

The constants $C_5, C_6, C_7, C_8, C_9$ are

$$\begin{aligned} C_9= & {} \frac{\Delta }{D}, \end{aligned}$$

(56a)

$$\begin{aligned} C_8= & {} \frac{F_2 A_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2} + \frac{E_2 B_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2}, \end{aligned}$$

(56b)

$$\begin{aligned} C_7= & {} \frac{E_2 A_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2} - \frac{F_2 B_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2}, \end{aligned}$$

(56c)

$$\begin{aligned} C_6= & {} \frac{\mathrm {e}^{-m_6t_0}}{m_6-m_5} \{(R_2-m_5 x_0) \nonumber \\&-\, u\mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0) \nonumber \\&+\, v\mathrm {e}^{ut_0}(C_7 \sin vt_0 - C_8 \cos vt_0) \nonumber \\&+\, m_5\mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0)\},\end{aligned}$$

(56d)

$$\begin{aligned} C_5= & {} \mathrm {e}^{-m_5t_0} \{x_0 - C_6 \mathrm {e}^{m_6 t_0} \nonumber \\&-\, \mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0) - C_9\}, \end{aligned}$$

(56e)

where

$$\begin{aligned} E_2= & {} v^2(m_5+m_6-2u), \\ F_2= & {} u^2 v -v^3 - (m_5+m_6)uv + m_5 m_6 v, \\ A_2= & {} \{((P_2 - m_5Q_2)- m_6(Q_2-m_5R_2)) \\&-\,u((Q_2-m_5R_2)-m_6(R_2-m_5 x_0))\} \cos vt_0 \\&+\, \{v(Q_2-m_5R_2)-m_6(R_2-m_5 x_0)\} \sin vt_0, \\ B_2= & {} \{((P_2 - m_5Q_2)- m_6(Q_2-m_5R_2)) \\&-\,u((Q_2-m_5R_2)-m_6(R_2-m_5 x_0))\} \sin vt_0 \\&-\, \{v(Q_2-m_5R_2)-m_6(R_2-m_5 x_0)\} \cos vt_0, \\ P_2= & {} \alpha _1 \beta _1 (\alpha _2 y_0-z_0-w_0) \\&+\, \alpha _1 (b^2 {\alpha _1}^2 - \alpha _1 \beta _1) (z_0-bx_0-(a-b)) \\&-\, \beta _1(\alpha _1 \beta _1+b {\alpha _1}^2) (y_0 - x_0-z_0), \\ Q_2= & {} \alpha _1 \beta _1 (y_0 - x_0 -z_0) - b {\alpha _1}^2 (z_0 - b x_0 - (a-b)), \\ R_2= & {} \alpha _1 z_0 - b \alpha _1 x_0 -\alpha _1 (a-b). \end{aligned}$$

3.1.3 $D_{-1}$ region

In this region, $h(x)=bx-(a-b)$, and the state equations are written as

$$\begin{aligned} \dot{x}= & {} \alpha _1 (z - bx + (a-b)), \end{aligned}$$

(57a)

$$\begin{aligned} \dot{y}= & {} \alpha _2 y - z - w,\end{aligned}$$

(57b)

$$\begin{aligned} \dot{z}= & {} \beta _1 (y - x - z), \end{aligned}$$

(57c)

$$\begin{aligned} \dot{w}= & {} \beta _2 y. \end{aligned}$$

(57d)

Differentiating eq. (57a) we get

$$\begin{aligned} \ddddot{x} + A \dddot{x} + B \ddot{x} + C \dot{x} + D x = \Delta , \end{aligned}$$

(58)

where $A=b \alpha _1+\beta _1-\alpha _2$, $B=\beta _1+\beta _2+\alpha _1 \beta _1(1+b)-\alpha _2 \beta _1 - b \alpha _1 \alpha _2$, $C=b \alpha _1(\beta _1+\beta _2)+\beta _1 \beta _2-\alpha _1\alpha _2 \beta _1 (1+b)$, $D=\alpha _1 \beta _1 \beta _2 (1+b)$ and $\Delta = \alpha _1 \beta _1 \beta _2 (a-b)$. In this region, the roots $m_5,m_7,m_8,m_6$ corresponding to eq. (58) are a real root, a pair of complex conjugates and a real root. Considering $m_5,m_6$ as the real roots and $m_{7,8} = u \pm iv$ as the pair of complex conjugates, the general solution is

$$\begin{aligned} x(t)= & {} C_5 \mathrm {e}^{m_5 t} + C_6 \mathrm {e}^{m_6 t} \nonumber \\&+ \mathrm {e}^{ut} (C_7 \cos vt + C_8 \sin vt) + C_9. \end{aligned}$$

(59)

Differentiating eq. (59) and using it in eq. (57), we get the state variables

$$\begin{aligned}&y(t)=\frac{\dot{z}(t)}{\beta _1} + x(t) + z(t), \end{aligned}$$

(60)

$$\begin{aligned}&z(t)=\frac{\dot{x}(t)}{\alpha _1} + b x(t) - (a-b), \end{aligned}$$

(61)

$$\begin{aligned}&w(t)=\alpha _2 y(t) - z(t) - \dot{y}(t). \end{aligned}$$

(62)

The constants $C_5, C_6, C_7, C_8, C_9, A_2, B_2$ are the same as given in §3.1.2 except that the terms $P_2, Q_2, R_2$ are to be changed as follows:

$$\begin{aligned} P_2= & {} \alpha _1 \beta _1 (\alpha _2 y_0-z_0-w_0) \\&+\, \alpha _1 (b^2 {\alpha _1}^2 - \alpha _1 \beta _1) (z_0-bx_0+(a-b)) \\&-\, \beta _1(\alpha _1 \beta _1+b {\alpha _1}^2) (y_0 - x_0-z_0), \\ Q_2= & {} \alpha _1 \beta _1 (y_0 - x_0 -z_0) - b {\alpha _1}^2 (z_0 - b x_0 + (a-b)), \\ R_2= & {} \alpha _1 z_0 - b \alpha _1 x_0 + \alpha _1 (a-b). \end{aligned}$$

The solutions obtained in each of the region is used to observe the trajectories in phase-space as presented in §2. The solutions can be used to observe the period-3 doubling sequence leading to hyperchaos in the system dynamics. The entire dynamics of the system is summarised using the bifurcation diagram and Lyapunov exponents as shown in figure 15. The analytically observed one-parameter bifurcation diagram obtained as a function of the resistance R in the R–y plane is shown in figure 15a. The three largest Lyapunov exponents obtained using numerical simulation of the state equations given in eq. (42) of the system is shown in figure 15b. The analytically observed phase portraits indicating the period-3 doubling route to hyperchaos in different phase planes is shown in figure 16. The Poincaré maps of the attractors given in the x–y plane are represented by red coloured dots. Figures 16a(i)–a(iv) show the period-3 limit cycle attractors in different phase planes for the parameters $\alpha _1=2.1429, \alpha _2=0.3263, \beta _1=0.2543,\beta _2=0.0099,a=-0.0761, b=5.0750$ corresponding to $R=725 \Omega$ while figures 16b(i)–b(iv) show the period-6 limit cycle attractors for the parameters $\alpha _1=2.1429, \alpha _2=0.3105, \beta _1=0.2304,\beta _2=0.0090,a=-0.0725, b=4.83$ obtained for $R=690 \Omega$. The chaotic and the hyperchaotic attractors observed in the system for the parameters $\alpha _1=2.1429, \alpha _2=0.2025, \beta _1=0.0980,\beta _2=0.0038,a=-0.0473, b=3.15$ and $\alpha _1=2.1429, \alpha _2=0.1283, \beta _1=0.0393,\beta _2=0.0015,a=-0.0299, b=1.995$ corresponding to $R=450 \,\Omega$ and $R=285\, \Omega$ are shown in figures 16c(i)–c(iv) and figures 16d(i)–d(iv), respectively. The analytical evolution of the hyperchaotic attractor of the modified canonical Chua’s circuit with time in the x–y–z phase-space is shown in the supplementary file. In the next section, we develop explicit analytical solutions for the complete synchronisation observed in the coupled modified canonical Chua’s circuit systems operating in the hyperchaotic state.

Fig. 17

Schematic diagram of the unidirectionally coupled modified canonical Chua’s circuit systems.

Fig. 18

Analytical results of the coupled modified canonical Chua’s circuits operating in the hyperchaotic state: (a) Unsynchronised and (b) synchronised states for $\epsilon =0$ and $\epsilon =0.57$, respectively. (i) Drive system attractor in the x–y plane; (ii) response system attractor in the $x'$–$y'$ plane; (iii) dynamical process in the x–$x'$ plane and (iv) time series of the drive system signal x (red) and response system signal $x'$ (blue) indicating the unsynchronised and synchronised states.

3.2 Analytical study of the synchronisation of modified canonical Chua’s circuit

In this section, we develop analytical solutions for the synchronisation of the coupled modified canonical Chua’s circuit systems operating in the hyperchaotic state. The schematic diagram of the unidirectionally coupled modified canonical Chua’s circuit systems is shown in figure 17. The system discussed in §3.1 acts as the drive and the response systems but operate with different initial conditions. The two systems are coupled through the x-variable of the systems. The state equations of the drive system is given in eq. (42) while the equations of the response system is given as

$$\begin{aligned} \dot{x}'= & {} \alpha _1 (z' - h(x')) + \epsilon (x-x'), \end{aligned}$$

(63a)

$$\begin{aligned} \dot{y}'= & {} \alpha _2 y' - z' - w', \end{aligned}$$

(63b)

$$\begin{aligned} \dot{z}'= & {} \beta _1 (y' - x' - z'), \end{aligned}$$

(63c)

$$\begin{aligned} \dot{w}'= & {} \beta _2 y', \end{aligned}$$

(63d)

where $x',y',z',w'$ are the state variables of the response system, $\epsilon$ is the coupling parameter and the function $h(x')$ is given in eq. (23). The difference system obtained from eqs (42) and (63) can be written as

$$\begin{aligned} \dot{x}^{*}= & {} \alpha _1 (z^{*} - h(x^{*})) + \epsilon x^{*}, \end{aligned}$$

(64a)

$$\begin{aligned} \dot{y}^{*}= & {} \alpha _2 y^{*} - z^{*} - w^{*},\end{aligned}$$

(64b)

$$\begin{aligned} \dot{z}^{*}= & {} \beta _1 (y^{*} - x^{*} - z^{*}), \end{aligned}$$

(64c)

$$\begin{aligned} \dot{w}^{*}= & {} \beta _2 y^{*}, \end{aligned}$$

(64d)

where $x^{*}=$ $x-x'$, $y^{*}=$ $y-y'$, $z^{*}=$ $z-z'$, $w^{*}=$ $w-w'$ and $h(x^{*}) = h(x) - h(x')$. The state variables of the response system are given as

$$\begin{aligned} x'(t)= & {} x(t) - x^{*}(t), \end{aligned}$$

(65a)

$$\begin{aligned} y'(t)= & {} y(t) - y^{*}(t), \end{aligned}$$

(65b)

$$\begin{aligned} z'(t)= & {} z(t) - z^{*}(t), \end{aligned}$$

(65c)

$$\begin{aligned} w'(t)= & {} w(t) - w^{*}(t). \end{aligned}$$

(65d)

The origin becomes the fixed point in all the regions and are given as

$$\begin{aligned}&\left. \begin{aligned}&D^{*}_{+1} = \{ (x^{*},y^{*},z^{*},w^{*})| x^{*} > 1 \}| P^{*}_+ = (0,0,0,0)\\&D^{*}_0 = \{ (x^{*},y^{*},z^{*},w^{*})|| x^{*} | \le 1 \}| O^{*} = (0,0,0,0)\\&D^{*}_{-1} = \{ (x^{*},y^{*},z^{*},w^{*})|x^{*} < -1 \}| P^{*}_- = (0,0,0,0) \end{aligned} \right\} . \nonumber \\ \end{aligned}$$

(66)

The stability of the fixed points given in eq. (66) is studied using the stability matrices. The stability matrix in the $D^{*}_0$ region is

$$\begin{aligned} J^{*}_{0} = \begin{pmatrix} -(a \alpha _1+\epsilon ) &{}&{}&{} 0 &{}&{}&{} \alpha _1 &{}&{}&{} 0 \\ 0 &{}&{}&{} \alpha _2 &{}&{}&{} -1 &{}&{}&{} -1 \\ -\beta _1 &{}&{}&{} \beta _1 &{}&{}&{} \beta _1 &{}&{}&{} 0 \\ 0 &{}&{}&{} \beta _2 &{}&{}&{} 0 &{}&{}&{} 0\\ \end{pmatrix}, \end{aligned}$$

(67)

while in the $D^{*}_{\pm 1}$ region it is given as

$$\begin{aligned} J^{*}_{\pm 1} = \begin{pmatrix} -(b \alpha _1+\epsilon ) &{}&{}&{} 0 &{}&{}&{} \alpha _1 &{}&{}&{} 0 \\ 0 &{}&{}&{} \alpha _2 &{}&{}&{} -1 &{}&{}&{} -1 \\ -\beta _1 &{}&{}&{} \beta _1 &{}&{}&{} \beta _1 &{}&{}&{} 0 \\ 0 &{}&{}&{} \beta _2 &{}&{}&{} 0 &{}&{}&{} 0\\ \end{pmatrix}. \end{aligned}$$

(68)

Fig. 19

Experimentally observed complete synchronisation in modified canonical Chua’s circuit for coupled hyperchaotic attractors. (i) Phase portraits (vertical scale: 500 mV/div., horizontal scale: 500 mV/div.) and (ii) time series of the drive (orange) and the response (red) signals (vertical scale: 1.0 V/div., horizontal scale: 5 ms/div.) indicating the (a) unsynchronised and (b) synchronised states.

Fig. 20

MSF $(\lambda ^{\perp }_{\mathrm{max}})$ as a function of the coupling parameter $\epsilon$ for coupled hyperchaotic attractors indicating stable synchronisation for the values of coupling parameter $0.0694 \le \epsilon \le 0.6166$.

For the given values of the parameters of the drive and the response systems operating in the hyperchaotic region, the stability of the fixed points is determined by the parameter $\epsilon$. In the $D^{*}_0$ region, the eigenvalues are two complex conjugates and two real roots for all the values of $\epsilon$. In the $D^{*}_{\pm 1}$ region, the eigenvalues are one real root, a pair of complex conjugates and a real root for all values of $\epsilon$. Under the uncoupled state, i.e. $\epsilon =0$, the drive and the response systems evolve independently and are unsynchronised as they operate with different initial conditions. For $\epsilon >0$, the response system is controlled by the drive through $\epsilon$. The analytical solutions of the state equations given in eq. (64) is summarised as follows:

3.2.1 Region $D^*_0$

In the $D^{*}_0$ region, $h(x^*) = ax^*$ and the state equations are

$$\begin{aligned} \dot{x}^{*}= & {} \alpha _1 z^{*} - (a \alpha _1+ \epsilon ) x^{*}, \end{aligned}$$

(69a)

$$\begin{aligned} \dot{y}^{*}= & {} \alpha _2 y^{*} - z^{*} - w^{*},\end{aligned}$$

(69b)

$$\begin{aligned} \dot{z}^{*}= & {} \beta _1 (y^{*} - x^{*} - z^{*}),\end{aligned}$$

(69c)

$$\begin{aligned} \dot{w}^{*}= & {} \beta _2 y^{*}. \end{aligned}$$

(69d)

Differentiating eq. (69a) we get

$$\begin{aligned} \ddddot{x}^{*} + A \dddot{x}^{*} + B \ddot{x}^{*} + C \dot{x}^{*} + D = 0, \end{aligned}$$

(70)

where $A= a \alpha _1 + \epsilon + \beta _1 -\alpha _2$, $B= \alpha _1 \beta _1 + \beta _1 (a \alpha _1 + \epsilon ) + \beta _1 + \beta _2 -\alpha _2 \beta _1 - \alpha _2 (a \alpha _1 + \epsilon )$, $C= \beta _1 (a \alpha _1 + \epsilon ) + \beta _2 (a \alpha _1 + \epsilon ) + \beta _1 \beta _2 - \alpha _1 \alpha _2 \beta _1 - \alpha _2 \beta _1 (a \alpha _1 + \epsilon )$ and $D= \beta _1 \beta _2 ( \alpha _1 + a \alpha _1 + \epsilon )$. The roots corresponding to eq. (70) are a pair of complex conjugates and two real root for all values of $\epsilon$. Considering $m_1, m_2$ as the real roots and $m_{3,4} = u \pm iv$ as the pair of complex conjugates, the general solution is written as

$$\begin{aligned} x^{*}(t)= & {} C_1 \mathrm {e}^{m_1 t} + C_2 \mathrm {e}^{m_2 t} \nonumber \\&+ \mathrm {e}^{ut} (C_3 \cos vt + C_4 \sin vt). \end{aligned}$$

(71)

Differentiating eq. (71) we get the state variables

$$\begin{aligned}&y^{*}(t) = \frac{\dot{z}^{*}(t)}{\beta _1} + x^{*}(t) + z^{*}(t), \end{aligned}$$

(72)

$$\begin{aligned}&z^{*}(t) = \frac{1}{\alpha _1} \{\dot{x}^{*}(t) + (a \alpha _1 + \epsilon ) x^{*}(t)\}, \end{aligned}$$

(73)

$$\begin{aligned}&w^{*}(t) = \alpha _2 y^{*}(t) - z^{*}(t) - \dot{y}^{*}(t). \end{aligned}$$

(74)

The constants $C_1, C_2, C_3, C_4$ are

$$\begin{aligned} C_4= & {} \frac{F_1 A_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2} + \frac{E_1 B_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2}, \end{aligned}$$

(75a)

$$\begin{aligned} C_3= & {} \frac{E_1 A_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2} - \frac{F_1 B_1 \mathrm {e}^{-ut_0}}{E_1^2 + F_1^2}, \end{aligned}$$

(75b)

$$\begin{aligned} C_2= & {} \frac{\mathrm {e}^{-m_2t_0}}{m_2-m_1} \{(R_1-m_1 x^{*}_0) \nonumber \\&-\, u\mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0) \nonumber \\&+\, v\mathrm {e}^{ut_0}(C_3 \sin vt_0 - C_4 \cos vt_0) \nonumber \\&+\, m_1\mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0)\},\end{aligned}$$

(75c)

$$\begin{aligned} C_1= & {} \mathrm {e}^{-m_1t_0} \{x^{*}_0 - C_2 \mathrm {e}^{m_2 t_0} \nonumber \\&-\, \mathrm {e}^{ut_0}(C_3 \cos vt_0 + C_4 \sin vt_0)\}, \end{aligned}$$

(75d)

where

$$\begin{aligned} E_1= & {} v^2(m_1+m_2-2u) \\ F_1= & {} u^2 v -v^3 - (m_1+m_2)uv + m_1 m_2 v \\ A_1= & {} [(P_1 - m_1Q_1)- m_2(Q_1-m_1R_1)] \\&-\,[u(Q_1-m_1R_1)-m_2(R_1-m_1 x^{*}_0)] \cos vt_0 \\&+\, [v(Q_1-m_1R_1)-m_2(R_1-m_1 x^{*}_0)] \sin vt_0, \\ B_1= & {} [(P_1 - m_1Q_1)- m_2(Q_1-m_1R_1)] \\&-\,[u(Q_1-m_1R_1)-m_2(R_1-m_1 x^{*}_0)] \sin vt_0 \\&-\,[v(Q_1-m_1R_1)-m_2(R_1-m_1 x^{*}_0)] \cos vt_0, \\ P_1= & {} \alpha _1 \beta _1 (\alpha _2 y^{*}_0-z^{*}_0-w^{*}_0) \\&+\, [{(a \alpha _1 + \epsilon )}^2 - \alpha _1 \beta _1) (\alpha _1 z^{*}_0 - (a \alpha _1 + \epsilon ) x^{*}_0] \\&-\, \alpha _1 \beta _1( \beta _1+ (a \alpha _1 + \epsilon )) (y^{*}_0 - x^{*}_0-z^{*}_0), \\ Q_1= & {} \alpha _1 \beta _1 (y^{*}_0 - x^{*}_0 -z^{*}_0) \\&-\, (a \alpha _1 + \epsilon ) (\alpha _1 z^{*}_0 - (a \alpha _1 + \epsilon ) x^{*}_0), \\ R_1= & {} \alpha _1 z^{*}_0 - (a \alpha _1 + \epsilon ) x^{*}_0. \end{aligned}$$

Using the state variables $x^{*}(t),~y^{*}(t),~z^{*}(t),~w^{*}(t)$ from eqs (71)–(74) and x(t),  y(t),  z(t),  w(t) from eqs (45)–(48), the state variables $x'(t)$, $y'(t)$, $z'(t)$, $w'(t)$ can be obtained from eq. (65), respectively.

3.2.2 Region $D^{*}_{\pm 1}$

In the $D^{*}_{\pm 1}$ regions, $h(x^{*}) = bx^{*}$ and the state equations are

$$\begin{aligned} \dot{x}^{*}= & {} \alpha _1 z^{*} - (b \alpha _1+ \epsilon ) x^{*}, \end{aligned}$$

(76a)

$$\begin{aligned} \dot{y}^{*}= & {} \alpha _2 y^{*} - z^{*} - w^{*},\end{aligned}$$

(76b)

$$\begin{aligned} \dot{z}^{*}= & {} \beta _1 (y^{*} - x^{*} - z^{*}), \end{aligned}$$

(76c)

$$\begin{aligned} \dot{w}^{*}= & {} \beta _2 y^{*}. \end{aligned}$$

(76d)

Differentiating eq. (76a) we get

$$\begin{aligned} \ddddot{x}^{*} + A \dddot{x}^{*} + B \ddot{x}^{*} + C \dot{x}^{*} + D = 0, \end{aligned}$$

(77)

where $A= b \alpha _1 + \epsilon + \beta _1 -\alpha _2$, $B= \alpha _1 \beta _1 + \beta _1 (b \alpha _1 + \epsilon ) + \beta _1 + \beta _2 -\alpha _2 \beta _1 - \alpha _2 (b \alpha _1 + \epsilon )$, $C= \beta _1 (b \alpha _1 + \epsilon ) + \beta _2 (b \alpha _1 + \epsilon ) + \beta _1 \beta _2 - \alpha _1 \alpha _2 \beta _1 - \alpha _2 \beta _1 (b \alpha _1 + \epsilon )$ and $D= \beta _1 \beta _2 ( \alpha _1 + b \alpha _1 + \epsilon )$. The roots corresponding to eq. (77) are a real root, a pair of complex conjugates and another real root for all values of $\epsilon$. Considering $m_5, m_6$ as the real roots and $m_{7,8} = u \pm iv$ as the pair of complex conjugates, the general solution to eq. (77) is written as

$$\begin{aligned} x^{*}(t)= & {} C_5 \mathrm {e}^{m_5 t} + C_6 \mathrm {e}^{m_6 t} \nonumber \\&+ \mathrm {e}^{ut} (C_7 \cos vt + C_8 \sin vt). \end{aligned}$$

(78)

Differentiating eq. (78), we get the state variables

$$\begin{aligned}&y^{*}(t)=\frac{\dot{z}^{*}(t)}{\beta _1} + x^{*}(t) + z^{*}(t), \end{aligned}$$

(79)

$$\begin{aligned}&z^{*}(t)=\frac{1}{\alpha _1} \{\dot{x}^{*}(t) + (b \alpha _1 + \epsilon ) x^{*}(t)\}, \end{aligned}$$

(80)

$$\begin{aligned}&w^{*}(t)=\alpha _2 y^{*}(t) - z^{*}(t) - \dot{y}^{*}(t). \end{aligned}$$

(81)

The constants $C_5, C_6, C_7, C_8$ are

$$\begin{aligned} C_8= & {} \frac{F_2 A_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2} + \frac{E_2 B_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2}, \end{aligned}$$

(82a)

$$\begin{aligned} C_7= & {} \frac{E_2 A_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2} - \frac{F_2 B_2 \mathrm {e}^{-ut_0}}{E_2^2 + F_2^2}, \end{aligned}$$

(82b)

$$\begin{aligned} C_6= & {} \frac{\mathrm {e}^{-m_6t_0}}{m_6-m_5} \{(R_2-m_5 x^{*}_0) \nonumber \\&-\, u\mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0) \nonumber \\&+\, v\mathrm {e}^{ut_0}(C_7 \sin vt_0 - C_8 \cos vt_0) \nonumber \\&+\, m_5\mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0)\}, \end{aligned}$$

(82c)

$$\begin{aligned} C_5= & {} \mathrm {e}^{-m_5t_0} \{x^{*}_0 - C_6 \mathrm {e}^{m_6 t_0} \nonumber \\&-\, \mathrm {e}^{ut_0}(C_7 \cos vt_0 + C_8 \sin vt_0)\}, \end{aligned}$$

(82d)

where

$$\begin{aligned} E_2= & {} v^2(m_1+m_2-2u) \\ F_2= & {} u^2 v -v^3 - (m_1+m_2)uv + m_1 m_2 v \\ A_2= & {} \{((P_2 - m_5Q_2)- m_6(Q_2-m_5R_2)) \\&-\,u((Q_2-m_5R_2)-m_6(R_2-m_5 x^{*}_0))\} \cos vt_0 \\&+\, \{v(Q_2-m_5R_2)-m_6(R_2-m_5 x^{*}_0)\} \sin vt_0, \\ B_2= & {} \{((P_2 - m_5Q_2)- m_6(Q_2-m_5R_2)) \\&-\,u((Q_2-m_5R_2)-m_6(R_2-m_5 x^{*}_0))\} \sin vt_0 \\&-\, \{v(Q_2-m_5R_2)-m_6(R_2-m_5 x^{*}_0)\} \cos vt_0, \\ P_2= & {} \alpha _1 \beta _1 (\alpha _2 y^{*}_0-z^{*}_0-w^{*}_0) \\&+\, ({(b \alpha _1 + \epsilon )}^2 - \alpha _1 \beta _1) (\alpha _1 z^{*}_0 - (b \alpha _1 + \epsilon ) x^{*}_0) \\&-\, \alpha _1 \beta _1( \beta _1+ (b \alpha _1 + \epsilon )) (y^{*}_0 - x^{*}_0-z^{*}_0), \\ Q_2= & {} \alpha _1 \beta _1 (y^{*}_0 - x^{*}_0 -z^{*}_0) \\&-\, (b \alpha _1 + \epsilon ) (\alpha _1 z^{*}_0 - (b \alpha _1 + \epsilon ) x^{*}_0), \\ R_2= & {} \alpha _1 z^{*}_0 - (b \alpha _1 + \epsilon ) x^{*}_0. \end{aligned}$$

Using the state variables $x^{*}(t),~y^{*}(t),~z^{*}(t),~w^{*}(t)$ from eqs (78)–(81) and x(t),  y(t),  z(t),  w(t) from eqs (52)–(55) or eqs (59)–(62), the state variables $x'(t)$, $y'(t)$, $z'(t)$, $w'(t)$ can be obtained from eq. (65) for the corresponding region of operation $D^{*}_{+1}$ or $D^{*}_{-1}$. The procedure presented in §3.1 can be followed to obtain the state variables of the difference system in each of the piecewise-linear region and hence to find the state variables of the response system.

The analytical solutions presented above are used to study the complete synchronisation of coupled modified canonical Chua’s circuit systems operating in the hyperchaotic states. The unsynchronised and the synchronised states of the coupled systems are shown in figures 18a and figure 18b for the values of coupling parameter $\epsilon =0$ and $\epsilon =0.57$, respectively. Figures 18a(i) and 18a(ii) show the hyperchaotic attractors of the drive and the response systems evolving from two different sets of initial conditions leading to their unsynchronised states as shown in figure 18a(iii). The time series of the signals corresponding to the drive (x) and the response $(x')$ systems indicating the unsynchronised nature of the attractors are shown in figure 18a(iv). The synchronised state of the systems for the coupling parameter value $\epsilon =0.57$ is presented in figure 18b. Figure 18b(ii) showing the hyeprchaotic attractor of the response system evolving is identical to that of the drive attractor shown in figure 18b(i) indicates the synchronised state of the system as shown in figure 18b(iii) in the x–$x'$ phase plane. The corresponding time series of the drive signal x (red) and response signal $x'$ (blue) indicating the synchronised nature of the attractors are shown in figure 18b(iv). The experimental observations indicating the unsynchronised and the synchronised states of the coupled hyperchaotic attractors of the modified canonical Chua’s circuit confirming the analytical results is shown in figure 19. The stability of synchronisation observed in coupled hyperchaotic attractors through the MSF $(\lambda ^{\perp }_{\mathrm{max}})$ is presented in figure 20. The region of stable synchronisation is observed in the range of the coupling parameter values $0.0694 \le \epsilon \le 0.6166$.

4 Summary and conclusions

Analytical solutions developed for higher-dimensional chaotic and hyperchaotic systems are reported in this paper. As every nonlinear system presents complexity of its own kind, a generalised approach or method for solving the differential equations of the nonlinear systems is indispensable but is quite uncommon in literature. The research presented in this paper enhances our understanding on the method for developing explicit analytical solutions for higher-dimensional systems with piecewise linear elements as the nonlinear component. The third-order Chua’s circuit and the fourth-order modified canonical Chua’s circuit were studied analytically for their chaotic and hyperchaotic dynamical behaviours, respectively, through phase portraits, Poincaré maps, basins of attraction and one-parameter bifurcation diagram. Further, the existence of multistability of attractors observed in the Chua’s circuit studied analytically has been confirmed through experimental results. Explicit analytical solutions were also developed to study the synchronisation process of the coupled systems and the emergence of complete synchronisation has been reported. The present work reports the applicability of the analytical method to explain the dynamics of higher-dimensional autonomous chaotic and hyperchaotic systems which has been studied earlier for non-autonomous second-order chaotic systems. The present work confirms the reliability of this method for studying the analytical dynamics of chaotic systems with piecewise linear elements in the circuits.