NSFD schemes for a class of nonlinear generalised advection–diffusion–reaction equation

Abstract

This paper deals with the nonlinear generalised advection–diffusion–reaction (GADR) equation subject to some initial and boundary conditions (BCs). Some exact finite difference (EFD) schemes and non-standard finite difference (NSFD) schemes are derived. Positivity and boundedness of the proposed NSFD schemes are analysed analytically and numerically. Theoretical results are very well supported by solved examples. The major achievements of NSFD schemes are that they give highly accurate solutions for very few spatial and temporal divisions.

1 Introduction

Advection–diffusion–reaction (ADR) equations are one of the basic partial differential equations (PDEs) which are used in modelling the heat and mass transfer. They play central roles in many disciplines of engineering, science and finances. One of the important research directions in numerical PDEs and computational fluid dynamics is to compute their numerical solutions. We investigate the following generalised versions of this class:

$$\begin{aligned}&\vartheta \xi _{rr}=\xi _{t}+ \eta \xi _{r}-\alpha \xi ^{\theta +1}+\beta \xi ^{2\theta +1},\nonumber \\&\quad 0\le r\le 1,~ t \ge 0, \end{aligned}$$

(1)

where $\xi (r,t)$ is the concentration or density, $\vartheta$ is the diffusion coefficient, $\eta$ is the advective or convective velocity and $\alpha ,\beta$ are the real constants. Here, we assume that $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$, $\eta \in {\mathbb {R}}$ and $\theta \in {\mathbb {N}}$ [1].

Exact finite difference (EFD) and non-standard finite difference (NSFD) methods were established for solving practical problems in applied sciences and engineering. The books [2,3,4] and the survey articles [5, 6] give a comprehensive treatment on EFD and NSFD methods. The main aim of these methods is to reduce the numerical instabilities which emerge in the standard finite difference (FD) methods. In this approach, non-trivial denominator functions (DFs), e.g., $\sin (\delta r )$, $({\mathrm {e}^{\delta r }-1})^2$ are used instead of trivial denominator terms, i.e., $\delta r,~(\delta r )^2$. Also the nonlinear term, e.g., $(\xi _j^n)^2$, is modelled by $\xi _{j-1}^{n+1} \xi _{j+1}^n$, which is non-local on the computational grid. We now give a brief literature review on the NSFD method for ADR equations.

Mickens and Shoosmith [7] proved that in best FD scheme for arbitrary step sizes $\delta t$ and $\delta r$, modified Burgers’ equation has exactly the same rational solutions as the PDE. Therefore, even for large step sizes we shall get highly accurate solutions. Mickens [8] gave exact solutions to a best difference equation model of a nonlinear advection–reaction PDE, $a \xi _t+ \eta \xi _r= \alpha \xi +\beta {\xi }^2$, where a, $\eta$, $\alpha$, $\beta$ are positive constants. The given scheme minimised or eliminated a number of issues related to numerical instabilities and ghost solutions. Then in [9], Mickens considered a particular class of one-space dimension, nonlinear reaction–diffusion PDEs. As an application, the reaction–diffusion equation $\xi _{rr}=\xi _t-\xi +{\xi }^2$ has been studied. The NSFD scheme proposed holds positivity, boundedness and symmetric property under some conditions. Further in [10], Mickens constructed the best FD scheme for $\vartheta \xi _{rr}= \xi _t+\xi _r+\alpha {\xi }$, where $\vartheta$ and $\alpha$ are positive parameters and studied its stability on the basis of positive constraints. Rucker [11] proposed EFD scheme for $\xi _t+ \xi _r= \xi (1-{\xi }^2)$. Chen et al [12] considered $\vartheta \xi _{rr}=a \xi _t-\alpha \xi +\beta {\xi }^3$ and studied the qualitative stability for $\vartheta =0.$ The numerical simulations illustrate that the scheme proposed is more robust than standard explicit methods such as forward Euler and the fourth-order Runge–Kutta method. Further, Chen et al [12] extended the semi-explicit and implicit scheme for the full equation. In [13], Mickens proposed the EFD scheme for $\xi _t+ \vartheta \xi _r= \alpha \xi + \beta \sqrt{\xi },$ where $\vartheta$, $\alpha$, $\beta$ are real constants and compared the discretisations with the standard one. Appadu [14] solved the one-dimensional advection diffusion equation using explicit Lax–Wendroff scheme, the implicit Crank–Nicolson scheme and an NSFD scheme. Appadu et al [15] used three methods to solve two test problems of advection–diffusion equation. First was the third-order upwind scheme, second was the fourth-order upwind scheme and third one was the NSFD scheme. The result illustrated that NSFD was much better than the third-order and fourth-order upwind scheme for all the cases considered. Wang and Roeger [16] considered the following generalised nonlinear convection–diffusion–reaction PDE:

$$\begin{aligned} \vartheta \xi _{rr}=\xi _{t}+ \eta \xi _{r}-\alpha \xi +\alpha \xi ^{\theta }, \end{aligned}$$

(2)

where $\vartheta$, $\eta$, $\alpha >0$ and $\theta >1$ is a real parameter and constructed two EFD schemes for the case of no diffusion. Due to its complicacy, NSFD schemes are proposed first for diffusionless form and then for full PDE which works for relatively large step sizes (see [16, figures 3(a), 3(b), pp. 1304]). In [17] and [18], Verma and Kayenat proposed the EFD and NSFD schemes for the generalised Burgers–Fisher and the generalised Burgers–Huxley equations, respectively. Recently, Mickens and Washington [19] considered the following advection–diffusion–reaction PDE:

$$\begin{aligned} \vartheta \xi _{rr}=\xi _{t}+ \eta \xi _{r}+\alpha \xi +\beta \xi ^{1/3}, \end{aligned}$$

(3)

where $(\vartheta ,\eta ,\alpha ,\beta )$ are non-negative parameters and proposed positivity preserving NSFD scheme for this.

In this paper, we propose two EFD schemes and three NSFD schemes for the GADR equation (1) which are novel and have not been analysed in the existing literature. Here we propose different NSFD schemes for different $\theta$s and the conditions for the positivity and boundedness of NSFD schemes are deduced and their local truncation errors are calculated. We compute the solutions through the proposed NSFD schemes to illustrate their efficiency.

Remark 1

In most of the cases, EFD scheme is very complicated to be programmed and very difficult to use for actual computation. Therefore, we define simpler version of EFD scheme which we refer as NSFD, such that this NSFD inherits certain property of the original equation and satisfies one or more of NSFD rules [2, p. 84]. As observed by Mickens and Shoosmith [7], we also observe that for very few spatial divisions we get highly accurate solutions, e.g. $10^{-10}$.

The article is organised as follows. We present the derivation of EFD schemes for the nonlinear GADR equation (1) in §2. It follows that different NSFD schemes are proposed for different $\theta$s and their positivity-boundedness properties are discussed in detail in §3. In §4, we calculate the local truncation errors of NSFD schemes. Section 5 presents several simulations aimed at establishing the validity of the methods and §6 closes this work with some concluding observations.

2 Derivation of EFD schemes

In this section, we derive EFD schemes for the nonlinear GADR equation (1). Kumar et al [1] derived the following solitary wave solution of (1) using homogeneous balance method:

$$\begin{aligned} \xi (r,t)= & {} \left[ \frac{p}{2}\left\{ 1+\tanh \left( \frac{pr+qt}{2} \right) \right\} \right] ^{{1}/{\theta }}\nonumber \\= & {} \left[ \frac{p}{1+\exp (- (pr+qt))}\right] ^{{1}/{\theta }}, \end{aligned}$$

(4)

where

$$\begin{aligned}&p=\frac{\alpha \theta ^2 }{\vartheta (1+\theta )}, ~ q=\frac{\alpha \theta ^2\left( \alpha \theta -\eta \theta -\eta \right) }{\vartheta (1+\theta )^2} \end{aligned}$$

and

$$\begin{aligned}&\beta =\frac{\vartheta (1+\theta ) }{\theta ^2}. \end{aligned}$$

(5)

From (4), we get

$$\begin{aligned}&\left( \frac{1}{\xi (r,t)}\right) ^\theta -\left( \frac{1}{\xi (r+\delta r,t)}\right) ^\theta \nonumber \\&\quad = \frac{1}{p}\left[ \left\{ 1+\exp (- (pr+qt))\right\} \right. \nonumber \\&\qquad \left. -\left\{ 1+\exp (- p(r+\delta r)+qt))\right\} \right] \nonumber \\&\quad = \left( \frac{1-\exp (- p\delta r)}{p}\right) \left\{ \exp (- (pr+qt))\right\} . \end{aligned}$$

(6)

Similarly, we compute the forward and backward differences in space and time with the non-trivial DFs given as follows:

$$\begin{aligned} \partial _{r}\xi= & {} \frac{\xi (r+\delta r,t)-\xi (r,t)}{ \tau _{1}}\nonumber \\= & {} \frac{(p-\left( \xi (r,t)\right) ^\theta )\left( \xi (r+\delta r,t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r,t)\right) ^{\theta -k-1} \left( \xi (r+\delta r,t)\right) ^k}, \end{aligned}$$

(7)

$$\begin{aligned} {\overline{\partial }}_{r}\xi= & {} \frac{\xi (r,t)-\xi (r-\delta r,t)}{ \tau _{2}}\nonumber \\= & {} \frac{(p-(\xi (r,t))^\theta )\left( \xi (r-\delta r,t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r,t)\right) ^{\theta -k-1} \left( \xi (r-\delta r,t)\right) ^k}, \end{aligned}$$

(8)

$$\begin{aligned}&\partial _{t}\xi =\frac{ \xi (r,t+\delta t)-\xi (r,t)}{ \chi _{2} }\nonumber \\&=\frac{q}{p}\frac{(p-\left( \xi (r,t)\right) ^\theta )\left( \xi (r,t+\delta t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r,t+\delta t)\right) ^{\theta -k-1} \left( \xi (r,t)\right) ^k}, \end{aligned}$$

(9)

$$\begin{aligned} {\overline{\partial }}_{t}\xi= & {} \frac{\xi (r,t)-\xi (r,t-\delta t)}{\chi _{1} }\nonumber \\= & {} \frac{q}{p}\frac{\left( p-\left( \xi (r,t)\right) ^\theta \right) \left( \xi (r,t-\delta t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r,t-\delta t)\right) ^{\theta -k-1} \left( \xi (r,t)\right) ^k}, \end{aligned}$$

(10)

where the notations of DFs are explained as follows:

$$\begin{aligned} \tau _{1}= & {} \frac{1-\exp (- p\delta r)}{ p},~\tau _{2}=\frac{\exp ( p\delta r)-1}{ p},\nonumber \\ \chi _{1}= & {} \frac{\exp (q\delta t)-1}{q},~\chi _{2}=\frac{1-\exp ( -q\delta t)}{q}. \end{aligned}$$

(11)

Now, we select $\xi _{rr}\approx \partial _{r}\overline{\partial }_{r}{\xi }$, then using (8), we get

$$\begin{aligned} \partial _{r}{{\overline{\partial }}}_{r}{\xi }= & {} \partial _{r}\left( \frac{\xi (r,t)-\xi (r-\delta r,t)}{\tau _{2}}\right) \nonumber \\= & {} \frac{ \partial _{r} \xi (r,t)- \partial _{r}\xi (r-\delta r,t)}{\tau _{2}}\nonumber \\= & {} \frac{ 1 }{\tau _{2}}\left\{ \frac{(p-\left( \xi (r,t)\right) ^\theta )\left( \xi (r+\delta r,t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r,t)\right) ^{\theta -k-1} \left( \xi (r+\delta r,t)\right) ^k}\right. \nonumber \\&\quad \left. - \frac{(p-(\xi (r-\delta r,t))^\theta )\left( \xi (r,t)\right) ^\theta }{\sum _{k=0}^{\theta -1} \left( \xi (r-\delta r,t)\right) ^{\theta -k-1} \left( \xi (r,t)\right) ^k}\right\} .\nonumber \\ \end{aligned}$$

(12)

We denote

$$\begin{aligned} \Psi _1= & {} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi (r,t)\right) ^{\theta -k-1} \left( \xi (r+\delta r,t)\right) ^k, \\ \Psi _2= & {} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi (r-\delta r,t)\right) ^{\theta -k-1} \left( \xi (r,t)\right) ^k \end{aligned}$$

and write $\xi _j^n$ as follows:

$$\begin{aligned} \xi _j^n=\xi (r_j,t_n) =\left[ \frac{p}{1+\exp (- (pr_j + qt_n))}\right] . \end{aligned}$$

(13)

Applying (13) in (12), we deduce the following:

$$\begin{aligned}&\vartheta \xi _{rr}\approx \vartheta (\partial _{r}{{\overline{\partial }}}_{r}{\xi }) \nonumber \\&\quad = \frac{\vartheta }{\tau _{2}}\left[ \frac{p((\xi _{j+1}^n)^\theta \Psi _2-(\xi _j^n)^\theta \Psi _1 )- (\xi _{j}^{n})^\theta ((\xi _{j+1}^n)^\theta \Psi _2-(\xi _{j-1}^n)^\theta \Psi _1 )}{\Psi _1 \Psi _2}\right] \end{aligned}$$

(14)

$$\begin{aligned}&=\frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\left[ (\xi _{j+1}^n)^\theta \left\{ (\xi _{j}^{n})^{\theta -1} +\xi _{j-1}^{n}(\xi _{j}^{n})^{\theta -2}\right. \right. \nonumber \\&\quad \left. \left. +\cdots +(\xi _{j-1}^{n})^{\theta -2}\xi _{j}^{n}+(\xi _{j-1}^{n})^{\theta -1} \right\} \right. \nonumber \\&\quad \left. - (\xi _{j}^{n})^{\theta } \left\{ (\xi _{j+1}^{n})^{\theta -1}\right. \right. \nonumber \\&\quad \left. \left. +\xi _{j}^{n}(\xi _{j+1}^{n})^{\theta -2}+\cdots +(\xi _{j}^{n})^{\theta -2}\xi _{j+1}^{n}+(\xi _{j}^{n})^{\theta -1}\right\} \right] \nonumber \\&\quad -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{\tau _{2} \Psi _1 \Psi _2}\left[ (\xi _{j+1}^n)^\theta \left\{ (\xi _{j}^{n})^{\theta -1}\right. \right. \nonumber \\&\quad \left. \left. +\xi _{j-1}^{n}(\xi _{j}^{n})^{\theta -2}+\cdots +(\xi _{j-1}^{n})^{\theta -2}\xi _{j}^{n}+(\xi _{j-1}^{n})^{\theta -1}\right\} \right. \nonumber \\&\quad \left. - (\xi _{j-1}^{n})^{\theta } \left\{ (\xi _{j+1}^{n})^{\theta -1} +\xi _{j}^{n}(\xi _{j+1}^{n})^{\theta -2}\right. \right. \nonumber \\&\quad \left. \left. +\cdots +(\xi _{j}^{n})^{\theta -2}\xi _{j+1}^{n}+(\xi _{j}^{n})^{\theta -1}\right\} \right] \nonumber \\&\quad = \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\left[ (\xi _{j}^{n})^{\theta -1} \left( (\xi _{j+1}^n)^\theta -(\xi _{j}^n)^\theta \right) \right. \nonumber \\&\quad \left. +(\xi _{j}^{n})^{\theta -2}\xi _{j+1}^{n} \left( (\xi _{j+1}^n)^{\theta -1}\xi _{j-1}^{n}-(\xi _{j}^n)^\theta \right) \right. \nonumber \\&\quad \left. +\cdots +(\xi _{j+1}^{n})^{\theta -1} \left( \xi _{j+1}^n (\xi _{j-1}^{n})^{\theta -1}(\xi _{j}^n)^\theta \right) \right] \nonumber \\&\quad -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{\tau _{2} \Psi _1 \Psi _2}\left[ (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1} \left( \xi _{j+1}^{n} -\xi _{j-1}^{n}\right) \right. \nonumber \\&\quad \left. +(\xi _{j+1}^n)^{\theta -2}(\xi _{j-1}^n)^{\theta -2} \xi _{j}^{n} \right. \left( (\xi _{j+1}^{n})^2 -(\xi _{j-1}^{n})^2\right) \nonumber \\&\quad +(\xi _{j+1}^n)^{\theta -3}(\xi _{j-1}^n)^{\theta -3} (\xi _{j}^{n})^2 \left( (\xi _{j+1}^{n})^3 \left. -(\xi _{j-1}^{n})^3\right) +\cdots \right. \nonumber \\&\quad + \xi _{j+1}^{n}\xi _{j-1}^{n}(\xi _{j}^{n})^{\theta -2} \left( (\xi _{j+1}^{n})^{\theta -1}-(\xi _{j+1}^{n})^{\theta -1} \right) \nonumber \\&\left. \quad +(\xi _{j}^{n})^{\theta -1} \left( (\xi _{j+1}^{n})^{\theta }-(\xi _{j-1}^{n})^{\theta } \right) \right] \end{aligned}$$

(15)

$$\begin{aligned}&=\frac{\vartheta p(\xi _{j}^{n})^{\theta -1}}{ \Psi _2}\left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) \nonumber \\&\quad +\frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\left\{ (\xi _{j}^{n})^{\theta -2}\xi _{j+1}^{n} \left( (\xi _{j+1}^n)^{\theta -1}\xi _{j-1}^{n}-(\xi _{j}^n)^\theta \right) \right. \nonumber \\&\quad +\cdots +(\xi _{j+1}^{n})^{\theta -1} \left. \left( \xi _{j+1}^n (\xi _{j-1}^{n})^{\theta -1}-(\xi _{j}^n)^\theta \right) \right\} \nonumber \\&\quad -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{\tau _{2} \Psi _1 \Psi _2}\left( \xi _{j+1}^{n} -\xi _{j-1}^{n}\right) \left\{ (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1} \right. \nonumber \\&\quad +(\xi _{j+1}^n)^{\theta -2} (\xi _{j-1}^n)^{\theta -2} \xi _{j}^{n}\left( \xi _{j+1}^{n} +\xi _{j-1}^{n}\right) \nonumber \\&\quad \left. + \cdots +(\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi _{j-1}^n\right) ^{\theta -k-1}\left( \xi _{j+1}^n\right) ^k\right\} \nonumber \\&\quad =\frac{q}{p}\left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) +\left( \frac{\vartheta p}{\theta }\frac{(\xi _{j}^{n})^{\theta -1}}{\frac{\Psi _2}{\theta }}\right. \nonumber \\&\left. \quad -\frac{q}{p}\right) \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{ \Psi _1 \Psi _2} \end{aligned}$$

(16)

$$\begin{aligned}&\left( \frac{\xi _{j+1}^{n}-\xi _{j-1}^{n}}{\tau _{2}}\right) \left\{ (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+\cdots \right. \nonumber \\&\quad \left. + (\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi _{j-1}^n\right) ^{\theta -k-1} \left( \xi _{j+1}^n\right) ^k\right\} . \end{aligned}$$

(17)

Here we denote

$$\begin{aligned} c= & {} (\xi _{j}^{n})^{\theta -2}\xi _{j+1}^{n} \left( (\xi _{j+1}^n)^{\theta -1}\xi _{j-1}^{n}-(\xi _{j}^n)^\theta \right) \\&+\cdots +(\xi _{j+1}^{n})^{\theta -1}\left( \xi _{j+1}^n (\xi _{j-1}^{n})^{\theta -1}-(\xi _{j}^n)^\theta \right) \end{aligned}$$

and verify that

$$\begin{aligned} \left( \frac{\vartheta p}{ \theta }\frac{(\xi _{j}^{n})^{\theta -1}}{\frac{\Psi _2}{\theta }}-\frac{q}{p}\right) \approx \left( \frac{\vartheta p}{ \theta }-\frac{q}{p}\right) =\eta . \end{aligned}$$

Case I: Choosing $\delta r=\left( {-q}/{p}\right) \delta t,$ we deduce from (4) and (11) as follows:

$$\begin{aligned} \xi (r+\delta r,t)=\xi (r,t-\delta t) \end{aligned}$$

and

$$\begin{aligned} \frac{1}{\chi _2}=\left( \frac{-q}{p}\right) \frac{1}{\tau _2}. \end{aligned}$$

(18)

Using (18) in (16), we arrive at

$$\begin{aligned}&\vartheta \xi _{rr}\approx \left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) +\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) \nonumber \\&\qquad +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{ \Psi _1 \Psi _2}\left( \frac{\xi _{j+1}^{n}-\xi _{j}^{n}+\xi _{j}^{n}-\xi _{j-1}^{n}}{\tau _{2}}\right) \nonumber \\&\qquad \times \left( (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots \right. \nonumber \\&\qquad \left. + (\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi _{j-1}^n\right) ^{\theta -k-1} \left( \xi _{j+1}^n\right) ^k\right) \nonumber \\&\quad = \left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) \!{+}\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) \!{+}\! \left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c\nonumber \\&\qquad -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{ \Psi _1 \Psi _2}\left( \frac{\left( p-(\xi _{j+1}^{n})^\theta \right) (\xi _{j}^{n})^\theta }{ \Psi _1}\right. \nonumber \\&\qquad \left. +\frac{\left( p-(\xi _{j}^{n})^\theta \right) (\xi _{j-1}^{n})^\theta }{\Psi _2}\right) \left( (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}\right. \nonumber \\&\qquad \left. + \cdots + (\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} \left( \xi _{j-1}^n\right) ^{\theta -k-1} \left( \xi _{j+1}^n\right) ^k\right) \nonumber \\&\quad =\left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) {+}\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) \!{+}\!\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c\nonumber \\&\qquad -\frac{\vartheta (\xi _{j}^{n})^{\theta }}{ \Psi _1 \Psi _2}\left[ p\left( \frac{(\xi _{j}^{n})^\theta \Psi _2+(\xi _{j-1}^{n})^\theta \Psi _1 }{ \Psi _1 \Psi _2}\right) -(\xi _{j}^{n})^{\theta }\right. \nonumber \\&\qquad \left. \times \left( \frac{(\xi _{j+1}^{n})^\theta \Psi _2+(\xi _{j-1}^{n})^\theta \Psi _1 }{ \Psi _1 \Psi _2}\right) \right] \nonumber \\&\qquad \times \left( (\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots \right. \nonumber \\&\qquad \left. + (\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k\right) \nonumber \\&\quad =\left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) +\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) \nonumber \\&\qquad +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c-\left[ \left( \frac{\vartheta p(\theta +1)}{\theta ^2}\right) \left( \frac{ (\xi _{j}^{n})^{\theta }}{\frac{\Psi _1}{\theta }}\right) \right. \nonumber \\&\qquad \times \left\{ \frac{1}{2}\left( \frac{(\xi _{j}^{n})^\theta }{\frac{\Psi _1}{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{\frac{\Psi _2}{\theta } }\right) \right\} \nonumber \\&\qquad - \left( \frac{\vartheta (\theta +1)}{\theta ^2}\right) (\xi _{j}^{n})^{\theta }\left( \frac{ (\xi _{j}^{n})^{\theta }}{\frac{\Psi _1}{\theta }}\right) \nonumber \\&\qquad \times \left. \left\{ \frac{1}{2}\left( \frac{(\xi _{j+1}^{n})^\theta }{\frac{\Psi _1}{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{\frac{\Psi _2}{\theta } }\right) \right\} \right] \end{aligned}$$

$$\begin{aligned}&\qquad \times \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) \nonumber \\&\quad =\left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) +\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c - \alpha \left( \frac{ (\xi _{j}^{n})^{\theta }}{\frac{\Psi _1}{\theta }}\right) \left\{ \frac{1}{2}\left( \frac{(\xi _{j}^{n})^\theta }{\frac{\Psi _1}{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{\frac{\Psi _2}{\theta } }\right) \right\} \nonumber \\&\qquad \times \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \displaystyle \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) +\beta (\xi _{j}^{n})^{\theta }\left( \frac{ (\xi _{j}^{n})^{\theta }}{{\Psi _1}/{\theta }}\right) \nonumber \\&\qquad \times \frac{1}{2}\left( \frac{(\xi _{j+1}^{n})^\theta }{\frac{\Psi _1}{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{\frac{\Psi _2}{\theta } }\right) \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) . \end{aligned}$$

(19)

Due to the non-local discrete representations, the term c of eq. (19) can be approximated to zero. Thus, we get the EFD scheme of eq. (1) as follows:

$$\begin{aligned}&\text{ EFDS}_1{:}\nonumber \\&\quad \vartheta \left( \frac{\xi _{j+1}^n-2\xi _{j}^n+\xi _{j-1}^n}{\tau _1 \tau _2}\right) = \left( \frac{\xi _j^n-\xi _{j}^{n-1}}{\chi _2}\right) +\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c- \alpha \left( \frac{ (\xi _{j}^{n})^{\theta }}{{\Psi _1}/{\theta }}\right) \nonumber \\&\quad \times \frac{1}{2}\left( \frac{(\xi _{j}^{n})^\theta }{{\Psi _1}/{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{{\Psi _2}/{\theta } }\right) \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) +\beta (\xi _{j}^{n})^{\theta }\nonumber \\&\quad \times \left( \frac{ (\xi _{j}^{n})^{\theta }}{{\Psi _1}/{\theta }}\right) \frac{1}{2}\left( \frac{(\xi _{j+1}^{n})^\theta }{{\Psi _1}/{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{{\Psi _2}/{\theta } }\right) \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) .\nonumber \\ \end{aligned}$$

(20)

Theorem 1

An implicit EFD scheme for the nonlinear GADR equation (1) is given by (20). The step-size satisfies $\delta r= -\left( {q}/{p}\right) \delta t,$ and the DFs satisfy (11).

Case II: Choosing $\delta r=\left( {q}/{p}\right) \delta t,$ we deduce from (4) and (11) as follows:

$$\begin{aligned}&\xi (r+\delta r,t)=\xi (r,t+\delta t) \end{aligned}$$

and

$$\begin{aligned} \frac{1}{\chi _1}=\left( \frac{q}{p}\right) \frac{1}{\tau _2}. \end{aligned}$$

(21)

Proceeding in the same fashion, we arrive at the following equation:

$$\begin{aligned}&\text{ EFDS}_2:\nonumber \\&\quad \vartheta \left( \frac{\xi _{j+1}^n-2\xi _{j}^n+\xi _{j-1}^n}{\tau _1 \tau _2}\right) = \left( \frac{\xi _j^{n+1}-\xi _{j}^{n}}{\chi _1}\right) +\eta \left( \frac{\xi _{j+1}^n-\xi _{j}^n}{\tau _{2}}\right) +\left( \frac{\vartheta p}{\tau _{2} \Psi _1 \Psi _2}\right) c- \alpha \left( \frac{ (\xi _{j}^{n})^{\theta }}{{\Psi _1}/{\theta }}\right) \nonumber \\&\quad \times \frac{1}{2}\left( \frac{(\xi _{j}^{n})^\theta }{{\Psi _1}/{\theta } }+\frac{(\xi _{j-1}^{n})^\theta }{{\Psi _2}/{\theta } }\right) \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}+ \cdots + (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) +\beta (\xi _{j}^{n})^{\theta }\nonumber \\&\quad \times \left( \frac{ (\xi _{j}^{n})^{\theta }}{{\Psi _1}/{\theta }}\right) \frac{1}{2}\left( \frac{(\xi _{j+1}^{n})^\theta }{{\Psi _1}/{\theta } }{+}\frac{(\xi _{j-1}^{n})^\theta }{{\Psi _2}/{\theta } }\right) \left( \frac{(\xi _{j+1}^n)^{\theta -1}(\xi _{j-1}^n)^{\theta -1}{+} \cdots {+} (\xi _{j}^{n})^{\theta -1} \sum _{k=0}^{\theta -1} (\xi _{j-1}^n)^{\theta -k-1} (\xi _{j+1}^n)^k}{\frac{\theta (\theta +1)}{2} \frac{\Psi _2}{\theta }} \right) . \end{aligned}$$

(22)

Theorem 2

An explicit EFD scheme for the nonlinear GADR equation (1) is given by (22). The step-size satisfies $\delta r= \left( {q}/{p}\right) \delta t,$ and the DFs satisfy (11).

3 Non-standard finite difference schemes

We propose the following non-standard FD schemes for the non-linear GADR equation (1) for $\theta \in {\mathbb {N}}$, where $\Gamma =\tau _1 \tau _2$, $R=\chi _2/\Gamma$ and $R_1=\chi _2/\tau _2.$

• Case I: For $\theta = \{1,2\}$

$$\begin{aligned}&\vartheta \left( \frac{\xi _{j+1}^n-2\xi _{j}^n+\xi _{j-1}^n}{\Gamma }\right) \nonumber \\&\quad = \left( \frac{\xi _j^{n+1}-\xi _{j}^{n}}{\chi _2}\right) +\eta \left( \frac{\xi _{j}^n-\xi _{j-1}^n}{\tau _{2}}\right) \nonumber \\&\qquad -\alpha (\xi _{j}^n)^{\theta +1} +\beta (\xi _{j}^n)^{2\theta } \xi _{j}^{n+1}, \end{aligned}$$

(23)

$$\begin{aligned}&\xi _j^{n+1}= \frac{(\vartheta R+ \eta R_1)\xi _{j-1}^n+(1-2\vartheta R- \eta R_1)\xi _{j}^n+\vartheta R \xi _{j+1}^n+\alpha \chi _2(\xi _{j}^n)^{\theta +1}}{1+\beta \chi _2 (\xi _{j}^n)^{2\theta }}. \end{aligned}$$

(24)

• Case II: For $\theta =3$

$$\begin{aligned}&\vartheta \left( \frac{\xi _{j+1}^n-2\xi _{j}^n+\xi _{j-1}^n}{\Gamma }\right) \nonumber \\&\quad = \left( \frac{\xi _j^{n+1}-\xi _{j}^{n}}{\chi _2}\right) +\eta \left( \frac{\xi _{j}^n-\xi _{j-1}^n}{\tau _{2}}\right) \nonumber \\&\qquad -\alpha (\xi _{j}^n)^{4} +\beta (\xi _{j}^n)^{5} \xi _{j-1}^n\xi _{j}^{n+1}, \end{aligned}$$

(25)

$$\begin{aligned}&\xi _j^{n+1}= \frac{(\vartheta R+ \eta R_1)\xi _{j-1}^n+(1-2\vartheta R- \eta R_1)\xi _{j}^n+\vartheta R \xi _{j+1}^n+\alpha \chi _2(\xi _{j}^n)^{4}}{1+\beta \chi _2\xi _{j-1}^n(\xi _{j}^n)^{5}}. \end{aligned}$$

(26)

• Case III: For $\theta \ge 4$

$$\begin{aligned}&\vartheta \left( \frac{\xi _{j+1}^n-2\xi _{j}^n+\xi _{j-1}^n}{\Gamma }\right) \nonumber \\&\quad = \left( \frac{\xi _j^{n+1}-\xi _{j}^{n}}{\chi _2}\right) +\eta \left( \frac{\xi _{j}^n-\xi _{j-1}^n}{\tau _{2}}\right) \nonumber \\&\qquad -\alpha (\xi _{j}^n)^{\theta +1} +\beta (\xi _{j}^n)^{2\theta -2} \xi _{j-1}^n \xi _{j+1}^n\xi _{j}^{n+1}, \end{aligned}$$

(27)

$$\begin{aligned}&\xi _j^{n+1}= \frac{(\vartheta R+ \eta R_1)\xi _{j-1}^n+(1-2\vartheta R- \eta R_1)\xi _{j}^n+\vartheta R \xi _{j+1}^n+\alpha \chi _2(\xi _{j}^n)^{\theta +1}}{1+\beta \chi _2 \xi _{j-1}^n (\xi _{j}^n)^{2\theta -2}\xi _{j+1}^n}. \end{aligned}$$

(28)

Theorem 3

Let $\exists ~p \in {\mathbb {R}}^+$ such that $0\le \vartheta R+ \eta R_1 \le 1-\vartheta R$ with $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$ and $\eta \in {\mathbb {R}}$. Then the NSFD scheme (24) satisfies the positivity and boundedness property for $\theta =1,$ i.e.,

$$\begin{aligned} 0\le \xi _{j}^n \le p\Rightarrow 0 \le \xi _{j}^{n+1}\le p, \end{aligned}$$

for all j, n.

From the given conditions, we have, $1-2\vartheta R- \eta R_1 \ge 0$. Thus from (24), we conclude that

$$\begin{aligned} \xi _{j}^n\ge 0 \Rightarrow \xi _{j}^{n+1}\ge 0,~ \forall ~ j ~\text{ and }~n. \end{aligned}$$

For boundedness, we have to show $\xi _{j}^{n+1}\le p.$ To prove this, we subtract upside of (24) with downside and arrive at

$$\begin{aligned}&(\vartheta R+ \eta R_1)\xi _{j-1}^n+(1-2\vartheta R- \eta R_1)\xi _{j}^n+\vartheta R \xi _{j+1}^n\nonumber \\&\qquad +\alpha \chi _2(\xi _{j}^n)^{2}-p-\beta p\chi _2 (\xi _{j}^n)^{2}\nonumber \\&\quad \le (\vartheta R+ \eta R_1)p+(1-2\vartheta R- \eta R_1)p+\vartheta R p\nonumber \\&\qquad +\alpha \chi _2(\xi _{j}^n)^{2}-p-\alpha \chi _2 (\xi _{j}^n)^{2} =0 \qquad (\because \alpha = \beta p).\nonumber \\ \end{aligned}$$

(29)

Thus, we have

$$\begin{aligned} 0 \le \xi _{j}^n \le p\Rightarrow 0 \le \xi _{j}^{n+1}\le p. \end{aligned}$$

(30)

Hence the proof is complete.

Theorem 4

Let $\exists ~p \in {\mathbb {R}}^+$ such that $0\le \vartheta R+ \eta R_1 \le 1-\vartheta R-\alpha \chi _2 p$ with $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$ and $\eta \in {\mathbb {R}}$. Then, the NSFD scheme (24) satisfies the positivity and boundedness property for $\theta =2,$ i.e.,

$$\begin{aligned} 0\le \xi _{j}^n \le \sqrt{p} \Rightarrow 0 \le \xi _{j}^{n+1}\le \sqrt{p}, \end{aligned}$$

for all j and n.

From the given conditions, we have $1-2\vartheta R- \eta R_1 \ge 0$. Thus, from (24), we conclude that

$$\begin{aligned} \xi _{j}^n\ge 0 \Rightarrow \xi _{j}^{n+1}\ge 0,~ \forall ~ j ~\text{ and }~n. \end{aligned}$$

For boundedness, we require $\xi _{j}^{n+1}\le \sqrt{p}.$ Similar to the proof of Theorem 1 we proceed to arrive at

$$\begin{aligned}&(\vartheta R+ \eta R_1)\xi _{j-1}^n\nonumber \\&\qquad +(1-2\vartheta R- \eta R_1-\beta \sqrt{p}\chi _2 (\xi _{j}^n)^{3})\xi _{j}^n\nonumber \\&\qquad +\vartheta R \xi _{j+1}^n+\alpha \chi _2(\xi _{j}^n)^{3}-\sqrt{p}\nonumber \\&\quad \le (\vartheta R+ \eta R_1)\sqrt{p}\nonumber \\&\qquad +(1-2\vartheta R- \eta R_1-\beta \sqrt{p}\chi _2 (\xi _{j}^n)^{3})\sqrt{p}\nonumber \\&\qquad +\vartheta R \sqrt{p}+\alpha \chi _2(\xi _{j}^n)^{3}-\sqrt{p} =0. \end{aligned}$$

(31)

This completes the proof.

Theorem 5

Let $\exists ~p \in {\mathbb {R}}^+$ such that $\vartheta R+ \eta R_1-\alpha \chi _2 p\ge 0$ and $1-2\vartheta R-\eta R_1-\alpha \chi _2 p\ge 0$ with $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$ and $\eta \in {\mathbb {R}}$. Then the NSFD scheme (26) satisfies the positivity and boundedness property for $\theta =3,$ i.e.,

$$\begin{aligned} 0\le \xi _{j}^n \le p^{{1}/{3}} \Rightarrow 0 \le \xi _{j}^{n+1}\le p^{{1}/{3}}, \end{aligned}$$

for all j and n.

From the given conditions, we have, $\vartheta R+ \eta R_1 \ge 0$ and $1-2\vartheta R- \eta R_1 \ge 0$. Thus from (26), we conclude that

$$\begin{aligned} \xi _{j}^n\ge 0 \Rightarrow \xi _{j}^{n+1}\ge 0,~ \forall ~ j ~\text{ and }~n. \end{aligned}$$

For boundedness, we require $\xi _{j}^{n+1}\le p^{{1}/{3}}.$ Similar to the above discussion, we arrive at

$$\begin{aligned}&(\vartheta R+ \eta R_1)\xi _{j-1}^n+(1-2\vartheta R- \eta R_1\nonumber \\&\quad -\beta p^{{1}/{3}}\chi _2 \xi _{j-1}^n(\xi _{j}^n)^{4})\xi _{j}^n+\vartheta R \xi _{j+1}^n+\alpha \chi _2(\xi _{j}^n)^{4}-p^{{1}/{3}}\nonumber \\&\,\, \le (\vartheta R+ \eta R_1-\beta p^{{2}/{3}}\chi _2 (\xi _{j}^n)^{4})\xi _{j-1}^n\nonumber \\&\quad +(1-2\vartheta R- \eta R_1)p^{{1}/{3}}+\vartheta Rp^{{1}/{3}}+\alpha \chi _2(\xi _{j}^n)^{4}-p^{{1}/{3}}\nonumber \\&\,\, \le (\vartheta R+ \eta R_1-\beta p^{{2}/{3}}\chi _2 (\xi _{j}^n)^{4})p^{{1}/{3}}\nonumber \\&\quad +(-\vartheta R- \eta R_1)p^{{1}/{3}}+\alpha \chi _2(\xi _{j}^n)^{4}=0. \end{aligned}$$

(32)

Thus, the proof is complete.

Theorem 6

Let $\exists ~p \in {\mathbb {R}}^+$ such that $\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) -\alpha \chi _2 p\ge 0$, $\vartheta R+ \eta R_1-\alpha \chi _2 p\ge 0$ and $\vartheta R-\alpha \chi _2 p\ge 0$ with $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$ and $\eta \in {\mathbb {R}}$. Then, the NSFD scheme (28) satisfies the positivity and boundedness property for $\theta \ge 4,$ i.e.,

$$\begin{aligned} 0\le \xi _{j}^n \le p^{1/\theta } \Rightarrow 0 \le \xi _{j}^{n+1}\le p^{1/\theta }, \end{aligned}$$

for all j and n.

Table 1 Comparison of maximum error for $\alpha =0.001$, $\eta =0.01$, $\vartheta =0.1$ for different values of N, t, $\delta t$ and $\theta$

From the given conditions, we have, $\vartheta R+ \eta R_1 \ge 0$ and $1-2\vartheta R- \eta R_1 \ge 0$. Hence, we have

$$\begin{aligned} \xi _{j}^n\ge 0 \Rightarrow \xi _{j}^{n+1}\ge 0,~ \forall ~ j ~\text{ and }~n. \end{aligned}$$

For boundedness, we have to show $\xi _{j}^{n+1}\le p^{1/\theta }.$ For proving this, we subtract upside of (28) with downside and arrive at

$$\begin{aligned} G= & {} \left( \vartheta R+ \eta R_1-\beta p^{1/\theta }\chi _2 \xi _{j+1}^n(\xi _{j}^n)^{2\theta -2}\right) \xi _{j-1}^n\nonumber \\&+(1-2\vartheta R- \eta R_1)\xi _{j}^n+\vartheta R\xi _{j+1}^n \nonumber \\&+\alpha \chi _2(\xi _{j}^n)^{\theta +1}-p^{1/\theta }\nonumber \\\le & {} (\vartheta R+ \eta R_1)p^{1/\theta }+(1-2\vartheta R- \eta R_1)\xi _{j}^n\nonumber \\&+\left( \vartheta R-\beta p^{2/\theta }\chi _2 (\xi _{j}^n)^{2\theta -2}\right) \xi _{j+1}^n\nonumber \\&+\alpha \chi _2(\xi _{j}^n)^{\theta +1}-p^{1/\theta }\nonumber ~\\\le & {} (2\vartheta R+ \eta R_1-1)p^{1/\theta }+\left( 1-2\vartheta R- \eta R_1\right) \xi _{j}^n\nonumber \\&-\beta p^{\frac{3}{\theta }}\chi _2 (\xi _{j}^n)^{2\theta -2}+\alpha \chi _2(\xi _{j}^n)^{\theta +1}. \end{aligned}$$

(33)

Now we write

$$\begin{aligned}&\left( 1-2\vartheta R- \eta R_1\right) \xi _{j}^n\nonumber \\&\quad =(\theta -3)\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) \xi _{j}^n\nonumber \\&\quad =\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) \overbrace{\left( \xi _{j}^n+\xi _{j}^n+\cdots +\xi _{j}^n\right) }^{(\theta -3)~\text {times}}. \end{aligned}$$

(34)

Using (34) in (33), we get

$$\begin{aligned} G\le & {} \left( \frac{ 1{-}2\vartheta R{-}\eta R_1}{\theta {-}3}-\beta p^{{3}/{\theta }}\chi _2 (\xi _{j}^n)^{\theta +1}(\xi _{j}^n)^{\theta -4}\right) \xi _{j}^n\nonumber \\&+\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) \overbrace{\left( \xi _{j}^n+\cdots +\xi _{j}^n\right) }^{(\theta -4)~\text {times}}\nonumber \\&+(2\vartheta R+ \eta R_1-1)p^{1/\theta }+\alpha \chi _2(\xi _{j}^n)^{\theta +1}\nonumber \\\le & {} \left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3} \right) p^{1/\theta }\nonumber \\&+\left( \frac{1{-}2\vartheta R{-}\eta R_1}{\theta {-}3}-\beta p^{\frac{4}{\theta }}\chi _2 (\xi _{j}^n)^{\theta +1}(\xi _{j}^n)^{\theta -5}\right) \xi _{j}^n\nonumber \\&+\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) \overbrace{\left( \xi _{j}^n+\cdots +\xi _{j}^n\right) }^{(\theta -5)~\text {times}}\nonumber \\&+(2\vartheta R+ \eta R_1-1)p^{1/\theta }+\alpha \chi _2(\xi _{j}^n)^{\theta +1}\nonumber \\\le & {} \left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3} \right) p^{2/\theta }\nonumber \\&+\left( \frac{1{-}2\vartheta R{-}\eta R_1}{\theta {-}3}-\beta p^{{5}/{\theta }}\chi _2 (\xi _{j}^n)^{\theta +1}(\xi _{j}^n)^{\theta -6}\right) \xi _{j}^n\nonumber \\&+\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) \overbrace{\left( \xi _{j}^n+\cdots +\xi _{j}^n\right) }^{(\theta -6)~\text {times}}\nonumber \\&+(2\vartheta R+ \eta R_1-1)p^{1/\theta }+\alpha \chi _2(\xi _{j}^n)^{\theta +1}. \end{aligned}$$

(35)

Proceeding in the same manner, after $(\theta -6)$ steps, we arrive at

$$\begin{aligned} G\le & {} -\beta p\chi _2 (\xi _{j}^n)^{\theta +1}\\&+\left( \frac{ 1-2\vartheta R-\eta R_1}{\theta -3}\right) (\theta -3)p^{1/\theta }\\&+(2\vartheta R+ \eta R_1-1)p^{1/\theta } +\alpha \chi _2(\xi _{j}^n)^{\theta +1}=0. \end{aligned}$$

Thus, we complete the proof.

Table 2 Comparison of maximum error for $\alpha =0.001$, $\eta =0.01$, $\vartheta =0.1$ for different values of N, t, $\delta t$ and $\theta$

Table 3 Comparison of maximum error for $\alpha =0.01$, $\vartheta =1$, $N=4$, $\delta t=0.0001$

Table 4 Comparison of maximum error for $\alpha =0.05$, $\vartheta =5$, $N=4$, $\delta t=0.001$

Table 5 Comparison of maximum error for $\eta =0.005$, $\vartheta =2.5$, $N=4$, $\delta t=0.01$

4 Local truncation error

To compute the truncation error, we apply Taylor’s series expansion on the proposed NSFD scheme given by eq. (1) where $\xi _{j}^{n}=\xi (r_{j},t_{n})$, $\bar{r_{i}}\in (r_{j},r_{j+1})$ and $\bar{t_{n}}\in (t_{n},t_{n+1})$. Following are the notations of the difference equations for the partial derivatives in time and space, respectively:

$$\begin{aligned}&\partial _{t}\xi _{j}^{n} = \frac{\xi _{j}^{n+1}-\xi _{j}^{n}}{\phi _2},\quad \partial _{r}\xi _{j}^{n} = \frac{\xi _{j}^{n}-\xi _{j-1}^{k}}{\tau _2},\\&\partial _{r} \bar{\partial _{r}}\xi _{j}^{n} = \frac{\xi _{j+1}^{n}- 2\xi _{j}^{n} +\xi _{j-1}^{n} }{\tau }. \end{aligned}$$

The local truncation error $\zeta _{j}^n$ of NSFD scheme (24) is as follows:

$$\begin{aligned} \zeta _{j}^n= & {} (\partial _{t} \xi _{j}^n-\xi _{t}(r_{j},t_{n}))-\vartheta (\partial _{r} \bar{\partial _{r}} \xi _{j}^n-\xi _{rr}(r_{j},t_{n}))\nonumber \\&+\eta (\partial _{r} \xi _{j}^n- \xi _{r}(r_{j},t_{n}))-\alpha ((\xi _{j}^{n})^{\theta +1}\nonumber \\&-(\xi (r_{j},t_{n}))^{\theta +1} ) + \beta ((\xi _{j}^{n})^{2\theta }\xi _{j}^{n+1}\nonumber \\&-(\xi (r_{j},t_{n}))^{2\theta +1})\nonumber \\= & {} \left( \frac{\delta t}{\chi _2}-1\right) \xi _{t}(r_{j},t_{n})-\vartheta \left( \frac{(\delta r)^2 }{\Gamma }-1\right) \xi _{rr}({r_{j}},t_{n})\nonumber \\&+\eta \left( \frac{\delta r}{\tau _2}-1\right) \xi _{r}(r_{j},t_{n})\nonumber \\&+\frac{(\delta t)^2}{2 \chi _2}\xi _{t t}(r_{j},t_{n})+\frac{(\delta t)^3}{6 \chi _2}\xi _{ttt}(r_{j},\bar{t_{n}})\nonumber \\&-\vartheta \frac{(\delta r)^4}{12\Gamma } \xi _{rrrr}(\bar{r_{j}},t_{n})- \frac{\eta (\delta r)^2 }{2\tau _2} \xi _{rr}(r_{j},t_{n})\nonumber \\&+\frac{\eta (\delta r)^3}{6\tau _2} \xi _{rrr}(\bar{r_{j}},t_{n})+\beta \delta t \xi _{t}(r_{j},t_{n})(\xi (r_{j},t_{n}))^{2\theta }\nonumber \\&+\beta \frac{(\delta t)^2}{2} \xi _{tt}(r_{j},t_{n})(\xi (r_{j},t_{n}))^{2\theta }\nonumber \\&+\beta \frac{(\delta t)^3}{6} \xi _{ttt}(r_{j},\bar{t_{n}})(\xi (r_{j},t_{n}))^{2\theta }. \end{aligned}$$

(36)

From eq. (36), we make the following analysis on the order of accuracy and consistency:

• (i) In the DFs (11),

  $$\begin{aligned}&\displaystyle \lim _{\delta r\rightarrow 0}\frac{\delta r}{\tau _2}\rightarrow 1 ,\quad \displaystyle \lim _{\delta t \rightarrow 0}\frac{\delta t}{\chi _2}\rightarrow 1 \quad \end{aligned}$$

  and

  $$\begin{aligned}&\displaystyle \lim _{\delta r\rightarrow 0}\frac{(\delta r)^2 }{\Gamma }\rightarrow 1. \end{aligned}$$

• (ii) $\zeta _{j}^n =O(\delta t)+ O(\delta r)$ if $\delta r\rightarrow 0$ and $\delta t \rightarrow 0$. Thus, we can say that the exact solution satisfies the difference equation (1) except for small error.

Similarly, we calculate the truncation error for the NSFD schemes given in eqs (26) (for $\theta =3$) and (28) (for case $\theta \ge 4$). They are also consistent with first order in time and first order in space for all appropriate values of j and n.

Theorem 7

$\mathrm {(Consistency~ Theorem)}$ For $\alpha ,\vartheta ,\beta \in {\mathbb {R}}^+$ and $\eta \in {\mathbb {R}}$, the NSFD schemes defined by (23), (26) and (28) are consistent with first order in time and first order in space for all appropriate values of j and n.

Fig. 1

Comparison of solutions for $\alpha$ when $\eta = 0.01$, $\vartheta =0.001$, $t = 0.1$, $\theta =3$ $\delta r = 0.0625$ and $\delta t = 0.001$.

Fig. 2

Comparison of solutions for $\vartheta$ when $\alpha =0.002$, $t = 5$, $\eta =0.0001$, $\delta r = 0.0625$ and $\delta t = 0.01$.

Fig. 3

Comparison of solutions for $\eta$ when $\vartheta =1$, $\alpha =0.0001$, $\theta =2$, $t = 0.5$, $\delta r = 0.0625$ and $\delta t = 0.001$.

Fig. 4

Comparison of solutions for $\eta$ when $\alpha =\vartheta =0.0001$, $\theta =1$, $t = 0.1$, $\delta r = 0.0625$ and $\delta t = 0.001$.

Fig. 5

Comparison of solutions for $\theta$ when $\eta = 0.1$, $\vartheta =0.0008$, $\alpha =0.005$, $t =0.1$, $\delta r = 0.0625$ and $\delta t = 10^{-4}$.

Fig. 6

Comparison of solutions for t when $\alpha =\vartheta = 0.0001$, $\eta =1$, $t = 5$, $\theta =2$, $\delta r = 0.0625$ and $\delta t = 0.001$.

Fig. 7

Graph of errors for various values of N when $\vartheta =0.1$, $\eta = 0.01$, $\alpha =0.001$, $\theta =3$, $t = 1$ and $\delta t = 0.001$.

Fig. 8

Graph of errors for various values of $\delta t$ when $\vartheta =\alpha =\eta = 0.001$, $t = 1$, $\theta =1$ and $\delta r = 0.03125$.

Fig. 9

NSFD solutions for $\eta = 0.5$, $\vartheta =\alpha =0.001$, $\theta =2$, $N=80$ and $\delta t = 0.01$.

Fig. 10

NSFD solutions for $\eta =-0.8$, $\vartheta =0.01$, $\alpha =0.1$, $\theta =1$, $N = 80$ and $\delta t = 0.001$.

5 Numerical results

We solve the non-linear GADR equation (1) through the proposed NSFD schemes along with the discretised initial condition in time and BCs in space given as follows:

$$\begin{aligned} \left. \begin{array}{ll} \xi _{j}^0=\left[ \dfrac{p}{1+\mathrm{e}^{ (- p r_{j})}}\right] ,~ j = 0, 1, 2, \ldots , N,\\ \xi _{0}^n=\left[ \dfrac{p}{1+\mathrm{e}^{ ( - q t_{n})}}\right] ,~ n=0, 1, 2, \ldots , M,\\ \xi _{j}^n=\left[ \dfrac{p}{1+\mathrm{e}^{ (- p - qt_{n})}}\right] ,~ n=0, 1, 2, \ldots , M. \end{array} \right\} \end{aligned}$$

(37)

The absolute maximum error is defined as:

$$\begin{aligned} \text{ Maximum } \text{ error }= \displaystyle {\max _j} | \varepsilon (r_{j},t_{n})-\xi (r_{j},t_{n})|. \end{aligned}$$

Here $\varepsilon (r_{j},t_{n})$ is the exact solution given in eq. (4) and $\xi (r_{j},t_{n})$ is the NSFD solution at the grid point $(r_{j},t_{n})$. The NSFD solutions hold conditions for positivity and boundedeness. We have done numerical implementation in Mathematica 11.3 with the hardware configuration: 64-bit operating system, $\times 64$-based processor, Intel(R) Core(TM) i7-4790 CPU @3.60 GHz, 4 GB of RAM and used the ‘TimeUsed’ command to compute the CPU time given in seconds. For plottings we have used Origin 8.5.

Tables 1 and 2 present the numerical results of GADR equation at different values of t, $\theta$, N and $\delta t$ for $\alpha =0.001$, $\eta =0.01$, $\vartheta =0.1$. In these tables, we have computed the absolute maximum error between the exact and the NSFD solutions. Here we get highly accurate solution at $N=4$ only. We have also taken less number of temporal division, i.e., for $t=\delta t=0.01$, we have $M=1$ only but then also we are getting $O(10^{-10})$ accurate solution. The increment in T also does not affect the accuracy much. Table 3 presents the absolute maximum error for different values of $\eta \ge 0$, $\theta$ and t when $\alpha =0.01$, $\vartheta =1$, $N=4$, $\delta t=0.0001.$ As we increase $\eta$ and $\theta$, the error also increases a little bit but we can see that the accuracy of the presented method is high for almost all the $\eta$s. Similarly, table 4 presents the absolute maximum error for different values of $\eta <0$, $\theta$ and t when $\alpha =0.05$, $\vartheta =5$, $N=4$, $\delta t=0.001.$ Here, as we decrease $\eta$, there is a slight increment in the error in the respective $\theta$s but overall here too we get good accuracy even at $\theta =4$ and $\eta =-5.$ Table 5 presents the absolute maximum error for different values of $\alpha$, $\theta$ and t when $\eta =0.005$, $\vartheta =2.5$, $N=4$, $\delta t=0.01.$ Here, as we increase $\alpha$ upto 0.1 the error increases, but here impact of time and $\theta$ is very less on the error. For $\alpha =1$, the case is quite different. Here, as we increase $\theta$ and t,  error decreases upto zero. Thus, our proposed method gives highly accurate solutions for very few spatial and temporal divisions. Average CPU time is given here in all the tables which is very less.

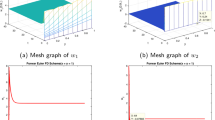
Here, we have plotted two-dimensional figures for the NSFD solutions of the GADR equation (1) by varying $\alpha$, $\vartheta$, $\eta$, $\theta$ and t. From figures 1–6, we can see that the NSFD solutions completely lie on respective exact ones. We have also plotted figures 7 and 8 for the errors in the NSFD solutions at different number of spatial and temporal divisions. From figure 7, we can depict that as we increase the spatial divisions, the error graph tends towards the straight line, and three-dimensional figures for the GADR equation (1). Figures 9 and 10 depict the three-dimensional simulation of NSFD solutions for $\eta >0$ and $\eta <0$, respectively.

6 Conclusions

In this paper, two EFD schemes are proposed for the GADR equation (1). The derived EFD schemes are very complicated, and hence it is difficult to compute solutions from them. Thus, we propose different explicit NSFD schemes for different $\theta$s and successfully used them to obtain the numerical solutions. The proposed NSFD schemes satisfy first four properties given by Mickens in [3, pp. 20–22] which enable them suffer less instabilities which we have verified by the examples. Our NSFD schemes preserve the positivity and boundedness property for all $\theta \in {\mathbb {N}}$ and their local truncation errors are calculated. Through numerical simulations, it is verified that the proposed NSFD schemes give highly accurate solutions for various values of $\alpha$, $\vartheta$, $\eta$, $\theta$, N, t and $\delta t.$ The proposed NSFD schemes are very simple, explicit, consume less computational time and gives high accuracy at very few spatial and temporal divisions. The proposed NSFD methods can also be applied to other types of BCs, e.g., Robin or Neumann BCs. Along with this, these results can also be extended to the GADR equation with variable coefficients in space or time.