1 Introduction

The nonlinear evolution equations (NLEE) are useful because many ideas in NLEEs are more easily understood in terms of simpler equations which model more complicated systems in various aspects. NLEEs appear not only in applied mathematics but also in theoretical physics. The general solutions of these types of equations in areas such as engineering, biology, chemistry, finance and mechanics, help scientists to obtain quite favourable information about the character of equations. Thus, these equations are critical in solving real-world problems and it is important to reach general solutions to make sense of this physical phenomenon. Following the progress on computer-aided calculations and the development of non-linear sciences based on algebraic systems, the application fields of NLEEs have also expanded. Examples of these fields include: optical fibres [1], fluid dynamics and condensed matter physics [2], plasma physics [3] and so on. Due to the efficiency, reliability, and ease of use of symbolic software packages such as Mathematica or Maple, many powerful techniques such as the (\(G^ \prime /G\))-expansion method [4, 5], the simplest equation method [6], the Jacobi elliptic function method [7, 8], the homotopy perturbation method [9, 10], the variational iteration method [11], the sine–cosine method [12], the tanh–coth method [13, 14], the exp-function method [15], the homogeneous balance method [16], first integral methods [17, 18], the Lie symmetry method [19], \(\exp (-\Psi (\xi ))\) expansion method [20], the Hirota bilinear method [21, 22] and so on have been constructed and developed. All these methods are effective methods to obtain travelling wave solutions of NLEEs.

Several important results have emerged for the two-dimensional (2D) systems obtained over the years and a wide variety of 2D systems have been available for the detailed experimental study to assess the suitability of various experimental theories. In recent years, there has been great interest in the impact of dimensionality on the behaviour of physical systems in relation to critical events occurring around phase transitions. The probable reason for the interest in 2D systems is that, while they are broadly similar in many respects to the three-dimensional (3D) systems, the theoretical analysis is somewhat simpler. The simplicity of calculating the geometry of a plane relative to the geometry of the volume, the easier evaluation of the integrals, the need for fewer particles in some numerical calculations are some of the advantages of 2D systems [23].

In this work, first we consider a generalised Hirota–Satsuma coupled KdV (HScKdV) equation. This equation was introduced by Wu et al [24]. They introduced a \(4 \times 4\) matrix spectral problem with three potentials and proposed a corresponding hierarchy of nonlinear equations. One of the typical equations in the hierarchy is the new generalised HScKdV equation as follows:

$$\begin{aligned}&u_t=\frac{1}{2}u_{xxx}-3uu_x+3(vw)_x \nonumber \\&v_t=-v_{xxx}+3uv_x \nonumber \\&w_t=-w_{xxx}+3uw_x . \end{aligned}$$
(1)

This equation has been proposed to explain shallow water waves whose dispersion is unidirectional. Equation (1) was first appeared as an interesting equation in hierarchy which was offered by Wu et al [24]. Substituting \(w = v^*\) in eq. (1), one can obtain a new complex coupled KdV equation [24] and similarly substituting \(w = v\) in eq. (1), the Hirota–Satsuma equation is reached [25]. The HScKdV equation has attracted the attention of many researchers recently, and it has been analysed using different techniques such as the homotopy perturbation approach [26], Jacobi elliptic function [27], the projective Riccati equations [28] etc. to find solutions.

Secondly, the \((2+1)\)-dimensional Nizhnik–Novikov–Veselov (NNV) system discussed in this study is

$$\begin{aligned}&u_t{+}ku_{xxx}{+}ru_{yyy}{+}su_x{+}qu_y{=}3k(uv)_x{+}3r(uw)_y,\nonumber \\&u_x=v_y,\quad u_y=w_x, \end{aligned}$$
(2)

where x, y and t are the scaled space and time coordinates respectively, and the coefficients s, k, r and q are some arbitrary constants [29, 30]. This equation is the only known isotropic Lax integrable extension of the familiar KdV equation [31]. As this system is useful for examining the degeneration of string configurations, membrane shapes and equilibrium shapes [32], it is very important in biomathematics and mathematical physics. Many scientists found solutions of NNV system with the help of different techniques. Some of them are \((G^ \prime /G\))-expansion method [33], the modified Kudryashov method [34], the extended tanh method [35], etc.

The study aims to build up exact solutions for the generalised HScKdV equation (1) and \((2 + 1)\)-dimensional NNV system (2) by using improved \(\tan (\varphi /2)\)-expansion method (ITEM). This technique is one of the most efficient and powerful methods that helps us to obtain solutions of these problems and of many other nonlinear equations. Additionally, this method allows to perform long-term, boring and confusing algebraic calculations by computer using symbolic softwares such as Maple, Matlab, etc.

This paper is arranged as follows: we give the steps of the ITEM in §2. In the next two sections, as an illustration of this method, we apply ITEM to the HScKdV equation (1) and to the NNV system (2) in §3 and §4, respectively. In §5, we discuss the modulation instability analysis. In the last chapter, we give some conclusions and discussions about the obtained solutions. Finally, some references contributing to this paper are given.

2 Algorithm of ITEM for NLEEs

This method was summarised and improved by Manafian et al [36] for achieving analytic solutions of NLEEs. Assume that a nonlinear partial differential equation is given in general form as follows:

$$\begin{aligned} {\mathfrak {F}}(q,q_x,q_t,q_{xx},q_{tt},\ldots )=0. \end{aligned}$$
(3)

After simple algebraic operations, this equation is transformed into an ordinary differential equation (ODE) with \(\xi =kx+vt\) transformation

$$\begin{aligned} {\mathfrak {Q}}(q,kq^{\prime },vq^{\prime },k^2q^{\prime \prime },v^2q^{\prime \prime },\ldots )=0. \end{aligned}$$
(4)

Then, assume that the searched wave solutions of eq. (4) have the following representation:

$$\begin{aligned} q(\xi )=S(\varphi )=\sum _{s=-m}^{m}A_s[\tau +\tan (\varphi /2)]^s, \end{aligned}$$
(5)

where \(A_s\) \((0\le s\le m) \) and \(A_{-s}=B_s\) \((1\le s\le m) \) are constants to be determined and \(\tau \) is an arbitrary constant, such that \(A_m \ne 0\), \(B_m \ne 0\) and \( \varphi =\varphi (\xi )\) is the solution of the following first-order differential equation:

$$\begin{aligned} \varphi ^{\prime }(\xi )=a\sin (\varphi (\xi ))+b\cos (\varphi (\xi ))+c. \end{aligned}$$
(6)

If we try to find the solution of (6), then we obtain special solutions that vary according to the state of the coefficients:

Family 1. When \(\Delta =a^2+b^2-c^2<0\) and \(b-c\ne 0\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}-\frac{\sqrt{-\Delta }}{b-c}\tan \left( \frac{ \sqrt{-\Delta }}{2}{\bar{\xi }}\right) \right] . \end{aligned}$$

Family 2. When \(\Delta =a^2+b^2-c^2>0\) and \(b-c\ne 0\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{a}{b-c}+\frac{\sqrt{\Delta }}{b-c}\tanh \left( \frac{\sqrt{\Delta }}{2}{\bar{\xi }}\right) \right] . \end{aligned}$$

Family 3. When \(\Delta =a^2+b^2-c^2>0\), \(b\ne 0\) and \(c=0\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{a}{b}+\frac{\sqrt{b^2+a^2}}{b}\tanh \left( \frac{ \sqrt{b^2+a^2}}{2}{\bar{\xi }}\right) \right] . \end{aligned}$$

Family 4. When \(\Delta =a^2+b^2-c^2<0\), \(c\ne 0\) and \(b=0\), then

$$\begin{aligned} \varphi (\xi ) = 2\tan ^{-1}\left[ \frac{-a}{c}{+}\frac{\sqrt{c^2-a^2}}{c}\tanh \left( \frac{ \sqrt{c^2-a^2}}{2}{\bar{\xi }}\right) \right] . \end{aligned}$$

Family 5. When \(\Delta =a^2+b^2-c^2>0\), \(b-c\ne 0\) and \(a=0\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \sqrt{\frac{b+c}{b-c}}\tanh \left( \frac{\sqrt{b^2-c^2}}{ 2}{\bar{\xi }}\right) \right] . \end{aligned}$$

Family 6. When \(a=0\) and \(c=0\), then

$$\begin{aligned} \varphi (\xi )=\tan ^{-1}\left[ \frac{\mathrm {e}^{2b{\bar{\xi }}}-1}{\mathrm {e}^{2b{\bar{\xi }}}+1},\frac{\mathrm {e}^{2b{\bar{\xi }}}}{\mathrm {e}^{2b\bar{ \xi }}+1}\right] . \end{aligned}$$

Family 7. When \(b=0\) and \(c=0\), then

$$\begin{aligned} \varphi (\xi )=\tan ^{-1}\left[ \frac{\mathrm {e}^{2a{\bar{\xi }}}}{\mathrm {e}^{2a{\bar{\xi }}}+1},\frac{\mathrm {e}^{2a{\bar{\xi }}}-1}{\mathrm {e}^{2a\bar{ \xi }}+1}\right] . \end{aligned}$$

Family 8. When \(a^2+b^2=c^2\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{{a{\bar{\xi }}}+2}{(b-c){\bar{\xi }}}\right] . \end{aligned}$$

Family 9. When \(a=b=c=ka\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}[{\mathrm {e}^{ka {\bar{\xi }}}-1}]. \end{aligned}$$

Family 10. When \(a=c=ka\) and \(b=-ka\), then

$$\begin{aligned} \varphi (\xi )=-2\tan ^{-1} \left[ \frac{\mathrm {e}^{ka{\bar{\xi }}}}{\mathrm {e}^{ka{\bar{\xi }}}-1}\right] . \end{aligned}$$

Family 11. When \(c=a\), then

$$\begin{aligned} \varphi (\xi )=-2\tan ^{-1}\left[ \frac{ (a+b)\mathrm {e}^{b{\bar{\xi }}}-1}{(a-b)\mathrm {e}^{b{\bar{\xi }}}-1}\right] . \end{aligned}$$

Family 12. When \(a=c\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{ (c+b)\mathrm {e}^{b{\bar{\xi }}}+1}{(b-c)\mathrm {e}^{b{\bar{\xi }}}-1}\right] . \end{aligned}$$

Family 13. When \(c=-a\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{\mathrm {e}^{b {\bar{\xi }}}+b-a}{\mathrm {e}^{b{\bar{\xi }}}-b-a}\right] . \end{aligned}$$

Family 14. When \(b=-c\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{a\mathrm {e}^{a {\bar{\xi }}}}{1-d\mathrm {e}^{a{\bar{\xi }}}}\right] . \end{aligned}$$

Family 15. When \(b=0\) and \(a=c\), then

$$\begin{aligned} \varphi (\xi )=-2\tan ^{-1}\left[ \frac{c{\bar{\xi }}+2}{c{\bar{\xi }}}\right] . \end{aligned}$$

Family 16. When \(a=0\) and \(b=c\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}[ c {\bar{\xi }}]. \end{aligned}$$

Family 17. When \(a=0\) and \(b=-c\), then

$$\begin{aligned} \varphi (\xi )=-2\tan ^{-1}\left[ \frac{1}{c{\bar{\xi }}}\right] . \end{aligned}$$

Family 18. When \(a=0\) and \(b=0\), then

$$\begin{aligned} \varphi (\xi )=c\xi +C. \end{aligned}$$

Family 19. When \(b=c\), then

$$\begin{aligned} \varphi (\xi )=2\tan ^{-1}\left[ \frac{\mathrm {e}^{a {\bar{\xi }}}-c}{a}\right] , \end{aligned}$$

where \({\bar{\xi }}=\xi +C\), \(p,A_0,A_s,B_s (s=1,2,\ldots ,m), a,b\) and c are constants to be determined later.

As usual, for determining m, the highest-order derivative should be balanced with the highest-order nonlinear terms in eq. (4). However, the positive integer m can be determined in this way. When \(m=r/ p\) (where \(m=r/ p\) is a fraction in the lowest term), we need to do a conversion on the unknown function q as follows:

$$\begin{aligned} q(\xi )=(v(\xi ))^{r/p}. \end{aligned}$$
(7)

Then substitute eq. (7) into eq. (4). By using the new eq. (4), the value of m can be determined. If m is a negative integer, similar process can be followed with the transformation

$$\begin{aligned} q(\xi )=(v(\xi ))^m. \end{aligned}$$

Following these operations, according to the obtained m value, substitute (5) into eq. (4). Therefore, we obtain a set of algebraic equations that contain \(\tan (\varphi /2)^s\), \(\cot (\varphi /2)^s\) \((s = 0, 1, 2, \ldots )\). Then setting each coefficient of \(\tan (\varphi /2)^s\), \(\cot (\varphi /2)^s\) to zero, we can get a set of overdetermined equations for \(A_0, A_s, B_s (s = 1, 2, \ldots ,m), a, b, c\) and \(\tau \). As it is difficult to solve the obtained algebraic equations manually, symbolic computation such as Maple can be used at this stage. Finally, \(A_0,A_1,B_1, \ldots , A_m,B_m, \tau \) are replaced in eq. (5).

3 Application of ITEM for HScKdV equation

In this section, we apply the ITEM to eq. (1) to obtain the travelling wave solutions. In this context, let us consider \(u(x,t)=u(\xi )\), \(v(x,t)=v(\xi )\), \(w(x,t)=w(\xi )\), \(\xi =x-kt\) and therefore eq. (1) becomes

$$\begin{aligned}&ku^{\prime }=-\frac{1}{2}u^{{\prime \prime \prime }}+3uu^{\prime }-3(vw)^{\prime } \nonumber \\&kv^{\prime }= v ^{\prime \prime \prime }-3uv^{\prime } \nonumber \\&kw^{\prime }= w ^{\prime \prime \prime }-3uw^{\prime }, \end{aligned}$$
(8)

where ‘\('\)’ shows the derivative according to \(\xi .\) With balancing procedure [39], we get the following two ansatze:

$$\begin{aligned} u(\xi )= & {} A_0+A_1\tan \left( \frac{\varphi (\xi )}{2}\right) +A_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^2\nonumber \\&+A_3\left( \tan \left( \frac{\varphi (\xi )}{2 }\right) \right) ^{-1}{+}A_4\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-2} \end{aligned}$$
$$\begin{aligned}&v(\xi )= B_0+B_1\tan \left( \frac{\varphi (\xi )}{2}\right) +B_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-1} \nonumber \\&w(\xi )= C_0+C_1\tan \left( \frac{\varphi (\xi )}{2}\right) +C_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-1}\nonumber \\ \end{aligned}$$
(9)

and

$$\begin{aligned} u(\xi )= & {} A_0+A_1\tan \left( \frac{\varphi (\xi )}{2}\right) +A_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^2\nonumber \\&+A_3\left( \tan \left( \frac{\varphi (\xi )}{2 }\right) \right) ^{-1}{+}A_4\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-2} \nonumber \\ v(\xi )= & {} B_0+B_1\tan \left( \frac{\varphi (\xi )}{2}\right) +B_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^2\nonumber \\&+B_3\left( \tan \left( \frac{\varphi (\xi )}{2 }\right) \right) ^{-1}{+}B_4\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-2} \nonumber \\ w(\xi )= & {} C_0+C_1\tan \left( \frac{\varphi (\xi )}{2}\right) +C_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^2\nonumber \\&+C_3\left( \tan \left( \frac{\varphi (\xi )}{2 }\right) \right) ^{-1}{+}C_4\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-2}.\nonumber \\ \end{aligned}$$
(10)

First, we substitute the expressions of u, v and w in (9) into (8) and collect all terms with the same order of \( \tan (\varphi (\xi )/2)\) together. Then, by equating the coefficient of each polynomial to zero, we obtain a set of algebraic equations of \( a,b,c,A_i,B_j,C_j\), \(i=0,\ldots ,4\) and \(j=0,\ldots ,2\) as

$$\begin{aligned}&\frac{3}{2}\,A_{{4}}{b}^{3}+\frac{9}{2}\,A_{{4}}{b}^{2}c-3A_{{4}}^{2}b+ \frac{3}{2}\,A_{{4} }{c}^{3}\nonumber \\&\quad -3A_{{4}}^{2}c+\frac{9}{2}\,A_{{4}}b{c}^{2}=0, \nonumber \\&\frac{5}{2}\,A_{{4}}{c}^{3}+kA_{{4}}c+3 B_{{2}}bC_{{2}}+3A_{{4}}^{2}b- \frac{5}{2} \,A_{{4}}{b}^{2}c\nonumber \\&\quad +\frac{5}{2}\,A_{{4}}b{c}^{2}-3 A_{{0}}A_{{4} }b+3 B_{{2}}cC _{{2}}\nonumber \\&\quad +\frac{19}{2}\,A_{{4}}{a}^{2}c-\frac{3}{2}A_{{3}}^{2}b+ \frac{3}{2}\,A_{{3}}a{b}^{2} \nonumber \\&\quad - 3A_{{4}}^{2}c+\frac{19}{2}\,A_{{4}}{a}^{2}b-9A_{{3}}A_{{4}}a-\frac{3 }{2}\,A_{{3 }}^{2}c\nonumber \\&\quad +3A_{{3}}abc-\frac{5}{2}A_{{4}}{b}^{3}+\frac{3}{2}\,A_{{3}}a {c}^{2}\nonumber \\&\quad +\,kA_{{4 }}b-3A_{{0}}A_{{4}}c=0, \nonumber \\&6\,B_{{2}}aC_{{2}}+\frac{3}{2}\,B_{{2}}bC_{{0}}+\frac{3}{2}\,B_{{0}}C_{{2}}b\nonumber \\&\quad +\frac{ 1}{2}\,kA_{{3}}b-\frac{3}{2}\,A_{{0}}A_{{3}}b-\frac{3}{2}\,A_{{1}}A_{{4}}b\nonumber \\&\quad + \frac{9}{2}\,A_{{3}}A_{{4}}b+4 \,A_{{4}}{a}^{3}+\frac{1}{2}\,A_{{3}}{c}^{3} \nonumber \\&\quad +\frac{1}{2}\,kA_{{3}}c-\frac{3}{2}\,A_{{0}}A_{{3} }c+\frac{3}{2}\,B_{{2} }cC_{{0}}+\frac{3}{2}\,B_{{0}}C_{{2}}c\nonumber \\&\quad -\frac{3}{2}\,A_{{1}}A_{{4}}c+\frac{1}{ 2} \,A_{{3}}b{c}^{2}+\frac{7}{4}A_{{3}}{a}^{2}b=0, \nonumber \\&\vdots \end{aligned}$$
(11)

Solving eqs (11) with the help of Maple, we have numerous sets of coefficients for the solutions of (9). We only choose some of them as follows:

Case I

We have the desired constants as

$$\begin{aligned}&a=a,\quad b=b,\quad c=c,\nonumber \\&k={\frac{2\,{b}^{3}c+{b}^{4}+{b}^{2}{a}^{2}+2\,b{ a}^{2}c+{c}^{2}{a}^{2}-12\,C_{{2}}B_{{2}}-2\,{c}^{3}b-{c}^{4}}{4(2cb+{c} ^{2}+{b}^{2})}}, \nonumber \\&A_{{0}}={\frac{-{b}^{4}-2{b}^{3}c+{b}^{ 2}{a}^{2}+2\,b{a} ^{2}c+{c}^{2}{a}^{2}+4\,C_{{2}}B_{{2}}+2\,{c}^{3}b+{c }^{4}}{4(2cb+{c}^{2}+{b }^{2})}},\nonumber \\&A_{{1}}=0,\quad A_{{2}}=0,\quad A_{{3}}=ab+ac, \quad A_{{4 }}=\frac{{b}^{2}}{2}+cb+ \frac{{c}^{2}}{2},\nonumber \\&B_{{0}}={\frac{\left( -bC_{{0}}-cC_{ {0}}+2\,C_{{2}}a \right) B_{{2}}}{C_{{2}} \left( b+c \right) }},\nonumber \\&B_{{1} }=0,\quad B_{{2}}=B_{{2}},\quad C_{{0}}=C_{{0}},\quad C_{{ 1}}=0,\quad C_{{2}}=C_{{2}}. \end{aligned}$$
(12)

By using Family 1, (9) becomes

$$\begin{aligned}&u_1(x,t)=-\frac{\left[ \begin{array}{c} 2a\left( \left( b+c\right) ^{2}\Delta +4B_{2}C_{2}\right) {\sqrt{ -\Delta }\tan ( {\sqrt{-\Delta }\xi }/{2}) } \\ {+\left( 4B_{2}C_{2}+( b+c) ^{2}( a^{2}-b^{2}+c^{2}) \right) \Delta ( \tan ( {\sqrt{-\Delta }\xi }/{2} ) ) ^{2}} \\ {-4\,C_{{2}}B_{{2}}{a}^{2}}-\left( b+c\right) ^{2}\Delta ( a^{2}+2b^{2}-2c^{2}) \end{array} \right] }{4\left( b+c\right) ^{2}( -a+\sqrt{-\Delta }\tan ( { \sqrt{-\Delta }\xi }/{2}) )^{2}}, \end{aligned}$$
(13)
$$\begin{aligned}&v_1\left( x,t\right) =\frac{B_{{2}}( (-bC_{{0}}-cC_{{0}}+2C_{{2}}a) \sqrt{-\Delta }\tan ( {\sqrt{-\Delta }\xi }/{2}) +(b+c)C_{{0} }a-\,C_{{2}}(2{a}^{2}+{b}^{2}-{c}^{2})) }{C_{{2}}\left( b+c\right) ( -a+\sqrt{-\Delta }\tan ({\sqrt{-\Delta }\xi }/{2}) ) }, \end{aligned}$$
(14)
$$\begin{aligned}&w_1(x,t) ={\frac{-C_{{0}}(a-\sqrt{-\Delta }\tan ( {\sqrt{-\Delta }\xi }/{2})) -C_{{2}}(b-c)}{-a+\sqrt{-\Delta }\tan ( {\sqrt{-\Delta }\xi }/{2}) }}, \end{aligned}$$
(15)

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 2, (9) becomes

$$\begin{aligned}&u_2(x,t) ={\frac{\left[ \begin{array}{c} \left( ( b+c\right) ^{2}( a^{2}-b^{2}+c^{2}) +4B_{2}C_{2}) \Delta \tanh ( {\sqrt{\Delta }\xi }/{2}) ^{2} \\ +2a( ( b+c) ^{2}\Delta +4B_{2}C_{2}) \sqrt{\Delta }\tanh ( {\sqrt{\Delta }\xi }/{2}) \\ 4C_{{2}}B_{{2}}{a}^{2}+\left( b+c\right) ^{2}\left( a^{2}+2b^{2}-2c^{2}\right) \Delta \end{array} \right] }{4\left( b+c\right) ^{2}( a+\sqrt{\Delta }\tanh ( { \sqrt{\Delta }\xi }/{2}) ) ^{2}}}, \end{aligned}$$
(16)
$$\begin{aligned}&v_2(x,t)={\frac{B_{{2}}( ( -(b+c)C_{{0}}+2C_{{2}}a) \sqrt{ \Delta }\tanh ( {\sqrt{\Delta }\xi }/{2}) -(b+c)C_{{0}}a+(-{c} ^{2}+2\,{a}^{2}+{b}^{2})C_{{2}}) }{C_{{2}}( b+c) ( a+ \sqrt{\Delta }\tanh ( {\sqrt{\Delta }\xi }/{2}) ) }}, \end{aligned}$$
(17)
$$\begin{aligned}&w_2(x,t) ={\frac{C_{{0}}(a+\sqrt{\Delta }\tanh ( {\sqrt{\Delta }\xi }/{ 2}) )+C_{{2}}(b-c)}{a+\sqrt{\Delta }\tanh ( {\sqrt{\Delta } \xi }/{2}) }}, \end{aligned}$$
(18)

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 8, (9) becomes

$$\begin{aligned}&u_3(x,t)={\frac{\left( b+c\right) ^{2}{a}^{2}+2C_{{2}}B_{{2}}}{2\left( b+c\right) ^{2}}} -\frac{\sqrt{{a}^{2}}{a}^{2}\left( x+Ft\right) .+\frac{ \left( b+c\right) ^{2}\left( b-c\right) ^{2}}{2}\left( x+Ft\right) ^{2}}{ a\left( x+Ft\right) +2}, \end{aligned}$$
(19)
$$\begin{aligned}&v_3(x,t)=\frac{B_{{2}}\left[ \begin{array}{c} -bC_{{0}}a\left( x+Ft\right) -2bC_{{0}}-cC_{{0} }a\left( x+Ft\right) \\ -2\,cC_{{0}}+2C_{{2}}{a}^{2}\left( x+Ft\right) +4C_{ {2}}a\\ +\left( x+Ft\right) C_{{2}}{b}^{2}-\left( x+Ft\right) C_{{2}}{c} ^{2} \end{array}\right] }{{C_{{2}}}\left( b+c\right) \left( a\left( x+Ft\right) +2 \right) }, \end{aligned}$$
(20)
$$\begin{aligned}&w_3(x,t)=\frac{\left( C_{{0}}a\left( x+Ft\right) +2C_{{0}}+\left( x+Ft\right) C_{{2}}b-\left( x+Ft\right) C_{{2}}c\right) }{a\left( x+Ft\right) +2}, \end{aligned}$$
(21)

where

$$\begin{aligned} F=3\,{\frac{C_{{2}}B_{{2}}}{2\,\sqrt{{a}^{2}+{b}^{2}}b+{a}^{2}+2\,{b} ^{2}}.} \end{aligned}$$

By using Family 12, (9) can be written as

$$\begin{aligned}&u_4(x,t) ={\frac{\left[ \begin{array}{c} \left( 8B_{2}C_{2}-6b^{2}\left( b+c\right) ^{2}\right) (b+c){\mathrm {e} ^{b\xi }} \\ +\left( 4B_{2}C_{2}+b^{2}\left( b+c\right) ^{2}\right) \left( b+c\right) ^{2} {\mathrm {e}^{2\,b\xi }} \\ +b^{2}\left( b+c\right) ^{2}+4\,C_{{2}}B_{{2}} \end{array} \right] }{4\left( b+c\right) ^{2}\left( 1+\left( b+c\right) {\mathrm {e} ^{b\xi }}\right) ^{2}}}, \end{aligned}$$
(22)
$$\begin{aligned}&v_4(x,t)={\frac{B_{{2}}\left( \left( C_{{2}}-C_{{0}}\right) (b+c)^{2}{\mathrm {e }^{b\xi }}+(-c-b)C_{{0}}+C_{{2}}(c-b)\right) }{C_{{2}}\left( b+c\right) \left( 1+\left( b+c\right) {\mathrm {e}^{b\xi }}\right) }}, \end{aligned}$$
(23)
$$\begin{aligned}&w_4(x,t) ={\frac{\left( C_{{0}}b+C_{{2}}b-C_{{2}}c+C_{{0}}c\right) {\mathrm {e} ^{b\xi }}-C_{{2}}+C_{{0}}}{1+\left( b+c\right) {\mathrm {e}^{b\xi }}}}, \end{aligned}$$
(24)

where \(\xi =x-kt\).

Case II

We get the following equations:

$$\begin{aligned}&a={\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) }{C_{{1}}B_{{1}}}},\quad b=-c,\quad c=c,\quad k={\frac{{c}^{4}C_{{0}}^{2}B_{{1}}^{ 2}+2\,{c}^{4}C_{{0}}B_{{1}}C_{{1}}B_{{0}}+{c}^{4}C_{{1}}^{2}B_{{0} }^{2}-3\,C_{{1}}^{3}B_{{1}}^{3}}{4C_{{1}}^{2}B_{{1}}^{2}{c}^{2} }}, \nonumber \\&A_{{0}}={\frac{{c}^{4}C_{{0}}^{2}B_{{1}}^{2}+2\,{c}^{4}C_ {{0}}B_{{1}}C_{{1}}B_{{0}}+{c}^{4}C_{{1}}^{2}B_{{0}}^{2}+C_{{1}} ^{3}B_{{1}}^{3}}{4C_{{1}}^{2}B_{{1}}^{2}{c}^{2}}},\quad A_{{1}}={\frac{2{c}^{2} \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) }{C_{{1}}B _{{1}}}},\nonumber \\&A_{{2}}=2{c}^{2},\quad A_{{3}}=0,\quad A_{{4}}=0,\quad B_{{0}}=B_{{0}},\quad B_{1}=B_{{1}},\quad B_{{2}}=0,\quad C_{{0}}=C_{{0}},\quad C_{{1}}=C_{{1}},\quad C_{{2}}=0. \end{aligned}$$
(25)

By using Family 1, (9) becomes

$$\begin{aligned}&u_5(x,t)=-{\frac{ ( ( 16\,C_{{0}}B_{{1}}C_{{1}}B_{{0}}+8C_{ {1}}^{2}B_{{0}}^{2}-8\,C_{{1}}^{2}B_{{1}}^{2}+8\,C_{{0}}^{2} B_{{1}}^{2} ) {c}^{6}+8\,{c}^{4}C_{{1}}^{2}B_{{1}}^{2}{b}^{ 2} ) \tan ({\sqrt{-\Delta }\xi }/{2}) ^{2}}{4{c}^{2}C_{{1}}^{2}B_{{1}}^{2} \left( b-c \right) ^{ 2}}}\\&\quad -2{\frac{\sqrt{-\Delta }{c}^{2} \left( C_{{0}}B_{{1}}{+}B_{{0}}C_{ {1}} \right) \left( c{+}b \right) \tan ({\sqrt{-\Delta }\xi }/{2}) }{B_{{1}}C_{{1}} \left( b-c \right) ^{2}}} {-}{\frac{ \left( C_{{0}}B_{{1}}{+}B_{{0}}C_{{1}} \right) ^{2}(-{c}^{6} {-}6b{c}^{5} -{b}^{2} {c}^{4}){-}B_{{1}}^{3}C_{{1}}^{3 } \left( b{-}c \right) ^{2}}{4{c}^{2}C_{{1}}^{2}B_{{1}}^{2} \left( b{-} c \right) ^{2}}}, \\&v_5(x,t)=- \left( -B_{{0}}b+B_{{0}}c-{\frac{c \left( C_{{0}}B_{{1}}+B_{{0}}C_{ {1}} \right) }{C_{{1}}}}+B_{{1}}\sqrt{-\Delta }\tan \left( \frac{\sqrt{-\Delta }\xi }{2}\right) \right) \left( b-c \right) ^{-1}, \\&w_5(x,t)=- \left( -C_{{0}}b+C_{{0}}c-{\frac{c \left( C_{{0}}B_{{1}}+B_{{0}}C_{ {1}} \right) }{B_{{1}}}}+C_{{1}}\sqrt{-\Delta }\tan \left( \frac{\sqrt{-\Delta }\xi }{2}\right) \right) \left( b-c \right) ^{-1}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 14, (9) can be written as

$$\begin{aligned} u_6(x,t)= & {} \frac{ ( 6 ( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} ) ^{2}{c}^{5}-2\,C_{{1}}^{3}B_{{1}}^{3}c ) {\mathrm{e}^{{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}}}{ 4C_{{1}}^{2}B_{{1}}^{2}{c}^{2} \left( -1+c{\mathrm{e}^ {{\frac{c ( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} ) \xi }{C_{{1}}B_ {{1}}}}}} \right) ^{2}}\\&+ \frac{ ( {c}^{6} ( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} ) ^{2}+C_{ {1}}^{3}B_{{1}}^{3}{c}^{2} ) {\mathrm{e}^{2\,{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}}+ \left( C_ {{0}}B_{{1}}+C_{{1}}B_{{0}} \right) ^{2}{c}^{4}+C_{{1}}^{3}B_{{1}} ^{3} }{ 4C_{{1}}^{2}B_{{1}}^{2}{c}^{2} \left( -1+c{\mathrm{e}^ {{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_ {{1}}}}}} \right) ^{2}}, \\ v_6(x,t)= & {} - \frac{ ( -B_{{0}}c+{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0 }} \right) }{C_{{1}}}} ) {\mathrm{e}^{{\frac{c \left( C_{{0}}B_{{1 }}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}}+B_{{0}} }{\left( -1+c{\mathrm{e}^{{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}} \right) }, \\ w_6(x,t)= & {} -\frac{( -C_{{0}}c+{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0 }} \right) }{B_{{1}}}} ) {\mathrm{e}^{{\frac{c \left( C_{{0}}B_{{1 }}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}}+C_{{0}} }{\left( -1+c{\mathrm{e}^{{\frac{c \left( C_{{0}}B_{{1}}+C_{{1}}B_{{0}} \right) \xi }{C_{{1}}B_{{1}}}}}} \right) }, \end{aligned}$$

where \(\xi =x-kt\).

Case III

We acquire the following constants:

$$\begin{aligned}&a=a,\quad b=b,\quad c=c,\quad k={\frac{-2\,{b}^{3}c+{b}^{4}+{b}^{2}{a}^{2}-2b{a}^{2}c+{c}^{2}{a}^{2}-12\,C_{{1}}B_{{1}}+2\,{c}^{3}b-{c}^{4}}{4( -2\,cb+{c}^{2}+{b}^{2})}},\nonumber \\&A_{{0}}={\frac{2{b}^{3}c-{b}^{4}+{b}^ {2}{a}^{2}-2\,b{a}^{2}c+{c}^{2}{a}^{2}+4C_{{1}}B_{{1}}-2\,{c}^{3}b+{ c}^{4}}{4(-2\,cb+{c}^{2}+{b}^{2})}},\quad A_{{1}}=-ab+ac,\quad A_{{2}}=-cb+\frac{{b}^{ 2}}{2}+\frac{{c}^{2}}{2},\nonumber \\&A_{{3}}=0,\quad A_{{4}}=0,\quad B_{{0}}=-{\frac{ \left( bC_{{0}}- cC_{{0}}+2\,C_{{1}}a \right) B_{{1}}}{C_{{1}} \left( b-c \right) }},\quad B_ {{1}}=B_{{1}},\quad B_{{2}}=0,\quad C_{{0}}=C_{{0}},\quad C_{{1}}=C_{{1}},\quad C_{{2}}=0. \end{aligned}$$
(26)

By using Family 1, we get

$$\begin{aligned}&u_7(x,t)=\frac{-\Delta }{2} \left( \tan \frac{\sqrt{-\Delta }\xi }{2} \right) ^{4}+{\frac{C_{{1}}B_{{1}}}{ \left( b-c \right) ^{2}}}-\frac{\Delta }{4}, \\&v_7(x,t) =-{\frac{B_{{1}} \left( bC_{{0}}{-}cC_{{0}}{+}C_{{1}}a{+}C_{{1}}\sqrt{- \Delta } \tan ({\sqrt{-\Delta }\xi }/{2} )\right) }{C_{{1}} \left( b{-}c \right) }}, \\&w_7(x,t)=-{\frac{-bC_{{0}}+cC_{{0}}-C_{{1}}a+C_{{1}}\sqrt{-\Delta } \tan ( {\sqrt{-\Delta }\xi }/{2} ) }{b-c}}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 2, (9) becomes

$$\begin{aligned}&u_8(x,t)=\frac{\Delta \tanh ( {\sqrt{\Delta }\xi }/{2} ) ^{2}}{2} +{\frac{C_{{1}}B_{{1}}}{ \left( b-c \right) ^{2}}}-\frac{ \Delta }{4},\quad v_8(x,t)={\frac{B_{{1}} ( -bC_{{0}}+cC_{{0}}-C_{{1}}a+C_{{1}}\sqrt{ \Delta }\tanh ( {\sqrt{\Delta }\xi }/{2} ) ) }{C_{{1}} \left( b-c \right) }}, \\&w_8(x,t)={\frac{bC_{{0}}-cC_{{0}}+C_{{1}}a+C_{{1}}\sqrt{\Delta }\tanh ( {\sqrt{\Delta }\xi }/{2} ) }{b-c}}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 8, (9) can be written as follows:

$$\begin{aligned}&u_9(x,t)={\frac{C_{{1}}B_{{1}}}{ \left( b-c \right) ^{2}}}+2{\xi }^{-2}, \\&v_9(x,t)=-{\frac{B_{{1}} \left( bC_{{0}}-cC_{{0}}+C_{{1}}a \right) }{C_{{1}} \left( b-c \right) }}+2\,{\frac{B_{{1}}}{ \left( b-c \right) \xi }}, \\&w_9(x,t)={\frac{bC_{{0}}-cC_{{0}}+C_{{1}}a}{b-c}}+2\,{\frac{C_{{1}}}{ \left( b-c \right) \xi }}, \end{aligned}$$

where \(\xi =x-kt\).

By using Family 12, (9) becomes

$$\begin{aligned}&u_{10}(x,t)={\frac{ ( 3{b}^{2} ( b-c ) ^{2}-4C_{{1}}B_{{ 1}} ) {\mathrm{e}^{b\xi }}}{ 2\left( b-c \right) ( -1+ \left( b -c \right) {\mathrm{e}^{b\xi }} ) ^{2}}}+{\frac{ ( {b}^{2 } ( b-c ) ^{2}+4\,C_{{1}}B_{{1}} ) {\mathrm{e}^{2b\xi } }}{4 \left( -1+ \left( b-c \right) {\mathrm{e}^{b\xi }} \right) ^{2}}}+{\frac{(b-c)^2 b^2 +4C_{{1}}B_{{1}}}{4 \left( b-c \right) ^{2} \left( -1+ \left( b-c \right) {\mathrm{e}^{b\xi }} \right) ^{2}}}, \\&v_{10}(x,t)=-{\frac{B_{{1}} \left( ( b-c \right) ^{2} \left( C_{{0}}-C_{{1} } \right) {\mathrm{e}^{b\xi }}+cC_{{0}}-C_{{1}}b-bC_{{0}}-C_{{1}}c ) }{C_{{1}} \left( b-c \right) ( -1+ \left( b-c \right) { \mathrm{e}^{b\xi }} ) }}, \\&w_{10}(x,t)={\frac{ \left( C_{{0}}b+C_{{1}}b+C_{{1}}c-C_{{0}}c \right) {\mathrm{e}^{ b\xi }}+C_{{1}}-C_{{0}}}{-1+ \left( b-c \right) {\mathrm{e}^{b\xi }}}}, \end{aligned}$$

where \(\xi =x-kt\).

Case IV

We have the following equations:

$$\begin{aligned}&a=0,\quad b=b,\quad c=c,\quad k={b}^{2}-{c}^{2}-3A_{{0}},\quad A_{{0}} = A_{{0}},\quad A_{{1}}=0,\quad A_{{2}}=-cb+\frac{{b}^{2}}{2}+\frac{{c}^{2}}{2},\quad A_{{3}}=0,\nonumber \\&A_{{4}}=\frac{ \left( b+c \right) ^{2}}{2}, \quad B_{{0}}=B_{{0}},\quad B_{{1}}={\frac{B_{{2}} \left( b-c \right) }{b+c}},\quad B_{{2}}=B_{{2}},\quad C_{{0}}=-{\frac{ \left( b +c \right) ^{2}B_{{0}}A_{{0}}}{B_{{2}}^{2}}},\nonumber \\&C_{{1}}={\frac{ \left( b+c \right) A_{{0}} \left( b-c \right) }{B_{{2}}}},\quad C_{{2}}={ \frac{ \left( b+c \right) ^{2}A_{{0}}}{B_{{2}}}}. \end{aligned}$$
(27)

By using Family 5, we get

$$\begin{aligned}&u_{11}(x,t)={\frac{ ( 2{b}^{2}-2{c}^{2}+2A_{{0}} ) \cosh ({\sqrt{\Delta }\xi }/{2} ) ^{4}+ ( -2 A_{{0}}-2{b}^{2}+2{c}^{2} ) \cosh ({\sqrt{\Delta }\xi }/{2} ) ^{2}+{b}^{2}-{c}^{2}}{2 ( \cosh ( {\sqrt{\Delta }\xi }/{2}) ^{2}-1 ) \cosh ({\sqrt{\Delta }\xi }/{2} ) ^{2}}}, \\&v_{11}(x,t)=B_{{0}}+\tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) B_{{2}}{\frac{1}{ \sqrt{{( {b+c})/({b-c)}}}}} +B_{{2}}{\frac{1}{\sqrt{{( {b+c})/({b-c) }}}}} \left( \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) \right) ^{-1 }, \\&w_{11}(x,t) =\frac{( b+c )^{2}A_{{0}}}{B_{{2}}} \left( \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) {\frac{1}{\sqrt{{( {b+c})/({b-c)}}}}}-{ \frac{B_{{0}}}{{B_{{2}}}}}+{\frac{1}{\sqrt{{ ( {b+c)/}{(b-c)}}}}} \left( \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) \right) ^{-1} \right) , \end{aligned}$$

where \(\Delta =b^{2}-c^{2}\), \(\xi =x-kt\).

Case V

We get

$$\begin{aligned}&a=a,\quad b=b,\quad c=c,\quad k=-\frac{{b}^{2}}{2}+\frac{{a}^{2}}{4}+\frac{{c}^{2}}{2},\quad A_{{0}}=-\frac{{b}^{2}}{2}+\frac{{a}^{2}}{4}+\frac{{c}^{2}}{2},\quad A_{{1}}=-ab+ac,\nonumber \\&A_{{2}}=-cb+\frac{{b}^{2}}{2}+\frac{{c}^{2}}{2},\quad A_{{3}}=a \left( b+c \right) ,\quad A_{{4}}= \frac{\left( b+c \right) ^{2}}{2},\quad B_{{0}}=-{\frac{ ( b+c ) ( {b}^{2}-{c}^{2}) a}{2C_{{2}}}},\quad B_{{1}}=0,\quad B_{{2}}=0,\nonumber \\&C_{{0 }}=C_{{0}},\quad C_{{1}}=-{\frac{C_{{2}} \left( b-c \right) }{b+c}},\quad C_{{2}} =C_{{2}}. \end{aligned}$$
(28)

By using Family 1, (9) becomes

$$\begin{aligned}&u_{12}(x,t)=\frac{2{\Delta }^{2} ( \tan ({\sqrt{-\Delta } \xi }/{2})) ^{4}+4\sqrt{-\Delta }a\Delta \, ( \tan {(\sqrt{-\Delta } \xi }/{2}) ) ^{3}-\Delta ( -2{b}^{2}+{a}^{2}+2{c}^{2}) ( \tan ({\sqrt{-\Delta } \xi }/{2})) ^{2}}{4( -a+ \sqrt{-\Delta }( \tan ( {\sqrt{-\Delta } \xi }/{2}) )) ^{ 2}}\\&\qquad \quad \quad \quad \quad + \frac{2{a}^{3}\sqrt{-\Delta }( \tan ( {\sqrt{-\Delta } \xi }/{2})) -{a}^{4}+2{b}^{4}-2{c}^{2} {a}^{2}-4{b}^{2}{c}^{2}+2{c}^{4}+2{b}^{2}{a}^{2}}{4 ( -a+ \sqrt{-\Delta }( \tan ({\sqrt{-\Delta } \xi }/{2}))) ^{ 2}}, \\&v_{12}(x,t)=-{\frac{ \left( b+c \right) ( -{c}^{2}+{b}^{2}) a}{ 2C_{{2}}}} \\&w_{12}(x,t)=-{\frac{\left[ \begin{array}{c} C_{{2}}\Delta ( \tan ({\sqrt{-\Delta }\xi }/{2}) ) ^{2}+\sqrt{-\Delta } \left( -C_{{0}}c-C_{{0}}b+2C_ {{2}}a \right) \tan ({\sqrt{-\Delta }\xi }/{2})\\ + ( {b }^{2}-{a}^{2}-{c}^{2}) C_{{2}}+C_{{0}}ab+C_{{0}}ac \end{array}\right] }{ \left( b+c \right) ( -a+\sqrt{-\Delta }\tan ({\sqrt{-\Delta }\xi }/{2} )) }} \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 2, (9) can be written as

$$\begin{aligned} u_{13}(x,t)= & {} \frac{\left[ \begin{array}{c} 2{\Delta }^{2} ( \tanh ( {\sqrt{\Delta }\xi }/{2} )) ^{4}+4\,{\Delta }^{3/2}a( \tanh ({\sqrt{\Delta }\xi }/{2} ) ) ^{3} +\Delta ( -2\,{b}^{2}+{a }^{2}+2\,{c}^{2})( \tanh ({\sqrt{\Delta }\xi }/{2} )) ^{2}\\ -(2{a}^{3}\sqrt{\Delta }\tanh ({\sqrt{\Delta }\xi }/{2} ) +2{b}^{2}{a}^{2}-2{c}^{2}{a}^{2}-4{b}^ {2}{c}^{2}+2{c}^{4}+2{b}^{4}-{a}^{4}) \end{array}\right] }{4( a+\sqrt{\Delta } \tanh ({\sqrt{\Delta }\xi }/{2} )) ^{2}}, \\ v_{13}(x,t)= & {} -{\frac{ \left( b+c \right) ( {b}^{2}-{c}^{2}) a}{2C _{{2}}}} \\ w_{13}(x,t)= & {} -{\frac{\left[ \begin{array}{c} C_{{2}}\Delta ( \tanh ({\sqrt{\Delta }\xi }/{2} )) ^{2}+\sqrt{\Delta }( -C_{{0}}c-C_{{0}}b+2\,C_{ {2}}a) \tanh ( {\sqrt{\Delta }\xi }/{2} )\\ -C_{{0}}ab-C _{{2}}{b}^{2}-C_{{0}}ac+C_{{2}}{a}^{2}+C_{{2}}{c}^{2}\end{array}\right] }{ \left( b+c \right) ( a+\sqrt{\Delta }\tanh ({\sqrt{\Delta }\xi }/{2} )) }}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 8, (9) becomes

$$\begin{aligned} u_{14}(x,t)= & {} -{\frac{-32+( {a}^{2}( {a}^{2}-2{b}^{2}+2{c}^{2} ) -2( b-c) ^{2}( b+c) ^{2}) {\xi }^{4}+4{a}^{3}{\xi }^{3}+ ( 8{b}^{2}-4{a}^{2}-8{c}^{2} ) {\xi }^{2}-32a\xi }{4( a\xi +2) ^{2}{\xi }^{2}}}, \\ v_{14}(x,t)= & {} -{\frac{( b+c)( {b}^{2}-{c}^{2}) a}{2C _{{2}}}}, \\ w_{14}(x,t)= & {} -{\frac{( -C_{{0}}ba+C_{{2}}{a}^{2}-C_{{0}}ca-C_{{2}}{b}^{2}+C_ {{2}}{c}^{2}) {\xi }^{2}+ \left( -2C_{{0}}b-2C_{{0}}c+4C_{ {2}}a \right) \xi +4\,C_{{2}}}{ \left( b+c \right) \xi \left( a\xi +2 \right) }}, \end{aligned}$$

where \(\xi =x-kt\).

Secondly, let us consider the process applied in the first ansatz and start with substituting (10) into eq. (8). If we collect all terms with the same order of \( \tan (\varphi (\xi )/2)\), the left-hand side of (10) can be transformed into polynomial according to \(\tan (\varphi (\xi )/ 2)\). Setting each coefficient of each polynomial to zero, we achieve a set of algebraic equations for the coefficients \(a,b,c,A_j,B_j,C_j\) \((j\,{=}\,0,1,2,3,4)\), as follows:

$$\begin{aligned}&-\,9B_{{4}}{b}^{2}c-9B_{{4}}b{c}^{2}-3B_{{4}}{c}^{3}-3B_{{4}}{b} ^{3}\nonumber \\&\quad +\,3A_{{4}}B_{{4}}b+3A_{{4}}B_{{4}}c= 0, \nonumber \\&-\frac{9}{4}B_{{3}}{b}^{2}c-\frac{9}{4}B_{{3}}b{c}^{2}-{\frac{27}{2}} B_{{4}}a{c}^{2}-\frac{3}{4}B_{{3}}{c}^{3} -\frac{3}{4}B_{{3}}{b} ^{3}\nonumber \\&\quad +\,3A_{{3}}B_{{4}}b+3A_{{3}}B_{{4}}c+\frac{3}{2}A_{{4}}B_{{3}}b -{\frac{27}{2} }B_{{4}}a{b}^{2} \nonumber \\&\quad +\,6A_{{4}}B_{{4}}a-27B_{{4}}abc+\frac{3}{2}A_{{4}}B_{{3}}c= 0, \nonumber \\&-\,19B_{{4}}{a}^{2}b+\frac{3}{2}A_{{3}}B_{{3}}b-6B_{{3}}abc-3B_{{3}}a {b}^{2}-5B_{{4}}b{c}^{2}\nonumber \\&\quad -\,5B_{{4}}{c}^{3}+5B_{{4}}{b}^{3} +kB_{{4} }c+3A_{{4}}B_{{3}}a-19B_{{4}}{a}^{2}c\nonumber \\&\quad +\frac{3}{2}A_{{3}}B_{{3}}c +kB_{{4}}b+5B_{{4}}{b}^{2}c+3A_{{0}}B_{{4}}c+6A_{{3}}B_{{4}}a\nonumber \\&\quad -\,3B_{{3 }}a{c}^{2} +3A_{{0}}B_{{4}}b+3A_{{4}}B_{{4}}c-3A_{{4}}B_{{4}}b=0, \nonumber \nonumber \\&\quad \vdots \end{aligned}$$
(29)

Solving the above system, we get many sets of coefficients for the solutions of (10) as given below:

Case I

We have the following equations:

$$\begin{aligned}&a={\frac{A_{{1}}}{2c}},\quad b=-c,\quad c=c,\quad k=-{\frac{-A_{{1}}^{2}+12A_{{0}}{c}^{2}}{4{c}^{2}}},\nonumber \\&A_{{0}}=A_{{0}},\quad A_{{1}}=A_{{1}},\quad A_{{2} }=2{c}^{2},\quad A_{{3}}=0,\quad A_{{4}}=0, \nonumber \\&B_{{0}}=-{\frac{A_{{1}}^{3}C_{{1}}{-}16 A_{{0}}A_{{1}}C_{{1}} {c}^{2}{-}2A_{{1}}^{2}C_{{0}}{c}^{2}{+}32\,C_{{0}}{c}^{4}A_{{0}}}{8C_{{1}} ^{2}{c}^{2}}},\nonumber \\&B_{{1}}={\frac{-A_{{1}}^{2}+16\,A_{{0}}{c}^{2}}{ 4 C_{{1}}}},\quad B_{{2}}=0,\quad B_{{3}}=0,\quad B_{{4}}=0, \nonumber \\&C_{{0}}=C_{{0}},\quad C_{{1}}=C_{{1}}, \quad C_{{2}}=0,\quad C_{{3}}=0,\quad C_{{4}}=0 . \end{aligned}$$
(30)

By the use of Family 14, (9) becomes

$$\begin{aligned}&u_{15}(x,t)={\frac{ \left( A_{{1}}a-2A_{{0}}c \right) {\mathrm{e}^{a\xi }}+ ( 2{c}^{2}{a}^{2}+A_{{0}}{c}^{2}-A_{{1}}ac) {\mathrm{e}^{2\,a\xi }} +A_{{0}}}{ \left( -1+c{\mathrm{e}^{a\xi }} \right) ^{2}}}, \\&v_{15}(x,t)=-{\frac{( -A_{{1}}^{2}+16{c}^{2}A_{{0}}) ( c( 2C_{{0}}{c}^{2}+2\,aC_{{1}}c-A_{{1}}C_{{1}} ) {\mathrm{e}^{a\xi }}+A_{{1}}C_{{1}}-2\,C_{{0}}{c}^{2}) }{8 C_{{1}}^{2}{c}^{2} \left( -1+c{\mathrm{e}^{a\xi }} \right) }}, \\&w_{15}(x,t)=-{\frac{ \left( -C_{{0}}c+C_{{1}}a \right) {\mathrm{e}^{a\xi }}+C_{{0}}}{ -1+c{\mathrm{e}^{a\xi }}}},\\&\text {where } \xi =x-kt.\\ \end{aligned}$$

By using Family 17, (10) can be written as

$$\begin{aligned}&u_{16}(x,t)={\frac{A_{{0}}c{\xi }^{2}-A_{{1}}\xi +2c}{c{\xi }^{2}}}, \\&v_{16}(x,t)= \left( -{\frac{2C_{{0}}{c}^{2}-A_{{1}}C_{{1}}}{C_{{1}}^{2}{c}^{2 }}}-2\,{\frac{1}{cC_{{1}}\xi }} \right) \\&\qquad \qquad \qquad \times \left( 2A_{{0}}{c}^{2}- \frac{ A_{{1}}^{2}}{8} \right) , \\&w_{16}(x,t)={\frac{C_{{0}}c\xi -C_{{1}}}{c\xi }}, \end{aligned}$$

where \(\xi =x-kt\).

Case II

$$\begin{aligned}&a\,{=}\,a,\quad b\,{=}\,b,\quad c\,{=}\,c,\quad k\,{=}\,-\frac{{b}^{2}}{2}+{a}^{2}+\frac{{c}^{2}}{2}-3A_{{0}},\quad A_{{0}}\,{=}\,A_{{0}},\quad A_{{1}}\,{=}\,-a \left( b-c \right) ,\nonumber \\&A_{{2}}\,{=}\,\frac{{b}^{2}}{2}-cb+ \frac{{c}^{2}}{2},\quad A_{{3}}\,{=}\,0,\quad A_{{4}}\,{=}\,0,\quad B_{{0}}\,{=}\,B_{{0}},\quad B_{{1}}\,{=}\,B_{{1}},\quad B_{{2 }}\,{=}\,0,\quad B_{{3}}\,{=}\,0,\quad B_{{4}}\,{=}\,0,\nonumber \\&C_{{0}}\,{=}\,{\frac{\left( b-c \right) \left( B_{{0}}b-B_{{0}}c+2B_{{1}}a \right) ( -{b}^{2}+{a}^{2}-4A_{{0}}+{c}^{2})}{4B_{{1}}^{2}} },\quad C_{{1}}\,{=}\,-{\frac{\left( b-c \right) ^{2}( -{b}^{2}+{a}^{2}-4A_{{0}}+{c}^{2} ) }{4B_{{1}}}},\nonumber \\&C_{{2}}\,{=}\,0,\quad C_{{3}}\,{=}\,0,\quad C_{{4}}\,{=}\,0. \end{aligned}$$
(31)

By utilising Family 1, we get

$$\begin{aligned}&u_{17}(x,t)=-\frac{\Delta }{2}\left( \tan \frac{\sqrt{-\Delta }\xi }{2} \right) ^{2}+A_{{0}}-\frac{{a}^{2}}{2}, \\&v_{17}(x,t)=-{\frac{-B_{{0}} \left( b-c \right) +B_{{1}} ( -a+\sqrt{-\Delta }\tan ({\sqrt{-\Delta }\xi }/{2})) }{b-c}}, \\&w_{17}(x,t)={\frac{ \left( b-c \right) ( -{b}^{2}-4A_{{0}}+{a}^{2}+{ c}^{2})( B_{{1}}a+B_{{0}}b-B_{{0}}c+B_{{1}}\sqrt{- \Delta }\tan ({\sqrt{-\Delta }\xi }/{2})) }{4B_{{1}}^{2}}}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 2, (10) becomes

$$\begin{aligned} u_{18}(x,t)= & {} \frac{\Delta }{2} \left( \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) \right) ^{2}+A_{{0}}-\frac{{a}^{2}}{2}, \\ v_{18}(x,t)= & {} {\frac{B_{{1}}\sqrt{\Delta }\tanh ({\sqrt{\Delta }\xi }/{2} ) }{b-c}}+{\frac{B_{{0}}b-B_{{0}}c+B_{{1}}a}{b-c}}, \\ w_{18}(x,t)= & {} -{\frac{ \left( b-c \right) ( -{b}^{2}+{c}^{2}+{a}^{2}-4A_{{0}})( -B_{{1}}a-B_{{0}}b+B_{{0}}c+B_{{1}}\sqrt{ \Delta }\tanh ({\sqrt{\Delta }\xi }/{2})) }{4B_{{1}}^{2}}}, \end{aligned}$$

where \(\Delta =a^{2}+b^{2}-c^{2}\), \(\xi =x-kt\).

By using Family 8, (10) becomes

$$\begin{aligned} u_{19}(x,t)= & {} -1/2\,{a}^{2}+A_{{0}}+2{\xi }^{-2}, \\ v_{19}(x,t)= & {} {\frac{B_{{0}}b-B_{{0}}c+B_{{1}}a}{b-c}}+2\,{\frac{B_{{1}}}{ \left( b-c \right) \xi }}, \\ w_{19}(x,t)= & {} \frac{\left( b-c \right) ( {a}^{2}-{b}^{2}+{c}^{2}-4A_{{0}} )}{4{B_{{1}}}} \left( {\frac{B_{{0}}b+B_{{1}}a-B_{{0}}c}{B_{{1}}}}-2{\xi }^{-1} \right) , \end{aligned}$$

where \(\xi =x-kt\).

By using Family 12, (10) can be written as

$$\begin{aligned}&u_{20}(x,t)={\frac{\left[ \begin{array}{c} 2 \left( b-c \right) ( {b}^{2}+2\,ac-{c}^{2}-2A _{{0}}) {\mathrm{e}^{b\xi }}-( b-c) ^{2}( ( b+c)( -b+2a-c) -2\,A_{{0}}) { \mathrm{e}^{2\,b\xi }}\\ +( b-c) \left( b+2\,a-c \right) +2A_ {{0}}\end{array}\right] }{2 \left( -1+ \left( b-c \right) {\mathrm{e}^{b\xi }} \right) ^{2}}}, \\&v_{20}(x,t) ={\frac{ \left( B_{{0}}b+B_{{1}}b+B_{{1}}c-B_{{0}}c \right) {\mathrm{e}^{ b\xi }}+B_{{1}}-B_{{0}}}{-1+ \left( b-c \right) {\mathrm{e}^{b\xi }}}}, \\&w_{20}(x,t) ={\frac{ \left( b-c \right) ( -{b}^{2}-4A_{{0}}+{a}^{2}+{ c}^{2}) \left[ \begin{array}{c} \left( b-c \right) \left( -B_{{1}}b+bB_{{0}}+ 2B_{{1}}a-B_{{0}}c-B_{{1}}c \right) {\mathrm{e}^{b\xi }}\\ +B_{{0}}c-bB_{{0 }}-2B_{{1}}a-B_{{1}}b+B_{{1}}c\end{array} \right] }{4B_{{1}}^{2} \left( -1+ \left( b-c \right) {\mathrm{e}^{b\xi }} \right) }} , \end{aligned}$$

where \(\xi =x-kt\).

By using Family 13, (10) becomes

$$\begin{aligned}&u_{21}(x,t) =\frac{ \left[ \begin{array}{c}( 2\left( b-c \right) ( {b}^{2}-ab-cb+2{ a}^{2}+ac) -4A_{{0}}a-4A_{{0}}b) {\mathrm{e}^{b\xi }}\\ + \left( - \left( b-c \right) \left( -b+c+2a \right) +2A_{{0}} \right) {\mathrm{e}^{2\,b\xi }}\\ +(- \left( b-c \right) \left( -b+a \right) ( 2{a}^{2}+ab+ac-cb+{b}^{2}) +2A_{{0}} \left( a+b \right) ^{2}) \end{array}\right] }{ 2\left( {\mathrm{e}^{b\xi }}-b-a \right) ^{2}}, \\&v_{21}(x,t) ={\frac{ \left( B_{{1}}+B_{{0}} \right) {\mathrm{e}^{b\xi }}+B_{{1}}b-B_{{0 }}b-B_{{0}}a-B_{{1}}a}{{\mathrm{e}^{b\xi }}-b-a}}, \\&w_{21}(x,t) ={\frac{( {a}^{2}-{b}^{2}-4A_{{0}}+{c}^{2}) \left( b-c \right) \left[ \begin{array}{c} \left( \left( -b+2a+c \right) B_{{1}}+ B_{{0}} \right) {\mathrm{e}^{b\xi }}\\ - (( ab-bc+{b}^{2}+2{a}^{2}+ac) B_{{1}}+( (b+a)) B_{{0}} ) \end{array}\right] }{4B_{{1}}^{2} \left( {\mathrm{e}^{b\xi }}-b-a \right) }}, \end{aligned}$$

where \(\xi =x-kt\).

Case III

We obtain

$$\begin{aligned}&a=0,\quad b=b,\quad c=c,\quad k=k,\quad \nonumber \\&A_{{0}}=-\frac{2{b}^{2}}{3}+\frac{2{c}^{2}}{3}-\frac{k}{3},\quad A_{{1}}=0,\nonumber \\&A_{{2}}= \left( b-c \right) ^{2},\quad A_{{3}}=0,\quad A_{{4}}= \left( b+c \right) ^{2}, \nonumber \\&B_{{0}}=-{\frac{( b+c ) ^{2} ( 3 ( b+c) ^{2}C_{{0}}+4C_{{4}}( 2k+{b}^{2}-{c}^{ 2})) }{12C_{{4}}^{2}}},\nonumber \\&B_{{1}}=0,\quad B_{{2}}={\frac{ ( b-c) ^{2}( b+c) ^{2}}{4C_{{4}}}},\nonumber \\&B_{{3}}=0,\quad B_{{4}}={\frac{ \left( b+c \right) ^{4}}{4C_{{4}}}}, C_{{0}}=C_{{0 }},\quad C_{{1}}=0,\nonumber \\&C_{{2}}={\frac{C_{{4}} \left( b-c \right) ^{2}}{ \left( b+c \right) ^{2}}},\nonumber \\&C_{{3}}=0,\quad C_{{4}}=C_{{4}}. \end{aligned}$$
(32)

By utilising Family 1, (10) becomes

$$\begin{aligned} u_{22}(x,t)= & {} -\Delta \left( \tan \left( \frac{\sqrt{-\Delta }\xi }{2} \right) \right) ^{2}-\frac{2{b}^{2}}{3}-\frac{k}{3}\nonumber \\&+\frac{2{c}^{2}}{3}-{\frac{\Delta }{ ( \tan ({ \sqrt{-\Delta }\xi }/{2} )) ^{2}}}, \end{aligned}$$
(33)
$$\begin{aligned}&v_{22}(x,t)=-{\frac{ \left( b+c \right) ^{2}\Delta ( \tan ({\sqrt{-\Delta }\xi }/{2} )) ^{2}}{4C_{{4}}}}\nonumber \\&\quad -{\frac{ ( ( 4{b}^{2}-4{c}^{2}+8k) C_{{4}}+3 ( b+c ) ^{2}C_{{0}}) \left( b+c \right) ^{2}}{12C_{{4}}^{2 }}}\nonumber \\&\quad -\frac{ \left( b+c \right) ^{2}\Delta }{4{C_{{4}} ( \tan ( {\sqrt{-\Delta }\xi }/{2})) ^{2}}}, \end{aligned}$$
(34)
$$\begin{aligned} w_{22}(x,t)= & {} -{\frac{C_{{4}} \left( b-c \right) ^{2} ( \tan ({ \sqrt{-\Delta }\xi }/{2})) ^{2}}{\Delta }}\nonumber \\&+C_{{0}}-{\frac{C_{ {4}} \left( b-c \right) ^{2}}{\Delta ( \tan ({\sqrt{ -\Delta }\xi }/{2})) ^{2}}}, \end{aligned}$$
(35)

where \(\Delta =b^2-c^2\), \(\xi =x-kt\).

By using Family 5, we get

$$\begin{aligned}&u_{23}(x,t)={\frac{( 4\Delta -k)( \cosh ( {\sqrt{\Delta }\xi }/{2}) ) ^{4}+( k-4\Delta ) ( \cosh ({\sqrt{\Delta }\xi }/{2})) ^{2}+3 \Delta }{ 3(( \cosh ( {\sqrt{\Delta }\xi }/{2}) ) ^{2}-1)( \cosh ({\sqrt{\Delta }\xi }/{2} )) ^{2}}}, \end{aligned}$$
(36)
$$\begin{aligned}&v_{23}(x,t)=-{\frac{( b+c) ^{2}((( 8\,k-2 \Delta ) C_{{4}}+3( b+c) ^{2}C_{{0}}) (( \cosh ({\sqrt{\Delta }\xi }/{2})) ^ {4}-( \cosh ({\sqrt{\Delta }\xi }/{2})) ^{2} ) -3C_{{4}}\Delta ) }{12(( \cosh ( {\sqrt{\Delta }\xi }/{2} )) ^{2}-1)( \cosh ({\sqrt{\Delta }\xi }/{2})) ^{2}C_{{4}}^{2}}}, \end{aligned}$$
(37)
$$\begin{aligned}&w_{23}(x,t)={\frac{(( 2b-2c) C_{{4}}+( b+c) C_{{0}})(( \cosh ({\sqrt{\Delta }\xi }/{2} )) ^{4}-( \cosh ({\sqrt{\Delta }\xi }/{2} ) ) ^{2}) +C_{{4}}( b-c) }{( ( \cosh ({\sqrt{\Delta }\xi }/{2})) ^{2}-1 ) ( \cosh ({\sqrt{\Delta }\xi }/{2})) ^{2}( b+c) }}, \end{aligned}$$
(38)

where \(\Delta =b^2-c^2\), \(\xi =x-kt\).

By using Family 16, (10) can be obtained as

$$\begin{aligned}&u_{24}(x,t)=-{\frac{k{\xi }^{2}-12}{3{\xi }^{2}}}, \\&v_{24}(x,t)=-{\frac{4{c}^{2}( 3{c}^{2}{\xi }^{2}C_{{0}}+2{\xi }^{2}kC _{{4}}-3C_{{4}}) }{3C_{{4}}^{2}{\xi }^{2}}}, \\&w_{24}(x,t)=-{\frac{k{\xi }^{2}-12}{3{\xi }^{2}}}, \end{aligned}$$

where \(\xi =x-kt\).

4 Application of ITEM for NNV system

The second example to illustrate ITEM implementation is the NNV system (2). Let us consider \(\xi = x + y -dt\) as the wave variable to convert this system into a system of ODEs

$$\begin{aligned}&(s+q-d) u'+(k+r)u'''=3k(uv)'+3r(uw)', \nonumber \\&u'=v', \quad u'=w'. \end{aligned}$$
(39)

If we integrate the second line equations, then we obtain

$$\begin{aligned} u=v,\quad u=w. \end{aligned}$$
(40)

As the next step, let us substitute (40) into the first equation in (39) and integrate the obtained equation. Hence we get

$$\begin{aligned} (s+q-d) u+(k+r)u''-3(k+r)u^2=0. \end{aligned}$$
(41)

If the terms \(u''\) and \(u^2\) in (41) are balanced, a simple algebraic equation \(M+2=2M\) is obtained so that \(M=2.\) Because of (40), determining only the function u(x, y, t) is sufficient. Therefore, we may assume the solution of (41) as

$$\begin{aligned} u(\xi )= & {} A_0+A_1\tan \left( \frac{\varphi (\xi )}{2}\right) +A_2\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{2}\nonumber \\&+A_3\left( \tan \left( \frac{\varphi (\xi )}{2 }\right) \right) ^{-1}\nonumber \\&+A_4\left( \tan \left( \frac{\varphi (\xi )}{2}\right) \right) ^{-2} . \end{aligned}$$
(42)

Substituting (42) into eq. (41) gives an algebraic equations set for \(a,b,c,d,A_j\) \((j=0,1,2,3,4)\). These algebraic equation systems are obtained as

$$\begin{aligned} H^8{:}&\quad \frac{3}{2}kA_{{2}}{c}^{2}+\frac{3}{2}rA_{{2}}{b}^{2}-3kA_{{2}}bc+\frac{3}{2}kA_{{2}}{ b}^{2}\\&\quad -3rA_{{2}}^{2}+\frac{3}{2}rA_{{2}}{c}^{2}-3kA_{{2}}^{2}-3rA_ {{2}}bc,&\\ H^7{:}&\quad -6rA_{{1}}A_{{2}}-rA_{{1}}bc+5rA_{{2}}ac+\frac{1}{2}kA_{{1}}{b}^{2}\\&\quad -5k A_{{2}}ab-kA_{{1}}bc+\frac{1}{2}kA_{{1}}{c}^{2}+\frac{1}{2}rA_{{1}}{b}^{2}\\&\quad +\frac{1}{2}rA _{{1}}{c}^{2}-6kA_{{1}}A_{{2}}+5kA_{{2}}ac-5rA_{{2}}ab,&\\ H^6{:}&\quad -2rA_{{2}}{b}^{2}+sA_{{2}}-6rA_{{0}}A_{{2}}+2rA_{{2}}{c}^{2}-dA_ {{2}}\\&\quad -6kA_{{0}}A_{{2}}-3rA_{{1}}^{2}-\frac{3}{2}kA_{{1}}ab+4rA_{{2}} {a}^{2}&\\&\quad +\frac{3}{2}kA_{{1}}ac - 2kA_{{2}}{b}^{2} - 3kA_{{1}}^{2} + qA_{{2}}+ 2kA_{{2}}{c}^{2}\\&\quad -\frac{3}{2}rA_{{1}}ab+\frac{3}{2}rA_{{1}}ac+4kA_{{2}}{a}^{2},&\\ H^5{:}&\quad -dA_{{1}}+3rA_{{2}}ac+3kA_{{2}}ab+kA_{{1}}{a}^{2}\\&\quad +qA_{{1}}+\frac{1}{2}rA _{{1}}{c}^{2}-\frac{1}{2}kA_{{1}}{b}^{2}+3rA_{{2}}ab\\&\quad -6kA_{{0}}A_{{1}}-\frac{1}{2}rA_{{1}}{b}^{2}&\\&\quad +3\,kA_{{2}}ac+\frac{1}{2}kA_{{1}}{c}^{2}-6rA_{{0}}A_{{1 }}+rA_{{1}}{a}^{2}\\&\quad -6rA_{{2}}A_{{3}}+sA_{{1}}-6kA_{{2}}A_{{3}},&\\ H^4{:}&\quad rA_{{2}}bc+\frac{1}{2}kA_{{1}}ab+\frac{1}{2}kA_{{1}}ac+\frac{1}{2}rA_{{1}}ab\\&\quad +\frac{1}{2}rA_{{1 }}ac-rA_{{4}}bc-kA_{{4}}bc-\frac{1}{2}kA_{{3}}ab&\\&\quad +\frac{1}{2}kA_{{3}}ac-\frac{1}{2}rA_{{3 }}ab+\frac{1}{2}rA_{{3}}ac+\frac{1}{2}rA_{{4}}{b}^{2}\\&\quad +\frac{1}{2}kA_{{4}}{b}^{2}+\frac{1}{2}kA _{{4}}{c}^{2}+\frac{1}{2}rA_{{4}}{c}^{2}-6kA_{{1}}A_{{3}}&\\&\quad -6kA_{{2}}A_{{4 }}-6rA_{{1}}A_{{3}}-6rA_{{2}}A_{{4}}+\frac{1}{2}rA_{{2}}{c}^{2}\\&\quad +\frac{1}{2}kA_ {{2}}{b}^{2}+\frac{1}{2}rA_{{2}}{b}^{2}+\frac{1}{2}kA_{{2}}{c}^{2}+sA_{{0}}\\&\quad +qA_{{0 }}-dA_{{0}}-3kA_{{0}}^{2}-3rA_{{0}}^{2}+kA_{{2}}bc,&\\ H^3{:}&\quad sA_{{3}}+rA_{{3}}{a}^{2}-\frac{1}{2},rA_{{3}}{b}^{2}-6rA_{{0}}A_{{3}}\\&\quad +\frac{1}{2} kA_{{3}}{c}^{2}+kA_{{3}}{a}^{2}+\frac{1}{2}rA_{{3}}{c}^{2}\\&\quad +3kA_{{4}}ac-3 kA_{{4}}ab+qA_{{3}}-\frac{1}{2}kA_{{3}}{b}^{2}\\&\quad +3rA_{{4}}ac-3rA_{{4}}ab-6 rA_{{1}}A_{{4}}-6kA_{{1}}A_{{4}}\\&\quad -dA_{{3}}-6kA_{{0}}A_{{3}},&\\ H^2{:}&\quad \frac{3}{2}kA_{{3}}ab+4kA_{{4}}{a}^{2}+2kA_{{4}}{c}^{2}+\frac{3}{2}rA_{{3}}ac+ sA_{{4}}\\&\quad +\frac{3}{2}kA_{{3}}ac+2rA_{{4}}{c}^{2}+\frac{3}{2}rA_{{3}}ab -6rA_{{0} }A_{{4}}&\\&\quad +qA_{{4}}-3kA_{{3}}^{2}-dA_{{4}}+4rA_{{4}}{a}^{2}-2\,rA_ {{4}}{b}^{2}\\&\quad -3rA_{{3}}^{2}-6kA_{{0}}A_{{4}}-2kA_{{4}}{b}^{2},&\\ H^1{:}&\quad \frac{1}{2}kA_{{3}}{c}^{2}-6rA_{{3}}A_{{4}}+5kA_{{4}}ac+5kA_{{4}}ab\\&\quad +5 rA_{{4}}ab +\frac{1}{2}rA_{{3}}{c}^{2}+kA_{{3}}bc-6kA_{{3}}A_{{4}}&\\&\quad +rA_{{3 }}bc+5rA_{{4}}ac+\frac{1}{2}kA_{{3}}{b}^{2}+\frac{1}{2}rA_{{3}}{b}^{2},&\\ H^0{:}&\quad \frac{3}{2}kA_{{4}}{c}^{2}-3kA_{{4}}^{2}-3rA_{{4}}^{2}+\frac{3}{2}rA_{{4}} {b}^{2}\\&\quad +3rA_{{4}}bc+\frac{3}{2}rA_{{4}}{c}^{2}+\frac{3}{2}kA_{{4}}{b}^{2}+3kA_ {{4}}bc, \end{aligned}$$

where \(H=\tan (\varphi (\xi )/2)\). Solving the equations corresponding to the coefficients of H, we get the following sets for the solutions of (42):

Case I

We have the following equations:

$$\begin{aligned}&a=\pm \sqrt{\frac{1}{2}{b}^{2}-\frac{1}{2}{c}^{2}+3A_{{0}}},\quad b=b,\quad c=c,\\&d=-\frac{3}{2}k{b}^{2}-\frac{3}{2}r{b}^{2}-3rA_{{0}}+s-3kA_{{0}}+q\\&\quad +\frac{3}{2}r{c}^{2}+\frac{3}{2}k{c}^{2},\quad k=k,\quad q=q,\quad r=r,\quad s=s,\\&A_{{0}}=A_{{0}},\quad A_{{1}}=0,\quad A_{{2}}=0,\quad A_{{3}} =ab+ac,\\&A_{{4}}=\frac{1}{2}{c}^{2}+\frac{1}{2}{b}^{2}+bc. \end{aligned}$$

By using Family 1, (42) can be written as

$$\begin{aligned}&u(\xi )^{(1)}= -{\frac{2A_{{0}}\Delta ( \tan ({\sqrt{-\Delta }\xi }/{2})) ^{2}+2\sqrt{-\Delta }a( -{c}^{2}+{ b}^{2}+2A_{{0}}) \tan ( {\sqrt{-\Delta }\xi }/{2} ) -2A_{{0}}{a}^{2}- ( {b}^{2}-{c}^{2})( \Delta +{a}^ {2}) }{ 2( -a+\sqrt{-\Delta }\tan ( {\sqrt{- \Delta }\xi }/{2})) ^{2}}},\\&\text {where } \xi = x + y -dt \text { and } \Delta =a^2+b^2-c^2. \end{aligned}$$

By using Family 2, (42) becomes

$$\begin{aligned}&u(\xi )^{(2)}={\frac{2A_{{0}}\Delta \left( \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) \right) ^{2}+2\,\sqrt{\Delta }a ( -{c}^{2}+{b}^{2}+ 2\,A_{{0}} ) \tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) +2A_{ {0}}{a}^{2}+ \left( {b}^{2}-{c}^{2} \right) \left( \Delta +{a}^{2} \right) }{2 \left( a+\sqrt{\Delta }\tanh \left( \frac{\sqrt{\Delta }\xi }{2} \right) \right) ^{2}}},\\&\text {where } \xi = x + y -dt \text { and } \Delta =a^2+b^2-c^2. \end{aligned}$$

By utilising Family 5, (42) becomes

$$\begin{aligned} u(\xi )^{(3)}=A_{{0}}+\frac{\Delta }{2} \left( \tanh \left( \frac{ \sqrt{\Delta }\xi }{2} \right) \right) ^{-2}, \end{aligned}$$

where \(\xi = x + y -dt\) and \(\Delta =b^2-c^2\).

By using Family 8, we get

$$\begin{aligned} u(\xi )^{(4)}=2\,{\frac{{a}^{2}}{ \left( a\xi +2 \right) ^{2}}}, \end{aligned}$$

where \(\xi = x + y -dt\).

Case II

We obtain another set of coefficients as

$$\begin{aligned}&a=a,\quad b=b,\quad c=c,\quad \\&d=k{b}^{2}+r{b}^{2} +k{a}^{2}+q+r{a}^{2}+s-r{c}^{2}-k{c}^{2},\\&k=k,\quad q=q,\quad r=r,\quad s=s,\\&A_{{0}}=-\frac{{b}^{2}}{2}+\frac{{c}^{2}}{2},\quad A_{{1}}=0 ,\quad A_{{2}}=0,\\&A_{{3}}=ab+ac,\quad A_{{4}}=\frac{{c}^{2}}{2}+\frac{{b}^{2}}{2}+bc. \end{aligned}$$

By using Family 1, (42) becomes

$$\begin{aligned}&u(\xi )^{(5)}\nonumber \\&\quad ={\frac{( b-c)( b+c) \Delta ( \tan ({\sqrt{-\Delta } \xi }/{2})) ^{2}+( b-c )( b+c) \Delta }{ 2( -a+\sqrt{-\Delta }\tan ({\sqrt{-\Delta } \xi }/{2})) ^{2}}},\nonumber \\ \end{aligned}$$
(43)

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2.\)

By utilising Family 3, (42) becomes

$$\begin{aligned}&u(\xi )^{(6)}\nonumber \\&\quad =-{\frac{{b}^{2}\Delta ( \tanh ({\sqrt{\Delta } \xi }/{2}) -1) ( \tanh ( {\sqrt{\Delta } \xi }/{2} ) +1) }{2 ( a+\sqrt{\Delta }\tanh ( {\sqrt{\Delta } \xi }/{2})) ^{2}}},\nonumber \\ \end{aligned}$$
(44)

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2.\)

By using Family 5, (42) can be written as follows:

$$\begin{aligned}&u(\xi )^{(7)}\nonumber \\&\quad =-{\frac{ \Delta ( \tanh ({\sqrt{\Delta } \xi }/{2}) -1)( \tanh ({\sqrt{\Delta } \xi }/{2}) +1) }{ 2( \tanh ({\sqrt{\Delta } \xi }/{2})) ^{2}}},\nonumber \\ \end{aligned}$$
(45)

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2\).

By using Family 8, (42) becomes

$$\begin{aligned} u(\xi )^{(8)}=4\,{\frac{ a^2 }{ \left( a\xi +2 \right) ^{2}}}, \end{aligned}$$
(46)

where \(\xi = x + y -dt\).

By using Family 11, (42) can be written as

$$\begin{aligned} u(\xi )^{(9)}=2{\frac{{b}^{2}{\mathrm{e}^{b\xi }} \left( b+a \right) }{ \left( { \mathrm{e}^{b\xi }}b+{\mathrm{e}^{b\xi }}a-1 \right) ^{2}}}, \end{aligned}$$
(47)

where \(\xi = x + y -dt\).

Case III

We have the following equations:

$$\begin{aligned}&a=0,\quad b=b,\quad c=c,\quad \\&d=-4\,r{c}^{2}-4\,k{c}^{2}+4\,k{b}^{2} +q+4\,r{b}^{2}+s,\quad \\&k=k,\quad q=q,\\&r=r,\quad s=s,\quad A_{{0}}={c}^{2}-{b}^{2},\\&A_{{1}}=0,\quad A_{{2}}=-bc+\frac{1}{2}\,{c}^{2}+\frac{1}{2}\,{b}^{2},\\&A_{{3}}=0,\quad A_{{4}}=\frac{1}{2}\,{c}^{2}+\frac{1}{2}\,{b}^{2}+bc. \end{aligned}$$

By using Family 1, (42) becomes

$$\begin{aligned}&u(\xi )^{(10)}\\&\quad ={\frac{\Delta }{2 ( \cos ( {\sqrt{-\Delta } \xi }/{2} )) ^{2}( -1+( \cos ({\sqrt{-\Delta } \xi }/{2})) ^{2}) }}, \end{aligned}$$

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2\).

By using Family 2, (42) becomes

$$\begin{aligned}&u(\xi )^{(11)}\\&\quad ={\frac{\Delta ( \tanh ( {\sqrt{\Delta } \xi }/{2} ) -1) ^{2}( \tanh ({\sqrt{\Delta } \xi }/{2} ) +1) ^{2}}{ 2( \tanh ({\sqrt{\Delta } \xi }/{2} )) ^{2}}}, \end{aligned}$$

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2\).

By using Family 5, (42) becomes

$$\begin{aligned} u(\xi )^{(12)}={\frac{\Delta }{ 2( ( \cosh ( {\sqrt{\Delta } \xi }/{2})) ^{2}-1)( \cosh ( {\sqrt{\Delta } \xi }/{2})) ^{2}}}, \end{aligned}$$

where \(\xi = x + y -dt\) and \(\Delta =a^2+b^2-c^2\).

By using Family 8, (42) becomes

$$\begin{aligned} u(\xi )^{(13)}=2\,{\xi }^{-2}, \end{aligned}$$

where \(\xi = x + y -dt\).

Remark 1

All results obtained in this study have been rewritten in the original equation and these results are verified by using Maple 13.

5 Stability analysis

In the previous two section, we presented some soliton solutions for eqs (1) and (2) with the help of ITEM. As a result of the instability in steady-state modulation, non-linear and dispersion effects occur in numerous nonlinear PDEs. The modulation instability of HScKdV and NNV are examined by using linear stability analysis in the following subsections respectively [37, 38].

5.1 Modulation instability of HScKdV

Assume that the perturbed steady-state solution of eq. (1) has the following form:

$$\begin{aligned} u(x,t)=\sqrt{P_0}+\sigma _1(x,t)\mathrm {e}^{\theta (t) }, \nonumber \\ v(x,t)=\sqrt{P_0}+\sigma _2(x,t)\mathrm {e}^{\theta (t) },\nonumber \\ w(x,t)=\sqrt{P_0}+\sigma _3(x,t)\mathrm {e}^{\theta (t) }, \end{aligned}$$
(48)

where \(\theta (t)=P_0(\gamma _1+P_0\gamma _2\varepsilon )t, P_0\) is the normalised optical power and \(\varepsilon \) is a sufficiently small parameter. We investigate the evolution of the perturbation \(\sigma (x,t)\) by utilising the linear stability analysis. Let us plug eq. (48) into eq. (1). If we linearise the expressions that we obtain, we reach the following equations:

$$\begin{aligned}&\frac{\partial \sigma _1}{\partial t}+P_0(\gamma _1+P_0\gamma _2\varepsilon )\sigma _1=\frac{1}{2}\frac{\partial ^3 \sigma _1}{\partial x^3} \nonumber \\&\quad -3\sqrt{P_0}\frac{\partial }{\partial x}(\sigma _1-\sigma _2-\sigma _3), \nonumber \\&\frac{\partial \sigma _2}{\partial t}+P_0(\gamma _1+P_0\gamma _2\varepsilon )\sigma _2 =-\frac{\partial ^3 \sigma _2}{\partial x^3}+3\sqrt{P_0}\frac{\partial \sigma _2}{\partial x},\nonumber \\&\frac{\partial \sigma _3}{\partial t}+P_0(\gamma _1+P_0\gamma _2\varepsilon )\sigma _3 = -\frac{\partial ^3 \sigma _3}{\partial x^3}+3\sqrt{P_0}\frac{\partial \sigma _3}{\partial x} .\nonumber \\ \end{aligned}$$
(49)

We consider the solution of (49) in the form

$$\begin{aligned}&\sigma _1(x,t)=\mu _1 \mathrm {e}^{(\nu x-kt)},\quad \sigma _2(x,t)=\mu _2 \mathrm {e}^{( \nu x-kt)},\nonumber \\&\sigma _3(x,t)=\mu _3 \mathrm {e}^{(\nu x-kt)}. \end{aligned}$$
(50)

Here k is the frequency of perturbation and \(\nu \) is the normalised wave number. Substituting eq. (50) into eq. (49), we get the following dispersion relation:

$$\begin{aligned}&k=\gamma _1P_0+\varepsilon \gamma _2P_0^2+\nu ^3-3\nu \sqrt{P_0},\nonumber \\&\mu _2=\frac{-\mu _1\nu ^2+(4\mu _1 -2\mu _3) \sqrt{P_0}}{\sqrt{P_0}}. \end{aligned}$$
(51)

The relations obtained above show that steady-state stability depends on the wave number. As the velocity dispersion k is real for all of wave numbers \(\nu \), steady state is stable against minor perturbations.

5.2 Modulation instability of NNV

The steady-state solution of eq. (2) is of the following form:

$$\begin{aligned}&u(x,t)=\sqrt{P_0}+\phi _1(x,y,t)\mathrm {e}^{\theta (t) }, \nonumber \\&v(x,t)=\sqrt{P_0}+\phi _2(x,y,t)\mathrm {e}^{\theta (t) },\nonumber \\&w(x,t)=\sqrt{P_0}+\phi _3(x,y,t)\mathrm {e}^{\theta (t) }, \end{aligned}$$
(52)

where \(\theta (t)=P_0(\gamma _1+P_0\gamma _2\varepsilon )t\) and \(P_0\) is the normalised optical power. Here we shall use the linear stability analysis to examine evolution of perturbations \(\phi (x,y,t)\). Putting eq. (52) into eq. (2) and linearising, we get

$$\begin{aligned}&\frac{\partial \phi _1}{\partial t}+P_0(\gamma _1+P_0\gamma _2\varepsilon )\phi _1+k\frac{\partial ^3 \phi _1}{\partial x^3}+r\frac{\partial ^3 \phi _1}{\partial y^3}+s\frac{\partial \phi _1}{\partial x}\nonumber \\&\quad +q\frac{\partial \phi _1}{\partial y}=3\sqrt{P_0}\left( k\frac{\partial }{\partial x}(\phi _1+\phi _2)+r\frac{\partial }{\partial y}(\phi _1+\phi _3)\right) , \nonumber \\&\frac{\partial \phi _1}{\partial x}=\frac{\partial \phi _2}{\partial y}, \quad \frac{\partial \phi _1}{\partial y}=\frac{\partial \phi _3}{\partial x}. \end{aligned}$$
(53)

We suppose the solution of (53) as

$$\begin{aligned}&\phi _1(x,y,t)=\beta _1 \mathrm {e}^{(\nu x+\mu y-dt)},\nonumber \\&\phi _2(x,y,t)=\beta _2 \mathrm {e}^{( \nu x+\mu y-dt)},\nonumber \\&\phi _3(x,y,t)=\beta _3 \mathrm {e}^{(\nu x+\mu y-dt)}. \end{aligned}$$
(54)

Here d is the frequency of perturbation and \(\nu ,\mu \) are the normalised wave numbers. Substituting eq. (54) into eq. (53), we get the following dispersion relation:

$$\begin{aligned} d= & {} P_0(\gamma _1+\gamma _2\varepsilon P_0)-\frac{3(\mu +\nu )(r\mu ^2+k\nu ^2)}{\mu \nu }\sqrt{P_0}\\&+\,k\nu ^3+s\nu +q\mu +r\mu ^3,\\ \beta _1= & {} \frac{\beta _3 \nu }{\mu },\ \ \beta _2=\frac{\beta _3 \nu ^2}{\mu ^2}. \end{aligned}$$

The velocity dispersion d is real for all of wave numbers \(\nu ,\mu \) if \(\mu \nu \ne 0 \). Hence the steady state is stable against minor perturbations.

Fig. 1
figure 1

Profiles of u, v and w solutions (13), (14) and (15) for (1) with \(a=1,b=2,c=3,B_2=1,C_0=1,C_2=1\), \(0\le t\le 25\pi /14\) and \(0\le x\le 2\pi \).

Full size image
Fig. 2
figure 2

Profiles of u, v and w solutions (16), (17) and (18) for (1) with \(a=1,b=2,c=1,B_2=1,C_0=1,C_2=1\) and \(-10\le t,x\le 10.\)

Full size image

6 Concluding remarks

In this paper, we considered the generalised HScKdV equation and \((2 + 1)\)-dimensional NNV system. To achieve exact solutions including exponential, rational, trigonometric and hyperbolic functions, we applied the ITEM to these equations. Various types of solutions play important roles in engineering and physical fields. These solutions may be useful to explain the physical phenomena in dynamical systems that are described by the system of equations HScKdV and NNV and to help for a deeper understanding of these systems. The type of solutions obtained is a guide to the interpretation of the physical properties and behaviour of the solutions. In this study, we have obtained different types of solutions (e.g. soliton, kink-type, bell-type, rational, trigonometric) each of which has its own features. For example, it is known that solitons appear as a result of a balance between weak nonlinearity and dispersion. A notable feature of solitons is that it can retain its identity when interacting with other solitons. Kink waves, which are travelling waves rising or descending from one asymptotic state to another, approaches a constant at infinity. Bell-shaped soliton solution is characterised by infinite wings or infinite tails [45].

The implemented method has been demonstrated to be more comprehensive and effective than the extended tanh-function method [39], the extended Jacobi elliptic function method [40] for HScKdV and the rational exp-function method [34], sine–cosine method [41] for NNV, because it allows us to obtain many different solutions. Therefore, using of the ITEM in seeking solutions of NLEEs which occur in real-world problems is beneficial too. Moreover, we examined the modulation instability analysis for the HScKdV and NNV via the linear stability analysis and determined the requirements for the stability of the solutions. Many nonlinear systems exhibit instability leading to modulation of the steady state as a result of the interaction between nonlinear and dispersive effects. The stability of solutions is important in physical problems because if slight deviations from the mathematical model caused by unavoidable errors in measurement do not have a slight effect on the solution accordingly, the mathematical equations defining the problem will not accurately predict the future outcome [37].

Fig. 3
figure 3

Profiles of u, v and w solutions (19), (20) and (21) for (1) with \(a=3,b=4,c=5,B_2=3,C_0=1,C_2=1\), \(-3.4\le t\) and \(x\le 3.4.\)

Full size image
Fig. 4
figure 4

Profiles of u, v and w solutions (22), (23) and (24) for (1) with \(a=1,b=2,c=1,B_2=1,C_0=1,C_2=1\), \(-4.4\le t\) and \(x\le 4.4.\)

Full size image
Fig. 5
figure 5

Profiles of u, v and w solutions (33), (34) and (35) for (1) with \(a=0,b=1,c=3,k=1,C_0=1,C_4=1\), \(-\sqrt{2}\pi \le t\) and \(x\le \sqrt{2}\pi \).

Full size image
Fig. 6
figure 6

Profiles of u, v and w solutions (36), (37) and (38) for (1) with \(a=0,b=3,c=1,k=1,C_0=1,C_4=1\), \(-0.71\le t\) and \(x\le 0.71.\)

Full size image

Gencoglu and Akgul [42] and Feng and Li [43] used ITEM and Fan sub-equation method respectively to obtain exact solutions of HScKdV. Comparing their special solutions with our solutions, we see that there are some structural similarities between these solutions. For example, eqs (13)–(15) in [42] and eq. (21) in [43] are structurally equivalent to the hyperbolic form of the solutions \(u_8,v_8,w_8\) in this paper. Ali [44] used the modified extended tanh-function method for solving eq. (1) and eqs (35)–(37) have the same mathematical structure as our solutions \(u_{22},v_{22},w_{22}\). On the other hand, Wazwaz in [35] investigated the system NNV by using several methods. If we compare solution (26) in [35] with our solution \(u^{(5)}\) in the case of \(a=0\), structural similarities can be seen between these solutions. It is seen that we omitted some family classification solutions in all ansatze. The reason for this is the inconsistency between the coefficient obtained in Maple calculations and the coefficient conditions of the family classification in \(\S \)2 (for instance Case 1, eq. (30)).

Fig. 7
figure 7

Profiles of u solutions (43) and (44) for eq. (2) with \(a=1,b=2,c=3,r=k=q=s=1\) at \(y=1\), \(0\le x\le \pi /3\) and \(0\le t\le 2\pi \).

Full size image
Fig. 8
figure 8

Profiles of u solutions (45), (46) and (47) for eq. (2) with \(\left\{ a=0,b=3,c=2,r=k=q=s=1\right\} \), \(\lbrace a=1,b=1,c=\sqrt{2},r=k=q=s=1\rbrace \) and \(\left\{ a=0.5,b=1,c=0.5,r=k=q=s=1\right\} \) respectively at \(y=1\), \(0\le x\le \pi /3\) and \(0\le t\le 2\pi \).

Full size image

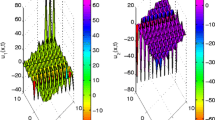
In figures 1–8, we depict the 3D plots of some exact solutions of eqs (1) and (2). These solutions have very important physical meanings. The reported results in this study may be useful in explaining the physical meaning of some nonlinear models arising in nonlinear sciences (solid-state physics, nonlinear optics, chemical kinetics, hydrodynamics, biological membranes, etc. [32, 46, 47]) and the mechanism of the nonlinear physical phenomena in a wave interaction. For instance, eqs (13)–(15) are periodic solutions which are presented in figure 1. Equation (16) is bell-type solution and eqs (17) and (18) are kink-type solutions. They are portrayed in figure 2. Equations (46) and (47) are rational and exponential function solutions respectively and they are plotted in figure 8.

In our study, we have not investigated the blow-up conditions of the aforementioned solutions. We have broadly tried to extract the physical structure of the solutions (containing the discontinuous point) and demonstrated some numerical simulations of the physical phenomena. We note that some of the solutions have singularity. For instance, the denominator of (13) should be non-zero, i.e.,

$$\begin{aligned} {4\left( b+c\right) ^{2}\left( -a+\sqrt{-\Delta }\tan \left( \frac{ \sqrt{-\Delta }(x-kt) }{2}\right) \right) ^{2}}\ne 0. \end{aligned}$$

Therefore, we have

$$\begin{aligned}&b+c\ne 0 \quad \\&\mathrm {and}\quad \\&-a+\sqrt{-\Delta }\tan \left( \frac{ \sqrt{-\Delta }(x-kt) }{2}\right) \ne 0 \end{aligned}$$

from which

$$\begin{aligned}&b\ne c, \ \ \ \ x-kt\ne \frac{2}{\sqrt{-\Delta }}\arctan \left( \frac{a}{\sqrt{-\Delta }}\right) +n\pi ,\\&n\in {\mathbb {Z}} \end{aligned}$$

are obtained. For example, for \(a=1,b=2,c=3,B_2=1,C_0=1,C_2=1\) and \(n=2\), if \(x-kt=\arctan ({1}/{2})+2\pi \) is considered, the \(0.4139710795\le t\le 6.023957962\) interval for t is obtained corresponding to \(0\le x\le 2\pi \). Accordingly, if t is selected outside this interval, such as \(x = 1\) and \(t = 7\), the singularity of the solution is eliminated. However, as it is not easy to see it with the help of graphics, it can be interpreted intuitively.