Analytical approaches to space- and time-fractional coupled Burgers’ equations

Abstract

We solve the one- and two-dimensional fractional coupled Burgers’ equations (FCBEs) by three different methods. The proposed methods are the Laplace–Adomian decomposition method (LADM), the Laplace-variational iteration method (LVIM) and the reduced differential transform method (RDTM). The solutions are obtained as rapidly convergent series with simply calculable terms. Numerical studies of the application of these approaches for a number of sample problems are given and are illustrated graphically. With these methods, it is possible to investigate the nature of solutions when the fractional derivative parameters are changed. The numerical results reveal the effectiveness and the correctness of the proposed methods.

1 Introduction

The Burgers’ equation is a vital partial differential equation (PDE) in fluid mechanics. It arises in numerous areas of applied mathematics, such as acoustic waves, heat conduction and modelling of dynamics [1,2,3]. Because of the wide variety of uses of the Burgers’ equation, it has been intensively studied, and many numerical techniques have been proposed to solve it. Most of these numerical techniques fall into either the finite difference method or the finite element and spectral method [4,5,6,7,8,9,10,11]. The mathematical structure of Burgers’ equation was introduced by Johannes Martinus Burgers (1895–1981) [12,13,14]. Recently, significant development has been reported in the field of fractional calculus (FC). FC has been applied in nearly every branch of science, engineering, economics and mathematics [15,16,17,18,19]. This is because the fractional derivatives offer more precise models of real-world problems than the integer-order derivatives. This is also the same reason why several models of fractional Burgers’ equations (FBEs) have been suggested and studied lately. These models are obtained by replacing integer-order space / time derivatives and ordinary initial / boundary conditions with their fractional counterparts. In [19], the existence and uniqueness of the solutions to a class of stochastic generalised Burgers’ equations driven by multiparameter fractional noises are proved. Garra [18] reported on an application of the time fractional Burgers’ equation in the framework of nonlinear wave propagation in porous media. Approximate solutions for various models of time and / or space FBEs are obtained by several methods. In [8], the Adomian decomposition method (ADM) is applied to find the approximate analytical solution of fractional coupled Burgers’ equations (FCBEs), variational iteration method (VIM) [20] was implemented to FBE with fractional time and space derivatives, homotopy perturbation method (HPM) [21] is used to find the approximate analytical solution to FCBEs with fractional space and time derivatives. The differential transform method (DTM) is applied to fractional Fisher equation in [22] while the coupled reduced differential transform was successfully implemented to the FCBEs for the two-dimensional space in [23]. It is obvious that there is a need to develop more efficient numerical and analytical methods to solve different models of FBEs.

The main objective of this work is to extend the application of Laplace–Adomian decomposition method (LADM), Laplace variational iteration method (LVIM) and reduced differential transform method (RDTM) to derive explicit analytical approximate solutions of the FCBE with time- and space-Caputo fractional derivatives for the following two models:

• (i) One-dimensional FCBE

  $$\begin{aligned} { D}_{t}^{\alpha _1 }u(x,t) =&\, { D}_{xx} u(x,t)+2u(x,t) { D}_{x}^{\alpha _2 } u(x,t)\nonumber \\&\quad -{ D}_{x} (u(x,t)v(x,t) ),\nonumber \\ { D}_t^{\beta _1 }v(x,t) =&\, { D}_{xx} v(x,t)+2v(x,t) {D}_x^{\beta _2 } v(x,t)\nonumber \\&\quad -{ D}_x (u(x,t)v(x,t)). \end{aligned}$$

  (1)

• (ii) Two-dimensional FCBE

  $$\begin{aligned}&{D}_{t}^{\alpha _1 }u(x,y,t)+u(x,y,t)\frac{\partial u(x,y,t)}{\partial x}\nonumber \\&\qquad +v(x,y,t) \frac{\partial u(x,y,t)}{\partial y}\nonumber \\&\quad =\frac{1}{\mathrm{Re}}\Bigg [\frac{\partial ^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2} u(x,y,t)}{\partial y^2}\Bigg ],\nonumber \\&{D}_{t}^{\beta _1 }v(x,y,t)+u(x,y,t)\frac{\partial v(x,y,t)}{\partial x}\nonumber \\&\qquad +v(x,y,t) \frac{\partial v(x,y,t)}{\partial y}\nonumber \\&\quad =\frac{1}{\mathrm{Re}}\Bigg [\frac{\partial ^{2} v(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2} v(x,y,t)}{\partial y^2}\Bigg ], \end{aligned}$$

  (2)

where $t>0,~A\le x$ and $y\le B$, the factors $\alpha _i$ and $\beta _i$, where $0<\alpha _i, \beta _i\le 1, i = 1,2$, stand for the order of the fractional time and space derivatives, respectively. ${\mathrm{Re}}$ is the Reynolds number, u(x, y, t) and v(x, y, t) are the velocity components along the x- and y-axes and it is worth noting that when at least one of the factors varies, different reaction systems are obtained. At $\alpha _i= \beta _i=1$, the fractional-order systems (1) and (2) define the traditional coupled Burgers’ equation in one- and two-dimensional spaces, respectively.

In the present paper, we apply LADM, LVIM and RDTM to the FCBEs (1) and (2). The proposed techniques are powerful and efficient in finding acceptable solutions for wide classes of nonlinear problems. The LADM is a smart mixture of the Laplace transformation and ADM [24,25,26,27,28], and was presented by Khuri [24, 25]. The LVIM [29] is a novel modification of the VIM. This technique was proposed by combining the Laplace transform and the variational method. The LVIM offers analytical approximate solutions to wide classes of differential equations. Zhou [30] proposed the concept of reduced differential transform and applied it to solve linear and nonlinear initial value electric circuit problems. RDTM is a numerical technique which depends on the Taylor series expansion. It is dissimilar from the familiar high-order Taylor’s series technique. It needs representative calculation of the essential derivatives of the data functions. RDTM yields a polynomial series solution by means of an iterative technique. In [30,31,32], RDTM was used to create analytical approximate solutions to fractional-order systems of linear and nonlinear PDEs. Numerical comparisons with graphical representation of the suggested methods with the exact solutions are given to illustrate the efficiency and the accuracy of the suggested methods. The results prove that the proposed methods are very effective and simple. This paper is structured as follows: some elementary definitions of the fractional Caputo derivative and mathematical preliminaries which are essential for creating our numerical results are in the following section. The applications of LADM, LVIM and RDTM on the fractional-order coupled Burgers’ equations are discussed in §3–5, respectively. Numerical applications are provided in §6. Our conclusions are presented in §7.

2 Basic definitions

DEFINITION 1

For $u(x,t)\in C_{-1}^{m}$ and m the smallest integer that exceeds $\alpha$ the (left side) Caputo time-fractional derivative operator of order $\alpha$ is defined as [15, 33, 34]

$$\begin{aligned} {D}_{t}^{\alpha } u(x,t)=\left\{ \begin{array}{l@{\quad }l} \displaystyle \frac{1}{\Gamma (m-\alpha ) } \int _{0}^{t} (t-\tau )^{m-\alpha -1} \frac{\partial ^{m}u(x,t)}{ \partial t^{m}}\,\mathrm {d}t, &{} m-1<\alpha <m, m\in N \cup \{0\},\\ \dfrac{\partial ^{m}u(x,t)}{ \partial t^{m}},&{} \alpha =m. \end{array} \right. \end{aligned}$$

(3)

DEFINITION 2

The Laplace transform $\mathscr {L}_{t}[\cdot ]$ of the Caputo fractional derivative is defined as [34]

$$\begin{aligned}&\mathscr {L}_{t}[{{D}^\alpha }{f(t)}]=s^\alpha F(s)-\sum _{k=0}^{m-1} {s^{\alpha -k-1}}{f^{(k)}}(0),\nonumber \\&\qquad m-1<\alpha <m. \end{aligned}$$

(4)

DEFINITION 3

The t-dimensional transformed function $F_{k}(x)$ of the analytical and continuously differentiable function f(x, t) with respect to t is defined as

$$\begin{aligned} F_{k}(x)=\frac{1}{\Gamma (k\alpha +1)}\bigg [\frac{\partial ^{\alpha k}}{\partial t^{\alpha k}} f(x,t)\bigg ]_{t=0}, \end{aligned}$$

(5)

where $\alpha$ signifies the order of time-fractional derivative [30,31,32].

DEFINITION 4

The inverse differential transform of $F_k (x)$ is defined as [30,31,32]

$$\begin{aligned} f(x,t)=\sum _{k=0}^{\infty }F_k (x) t^{k\alpha }. \end{aligned}$$

(6)

3 LADM for solving space and time FCBEs

Consider the FCBEs represented by (1). For convenience, we just discuss the case: $\alpha _1=\alpha _2=\alpha$ and $\beta _1=\beta _2=\beta ;$ other cases are similar. In order to offer analytical approximate solutions for (1) using LADM, we first rewrite the equation in the following operator form:

$$\begin{aligned} \begin{aligned} {D}_{t}^{\alpha }u(x,t)&= L_{2x} u(x,t)+2u(x,t) {D}_{x}^{\alpha } u(x,t)\\&\qquad \, -L_{x} (u(x,t)v(x,t) ),\\ {D}_t^{\beta }v(x,t)&= L_{2x} v(x,t)+2v(x,t) {D}_x^{\beta } v(x,t)\\&\qquad \, -L_x (u(x,t)v(x,t)), \end{aligned} \end{aligned}$$

(7)

with initial conditions

$$\begin{aligned} u(x,0)=f(x),\quad v(x,0)=g(x), \end{aligned}$$

(8)

where $L_{nx}={\partial ^{n}}/{\partial x^{n}}.$ The operators ${D}_{t}^{\alpha }, { D}_{x}^{\alpha }, {D}_{t}^{\beta }$ and ${D}_{x}^{\beta }$ denote the fractional derivatives defined in (3). The LADM method begins by applying the Laplace transform to (7), and then, by using the initial conditions (8), we obtain

$$\begin{aligned} \mathscr {L}_{t}[u(x,t)]= & {} \frac{1}{s}f(x)+\frac{1}{s^\alpha }\mathscr {L}_{t}[L_{2x} u(x,t)\nonumber \\&+\,2u(x,t) {D}_{x}^{\alpha } u(x,t)-v(x,t)L_{x}(u(x,t))\nonumber \\&-u(x,t)L_{x}(v(x,t))], \end{aligned}$$

$$\begin{aligned} \mathscr {L}_{t}[v(x,t)= & {} \frac{1}{s}g(x)+\frac{1}{s^\beta }\mathscr {L}_{t}[L_{2x} v(x,t)\nonumber \\&+\,2v(x,t) {D}_{x}^{\beta } v(x,t)-v(x,t)L_{x}(u(x,t))\nonumber \\&-u(x,t)L_{x}(v(x,t))]. \end{aligned}$$

(9)

In the LADM, the solutions u(x, t) and v(x, t) are defined by the infinite series as

$$\begin{aligned} u(x, t)=\sum _{n=0}^{\infty }u_{n}(x, t), \quad v(x, t)=\sum _{n=0}^{\infty }v_{n}(x, t). \end{aligned}$$

(10)

The nonlinear terms $N_{1}=u(x, t){D}_{x}^{\alpha } u(x,t), N_{2}= v(x, t){D}_{x}^{\beta } v(x,t), N_3= v(x, t)L_x u(x, t)$ and $N_4= u(x, t)L_x v(x, t)$ are generally expressed as an infinite series of the Adomian polynomials as

$$\begin{aligned}&N_1( u)= \sum _{n=0}^{\infty } A_{n}, \quad N_2 ( v)=\sum _{n=0}^{\infty } B_{n},\nonumber \\&N_3 ( u,v)=\sum _{n=0}^{\infty } C_{n},\quad N_4 ( u,v)=\sum _{n=0}^{\infty } {D}_{n}, \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{aligned} A_{n}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [N_1 \left( \sum _{k=0}^{\infty } \lambda ^k u_{k}\right) \Bigg ]\Bigg ]_{\lambda =0}\\&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [\Bigg (\sum _{k=0}^{\infty } \lambda ^k u_{k}\Bigg )\Bigg ({ D}_{x}^{\alpha }\Bigg (\sum _{k=0}^{\infty } \lambda ^k u_{k}\Bigg )\Bigg )\Bigg ]\Bigg ]_{\lambda =0},\\ B_{n}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [N_2 \Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg ]\Bigg ]_{\lambda =0}\\ {}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [ \Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg ({D}_{x}^{\beta }\Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg )\Bigg ]\Bigg ]_{\lambda =0},\\ C_{n}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [N_3 \Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k},\sum _{k=0}^{\infty } \lambda ^k u_{k}\Bigg )\Bigg ]\Bigg ]_{\lambda =0}\\ {}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [ \Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg (L_{x}\Bigg (\sum _{k=0}^{\infty } \lambda ^k u_{k}\Bigg )\Bigg )\Bigg ]\Bigg ]_{\lambda =0},\\ {D}_{n}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [N_4 \Bigg (\sum _{k=0}^{\infty } \lambda ^k u_{k},\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg ]\Bigg ]_{\lambda =0}\\ {}&=\frac{1}{n!}\Bigg [\frac{\mathrm{d}^n}{\mathrm{d}\lambda ^n}\Bigg [ \Bigg (\sum _{k=0}^{\infty } \lambda ^k u_{k}\Bigg )\Bigg (L_{x}\Bigg (\sum _{k=0}^{\infty } \lambda ^k v_{k}\Bigg )\Bigg )\Bigg ]\Bigg ]_{\lambda =0}. \end{aligned} \end{aligned}$$

(12)

The Adomian polynomials (12) can be easily calculated. Here we give some of them: $A_0=u_0 {D}_x ^\alpha u_0, A_1=u_0 {D}_x ^\alpha u_1 +u_1 {D}_x ^\alpha u_0, A_2=u_0 {D}_x ^\alpha u_2 +u_1 {D}_x ^\alpha u_1 +u_2 {D}_x ^\alpha u_0,\ldots , B_0=v_0 {D}_x ^\beta v_0, B_1=v_0 {D}_x ^\beta v_1 +v_1 {D}_x ^\beta v_0, B_2=v_0 {D}_x ^\beta v_2 +v_1 {D}_x ^\beta v_1 +v_2 {D}_x ^\beta v_0,\ldots , C_0=u_0 L_x v_0, C_1=u_1 L_x v_0 +u_0 L_x v_1, C_2=u_2 L_x v_0 +u_1 L_x v_1 +u_0 L_x v_2,\ldots , D_0=v_0 L_x u_0, D_1=v_1 L_x u_0 +v_0 L_x u_1, D_2=v_2 L_x u_0 +v_1 L_x u_1 +v_0 L_x u_2,\ldots$.

Substituting (10) and (11) into (9) gives

$$\begin{aligned}&\mathscr {L}_{t}\Bigg [\sum _{n=0}^{\infty }u_{n}(x, t)\Bigg ]\nonumber \\&\quad =\frac{1}{s}f(x)+\frac{1}{s^\alpha }\mathscr {L}_{t}\Bigg [L_{2x}\Bigg (\sum _{n=0}^{\infty }u_{n}(x, t)\Bigg )\nonumber \\&\qquad +2A_n - C_n - { D}_n\Bigg ],\nonumber \\&\mathscr {L}_{t}\Bigg [\sum _{n=0}^{\infty }v_{n}(x, t)\Bigg ]\nonumber \\&\quad =\frac{1}{s}g(x)+\frac{1}{s^\beta }\mathscr {L}_{t}\Bigg [L_{2x}\Bigg (\sum _{n=0}^{\infty }v_{n}(x, t)\Bigg )\nonumber \\&\qquad +2B_n - C_n - {D}_n\Bigg ]. \end{aligned}$$

(13)

By using the linearity property of the Laplace transform, the following recursive formulas are obtained:

$$\begin{aligned} \mathscr {L}_{t} \big [u_{0}(x, t) \big ]= & {} \frac{1}{s}f(x),\quad \nonumber \\ \mathscr {L}_{t} \big [v_{0}(x, t) \big ]= & {} \frac{1}{s}g(x), \end{aligned}$$

(14)

$$\begin{aligned} \mathscr {L}_{t}\big [u_{1}(x, t)\big ]= & {} \frac{1}{s^\alpha }\mathscr {L}_{t}\big [(u_{0})_{xx}+2A_0 - C_0 - {D}_0\big ],\nonumber \\ \mathscr {L}_{t}\big [v_{1}(x, t)\big ]= & {} \frac{1}{s^\beta }\mathscr {L}_{t}\big [(v_{0})_{xx}+2B_0 - C_0 - { D}_0\big ].\nonumber \\ \end{aligned}$$

(15)

In general, for $k\ge 1,$ we obtain

$$\begin{aligned} \begin{aligned} \mathscr {L}_{t}\big [u_{k+1}(x, t)\big ]&=\frac{1}{s^\alpha }\mathscr {L}_{t}\big [(u_{k})_{xx}+2A_k - C_k - {D}_k\big ],\\ \mathscr {L}_{t}\big [v_{k+1}(x, t)\big ]&=\frac{1}{s^\beta }\mathscr {L}_{t}\big [(v_{k})_{xx}+2B_k - C_k - {D}_k\big ]. \end{aligned} \end{aligned}$$

(16)

By applying the inverse Laplace transform, $u_{k}$ and $v_{k}$ ($k\ge 0$ ) are evaluated as

$$\begin{aligned} u_{0}(x, t)= & {} f(x),\nonumber \\ v_{0}(x, t)= & {} g(x),\nonumber \\ u_{1}(x, t)= & {} f_{1}(x)\frac{t^{\alpha }}{\Gamma (\alpha +1)},\nonumber \\ v_{1}(x, t)= & {} g_{1}(x)\frac{t^\beta }{\Gamma (\beta +1)},\nonumber \\ u_{2}(x, t)= & {} f_{2}(x)\frac{t^{2 \alpha }}{\Gamma (2\alpha +1)}-f_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)},\nonumber \\ v_{2}(x, t)= & {} g_{2}(x)\frac{t^{2 \beta }}{\Gamma (2\beta +1)}\nonumber \\&-g_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)},\ldots . \end{aligned}$$

(17)

Hence, the solution in the series form is given by

$$\begin{aligned} u(x, t)= & {} f(x)+f_{1}(x)\frac{t^{\alpha }}{\Gamma (\alpha +1)}+f_{2}(x)\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&-f_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}+\cdots ,\nonumber \\ v(x, t)= & {} g(x)+g_{1}(x)\frac{t^{\beta }}{\Gamma (\beta +1)}+g_{2}(x)\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&-g_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}+\cdots , \end{aligned}$$

(18)

where

$$\begin{aligned} f_{1}(x)=&\,f''(x)+2f(x){ D}_x ^\alpha f(x)-f(x) g'(x)\nonumber \\&- g(x) f'(x),\nonumber \\ f_{2}(x)=&\,f_1 ''(x)+2f(x){D}_x ^\alpha f_1 (x)+2f_1 (x){D}_x ^\alpha f (x)\nonumber \\ {}&- f_1 (x) g'(x)- g(x)f_1 '(x),\nonumber \\ f_{3}(x)=&\,f(x) g_1 '(x)+ g_1 (x) f'(x),\nonumber \\ g_{1}(x)=&\,g''(x)+2g(x){D}_x ^\beta g(x)-f(x) g'(x)\nonumber \\&- g(x) f'(x),\nonumber \\ g_{2}(x)=&\,g_1 ''(x)+2g(x){ D}_x ^\beta g_1 (x)+2g_1 (x){D}_x ^\beta g (x)\nonumber \\ {}&- f(x) g_1 '(x)- g_1 (x) f '(x),\nonumber \\ g_{3}(x)=&\,f_1 (x) g '(x)+ g (x) f'_1 (x). \end{aligned}$$

(19)

The exact solution in the closed form may also be found in some cases. The theoretical treatment of the convergence of ADM has been considered in [35,36,37,38]. El-Kalla [38, Theorem 1] introduced the sufficient condition that guarantees the existence of a unique solution. The convergence of the series solution obtained by ADM is proved in Theorem 2 of [38]. Finally, the maximum absolute errors of the series solution obtained by ADM are proved in Theorem 3 in [38].

4 LVIM for solving space- and time FCBEs

In this section, we present LVIM [29] for solving (7). The first step of the method is applying the Laplace transform to (7) and by using the initial conditions (8) we obtain

$$\begin{aligned}&\mathscr {L}_{t}\big [u(x, t)\big ]-\sum _{k=0}^{m-1}s^{\alpha -1-k}\left. \frac{\partial ^{k} u(x,t)}{\partial t^{k}}\right| _{t=0}\nonumber \\&\quad =\mathscr {L}_{t}\big [ L_{2x}u(x,t)+2u(x,t){D}_{x}^{\alpha }u(x,t) \nonumber \\&\qquad \,-v(x,t)L_{x}u(x,t)-u(x,t)L_{x}v(x,t)\big ],\nonumber \\&\mathscr {L}_{t}\big [v(x, t)\big ]-\sum _{k=0}^{m-1}s^{\beta -1-k}\left. \frac{\partial ^{k} v(x,t)}{\partial t^{k}}\right| _{t=0}\nonumber \\&\quad =\mathscr {L}_{t}\big [ L_{2x}v(x,t)+2v(x,t){D}_{x}^{\beta }v(x,t)\nonumber \\&\qquad \,-v(x,t)L_{x}u(x,t)-u(x,t)L_{x}v(x,t)\big ]. \end{aligned}$$

(20)

The iteration formula of (20) may then be used to generate the main iterative scheme involving the Lagrange multiplier as

$$\begin{aligned} \begin{aligned}&\mathscr {L}_{t}\big [u_{n+1}(x, t)\big ]\\&\quad =\mathscr {L}_{t}\big [u_{n}(x, t)\big ]+\lambda _{1}(s)\Big [s^{\alpha }\mathscr {L}_{t}\big [u_{n}(x, t)\big ] \\&\qquad -\sum _{k=0}^{m-1}s^{\alpha -1-k}\left. \frac{\partial ^{k} u(x, t)}{\partial t^{k}}\right| _{t=0}\\&\qquad + \mathscr {L}_{t}\big [L_{2x}u_{n}(x, t)+2u_{n}(x, t){D}^{\alpha }_{x}u_{n}(x, t)\\&\qquad -v_{n}(x, t)L_{x}u_{n}(x, t)-u_{n}(x, t)L_{x}v_{n}(x, t)\big ]\Big ],\\&\mathscr {L}_{t}\big [v_{n+1}(x, t)\big ]\\&\quad =\mathscr {L}_{t}\big [v_{n}(x, t)\big ]+\lambda _{2}(s)\Big [s^{\beta }\mathscr {L}_{t}\big [v_{n}(x, t)\big ]\\&\qquad \left. -\sum _{k=0}^{m-1}s^{\beta -1-k}\frac{\partial ^{k} v(x, t)}{\partial t^{k}}\right| _{t=0}\\&\qquad + \mathscr {L}_{t}\big [L_{2x}v_{n}(x, t)+2v_{n}(x, t){D}^{\beta }_{x}v_{n}(x, t)\\&\qquad -v_{n}(x, t)L_{x}u_{n}(x, t)-u_{n}(x, t)L_{x}v_{n}(x, t)\big ]\Big ]. \end{aligned} \end{aligned}$$

(21)

Consider $\mathscr {L}_{t}\big [2u(x, t){D}^{\alpha }_{x}u(x, t)-v(x, t)L_{x}u(x, t)-u(x, t)L_{x}v(x, t)\big ]$ and $\mathscr {L}_{t}\big [2v(x, t){D}^{\beta }_{x}v(x, t) -v(x, t)L_{x}u(x, t)-u(x, t)L_{x}v(x, t)\big ]$ as restricted terms. One can derive the Lagrange multipliers as

$$\begin{aligned} \lambda _{1}(s)=-\frac{1}{s^\alpha },\quad \lambda _{2}(s)=-\frac{1}{s^\beta } \end{aligned}$$

(22)

with (21) and the inverse Laplace transform $\mathscr {L}_{t}^{-1},$ the iterative formula of (21) is given as

$$\begin{aligned} \begin{aligned}&u_{n+1}(x, t)\\&\quad = \mathscr {L}_{t}^{-1}\Bigg [\frac{1}{s^\alpha }\Bigg [\sum _{k=0}^{m-1}s^{\alpha -1-k}\frac{\partial ^{k} u(x, t)}{\partial t^{k}}\bigg |_{t=0}\\&\qquad \, -\mathscr {L}_{t}\big [L_{2x}u_{n}(x, t)+2u_{n}(x, t){D}^{\alpha }_{x}u_{n}(x, t)\\&\qquad \, -v_{n}(x, t)L_{x}u_{n}(x, t)-u_{n}(x, t)L_{x}v_{n}(x, t)\big ]\Bigg ]\Bigg ], \\&v_{n+1}(x, t)\\&\quad = \mathscr {L}_{t}^{-1}\Bigg [\frac{1}{s^\beta }\Bigg [\sum _{k=0}^{m-1}s^{\beta -1-k}\frac{\partial ^{k} v(x, t)}{\partial t^{k}}\bigg |_{t=0}\\&\qquad \, - \mathscr {L}_{t}\big [L_{2x}v_{n}(x, t)+2v_{n}(x, t){D}^{\beta }_{x}v_{n}(x, t)\\&\qquad \, -v_{n}(x, t)L_{x}u_{n}(x, t)-u_{n}(x, t)L_{x}v_{n}(x, t)\big ]\Bigg ]\Bigg ], \end{aligned} \end{aligned}$$

(23)

where the initial iterations $u_{0}(x, t)$ and $v_{0}(x, t)$ are determined by

$$\begin{aligned} u_{0}(x, t)= & {} \mathscr {L}_{t}^{-1}\Bigg [\frac{1}{s^\alpha }\Bigg [\sum _{k=0}^{m-1}s^{\alpha -1-k}\frac{\partial ^{k} u(x, t)}{\partial t^{k}}\bigg |_{t=0}\Bigg ]\Bigg ]\nonumber \\= & {} f(x),\nonumber \\ v_{0}(x, t)= & {} \mathscr {L}_{t}^{-1}\Bigg [\frac{1}{s^\beta }\Bigg [\sum _{k=0}^{m-1}s^{\beta -1-k}\frac{\partial ^{k} v(x, t)}{\partial t^{k}}\bigg |_{t=0}\Bigg ]\Bigg ]\nonumber \\= & {} g(x), \end{aligned}$$

(24)

then we have

$$\begin{aligned} u_{1}(x, t)&=f(x)+f_{1}(x)\frac{t^{\alpha }}{\Gamma (\alpha +1)},\nonumber \\ v_{1}(x, t)&=g(x)+g_{1}(x)\frac{t^\beta }{\Gamma (\beta +1)},\nonumber \\ u_{2}(x, t)&=f(x)+f_{1}(x)\frac{t^{\alpha }}{\Gamma (\alpha +1)}\nonumber \\&\quad +f_{2}(x)\frac{t^{2 \alpha }}{\Gamma (2\alpha +1)}\nonumber \\&\quad -f_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}\nonumber \\&\quad -f_{4}(x)\frac{t^{2\alpha +\beta }}{\Gamma (2\alpha +\beta +1)}\nonumber \\&\quad +f_{5}(x)\frac{t^{3\alpha }}{\Gamma (3\alpha +1)},\nonumber \\ v_{2}(x, t)&=g(x)+g_{1}(x)\frac{t^{\beta }}{\Gamma (\beta +1)}\nonumber \\&\quad +g_{2}(x)\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&\quad -g_{3}(x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}\nonumber \\&\quad -f_{4}(x)\frac{t^{2\beta +\alpha }}{\Gamma (2\beta +\alpha +1)}\nonumber \\&\quad +g_{5}(x)\frac{t^{3\beta }}{\Gamma (3\beta +1)},\ldots , \end{aligned}$$

(25)

where

$$\begin{aligned} f_{4}(x)= & {} (f'_1 (x)g_{1}(x))\nonumber \\&+\,g'_{1}(x)f_{1}(x))\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha +1)\Gamma (\beta +1)},\nonumber \\ f_{5}(x)= & {} (2f_1 (x){D}^{\alpha }_{x}f_{1}(x))\frac{\Gamma (2\alpha +1)}{(\Gamma (\alpha +1))^{2}},\nonumber \\ g_{4}(x)= & {} (2g_1 (x){D}^{\beta }_{x}g_{1}(x))\frac{\Gamma (2\beta +1)}{(\Gamma (\beta +1))^{2}}, \end{aligned}$$

(26)

while $f_1(x), f_2(x), f_3(x), g_1(x), g_2(x)$ and $g_3(x)$ are defined by (19). The sufficient condition for the convergence of VIM is proved in Theorem 1 in [39] and Theorem 2 in [40]. The maximum errors of the series solution of VIM are derived in [39, 40] (Theorem 3).

5 RDTM for solving space and time FCBEs

In this section we use RDTM to solve the FCBEs with space- and time-fractional derivatives (7). By applying RDTM to (7), the following iterative relations are obtained:

$$\begin{aligned}&\frac{\Gamma (k\alpha +\alpha +1)}{\Gamma (k\alpha +1)}U_{k+1}(x,t)\nonumber \\&\quad =\frac{\partial ^{2}}{\partial x^{2}}U_{k}(x,t)+2U_{k}(x,t){D}^{\alpha }_{x}U_{k}(x,t)\nonumber \\&\qquad \,\, -\frac{\partial }{\partial x}(U_{k}(x,t)V_{k}(x,t)),\nonumber \\&\frac{\Gamma (k\beta +\beta +1)}{\Gamma (k\beta +1)}V_{k+1}(x,t)\nonumber \\&\quad =\frac{\partial ^{2}}{\partial x^{2}}V_{k}(x,t)+2V_{k}(x,t){D}^{\beta }_{x}V_{k}(x,t)\nonumber \\&\qquad \,\, -\frac{\partial }{\partial x}(U_{k}(x,t)V_{k}(x,t)). \end{aligned}$$

(27)

For the initial conditions (8), we have

$$\begin{aligned} U_{0}(x,t)= & {} f(x),\nonumber \\ V_{0}(x,t)= & {} g(x). \end{aligned}$$

(28)

Putting $k =0$ in (27), we have

$$\begin{aligned} \begin{aligned}&U_{1}(x,t)=\frac{\Gamma (k\alpha +1)}{\Gamma (k\alpha +\alpha +1)}\\&\quad \times \bigg (\frac{\partial ^{2}}{\partial x^{2}}U_{0}(x,t)+2U_{0}(x,t){D}^{\alpha }_{x}U_{0}(x,t)\\&\quad -\frac{\partial }{\partial x}(U_{0}(x,t))V_{0}(x,t)-\frac{\partial }{\partial x}(V_{0}(x,t))U_{0}(x,t)\bigg ),\\&V_{1}(x,t) =\, \frac{\Gamma (k\beta +1)}{\Gamma (k\beta +\beta +1)}\\&\quad \times \bigg (\frac{\partial ^{2}}{\partial x^{2}}V_{0}(x,t) +2V_{0}(x,t){D}^{\beta }_{x}V_{0}(x,t)\\&\quad -\frac{\partial }{\partial x}(U_{0}(x,t))V_{0}(x,t)-\frac{\partial }{\partial x}(V_{0}(x,t))U_{0}(x,t)\bigg ), \end{aligned} \end{aligned}$$

which can be written as

$$\begin{aligned} U_{1}(x,t)= & {} f_{1}(x)\frac{1}{\Gamma (\alpha +1)},\nonumber \\ V_{1}(x,t)= & {} g_{1}(x)\frac{1}{\Gamma (\beta +1)}. \end{aligned}$$

(29)

In the same way and by using iterative relation (27), we have

$$\begin{aligned} U_{2}(x,t)= & {} f''_{1}(x)\frac{1}{\Gamma (2\alpha +1)}\nonumber \\&+2f_{1}(x){D}^{\alpha }_{x}f_{1}(x)\frac{1}{\Gamma (\alpha +1)\Gamma (2\alpha +1)}\nonumber \\&-f_{6}(x)\frac{1}{\Gamma (\beta +1)\Gamma (2\alpha +1)},\nonumber \\ V_{2}(x,t)= & {} g''_{1}(x)\frac{1}{\Gamma (2\beta +1)}\nonumber \\&+2g_{1}(x){D}^{\beta }_{x}g_{1}(x)\frac{1}{\Gamma (\beta +1)\Gamma (2\beta +1)}\nonumber \\&-f_{6}(x)\frac{1}{\Gamma (\alpha +1)\Gamma (2\beta +1)},\ldots , \end{aligned}$$

(30)

where $f_6 (x) =f'_1 (x)g_1 (x) + f_1 (x)g'_1(x)$ and $f_1(x), f_3(x), g_1(x), g_3(x)$ are defined in (19). Finally, applying the differential inverse transforms to $U_k (x,t)$ and $V_k (x,t)$ gives

$$\begin{aligned} \begin{aligned} u(x, t)=&\,\sum _{k=0}^{\infty }U_{k}(x, t)t^{k\alpha }\\ =&\,f(x)+f_{1}(x)\frac{t^{\alpha }}{\Gamma (\alpha +1)}+f''_{1}(x)\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\\&+2f_{1}(x){D}_{x}^{\alpha }f_{1}(x)\frac{t^{2\alpha }}{\Gamma (\alpha +1)\Gamma (2\alpha +1)}\\&-f_{6}(x)\frac{t^{2\alpha }}{\Gamma (\beta +1)\Gamma (2\alpha +1)}+\cdots ,\\ v(x, t)=&\,\sum _{k=0}^{\infty }V_{k}(x, t)t^{k\beta }\\ =&\,g(x)+g_{1}(x)\frac{t^{\beta }}{\Gamma (\beta +1)}+g''_{1}(x)\frac{t^{2\beta }}{\Gamma (2\beta +1)}\\&+2g_{1}(x){D}_{x}^{\beta }g_{1}(x)\frac{t^{2\beta }}{\Gamma (\beta +1)\Gamma (2\beta +1)}\\&-f_{6}(x)\frac{t^{2\beta }}{\Gamma (\alpha +1)\Gamma (2\beta +1)}+\cdots . \end{aligned} \end{aligned}$$

(31)

In a similar way, the proposed techniques of LADM, LVIM and RDTM can be applied to obtain analytical approximate solutions of (2) by LADM, LVIM and RDTM.

6 Numerical applications

In this section, two numerical examples representing the one- and two-dimensional FCBEs are given to illustrate the accuracy and efficiency of the proposed methods. The numerical results are computed for only five terms of the LADM and RDTM with the fourth iteration of LVIM.

Example 1

[9]. For the following one-dimensional time FCBEs:

$$\begin{aligned} {D}^{\alpha }_{t}u(x,t)= & {} \, L_{2x}u(x,t)+2u(x,t)L_{x}u(x,t)\nonumber \\&\,-L_{x}(u(x,t)v(x,t)),\quad 0<\alpha \le 1,\nonumber \\ {D}^{\beta }_{t}v(x,t)= & {} \, L_{2x}v(x,t)+2v(x,t)L_{x}v(x,t)\nonumber \\&\,-L_{x}(u(x,t)v(x,t)),\quad 0<\beta \le 1, \end{aligned}$$

(32)

with initial conditions

$$\begin{aligned}&u(x,0)= f (x) = \sin (x),\quad \nonumber \\&v(x,0)= g(x) = \sin (x). \end{aligned}$$

(33)

The exact solution of (32) at the special case, $\alpha =\beta =1$, is

$$\begin{aligned} u(x,t) = \mathrm{e}^{-t} \sin (x),\quad v(x,t)= \mathrm{e}^{-t}\sin (x). \end{aligned}$$

(34)

6.1 Solution using LADM

By using the initial conditions (33), (19) takes the form

$$\begin{aligned} f_1(x)&=-\sin (x)=g_1(x),\nonumber \\ f_2(x)&=\sin (x)-2\sin (x) \cos (x)=g_2(x),\nonumber \\ f_3(x)&=-2\sin (x) \cos (x)=g_3(x), \end{aligned}$$

(35)

then using (32), (35) and (18) we have

$$\begin{aligned} u_0(x,t)= & {} \sin (x),\nonumber \\ v_0(x,t)= & {} \sin (x),\nonumber \\ u_1(x,t)= & {} -\sin (x)\frac{t^\alpha }{\Gamma (\alpha +1)},\nonumber \\ v_1(x,t)= & {} -\sin (x)\frac{t^\beta }{\Gamma (\beta +1)},\nonumber \\ u_2(x,t)= & {} \big (\sin (x) -2\sin (x)\cos (x)\big )\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)},\nonumber \\ v_2(x,t)= & {} \big (\sin (x) -2\sin (x)\cos (x)\big )\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)},\ldots . \end{aligned}$$

(36)

Hence, the solution in series form is

$$\begin{aligned} \begin{aligned} u(x,t)=&\, u_0(x,t)+u_1(x,t)+u_2(x,t)\\&+u_3(x,t)+\cdots ,\\ v(x,t)=&\, v_0(x,t)+v_1(x,t)+v_2(x,t)\\&+v_3(x,t)+\cdots , \end{aligned} \end{aligned}$$

i.e.

$$\begin{aligned} \begin{aligned} u(x,t)=&\sin (x) -\sin (x)\frac{t^\alpha }{\Gamma (\alpha +1)}\\&+\big (\sin (x) -2\sin (x)\cos (x)\big )\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}+\cdots ,\\ v(x,t)=&\sin (x) -\sin (x)\frac{t^\beta }{\Gamma (\beta +1)}\\&+\big (\sin (x) -2\sin (x)\cos (x)\big )\frac{t^{2\beta }}{\Gamma (2\beta +1)}\\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}+\cdots . \end{aligned} \end{aligned}$$

(37)

Table 1 The $L_{2}$-norm errors for the suggested methods when $-5\le x\le 5, h=0.1$ for u(x, t).

6.2 Solution using LVIM

From (33), (35) and (26), we have

$$\begin{aligned} f_4(x)= & {} 2\sin (x)\cos (x)\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha +1)\Gamma (\beta +1)},\nonumber \\ f_5(x)= & {} 2\sin (x)\cos (x)\frac{\Gamma (2\alpha +1)}{(\Gamma (\alpha +1))^{2}},\nonumber \\ g_4(x)= & {} 2\sin (x)\cos (x)\frac{\Gamma (2\beta +1)}{(\Gamma (\beta +1))^2} \end{aligned}$$

(38)

and by substituting (38) into (25) we have

$$\begin{aligned} u_0(x,t)= & {} \sin (x),\nonumber \\ v_0(x,t)= & {} \sin (x),\nonumber \\ u_1(x,t)= & {} \sin (x) -\sin (x)\frac{t^\alpha }{\Gamma (\alpha +1)},\nonumber \\ v_1(x,t)= & {} \sin (x) -\sin (x)\frac{t^\beta }{\Gamma (\beta +1)},\nonumber \\ u_2(x,t)= & {} \sin (x) -\sin (x)\frac{t^\alpha }{\Gamma (\alpha +1)}\nonumber \\&+(\sin (x) -2\sin (x)\cos (x))\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}\nonumber \\&-2\sin (x)\cos (x)\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha +1)\Gamma (\beta +1)}\nonumber \\&\times \frac{t^{2\alpha +\beta }}{\Gamma (2\alpha +\beta +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{\Gamma (2\alpha +1)}{(\Gamma (\alpha +1))^{2}}\frac{t^{3\alpha }}{\Gamma (3\alpha +1)},\nonumber \\ v_2(x,t)= & {} \sin (x) -\sin (x)\frac{t^\beta }{\Gamma (\beta +1)}\nonumber \\&+\big (\sin (x) -2\sin (x)\cos (x)\big )\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{t^{\alpha +\beta }}{\Gamma (\alpha +\beta +1)}\nonumber \\&-2\sin (x)\cos (x)\frac{\Gamma (\alpha +\beta +1)}{\Gamma (\alpha +1)\Gamma (\beta +1)}\nonumber \\&\times \frac{t^{2\alpha +\beta }}{\Gamma (2\alpha +\beta +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{\Gamma (2\beta +1)}{(\Gamma (\beta +1))^{2}}\nonumber \\&\times \frac{t^{3\beta }}{\Gamma (3\beta +1)},\ldots . \end{aligned}$$

(39)

6.3 Solution using RDTM

Using (29), (30) and (35), we have

$$\begin{aligned} \begin{aligned} U_0(x,t)&= \sin (x),\\ V_0(x,t)&= \sin (x),\\ U_1(x,t)&= -\sin (x)\frac{1}{\Gamma (\alpha +1)},\\ V_1(x,t)&= -\sin (x)\frac{1}{\Gamma (\beta +1)},\\ U_2(x,t)&= \sin (x) \frac{1}{\Gamma (2\alpha +1)}\\&\quad \, +2\sin (x)\cos (x)\frac{1}{\Gamma (\alpha +1)}\frac{1}{\Gamma (2\alpha +1)}\\&\quad \, -2\sin (x)\cos (x)\frac{1}{\Gamma (2\alpha +1)}\frac{1}{\Gamma (\beta +1)},\\ V_2(x,t)&= \sin (x) \frac{1}{\Gamma (2\beta +1)}\\&\quad \, +2\sin (x)\cos (x)\frac{1}{\Gamma (\beta +1)}\frac{1}{\Gamma (2\beta +1)}\\&\quad \, -2\sin (x)\cos (x)\frac{1}{\Gamma (2\beta +1)}\frac{1}{\Gamma (\alpha +1)},\ldots \end{aligned} \end{aligned}$$

(40)

and the series solution takes the form

$$\begin{aligned} u(x,t)= & {} \sin (x) -\sin (x)\frac{t^{\alpha }}{\Gamma (\alpha +1)}\nonumber \\&+\sin (x)\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{1}{\Gamma (\alpha +1)}\frac{t^{2\alpha }}{\Gamma (2\alpha +1)}\nonumber \\&-2\sin (x)\cos (x)\frac{1}{\Gamma (\beta +1)}\nonumber \\&\times \frac{t^{2\alpha }}{\Gamma (2\alpha +1)}+\cdots ,\nonumber \\ v(x,t)= & {} \sin (x) -\sin (x)\frac{t^{\beta }}{\Gamma (\beta +1)}\nonumber \\&+\sin (x)\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&+2\sin (x)\cos (x)\frac{1}{\Gamma (\beta +1)}\frac{t^{2\beta }}{\Gamma (2\beta +1)}\nonumber \\&-2\sin (x)\cos (x)\frac{1}{\Gamma (\alpha +1)}\nonumber \\&\times \frac{t^{2\beta }}{\Gamma (2\beta +1)}+\cdots . \end{aligned}$$

(41)

6.4 Some numerical results

We suppose that the function u(x, t) is defined for $A\le x\le B$ and $0\le t\le L$. The solution domain is discretised into cells described by the node set $(x_{i},t_{n})$ in which $x_{i}=A+ih$ $(i=0,1,2,\ldots ,M)$ and $t_{n}=nk$ $(n=0,1,2,\ldots ,K), h=\Delta x=({B-A})/{M}$ is the spatial mesh size and $k=\Delta t={L}/{K}$ is the time step. Numerical results of Example 1 are given in tables 1 and 2 which represent the $L_{2}$-norm errors for the three proposed methods at: $- 5 \le x\le 5$.

Table 2 The $L_{2}$-norm errors for the suggested methods when $-5\le x\le 5, h=0.1$ for v(x, t).

Fig. 1

The space–time surfaces of the absolute errors for u(x, t) by (a) LADM, (b) LVIM and (c) RDTM when $-5 \le x\le 5, 0 \le t\le 1$ and $\alpha =\beta =1$.

Fig. 2

The space–time surfaces of the absolute errors for v(x, t) by (a) LADM, (b) LVIM and (c) RDTM when $-5 \le x\le 5, 0 \le t\le 1$ and $\alpha =\beta =1$.

Fig. 3

The approximate solutions for u(x, t) at various values of $\alpha ,\beta$: (a) LADM, (b) LVIM and (c) RDTM.

Fig. 4

The approximate solutions for v(x, t) at various values of $\alpha ,\beta$: (a) LADM, (b) LVIM and (c) RDTM.

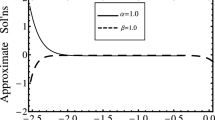
Figures 1 and 2 illustrate the absolute errors between the exact solutions of u(x, t) and v(x, t) and the analytical approximate solutions at $\alpha =\beta =1$ obtained by LADM, LVIM and RDTM when $-5 \le x\le 5, 0 \le t \le 1,$ respectively. The behaviours of the estimated solutions of u(x, t) and v(x, t) by using LADM, LVIM, and RDTM at different values of $\alpha , \beta$ ($\alpha =\beta =1, 0.95, 0.75$ and 0.5), $t=0.1, -5 \le x\le 5$ with exact solution are displayed in figures 3 and 4, respectively. There are some remarkable results that should be mentioned. First, the LADM has many advantages as it can be applied directly without linearisation. Also, the method is capable of reducing greatly the size of computational work while still maintaining high accuracy of the numerical solution. However, although the series can be rapidly convergent in a very small region, it has a very slow convergence rate in wide regions. Secondly, the main advantage of LVIM is to identify the Lagrange multipliers of the VIM, and to propose a new concept of the Laplace–Lagrange multipliers from the Laplace transform. Thirdly, with RDTM, it is possible to obtain highly accurate results or exact solutions for differential equations without linearisation or perturbations. However, RDTM has some drawbacks that the series solution gives a good approximation to the true solution in a very small region. The numerical results show that the three proposed methods are very effective and are in good agreement with each other.

Example 2

[9, 11]. For the following two-dimensional time FCBEs:

$$\begin{aligned}&{D}^{\alpha }_{t} u(x,y,t)+u(x,y,t)\frac{\partial u(x,y,t)}{\partial x}\nonumber \\&\qquad +v(x,y,t)\frac{\partial u(x,y,t)}{\partial y}\nonumber \\&\quad =\frac{1}{\mathrm{Re}}\Bigg [ \frac{\partial ^{2} u(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2} u(x,y,t)}{\partial y^{2}}\Bigg ],\nonumber \\&{D}^{\beta }_{t} v(x,y,t)+u(x,y,t)\frac{\partial v(x,y,t)}{\partial x}\nonumber \\&\qquad +v(x,y,t)\frac{\partial v(x,y,t)}{\partial y}\nonumber \\&\quad =\frac{1}{\mathrm{Re}}\Bigg [ \frac{\partial ^{2} v(x,y,t)}{\partial x^{2}}+\frac{\partial ^{2} v(x,y,t)}{\partial y^{2}}\Bigg ] \end{aligned}$$

(42)

with the initial conditions

$$\begin{aligned} u(x,y,0)= & {} \tfrac{3}{4}-\big (4(1+\mathrm{e}^{(\mathrm{Re}/{8})(-x+y)})\big )^{-1},\nonumber \\ v(x,y,0)= & {} \tfrac{3}{4}+\big (4(1+\mathrm{e}^{(\mathrm{Re}/{8})(-x+y)})\big )^{-1}. \end{aligned}$$

(43)

The exact solutions of (42) at the special case, $\alpha =\beta =1$, are

$$\begin{aligned} u(x,y,t)= & {} \tfrac{3}{4}-\big (4(1+\mathrm{e}^{(\mathrm{Re}/{32})(-t-4x+y)})\big )^{-1},\nonumber \\ v(x,y,t)= & {} \tfrac{3}{4}+\big (4(1+\mathrm{e}^{(\mathrm{Re}/{32})(-t-4x+y)})\big )^{-1}. \end{aligned}$$

(44)

6.5 Solution using LADM

By using the initial conditions (43), the first components of u(x, y, t) and v(x, y, t) will be

$$\begin{aligned} \begin{aligned}&u_{0}(x,y,t)=\frac{3}{4}-\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\&v_{0}(x,y,t)=\frac{3}{4}+\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\&u_{1}(x,y,t)=-\frac{b\mathrm{e}^{b(-x+y)}\big (1{+}4ab(-1{+}\mathrm{e}^{b(-x+y)})\big )t^\alpha }{8(1{+}\mathrm{e}^{b(-x+y)})^{3}\Gamma (1{+}\alpha )},\\&v_{1}(x,y,t)=\\&\quad \quad -\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\beta }{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\beta )}, \ldots , \end{aligned} \end{aligned}$$

where $a={1}/{\mathrm{Re}}, b={\mathrm{Re}}/{8}$. So the solution will take the following form:

$$\begin{aligned} \begin{aligned} u(x,y,t)&=u_{0}(x,y,t)+u_{1}(x,y,t)\\&\quad +u_{2}(x,y,t)+\cdots \\&=\frac{3}{4}-\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )}\\&\quad -\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\alpha }{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\alpha )}\\&\quad +\cdots ,\\ v(x,y,t)&=v_{0}(x,y,t)+v_{1}(x,y,t)\\&\quad +v_{2}(x,y,t)+\cdots \\&=\frac{3}{4}+\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )}\\&\quad +\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\beta }{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\beta )}\\&\quad +\cdots . \end{aligned} \end{aligned}$$

Table 3 The $L_{2}$-norm errors for the suggested methods when $0\le x\le 1, 0\le y\le 1, h=0.1$ for u(x, y, t).

Table 4 The $L_{2}$-norm errors for the suggested methods when $0\le x\le 1, 0\le y\le 1, h=0.1$ for v(x, y, t).

6.6 Solution using LVIM

According to the procedure of LVIM and by using the initial conditions (43), the first components of u(x, y, t) and v(x, y, t) are

$$\begin{aligned} \begin{aligned} u_{0}(x,y,t)&=\frac{3}{4}-\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\ v_{0}(x,y,t)&=\frac{3}{4}+\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\ u_{1}(x,y,t)&=-\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\alpha +2(1+\mathrm{e}^{b(-x+y)})^{2}(2+3\mathrm{e}^{b(-x+y)})\Gamma (1+\alpha )}{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\alpha )},\\ v_{1}(x,y,t)&=\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\beta +2(1+\mathrm{e}^{b(-x+y)})^{2}(4+3\mathrm{e}^{b(-x+y)})\Gamma (1+\beta )}{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\beta )}, \ldots .\\ \end{aligned} \end{aligned}$$

Fig. 5

The space–time graph of absolute errors of u(x, y, t) obtained by (a) LADM, (b) LVIM and (c) RDTM when $\alpha =\beta =1, 0\le y\le 1, 0\le t\le 0.5$ and $x=0.9$.

Fig. 6

The space–time graph of absolute errors of v(x, y, t) obtained by (a) LADM, (b) LVIM and (c) RDTM when $\alpha =\beta =1, 0\le y\le 1, 0\le t\le 0.5$ and $x=0.9$.

Fig. 7

The space–time graph of absolute errors of u(x, y, t) obtained by (a) LADM, (b) LVIM and (c) RDTM when $\alpha =\beta =1, 0\le x\le 1, 0\le t\le 0.5$ and $y=0.9$.

Fig. 8

The space–time graph of absolute errors of v(x, y, t) obtained by (a) LADM, (b) LVIM and (c) RDTM when $\alpha =\beta =1, 0\le x\le 1, 0\le t\le 0.5$ and $y=0.9$.

6.7 Solution using RDTM

By applying RDTM to solve (42) and using the initial conditions (43), the first components will be

$$\begin{aligned}&U_{0}(x,y,t)=\frac{3}{4}-\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\&V_{0}(x,y,t)=\frac{3}{4}+\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )},\\&U_{1}(x,y,t)=-\frac{b\mathrm{e}^{b(-x+y)}\big (1{+}4ab(-1{+}\mathrm{e}^{b(-x+y)})\big )}{8(1{+}\mathrm{e}^{b(-x+y)})^{3}\Gamma (1{+}\alpha )},\\&V_{1}(x,y,t)=\\&\quad -\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )}{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\beta )},\ldots . \end{aligned}$$

So, the solution takes the following form:

$$\begin{aligned} \begin{aligned} u(x,y,t)&=U_{0}(x,y,t)+U_{1}(x,y,t)t^{\alpha }\\&\quad +U_{2}(x,y,t)t^{2\alpha }+\cdots \\&=\frac{3}{4}-\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )}\\&\quad -\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\alpha }{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\alpha )}\\&\quad +\cdots ,\\ v(x,y,t)&=V_{0}(x,y,t)+V_{1}(x,y,t)t^{\beta }\\&\quad +V_{2}(x,y,t)t^{2\beta }+\cdots \\&=\frac{3}{4}+\frac{1}{4\big (1+\mathrm{e}^{b(-x+y)}\big )}\\&\quad +\frac{b\mathrm{e}^{b(-x+y)}\big (1+4ab(-1+\mathrm{e}^{b(-x+y)})\big )t^\beta }{8(1+\mathrm{e}^{b(-x+y)})^{3}\Gamma (1+\beta )}\\&\quad +\cdots . \end{aligned} \end{aligned}$$

Fig. 9

The behaviours of u(x, y, t) by using (a) LADM, (b) LVIM and (c) RDTM for various values of $\alpha ,~\beta$ at $x=y=0.5, 0\le t\le 0.5$ with the exact solution.

Fig. 10

The behaviours of v(x, y, t) by using (a) LADM, (b) LVIM and (c) RDTM for various values of $\alpha ,~\beta$ at $x=y=0.5, 0\le t\le 0.5$ with the exact solution.

Fig. 11

The behaviours of u(x, y, t) and v(x, y, t) by using (a) LADM, (b) LVIM and (c) RDTM at $\alpha =\frac{1}{3}, \beta =\frac{1}{5}$.

Tables 3 and 4 tabulate the $L_2$-norm errors for our three proposed methods at $0\le x\le 1, 0\le y\le 1$ and $\mathrm {Re}=1$ for different values of t. It is remarkable that in Example 2, the estimated solutions obtained using LADM, RDTM and LVIM converge faster than the approximate solutions obtained using methods in [9, 11] to exact solution. To show the efficiency of the proposed methods, graphical representation of the absolute error surfaces between the exact and the analytical approximate solutions of u(x, y, t) and v(x, y, t) at $\alpha =\beta =1,~0\le t\le 0.5, a=1, b=\frac{1}{8},$ obtained by LADM, LVIM and RDTM when $0\le y\le 1 , x=0.9$, is shown in figures 5 and 6, respectively, and for $0\le x\le 1$, $y=0.9$ in figures 7 and 8, respectively. It is noted that the same numerical results are obtained in two cases.

Figures 9 and 10 illustrate the behaviours of the computed solutions of u(x, y, t) and v(x, y, t), respectively, using LADM, LVIM and RDTM at various values of the parameters $\alpha$ and $\beta$ ($\alpha =\beta =1, 0.95, 0.75$ and $0.5), x=y=0.5, 0\le t\le 0.5$ with exact solution. In figure 11 the behaviours of the approximate solutions of u(x, y, t) and v(x, y, t) obtained by the three proposed methods at a fixed value of $\alpha$ and $\beta$ ($\alpha =\frac{1}{3}, \beta =\frac{1}{5}$) are plotted. These figures show that the obtained solutions cover the classical results when the value of the fractional order tends to unity. Also, the three methods are very effective and are in good agreement with each other.

7 Conclusions

The main objective of this paper was to construct efficient approximate analytical solutions to the one- and two-dimensional FCBEs. We successfully achieved this target by using three methods: namely, LADM, LVIM and RDTM. The obtained solutions approved the reliability and accuracy of the proposed methods. Numerical analysis showed that the same results are obtained for the one-dimensional FCBE by the three suggested methods, while in the two-dimensional FCBE, the solutions obtained by means of LADM and RDTM converge faster than the approximate solution by LVIM.