1 Introduction

Recent developments in the nanoscience-driven world enforce the scientists and researchers to explore the field of thermal engineering more and more. One crucial pursuit of the thermal engineers is to provide new types of heat transfer liquids. They found that nanoscale additives to the base liquid can provide a liquid that has enhanced heat transfer capability. Based on this perception, a new fluid named ‘nanofluid’ has been in the field for the last two decades. These nanoliquids have the potential to provide erosion reduction, better stability and controlled chemical processes with other chemicals existing in the system. Recently, nanoliquids have received substantial attention in heat transfer mechanisms because of their promising performance as cooling and heating liquids. Heat dissipation in electronic devices has become a significant factor in designing electronic instruments. It is observed that by utilising nanoliquid in thermosiphons and heat pipes, we can enhance the rate of heat transfer from one point to another. The concept of nanoliquid was initially conceived by Choi et al [1], to rise the rate of heat transfer. Oztop and Abu-Nada [2] scrutinised numerically the natural convection flow of nanofluids in partially heated rectangular enclosures. The boundary layer flow of viscous nanofluid towards a convectively heated plate was numerically addressed by Makinde and Aziz [3]. Pal and Mondal [4] scrutinised the magnetohydrodynamic (MHD) convective stagnation-point flow of nanofluids over a non-isothermal stretching sheet with induced magnetic field. The mixed convection stagnation-point flow of nanofluids over a stretching / shrinking sheet in a porous medium with internal heat generation / absorption was studied by Pal and Mondal [5]. Effects of heat and mass transfer on the hydromagnetic flow of a viscous fluid under slip conditions and different types of nanoparticles were considered by Turkyilmazoglu [6]. Khan et al [7] analysed the three-dimensional (3D) flow of an Oldroyd-B nanofluid towards a stretching sheet with heat generation / absorption. Their observations revealed that with the Brownian motion and thermophoresis parameters, the temperature field increases, however, an opposite behaviour was found in the concentration field. Furthermore, Khan et al [8] scrutinised the two-dimensional (2D) boundary layer flow and heat transfer to Sisko nanofluid over a stretching sheet in the concerned study. Their results showed that the temperature distribution increases with the thermophoresis and Brownian motion parameters. Kuznetsou and Nield [9] provided a revised model of the natural convective boundary-layer flow of nanofluid on a vertical plate under the newly proposed boundary condition. Hayat et al [10] studied the mixed convection flow of viscoelastic nanofluid by a cylinder with variable thermal conductivity and heat source / sink. The magneto-nanoliquids are utilised in significant areas of science and technology such as optical modulators, magneto-optical wavelength filters, wound treatment and MHD power generators. These applications of magneto-nanoliquids are justified because the utilisation of MHD in the working liquid creates a retarding force, which controls the cooling rate that is essential in these devices. Hayat et al [11] developed the MHD 3D flow of nanofluid under convective conditions. Hayat et al [12] presented the impact of MHD on the bidirectional flow of nanofluid subject to a second-order slip velocity and homogeneous–heterogeneous reactions. Khan and Khan [13, 14] inspected the characteristics of nonlinear mechanics by utilising the aspects of thermophoresis and Brownian motion. Peddisetty [15] considered the problem of transient-free convective flow for nanofluid with thermal stratification. Khan and Khan [16] analysed the non-Newtonian Burgers nanofluid over the stretched surface under the influence of heat sink–source. Sheikh et al [17] presented the applications of nanofluids for improving the efficiency of solar collectors. Khan et al [18] scrutinised the features of magneto-Carreau nanofluid by considering the aspects of solar energy.

Chemical processes are an essential piece of innovation, of culture and in fact, of life itself. Chemical reactions are absolutely distinguished from the physical change. In physical processes, only states are changed. In physical change, the chemical properties of the substance will remain the same as before. Chemical reaction is the mechanism, which takes place between two or more reactants to generate one or more new compounds. There are many chemical reactions, which are slow and require heat or an accelerator to start the reaction. Chemical reaction is classified as homogeneous reaction if the reactant and catalyst are in one phase and heterogeneous reaction if they are in at least two phases. Example of this mechanism is the interaction between a liquid and a solid. These chemical processes have several applications like food processing, fog formation and polymer production. Pizza et al [19] showed the capability of catalytically coated walls in moderating characteristic fire hazards of meso / smaller scale channels. Additionally, Hayat et al [20, 21] have done a lot of work related to chemical reactions. Khan et al [22] also reported the outcome of a chemically reactive aspect in the flow of tangent hyperbolic materials. Wang et al [23] reported the reaction intensity between catalytic and non-catalytic combustors. Li et al [24] investigated the characteristics of heterogeneous-homogeneous reactions by utilizing the aspects of catalyst segmentation with cavities. The outcomes demonstrated that the catalytic combustor showed high stability and powerless reaction intensity. Yasmeen et al [25] examined the homogeneous–heterogeneous reactions of the ferrofluid flow by a stretched surface in the incidence of a magnetic dipole. They detected from their graphical data that temperature of ferrofluid declines for higher values of Prandtl number while opposite trend is observed for thermal radiation. On the other hand, the temperature and skin friction were found to enhance conductivity while using increasing values of embedded parameters. Moreover, Khan et al [26] illustrated the characteristics of the homogeneous–heterogeneous processes in the 3D Burgers fluid flow.

The rheology of nonlinear mechanics [27,28,29,30,31,32,33,34,35,36,37,38] has been an inspiring and fascinating subject for investigators because of its growing technical and industrial importance such as in polymer, petroleum, chemical and food processing industries. Owing to the significance of nonlinear mechanics, Powell and Eyring anticipated a novel fluid relation known as the Eyring–Powell fluid model. Hayat et al [39] inspected the flow of Eyring–Powell fluid by considering a moving surface. The characteristics of the 3D flow for Powell–Eyring nanfluid over a stretched surface was studied numerically by Gireesha et al [40]. Khan et al [41] assessed the flow behaviour of the 3D magneto Eyring–Powell nanofluid under the influence of thermal radiation.

Fig. 1
figure 1

The physical geometry of the problem.

Full size image

Thermal radiation is a phenomenon in which energy spreads from a heated surface to its absorption point in all directions in the form of electromagnetic waves. It is generated by the thermal agitation of composite molecules of the body. A common example of thermal radiation is the heating of a room by an open fireplace. The typical examples are heat from the sun, fire, light-bulb and microwave radiation. Moreover, its technological applications can be seen in nuclear power plants, solar power technology, chemical processes and combustion chambers. Stefan–Boltzmann law of radiative heat transfer states that heat energy emitted by the heated surface per unit area per second is directly proportional to the fourth power of the surface’s absolute temperature. It has been observed that when the temperature difference between the object and free stream fluid is large, thermal radiation is capable of inverting thermal boundary layers and related rate of heat transfer. Khan et al [42] considered the aspect of gyrotactic microorganisms for magneto-Burgers nanofluid in the presence of thermal radiation. Ali et al [43] studied the hidden mechanisms for unsteady flow by utilising a porous medium. Bhatti et al [44] investigated the heat transfer mechanism for MHD particle-fluid suspension under the influence of thermal radiation induced by a metachronal wave. Khan et al [45] used the idea of suspension of nanoparticles in 3D Sisko fluid flow over a stretched surface.

From the above-mentioned discussion, it is found that the current consideration is unique and no such investigation has been considered in the literature. Therefore, the objective of the current research is to explore the features of unsteady 3D flow of the Eyring–Powell nanofluid in the presence of constructive / destructive reactions and nonlinear thermal radiation over a bidirectional stretchable surface. Additionally, the heat transfer mechanism is demonstrated in the presence of heat sink / source. The bvp4c scheme is used to find numerical solution to the obtained ODEs.

2 Theory and flow field exploration

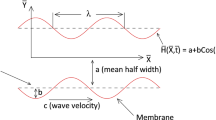
We shall consider here the unsteady 3D forced convective flow of an electrically conducting Eyring–Powell nanofluid associated with the heat and mass transfer. The sheet coincides with the plane \(z=0\) and the motion of the Eyring–Powell nanoliquid is confined in the half space \(z>0\). Constructive / destructive chemical reactions and heat source / sink mechanisms are also taken into account. Moreover, Reynolds number is supposed to be small neglecting the impact of the induced magnetic field on the Eyring–Powell nanofluid. The surface of the sheet is heated by a hot liquid having temperature \( T_{\mathrm {f}}\), whereas the nanofluid outside the boundary is maintained at a uniform temperature and concentration \(\left( T_{\infty },C_{\infty }\right) \). The physical geometry of the problem considered here is shown in figure 1. The boundary layer equations take the form:

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w }{\partial z}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}=\left( \nu +\frac{1}{\beta d_{1}\rho _{f}}\right) \frac{\partial ^{2}u}{\partial z^{2}}\nonumber \\&\quad -\,\frac{1}{2\beta d_{1}^{3}\rho _{f}}\left( \frac{\partial u}{\partial z}\right) ^{2}\frac{ \partial ^{2}u}{\partial z^{2}}-\frac{\sigma B_{0}^{2}\left( t\right) }{\rho _{f}}u, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}=\left( \nu +\frac{1}{\beta d_{1}\rho _{f}}\right) \frac{\partial ^{2}v}{\partial z^{2}}\nonumber \\&\quad -\,\frac{1}{2\beta d_{1}^{3}\rho _{f}}\left( \frac{\partial v}{\partial z}\right) ^{2}\frac{ \partial ^{2}v}{\partial z^{2}}-\frac{\sigma B_{0}^{2}\left( t\right) }{\rho _{f}}v, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z} =\alpha _{1}\frac{\partial ^{2}T}{\partial z^{2}}\nonumber \\&\quad \,\, +\,\tau \left[ D_{B}\frac{\partial C}{\partial z}\frac{ \partial T}{\partial z}+\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{ \partial z}\right) ^{2}\right] \nonumber \\&\quad \,\, -\,\frac{1}{(\rho c)_{f}}\frac{\partial q_{r}}{\partial z}+\frac{Q_{0}}{ (\rho c)_{f}}(T-T_{\infty }), \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial C}{\partial t}+u\frac{\partial C}{\partial x}+v\frac{\partial C}{\partial y}+w\frac{\partial C}{\partial z}=D_{B}\frac{\partial ^{2}C}{ \partial z^{2}}\nonumber \\&\quad \,\, +\,\frac{D_{T}}{T_{\infty }}\frac{\partial ^{2}T}{\partial z^{2} }-k_{c}\left( C-C_{\infty }\right) . \end{aligned}$$
(5)

The boundary conditions for the present flow analysis are

$$\begin{aligned}&u =U_{w}(x,t)=\frac{ax}{1-\beta _{1}},\quad v=V_{w}(x,t)=\frac{by}{ 1-\beta _{1}},\nonumber \\&\quad w=0, \nonumber \\&-\,k\frac{\partial T}{\partial z} =h_{f}[T_{f}-T],\quad D_{B}\frac{ \partial C}{\partial z}+\frac{D_{T}}{T_{\infty }}\frac{\partial T}{\partial z }=0\nonumber \\&\quad \text { at }z=0, \end{aligned}$$
(6)
$$\begin{aligned}&u \rightarrow 0,\text { }v\rightarrow 0, \ T\rightarrow T_{\infty }, \ C\rightarrow C_{\infty }\quad \text {as }z\rightarrow \infty ,\nonumber \\ \end{aligned}$$
(7)

where \(u,v,w,T,C,\nu ,\beta ,d_{1},\rho _{_{f}},\alpha _{1},\tau ,D_{B},\) \( D_{T},k_{c},q_{r}\) are, respectively, the velocity components in the x, y and z directions, temperature, concentration, kinematic viscosity, fluid parameters, fluid density, thermal diffusivity of base liquid, ratio of effective heat capacity of the nanoparticle to heat capacity of Eyring–Powell fluid, Brownian diffusion coefficient, thermophoresis diffusion coefficient, rate of chemical reaction and radiative heat flux. The radiative heat flux \( q_{r}\) is given by

$$\begin{aligned} q_{r}=-\frac{4\sigma ^{*}}{3k^{*}}\frac{\partial T^{4}}{\partial z}=- \frac{16\sigma ^{*}}{3k^{*}}\frac{\partial }{\partial z}\left( T^{3} \frac{\partial T}{\partial z}\right) , \end{aligned}$$
(8)

where \(\sigma ^{*}\) is the Stefan–Boltzman constant and \(k^{*}\) is the mean absorption coefficient.

Substituting eq. (8) into eq. (4), we have the following energy equation:

$$\begin{aligned}&\frac{\partial T}{\partial t}+u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}\nonumber \\&\quad =\alpha _{1}\frac{\partial ^{2}T}{\partial z^{2}}+\tau \left[ D_{B}\frac{\partial C}{\partial z}\frac{ \partial T}{\partial z}+\frac{D_{T}}{T_{\infty }}\left( \frac{\partial T}{ \partial z}\right) ^{2}\right] \nonumber \\&\qquad +\frac{1}{(\rho c)_{f}}\frac{16\sigma ^{*}}{3k^{*}}\frac{\partial }{\partial z}\left( T^{3}\frac{\partial T}{\partial z}\right) \nonumber \\&\qquad +\frac{Q_{0}}{ (\rho c)_{f}}(T-T_{\infty }). \end{aligned}$$
(9)

By presenting the following suitable conversions:

$$\begin{aligned}&u =\frac{axf^{\prime }(\eta )}{1-\beta _{1}},\quad v=\frac{ ayg^{\prime }(\eta )}{1-\beta _{1}},\nonumber \\&w=-\sqrt{\frac{a\nu }{1-\beta _{1}}}\left[ f(\eta )+g(\eta )\right] , \nonumber \\&\theta (\eta ) =\frac{T-T_{\infty }}{T_{f}-T_{\infty }},\quad \phi (\eta )=\frac{C-C_{\infty }}{C_{\infty }},\nonumber \\&\eta =z\sqrt{\frac{a }{\nu \left( 1-\beta _{1}\right) }}, \end{aligned}$$
(10)

eq. (1) is automatically satisfied and eqs (2)–(7) and (9) yield

$$\begin{aligned}&(1+\epsilon )f^{\prime \prime \prime }-S\left( f^{\prime }+\frac{1}{2}\eta f^{\prime \prime }\right) \nonumber \\&\quad +\,(f+g)f^{\prime \prime }-f^{{\prime }2}-\epsilon \delta _{1}f^{{\prime \prime }2}f^{{\prime \prime \prime }}-M^{2}f^{\prime }=0, \end{aligned}$$
(11)
$$\begin{aligned}&(1+\epsilon )g^{\prime \prime \prime }-S\left( g^{\prime }+\frac{1}{2}\eta g^{\prime \prime }\right) \nonumber \\&\quad +\,(f+g)g^{{\prime \prime }}-g^{{\prime }2}-\epsilon \delta _{2}g^{{\prime \prime }2}g^{{\prime \prime \prime }}-M^{2}g^{\prime }=0, \end{aligned}$$
(12)
(13)
$$\begin{aligned}&\phi ^{{\prime \prime }}-{\mathrm {Le}}\Pr S\left( \phi +\frac{1}{2}\eta \phi ^{\prime }\right) +\,{\mathrm {Le}}\Pr (f+g)\phi ^{{\prime }}\nonumber \\&\quad -{\mathrm {Le}}\Pr \delta \phi +\frac{N_{t}}{N_{b} }\theta ^{{\prime \prime }}=0, \end{aligned}$$
(14)
$$\begin{aligned}&f =0,\ \ g=0,\ \ \ \ f^{{\prime }}=1,\ \ g^{{\prime }}=\alpha , \nonumber \\&\theta ^{{\prime }}(0) =-\gamma [1-\theta (0)],\ \ N_{b}\phi ^{\prime }(0)+N_{t}\theta ^{\prime }(0)=0,\nonumber \\&\quad {\mathrm {at}}\ \ \ \eta =0, \end{aligned}$$
(15)
$$\begin{aligned}&f^{\prime }\rightarrow 0, \ \ g^{{\prime }}\rightarrow 0, \ \ \theta \rightarrow 0, \ \ \phi \rightarrow 0,\text { as }\eta \rightarrow \infty .\nonumber \\ \end{aligned}$$
(16)

In the above expressions, \(\epsilon = {1}/{\beta d_{1}\rho _{f}},\) \(\delta _{1}= {a^{3}x^{2}}/{2vd_{1}^{2}}\) and \( \delta _{2}= {a^{3}y^{2}}/{2vd_{1}^{2}}\) are the Eyrin–Powell fluid parameters, \(M ={\sigma B_{0}^{2}}/{(\rho c)_{f}}\) denotes the magnetic parameter, \(R_{d}={16\sigma ^{*}T_{\infty }^{3}}/{3kk^{*}}\) is the radiation parameter, \({\mathrm {Pr}} ={\nu }/{\alpha _{1}}\) is the Prandtl number, \( \theta _{f}={T_{f}}/{T_{\infty }} \) is the temperature parameter, \(N_{b}= {\tau D_{B}C_{\infty }}/{\nu }\) is the Brownian motion parameter, \(N_{t}={\tau D_{T}(T_{f}-T_{\infty })}/{\nu T_{\infty }}\) is the thermophoresis parameter, \({\mathrm {Le}} = {\alpha _{1}}/{D_{B}} \) is the Lewis number, \(\ \alpha ={b}/{a}\) is the ratio of stretching rate parameter, \(\gamma =( ({h_{f}}/{k})\sqrt{{\nu }/{a}}) \) is the Biot number, \(\lambda =({Q_{0}( 1-\beta _{1})) }/{a(\rho c)_{f}} \) is the heat source / sink parameter and \(\delta ={k_{c}}/{a}\) for the chemical reaction parameter. The prime stands for differentiation with respect to \(\eta \).

Table 1 Numerical values of the local Nusselt number \(-\theta ^{\prime }(0)\) for distinct values of growing parameters for fixed value of \(\alpha =0.3\) and \(\gamma =0.3.\)
Full size table

After somatic opinion, the vital characteristic of the flow is the local Nusselt number \({\mathrm {Nu}}_{x}\) which can be characterised as

$$\begin{aligned} {\mathrm {Nu}}_{x}=-\frac{x}{( T_{f}-T_{\infty }) }\left. \left( \frac{\partial T}{\partial z}\right) \right| _{z=0}+\frac{xq_{r}}{k(T_{f}-T_{\infty }) }.\nonumber \\ \end{aligned}$$
(17)

The above quantities are reduced to the following dimensionless form:

$$\begin{aligned} \left( {\mathrm{Re}}_{x}\right) ^{-{1}/{2}}{\mathrm {Nu}}_{x}=-[ 1+R_{d}\{\theta _{f}+(1-\theta _{f})\theta \}^{3}] \theta ^{\prime }(0),\nonumber \\ \end{aligned}$$
(18)

where \({\mathrm{Re}}_{x}=({ax^{2}})/{\nu }\) is the local Reynolds numbers.

Fig. 2
figure 2

Profiles of temperature \(\theta (\eta )\) for various values of (a) unsteadiness parameter S and (b) magnetic parameter M.

Full size image
Fig. 3
figure 3

Profiles of temperature \(\theta (\eta )\) for various values of (a) ratio of temperature parameter \(\theta _{f}\) and (b) heat absorption parameter \(\lambda \).

Full size image
Fig. 4
figure 4

Profiles of temperature \(\theta (\eta )\) for various values of (a) Biot number \(\gamma \) and (b) thermophoresis parameter \(N_{t}\).

Full size image
Fig. 5
figure 5

Profiles of concentration \(\phi (\eta )\) for various values of (a) unsteadiness parameter S and (b) magnetic parameter M.

Full size image
Fig. 6
figure 6

Profiles of concentration \(\phi (\eta )\) for various values of (a) Brownian motion parameter \(N_{b}\) and (b) thermophoresis parameter \(N_{t}\).

Full size image

3 Graphical results and discussion

A thorough analysis is made for the constructive / destructive effects on the MHD 3D forced convective flow of the Erying–Powell nanofluid. Heat source / sink and nonlinear radiation effects are taken into consideration. The governing ODEs and boundary conditions are analysed by utilising the bvp4c function in Matlab. A detailed graphical analysis has been made for the temperature and concentration fields and discussed for various parameters of interest. Furthermore, heat transfer rate for fluctuating various parameters is included in table 1. From table 1, we perceived that heat transfer rate enriches for accumulative values of Pr, \(\epsilon \) and \(\alpha \) while it illustrates diminishing behaviour for \(\delta _1\), \(\delta _2\), M, \(N_b\) and \(N_t\).

3.1 Temperature field

The temperature profiles of the Eyrin–Powell nanofluid exhibit a remarkable change with the variation of S,  M,  \(\theta _{f},\) \(\lambda ,\) \(\gamma \) and \(N_{t}\). The variation of temperature profile with these parameters is illustrated in figures 2–4. To exhibit the effects of unsteadiness parameter S and magnetic parameter M on the temperature profile, we have plotted figures 2a and 2b. These sketches show that the temperature of the Eyrin–Powell nanofluid increases as the values of S and M are increased. Physically, as we enhance M,  Lorentz’s force increases due to which collision between the particles of the Eyrin–Powell nanofluid increases. As a result, the temperature of the Eyrin–Powell nanofluid rises. The ratio of the temperature parameter \(\theta _{f}\) and heat absorption parameter \( \lambda \) plays a vital role in the forced convective 3D flow of the Eyrin–Powell nanofluid. Figures 3a and 3b present the impact of these parameters on the temperature profile. These figures show that the augmented values of \( \theta _{f}\) and \(\lambda \) affect the heat transfer strongly. Physically, as \(\theta _{f}\) increases, the temperature of the wall becomes higher than the temperature of the nanoliquid at infinity. As a result, the temperature of the nanofluid increases. Figures 4a and 4b interpret the dependence of the Biot number \(\gamma \) and thermophoresis parameter \(N_{t}\) on the nanofluid temperature. The exploration of these plots imparts that leads to enhancement of nanofluid temperature. The physical reason behind this trend of \( \gamma \) is that less resistance is faced by the thermal wall which causes an enhancement in convective heat transfer to the fluid.

3.2 Concentration field

The dependence of various parameters on the concentration of the Eyrin–Powell nanofluid is exhibited graphically in figures 5–9. The influence of unsteadiness parameter S and magnetic parameter M on the concentration profile is displayed in figures 5a and 5b. It is analysed from these figures that the concentration profile enhances with an increase in S and M. The concentration of the Erying–Powell nanofluid increases due to the heat produced by M. Figure  6a reveals the effect of parameter \(N_{b}\) on fluid concentration. The concentration profile reduces as \(N_{b}\) increases. Figure 6b shows that the concentration profile enhances with elevation in the thermophoresis parameter \(N_{t}\) as a higher value of \(N_{t}\) stands for a greater temperature difference. Additionally, it is detected that physically, an increase in the magnitude of \(N_{b}\) corresponds to an increase in the rate at which nanoparticles in the base liquid move in random directions with different velocities. This movement of nanoparticles augments transfer of heat and therefore, declines the concentration profile. Demonstration of the effects of Prandtl number \({\mathrm {Pr}}\) and Lewis number \({\mathrm {Le}}\) on the concentration of the Eyrin–Powell nanofluid is shown in figures 7a and 7b. These figures show that the increasing values of \({\mathrm {Pr}} \) and \({\mathrm {Le}}\) result in a reduction of the concentration profile. To investigate the effects of the ratio of stretching rate parameter \(\alpha \) and Biot number \( \gamma \) on the concentration profile, we have plotted figures 8a and  8b. These figures reveal that the concentration profile declines as the value of \(\alpha \) is augmented while an opposite behaviour is observed for \(\gamma \). Figures 9a and 9b show the impact of chemical reaction parameter \(\delta \) and ratio of temperature parameter \(\theta _{f}\) on the concentration profile. It is detected that the concentration of nanoliquids decreases with an increase in \(\delta , \) whereas a reverse behaviour is detected for \( \theta _{f}\). Furthermore, these plots show that the concentration profile is significantly affected by the variation of \(\delta \).

Fig. 7
figure 7

Profiles of concentration \(\phi (\eta )\) for various values of (a) Prandtl number \(\Pr \) and (b) Lewis number \({\mathrm {Le}}\).

Full size image
Fig. 8
figure 8

Profiles of concentration \(\phi (\eta )\) for various values of (a) ratio of stretching rate parameter \(\alpha \) and (b) Biot number \(\gamma \).

Full size image
Fig. 9
figure 9

Profiles of concentration \(\phi (\eta )\) for various values of (a) chemical reaction parameter \(\delta \) and (b) ratio of temperature parameter \(\theta _{f}\).

Full size image

4 Conclusions

The current paper reported the forced convective 3D flow of the Eyring–Powell magneto-nanofluid in the presence of heat source / sink. Additionally, the impacts of the constructive / destructive reactions and newly suggested relation for nanofluid were considered here. The modelled equations of the Eyring–Powell magneto-nanofluid were simplified by applying suitable similarity transformations and numerical solutions of these equations were found with the help of the bvp4c scheme. The graphical data led us to conclude that

  • the increasing values of S and \(\theta _{f}\) resulted in the increase of the liquid temperature,

  • temperature field and thermal layer structures exhibited descending trend for increasing values of the heat sink parameter,

  • \(N_{t}\) and \(N_{b}\) have opposite effects on the nanofluid concentration,

  • the concentration of the nanofluid decreased gradually with the increasing values of chemical reaction parameter \(\delta \).