1 Introduction

Nonlinearity of Einstein’s equation is the reason for non-linearity of Einstein’s general theory of relativity. So, there may be a certain link between nonlinear Einstein’s general theory of relativity and non-linear dynamics. Particularly, Lyapunov exponent [1] is one of the bridges between them. In this paper, we shall focus on the analytical calculations involving the Lyapunov exponent in terms of the equation of circular geodesics around a BH space-time. These equatorial circular geodesics around a BH space-time play crucial roles in general relativity for the classification of the orbits. They also determine important features of the space-time and give important information on the background geometry.

The Lyapunov exponent (λ) has been used to probe the instability of circular null geodesics and in terms of the quasinormal modes (QNMs) for spherically symmetric space-time of arbitrary dimensions [2], but the focus there is on null circular geodesics. It has been shown in ref. [2] that in the eikonal approximation, the real and imaginary parts of the QNMs of any dimensions of spherically symmetric, asymptotically flat space-time are given by (multiples of) the frequency and instability time-scale of the unstable circular photon geodesics.

Note however that the principal Lyapunov exponents have been computed in [2–5] using coordinate time t, where t is measured by the asymptotic observers. Thus, these exponents are explicitly coordinate-dependent and therefore have a degree of un-physicality. Here, we compute the principal Lyapunov exponent analytically by using the proper time as well as coordinate time and prove that their ratio i.e., λ p /λ c is not an invariant quantity. Then we compare the results obtained using both coordinate time and proper time. Using λ, we also study the stability properties of the equatorial circular geodesics for RN BH space-time.

We further elucidate the connection between the Lyapunov exponent of the circular null geodesics in terms of the frequency of QNMs for RN BH in the eikonal limit. Interestingly, for extremal BH this frequency goes to zero. i.e.,

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}}=0 \end{array} $$
(1)

and for non-extremal RN BH, the frequency of QNM is

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}}&=&\ell \sqrt{\frac{Mr_{c}-Q^{2}}{{r_{c}^{4}}}} - i\left( n+\frac{1}{2}\right)\\ &&\times\sqrt{\frac{(Mr_{c}-Q^{2})(3Mr_{c}-4Q^{2})}{{r_{c}^{6}}}} , \end{array} $$
(2)

where n is the overtone number and ℓ is the angular momentum of perturbation.

For Schwarzschild BH, the QNM frequency becomes

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}}=\ell \sqrt{\frac{M}{{r_{c}^{3}}}} - i\left( n+\frac{1}{2}\right)\frac{\sqrt{3}M}{{r_{c}^{2}}} . \end{array} $$
(3)

Another interesting feature we have studied here is that, when we use the proper time, the principal Lyapunov exponent for RN space-time can be obtained as

$$\begin{array}{@{}rcl@{}} \lambda_{p}=\sqrt{\frac{-(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4})} {{r_{0}^{4}}({r_{0}^{2}}-3Mr_{0}+2Q^{2})}} . \end{array} $$
(4)

When we use the coordinate time, the Lyapunov exponent for RN space-time can be obtained as

$$\begin{array}{@{}rcl@{}} \lambda_{c}=\sqrt{\frac{-(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9M Q^{2}r_{0}-4Q^{4})} {{r_{0}^{6}}}} \end{array} $$
(5)

and also their ratio

$$\begin{array}{@{}rcl@{}} \frac{\lambda_{p}}{\lambda_{c}} =\frac{r_{0}}{\sqrt{{r_{0}^{2}}-3M r_{0}+2Q^{2}}} \end{array} $$
(6)

is not an invariant quantity.

We would like to mention here for the reader a few works that have addressed Lyapunov exponent for different types of BHs. The invariant properties of the Lyapunov exponent were first discussed in [6] (see also [7,8]). Sota et al [9] have first proposed and used the invariant form of Lyapunov exponent, where the proper time is employed for the exponents as an invariant measure of time. Wu et al [10] have tested the same problem using different approaches. More recent proposals and discussions on that topic can be found in [11,12]. A review on Lyapunov exponent can be found in [13].

The paper is organized as follows: In §2, we provide the fundamentals of the Lyapunov exponent. In §3, we shall completely describe the equatorial circular geodesics, both time-like and null cases for RN BH and also compute the proper time Lyapunov exponent as well as coordinate time Lyapunov exponent. In §4, we discuss similar features for extremal RN space-time. In §5, we relate the QNMs of null circular geodesics in terms of the Lyapunov exponent for a spherically symmetric RN space-time and Schwarzschild BH. In §6, we present our conclusions.

2 Fundamentals of the Lyapunov exponent

Lyapunov exponent in a classical phase-space is a measure of the average rates of expansion and contraction of trajectories surrounding it. They are asymptotic quantities defined locally in state space, and describe the exponential rate at which a perturbation to a trajectory of a system grows or decays with time at a certain location in the state space. A positive Lyapunov exponent indicates a divergence between two nearby geodesics, the paths of such a system are extremely sensitive to changes of the initial conditions. A negative Lyapunov exponent implies a convergence between two nearby geodesics.

Let x(t), i.e., x(t = 0) = x 0 denote a trajectory of a system of equations governed by the following n-dimensional autonomous system [14]:

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}x}{\mathrm{d}t} = F(x;M). \end{array} $$
(7)

The vector x consists of n state variables, the function F describes the non-linear evolution of the dynamical system and M is a vector control parameter, while t is the time parameter. The solutions are fixed points or critical points when F(x; M) = 0. Let its solution for M = M 0 be x 0, where \(x_{0}\in \mathcal {R}^{n}\) and \(M_{0} \in \mathcal {R}^{m}\). To calculate stability, we simply apply on x(t), a small perturbation y(t) and obtain

$$\begin{array}{@{}rcl@{}} x(t) = x_{0}+y(t). \end{array} $$
(8)

Substituting eq. (8) into eq. (7) yields

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}y}{\mathrm{d}t} = F(x_{0}+y;M). \end{array} $$
(9)

Note that the fixed point x = x 0 of eq. (7) has been transformed into the fixed point y=0 of eq. (9). Expanding eq. (9) in a Taylor series about x 0 and keeping only linear terms in the perturbation leads to

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}y}{\mathrm{d}t} = F(x_{0};M_{0})+\frac{\partial F(x_{0};M_{0})}{\partial x} y +O(\| y\|^{2}) \end{array} $$
(10)

or

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}y}{\mathrm{d}t} = \frac{\partial F(x_{0};M_{0})}{\partial x} y = Ay , \end{array} $$
(11)

where the matrix A is called the Jacobian matrix. If the components of F are F 1(x 1,x 2,x 3,...,x n ), F 2(x 1,x 2,x 3,...,x n ), F 3(x 1,x 2,x 3,...,x n ), then

$$\begin{array}{@{}rcl@{}} A= \left( \begin{array}{cccc} \frac{\partial F_{1}}{\partial x_{1}} & \frac{\partial F_{1}}{\partial x_{2}} & ... &\frac{\partial F_{1}}{\partial x_{n}} \\ \frac{\partial F_{2}}{\partial x_{1}} & \frac{\partial F_{2}}{\partial x_{2}} & ... &\frac{\partial F_{2}}{\partial x_{n}} \\ .& . & . & . \\ .& . & . & . \\ .& . & . & . \\ \frac{\partial F_{n}}{\partial x_{1}} & \frac{\partial F_{n}}{\partial x_{2}} &... &\frac{\partial F_{n}}{\partial x_{n}}\\ \end{array} \right). \end{array} $$
(12)

The eigenvalues of the constant matrix A provide information about the local stability of the fixed point x 0. The eigenvalues of A are also known as characteristic exponents or Lyapunov exponents associated with F at (x 0,M 0).

If we consider an initial deviation y(0), its evolution is described by

$$\begin{array}{@{}rcl@{}} y(t)={\Phi}(t) y(0), \end{array} $$
(13)

where Φ(t) is the fundamental(transition) matrix solution of eq. (11) associated with the trajectory, say x(t), which governs the dynamical equation (7). For an appropriately chosen value of y(0), the rate of exponential expansion or contraction in the direction of y(0) on the trajectory passing through x 0 (trajectory at t = 0) is given by

$$\begin{array}{@{}rcl@{}} \lambda_{i}= \lim_{t \rightarrow \infty} \left( \frac{1}{t}\right)\ln\!\left( \frac{\parallel \!\!y(t)\! \!\parallel}{ \parallel\! \!y(0)\!\! \parallel}\right), \end{array} $$
(14)

where ∥∥ denotes a vector norm. The asymptotic quantity λ i is called the Lyapunov exponent.

If there exists a set of n Lyapunov exponents associated with an n-dimensional autonomous system, they can be ordered by size, i.e.,

$$\begin{array}{@{}rcl@{}} \lambda_{1}\geq \lambda_{2} \geq \lambda_{3}\geq {\cdots} \geq \lambda_{n}. \end{array} $$
(15)

The set of n-numbers λ i is called the Lyapunov spectrum.

Following Lyapunov [1], the fundamental matrix Φ(t) is called regular if

$$\begin{array}{@{}rcl@{}} \lim_{t \rightarrow \infty} \ln |\!\det\!\,{\Phi}(t)\,\!| \end{array} $$
(16)

exists and is finite and if there exists a normal basis of the n-dimensional state space such that

$$\begin{array}{@{}rcl@{}} \sum\limits_{i=1}^{n}\lambda_{i}=\lim_{t \rightarrow \infty} \ln |\! \det\,\!{\Phi}(t)\,\!|\,\!. \end{array} $$
(17)

If Φ(t) is regular, then according to a theorem by Oseldec [15], the asymptotic quantity defined in eq. (14) exists and is finite for any initial deviation y(0) belonging to the n-dimensional space.

The asymptotic quantity λ i given by eq. (14) is also known as a one-dimensional exponent. For p dimensions, the p-dimensional Lyapunov exponent λ is defined as

$$ \lambda^{p}\! =\! \lim_{t \rightarrow \infty} \left( \frac{1}{t}\right)\ln \left( \frac{\parallel\! y_{1}(t)\wedge y_{2}(t)\wedge \cdots\wedge y_{p}(t)\!\parallel} {\parallel\! y_{1}(0)\wedge y_{2}(0)\wedge {\cdots} \wedge y_{p}(0)\!\parallel}\right), $$
(18)

where ∧ is an exterior or vector cross product.

In the next section, we shall derive the expression for Lyapunov exponent, using both coordinate time and proper time.

2.1 Lyapunov exponent and radial effective potential

Now we compute second derivative of the square of the radial component of the four-velocity in terms of the Lyapunov exponent. Therefore, the Lagrangian of a test particle in the equatorial plane for any static spherically symmetric space-time can be written as

$$\begin{array}{@{}rcl@{}} \mathcal{L} = \frac{1}{2}\left[g_{tt}\,\dot{t}^{2}+g_{rr}\,\dot{r}^{2} +g_{\phi\phi}\,\dot{\phi}^{2}\right]. \end{array} $$
(19)

Now, we define the canonical momenta as

$$\begin{array}{@{}rcl@{}} p_{q}= \frac{\partial {\mathcal{L}}}{\partial\dot{q}}. \end{array} $$
(20)

Using this, the generalized momenta can be derived as

$$\begin{array}{@{}rcl@{}} p_{t}&=&g_{tt}\,\dot{t}=-E =\text{Const}. \end{array} $$
(21)
$$\begin{array}{@{}rcl@{}} p_{\phi}&=&g_{\phi\phi}\,\dot{\phi}=L=\text{Const}. \end{array} $$
(22)
$$\begin{array}{@{}rcl@{}} p_{r}&=&g_{rr}\, \dot{r} . \end{array} $$
(23)

Here \((\dot {t},\dot {r},\dot {\phi })\) denotes differentiation with respect to the proper time (τ). Again, from the Euler–Lagrange equations of motion

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}p_{q}}{\mathrm{d}\tau} &=& \frac{\partial{\mathcal{L}}}{\partial q}. \end{array} $$
(24)

Using this, we get the non-linear differential equation in two-dimensional phase-space with phase-space variables x i (t)=(p r ,r).

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}p_{r}}{\mathrm{d}\tau} = \frac{\partial {\mathcal{L}}}{\partial r} \quad\text{and}\quad \frac{\mathrm{d}r}{\mathrm{d}\tau} = \frac{p_{r}}{g_{rr}}. \end{array} $$
(25)

Now, linearizing the equation of motion about the circular orbits of constant r, we get the infinitesimal evolution matrix as

$$\begin{array}{@{}rcl@{}} M_{ij}=\left.\left( \begin{array}{cc} 0 & \displaystyle\frac{\mathrm{d}}{\mathrm{d}r}\left( \frac{\partial {\mathcal{L}}}{\partial r}\right)\\ \displaystyle\frac{1}{g_{rr}} & 0 \\ \end{array} \right)\right|_{r=r_{0}} . \end{array} $$
(26)

For circular orbits of constant r = r 0, the characteristic values of the matrix gives information about the stability of the orbit. The eigenvalues of this matrix are called principal Lyapunov exponent. Therefore, the eigenvalues of the evolution matrix along circular orbits can be written as

$$\begin{array}{@{}rcl@{}} \lambda^{2}= \frac{1}{g_{rr}} \frac{\mathrm{d}}{\mathrm{d}r}\left.\left( \frac{\partial {\mathcal{L}}}{\partial r}\right)\right|_{r=r_{0}}. \end{array} $$
(27)

Again, from Lagrange’s equation of motion

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}}{\mathrm{d}\tau}\left( \frac{\partial {\mathcal{L}}}{\partial \dot{r}}\right) -\frac{\partial {\mathcal{L}}}{\partial r}=0. \end{array} $$
(28)

Thus, the Lyapunov exponent (which is the inverse of the instability time-scale associated with the geodesic motions) in terms of the square of the radial velocity (\(\dot {r}^{2}\)) can be written as

$$\begin{array}{@{}rcl@{}} \frac{\partial {\mathcal{L}}}{\partial r}=\frac{1}{2g_{rr}} \frac{\mathrm{d}}{\mathrm{d}r}\left( \dot{r}g_{rr}\right)^{2}. \end{array} $$
(29)

Finally, the principal Lyapunov exponent can be rewritten as

$$\begin{array}{@{}rcl@{}} \lambda^{2}= \frac{1}{2} \frac{1}{g_{rr}} \frac{\mathrm{d}}{\mathrm{d}r}\left[\frac{1}{g_{rr}}\frac{\mathrm{d}}{\mathrm{d}r}\left( \dot{r}g_{rr}\right)^{2}\right]. \end{array} $$
(30)

Again for circular geodesics [16]

$$\begin{array}{@{}rcl@{}} \dot{r}^{2}=(\dot{r}^{2})^{\prime}=0, \end{array} $$
(31)

where prime denotes the derivative with respect to r. Thus, for proper-time Lyapunov exponent eq. (30) must be reduced to

$$\begin{array}{@{}rcl@{}} \lambda_{p} & =& \pm \sqrt{\frac{(\dot{r}^{2})^{\prime\prime}}{2}} \end{array} $$
(32)

and for coordinate-time Lyapunov exponent [2], eq. (30) is given by

$$\begin{array}{@{}rcl@{}} \lambda_{c} & =& \pm \sqrt{\frac{(\dot{r}^{2})^{\prime\prime}}{2\dot{t}^{2}}}. \end{array} $$
(33)

The Lyapunov exponent must be in ± pairs to conserve the volume of the phase-space. From now on we shall take only the positive Lyapunov exponent. The circular orbit is unstable when λ p or λ c is real, the circular orbit is stable when the λ p or λ c is imaginary and the circular orbit is marginally stable when λ p = 0 or λ c = 0.

(Note that Cardoso et al [2] have derived a coordinate-time Lyapunov exponent, i.e., \(\lambda _{c} = \sqrt {{V_{r}^{\prime \prime }}/{2\dot {t}^{2}}}\) with \(V_{r}=\dot {r}^{2}\)).

The above expression for λ is valid for any spherically symmetric BH space-times [17–19], i.e., (Schwarzschild, Reissner–Nordstrøm, Schwarzschild–de Sitter, Schwarzschild–anti-de Sitter, Reissner–Nordstrøm–de Sitter, Reissner–Nordstrøm–anti-de Sitter etc.). Also, it is valid for any axisymmetric space-time [20–22].

2.2 Critical exponent and radial effective potential

Following Pretorius and Khurana [23], we can define a critical exponent which is the ratio of Lyapunov time-scale or instability time-scale T λ and orbital time-scale T Ω can be written as

$$\begin{array}{@{}rcl@{}} \gamma = \frac{\Omega}{2\pi\lambda} =\frac{T_{\lambda}}{T_{\Omega}}=\frac{\text{Lyapunov~time-scale}}{\text{Orbital~ time-scale}} , \end{array} $$
(34)

where T λ =1/λ and T Ω=2π/Ω. This is important for black-hole merger in the ring down radiation. In terms of the second derivative of the square of the radial velocity (\(\dot {r}^{2}\)), critical exponent can be written as

$$\begin{array}{@{}rcl@{}} \gamma_{p} &=& \frac{1}{2\pi}\sqrt{\frac{2{\Omega}^{2}}{(\dot{r}^{2})^{\prime\prime}}},\quad \gamma_{c} = \frac{1}{2\pi}\sqrt{\frac{2\dot{\phi}^{2}}{(\dot{r}^{2})^{\prime\prime}}} . \end{array} $$
(35)

Here, Ω is the angular velocity.

We shall now calculate the equatorial circular geodesics for a spherically symmetric RN space-time.

3 Equatorial circular geodesics in spherically symmetric RN space-time

First, we shall consider a static, spherically symmetric, asymptotically flat solution of the coupled Einstein–Maxwell equations in general relativity. They are described by the RN space-time and the metric for such space-time is given by

$$\begin{array}{@{}rcl@{}} \mathrm{d}s^{2}&=&-\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)}\\ &&+r^{2}\left( \mathrm{d}\theta^{2}+\sin^{2}\theta \mathrm{d}\phi^{2}\right). \end{array} $$
(36)

To compute the geodesics in the equatorial plane for this space-time, we follow [16]. To determine the geodesic motion of a test particle in this plane we set \(\dot {\theta }=0\) and 𝜃=constant = π/2.

Therefore, the necessary Lagrangian for this motion is given by

$$\begin{array}{@{}rcl@{}} \mathcal{L} &=& \frac{1}{2}\left[\vphantom{\frac{\dot{r}^{2}} {\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)}}-\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)\,\dot{t}^{2}\right.\\ &&\left.\qquad+\frac{\dot{r}^{2}} {\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)}\, +r^{2}\,\dot{\phi}^{2}\right]. \end{array} $$
(37)

Using eq. (20), the generalized momenta can be derived as

$$\begin{array}{@{}rcl@{}} p_{t} &=&-\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)\!\dot{t}=-E =\text{Const}. \end{array} $$
(38)
$$\begin{array}{@{}rcl@{}}[-2pt] p_{\phi} &=&r^{2}\,\dot{\phi}=L=\text{Const}. \end{array} $$
(39)
$$\begin{array}{@{}rcl@{}}[-2pt] p_{r}&=&\frac{\dot{r}}{\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)}. \end{array} $$
(40)

Here, overdot denotes differentiation with respect to the proper time (τ). As the Lagrangian does not depend on both t and ϕ, p t and p ϕ are conserved quantities. Solving eqs (38) and (39) for \(\dot {t}\) and \(\dot {\phi }\), we find

$$\begin{array}{@{}rcl@{}} \dot{t}=\frac{E}{\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)} \quad \text{and} \quad \dot{\phi}=\frac{L}{r^{2}}, \end{array} $$
(41)

where E and L are the energy and angular momentum per unit rest mass of the test particle.

The normalization of the four-velocity (u μ) gives another integral equation for the geodesic motion:

$$\begin{array}{@{}rcl@{}} g_{\mu\nu}u^{\mu}u^{\nu} &=& \epsilon, \end{array} $$
(42)

or

$$\begin{array}{@{}rcl@{}} -E\dot{t}+L\dot{\phi}+\frac{\dot{r}^{2}}{\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right)}&=&\epsilon. \end{array} $$
(43)

Here 𝜖 = −1 for time-like geodesics, 𝜖 = 0 for light-like geodesics and 𝜖 = +1 for space-like geodesics. Substituting the value of \(\dot {t}\) and \(\dot {\phi }\) from eq. (41) in eq. (42), we obtain the radial equation for spherically symmetric RN space-time:

$$\begin{array}{@{}rcl@{}} \dot{r}^{2}=E^{2}-\left( \frac{L^{2}}{r^{2}}-\epsilon \right)\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right). \end{array} $$
(44)

3.1 Time-like case

Now, the radial equation of the test particle for time-like circular geodesics [17,18]:

$$\begin{array}{@{}rcl@{}} \dot{r}^{2}=E^{2}- \left( 1+\frac{L^{2}}{r^{2}}\right)\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right). \end{array} $$
(45)

To investigate the circular geodesic motion of the test particle in the Einstein–Maxwell gravitational field, for circular geodesics we must have constant r = r 0 and using the condition for circular orbit (31), we get the energy and angular momentum per unit mass of the test particle for time-like orbit as

$$\begin{array}{@{}rcl@{}} &&{E_{0}^{2}} =\frac{\left( {r_{0}^{2}}-2Mr_{0}+Q^{2}\right)^{2}}{{r_{0}^{2}}({r_{0}^{2}}-3Mr_{0}+2Q^{2})}\quad\\ &&\text{and}\\&&{L_{0}^{2}}= \frac{{r_{0}^{2}}\left( Mr_{0}-Q^{2}\right)}{{r_{0}^{2}}-3Mr_{0}+2Q^{2}}. \end{array} $$
(46)

Circular motion is possible when both the energy and the angular momentum are real and finite; therefore, we must have \({r_{0}^{2}}-3Mr_{0}+2Q^{2}>0\) and r 0>(Q 2/M), and the angular frequency at r = r 0 is

$$\begin{array}{@{}rcl@{}} {\Omega}_{0}=\frac{\dot{\phi}}{\dot{t}}=\frac{\sqrt{\left( Mr_{0}-Q^{2}\right)}}{{r_{0}^{2}}} . \end{array} $$
(47)

Hence, for non-extremal RN BH, the proper-time Lyapunov exponent and coordinate-time Lyapunov exponent are

$$\begin{array}{@{}rcl@{}} \lambda_{p}^{\text{RN}}&=& \sqrt{\frac{-(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4})}{{r_{0}^{4}} ({r_{0}^{2}}-3Mr_{0}+2Q^{2})}}. \end{array} $$
(48)
$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{RN}}&=& \sqrt{\frac{-(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4})}{{r_{0}^{6}}} } . \end{array} $$
(49)

Thus, the time-like circular geodesics of non-extremal RN BH is stable when \(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4}>0\) such that λ p or λ c is imaginary, the circular geodesics is unstable when \(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4}<0\), i.e., λ p or λ c is real and the time- like circular geodesics is marginally stable when \(M{r_{0}^{3}}-6M^{2}{r_{0}^{2}}+9MQ^{2}r_{0}-4Q^{4}=0\) such that λ p or λ c is equal to zero.

For completeness, we have also computed the ratio λ p /λ c for RN space-time which is given by

$$\begin{array}{@{}rcl@{}} \frac{\lambda_{p}}{\lambda_{c}} &=& \frac{r_{0}}{\sqrt{{r_{0}^{2}}-3Mr_{0}+2Q^{2}}}. \end{array} $$
(50)

For extremal RN BH, this ratio is

$$\begin{array}{@{}rcl@{}} \frac{\lambda_{p}}{\lambda_{c}} &=& \frac{r_{0}}{\sqrt{(r_{0}-M)(r_{0}-2M)}}. \end{array} $$
(51)

For Schwarzschild BH, this ratio has been reduced to

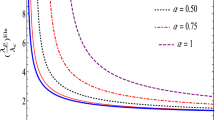
$$\begin{array}{@{}rcl@{}} \frac{\lambda_{p}}{\lambda_{c}} &=& \frac{\sqrt{r_{0}}}{\sqrt{r_{0}-3M}}. \end{array} $$
(52)

Now, we shall see the variation of the ratio of λ p and λ c graphically (see figure 1) for Schwarzschild BH (Q = 0) and RN BH.

Figure 1
figure 1

The variation of λ p /λ c with r 0/M for RN BH. We choose different values of (Q/M), i.e., (Q/M)=0,0.5,1.0,2.0,5.0. The range of validity for the charge to mass ratio Q/M is 0≤(Q/M)≤1. In the graph, red indicates the value of charge Q=0, green indicates Q=0.5M, yellow indicates Q=1.0M, blue indicates Q=2.0M and violet indicates Q=5.0M.

Full size image

It can be easily seen from figure 1 that, the ratio of λ p and λ c varies from orbit to orbit for different charge parameters.

Thus, the solution of the system \(\dot {r}^{2}=(\dot {r}^{2})^{\prime }=(\dot {r}^{2})^{\prime \prime }=0\) gives the radius of ISCO at r 0 = r ISCO for non-extremal RN BH which is given by

$$\begin{array}{@{}rcl@{}} \frac{r_{\text{ISCO}}}{M}&=& 2+Z^{{1}/{3}}+\frac{4-3\left( {Q}/{M}\right)^{2}}{Z^{{1}/{3}}}, \end{array} $$
(53)

where

$$\begin{array}{@{}rcl@{}} Z &=& 8-9\left( \frac{Q}{M}\right)^{2}+2\left( \frac{Q}{M}\right)^{4}\\ &&+\sqrt{5\left( \frac{Q}{M}\right)^{4}-9\left( \frac{Q}{M}\right)^{6}+4\left( \frac{Q}{M}\right)^{8}}. \end{array} $$
(54)

As Schwarzschild space-time is a special case of RN space-time which occurs in the limit Q=0, we find the radius of ISCO, r ISCO=6M.

Now the reciprocal of critical exponent for RN BH is given by

$$ \frac{1}{\gamma_{p}}\! =\! \frac{T_{\Omega}}{T_{\lambda}}\! =\! 2\pi \sqrt{\frac{-(M{r_{0}^{3}}\! -\! 6M^{2}{r_{0}^{2}}\! +\! 9MQ^{2}r_{0}-4Q^{4})}{(Mr_{0}-Q^{2}) ({r_{0}^{2}}-3Mr_{0}+2Q^{2})}}. $$
(55)

For any unstable circular orbit, T Ω>T λ , i.e., Lyapunov time-scale is shorter than the gravitational time-scale making the instability observationally relevant [4].

3.2 Special case

For Schwarzschild BH Q = 0, the Lyapunov exponent is

$$\begin{array}{@{}rcl@{}} \lambda_{p}^{\text{Sch}} &=& \sqrt{-\frac{M(r_{0}-6M)}{{r_{0}^{3}}(r_{0}-3M)}}. \end{array} $$
(56)
$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{Sch}} &=& \sqrt{-\frac{M(r_{0}-6M)}{{r_{0}^{4}}}}. \end{array} $$
(57)

The reciprocal of critical exponent for Schwarzschild BH is given by

$$\begin{array}{@{}rcl@{}} \frac{1}{\gamma_{p}} &=& \frac{T_{\Omega}}{T_{\lambda}}= 2\pi \sqrt{\frac{-(r_{0}-6M)}{(r_{0}-3M)}}. \end{array} $$
(58)

For any unstable circular orbit say for r 0 = 4M, γ becomes \({1}/{2\sqrt {2}\pi }\). Therefore, T λ <T Ω, i.e., Lyapunov time-scale is shorter than the gravitational time- scale [4].

3.3 Null case

As there is no proper time for photons, we have to only compute the coordinate-time Lyapunov exponent. To proceed this for null geodesics, the radial equation is given by

$$\begin{array}{@{}rcl@{}} \dot{r}^{2}=E^{2}- \frac{L^{2}}{r^{2}}\left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right). \end{array} $$
(59)

Therefore, the energy and angular momentum evaluated at r = r c for circular null geodesics are

$$\begin{array}{@{}rcl@{}} &&\frac{E_{c}}{L_{c}}=\pm \sqrt{\frac{{r_{c}^{2}}-2M r_{c}+Q^{2}}{{r_{c}^{4}}}}\\ &&\text{and}\\&&{r_{c}^{2}}-3Mr_{c}+2Q^{2}= 0. \end{array} $$
(60)

After introducing the impact parameter D c = L c /E c , the above equation is reduced to

$$\begin{array}{@{}rcl@{}} \frac{1}{D_{c}}=\frac{E_{c}}{L_{c}}=\sqrt{\frac{Mr_{c}-Q^{2}}{{r_{c}^{4}}}}={\Omega}_{c}= \frac{\dot{\phi}}{\dot{t}}, \end{array} $$
(61)

where Ω c is the angular frequency measured by an asymptotic observer at infinity.

Solving eq. (60), we obtain the radius of null circular orbits as [24]

$$\begin{array}{@{}rcl@{}} {r_{c}}_{\pm} &=& \frac{3M}{2}\left[1\pm\sqrt{1-\frac{8}{9}\left( \frac{Q^{2}}{M^{2}}\right)}\right]. \end{array} $$
(62)

Using (32), the Lyapunov exponent for the null circular geodesics is given by

$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{null}}|_{\text{RN}} &=& \sqrt{\frac{(Mr_{c}-Q^{2})(3Mr_{c}-4Q^{2})}{{r_{c}^{6}}}} . \end{array} $$
(63)

So, the circular geodesics r c = r c + and r c = r c − are unstable because \(\lambda _{c}^{\text {null}}|_{\text {RN}}\) is real.

For Schwarzschild BH Q=0, the Lyapunov exponent reads as

$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{null}}|_{\text{Sch}} &=& \frac{\sqrt{3}M}{{r_{c}^{2}}}. \end{array} $$
(64)

It can be easily checked that for r c =3M, \(\lambda _{c}^{\text {null}}|_{\text {Sch}}\) is real which means that Schwarzschild photon sphere is unstable.

4 Extremal RN space-time

4.1 Lyapunov exponent and equation of ISCO

For extremal RN BH, the radial equation of the test particle for time-like circular geodesics is

$$\begin{array}{@{}rcl@{}} \dot{r}^{2}=E^{2}- \left( 1+\frac{L^{2}}{r^{2}}\right)\left( 1-\frac{M}{r}\right)^{2}. \end{array} $$
(65)

Thus, the Lyapunov exponent becomes

$$\begin{array}{@{}rcl@{}} \lambda_{p}^{\text{ex}} &=& \frac{\sqrt{M(r_{0}-M)}}{{r_{0}^{2}}\sqrt{(r_{0}-2M)}}\sqrt{-\left( r_{0}-4M\right)}. \end{array} $$
(66)
$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{ex}}&=& (r_{0}-M)\sqrt{\frac{-M(r_{0}-4M)}{{r_{0}^{6}}} }. \end{array} $$
(67)

So, the time-like circular geodesics of the extremal RN BH is stable when r 0 > 4M such that λ p or λ c is imaginary, the circular geodesics is unstable when 2M < r 0 < 4M, i.e., λ p or λ c is real and the time-like circular geodesics is marginally stable when r 0 = 4M, such that λ p or λ c is equal to zero.

4.2 Lyapunov exponent and null circular geodesics

Analogously, using (32), the Lyapunov exponent for the null circular geodesics is

$$\begin{array}{@{}rcl@{}} \lambda_{c}^{\text{exn}} &=& \sqrt{\frac{M^{2}(r_{c}-M)(3r_{c}-4M)}{{r_{c}^{6}}}}. \end{array} $$
(68)

So the circular geodesics r c = 2M are unstable as \(\lambda _{c}^{\text {exn}}\) is real. Note that, for extremal BH, this result is valid for only single null geodesics, i.e., r 0≠r c . For r 0 = r c = M, the Lyapunov exponent becomes zero, i.e., \(\lambda _{p}^{\text {ex}}=\lambda _{c}^{\text {ex}}=\lambda _{c}^{\text {exn}}=0\).

Now we shall make a link between the Lyapunov exponent of the null circular geodesics and the QNM for RN BH in the eikonal limit.

5 Null circular geodesics and QNM for RN BH in the eikonal limit

This section is devoted to study the QNM frequencies for RN BH in the eikonal limit following the work by Cardoso et al [2]. It is well known that the unstable null circular geodesics is very useful to determine the characteristic modes of BH, which is so called QNMs [25–30]. To compute QNMs, we first consider the wave equation for a massless scalar field in the background of RN space-time which may be cast in the form

$$\begin{array}{@{}rcl@{}} \frac{\mathrm{d}^{2}X}{\mathrm{d}r_{\ast}^{2}}+Q_{0}X &=&0, \end{array} $$
(69)

where

$$Q_{0} = \omega^{2}-V_{s}(r) $$

and

$$ V_{s}(r)= \frac{\ell(\ell+1)} {r^{2}}+\frac{2(Mr-Q^{2})(r^{2}-2Mr+Q^{2})}{r^{6}}. $$
(70)

Here, ℓ denotes the spherical harmonic index and r ∗ is the tortoise coordinates, ranging from −∞ to + ∞.

In the eikonal limit, i.e., ℓ→∞, we get

$$\begin{array}{@{}rcl@{}} Q_{0} &\approx & \omega^{2}-\frac{\ell}{r^{2}} \left( 1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}\right). \end{array} $$
(71)

Using eq. (71), one may be able to find maximum value of Q 0 which occurs at r = r z :

$$\begin{array}{@{}rcl@{}} {r_{z}^{2}}-3Mr_{z}+2Q^{2} &=& 0. \end{array} $$
(72)

Again we know that for null circular geodesics, the radial equation is determined by eq. (60). Therefore, unstable circular orbits could be determined when \(\dot {r}^{2}=0\), leading to

$$\begin{array}{@{}rcl@{}} {r_{c}^{2}}-3Mr_{c}+2Q^{2} &=& 0. \end{array} $$
(73)

The maximum value of Q 0 and the location of the null circular geodesics are coincident at r z = r c . Therefore, from eq. (69), one may find the QNM conditions [31–33] as

$$ \frac{Q_{0}(r_{z})}{\sqrt{-2\frac{\mathrm{d}^{2}Q_{0}}{\mathrm{d} r_{\ast}^{2}}}}= i\left( n+{1}/{2}\right). $$
(74)

Equation (72) is evaluated at the extremum of Q 0, i.e., the point r 0 at which (dQ 0/dr ∗)=0. Therefore, in the large- ℓ limit eq. (74) gives

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}}&=&\ell \sqrt{\frac{Mr_{c}-Q^{2}}{{r_{c}^{4}}}} - i\left( n+\frac{1}{2}\right)\\ &&\times\sqrt{\frac{(Mr_{c}-Q^{2})(3Mr_{c}-4Q^{2})}{{r_{c}^{6}}}} . \end{array} $$
(75)

The significance of eq. (75) is that in the eikonal limit, the real and imaginary parts of the QNMs of RN BH are given by the frequency and instability time-scale of the unstable null circular geodesics. This is one of the key results of the paper.

It should be noted that for extremal RN BH, as \(\lambda _{c}^{\text {null}}=0\) for r 0 = r c = M, the value of ω QNM becomes

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}}=0 . \end{array} $$
(76)

For Schwarzschild BH, in the eikonal limit the frequency of QNM is given by

$$\begin{array}{@{}rcl@{}} \omega_{\text{QNM}} &=& \ell \sqrt{\frac{M}{{r_{c}^{3}}}} - i\!\left( n+\frac{1}{2}\right)\! \frac{\sqrt{3}M}{{r_{c}^{2}}}. \end{array} $$
(77)

Thus, by calculating the Lyapunov exponent, which is the reciprocal of the instability time-scale associated with the geodesic motion, we found that, in the eikonal limit, the frequency of QNMs of Schwarzschild BH could be determined by parameters of the null circular geodesics.

6 Discussion

In this article, we have used the Lyapunov exponent to give a full description of time-like circular geodesics and null circular geodesics in a spherically symmetric RN BH space-time. Then, we explicitly derived the proper-time Lyapunov exponent and coordinate-time Lyapunov exponent for RN BH. We found that the ratio of proper-time Lyapunov exponent and coordinate-time Lyapunov exponent for RN space-time is

$$({\lambda_{p}}/{\lambda_{c}}) ={r_{0}}/{\sqrt{{r_{0}^{2}}-3Mr_{0}+2Q^{2}}}. $$

For time-like circular geodesics and for Schwarzschild BH, the ratio is \(({\lambda _{p}}/{\lambda _{c}})={\sqrt {r_{0}}}/{\sqrt {r_{0}-3M}}\). This ratio also varies from orbit to orbit and may not contain any generic information. For example, for Schwarzschild BH at ISCO the ratio is \(({\lambda _{p}}/{\lambda _{c}})|_{r_{\text {ISCO}}=6M}\) \(=\sqrt {2}\) and at marginally bound circular orbit (MBCO), the ratio is calculated to be \(({\lambda _{p}}/{\lambda _{c}})|_{r_{\text {mb}}=4M}=2\). Similarly, for extremal RN BH, the ratio is at ISCO \(({\lambda _{p}}/{\lambda _{c}})|_{r_{\text {ISCO}}=4M}\! =\! ({2\sqrt {2}}/{\sqrt {3}})\) and at MBCO is \(({\lambda _{p}}/{\lambda _{c}})|_{r_{\text {mb}}=({3+\sqrt {5}})/{2}M}={(3+\sqrt {5})}/{2}\).

We further showed that the Lyapunov exponent can be used to determine the stability and instability of equatorial circular geodesics, both time-like and null case for RN BH space-time. Finally, we computed the QNM frequencies for RN BH in the eikonal limit. We found that in the eikonal limit, the real and imaginary parts of the QNMs of RN BH is given by the frequency and instability time-scale of the unstable null circular geodesics. For Schwarzschild BH, in the eikonal limit, the real part of the complex QNM frequencies are determined by the angular velocity of the null circular geodesics and imaginary part is related to the coordinate-time Lyapunov exponent of null circular geodesics.

Besides, the theory of Lyapunov exponent has important applications in the study of critical phenomena in BH binaries [5]. It also plays a crucial role for the physical understanding of ring-down radiation, interpretation of numerical simulations of BH merger and gravitational wave data analysis [23,34,35].