Evolution of entropy in different types of non-Markovian three-level systems: Single reservoir vs. two independent reservoirs

Abstract

We solve the Nakajima–Zwanzig (NZ) non-Markovian master equation to study the dynamics of different types of three-level atomic systems interacting with bosonic Lorentzian reservoirs at zero temperature. Von Neumann entropy (S) is used to show the evolution of the degree of entanglement of the subsystems. The results presented are also compared with some recently published reports.

1 Introduction

Schrödinger equation is used to describe the evolution of closed systems, while real physical systems interact with their environment and these interactions are the non-coherence source. This means that we cannot use Schrödinger equation to describe such real physical systems. Therefore, we need a new formulation to study open quantum systems [1,2]. Investigating the evolution of open quantum systems is not easy and some approximations are required to obtain equations of motion [3]. Open quantum systems are divided into two systems: Markovian and non-Markovian systems [4]. The most important difference between Markovian and non-Markovian systems lies in the memory effects (environment flow-back information to system) [5]. There are several approaches to describe the evolution of non-Markovian open quantum systems, for example, pseudomode approach [6,7] and time convolutionless projection operator (TCL) [8]. Dalton and Garraway [9,10] used pseudomode method to describe the evolution of the Ξ-type atom coupled to an electromagnetic field (single bosonic reservoir and two independent reservoirs). The two-level atomic systems have been studied using NZ approach in [11] and the three-level atomic systems in Ξ, Λ and V atomic types have been studied in [12–20].

In recent years, research on quantum entanglement has attracted a lot of attention, which has a lot of application in quantum information theory [21]. Interaction of atom–reservoir, will lead to entanglement between the atom and the reservoir. Time evolution of entropy of reservoir or the atom shows the time evolution of degree of entanglement between subsystems [22]. According to Araki and Leib’s [23] theorem, for any two-component systems (here atom (A) and reservoir (R)), the total entropy (S _AR) is limited by

$$ \left|S_{\mathrm{A}}(t)-S_{\mathrm{R}}(t)\right|\leq S_{\text{AR}}(t)\leq S_{\mathrm{A}}(t)+S_{\mathrm{R}}(t). $$

(1)

The motivation of our work is to compare different types of three-level atoms in single bosonic reservoir and two independent reservoirs and thus find the effect of reservoir on atoms.

In this paper, after a brief review of three different types of three-level atoms in §2, we introduce the Hamiltonians for three-level atoms in a single reservoir in §3.1. Then in §3.2, we solve the NZ equation to describe the evolution of different types of three-level atoms in a single reservoir. We write the entropy evolution of the atoms in single reservoirs to measure the degree of entanglement in §3.3 and then we compare entanglement in different types of atoms for two different states in §3.4. In §4, we do the above mentioned procedures for three-level atoms in two independent reservoirs and finally in §5, we compare the entropy of three-level atoms in single and two independent reservoirs.

2 Three-level atoms

2.1 Λ-type three-level atomic system

The Λ-type three-level atomic system is shown in figure 1a. The dipole transitions allowed in this system are |1〉 ⇔ |2〉, with atomic transition frequency ω ₁ and |0〉 ⇔ |2〉 with atomic transition frequency ω ₂. The dipole transition |2〉⇔|1〉 is forbidden. The couplings between the atom and the reservoir are respectively $g^{(1)}_{k}$ and $g^{(2)}_{k}$ for these transitions [12,24].

Figure 1

Three-level atoms: (a) Λ-type, (b) V-type and (c) Ξ-type.

2.2 V-type three-level atomic system

Figure 1b presents the V-type three-level atomic system. The dipole transitions allowed in this system are |0〉⇔|1〉, with atomic transition frequency ω ₁ and |0〉⇔|2〉 with atomic transition frequency ω ₂. The dipole transition |1〉⇔|2〉 is forbidden. The couplings between the atom and the reservoir are respectively $g^{(1)}_{k}$ and $g^{(2)}_{k}$ for these cases [14,24].

2.3 Ξ-type three-level atomic system

The Ξ-type three-level atomic system is shown in figure 1c. The dipole transitions allowed are |0〉 ⇔ |1〉, with atomic transition frequency ω ₁ and |1〉 ⇔ |2〉 with atomic transition frequency ω ₂ and dipole transition |0〉 ⇔ |2〉 is forbidden. The couplings between the atom and the reservoir are respectively $g^{(1)}_{k}$ and $g^{(2)}_{k}$ for these cases [9,24].

3 Three-level atoms in a single reservoir

3.1 Models

The Hamiltonian for a three-level atom in different types interacts with a single bosonic Lorentzian reservoir at zero temperature in rotating wave approximation (RWA) and can be written as follows [5,25]:

$$\begin{array}{@{}rcl@{}} H_{0{\Lambda}}&=& (\omega_{2}-\omega_{1}) \left| 1 \right>\left< 1 \right|+\omega_{2} \left| 2 \right>\left< 2 \right|+{\sum}_{k}\omega_{k}a^{\dagger}_{k}a_{k},\\\ H_{I{\Lambda}}&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} |1\rangle\left\langle {2} \right|)+\ g^{(2)}_{k} (a_{k}^{\dagger} |0\rangle\!\left\langle {2} \right|)+\text{h.c.}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} \ H_{0V}& =& \omega_{1} \left| 1 \right>\left< 1 \right|+\omega_{2} \left| 2 \right>\left< 2 \right|+{\sum}_{k}\omega_{k}a_{k}^{\dagger} a_{k},\\ \ H_{IV}&=& {\sum}_{k}\ g^{(1)}_{k} (a_{k}^{\dagger} |0\rangle\left\langle {1} \right|)+\ g^{(2)}_{k} (a_{k}^{\dagger} |0\rangle\!\left\langle {2} \right|)+\text{h.c.}, \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} \ H_{0{\Xi}}&=& \omega_{1} \left| 1 \right>\left< 1 \right|+(\omega_{1}+\omega_{2}) \left| 2 \right>\!\left< 2 \right|+{\sum}_{k}\omega_{k}a^{\dagger}_{k}a_{k},\\\ H_{I{\Xi}}&=& {\sum}_{k}\ g^{(1)}_{k} (a_{k}^{\dagger} |1\rangle\left< {2} \right|)+\ g^{(2)}_{k} (a_{k}^{\dagger} |0\rangle\!\left\langle {1} \right|)+\mathrm{h.c.}, \end{array} $$

(4)

where ω ₁, ω ₂ are defined in §2 and ω _k is the field frequency of the kth field mode. The constant g _k describes the strength of coupling between the atom and the reservoir. a _k and $a_{k}^{\dagger }$ are annihilation and creation operators respectively.

3.2 Dynamics of an atom in a single reservoir

First, we write Hamiltonians in the interaction picture and then we use the NZ master equation to get dynamics of each models. NZ master equation is:

$$ \frac{\mathrm{d}\rho_{{S}}(t)}{\mathrm{d}t}=-{{\int}_{0}^{t}}\mathrm{d}t^{\prime} TR_{\mathrm{R}}[H_{\mathrm{I}}(t),[H_{\mathrm{I}}(s),\rho_{{S}}(s)\otimes\rho_{\mathrm{R}}]]. $$

(5)

H _I(t) is Hamiltonian in the interaction picture. Temperature is zero and density matrix of the reservoir is ρ _R=|0〉〈0|.

Hamiltonians for three types of atoms in the interaction picture are

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}{\Lambda}}(t)&=& {\sum\limits}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \left| 1 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+ g^{(2)}_{k} (a_{k}^{\dagger} \left| 0 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{k})t}+ \text{h.c}., \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}V}(t)&=& {\sum\limits}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \left| 0 \right>\!\left< 1 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+ g^{(2)}_{k} (a_{k}^{\dagger} \left| 0 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{k})t}+\text{h.c.}, \end{array} $$

(7)

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}{\Xi}}(t)&=& {\sum\limits}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \left| 0 \right>\!\left< 1 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+ g^{(2)}_{k} (a_{k}^{\dagger} \left| 1 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{k})t}+\text{h.c.} \end{array} $$

(8)

We put the general density matrix ρ _S (t)

$$\begin{array}{@{}rcl@{}} \rho_{S}(t)=\left[\begin{array}{ccc} \rho_{{11}}(t)&\rho_{{12}}(t)&\rho_{{13}}(t) \\ \rho_{{21}}(t)&\rho_{{22}}(t)&\rho_{{23}}(t) \\ \rho_{{31}}(t)&\rho_{{32}}(t)&\rho_{{33}}(t)\end {array} \right], \end{array} $$

(9)

ineqs (6)–(8). The NZ master equation for these models becomes

$$\begin{array}{@{}rcl@{}} \dot{\rho_{S{\Lambda}}}(t)&=&{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t-t^{\prime}) \left( 2\rho_{S}(t^{\prime})|2\rangle\left\langle {2} \right|-|0\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|-|0\rangle\right.\\ &&\times\left.\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|-|1\rangle\left\langle {2}\right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|-|1\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|\right)\\ &&+{\int}_{0}^{t} \mathrm{d}t^{\prime} f^{*}(t-t^{\prime})\left( -|0\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|+2|2\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})-\-|1\rangle\right.\\ &&\times\left.\left\langle{2} \right|\rho_{S}(t^{\prime})|2\rangle\left\langle {0} \right|{\kern-1.5pt}-{\kern-1.5pt}|0\rangle{}\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|{\kern-1.5pt}-{\kern-1.5pt}|1\rangle{}\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|\right). \end{array} $$

(10)

The set of equations can be solved by employing the Laplace transform. The results are

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{11}(s)&=&\frac{\rho_{11}(0)}{s +2\tilde{f}^{*}(s )+2\tilde{f}(s )},\\ \tilde{\rho}_{12}(s )&=&\frac{\rho_{12}(0)}{s +2\tilde{f}^{*}(s )},\\ \tilde{\rho}_{13}(s )&=&\frac{\rho_{13}(0)}{s +2\tilde{f}^{*}(s )},\\ \end{array} $$

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{22}(s )&=&\frac{{\rho}_{22}(0)s +2{\rho}_{22}(0)\tilde{f}(s )+2{\rho}_{22}(0)\tilde{f^{*}}(s )+2\tilde{\rho}_{11}(0)\tilde{f^{*}}(s )}{(s +2\tilde{f(s)}+2\tilde{f^{*}}(s ))},\\ \tilde{\rho}_{23}(s )&=&\frac{{\rho}_{23}(0)s +2{\rho}_{23}(0)\tilde{f}(s )+2{\rho}_{23}(0)\tilde{f^{*}}(s )+2\tilde{\rho}_{11}(0)\tilde{f^{*}}(s )}{(s +2\tilde{f}(s )+2\tilde{f^{*}}(s ))},\\ \tilde{\rho}_{33}(s )&=&\frac{{\rho}_{33}(0)s +2{\rho}_{33}(0)\tilde{f}(s )+2{\rho}_{33}(0)\tilde{f^{*}}(s )+2\tilde{\rho}_{11}(0)\tilde{f^{*}}(s )}{(s +2\tilde{f}(s )+2\tilde{f^{*}}(s ))}, \end{array} $$

(11)

where $\tilde {\rho }_{ij}(s)$ (i,j=1,2,3), $\tilde {f}(s)$ and $\tilde {f^{*}}(s)$ are Laplace transforms of ρ _{i j} (t), f(t−t ^′) and f ^∗(t−t ^′) respectively. Finally, we need to use an inverse Laplace transform to find the solution. The above procedure can be done for V- and Ξ-type atoms also.

$$\begin{array}{@{}rcl@{}} \dot{\rho_{SV}}(t)&=&{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t-t^{\prime}) (\rho_{S}(t^{\prime})|1\rangle\!\left\langle {1} \right|-|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-|0\rangle\!\left\langle {1} \right|\rho_{S}|2\rangle\\ &&\times\left\langle {0} \right|-|0\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|1\rangle\left\langle {0} \right|+\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|+\rho_{S}|1\rangle\!\left\langle {2} \right|-|0\rangle\\ &&\times\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|-|0\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-\rho_{S}(t^{\prime})|2\rangle\!\left\langle {2} \right|)\\ &&+{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f^{*}(t-t^{\prime}) (|1\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})-|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-|0\rangle\\ &&\times \left\langle {2} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|+\rho_{S}(t^{\prime})|2\rangle\!\left\langle {2} \right|-|0\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|+\rho_{S}(t^{\prime})|1\rangle\\ &&\times\left\langle {2} \right|+\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|-|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|) \end{array} $$

(12)

and

$$\begin{array}{@{}rcl@{}} \dot{\rho_{S{\Xi}}}(t)&=&{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t-t^{\prime}) (-|1\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right| -|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0}\right|-|0\rangle\\ &&\times\left\langle {1} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|-|1\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|+\rho_{S}(t^{\prime})|1\rangle\!\left\langle {1}\right|+\rho_{S}(t^{\prime})|2\rangle\\ &&\times\left\langle {2} \right|)\mathrm{e}^{-i(\omega_{0}-\omega_{k})(t-t^{\prime} )}+{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f^{*}(t-t^{\prime}) (|1\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})-|0\rangle\\ &&\times\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-|1\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|2\rangle\\ &&\times\left\langle {1} \right|-|1\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|+|2\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})). \end{array} $$

(13)

Assuming three-level atoms are degenerate, it means ω ₁ = ω ₂≡ω ₀ and suppose $g_{k}^{(1)}=g_{k}^{(2)}\equiv g_{k}$, the correlation function becomes

$$ f(t-t^{\prime})={\sum\limits}_{k}\left|g_{k}\right|^{2}\mathrm{e}^{-i(\omega_{k}-\omega_{0})(t-t^{\prime})}. $$

(14)

In continuous field frequency, we replace ${\sum }_{k}\left |g_{k}\right |^{2}$ by $\int \!\mathrm {d}\omega J(\omega )\delta (\omega _{k}-\omega )$. Here J(ω) is Lorentzian spectral density which is defined as

$$ J(\omega)= \frac{1}{2\pi}\frac{\Omega\lambda^{2}}{(\lambda^{2}+(\omega-\omega_{0})^{2})} $$

(15)

and correlation function becomes

$$ f(t-t^{\prime})= \frac{1}{2}{\Omega}\lambda \mathrm{e}^{-\lambda t}, $$

(16)

where λ is the bandwidth of the reservoir and Ω is the coupling strength. The condition ${\Omega } > \frac { \lambda }{2}$ (${\Omega } < \frac { \lambda }{2}$) defines strong coupling (weak coupling) regime. We have used the initial state $|\psi (0)\rangle =(p|2\rangle +\sqrt {1-p^{2}}|1\rangle )\otimes |0\rangle$ for 0≤p≤1 and λ=0.01Ω in our calculations.

3.3 Degree of entanglement in a single reservoir

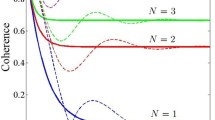
The reduced density matrix for atoms described in §3.2 has been calculated with initial state |ψ(0)>. Figure 2 demonstrates the evolution of entropy in a single reservoir with different values of parameter p. The entropy value for the Ξ-type atom is smaller than the entropy peak of Λ- and V-types for p>0.85. The peak of entropy in the Ξ-type is 0.5 (for p=0 and 1), while its entropy is minimum for p≈0.8. The entropy increases in time for a fixed value of the parameter p in all atom types. For a fixed time, the Λ-type atom finds its maximum value of entropy in p=1 and its minimum value in p=0, while for the V-type atom, entropy finds its minimum value at p=0 and 1 and its maximum value is located at p≈0.4. In [20], when the atom interacts with a single mode-field, the revival times in the Ξ-type atom is greater than those in the Λ- and V-type atoms. This means that the reservoir has greater correlation with the Λ- and V-type atoms in comparison with Ξ-type. But our simulation shows that for a k-mode reservoir in initial states |ψ(0)〉, V- and Ξ-type atoms at p>0.85 have less correlation with the reservoir while in some cases like p<0.85, Λ-type atom has lower correlation with the reservoir.

Figure 2

Evolution of entropy in a single reservoir. (a) Λ-type atom, (b) Ξ-type atom and (c) V-type atom.

3.4 Entropy evolution in three-level atoms with different initial states

Figure 3a demonstrates the evolution of entropy for initial state ψ ₁(0)=|2>. This figure shows that Λ atom has the greatest entropy. One may assume that the Λ atom has greatest entropy in all the cases. But it is not true and the situation is very sensitive to the initial state. Figure 3b presents the entropy evolution for initial state $|\psi _{2}{(0)}\rangle =\frac {1}{\sqrt {2}}({2}+|1\rangle )$. This figure clearly shows that the V-type atom has the greatest value of entropy in comparison with other types of atoms, while the Λ atom has the lowest entropy.

Figure 3

Evolution of entropy in a single reservoir for different states. (a) ψ ₁(0)=|2〉, (b) $|\psi _{2}{(0)}\rangle =\frac {1}{\sqrt {2}}(|2\rangle +|1\rangle )$.

4 Three-level atoms in two independent reservoirs

4.1 Models

The Hamiltonian of three-level atoms in different types interacting with two independent bosonic Lorentzian reservoirs at zero temperature in the RWA can be written as follows [5]:

$$\begin{array}{@{}rcl@{}} H_{0{\Lambda}}&=& (\omega_{2}-\omega_{1}) \left| 1 \right>\!\left< 1 \right|+\omega_{2} \left| 2 \right>\!\left< 2 \right|+{\sum}_{k}\omega_{k}a^{\dagger}_{k}a_{k}+{\sum}_{l}\omega_{l}b^{\dagger}_{l}b_{l},\\ H_{\mathrm{I}{\Lambda}}&=& {\sum}_{k}g^{(1)}_{k} (a_{k}^{\dagger} |1\rangle\!\left\langle{2} \right|)+{\sum}_{l} g^{(2)}_{l} (b_{l}^{\dagger} |0\rangle\!\left\langle {2} \right|)+\mathrm{h.c.}, \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}} H_{0V}& =& \omega_{1}\! \left| 1 \right>\!\left< 1 \right|+\omega_{2} \left| 2 \right>\!\left< 2 \right|+{\sum}_{k}\omega_{k}a^{\dagger}_{k}a_{k}+{\sum}_{l}\omega_{l}b^{\dagger}_{l}b_{l},\\ H_{\mathrm{I}V}&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} |0\rangle\!\left\langle {1} \right|)+{\sum}_{l} g^{(2)}_{l} (b_{l}^{\dagger} |0\rangle\!\left\langle {2}\right|)+\mathrm{h.c.}, \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}} H_{0{\Xi}}&=& \omega_{1} \!\left| 1 \right>\!\left< 1 \right|+(\omega_{1}+\omega_{2}) \left| 2 \right>\!\left< 2 \right|+{\sum}_{k}\omega_{k}a^{\dagger}_{k}a_{k}+{\sum}_{l}\omega_{l}b^{\dagger}_{l}b_{l},\\ H_{\mathrm{I}{\Xi}}&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} |1\rangle\!\left\langle {2} \right|)+{\sum}_{l} g^{(2)}_{l} (b_{l}^{\dagger} |0\rangle\!\left\langle {1} \right|)+\mathrm{h.c.}, \end{array} $$

(19)

where ω ₁, ω ₂, ω _k and g _k are defined in §2, while a _k (b _l ) and $a_{k}^{\dagger }~(b_{l}^{\dagger })$ are annihilation and creation operators respectively.

4.2 Dynamics of atom in two independent reservoirs

Like §3.2, we get Hamiltonian in the interaction picture. Then, one can use eq. (1) to find the dynamics of each model. The interaction part of the Hamiltonian for different types of atoms are:

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}{\Lambda}}(t)&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \!\left| 1 \right>{}\left< 2 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+{\sum}_{l} g^{(2)}_{l}(b_{l}^{\dagger} \!\left| 0 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{k})t}+\text{h.c.}, \end{array} $$

(20)

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}V}(t)&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \!\left| 0 \right>\!\left< 1 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+{\sum}_{l} g^{(2)}_{l} (b_{l}^{\dagger} \!\left| 0 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{k})t}+\text{h.c.}, \end{array} $$

(21)

$$\begin{array}{@{}rcl@{}} H_{\mathrm{I}{\Xi}}(t)&=& {\sum}_{k} g^{(1)}_{k} (a_{k}^{\dagger} \!\left| 0 \right>\!\left< 1 \right|)\mathrm{e}^{-i(\omega_{1}-\omega_{k})t}\\ &&+{\sum}_{l} g^{(2)}_{l} (b_{l}^{\dagger} \!\left| 1 \right>\!\left< 2 \right|)\mathrm{e}^{-i(\omega_{2}-\omega_{l})t}+\text{h.c.} \end{array} $$

(22)

Therefore we have

$$\begin{array}{@{}rcl@{}} \dot{\rho}_{S{\Lambda}}(t)&=& {{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t-t^{\prime}) (\left| 2 \right>\!\left< 2 \right|\rho_{S}(t^{\prime})-2\left| 0 \right>\!\left< 2 \right|\rho_{S}(t^{\prime})\left| 2 \right>\!\left< 0 \right|\\&&+\rho_{S}(t^{\prime})\left| 2 \right>\!\left< 2 \right|)+{\int}_{0}^{t^{\prime}} \mathrm{d}s f^{*}(t-t^{\prime}) (|2\rangle\!\left\langle {2} \right|\rho_{S}(t^{\prime})-2|1\rangle\\ &&\times\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {1} \right|+\rho_{S}(t^{\prime})|2\rangle\!\left\langle {2} \right|). \end{array} $$

(23)

For Λ-type atom, Laplace transform of density matrix becomes

$$\begin{array}{@{}rcl@{}} \tilde{\rho}_{11}(s)&=&\frac{\rho_{11}(0)}{s+2\tilde{f}^{*}(s)+2\tilde{f}(s)},\\ \tilde{\rho}_{12}(s)&=&\frac{\rho_{12}(0)}{s+2\tilde{f}^{*}(s)},\\ \tilde{\rho}_{13}(s)&=&\frac{\rho_{13}(0)}{s+2\tilde{f}^{*}(s)},\\ \tilde{\rho}_{22}(s)&=&\frac{\rho_{22}(0)+\tilde{f}(s)\tilde{\rho}_{11}(s)+\tilde{f}^{*}(s)\tilde{\rho}_{11}(s)}{s},\\ \tilde{\rho}_{23}(s)&=&\frac{\rho_{23}(0)}{s},\\ \tilde{\rho}_{33}(s)&=&\frac{\rho_{33}(0)+\tilde{f}(s)\tilde{\rho}_{11}(s)+\tilde{f}^{*}(s)\tilde{\rho}_{11}(s)}{s}, \end{array} $$

(24)

where $\tilde {\rho }_{ij}(s)$ (i,j=1,2,3), $\tilde {f}(s)$ and $\tilde {f^{*}}(s)$ are Laplace transforms of ρ _{i j} (t), f(t−t ^′) and f ^∗(t−t ^′) respectively. Finally, we need to use an inverse Laplace transform to find the solution. The above procedure can be done for V- and Ξ-type atoms also.

$$\begin{array}{@{}rcl@{}} \dot\rho_{SV}(t)&=&{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t{\kern-1.3pt}-{\kern-1.3pt}t^{\prime}) (\left| 1 \right>\!\left< 1 \right|\rho_{S}(t^{\prime}){\kern-1.3pt}-{\kern-1.3pt}2\left| 0 \right>\!\left< 1 \right|\rho_{S}(t^{\prime})\left| 1 \right>\!\left< 0 \right|+\rho_{S}(t^{\prime})\left| 1 \right>\!\left< 1 \right|\\ &&+{{\int}_{0}^{t}} \mathrm{d}s f^{*}(t-t^{\prime}) (|1\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})-|0\rangle\!\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle\!\left\langle {0} \right|-|0\rangle\\ &&\times\left\langle {2} \right|\rho_{S}(t^{\prime})|2\rangle\!\left\langle {0} \right|+\rho_{S}(t^{\prime})|2\rangle\!\left\langle {2} \right|) \end{array} $$

(25)

and

$$\begin{array}{@{}rcl@{}} \dot{\rho_{S{\Xi}}}(t){}&=&{}{{\int}_{0}^{t}} \mathrm{d}t^{\prime} f(t{\kern-1.5pt}-{\kern-1.5pt}t^{\prime}) (|1\rangle{}\left\langle {1} \right|\rho_{S}(t^{\prime}){\kern-1.5pt}-{\kern-1.5pt}|0\rangle{}\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle{}\left\langle {0} \right| {\kern-1.5pt}-{\kern-1.5pt}|0\rangle{}\left\langle {1} \right|\rho_{S}(t^{\prime})|1\rangle{}\left\langle {0} \right|\\ &&+\rho_{S}(t^{\prime})\left| 1 \right>\!\left< 1 \right|)+{}{{\int}_{0}^{t}} \mathrm{d}s f^{*}(t{}-{}t^{\prime}) (\left| 1 \right>{}\!\left< 1 \right|\rho_{S}(t^{\prime}){}-{}\left| 2 \right>{}\left< 1 \right|\rho_{S}(t^{\prime})\left| 1 \right>{}\left< 2 \right|\\ &&+\rho_{S}(t^{\prime})\left| 2 \right>\!\left< 2 \right|-\left| 1 \right>\!\left< 2 \right|\rho_{S}(t^{\prime})\left| 2 \right>\!\left< 1 \right|). \end{array} $$

(26)

Considering ω ₁ = ω ₂ ≡ ω ₀, $g_{k}^{(1)}=g_{k}^{(2)}\equiv g_{k}$ and $g_{l}^{(1)}=g_{l}^{(2)}\equiv g_{l}$, we have

$$\begin{array}{@{}rcl@{}} f(t-t^{\prime})&=&{\sum\limits}_{k}\left|g_{k}\right|^{2}\mathrm{e}^{-i(\omega_{k}-\omega_{0})(t-t^{\prime})}\\ &=&{\sum}_{l}\left|g_{l}\right|^{2}\mathrm{e}^{-i(\omega_{l}-\omega_{0})(t-t^{\prime})}=\frac{1}{2}{\Omega}\lambda \mathrm{e}^{-\lambda t}. \end{array} $$

(27)

We have taken initial state as $\left | \psi (0) \right >=(p\left | 2 \right >+\sqrt {1-p^{2}}\left | 1 \right >)\otimes \left | 0 \right >$ for 0≤p≤1 and λ=0.01Ω in our numerical calculations.

4.3 Entanglement in two independent reservoirs

Reduced density matrix for different types of atoms interacting with two independent reservoirs with initial state |2ψ(0)〉 has been calculated numerically. Figure 4 shows the evolution of entropy for different types of atoms in two independent reservoirs with a different parameter p. This figure clearly shows that the maximum value of entropy for Ξ- and V-type atoms is smaller than the entropy peak of the Λ-type atom when p>0.85. For a given value of time, the Ξ-type atom has a minimum value for p≈0.6, while the Λ-type atom has maximum value of entropy when p = 1 and minimum value when p=0. In [20], in a two-mode field, V and Ξ configurations have the maximum values of revival time and therefore they have lower correlation with reservoirs, while in our simulation, in two independent reservoirs for p>0.85 it is true but for p<0.85, Λ atom has lower interaction with the medium.

Figure 4

Evolution of entanglement in a single reservoir. (a) Λ-type atom, (b) Ξ-type atom and (c) V-type atom.

4.4 Behaviour of entropy evolution in different types of atoms with respect to different initial states

Figure 5a demonstrates evolution of the entropy calculated with initial state ψ ₁(0)=|2〉. This figure shows that Λ atom has the greatest entropy. Figure 5b presents the entropy evolution for initial state $|\psi _{2}{(0)}\rangle =\frac {1}{\sqrt {2}}(|2\rangle +|1\rangle )$. One can find that the V-type atom has the greatest value of entropy with the new initial state |ψ ₂(0)〉.

Figure 5

Evolution of entropy for different initial states. (a) |ψ ₁(0)〉=|2〉, (b) $|\psi _{2}(0)\rangle =\frac {1}{\sqrt {2}}(|1\rangle +|2\rangle )$.

5 Comparison of the entropy of three-level atoms in a single and two independent reservoirs

Figure 6 presents evolution of entropy in a single reservoir and also two reservoirs for different types of atoms with initial state $|\psi _{2}(0)\rangle =\frac {1}{\sqrt {2}}(|1\rangle +|2\rangle )$. This figure already shows that the entropy of the system in two reservoirs are greater than that in one reservoir for Λ and Ξ, while V-type finds its greater entropy in a single reservoir.

Figure 6

Evolution of entropy in a single and two independent reservoirs. (a) Λ-type atom, (b) V-type atom and (c) Ξ-type atom.

6 Conclusions and remarks

We have shown that entropy (S) of the system monotonically increases in time for any fixed value of the parameter p in all kinds of atoms. Our calculations show that a Λ-type atom has the greatest degree of entropy when compared with Ξ- and V-type atoms when p>0.85, while Λ-type atom has the smallest degree of entropy when compared with Ξ- and V-type atoms when p<0.85. We chose |ψ ₁(0)〉=|2〉 as the initial state and showed that Λ-type atom has the greatest entropy with this initial state. Also, it is shown that the V-type atom has the greatest entropy with initial state $|\psi _{2}(0)\rangle =\frac {1}{\sqrt {2}}(|1\rangle +|2\rangle )$. It is possible that an atom in a single reservoir has greater entropy in comparison with its entropy in two independent reservoirs.

Our investigation has been done with the same correlation function f(t−t ^′) because we assume ω ₁ = ω ₂ ≡ ω ₀ and $g_{k}^{(1)}=g_{k}^{(2)}\equiv g_{k}$. It is interesting to study the evolution of the system using different correlation functions. On the other hand, the effect of phase damping, phase and amplitude damping or other medium perturbations has not been considered here. These situations can be studied in further works.