Introduction

The reduction in the cost and rapid development of next-generation sequencing and related statistical computing tools have materially assisted quantitative-trait locus (QTL) mapping in various species (Glazner and Thompson 2015). To improve livestock production and reproduction, genome scanning to detect QTLs associated with economically important traits are important activity in animal breeding and genetics (Sham and Purcell 2014). This task often requires two pivotal approaches: linkage analysis and association mapping (Ott et al. 2011; Sha et al. 2011). Within a family that has pedigrees of related individuals and a phenotype, linkage is the inclination towards cosegregation of a marker allele with QTLs as they are closed in the position on the same chromosome (Won et al. 2009). Linkage analysis in animals establishes a base on the construction of a genetic linkage map and subsequent molecular biology tests using the map, as evidenced in phenotypes of individuals in known pedigree relationships (Murphy et al. 2010). QTL mapping using linkages was performed in almost all livestock species for an enormous scope of traits. An alternative to association mapping would be to use linkage disequilibrium (LD) to map QTLs (Zuryn et al. 2010). LD, which refers to the nonrandom association of combinations of variants between alleles at different loci, is better termed as ‘haplotype structure’ or ‘allelic association’ (Arelin et al. 2013). The patterns of LD can be transferred from generation to generation and can be spread in a population. They are locally associated and are used to construct the LD blocks. Using this specific correlation form, the sampled genetic markers can partially capture information of the unsampled single-nucleotide polymorphisms (SNPs). Exploiting these phenomena, LD can be used for a genomewide association study (GWAS), which is commonly based on historic LD that links phenotypes to genotypes. Numerous efforts were devoted to the study of GWAS based on LD. The combination of association and linkage information should generally provide more powerful and robust methods to identify the causes of mutations (Korte and Farlow 2013).

However, little attention was paid to the framework of GWASs with only linkage information. In this study, we proposed the development of a novel multiple regression method for GWAS using only linkage information in half-sib families. The new method adopted a sliding window approach to identify QTLs; thus, F-statistics can be obtained from regressing the phenotype on the window of markers (Haley and Knott 1992; Hodge 1993). We expect that this method may build a new theoretical foundation for GWAS. In the following sections, we first provide a theoretical basis for the modelling framework of GWAS, which exploits only linkage information. In this study, we establish the statistical basis of the model using a mixed linear model with details on hypothesis testing and parameter estimation. In addition, we further evaluate the model performance using extensive simulation studies. Finally, we assess the impacts of various factors on the model, followed by further discussion about their features.

Materials and methods

Mapping QTL using LD versus linkage

LD mapping is based on population-level associations between QTLs and markers. The reason for this association phenomenon is that small segments of a chromosome from the same common ancestor descended to the offspring in the current population. These chromosome segments, without intervening recombination events, might carry identical haplotypes or alleles. If there is a QTL within a certain segment, it might also harbour identical QTL alleles. Meanwhile, adjacent stretches of ancestral chromosomes are decreased in size of the initial generation, as continuous recombination occurs between every probable locus on the chromosome. Over many generations, segments on a chromosome in the population change from LD to linkage equilibrium (LE). A number of QTL mapping strategies, especially in GWASs, exploit only LD information.

Linkage appears when chromosomal regions remain joined together rather than being fragmented by recombination during meiosis. In a population, recombination events sequentially cause linkage decay over successive generations. LD does not require linkage and does not particularly represent disequilibrium on a chromosome, and the distinction between LD and linkage analysis is moderately artificial. The difference between these two metrics is as follows. Linkage analysis only uses the LD that occurs within families, which can extend for tens of cM and is reduced by recombination after only a few generations. However, LD mapping requires a marker to associate with a QTL in LD across the entire population. This association as a property of the population should have endured for many generations; therefore, the markers and QTLs should be closely linked.

mMLM

The following mMLM for GWAS was used to estimate the effects of SNP windows, extending from Henderson’s method as follows:

$$\begin{aligned} y=\mu +X_{js} \beta +X_{-js} u+e, \end{aligned}$$

where y is the phenotype of animals; \(\mu \) denotes the mean; \(\beta \) represents the unknown fixed effects, i.e. the effects of SNP windows consisting of j rows of SNPs; and \(u\sim \mathrm{N}\left( {0,G\sigma _a^2 } \right) \) is the unknown random polygenic effects of size p, the number of SNPs excluding j rows, where G is the genomic relationship matrix and \(\sigma ^{2}_{a}\) is the genetic variance. \(X_{js}\) and \(X-_{js}\) are the incidence matrices for \(\beta \) and u, respectively. \(e\sim \mathrm{N}\left( {0,\sigma _e^2 } \right) \) represents residual effects, where \(\sigma ^{2}_{e}\) represents the residual variance. To test the association between SNP windows and phenotype, the null hypothesis (\(H_{\mathrm{o}})\) is \(\beta = 0\), and the alternative hypothesis is \(\beta \ne 0\). Then, the above mMLM can be described as the mixed model equation:

$$\begin{aligned}&\left[ {{\begin{array}{ll} {{X}'_{js} R^{-1}X_{js} }&{}\quad {{X}'_{js} R^{-1}X_{-js} } \\ {{X}'_{-js} R^{-1}X_{js} }&{}\quad {{X}'_{-js} R^{-1}X_{js} +\frac{\sigma _{{e}}^2 }{\sigma _a^\mathrm{2} }G^{\mathrm{-}1}} \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\hat{{\beta }}} \\ {\hat{{u}}} \\ \end{array} }} \right] \\&\quad =\left[ {{\begin{array}{l} {{X}'_{js} R^{-1}y} \\ {{X}'_{-js} R^{-1}y} \\ \end{array} }} \right] . \end{aligned}$$

An F test can be performed to test the null hypothesis using multiple regression analysis. The F-value can be calculated as:

$$\begin{aligned} F=\frac{{\hat{{\beta }}}'\left( {X_{js} V^{-1}X_{js} } \right) ^{-1}\hat{{\beta }}}{\hat{{\sigma }}_e^2 \left( {n-1} \right) }, \end{aligned}$$

where \(V=\left( {X_{-js} G{X}'_{-js} +R} \right) \), n is the number of phenotypes of the animal, and the degrees of freedom of the F test are j and \(n-j\). The genomewide significance P value threshold is \(\frac{0.05}{\hbox {No windows}}=2.5\times 10^{\mathrm{-}4}\).

PRESS statistic for the genomic relationship matrix (G)

To estimate SNP effects using the mixed model, the genomic relationship (G) matrix can be calculated as follows:

$$\begin{aligned} G=TT^{\prime }/\left( {\sum {2p_i q_i } } \right) , \end{aligned}$$

where T is the \(q\times m\) matrix, and q indicates the number of animals, whereas m denotes the number of SNPs; the frequencies of the two alleles are denoted as p and q, respectively. The subscript i is the \(i\hbox {th}\) marker.

Successively eliminating each SNP window, the calculation of the G matrix must be repeated \(\hbox {L}=\frac{\hbox {No. total markers}}{\hbox {SNPs in a window}}\) times, which is computationally expensive. Therefore, we used the PRESS (prediction sum of squares) statistic:

$$\begin{aligned} \left( {X_{-js} X_{-js} } \right) ^{-1}= & {} \left( {XX^{\prime }} \right) ^{-1}+\left( {XX^{\prime }} \right) ^{-1}X_{js} \\&\left( {I-X_{js}^{\prime } \left( {XX^{\prime }} \right) ^{-1}X_{js} } \right) ^{-1}X_{js}^{\prime } \left( {XX^{\prime }} \right) ^{-1}, \end{aligned}$$

where I is an identity matrix (Chen et al. 2004).

Simulation study

Comparisons between GWASs using single marker regression and multiple regression were made for different scenarios. The simulated genome consisted of 10 chromosomes, and each was 1 Morgan. Each chromosome consisted of 2000 SNP markers that were almost evenly spaced and 10 randomly distributed QTLs, giving 20,000 markers and 19,900 potential QTLs in total. The gamma distribution (1.66, 0.4) was used to draw the allele substitution effect (\(\upalpha \)) of the major QTLs, and the effect of the polygene was one hundredth of \(\upalpha \) (Meuwissen et al. 2001). All markers were biallelic with starting allele frequencies of 0.5 and a mutation rate of \(2.5 \times 10^{-8}\) per generation. Haldane’s mapping function was used to model recombination between adjacent loci on a chromosome; this recombination relies only on the distance between loci. Other parameters, including allele frequencies and locus positions, were held constant. To study the performance of the model, two groups of scenarios were simulated. In the first group, the simulation started with 100 unrelated individuals as a base population, followed by only one discrete historical generation, which was 20 times the population size and was randomly mated to create linkages without LD. In the base and following historical generation, one male mated randomly with 20 females, and each female produced two progenies. For the second scenario, the simulation started with 2000 unrelated individuals as a base population to create populations without linkages and LD between the loci. True breeding values and genotypes were simulated for all individuals, and phenotypic records of a continuous trait were assigned by \(y=\mu +\upalpha +e\), where e is the residual variance and \(e\sim \mathrm{N}\left( {0,\upsigma _e^2 } \right) \). To study the effect of heritability and the number of QTLs on the statistical power of multiple regression using only linkage information, two other groups of scenarios were simulated. In the first group, four levels of heritability were simulated: 0.05, 0.1, 0.3 and 0.5. In another group, we simulated different numbers of QTLs: 10, 20, 50 and 100. For two scenarios, 10 simulation replications using different random seeds were performed to investigate the effect of linkage analysis using multiple regression. The software Xsim (http://qtl.rocks/XSim/index.html) was used to simulate all the data.

Fig. 1
figure 1

\(r^{2}\) values for increasing chromosome segment length.

Full size image
Fig. 2
figure 2

Distribution of genomic relationships.

Full size image

Results and discussion

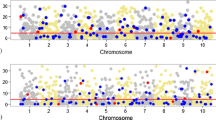
In total, figures 1 and 2 show the extent of LD of the simulated data. Because only one historical generation is included, nearly all marker pairs at different points in the genome have very low \(r^{2}\) values, close to zero. Additionally, the genomic relationships are the same as the \(r^{2}\) values with most coefficients towards zero. And the t-value is almost evenly distributed throughout the chromosome without any clear peaks (figure 3).

Effect of heritability

Figures 4 and 5 (left panel) shows the power of multiple regression analysis under different heritabilities. By increasing the heritability from 0.05 to 0.5, the power of the method increased as expected, from 0.27 to 0.48.

Fig. 3
figure 3

T-statistic of linkage analysis on chromosome 1.

Full size image
Fig. 4
figure 4

Mean sum of squares (mSS) of linkage analysis on chromosome 1.

Full size image
Fig. 5
figure 5

Power of multiple regression for different heritabilities and the number of QTLs in the simulated datasets. The number of QTLs in the left graph is 20, while the heritability changed from 0.05 to 0.5. The heritability in the right graph is 0.3, while the number of QTLs increased from 10 to 100.

Full size image

Effect of QTL number

As shown in figure 5 (right panel), the power of the method is sensitive to the number of QTLs. With an increase in this number, the power declined consistently, despite fluctuations in the middle of the line, from 0.48 to 0.29. Many QTL mapping approaches exploit LD or linkages. Classical GWAS utilizes population-level associations between QTL and markers (De La Vega et al. 2006). In this study, we developed a new pedigree-free linkage analysis using multiple regression analysis. Although we use only linkages without LD information in our simulation data, our approach relies on flanking the SNP region surrounding each QTL to identify the mutation that is affecting the gene.

Fig. 6
figure 6

Linkage and LD. The mutation is represented by red stars. Chromosomal stretches originating from the founder of all mutant loci are shown in red. Segments that are physically adjacent, tend to remain linked to the founder’s mutation, even as recombination events restrict the extent of the loci of linkages over time.

Full size image

Linkage analysis was one of the traditional means for mapping Mendelian traits and is highly successful in identifying locations on chromosomes with large genetic effects (Kitsios and Zintzaras 2009). Meanwhile, association mapping has also successfully revolutionized methods to discover common SNPs associated with many traits. Although association and linkage mapping share the same underlying principle, recombination, in practice, these methods have various features for identifying trait loci, and each method has particular advantages and disadvantages (figure 6, Nsengimana and Barrett 2008). For linkage analysis, the recombination phenomenon can be directly inferred or observed from the pedigree within several generations. However, association analysis utilizes inferences of nonrecombination over many historical generations within short genomic intervals encompassing mutation loci (Laird and Lange 2008).

Moreover, the essential distinction between the two methods frequently results in the identification of different types of genetic variants that cause phenotypic differences. These distinctions might partially provide an explanation for the repeated poor coherence of identifying meaningful mutations between the genetic linkages and GWASs (Fardo et al. 2011; Smith 2012). In fact, some studies appear to confuse the two concepts. However, the phenomena of association and linkage are not actually the same. The distinction between the two terms is not only an abstract measurement of one, but also might show the underlying differences of the genetic architecture of quantitative traits to be studied. Therefore, in the condition of linkage, but no LD, family association tests certainly could not note linkage (Fulker et al. 1999).

Although many QTL mapping strategies mainly employ LD, we combined multiple regression and only linkage information to capture QTL signals. In this paper, a simulation study was conducted to investigate the statistical power of the method in terms of different heritabilities and QTL numbers. We demonstrated that the power decreased with the increase in the number of QTLs, from 0.48 to 0.29, and the power of the multiple mixed linear model (mMLM) was sensitive to heritability. However, the cause of this phenomenon remains unknown.