1 Introduction

A number of lakes in India have been facing water scarcity problems in recent times. Watershed management practice, such as the construction of silt detention structures to arrest erosion in the catchment, is one of the main reasons for this water scarcity. This is because, these silt detention structures also act as water-storing structures, thereby abstracting water in the catchment and not allowing it to flow to the water bodies, as in the case of Sukhna lake in Chandigarh, India. As most of these water-retaining structures are very shallow water bodies, quite often shallow sheets of water, evaporation losses from them could be very significant. As such, it is important to understand the impact of evaporation losses from such structures on the run-off from the catchment, which in turn determines the inflow regime of the lakes. Knowledge of evaporation losses from such shallow water bodies is, therefore, very important.

There is no single reliable direct method for measuring evaporation from open-water surfaces. Although a number of models are available for indirectly estimating evaporation, most of these models are intended for use in climates similar to where they were developed and have a wide range of data requirement (Winter et al. 1995). Some of these models, such as the energy balance models, have extensive data requirements which cannot always be met. For a developing country like India, where data availability may be a limiting factor, there is a need for simple models with less data requirements, for most practical purposes. Many such models, e.g., the mass transfer-based models, have been developed. However, most of these models were developed for temperate climates. These models need to be evaluated and calibrated before using them for tropical or subtropical climates.

Pan method is one of such popular simple methods of evaporation estimation, particularly in India. It is popular mainly because of the fact that it is simple to use, requires only pan coefficients and it also has an element of observed evaporation. The method is used not only for the estimation of evaporation from open-water surfaces (Fu et al. 2004; Alvarez et al. 2007) but also for reference crop evapotranspiration estimation (Irmak et al. 2002). Different types of pans are available. The USWB Class A pan is used most widely throughout the world for the measurement of evaporation (Linsley et al. 1975). India Meteorological Department has also adopted USWB Class ‘A’ pan for the measurement of evaporation in different parts of the country.

1.1 Pan coefficients

The thermodynamics of a pan is different from that of water bodies like lakes, ponds and reservoirs. Sensible heat transfer from the sides and bottom of the pan is appreciable, while for lakes and reservoirs, the heat through the bottom is almost zero (Linsley et al. 1975). Consequently, a coefficient has to be applied to the pan data for converting it into the water surface evaporation. This coefficient, called the pan coefficient (\(K_{\mathrm{p}}\)), is the ratio between the observed pan evaporation and the evaporation from the water surface. Multiplying pan evaporation data with the pan coefficient directly gives open-water surface evaporation.

A number of pan coefficients models have been suggested for estimating evaporation (Snyder 1992; Pereira et al. 1995; Allen et al. 1998; Wahed and Snyder 2008; Tabari et al. 2011). A number of studies have also been reported comparing the performance of these models (Irmak et al. 2002; Gundekar et al. 2008; Rahimikhoob 2009; Sabziparvar et al. 2010; Trajkovic and Kolakovic 2010; Mohammadi et al. 2012; Pradhan et al. 2013; Heydari and Heydari 2014). Pradhan et al. (2013), e.g., five empirical methods of pan coefficients for Delhi were evaluated and the \(K_{\mathrm{p}}\) values observed ranged between 0.72 and 0.93, being lower in the summer months and higher in the rainy and winter months. Out of the five methods, the Snyder method was found to be the best for estimating \(K_{\mathrm{p}}\). However, it may be noted that the pan coefficients developed in many of these studies were for the estimation of reference evapotranspiration and not for open-water surface evaporation. The reference evapotranspiration, obtained from these models, therefore, needs to be multiplied by a coefficient for water to get open-water surface evaporation (Allen et al. 1998; Jensen 2010).

There are only a few reported studies which have obtained pan coefficients directly for open-water evaporation. A value of 0.69 was obtained for the annual pan coefficient in the lake Hefner studies (Harbeck 1954). Based on the reported data of 18 studies, Linacre (1994) observed that the annual pan coefficient values for US Class-A pan are scattered around 0.77. Turbak and Muttair (1994) estimated pan coefficients by the Penman method using different forms of vapour pressure deficit estimation methods for two lakes in Saudi Arabia. Annual pan coefficient was found to vary in the range of 0.53–0.59. Abtew (2001) obtained a value of 0.76 of the annual lake coefficient for lake Okeechobee, USA. Fu et al. (2004) observed that annual pan coefficients for different years, obtained from mean values of different months, varied from 0.60 to 1.07 for the Naninshu lake in China. It was observed that the pan coefficients varied from year to year but their variations between the maximum and minimum values were between 0.06 and 0.6. For irrigation water reservoirs in south-eastern Spain, the annual values have been observed to vary between 0.76 and 0.86 by Alvarez et al. (2007).

Commonly, annual pan coefficients are applied even for monthly and seasonal time scales or, monthly and seasonal coefficients derived in some other investigations are used (Nordenson 1963). There is also a tendency to use a uniform coefficient of 0.7 for all time scales, particularly in design problems. Most of the State Irrigation Departments in India also use a uniform value of 0.7. However, pan coefficients are observed to be different for different regions and are also different for different time scales (Nordenson 1963; Fu et al. 2004). Winter (1981) observed that monthly pan coefficients differ from the commonly used coefficient of 0.7 by more than 100%. Linacre (1994) reported that the seasonal values of pan coefficients vary between 0.62 and 0.80. The coefficient is dependent on the local climate and physical conditions, and should be determined locally from a standard method such as the Penman–Monteith or FAO-24 Radiation method (Chiew et al. 1995). Chiew et al. (1995) have suggested seasonal pan coefficients for 16 locations in Australia. Abtew (2001) proposed monthly values of \(K_{\mathrm{p}}\) for lake Okeechobee, located in subtropical South Florida. The values ranged from 0.64 for January to 0.91 for June. Alvarez et al. (2007) derived pan coefficients for irrigation water reservoirs in south-eastern Spain. Monthly \(K_{\mathrm{p}}\) values were observed to vary significantly throughout the year. The variation was found to be \(0.5< K_{\mathrm{p}} < 1.5\) for deep waters and \(0.8< K_{\mathrm{p}} < 1.2\) for shallow waters. McJannet et al. (2013) determined pan coefficients for Class-A pan for Logan’s dam in south-east Australia. The monthly pan coefficients were observed to vary in the range of 0.67 in July to 1.17 in April.

Thus, pan coefficients are found to be different for different regions and are also different for different time scales and have to be calibrated from other accurate methods. Although pan coefficients vary with local climates, they are not available for all regions. A review indicates that most of the studies related to pan coefficients for open-water surface evaporation are for arid and humid regions in temperate climates. There are only a few studies on humid tropical monsoon climates, such as those in India. Pan coefficients, for estimating open-water surface evaporation, are not reported for most climatic regions of India and generally a coefficient of 0.7 is being used by most field organisations in India for all time scales, although it is meant only for the annual time scale. It is, therefore, required to develop region-specific pan coefficients for humid tropical monsoon climate regions in India, as a number of lakes exist in this region, so that the coefficients can be used for estimating open-water surface evaporation from these water bodies. This is particularly important because, sophisticated evaporation models such as the energy balance models, which are considered as very precise, cannot be used for such water bodies for the want of detailed energy balance data whereas a simple technique such as the pan model is desirable for some practical applications or routine field purposes, in view of the easily available pan evaporation data in most parts of the country.

Fig. 1
figure 1

Location map of the study area.

Full size image

1.2 Objectives

Keeping in view the need to develop a region-specific simple methodology, such as the pan model, for estimating open-water surface evaporation for practical applications and routine field purposes, the present study has been undertaken with an objective to develop pan coefficients for Sukhna lake in the union territory of Chandigarh which is a humid tropical monsoon climatic region in India so that the coefficients can be used directly for estimating evaporation from other shallow open-water surfaces in the region using pan data, so that complex calculations to estimate evaporation can be avoided. Another objective of the present investigations is to evaluate the pan coefficients developed for different climatic regions, for their suitability in estimating evaporation from shallow open-water surfaces of the tropical monsoon climate of the Chandigarh region in India.

2 Methods and materials

2.1 Study area

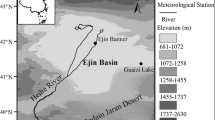
The present study has been carried out for the Chandigarh region in India which lies between \(30{^{\circ }}44'\hbox {N}\) and \(30{^{\circ }}48'\hbox {N}\) and between \(76{^{\circ }}48'\hbox {E}\) and \(76{^{\circ }}54'\hbox {E}\) at an elevation of 350 m above mean sea level. Sukhna lake, an important tourist spot in north India and a hot spot of biodiversity, has been facing water scarcity in recent years. The inflow to the lake from the catchment has been reported to be declining in recent years due to the large number of silt detention structures constructed in the catchment (Khobragade et al. 2013). About 150 such structures have been mapped for the \(42.14\ \hbox {km}^{2}\) catchment area (Semwal et al. 2013). Most of these structures are small and shallow water bodies with an average storage capacity of 0.98 ha m, average water spread area of 0.52 ha and an average depth of less 1.9 m (Grewal 2009).

The climate of the study area is humid tropical with an average annual rainfall of about 1121.6 mm (Agnihotri et al. 2006), of which about 80% occurs in the three monsoon months of July–September (Grewal 2009). There are four distinct seasons. Summer is from about mid-March to mid-June which is followed by the monsoon season that lasts up to mid-September. Mid-September to mid-November is the post-monsoon autumn/transition season. The winter season is from mid-November to mid-March. Average annual rainfall of the study area is 1121.6 mm of which about 80% rainfall occurs in the three monsoon months of July–September (Agnihotri et al. 2006). May and June are the hottest months of the year with temperatures soaring to about \(40{^{\circ }}\hbox {C}\) and above. January is the coldest month with minimum temperatures generally going down to about \(3{^{\circ }}\hbox {C}\) and sometimes even below. Winds are generally light. Figure 1 shows the location map of the study area.

Review brings out that the pan coefficient varies with the time scale such as by month, season and year, and depends on the local climate (Nordenson 1963; Fu et al. 2004). So it has to be determined locally from a standard method (Chiew et al. 1995). This section describes the methodology used for determination of pan coefficients for the study area.

2.2 Determination of open-water surface evaporation

As mentioned earlier, the development of pan coefficients needs data on evaporation from water bodies, obtained from standard methods of open-water surface evaporation. The energy balance is considered to be the most accurate of all the available methods of estimating open-water surface evaporation and is often used as a reference against which other methods are compared (Jensen et al. 1990; Sturrock et al. 1992; Rosenberry et al. 2007; Duan and Bastiaanssen 2017). However, extensive data and instrumentation requirements, associated costs and the requirement of precision in data, often limit their use. The Bowen ratio energy budget (BREB) method is considered to be the most robust and most accurate method for determining evaporation (Harbeck et al. 1958; Gunaji 1968; Sturrock et al. 1992; Lenters et al. 2005; Rosenberry et al. 2007). It is particularly useful in view of the elimination of some of the energy balance components such as heat flux and advected energy. Therefore, for the purpose of the present study, the BREB method has been used for estimating open-water surface evaporation. The BREB equation for estimating open-water evaporation (Ikebughi et al. 1988; Stannard and Rosebarry 1991; Ali et al. 2008) is

$$\begin{aligned} E_{\mathrm{BR}} =\frac{R_{\mathrm{n}} -(G+Q_{\mathrm{b}} +Q_{\mathrm{a}})}{\lambda (1 + \beta )}, \end{aligned}$$
(1)

where \(E_{\mathrm{BR}}\) is the open-water evaporation (\(\hbox {mm d}^{-1}\)), \(R_{\mathrm{n}}\) is net radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), G is the heat gained or lost by the upper layer of the water surface (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), \(Q_{\mathrm{b}}\) is the heat flux into the bottom of the water body (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), \(Q_{\mathrm{a}}\) is the energy advection into the water body (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), \(\lambda \) is the latent heat of evaporation of water (\(2.45\ \hbox {MJ kg}^{-1}\)) and \(\beta \) is the Bowen ratio (dimensionless).

\(Q_{\mathrm{b}}\) and \(Q_{\mathrm{a}}\) often are very small and are commonly ignored (Rosenberry et al. 2007). The reduced form of equation (1), obtained by neglecting \(Q_{\mathrm{b}}\) and \(Q_{\mathrm{a}}\), has been used by many researchers (Simon and Mero 1985; Assouline and Mahrer 1993) and the variation was found to be less than 7% for the annual evaporation (Ali et al. 2008). The reduced form of the BREB equation is

$$\begin{aligned} E_{\mathrm{BR}} =\frac{R_{\mathrm{n}} -G}{\lambda (1 + \beta )}. \end{aligned}$$
(2)

Equation (2) has been used in the present study for estimating open-water surface evaporation.

2.2.1 Parameters estimation for the BREB model

Net radiation (\(R_{\mathrm{n}}\)) has been calculated as the difference between the incoming net shortwave radiation (\(R_{\mathrm{ns}}\)) and outgoing long wave radiation (\(R_{\mathrm{nl}}\)) as per Allen et al. (1998) is

$$\begin{aligned} R_{\mathrm{n}} =R_{\mathrm{ns}} - R_{\mathrm{nl}}, \end{aligned}$$
(3)

where \(R_{\mathrm{n}}\) is the net radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), \(R_{\mathrm{ns}}\) is the net shortwave radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)) and \(R_{\mathrm{nl}}\) is the net long wave radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)).

\(R_{\mathrm{ns}}\) has been computed as

$$\begin{aligned} R_{\mathrm{ns}} = (1 - \alpha )R_{\mathrm{s}}, \end{aligned}$$
(4)

where \(R_{\mathrm{s}}\) is the measured or estimated incoming solar radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)) and \(\alpha \) is the albedo or reflection coefficient for the water surface (dimensionless).

The value of \(\alpha \) for the water surface varies between 0.05 and 0.1 (Shuttleworth 1993) and generally a value of 0.05 is assumed. However, \(\alpha \) is a function of solar radiation. In the present study, \(\alpha \) has been calculated as a function of solar radiation according to the equation developed by Koberg (1964) (see Dingman 1994) as

$$\begin{aligned} \alpha =0.127 \times \exp (-0.00108 \times R_{\mathrm{s}}), \end{aligned}$$
(5)

where \(\alpha \) is the albedo (reflection coefficient) and \(R_{\mathrm{s}}\) is the incoming solar radiation (\(\hbox {Cal cm}^{-2}\ \hbox {d}^{-1}\)).

The value of \(R_{\mathrm{s}}\) has been calculated as per Allen et al. (1998) as

$$\begin{aligned} R_{\mathrm{s}} = \left( a_{\mathrm{s}} + b_{\mathrm{s}} \frac{n}{N}\right) R_{\mathrm{a}} , \end{aligned}$$
(6)

where \(a_{\mathrm{s}}\) is the regression constant, expressing the fraction of extra-terrestrial radiation reaching the Earth on overcast days (\(n = 0\)), \(b_{\mathrm{s}}\) is the fraction of extra-terrestrial radiation reaching the Earth surface on clear days, n is the actual duration of sunshine (hours) and \(N=(24/\pi )\omega _{\mathrm{s}}\), the maximum possible duration of sunshine or daylight hours (hours). The value of \(a_{\mathrm{s}}\) and \(b_{\mathrm{s}}\) has been taken as 0.25 and 0.5, respectively, as suggested by Allen et al. (1998), as locally obtained values are not available.

The extra-terrestrial radiation \(R_{\mathrm{a}}\) has been calculated as

$$\begin{aligned} R_{\mathrm{a}}= & {} \left( \frac{24 \times 60}{\pi }\right) G_{\mathrm{sc}} d_{\mathrm{r}} (\omega _{\mathrm{s}} \sin (\phi )\sin (\delta )\nonumber \\&+\cos (\phi )\cos (\delta )\sin \ (\omega _{\mathrm{s}})), \end{aligned}$$
(7)

where \(G_{\mathrm{sc}} = \hbox {solar constant} = 0.0820 \,(\hbox {MJ m}^{-2} \hbox {min}^{-1})\); \(d_{\mathrm{r}} = 1+0.033\cos (\frac{2\pi }{365}J)\), inverse relative distance between the Earth and Sun; \(\omega _{\mathrm{s}} = \hbox {arccos}(-\tan (\phi ) \tan (\delta ))\), sunset hour angle in radian; \({\varPhi } =\) latitude in radian and estimated to be 0.537; \(\delta = 0.409\ \hbox {sin}(\frac{2\pi }{365}J-1.39)\), solar decimation in radian; \(J = \hbox {Julian day}\) (the number of days in the year between 1 (1st January) and 365 or 366 (31st December).

The net long-wave radiation (\(R_{\mathrm{nl}}\)) has been calculated as per Allen et al. (1998) as

$$\begin{aligned} R_{\mathrm{nl}}= & {} \sigma \times \left( \frac{T_{\mathrm{max},\mathrm{k}}^{4} +T_{\mathrm{min},\mathrm{k}}^{4}}{2}\right) \nonumber \\&\times \,\, (0.34 -0.14\ \sqrt{e_{\mathrm{a}}}) \times \left( 1.35 \times \frac{R_{\mathrm{s}}}{R_{\mathrm{so}}}-0.35\right) ,\nonumber \\ \end{aligned}$$
(8)

where \(R_{\mathrm{nl}}\) is the net long-wave radiation (\(\hbox {MJ} \hbox {m}^{-2} \,\hbox {d}^{-1}\)), \(\sigma \) is the Stefan–Boltzmann constant (\(=4.903*10^{-9}\) \(\hbox {MJK}^{-4}\ \hbox {m}^{-2}\ \hbox {d}^{-1})\), \(T_{\mathrm{max, k}}\) is the maximum absolute temperature during the 24-hr period (\(={^{\circ }}\hbox {C} + 273.16\)), \(T_{\mathrm{min,k}}\) is the minimum temperature during the 24-hr period (\(={^{\circ }}\hbox {C} + 273.16\)), \(e_{\mathrm{a}}\) is the actual vapour pressure (kPa), \(R_{\mathrm{s}}\) is the solar radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)), \(R_{\mathrm{so}}\) is the clear sky radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)) and \(R_{\mathrm{s}}/R_{\mathrm{so}}\) is the relative shortwave radiation (limited to \({\le }1.0\)).

The clear sky radiation \(R_{\mathrm{so}}\) has been calculated as per Allen et al. (1998):

$$\begin{aligned} R_{{\mathrm{so}}} =(0.75 +2 \times 10\ ^{-5} \times z)R_{\mathrm{a}}, \end{aligned}$$
(9)

where z is the station elevation above sea level (m) and \(R_{\mathrm{a}}\) is the extra-terrestrial radiation (\(\hbox {MJ m}^{-2}\ \hbox {d}^{-1}\)).

The daily meteorological data for the period July 2010–October 2014 has been used in the study. The data contained one leap year (2012) while the remaining were non-leap years. Calculation of various factors like \(d_{\mathrm{r}}\), \(\delta \), \(\omega _{\mathrm{s}}\), N, \(R_{\mathrm{a}}\) and \(R_{\mathrm{so}}\) were done separately for leap year and non-leap years and the data were used accordingly for the calculation of evaporation for different years.

The heat gained or lost by the upper layer of the water surface (G) has been calculated as per Finch and Hall (2001) as

$$\begin{aligned} G= \rho cz(T_{\mathrm{w},j} -T_{{\mathrm{w}}, j-1}), \end{aligned}$$
(10)

where \(\rho \) is the \(\hbox {density of water} = 1000\ (\hbox {kg m}^{-3})\), c is the specific \(\hbox {heat of water} {\,=\,} 0.0042 (\hbox {MJ kg}^{-1} {^{\circ }}\hbox {C}^{-1})\), z is the depth of the water (mean depth 3.3 m), \(T_{\mathrm{w},j}\) is the water temperature on day j and \(T_{\mathrm{w}, j-1}\) is the water temperature on day \(j-1\).

de Bruin (1982) showed that the water temperature on day j, \(T_{\mathrm{w},j}\), could be calculated as

$$\begin{aligned} T_{\mathrm{w},j} = T_{\mathrm{e}} +(T_{\mathrm{w}, j-1} - T_{\mathrm{e}})\hbox {e}^{t/\tau }, \end{aligned}$$
(11)

where \(T_{\mathrm{e}}\) is the equilibrium temperature, t is the model time step in days and \(\tau \) is the time constant.

The equilibrium temperature (\(T_{\mathrm{e}}\)) has been calculated as per Finch and Hall (2001) as

$$\begin{aligned} T_{\mathrm{e}} = T_{\mathrm{n}} + \frac{R_{\mathrm{n}}}{4\sigma (T_{\mathrm{n}} + 273.13)^{3} + \lambda f (u)(\varDelta +\gamma )},\nonumber \\ \end{aligned}$$
(12)

where \(T_{\mathrm{n}}\) is the wet bulb temperature (\({^{\circ }}\hbox {C}\)) and \(\varDelta \) is the slope of the temperature–saturation water vapour curve at the wet bulb temperature (\(\hbox {kPa}\ {^{\circ }}\hbox {C}^{-1}\)). The wind function, \(\lambda f\)(u) as per Sweers (1976) is

$$\begin{aligned} \lambda f(u)=0.864\ (4.4 + 1.82\ u_{\mathrm{z}}), \end{aligned}$$
(13)

where \(u_{\mathrm{z}}\) is the wind speed.

The time constant (\(\tau \)) has been calculated as per Finch and Hall (2001) as

$$\begin{aligned} \tau = T_{\mathrm{n}} + \frac{\rho cz}{4\ \sigma (T_{\mathrm{n}} + 273.13)^{3} +\lambda f(u)(\varDelta + \gamma )}. \end{aligned}$$
(14)

The Bowen ratio (\(\beta \)) is the ratio of sensible to latent heat. It has been calculated as per Rosenberry et al. (2007) as

$$\begin{aligned} C_{\mathrm{B}} P\,\frac{T_{0} - T_{\mathrm{a}}}{e_{\mathrm{o}} -e_{\mathrm{a}}}, \end{aligned}$$
(15)

where \(C_{\mathrm{B}}\) is the empirical constant determined by Bowen (1926) to be 0.61 (\({^{\circ }}\hbox {C}^{-1})\), P is the standard pressure at a specific altitude (kPa) (for the altitude of the study area, P is 97.18 kPa), \(T_{\mathrm{a}}\) is the air temperature (\({^{\circ }}\hbox {C}\) unless indicated otherwise), \(e_{\mathrm{o}}\) is the saturation vapour pressure at the water-surface temperature (Pa) and \(e_{\mathrm{a}}\) is the atmospheric vapour pressure (Pa). This formulation of the Bowen ratio ignores any covariance between wind speed and vapour pressure or temperature differences, which might cause additional errors in BREB calculations (Rosenberry et al. 2007).

2.3 Determination of pan coefficients

A pan model for Class A pan can be described as

$$\begin{aligned} E_{\mathrm{L}} = K_{\mathrm{p}} \times E_{\mathrm{pan}}, \end{aligned}$$
(16)

where \(E_{\mathrm{L}}\) is the open-water surface evaporation (\(\hbox {mm d}^{-1}\)), \(E_{\mathrm{pan}}\) is Class A pan evaporation (\(\hbox {mm d}^{-1}\)) and \(K_{\mathrm{p}}\) is the pan coefficient (non-dimensional).

Thus, the pan model can be considered as one parameter linear model with \(K_{\mathrm{p}}\) as the parameter to be determined. The parameter can be determined by minimising the sum of the square of error function as per the least squares optimisation technique.

The error function is given as

$$\begin{aligned} \hbox {Error}= E_{\mathrm{L}i} - E_{\mathrm{pan}i}, \end{aligned}$$
(17)

where \(E_{\mathrm{L}i}\) is the open-water surface evaporation for the \(i\hbox {th}\) term (\(\hbox {mm d}^{-1}\)) and \(E_{\mathrm{pan}i}\) is Class A pan evaporation for the \(i\hbox {th}\) term (\(\hbox {mm d}^{-1}\)). Then, the objective function is to minimise the sum of the squares of error. Let Z be the objective function such that

$$\begin{aligned} Z= \sum _{i=1}^n (E_{{\mathrm{L}}i} - K_{\mathrm{p}} \times E_{\mathrm{pan}i})^{2}. \end{aligned}$$
(18)

Then, \(K_{\mathrm{p}}\) can be estimated by minimising the objective function Z, i.e., by taking

$$\begin{aligned} \frac{\hbox {d}Z}{\hbox {d}K_{\mathrm{p}}}=0. \end{aligned}$$
(19)

Substituting Z from equation (18) in equation (19) we get

$$\begin{aligned}&\frac{\hbox {d}\left( \sum _{i=1}^n (E_{\mathrm{L}i} - K_{\mathrm{p}} \times E_{\mathrm{pan}i})^{2}\right) }{\hbox {d}K_{\mathrm{p}}}=0 \end{aligned}$$
(20)
$$\begin{aligned}&\quad =2 \times \sum _{i=1}^{n} (E_{\mathrm{L}i} - K_{\mathrm{p}} \times E_{\mathrm{pan}i}) (-E_{\mathrm{pan}i})=0 \end{aligned}$$
(21)
$$\begin{aligned}&\quad =\sum _{i=1}^{n}(E_{\mathrm{L}i} - K_{\mathrm{p}} \times E_{\mathrm{pan}i}) (-E_{\mathrm{pan}i})=0 \end{aligned}$$
(22)
$$\begin{aligned}&\quad =\sum _{i=1}^{n} (-E_{\mathrm{L}i} \times E_{\mathrm{pan}i} +K_{\mathrm{p}} \times E_{\mathrm{pan}i})^{2} =0.\qquad \quad \end{aligned}$$
(23)

Simplifying equation (23) gives

$$\begin{aligned} K_{\mathrm{p}} =\frac{\sum _{i=1}^{n} E_{\mathrm{L}i} \times E_{\mathrm{pan}i}}{\sum _{i=1}^{n} E^{2}_{\mathrm{pan}i}}. \end{aligned}$$
(24)

Using equation (24) above for \(K_{\mathrm{p}}\), pan coefficients for different time scales have been obtained. Pan coefficients were determined for annual, monthly and seasonal time scales.

Table 1 Various pan coefficient models.
Full size table
Table 2 Statistical parameters used to evaluate various evaporation models.
Full size table

2.4 Data used

For estimating open-water evaporation using BREB, equation (2), and pan coefficients using equation (24), various meteorological data such as air temperature, water temperature, wet bulb temperature, maximum relative humidity, minimum relative humidity, wind velocity, sunshine hours, pan evaporation, etc. are required. The data were collected from the Central Soil Conservation Research and Training Institute, Chandigarh, for the period of 52 months duration from July 2010 to October 2014. The meteorological observatory is located at a distance of 2 km from the Sukhna lake in Chandigarh. As the pan data available is for the mesh covered pan, a correction factor of 1.144 has been applied to the pan data covered with the mesh, to get the open pan evaporation data as suggested by WMO (1966). Applying this correction factor, open pan evaporation values were obtained and with this data, pan coefficients for open pan were determined.

To obtain the water temperature data for the study area, water temperature was measured for Sukhna lake in the study area on a daily basis for the period, March 2013–September 2014. To generate the water temperature data for the remaining study period, a linear relationship was developed between water temperature and air temperature as per Duan and Bastiaanssen (2017). The average slope and intercept of the developed relationship (\(T_{\mathrm{o}} =a \times T_{\mathrm{a}} + b\) expressed in \({^{\circ }}\hbox {C}\)) are 0.93 and 1.47, respectively, with an \(R^{2}\) value of 0.90. Out of the 52 months data, 40-month daily data were used for determining the pan coefficients \(K_{\mathrm{p}}\), while 1-year data were used for verification. The data of the year 2013 (1 January 2013–31 December 2013) were randomly selected for verification. Annual pan coefficient was obtained as a single value of pan coefficient, using the complete daily calibration data set. This single daily value can be applied to the daily data of pan evaporation to get the open-water evaporation value. For determining monthly and seasonal pan coefficients, data of only the concerned months or seasons of the calibration data set were considered. Thus, e.g., for determining the pan coefficients for the month of January, a daily data of pan and evaporation belonging to only January, from the calibration data set, was used. Similarly, for determining the seasonal values of pan coefficients, four seasons namely, winter (16th November–15th March), summer (16th March–15th June), monsoon (16th June–15th September) and post-monsoon (16th September–15th November) were considered. All daily values falling in respective seasons were considered for determining the pan coefficient for that season.

2.5 Comparison with other methods

Pan coefficients have also been estimated using various other popular models and their performance has been compared with the pan coefficients developed in the present study. The various models used for comparison are described in table 1. As these models provide daily pan coefficients, to obtain the monthly coefficients, the average of all daily pan coefficients was obtained for a particular month to obtain an average pan coefficient for that month. The seasonal pan coefficients were also obtained in the same manner. The performance of the various models was evaluated using various statistical parameters. Three statistical parameters were used for the purpose (table 2), besides carrying out the error analysis.

3 Results and discussion

The pan coefficients obtained for the study area using the optimisation technique are presented in table 3. A value of 0.92 was obtained as the optimised pan coefficient for the annual time scale. However, a single annual value is only indicative of the average pan coefficient for the daily time scale. As can be seen from table 3, the values of pan coefficients vary significantly both by month and season. For the values by month, the variation is in the range of 0.72–1.40. For seasonal values, the variation is in the range of 0.81–1.16 for pan coefficients. It is also observed that except for the months of April, May and June, pan evaporation is generally lower than the open-water surface evaporation, giving pan coefficients of more than 1.

Table 3 Pan coefficients for the study area.
Full size table
Fig. 2
figure 2

Performance of developed pan coefficients to estimate the open-water surface evaporation for the study area: (a) annual, (b) monthly, and (c) seasonal.

Full size image
Fig. 3
figure 3

Errors of the open-water surface evaporation estimation for developed pan coefficients.

Full size image
Table 4 Pan coefficients obtained using various pan coefficient models.
Full size table
Fig. 4
figure 4

Performance of the various pan models: (a) Cuenca model, (b) Snyder model, (c) modified Snyder model, (d) Pereira model, (e) Orang model, (f) FAO model, and (g) Wahed and Snyder model.

Full size image

The performance of the pan coefficients obtained in the present study is shown in figure 2. It can be seen from the scatter plot that the performance is highly varying for the annual time scale (figure 2a). Similarly, for the seasonal time scale also, there is only a marginal improvement in the performance of the pan coefficients (figure 2c). However, the use of monthly pan coefficients shows a significant improvement (figure 2b). Furthermore, it can be seen that the performance of both (monthly and seasonal) types of pan coefficients is satisfactory and both can estimate evaporation with a fair degree of accuracy, as majority of the data points fall on or along the 1:1 line, although some scatter has been observed for some individual points both for summer and winter, the scatter being more for summer than winter.

Figure 3 presents the errors of open-water surface evaporation estimation obtained using the developed pan coefficients. As was mentioned earlier, in India, it is a general practice for the irrigation departments and field organisations to use 0.7 as the pan coefficient for all time scales. So errors caused due to the use of \(K_{\mathrm{p}} = 0.7\) were also estimated. It can be observed from figure 3 that the errors of annual, monthly or seasonal pan coefficients developed using the optimisation technique are generally below 20–25% for most of the months. As far as the errors of the cooler months of November and December are concerned, these are higher for seasonal pan coefficients and are reduced drastically after using the annual and monthly pan coefficients. As far as the results of using a pan coefficient of 0.7 is concerned, it is observed that the errors caused are much higher compared to the pan coefficients developed in the study except for the cooler months of November–January, indicating that use of 0.7 as the pan coefficient could be highly erroneous. These errors are particularly very high for the monsoon months, when they are almost in the range of about 40%.

Pan coefficients have also been estimated using various other popular models. These are presented in table 4. It can be seen that except for the Snyder model, which gives significantly higher pan coefficients compared to the pan coefficients obtained in the present study, all other models give significantly lower coefficients. As most of these coefficients were developed for site-specific conditions in temperate climate, it is clearly visible that they do not represent the local tropical conditions where the coefficients are much higher, as obtained in the present study.

The suitability of the pan coefficients to estimate open-water evaporation obtained from the various models has been evaluated for the study area. To make the results comparable with the pan coefficients developed in the present study, the same data set used for the verification of the developed pan coefficients, was used and comparisons have been made on a monthly basis. The results are shown in figure 4. It can be seen that none of the models is able to predict the evaporation satisfactorily. There is a gross underestimation of evaporation by all models, except the Snyder model (figure 4a–g). This is obvious as the pan coefficients obtained for these models are significantly lower than the ones obtained in the present study, which give far more superior results. As far as the Snyder model (figure 4b) is concerned, evaporation is observed to be overestimated due to the higher pan coefficients, compared to those obtained in the present study. The performance appears to be better in general for winter months, but for the other months, the error is generally very high.

Fig. 5
figure 5

Comparative errors of different models used in the study.

Full size image

The monthly errors of the various models have been compared with the errors obtained using the pan coefficients developed in the present study. These are presented in figure 5. It can be easily seen that all models show very high errors compared to the errors of the developed pan coefficients, except for the winter month. The errors of the Snyder model and the modified Snyder model, in particular, are very high ranging from 9.54% in August to 64.25% in December for the Snyder model and 33.89% in December to 63.58% in August for the modified Snyder model. Other models also show errors ranging about 20–40% for most of the months, the errors being particularly higher in the monsoon months and also during February–April.

Further evidence of the better performance of the pan coefficients developed in the present study is presented in table 5 which compares the statistical parameters of the various models. The coefficient of determination (\(R^{2}\)) is 0.79 with pan coefficients developed in the present study. However, it is less than 0.70 for all other models. The difference in performance is very much visible in the other statistical parameters, namely, RMSE and EF. The RMSE values of the models based on the coefficients obtained in the present study are less than \(1\ \hbox {mm d}^{-1}\), while for all the other models it is much higher at above \(1.6\ \hbox {mm d}^{-1}\). More importantly, the model efficiency (coefficient of efficiency, EF) is very high for the coefficients developed in the present study, but for the other models, the efficiency is very poor.

Table 5 Statistical performance of the various pan coefficient models.
Full size table

The various results obtained in the study clearly indicate better performance of the pan coefficients developed in the present study for estimating evaporation from the Sukhna lake located in the humid tropical monsoon climatic region of India. However, as evaporation is a complex process involving the complex interaction of many causative meteorological parameters, the relative significance of which may vary both temporally and spatially, it cannot be said with certainty that the developed coefficients would be performing equally well under other similar climatic conditions also. The coefficients, therefore, need to be evaluated for various other locations with similar climatic conditions, for their general applicability and acceptability under the humid tropical monsoon climatic conditions.

4 Conclusions

Pan coefficients have been developed for a humid tropical monsoon region, Chandigarh in India, using the optimisation technique. A value of 0.92 as an optimised pan coefficient for the annual time scale has been obtained. However, the pan coefficient has been observed to vary significantly both by month and season for the study area. For the monthly time scale, the variation is in the range of 0.72–1.40 and for the seasonal time scale, the variation is in the range of 0.81–1.16. The coefficients are found to be significantly different than the reported pan coefficients for most temperate climates. The developed pan coefficients are found to estimate evaporation with a fair degree of accuracy for the Sukhna lake located in the humid tropical climatic region of Chandigarh in India and the errors of estimation are well within the acceptable limits. Furthermore, it is concluded that using a pan coefficient of 0.7, as being done by most field organisations in India, may lead to significantly erroneous estimates of evaporation as the respective errors are very high. Also, most of the other popular models of pan coefficients are found to be unsuitable for the humid tropical monsoon climate of the study area and hence, are not recommended for use, before local calibration. Most of these models are found to underestimate evaporation, except the Snyder model, which overestimates evaporation. However, keeping in view the fact that pan coefficients vary both temporally and spatially due to the variation in relative significance of various causative meteorological parameters, the pan coefficients developed in the present study need to be further evaluated for their suitability to other similar climatic regions of India.