Comparison of surrogate models with different methods in groundwater remediation process

Abstract

Surrogate modelling is an effective tool for reducing computational burden of simulation optimization. In this article, polynomial regression (PR), radial basis function artificial neural network (RBFANN), and kriging methods were compared for building surrogate models of a multiphase flow simulation model in a simplified nitrobenzene contaminated aquifer remediation problem. In the model accuracy analysis process, a 10-fold cross validation method was adopted to evaluate the approximation accuracy of the three surrogate models. The results demonstrated that: RBFANN surrogate model and kriging surrogate model had acceptable approximation accuracy, and further that kriging model’s approximation accuracy was slightly higher than RBFANN model. However, the PR model demonstrated unacceptably poor approximation accuracy. Therefore, the RBFANN and kriging surrogates were selected and used in the optimization process to identify the most cost-effective remediation strategy at a nitrobenzene-contaminated site. The optimal remediation costs obtained with the two surrogate-based optimization models were similar, and had similar computational burden. These two surrogate-based optimization models are efficient tools for optimal groundwater remediation strategy identification.

1 Introduction

Groundwater contamination problem arises along with the rapid development of industry and agriculture. Since groundwater remediation is a time consuming and costly process, finding methods to increase the remediation efficiency and reduce the remediation cost gradually becomes a crucial problem. Simulation and optimization technique is an effective tool to solve this problem (Ahlfeld et al. 1988; Guan and Aral 1999; Liu et al. 2000; Schaerlaekens et al. 2006; Md Azamathulla et al. 2008). However, the enormous computational cost of running such simulations multiple times, limits the applicability of the simulation optimization techniques in a complex groundwater remediation optimization process (Qin et al. 2007; Razavi et al. 2012). One method that reduces this computational burden is replacing the numerical models with efficient surrogate models (Sreekanth and Datta 2010; Jin et al. 2001).

Surrogate models, also called metamodels or response surface models, are used as particular substitutes for the complex numerical models, while being computationally cheaper to evaluate (Blanning 1975; Kourakos and Mantoglou 2013). Polynomial regression (PR), artificial neural network (ANN), kriging, support vector machine, and multivariate adaptive regression spline, etc., are common methods to build surrogate models, and these surrogate models have been widely used in space approximation problems (Jin et al. 2001; Giannakoglou 2002; Jin 2005; Forrester and Keane 2009).

To improve the computation efficiency of an optimization process, surrogate models have been used to approximate the computational simulation model in groundwater simulation optimization field in recent years. Huang et al. (2003), Qin et al. (2007), He et al. (2008), and Fen et al. (2009) used PR surrogate models to improve the optimization efficiency in contaminated groundwater remediation system. Rogers et al. (1995), Morshed and Kaluarachchi (1998), Johnson and Rogers (2000), Arndt et al. (2005), Yan and Minsker (2006), Nikolos et al. (2008), Behzadian et al. (2009), Dhar and Datta (2009), Kourakos and Mantoglou (2009), Yan and Minsker (2011) and Papadopoulou et al. (2010) used artificial neural network surrogate models in optimal groundwater remediation strategy identification, groundwater engineering facility optimization, optimal water supply design, and sea water intrusion management problems. Hemker et al. (2008) used kriging method to build the surrogate model of simulation model to reduce optimization computation cost in groundwater management problem.

It is difficult to say if one of these surrogate modelling methods is generally superior to others. For any specific engineering optimization design problem, conducting a comprehensive comparison analysis of the surrogate models that are built with different methods, and selecting the proper one to be used in the optimization process is of great importance. Mirfendereski and Mousavi (2011) compared support vector machines and polynomial-based surrogate models to approximate the MODSIM river basin simulation model, and applied it in Atrak river basin water allocation problem. Shyy et al. (2001) compared the relative performance between polynomials and neural networks surrogate models, and applied them on aerodynamics and rocket propulsion components. Simpson et al. (1998) compared the polynomial-based response surface and kriging surrogates in aerodynamic design optimization of hypersonic spiked blunt bodies. However, the comparisons of different surrogate modelling methods are limited in groundwater remediation optimization field.

During the model validation and selection process, the commonly used method is dividing the data into two mutually exclusive subsets called the training set and the validation set, which is called the holdout method (Kohavi 1995). This method only uses part of the data to train the surrogate model and uses the rest of data to validate the surrogate model (Namura et al. 2012), which may result in overfitting of the training data, and underfitting of the other data. Cross validation is an improvement of holdout method because it uses all data for both training and validation. In groundwater optimization field, cross validation is rarely used for surrogate model accuracy estimation (Razavi et al. 2012).

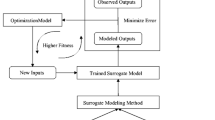
As an extension of previous researches, this study attempts to develop an optimization process based on multi-surrogate models and cross validation method for identifying the optimal remediation strategy at a nonaqueous phase liquids (NAPLs) contaminated aquifer. This objective entails the following tasks:

• build a multiphase flow simulation model in a nitrobenzene contaminated aquifer;

• develop surrogate models of multiphase flow simulation model using PR, RBFANN, and kriging methods, and estimate the accuracy of different surrogate models with cross validation method;

• surrogate models with acceptable accuracy are then selected and used in the nonlinear optimization model for identifying the most cost effective remediation strategy.

The novelty of the paper is:

• different surrogate modelling methods were used and compared in groundwater remediation optimization field;

• cross validation method was used to estimate the accuracy of different surrogate models in groundwater optimization field.

2 Methods

2.1 Surrogate modelling method

Polynomial regression is the simplest approximation method to build surrogate models (Forrester and Keane 2009). The most widely used polynomial regression model is the second-order polynomial model which has the following form (Jin 2005):

$$ y=\beta_{0} +\sum\limits_{i=1}^{n} {\beta_{i} x_{i} } +\sum\limits_{i=1}^{n}\sum\limits_{j\ge i}^{n} {\beta_{ij} x_{i} x_{j} } +\cdots $$

(1)

where β ₀, β _i , β _ii , and β _ij are the regression coefficients, n is the number of variables, x _i and x _j are the variables. Using least square method (LSM), the regression coefficients can be solved.

RBFANN is a 3-layer feed forward neural network consisting of an input layer, a hidden layer, and an output layer (Shen et al. 2010).

X is an N dimensional input vector. The output of the neurons in the RBFANN hidden layer is assumed as:

$$ q_{i} =\varPhi \left( {\left\| {\mathbf{X}-\mathbf{c}_{i} } \right\|} \right) $$

(2)

where c _i is the center associated with the ith neuron in the radial basis function hidden layer, i = 1, 2, …, H, where H is the number of hidden units, ∥X−c _i ∥ is the norm of X−c _i , Φ(⋅) is a radial basis function (Chen et al. 1991; Baddari et al. 2009). Outputs of the kth neuron in RBFANN output layer are linear combinations of the hidden layer neuron outputs as:

$$ y_{k} =\sum\limits_{i=1}^{H} {w_{ki} q_{i} -\theta_{k} }\quad(k=1,2,\ldots ,M) $$

(3)

where w _ki is the connecting weights from the ith hidden layer neuron to the kth output layer, 𝜃 _k is the threshold value of the kth output layer neuron.

The kriging method was developed by the French mathematician Georges Matheron based on the Master’s thesis of Daniel Gerhardus Krige (Matheron 1963), it was first used as a geostatistical method.

Sacks et al. (1989) firstly introduced kriging method as a surrogate modelling method, in the paper of Sacks et al. (1989), kriging surrogate model was also called design and analysis of computer experiment (DACE). From that time, many researchers have used kriging method for surrogate modelling (Booker et al. 1998; Simpson et al. 2001; Ryu et al. 2002; Hemker et al. 2008; Coetzee et al. 2012).

The kriging model is a combination of two components (Queipo et al. 2005): deterministic functions and localized deviations.

$$ Y(x)=\sum\limits_{i=1}^{k} {f_{i} \left( x \right)\beta_{i} } +z\left(x\right) $$

(4)

where $\sum \nolimits _{i=1}^{k} {f_{i} \left (x \right )\beta _{i} }$ is the term of deterministic functions, β _i are coefficients of deterministic functions, f _i (x) are k known regression functions, which are usually polynomial functions. z(x) is term of localized deviations with mean zero, variance σ ², and covariance expressed as:

$$ \text{Cov}\left[ {z\left( {x_{i} } \right),z\left( {x_{j} } \right)} \right]=\sigma^{2}R\left( {x_{i} ,x_{j} } \right) $$

(5)

where R(x _i , x _j ) is the correlation function between any two of the n _s samples The common types of correlation functions are linear function, exponential function, Gauss function, spline function, etc. (Ryu et al. 2002).

The prediction of unsampled points response y(x) can be expressed as:

$$ \mathord{\buildrel{\lower3pt\hbox{\(\scriptscriptstyle\frown\)}}\over {y}} \left( x \right)=f\left( x \right)^{\mathrm{T}}\beta +r^{\mathrm{T}}R^{-1}\left( {Y-F\beta } \right) $$

(6)

where Y is the vector of n _s samples response, r is the correlation vector between samples and prediction points.

$$ r = [R(x,x_{1} ),R(x,x_{2} ),\cdots, R(x,x_{n_{x} } )]^{\mathrm{T}}, $$

(7)

$$ F = [f(x_{1} ){\cdots} f(x_{n_{x} } )]^{\mathrm{T}}.$$

(8)

2.2 Cross validation – an accuracy estimating method

Cross validation is a technique for estimating the generalization errors of a predictive model. In cross validation process, all available data can be used both for validation and training, which helps avoid overfitting of the training data (Cheng and Pecht 2012). In k-fold cross validation, the data are divided into k subsets of approximately equal size. The surrogate model is built k times, each time leaving out one of the subsets as the validation data for validating the model, and using the remaining k–1 subsets for training. Total error of k times prediction is averaged to assess the approximation accuracy of surrogate models (Jiawei and Kamber 2001).

3 Case study

3.1 Site overview

To evaluate the advantages and disadvantages of different surrogate models of groundwater simulation model, three different surrogate models (PR model, RBFANN model, and kriging model) were applied to a test aquifer contaminated by nitrobenzene. The contaminated site is located in the second terrace of a valley alluvial plain in the lower Songhua River. The contaminated site is flat with an average altitude of 193 m. The upper part of the soil consists of an upper Pleistocene silt and silty clay with a thickness of 1–2 m, while the lower part is made up of medium sand and gravel, with a thickness of about 15 m. The main recharge sources are precipitation and runoff, while the main discharge source is runoff. Groundwater flows from northeast to southwest. The objective simulation layer is pore phreatic water in loose rock mass, the buried depth is about 4 m, and the single well yield is about 500–1000 m³/d. The study area and initial contaminant plume are shown in figure 1.

Figure 1

Contaminant conditions, and injection and extraction wells’ conditions.

Based on the contaminant distribution, a surfactant enhanced aquifer remediation (SEAR) with sodium lauryl sulfate as surfactant was designed with four injection wells and one extraction well (figure 1). 10% surfactant solution (volume fraction) was injected into the injection wells. To maintain hydraulic balance, the total extraction rates and injection rates were equal.

The optimization objective was to identify the most cost-effective strategy which can satisfy:

• more than 60% of the contaminant is removed;

• injection rate of each well is smaller than 70 m³/d; and the remediation duration is smaller than 20 days.

3.2 Numerical simulation model developed

The simulation domain was generalized as a heterogeneous and anisotropic 3-D multiphase flow and transport model. A first-type boundary condition was assigned at the northeast and southwest boundaries of the site. The other boundaries were no-flux boundaries. The simulation domain was discretized into 17 vertical layers, and each layer further discretized into 35 × 19 grids. Each grid dimension was 3 m × 3 m × 1 m in the x, y, and z axes directions respectively. The physical and chemical parameters of the site are presented in table 1.

Table 1 Physical and chemical parameters in simulation model.

A three-dimensional mathematical model was built to evaluate the efficiency of SEAR strategies. The basis mass conservation equation for each component can be written as (Delshad et al. 1996):

$$ \frac{\partial ({\phi \tilde{C}_{k} \rho_{k} })}{\partial t}+\vec{\nabla} \!\left[ \!{\sum\limits_{l=1}^{3} {\rho _{k} ({C_{kl} \vec{v}_{l}\,-\,\phi S_{l} \vec{{\vec{{K}}}}_{kl} \vec{\nabla} C_{kl} })} } \right]\,=\,R_{k} $$

(9)

where k is component index, including water (k = 1), oil (k = 2) and surfactant (k = 3), l is phase index including water (l = 1), oil (l = 2) and microemulsion (l = 3) phases, ϕ is porosity, $\tilde {{C}}_{k}$ is overall concentration of component k (volume fraction), ρ _k is density of component k (kg/m³), C _kl is concentration of component k in phase l (volume fraction), $\vec{{v}}_{l}$ is Darcy velocity of phase l (m/s), S _l is saturation of phase l, $\vec {{\vec {{K}}}}_{kl}$ is dispersion tensor (m²/s), R _k is total source/sink term for component k (kg/m³ s).

The mathematical model was constructed with the above mass conservation equation and corresponding initial conditions and boundary conditions. University of Texas Chemical Compositional Simulator (UTCHEM) was used to solve the mathematical model. UTCHEM is a three-dimensional, multiphase, multicomponent finite difference numerical simulator (Delshad et al. 1996; Bhattarai 2006). The simulator was originally developed by Pope and Nelson (1978) to simulate the enhanced recovery of oil using surfactant and polymer processes, and then was modified to simulate the remediation process of aquifers contaminated by NAPLs (Delshad et al. 1996; Delshad 1997; Qin et al. 2007).

3.3 Surrogate model developed

There are many factors that influence the remediation efficiency and remediation costs. In this study, we chose the well rates and remediation duration as the input variables. Due to the assumption that total extraction rates were equal to the total injection rates and there was only one extraction well, there were five input variables, which were remediation duration, rates of injection well In1, In2, In3, and In4 (table 2). The output variable was average contaminant removal rate.

Table 2 Input variables and its value range.

Forty input samples were collected through sampling in the feasible region of input variables of multiphase flow numerical simulation model, and the output responses were obtained through running the developed simulation model.

With these 40 input–output data, PR, RBFANN, and kriging methods were used separately to build three surrogate models of multi-phase flow numerical simulation model. Ten-fold cross validation method was adopted to evaluate the approximation accuracy of the three surrogate models.

In the 10-fold cross validation process, the 40 input–output data were randomly divided into 10 subsets, with each subset containing four samples. The surrogate model was built 10 times, with each time the surrogate model had 36 training data and four validation data. For PR model, first-order, second-order, and third-order polynomials were adopted to build the relationship between average contaminant removal rate, remediation duration, and four injection rates for each fold, using least square method (LSM), a set of regression coefficients were solved, and a total of 10 different polynomial regression models were obtained.

For RBFANN model, the input layer of the network represented the remediation duration and four injection rates, a total of five neurons. The output layer of the network contained only one neuron, which represented the average contaminant removal rate. The hidden neuron number is set as 10, 20, 30, and 40. In this study, the Gauss function was used as transfer function, and the orthogonal least square method was used for network training. After the RBFANN model training, a total of 10 RBFANN models with different parameters were obtained.

For kriging model, polynomial functions of orders 0, 1, and 2 were used as regression functions, while Gauss function was used as correlation function. Through training the kriging modela total of 10 kriging models with different parameters were also obtained.

3.4 Optimization model developed

To identify the optimal remediation strategy, a nonlinear optimization model was developed using the minimal remediation cost as the objective function, with the remediation duration and rates of injection well In1, In2, In3, and In4 as the decision variables. The optimization model can be represented as follows:

$$\begin{array}{@{}rcl@{}} && \min f\left( {Q,t} \right)=f_{\text{installation}} +f_{\text{operation}} \\ && =C_{1} m+C_{2} n+C_{3} t\sum\limits_{i=1}^{m} {Q_{i}^{In} } +C_{4}t\sum\limits_{j=1}^{n} {Q_{j}^{Ex} } \\ \end{array} $$

(10a)

Subject to:

$$ 0\le Q_{i}^{\text{In}} \le Q_{M}^{\text{In}} \, $$

(10b)

$$ 0\le Q_{j}^{\text{Ex}} \le Q_{M}^{\text{Ex}} \, $$

(10c)

$$ \sum\limits_{i=1}^{m} {Q_{i}^{\mathrm{In}} } =\sum\limits_{j=1}^{n} {Q_{j}^{\text{Ex}} } $$

(10d)

$$ 0\le t\le t_{M} $$

(10e)

$$ g(Q,t)\ge g_{0} $$

(10f)

where equation (10a) is the objective function, equation 10(b–d) are the injection and extraction rate constraints, equation (10e) is the remediation duration constraint, equation (10f) is the remediation efficiency constraint. f is total cost of the remediation system ($), the first two terms of equation (10a) account for the installation cost and the last two terms account for the operation cost, C ₁ and C ₂ are injection wells and extraction wells installation cost coefficients ($), respectively, C ₃ and C ₄ are injection and extraction operation cost coefficients ($/m³) respectively, m and n are injection and extraction wells number respectively, $Q_{i}^{\text {In}}$ is the rate of ith injection well (m³/d), $Q_{j}^{\text {Ex}}$ is the rate of jth extraction well (m³/d), $Q_{\textit {M}}^{\text {In}}$ and $Q_{\textit {M}}^{\text {Ex}}$ are maximum allowable injection rate and extraction rate of wells (m³/d), t is the remediation duration (d), t _M is the maximum allowable remediation duration (d), g(Q, t) is the average contaminant removal rate, which is an output response of the surrogate model, and g ₀ is the minimum allowable value of the contaminant average removal rate. The constant of the equation is in table 3.

Table 3 Constants included in the optimization model.

4 Results and discussion

4.1 Surrogate model accuracy analysis

For each surrogate modelling method, there are 10 folds, and in each fold, the output responses of the four validation samples were predicted with the developed surrogate models. Therefore, 40 samples’ output responses can be obtained with surrogate models.

In this study, absolute error (AE) and relative error (RE) were selected as the loss function to estimate the accuracy of the surrogate models. Figures 2, 3, and 4 show the boxplots of absolute and relative error of different surrogate models. The results demonstrated that: for PR model, approximation accuracy of second order polynomial is higher than that of first-order polynomial and third-order polynomial; for RBFANN model, the RBFANN with 40 hidden neurons obtained highest approximation accuracy; for kriging model, kriging model with second order polynomial function as regression function obtained the highest approximation accuracy. Therefore, second-order polynomial model, RBFANN model with 40 hidden neurons, and kriging model with second order polynomial function as regression function are selected as the surrogates, and their parameters are in table A1, table A2, and table A3 (Appendix).

Figure 2

Boxplots of the PR models: (a) boxplot of absolute errors and (b) boxplot of relative errors.

Figure 3

Boxplots of the RBFANN models: (a) boxplot of absolute errors and (b) boxplot of relative errors.

Figure 4

Boxplots of the kriging models: (a) boxplot of absolute errors and (b) boxplot of relative errors.

The relationship between simulation model results and surrogate model results of 40 validation samples are shown in figure 5, which shows that the accuracy of kriging and RBFANN models are greater than PR model. From the mean error (mean AE and mean RE) and maximum error (maximum AE and maximum RE) of the three surrogate models (figures 2, 3, and 4), we can conclude that the RBFANN model and kriging model had acceptable approximation accuracy, and further that the approximation accuracy of kriging model was slightly higher than that of RBFANN model. However, PR model’s approximation accuracy was unacceptable (the mean relative error is 80%), this probably due to its limited fitting ability for nonlinear problem, especially for the high-order nonlinear problem. From the distribution of surrogate models we can conclude that the distribution of RBFANN model and kriging model (most of the relative error values are between 3% and 18%) are much more concentrated than that of PR model (there are many samples with relative error greater than 100%). In summary, RBFANN model and kriging model had acceptable accuracy and robustness, and can be used in the flowing optimization process.

Figure 5

Simulation model results vs. surrogate model results.

4.2 Optimization result analysis

From the above observations, both the RBFANN model and kriging model were embedded in the optimization model, as the linking of the average contaminant removal rate, injection rates, and remediation duration. The genetic algorithm was adopted to solve the developed nonlinear optimization model on MATLB platform. In the genetic algorithm searching process, the surrogate model was invoked instead of the computational simulation model. The parameters of the genetic algorithm were set the same in the RBFANN surrogate based optimization model and in kriging surrogate based optimization model. Selection probability, crossover probability, and mutation probability are usually set between 0.7–1.0, 0.7–1.0, 0.01–0.05 (Simpson et al. 1994), and in this paper they are set as 0.9, 0.7 and 0.05; the generation number is set as 100. The population size is set as 500, and the obtained optimal remediation strategies are in table 4. The optimal remediation strategies obtained with RBFANN and kriging were evaluated using the multiphase flow numerical simulation model, and the predicted average contaminant removal rates were 0.6 and 0.6, which satisfies the contaminant removal rate constraint. The optimal solutions obtained with the two optimization models were different, but the optimal remediation costs were similar, this may be because the complex optimization problem had multioptimal solution. We can conclude that both the RBFANN and kriging surrogate-based optimization models obtained satisfactory solutions.

Table 4 Optimal remediation strategy.

4.3 Computational burden analysis

Generally, there are three parts for the computational burden in the surrogate-based optimization process: repeated running of the numerical simulation model, surrogate model construction, and the optimization searching process with genetic algorithm.

The main computational burden was resulted from the repeated running of the numerical simulation model. The SEAR optimization for the nitrobenzene-contaminated site required 295 seconds of CPU time to run every simulation model on a 3.0 GHz AMD CPU and 2 GB RAM PC platform. 40 input data were sampled randomly, and the output responses were obtained with the simulation model, so the simulation model needed to be run 40 times; thus, 11,800 s were required in this process with both of this two optimization models.

An average of 1.3 s were needed to train the RBFANN model for one time, while an average of 0.12 s were needed to train the kriging model. In the cross validation process, each surrogate model needed to be constructed 10 times, so the construction of RBFANN model and kriging model totally needed 13 and 1.2 s respectively.

In the optimization searching process, RBFANN surrogate-based optimization model needed 2.61 s before the genetic algorithm converged, while the kriging surrogate-based optimization needed 2.81 s.

Compared with the computational burden of repeated running of the numerical simulation model, the computational burden resulted from the surrogate model construct and the optimization searching process can be negligible. The whole process of surrogate-based optimization model solving needed nearly 3 hr (11,800 s), no matter which surrogate model was used. In GA process, 4000 evaluations were used as a termination criterion (maximum evaluation times). Therefore if the numerical model was used instead of the surrogate model, then the total CPU time would have been 1180,000 s (14 days).

5 Conclusions

In this study, three different surrogate models: polynomial regression, radial basis function artificial neural network, and kriging were used to build surrogate model at a nitrobenzene contaminated aquifer remediation problem.

Ten-fold cross validation was adopted to compare the approximation accuracy of the three surrogate models. The results showed that the radial basis function artificial neural network and kriging models had better approximation accuracy and robustness than the polynomial regression model. Therefore, the radial basis function artificial neural network and kriging-based optimization models were preferred and selected to identify the optimal remediation strategy for a nitrobenzene contaminated site. The two surrogate-based optimization models obtained similar optimal costs, with a similar computational burden. In addition, these two surrogate-based optimization models considerably reduced the computational burden compared with the conventional simulation optimization model. Therefore, we can conclude that the surrogate-based optimization models are efficient tools for optimal groundwater remediation strategy identification, and radial basis function artificial neural network method and kriging method are effective surrogate modelling methods.

Appendix

Table A1 Parameters of second-order polynomial models.

Table A2 Parameters of RBFANN models.

Table A3 Parameters of kriging models.