1 Introduction

Nonlinear chemical reactions, especially autocatalytic type, have been studied experimentally by many researchers.[1,2] Reactions of this type can be reversible or irreversible, with or without the inflow of the intermediate product X. Many processes in nature are autocatalytic, such as the self-replication exhibited by ligase ribozyme[3] and peptides[4] self-perpetuating conformational changes such as those known to be exhibited by prions[5] or reproduction events in biological populations.[6] The effect of a reversible autocatalytic process of spontaneous decay of the catalyst population was considered.[7] The authors consider the system for which the spontaneous production of the autocatalytic reagent is exceedingly rare over the time scale of the experiment. Micro-fluid experiments and blood coagulation have proved that the rate of mixing controls the rate and can regulate the rate and outcome of both biological and non-biological autocatalytic reaction systems.[8]

The autocatalytic stage is involved in many chemical and biochemical cycles. Well known and often considered by many researches are the following: the Belousov-Zhabotynski reactions[9–17] oxidation of bromates by nitric acid[18] or Landolt reactions,[19] ferrous-bromate,[20] iodide – areniate,[21] chlorite-iodide, and hydroxylamine-nitric acid,[22] Fe(I1)-HNO[23] reactions. Autocatalytic processing of β-pro’-tryptase to β-pro’-tryptase is described.[24] These autocatalytic processes possess bistable steady states observed in a stirred tank reactor (CSTR) experiments.[25] Minimal self-replicating systems based on autocatalytic processes were analyzed.[26] Some autocatalytic reactions, for example, may exhibit propagating reaction fronts.[27–33]

A theoretical work is concerned with a model of the enzymatic system of two coupled autocatalytic reactions based on three variables.[34–36] A three-variable model of deterministic chaos in the Belousov–Zhabotinsky reaction, has been described too.[37] The autocatalytic stage appears also in the hipercycle model described by Eigen.[38] A simple three-variable model for complex oscillations with an autocatalytic stage in an isothermal chemical system was considered.[39] Theoretical approaches used in the Belousov–Zhabotinsky (BZ) reactions[40] and arsenite-iodate waves,[41] iodate oxidation,[42] aerobic oxidation of NADH by horseradish peroxidase enzyme model[43] and many others. Time-periodic reaction-diffusion systems with application to the autocatalysis in chemistry were considered too.[44] The simulation of a complex kinetic scheme and the results verified considering the thermal decomposition of cumene hydroperoxide can be easily generalized to different kinetic models and is devoted to identify autocatalytic processes by means of dynamical DSC experiment.[45] Autocatalytic set concept introduced in 1860 by Darwin was recently used to describe the chemical reactions in combustion process in circulating fluidized bed boiler.[46]

The model of a simple autocatalytic type reaction with oscillatory, cosine-like inflow of intermediate product X to the reaction medium (reaction field) is presented in this paper. Numerical solutions and analytical attempts to solve the non-linear differential equation indicates a phase shift between the oscillatory influx of intermediate reagent X to the reaction medium and change of its concentration in this medium. Attempts for analytical solutions indicate that this shift may be associated with the reaction rate constants k 1 and k 2 and the relaxation time τ. The relationship between the phase shift and the oscillatory flow of reactant X seems to be similar to that obtained in the case of linear chemical reactions, as described previously,[47] however, is much more complex (table 1).

Table 1 Comparison between the linear and nonlinear processes with oscillatory, cosine-like inflow of X reactant to the reaction medium.
Full size table

This raises the question: is it possible to use a forced phase shift effect in the simplest nonlinear chemical processes occurring especially in the biological systems, for example DNA replication or formation of thiodiglycol from thioglycolates or that which occurs in the initial transcript of rRNA and many other auto-processing ones? In this paper, we would like to give an answer to this question. This work is a supplement to our earlier work.[47]

2 Theory

Nonlinear reactions with oscillatory inflow of reactant to the reaction medium are considered.

The main subject is the simplest nonlinear autocatalytic reaction with inflow I X of intermediate reactant to the reaction field:

$$ A+X\overset{k_{1} k_{2}}{\longleftrightarrow} 2X $$
(1)

Where, A stands for the initial product and X is the intermediate product.

The kinetic equation of reaction (1) takes the form:

$$ \frac{dX}{dt}=k_{1} AX-k_{2} X^{2}+I_{X} $$
(2)

We assume that inflow I X of the intermediate product X is not constant in time, but it changes periodically (cosine-like), according to the following function:

$$ \quad I_{X} =a\cos^{2}\left({\omega t} \right) $$
(3)

Where, a is the oscillation amplitude and ω is the rate (frequency) of X inflow to the reaction medium.

The equation (2) takes the form of:

$$ \frac{dX}{dt}=k_{1} AX-k_{2} X^{2}+a\cos^{2}\left({\omega t} \right) $$
(4)

The equation (4) is nonlinear and non-homogenous. The equation (4) has two variables: concentration of intermediate product X and time variable t. For this reason the analytical solution of this type equation is impossible. In the case of equation (4) it can only find a default solution of change of X product. It is true, that the reaction (4) has two changes over time in oscillating manner stationary states:

$$ x_{1} =\frac{k_{1} A+\sqrt {\Delta}} {2k_{2}} ~\text{and}~x_{1} =\frac{k_{1} A-\sqrt {\Delta}} {2k_{2}} $$
(5)

where:

$$\begin{array}{@{}rcl@{}} \sqrt {\Delta} &\!\!\!\,=\,\!\!&\sqrt {\left({k_{1} A} \right)^{2}+4k_{2} a\cos^{2}(\omega t)}{}\quad\text{i{\kern-.8pt}n{\kern-.2pt} c{\kern-.5pt}a{\kern-.2pt}s{\kern-.2pt}e o{\kern-.2pt}u{\kern-.2pt}t{\kern-.2pt}f{\kern-.2pt}l{}o{\kern-.2pt}w{\kern-.2pt} o{\kern-.2pt}f}~X, \\ &&{\Delta} > 0 \end{array} $$
(5a)
$$\begin{array}{@{}rcl@{}} \sqrt {\Delta} &\!\,=\,\!&\sqrt {\left({k_{1} A} \right)^{2}-4k_{2} a\cos^{2}(\omega t)}{}\quad\text{in case inflow of}~X, \\ &&{\Delta} > 0~\text{or}~{\Delta} < 0 \end{array} $$
(5b)

The formula (5) contains changing time t variable and it is not possible to solution. For this reason the eq. (4) is also impossible to analytical resolve. We assume that Δ is positive as in a constant inflow of X, because it has a definite physical meaning. Based on the analytical solution of nonlinear equation with a constant inflow of product X to the reaction medium (see Appendix) and on the analytical solve of linear type equation with a periodically inflow of X to the reaction medium described in our earlier paper and confirmed experimentally[47] we assume that approximate solution of the eq. (4) can take the following form:

$$\begin{array}{@{}rcl@{}} X&=&\frac{k_{1} A-\sqrt {\Delta} - [ {({k_{1} A+\sqrt {\Delta}} )} ]c\exp ({\sqrt {\Delta} t} )}{2k_{2} [ {({1-c\exp (-\sqrt {\Delta} t} )} ]}\\ &&\times ({\sqrt {\Delta} \cos 2\omega t+2\omega \sin 2\omega t} ) \end{array} $$
(6)

Where, pre-exponential factor c is,

$$ c=\frac{-X_{0} 2k_{2} +k_{1} A-\sqrt {\Delta}} {-X_{0} 2k_{2} + ({k_{1} A+\sqrt {\Delta}} )\sqrt {\Delta}} $$
(7)

X 0– is the initial concentration of the product X. X 0 is calculated from the following initial conditions: when X = X 0→t=0 and it takes the form:

$$ X_{0} =\frac{k_{1} A-\sqrt {\Delta} -({k_{1} A+\sqrt {\Delta}} )c\sqrt {\Delta}} {2k_{2} -c2k_{2}} $$
(8)

The relaxation time τ follows from the eq. (6) and takes the form:

$$ \tau =\frac{1}{\sqrt {\Delta}} =\frac{1}{\sqrt {\left({k_{1} A} \right)^{2}\pm 4k_{2} a\cos^{2}(\omega t)}} $$
(9)

As follows from eqs. (9) and (8) the determination of τ is impossible in this case, namely, nonlinear chemical processes with the oscillatory, cosine-like inflow to the reaction medium. The problem here is the time variable delta. This factor indicates the fundamental difference between linear and nonlinear reaction with oscillatory in time inflow of chemical reagent X to the reaction medium.

As in the linear reaction with oscillatory inflow of X to the reaction medium[47] the sum of two trigonometric functions in brackets in eq. (6) can be replaced by a single trigonometric function after introducing an auxiliary angle ϕ defined as:

$$ \tan \phi =\frac{2\omega} {\sqrt {\Delta}} =2\omega \tau $$
(10)

where,

$$ \phi =\arctan \frac{2\omega} {\sqrt {\Delta}} =\arctan 2\omega \tau $$
(11)

After substitution eq. (11) into eq. (6) and some mathematical transformations we obtain:

$$\begin{array}{@{}rcl@{}} X&\!\!\!=\!\!\!&\frac{k_{1} A-\sqrt \Delta -[ {( {k_{1} A+\sqrt \Delta} )} ]c\exp ( {\sqrt \Delta t} )\sqrt \Delta} {2k_{2} [ {( {1-c\exp (-\sqrt \Delta t} )} ]}\notag\\ &&\times\frac{1}{\cos \phi} \cos (2\omega t-\phi ) \end{array} $$
(12)

where,

$$ \quad \cos \phi =\frac{\sqrt {\Delta}} {\sqrt {({\sqrt {\Delta}} )^{2}+4\omega^{2}}} $$
(12a)

Let us consider now a high-order autocatalysis level reaction type:

$$ A+2X\overset{k_{1} k_{2}}{\longleftrightarrow} 3X $$
(13)

with a time constant inflow I X of X reagent to the reaction medium is described by the kinetic equation:

$$ \frac{dX}{dt}=k_{1} AX^{2}-k_{2} X^{3}+I_{X} $$
(14)

The reaction has two stable stationary states. The analytical solution for these states is given by eq. (5).

When the inflow is oscillatory and time dependent, described by the eq. (3) approximate solution of the eq. (14) takes the form similar to eq. (6). The solution of eq. (14) applies only for one of the stable stationary state. It is known that the system tends to only one stable stationary state.

For the higher degrees of the nonlinear and oscillatory autocatalytic processes, seems to be that there is a dependency similar to eq. (2). For the higher degrees of autocatalysis in real space, i.e., three-dimensional space, there are only two stable steady states and the system seeks one of them.

It seems that the formula (6) also can apply to the one of the stable stationary state to the high-order autocatalytic reactions with the general formula:

$$ \frac{dX}{dt}=k_{1} AX^{(n-1)}-k_{2} X^{n}+a\cos^{2}(\omega t) $$
(15)

In general the formula (6) takes the form:

$$\begin{array}{@{}rcl@{}} X&=&\frac{k_{1} A-\sqrt[n]{\Delta} - [ {({k_{1} A+\sqrt[n]{\Delta} } )} ]c\exp ({\sqrt[n]{\Delta} t} )}{2k_{2} [ {({1-c\exp (-\sqrt[n]{\Delta} t} )} ]}\\ &&\times({\sqrt[n]{\Delta} \cos 2\omega t+2\omega \sin 2\omega t} ) \end{array} $$
(16)

where, n denotes the order of autocatalysis.

X 0 and c are as described for n=2 by eq. (7) and eq. (8) but with \(\sqrt [n]{\Delta } \).

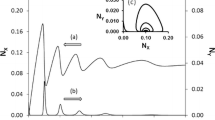
The equation (4) can be numerically solved using four-order Runge-Kutta algorithm (figure 1). Figures 1a, 1b and 1c present the numerical analysis (based on the Runge-Kutta algorithm) of a delay effect and an amplitude modification in the case of high-order nonlinear autocatalytic processes. All simulations were performed for the initial conditions: X=1, t=0 and an integration step h=0.01. The numerical calculations show a delay between the concentration of inflow product X to the reaction medium (field) and its concentration in this medium. The amplitude of X in the reaction field is modified too. The phase shift and amplitude modification depends on frequency ω of X inflow, as well as on values of k 1 A and k 2. For a given level of autocatalysis the numerical solution shows the following dependence: when the influx of reagent X to the field (medium) reaction is more intense, the delay in concentration in the reaction field is less or unchanged. (figures 1a–c, 2a–b, 3a–b and table 2).

Figure 1
figure 1

The results of numerical calculation for the autocatalytic reactions with oscillatory stimulus (described by eq. (4)) both for k 1 A>k 2 (upper lines) and k 1 A<k 2 (lower lines) for a) ω=0.2, b) 0.6 and c) 1.2. For k 1 A<k 2 (lower lines) from the bottom, the lines correspond 2X, 3X, 4X, 5X and 6X; for k 1 A>k 2 (upper lines) from the top (upper lines), the lines correspond 2X, 3X, 4X, 5X and 6X. The black line at the bottom of figure is a periodical, cosine-like inflow of the intermediate product X. The calculation parameters are initial concentration of X: X 0=1, initial time: t 0=0, integration step h=0.01, k 1 A=0.5, k 2=0.3, a=0.1.

Full size image
Figure 2
figure 2

Illustration of a) the phase delay ϕ maximum and b) the phase delay minimum, dependence on frequency ω; 0.2, 0.4, 0.6, 0.9, 1.2 of the X inflow and on autocatalysis degree for k 1 A>k 2:k 1 A=0.5, k 2=0.3.

Full size image
Figure 3
figure 3

Illustration of a) the phase delay ϕ maximum and b) the phase delay minimum, dependence on frequency ω; 0.2, 0.4, 0.6, 0.9, 1.2 of the X inflow and on autocatalysis degree for k 1 A<k 2:k 1 A=0.3, k 2=0.5.

Full size image
Table 2 Juxtaposition of the values of amplitude obtained from the numerical calculations for the case: k 1 A>k 2, k 1 A=0.5, k 2=0.3. ω is a frequency of X supply, 2X, 3X, 4X, 5X and 6X denote the degree of autocatalysis.
Full size table

In the linear type reaction with oscillatory, cosine-like inflow of the intermediate product X to the reaction medium (field), the analytical solution of linear kinetic equation shows that the delay is ruled by the formula: tanΦ=ω t.[47] This formula was confirmed experimentally and was used to determination of the rate constant k of the saponification of ethyl acetate (used as a reagent A) with sodium hydroxide (used as a reagent X).

In the presented model \(\sqrt {\Delta } \) probably depends on the order of autocatalysis in case when \(\sqrt {\Delta } \) is positive this is, for k 1 A>k 2. For higher levels of autocatalysis a sign of the delta (positive or negative) probably determines whether a system oscillations disappear or not (at a fixed frequency inflow of X reagent, see figures 1a–c,). When the k 1 A is greater than k 2 (delta is positive) the damping of the amplitude of the oscillations and decrease in the phase shift are observed in the system with an increase in the degree of autocatalysis (figures 1a–c (upper lines) and figures 2a–b and table 2) (the shift between the oscillatory inflow of X reagent to the reaction medium and its concentration in this medium). This is visible both in maximum and minimum of X inflow (figures 2a–b). As shown in the figures 2a and 2b, when the k 1 A is greater than k 2 the phase shift depends strictly on the frequency ω of supply of X reagent to the reaction medium – decreases with increasing of ω inflow of reactant X at the given degree of autocatalysis. As shown in the figures 2a and 2b, with the increase in the degree of autocatalysis, phase shift between the concentration of the reactant X and the inflow is reduced. At six-order of autocatalysis the phase shift does not seem to depend on frequency ω of flow of X. A similar correlation is observed in the amplitude values obtained from numerical calculation as show in table 2. When the k 1 A is smaller than the k 2 (Δ is negative) the oscillation of X are sustained (with

increase of degree of autocatalysis ((figure 1a), figure 1b), figure 1c) – lower graphs)) and the phase delay does not change with increasing of degree of autocatalysis at the given frequency ω of X inflow (figures 3a and 3b). But, in this case, the phase shift depends on frequency ω of X inflow at the given degree of autocatalysis (figures 3a and 3b). In both cases (when k 1 A is greater than k 2 or k 1 A is smaller than the k 2) the phase shift depends on frequency ω of inflow of X at the given degree of autocatalysis. When the frequency ω of X inflow to the reaction medium is greater, the phase shift (phase delay) of the concentration of X in this medium is reduced at a given order of autocatalysis as shown in the figure 2 and figure 3. It is opposite to the effect in linear reactions.[47] Apart from that, bifurcation point is visible in figures 1a–c.

3 Results and Discussion

3.1 Physical interpretation - connection between the exponential relaxation and the forced delay effect in the linear and nonlinear systems and some examples

In nature the most of relaxation processes have an exponential character. In the biological and chemical systems, relaxation takes place exponentially in almost 70–80%. In chemistry the first order and autocatalytic non oscillating type of reactions have an exponential relaxation. Especially the nonlinear autocatalytic processes play an important role in biological systems.

If (in the non-oscillating and exponentially relaxing systems) intermediate product X flows in the oscillatory manner to the reaction medium (as a variable time cosine type function) it will be seen the phase shift in the concentration of X in response to the supply of this component to the medium. This process is called as a forced (by the oscillating stimulus), the effect of phase shift. Phase shift (phase delay) is strictly connected with the relaxation process.

There is a one common formula for all oscillating and non-oscillating linear systems relaxing exponential and forced by a periodical stimulus: tanΦ=ω t, where ω – is a frequency of stimulus, τ – is a relaxation time. This formula is mainly used for determination of the relaxation time τ, especially in physical systems. In the linear first-order chemical reactions, the forced phase delay effect turned out to as a good method for determination of the rate constant k 1 and the relaxation time τ.[47]

There are common factors relating to all the linear relaxing exponentially systems both oscillatory and non oscillatory forced by oscillatory stimulus. Parameters of the forced oscillation do not depend on the initial conditions. These oscillations have the frequency of driving force and are characterized by amplitude and phase shift (with respect to the appropriate stimulus).

There are some differences characterizing the nonlinear systems with respect to the linear ones. There are the common characteristic for the nonlinear systems, both oscillatory and non oscillatory, forced by oscillatory stimulus. In this work we present the non-oscillating and nonlinear system forced by oscillatory stimulus. Parameters of the forced oscillation strictly depend on the initial conditions. Nonlinear systems are sensitive to the initial conditions. The oscillations have the frequency of driving force and are characterized by amplitude and phase shift (as in the linear systems). There is no one set rule which describes the behaviour of the nonlinear systems. This is due to the fact that the nonlinear systems are far from thermodynamic equilibrium.

The forced phase shift in the nonlinear systems is even less frequent than in the linear ones. There are known examples of nonlinear physical systems in which there is a forced phase shift effect. It is difficult to find examples of nonlinear chemical systems in which the forced phase shift effect is observed. A special class of reaction-diffusion equations to a system incorporating time delay effects were theoretically considered.[48] The equations applied e.g., to a nonlinear reaction-diffusion Lotka-Volterra system.

3.2 Discussion

The nonlinear, non-oscillating and an auto-processing- autocatalytic chemical reactions are considered in this paper. The simplest nonlinear autocatalytic type reaction with the oscillatory inflow of X reagent to the reaction medium (reaction field) is much more complicated in comparison to the linear first-order reaction with the X reagent inflow to the reaction medium. In our case, the delay in the concentration of X chemical reagent in the reaction medium is connected with its frequency of inflow to the reaction medium. As in the linear first-order process we also observed the phase shift between the X inflows to the reaction medium and change its concentration in this medium. The amplitude modification is observed too. However in the nonlinear autocatalytic processes the Δ is connected with an oscillatory time dependent inflow of X and is variable in time (Eqs. 5a and 5b). Connected with the Δ the relaxation time τ is also variable in time. Apart from Δ and τ are also dependent on k 1 A and k 2. For this reason the relaxation time τ as well as k 1 A and k 2 are not possible to determination. Nonlinear autocatalytic processes of high-order have also a one stable stationary state, which rule this same or similar formula as the simplest autocatalytic process one. Determination of the relaxation time τ and rate constants k 1 and k 2 are impossible too.

We observe that with increasing frequency of X inflow to the reaction medium the phase shift tends to zero. In the linear first-order reaction, the phase shift tends to π/2 with increasing frequency of X inflow. It may be connected with the fundamental difference between the systems linear and nonlinear. It is probably connected with Δ oscillating in time. The fact that the phase shift decreases with increasing ω inflow X seems to be important especially in the biological systems. High frequency ω X component supply needed for the occurrence of a chemical reaction reduces the delay of its delivery. This is very important for the proper conduct of the chemical process in a living organism. Most nonlinear biological processes, such as, enzymatic reactions, DNA replication, biosynthesis of protein and many others occurs with very great speed of 10 12 s. It follows that the reagent X must also be provided at the same rate. It is the rate of 1000 times greater than the rate of transmission of any signal, which is 10 9 s. When the delivery rate of reagent X is very rapid, about 1012 s, a delay in phase is observed. Also, any oscillations are extinguished. In the linear reactions it is inverse; the higher the frequency of reactant X supply to the reaction medium, the greater is the phase delay, and tends to a maximum of 90∘ (but does not exceed this value). This explains the very important role of nonlinearity in biology. For a biological system to function effectively there can be no delay in the chemical process. If the reactant flow rate decreases, the delay may occur, which may have an adverse effect on the functioning of the biological system. Presented model explains the behavior of the nonlinear system, depending on the frequency of X reagent flow to the reaction field. In some cases, when k 1 A<k 2 (Δ probably is negative) the oscillations are sustained in system. This fact is also important in the living systems that allows to preserve stability.

Table 1 presents a comparison between the linear and nonlinear chemical processes referring to the forced phase delay effect. Large differences are apparent between the linear first order chemical reactions with the oscillatory inflow of X reactant and the nonlinear autocatalytic ones with the same inflow. It is a fundamental difference between the linear chemical reactions with forced delays effect[47] (table 1). In the linear first-order reactions with an oscillatory inflow of X reagent to the reaction medium there is only one stationary state and there is only one analytical solution. The relaxation time τ is strictly connected with k 1 A and tan ϕ=2ω τ. In the nonlinear processes with the oscillatory inflow of X reagent to the reaction medium is much more complicated. In the first-order linear reactions with oscillatory inflow of X to the reaction medium, the phase delay ϕ is greater with increase of frequency ω of its inflow. In the autocatalytic nonlinear reactions, the phase shift is reduced with an increase in frequency ω of X inflow to the reaction medium (figures 2a and 2b, figures 3a and 3b) at a given degree of autocatalysis. For the higher order of autocatalysis (five and six), the phase delay seems to not depend on frequency ω of X inflow in some cases (when k 1 A>k 2, see figures 2a and 2b).

The following question arises: is it possible that any application of the forced phase delay affect in the nonlinear autocatalytic processes? In order to answer this question let’s cite one researcher - Laister. Laister[48] in the abstract of his article writes:

“For a significant class of nonlinear equations it is shown that an unstable equilibrium solution of the reaction-diffusion system cannot be stabilized by the introduction of delay”.[48] In our case the nonlinear autocatalytic but without diffusion processes, cannot be stabilized by forced delay effect. For this reason the forced delay effect in the nonlinear chemical processes cannot be applied for determination of a rate constant or a relaxation time.

The phase delays’ phenomena seem also to play an important role in some biological processes. It has been proved that the p19 protein induces G1/S phase delay, thereby maintaining cells in a reversible quiescence state and preventing entry into apoptosis[49] N-methyl-D Revised: aspartate (NMDA) induces a rapid phase shift of mPer 1promotor gene in cultured SCN. It has been shown that NMDA induces phase shifts at various time points.[50]

Autocatalytic processes are connected with the class of reactions which are most closely associated with creation. Stuart Kauffman in his book wrote that life initially arose as autocatalytic chemical networks.[51]

The theoretical model presented in this paper can also be applied to the theory of heterogeneous catalysis. In practice, the present model does not apply here, because of the intermediate species which are not available outside reactor. But this model may be useful to explain the role of autocatalytic stage occurring during heterogeneous catalysis.

4 Conclusions

Our theory shows that in the nonlinear and non-oscillating chemical processes, the phase shift and oscillation amplitude decrease with increasing flow frequency of the intermediate product X to the reaction medium. For this reason, the forced phase delay effect seems to play an important role in all nonlinear processes in biological systems.

The phase delay effect (phase shift) in the nonlinear and non-oscillating chemical processes forced by the oscillatory inflow of chemical reagent cannot be used for determination of both a rate constant and a relaxation time because of a time variable Δ.

It seems that there is one common mathematical formula possible to describe nonlinear autocatalytic processes of all orders.