Exact solutions and constraints on the dark energy model in FRW Universe

Abstract

The inflationary epoch and the late time acceleration of the expansion rate of universe can be explained by assuming a gravitationally coupled scalar field. In this article, we propose a new method of finding exact solutions in the background of flat Friedmann–Robertson–Walker (FRW) cosmological models by considering both scalar field and matter where the scalar field potential is a function of the scale factor. Our method provides analytical expressions for equation of state parameter of scalar field, deceleration parameter and Hubble parameter. This method can be applied to various other forms of scalar field potential, to the early radiation dominated epoch and very early scalar field dominated inflationary dynamics. Since the method produces exact analytical expression for H(a) (i.e., H(z) as well), we then constrain the model with currents data sets, which includes-Baryon Acoustic Oscillations, Hubble parameter data and Type 1a Supernova data (Pantheon Dataset). As an extension of the method, we also consider the inverse problem of reconstructing scalar field potential energy by assuming any general analytical expression of scalar field equation of state parameter as a function of scale factor.

1 Introduction

The observations of Type 1a Supernovae indicate that expansion rate of the universe in the recent past (on cosmological time scale) is speeding up (Riess et al. 1998; Perlmutter et al. 1999; Tegmark et al. 2004; Spergel et al. 2007; Davis et al. 2007; Kowalski et al. 2008; Hicken et al. 2009; Komatsu et al. 2009; Hinshaw et al. 2009; Lima & Alcaniz 2000; Lima et al. 2009; Basilakos & Plionis 2010; Komatsu et al. 2011; Planck Collaboration et al. 2014, 2020). This discovery serves as a paradigm shift in our understanding of cosmology by postulating the existence of a component named ‘dark energy’. The analysis of current cosmological observations (Planck Collaboration et al. 2020) indicates that the ‘dark energy’ provides dominant contribution to the present total energy density of the universe. The accelerated expansion took place also in a widely separated time epoch, before the Universe became radiation dominated, during inflation (Guth 1981), the theory of which was subsequently developed by Guth (1981) and Linde (1982, 1983). The inflationary epoch as well as the recent accelerated expansion can be modelled by postulating existence of a scalar field dynamically coupled to gravitation. Since a scalar field is a simple, yet natural candidate which causes accelerated expansion it plays a fundamental role in cosmology. Scalar fields have been extensively studied in cosmology (see Linde 1982, 1983; Ratra & Peebles 1988; Peebles & Ratra 2003; Bamba et al. 2012, and references therein). The scalar field, in this context, serves as the model of dark-energy. For the purpose of constraining the nature of dark-energy understanding the evolution of the universe during the accelerated expansion epoch of universe is an area of great research interest.

Currently, there is no unique underlying principle can uniquely specify the potential of the scalar field that gives rise to earlier inflationary epoch and the late time accelerated epoch of the universe. Many proposals based on new particle physics and gravitational theories were introduced (see Linde 2005, and references therein) and others were based on ad-hoc assumption so as to get the desired evolution of the universe (Ellis & Madsen 1991). There is also a formalism where we can reconstruct the potential by using the knowledge of tensor gravitational spectrum and the scalar density fluctuation spectrum (Copeland et al. 1993; Liddle & Turner 1994). Though there are numerous scalar field potential which can give rise to accelerated expansion, the exact solutions of these cosmological models are less known. As the exact solutions of cosmological models gives rise to exact cosmological parameters, they have a vital role in the present cosmological scenario. There are several methods by which one can explore the exact solutions of Friedman equations in a scalar field dominated universe. The construction of exact solutions for an inflationary scenario was started with Muslimov (1990). The author, by starting with the assumption of scalar field potential $V(\phi )$, found the remaining parameters, i.e., a(t) and $\phi (t)$ based upon the model. A method of generating exact solutions in scalar field dominated cosmology by considering scalar field potential as a function of time V(t) has been explored in Zhuravlev et al. (1998). By assigning the time dependence of scale factor a(t), we can also find the scalar field $\phi (t)$ and potential V(t) as seen in Ellis and Madsen (1991). One can also find the analytical expressions for a(t) and $V(\phi )$ by assigning time dependence of scalar field $\phi (t)$ which is explored in Barrow (1993). Barrow (1990) showed a simple method of finding exact solutions of cosmological dynamic equations in terms of a pressure–density relationship.

One can also reduce the scalar field cosmology equations to a known type of equation whose solution has already been developed. In Harko et al. (2014) and Chakrabarti (2017) we can see a method in which the Klein–Gordon equation which describes the dynamics of the scalar field is transformed to a first order non-linear differential equation. This equation immediately leads to the identification of some exact classes of scalar field potentials $V(\phi )$ for which the field equations can be solved exactly and there by obtaining analytical expressions for a(t), $\phi (t)$ and q(t). The solutions of the Friedman equations in a scalar field dominated universe is explored by its connection with the Abel equations of first kind is seen in Yurov & Yurov (2010). Here for a given $V(\phi )$ one can obtain a(t) and $\phi (t)$ analytically. The exact solutions for exponential form of the potential $V(\phi )$ by rewriting the Klein–Gordon equation in the Riccati form and thereby transforming it into a second-order linear differential equation is investigated in Andrianov et al. (2011). Analytical solutions to the field equations can also be obtained by considering suitable generating functions. Here the generating functions are chosen as a function of one of the parameters of the model (Kruger & Norbury 2000; Charters & Mimoso 2010; Harko et al. 2014; Chervon et al. 2018) and thus by simplifying the scalar field cosmology equation one can obtain all the parameters of the model. In Salopek & Bond (1990) a method was proposed by simplifying scalar field cosmology equation by assuming Hubble function as a function of scalar field $\phi$. By making use of the Noether symmetry for exponential potential (de Ritis et al. 1990; Paliathanasis et al. 2014), Hojman’s conservation law (Capozziello & Roshan 2013), and other non-canonical conservation laws (Dimakis et al. 2016) for arbitrary potential and also by the form-invariant transformations of scalar field cosmology equations (Chimento et al. 2013) one can obtain the exact solutions for the parameters of the model. Moreover analytical solutions for field equations by considering a homogeneous scalar field in the Szekeres cosmological metric has been investigated in Barrow & Paliathanasis (2018).

Though there are various ways for finding exact solutions in scalar field cosmology, the solutions are limited if we incorporate the contributions by a perfect fluid source. In Chimento & Jakubi (1996) the authors showed that the Einstein’s equations with a self-interacting minimally coupled scalar field, a perfect fluid source and cosmological constant can be reduced to quadrature in the Robertson–Walker metric. Here the scale factor is considered as the independent variable and the scalar field potential is expressed in terms of scale factor. Barrow & Saich (1993) presented exact solutions of Friedman universes which contain a scalar field and a perfect fluid with the requirement that the kinetic and potential energies of the scalar field be proportional. The classes of scalar field potentials $V(\phi )$, which provide exact solutions for scalar field with scaling behavior had been investigated in Liddle & Scherrer (1999). In Barrow & Paliathanasis (2016) specific closed-form solutions of field equations (with and without matter source) have been derived by assuming special inflationary functions for the scale factor and special equation of state parameters of the scalar field. The application of lie symmetry methods in finding the exact cosmological solutions for scalar field dark energy in the presence of perfect fluids has been investigated in Paliathanasis et al. (2015). In Socorro et al. (2015), a scenario of time varying cosmological term is investigated by using a special anartz were energy density of the scalar field is proportional to energy density of the barotropic fluid. Fomin (2018) explored the exact solutions by considering scalar field and matter fields or non-zero curvature by representing the main cosmological parameters as a function of number of e-folds and also by the direct substitution of the scale factor. The study of late-time cosmology in a (phantom) scalar-tensor theory with an exponential potential had been investigated in Elizalde et al. (2004). In Elizalde et al. (2008), the unification of inflation and late-time acceleration epochs within the context of a single field theory had been studied. Moreover, the exact and semiclassical solutions of the Wheeler–DeWitt equation for a particular family of scalar field potential had been explored in Guzmán et al. (2007).

In this paper, we propose a new method of finding analytical solutions of equation of state parameter of scalar field, deceleration parameter and also the Hubble parameter as a function of scale factor. Using the continuity equation for the scalar field we form a first order linear inhomogeneous equation of the independent variable $\dot{\phi}^2$ and dependent variable a. Since the inhomogeneous term is given by − dV/da, derivative of the scalar field a the linear equation is exactly solvable for any choice of V = V(a). As some test applications we present solutions for some chosen forms of V(a). Since the linear equation is completely decoupled from the other source terms of the Friedmann equation the solution of $\dot{\phi}^2$(a) and the chosen form of V(a) can be used in the right hand side of first Friedmann equation together with the other source terms. Therefore, apart from the scalar field, our method can incorporate matter or radiation as a perfect fluid source to obtain an exact solution of H(a) or H(z), which can be constrained using observations. Since the method is applicable for any well behaved (e.g., differentiable w.r.t. a) chosen form of V(a) it can be applied to understand the physics of the inflation, as well as the late time acceleration of expansion rate.

The paper is organized as follows. In Section 2 we explore the basis equations in scalar field cosmology. In Section 3 we consider the scalar field potential energy of power law form. The Section 4 is dedicated to the reconstruction of scalar field potential energy. After discussing the relationship of the scalar field potential with the particle physics models in Section 5, we constrain the model parameters in Section 6. Finally, in the last Section 7 we discuss and conclude upon our results.

2 Formalism

In the spatially flat Friedman–Robertson–Walker (FRW) model of the universe the space-time interval ds between two events in a global comoving Cartesian coordinate system follows,

$$ ds^2=dt^2-a^2(t)(dx^2+dy^2+dz^2), $$

(1)

where a and t represent the scale factor and comoving time respectively and we have used c = 1 unit. If the universe is dominated by the non-relativistic matter (e.g., baryon and cold dark matter) and a spatially homogeneous and time varying scalar field, $\phi$ which is minimally coupled to gravity, the evolution of a(t) is determined by the following system of equations,

$$ H^2 \equiv \left( \frac{{\dot{a}}}{a}\right) ^2=\frac{8\pi G}{3}[\rho _\phi +\rho _m], $$

(2)

$$ \frac{\ddot{a}}{a} =-\frac{4\pi G}{3}[\rho _m +\rho _\phi +3(p_m+p_\phi )], $$

(3)

where an over-dot represents derivative with respect to the comoving time t, and $\rho _{\phi }$ and $\rho _m$ represent the scalar field and matter density respectively. The time evolution of $\phi (t)$ couples to a(t) and $V(\phi )$ and is governed by the second order generally non-linear differential equation,

$$ \ddot{\phi }+3H{\dot{\phi }}+\frac{dV}{d\phi }=0. $$

(4)

We also have the continuity equation which holds separately for each component,

$$ {\dot{\rho }}+3H \rho (1+\omega )=0, $$

(5)

where ${\omega } \equiv p/\rho$ represents the equation of state parameter for the component under consideration. The fluids filling the universe have equation of state given by,

$$ p_m=0, \quad p_\phi =\omega _\phi \rho _\phi , $$

(6)

with

$$ \rho _m={\frac{\rho ^0_{m}}{a^3}}^1, \quad \rho _{\phi } =\frac{\dot{\phi}^2}{2}+V, \quad p_\phi =\frac{\dot{\phi}^2}{2}-V. $$

(7)

¹Using $p_{\phi }$ and $\rho _{\phi }$ from Equation (7) in Equation (5) along with $p_{\phi } =\omega _{\phi } \rho _{\phi }$, we can rewrite continuity equation as follows,

$$ \frac{d}{da}\left( \frac{\dot{\phi}^2}{2}\right) +\frac{dV}{da} +\frac{3}{a}\left( \frac{\dot{\phi}^2}{2}\right) =0. $$

(8)

Now, by considering V = V(a) and using the transformation $\dot{\phi}^2(a)=y(a)$ we get the following linear differential equation

$$ \frac{dy}{da}+2\frac{dV}{da}+\frac{6}{a}y=0, $$

(9)

where we have assumed that y and V are in units of present day critical energy density $\rho ^0_{c}$ such that

$$ y\rightarrow y'=\frac{y}{\rho ^0_{c}}, \quad V\rightarrow V'=\frac{V}{\rho ^0_{c}}, $$

(10)

and omitted any primes in our forthcoming analysis of this work. The solution of linear differential Equation (9) gives ${{\dot{\phi}^2}}(a)$.² Using Equation (10) the Friedmann Equations (2) and (3) become

$$ H^2(a) = H^2_0\left( \frac{{{\dot{\phi^2 }}}}{2} + V(a) + \frac{\Omega ^0_m}{a^3}\right) $$

(11)

and

$$ \frac{\ddot{a}}{a} = -H^2_0\left( {{{\dot{\phi^2 }}}} - V(a) + \frac{\Omega ^0_m}{2a^3}\right) , $$

(12)

where we have assumed $p_m = 0$. At this point, we mention that once a form of V(a) is assumed, Equation (9) may be considered to be decoupled from the expansion dynamics of the universe, i.e., it does not depend on the exact solution of a(t) which is obtained from first and second Friedman equations, Equations (11) and (12). This is an excellent advantage since the independent variable y(a) can now be evolved irrespective of evolution of other components that contribute to the total energy momentum tensor. Another advantage of Equation (9) is that using its solution we immediately obtain the equation of state parameter of scalar field as, $\omega _\phi$ as

$$ \omega _{\phi }(a)=\frac{{\dot{\phi}^2}/{2}-V}{{\dot{\phi}^2}/{2}+V}, $$

(13)

which serve as an important physical parameter to describe and constrain the nature of dark energy from both observational and theoretical point view. In this work, we focus ourselves for cases where both ${{\dot{\phi}^2}}$ and V(a) are positive (semi) definite, resulting in $-1 \le \omega _\phi (a) \le 1$.

Once ${{\dot{\phi}^2}}(a)$ is solved using Equation (9) for the assumed model of V(a) one can relate the dynamics of the $\phi$ sector with some important dynamical variables of the dynamics of a(t). One such variable is the total effective equation of state parameter, $\omega _{\mathrm{tot}}$ taking into account all components of the universe

$$ \omega _{\text {tot}}(a)\equiv \frac{p_\phi + p_m}{\rho _\phi + \rho _m} \equiv \frac{{\dot{\phi}^2(a)}/{2}-V(a)}{{\dot{\phi}^2(a)} {/2}+V(a)+{\Omega ^0_{m}}/{a^3}}, $$

(14)

where $\Omega ^0_{m}$ represents the present day energy density parameter for matter. The effective equation of state parameter, $\omega _{\text {tot}}$ has great significance because it tells us whether the universe undergoes an accelerated expansion ($\omega _{\text {tot}}\,<\,-1/3$) or decelerating expansion ($\omega _{\text {tot}}\,>\,-1/3$) at any particular epoch of time. Another useful parameter which encodes the information of acceleration or deceleration phases of a(t) in its sign is the so-called deceleration parameter, q, defined as

$$ q=-\frac{\ddot{a}}{\dot{a^2}}a= -\frac{\ddot{a}}{a}\left( \frac{{\dot{a}}}{a}\right) ^{-2} = -\frac{\ddot{a}}{a}(H)^{-2}. $$

(15)

A transition between the two phases always corresponds to zeros of the q parameter. Since $\dot{\phi}^2(a)$, V(a) and $\rho _m(a)$ are now known functions of scale factor, by using Equation (2) we can easily obtain the Hubble parameter, H(a).³ Knowing the numerator of Equation (15) using Equation (12) and denominator using Equation (11) we find an exact expression of q(a) as well.

Before we proceed to discuss solution of Equation (9) for specific choice of V(a) let us discuss some general features of these solutions. First, a = 0 is a singular point of Equation (9). This means that the solution ${{\dot{\phi}^2}}(a)$ is not analytic at a = 0. One common feature of ${{\dot{\phi}^2}}$ may be obtained by considering the associated homogeneous equation corresponding to Equation (9) by setting either V = 0 or $V = V_0$, a constant for all a, so that dV/da = 0. In this case, ignoring the trivial solution, ${{\dot{\phi}^2}}(a) = 0$, we have ${{\dot{\phi}^2}}(a) = {{\dot{\phi}^2}}_0/a^6$. In fact, presence of a modulation factor of ${\sim }1/a^6$ is ubiquitous in the solution of ${{\dot{\phi}^2}}(a)$ through the integrating factor of Equation (9) for any other choice of V(a). Thus ${{\dot{\phi}^2}}$ diverges in general, as $a \rightarrow 0$. This can be contrasted with the corresponding behavior for matter (or radiation) density, $\rho _m(a) = \rho ^0_m/a^3(\rho _r(a) = \rho ^0_r/a^4)$. We note that, such divergence of ${{\dot{\phi}^2}}(a)$ does not necessarily imply divergence of $\omega _\phi$, for a general V(a). If $V = V_0$ we have $\omega _\phi (a) =(\dot\phi^2_0 - 2a^6V_0)/(\dot\phi^2_0 + 2a^6V_0)$, which tends to unity as $a \rightarrow 0$.⁴

3 Applications

3.1 Power law potential

Let us consider the power law form of potential energy density

$$ V(a)=V_{0} a^n, $$

(16)

where $V_{0}$ is a dimensionless constant and n is a real number. By direct observation of Equation (9) we see that in this case, ${{\dot{\phi}^2}}(a) \sim a^n$ is a solution. If $n > 1$ all terms of Equation (9) remains finite for all a. In fact, for any polynomial choice of

$$ V(a) = \sum _{p=0}^nV_pa^{p+1}, $$

(17)

where $V_p$ for $p =1, \ldots , n$ are constants, ${{\dot{\phi}^2}}(a)$ also admits a polynomial solution

$$ {{\dot{\phi}^2}}(a) = \sum _{p\,=\,0}^nA_pa^{p+1}, $$

(18)

which is finite for all a. In this case, (9) becomes

$$ \sum _{p\,=\,0}^nA_p(p+7)a^p = -2\sum _{p\,=\,0}^nV_p(p+1)a^p, $$

(19)

which leads to a solution of the form

$$ {{\dot{\phi^2 }}}(a) = -2\sum _{p\,=\,0}^n \frac{V_p(p+1)}{(p+7)}a^{p+1}. $$

(20)

Equation (20) does not capture the complete picture of the most general solution ${{\dot{\phi}^2}}(a)$ since it only corresponds to the solution of the in-homogeneous Equation (9). The general solution of Equation (9) is obtained after adding with Equation (20) $C/a^6$, which is the solution corresponding to the homogeneous equation of Equation (9), where C is a constant. The general solution is therefore

$$ {{\dot{\phi}^2}}(a) = -2\sum _{p\,=\,0}^n \frac{V_p(p+1)}{(p+7)}a^{p+1} + \frac{C}{a^6}. $$

(21)

The constant C is fixed by imposing suitable boundary condition. If the potential energy density consists of a single power law as given by Equation (16), the only value of p in Equation (21) becomes $p = n -1$. Equation (21) now becomes

$$ \dot{\phi}^2(a)\equiv y(a)= \frac{1}{a^6}\left( -\frac{2V_{0} n a^{n+6}}{n+6}+C \right) , $$

(22)

where $n \ne -6$. If at $t = t_0$, $a=a_{0}=1$ and $\dot{\phi}^2(1)=y_{0}$, then $\rho ^0_{\phi } +\rho ^0_{m} = \rho ^0_{c} = 3H^2_0/(8\pi G)$, which following the definitions of Equation (10) implies

$$ {y_0} = 2(1-V_0-\Omega ^0_{m}). $$

(23)

Using Equations (22) and (23) we obtain

$$ C= y_{0}+\frac{2V_{0}n}{n+6} = 2\left[ \frac{n+6(1-V_0)}{n+6}\right] - 2\Omega ^0_m. $$

(24)

Finally using Equations (22) and (24) we obtain

$$\begin{aligned} \dot{\phi}^2(a)= & \frac{1}{a^6}\left[ 2 \left( \frac{n+6(1-V_0)}{n+6}\right) \right. \\&\left. -\frac{2V_{0} n a^{n+6}}{n+6} - 2\Omega ^0_m\right] . \end{aligned}$$

(25)

To get some insight into the nature of the solution given by Equation (25) we first consider a simple case for which n = 0 (implying $V = V_0$, a constant) and $\Omega ^0_m = 0$ as well. This corresponds to a dark energy dominated flat universe with $\dot\phi ^2_{0} = 2(1-V_0)$. If $V_0 \ne 1$, $V \ne 1$ for always and using Equation (25),

$$ {{\dot{\phi}^2}}(a) = \frac{2(1-V_0)}{a^6}, $$

(26)

implying the kinetic energy density of the scalar field decays as $\sim a^{-6}$ as the universe expands. One can further consider two limiting values of $V_0$, namely, 1 and 0 respectively. If $V_0 =1$ then from Equation (25) ${{\dot{\phi^2 }}}(a) = 0$ for all a implying $\phi$ is a constant. In this case, as expected, we recover the cosmological model with cosmological constant with $\omega _{\phi }(a) = -1$. If $V_0 =0$, $\dot\phi^2_0 = 2$ to satisfy the flatness condition today. In this case, $\omega _{\phi } = 1$ always and hence the particular scalar field theory does not cause inflation. Using Equation (26) we obtain ${{\dot{\phi}^2}}(a) = 2/a^6$. Substituting this in first Friedmann equation with $\Omega ^0_m = 0$ and after some algebra one finds

$$ a(t) = (H_0)^{1/3}t^{1/3}, $$

(27)

where we have used boundary condition a = 0 at t = 0. Clearly this particular scalar field does not cause inflation as argued earlier since $\omega _{\phi } =1$. In summary, we conclude that for different choices of numerical values of $V_0$ and specific choice of exponent n in Equation (16) the solutions ${{\dot{\phi}^2}}(a)$ as given by Equation (9) are capable of capturing a wide range of dynamical behavior of scale factor a(t).

Using the general solution ${{\dot{\phi}^2}}(a),$ Equations (25) and (16) in Equations (13) and (14) respectively, we obtain

$$ \omega _{\phi } = \frac{n +6(1-V_0) - \Omega ^0_m(n+6) - 2V_0(n+3)a^{n+6}}{n +6(1-V_0) - \Omega ^0_m(n+6) +6V_0a^{n+6}} $$

(28)

and

$$\begin{aligned} \omega _{\mathrm{tot}}&=(n +6(1-V_0) - \Omega ^0_m(n+6)- 2V_0(n+3)a^{n+6})/ \\& \times (n +6(1-V_0) - \Omega ^0_m(n+6)+6V_0a^{n+6} \\& + \Omega ^0_ma^3(n+6)). \end{aligned}$$

(29)

One can also easily calculate the Hubble parameter H(a) as a function of scale factor using the Equation (11)

$$\begin{aligned} H^2(a)&= H_0^2 \left[ \frac{1}{a^6}\left( \frac{n+6(1-V_0)}{n+6}- \Omega ^0_m-\frac{V_{0} n a^{n+6}}{n+6} \right) \right. \\&\quad \left. +V_{0} a^n+\frac{\Omega _{m0}}{a^3} \right] .^{5} \end{aligned}$$

(30)

⁵The deceleration parameter q(a) can be obtained from the Equation (15)

$$\begin{aligned} q(a)&= (\Omega ^0_m(a^3-4)(6+n)+n(4-6a^{n+6}V_0) \\&\quad -12(-2+(2+a^{n+6})V_0))/(2(6+n+\Omega ^0_m(n+6) \\&\quad \times (a^3-1)-6 V_0+6a^{n+6}V_0)). \end{aligned}$$

(31)

4 Reconstruction of scalar field potential energy

The first order differential Equation (9) has another great advantage. It can be used as a tool to reconstruct V(a) and ${{\dot{\phi}^2}}(a)$ from any general equation of state parameter, $w_\phi (a)$ of the scalar field. To illustrate this, we first note that

$$ {{{\dot{\phi}^2}}}(a) = \left[ \frac{\omega _\phi +1}{1-\omega _{\phi }}\right] (2V(a)), $$

(32)

where we have used Equation (13),⁶ after calculation, we obtain

$$ \frac{d{{\dot{\phi}^2}}(a)}{da} = \frac{2V}{(1-\omega _\phi )^2}\frac{d\omega _\phi }{da} + 2\frac{dV}{da}\left[ \frac{1+\omega _\phi }{1-\omega _\phi }\right] . $$

(33)

Using Equations (32) and (33) in Equation (9), after calculation we obtain

$$ \frac{dV}{da} + V\left[ \frac{3 (1 + \omega _\phi )}{a} + \frac{1}{2(1-\omega _\phi )}\frac{d\omega _\phi }{da}\right] = 0, $$

(34)

which has the solution,

$$\begin{aligned} V(a)= & V_0 \exp \left[ -\int ^a_{1} \left\{ \frac{3 (1 + \omega _\phi )}{a}\right. \right. \\&\left. \left. + \frac{1}{2(1-\omega _\phi )} \frac{d\omega _\phi }{da}\right\} da\right] , \end{aligned}$$

(35)

where $V_0 = V(a = a_0 = 1)$ as earlier. It is evident from Equation (35) that given any general form of $\omega _\phi$ an analytical expression of scalar field potential energy density can be obtained as long as the first and second integrands in the exponent of this equation are integrable. The second integral in the exponent can further be carried out analytically. Performing integration by parts on the first integrand, and after calcutation as in Appendix we find

$$\begin{aligned} V(a)&= V_0\left[ \frac{1-\omega _\phi (1)}{1-\omega _\phi (a)} \right] ^{1/2}a^{-3(1+\omega _\phi (a))} \\&\quad \times \exp \left\{ 3\int _1^a\frac{d\omega _\phi }{da}\ln (a)da\right\} . \end{aligned}$$

(36)

It is interesting to note from Equation (36) that apart from the scale factor dependence through $\omega _\phi$ induced by the first term $[(1-\omega _\phi (1))/(1-\omega _\phi (a))]^{1/2}$, V(a) is determined by the product of one power law and another exponential function in a. As a simple application of Equation (36) if we assume $\omega _\phi = -1$ for all a, the exponential function on a becomes unity and since $d\omega _\phi /da =0$, the integral in the exponent disappear as well, implying $V = V_0$, a constant. In this case, ${{\dot{\phi}^2}} = 0$ by using Equation (32), as expected. Therefore, starting from $\omega _{\phi } = -1$ we reproduce the well known case of a cosmological constant by using the general solution of V(a) (Equation 36) and definition of $\omega _\phi$ (Equation 32). If we assume $\omega _\phi (a) =0$ for all a, then using Equation (36) we obtain $V(a) = V_0/a^3$ and ${{\dot{\phi}^2 }}/2 = V(a)$ using Equation (13), i.e., the kinetic energy of the scalar field traces the potential energy exactly for all a. In the case, the scalar field behaves like pressure less non relativistic matter. One can also reconstruct the scalar field potential from the observed spectral indices for the density perturbation $n_s$ and the tensor to scalar ratio r as seen in Barrow & Paliathanasis (2016).

An interesting application of Equation (35) is to obtain potential energy density for the CPL equation state

$$ \omega _\phi (a) = \omega _0 + \omega _1a, $$

(37)

where $\omega _0$ and $\omega _1$ are constants.⁷ Using Equation (37) in Equation (36) we obtain

$$ V(a) = V_0\left[ \frac{1-\omega _0-\omega _1}{1-\omega _0 -\omega _1a}\right] ^{1/2}a^{-3(1+\omega _0 + \omega _1a )} a^{\omega _1}. $$

(38)

If $\omega _1 = 0$ in Equation (37) so that $\omega _\phi = \omega _0 \ne 1$, Equation (38) leads to

$$ V(a) = V_0a^{-3(1+\omega _0)}. $$

(39)

By using Equation (13) we can also obtain

$$ {{\dot{\phi}^2}}(a) = 2V_0^{-3(1+\omega _0)}(1+\omega _0)/(1-\omega _0). $$

(40)

5 Relation with the particle physics models

Once we obtain ${{\dot{\phi}^2}}(a)$ analytically, it is possible to get an analytical expression for the Hubble parameter H(a) using Equation (11). Then by a numerical evaluation one can easily obtain $\phi (a)$ and finally the particle physics motivated form, i.e., potential in terms of the scalar field, $V(\phi )$. This can be achieved by the following procedure. It is simple to estimate $\dot{a} = aH(a)$, where we already obtained an analytical expression for the Hubble parameter H following our method. Using identity $\dot{a} = (da/d\phi ){{\dot{\phi }}}$ and knowing ${{\dot{\phi }}}$ following the method of this article, one obtains $\phi (a)$ after employing a numerical integration. From the graph of $\phi (a)$ and V(a) one can readily estimate $V(\phi )$ numerically. This makes a connection of our method with the theory of particle physics, since there $V(\phi )$ is directly model led following symmetry conditions of the theory. Thus for any choice of potential V(a), one can obtain its corresponding form of $V(\phi )$. For instance, considering the case of the potential V(a) in the power law form discussed in Section 3.1, one can easily obtain the corresponding form of $V(\phi )$ using the method mentioned above. Here the scalar field $\phi$ is scaled by $\sqrt{8\pi G}= M_p^{-1}$. Figure 1 shows the variation of scalar field potential as a function of scalar field for the case of the potential $V(a)=V_0 a^n$ with $V_0=0.672$ and n = − 0.24. It is very interesting to note that, this potential approximates an inverse power law potential of the form $V(\phi )=V^\prime _0 (\phi + \phi _0)^{-m}$ with $V^\prime _0= 0.16$, $\phi _0=0.00049$ and m = 0.257 with some level of clearly visible differences. This is shown in blue in Figure 1. It is noteworthy to mention that the derived potential $V(\phi )$ resembles to the class of quintessential tracker potentials (inverse power law models) proposed by Ratra & Peebles (1988).

Figure 1

The reconstructed potential $V(\phi )$ (in red) with $\phi$ when $V(a)=V_0 a^n$. The blue curve shows the potential $V(\phi )=V^\prime _0 (\phi + \phi _0)^{-m}$ with $V^\prime _0= 0.16$, $\phi _0=0.00049$ and m = 0.257.

6 Observational constraints

After obtaining the analytical expressions for Hubble parameter as a function of redshift (or scale factor) for different cosmological models, one can constrain its model parameters using the observational probes in the cosmology. The observational probes utilized for the data analysis includes the Type 1a supernovae, Baryon acoustic oscillations and Hubble parameter data sets. We constrain the parameters by employing the $\chi ^2$ statistics. The total likelihood function for the joint data is given by

$$ {\mathcal {L}}_{\mathrm{tot}}(\theta ) = e^{- \chi _{\mathrm{tot}}^2(\theta )/2}, $$

(41)

where

$$ \chi _{\mathrm{tot}}^2=\chi _{\mathrm{SN}}^2+\chi _{\mathrm{Hub}}^2+\chi _{\mathrm{BAO}}^2, $$

(42)

where $\theta$ denotes the parameters of the model under consideration. The best fit values of the model parameters ($\theta$) are the values corresponding to the minimum $\chi ^2$ value.

6.1 Observational probes

6.1.1 Hubble data (H)

The Hubble parameter data set consists of measurements of the Hubble parameter H(z) at different redshifts. We use H(z) data which is compiled and listed in Table 1 of Farooq et al. (2017). The table contains 38 measurements of Hubble parameter and its associated errors in measurements up to a redshift of z = 2.36. From the total of 38 data sets, we have considered only 32 points as we do not consider three data points taken from Alam et al. (2016) at reshifts z = 0.38, 0.51, 0.61 and we also removed the data points corresponding to the redshits z = 0.44, 0.6, 0.72 as they are already included in the BAO dataset. The chi-squared function of Hubble data is given by

$$ \chi _{\mathrm{Hub}}^2(\theta )=\sum _{i=1}^{32} \frac{[H_{\mathrm{th}}(z_i,\theta )-H_{\mathrm{obs}}(z_i)]^2}{ \sigma ^2_H(z_i)}, $$

(43)

were $\sigma _H$ is the error associated with each measurements.

6.1.2 Type 1a supernovae (SN 1a)

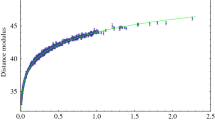
The Type 1a supernovae are the result of the explosion of a white dwarf star in a binary when it crosses the Chandrasekhar limit. These Type 1a supernovae is an ideal probe for the study of the cosmological expansion. As they all have the same luminosity, they are considered as a good standard candle. So the first data set which we used for the analysis is the Type 1a supernovae data from the Pantheon compilation (Scolnic et al. 2018). This data set consists of 1048 supernovae in the redshift range $0.01< z <2.26$.

The luminosity distance of a Type 1a supernova at given redshift z reads as

$$ D_L(z)=(1+z) \int _0^z\frac{H_0dz'}{H(z')}. $$

(44)

Moreover the luminosity distance is directly related to the observed quantity, distance modulus $\mu (z)$ given by

$$ \mu (z)=m - M=5 \log D_L(z)+\mu _0, $$

(45)

where M and m are the absolute and apparent magnitude of the supernovae. Here the quantity $\mu _0=5 \log ({H_0^{-1}}/\mathrm{Mpc})+25$ is a nuisance parameter which should be marginalized.

So for the case of SN 1a, the $\chi ^2_{\mathrm{SN}}$ estimator is defined as

$$ \chi _{\mathrm{SN}}^2(\mu _0,\theta )=\sum _{i\,=\,1}^{1048} \frac{[\mu _{th}(z_i,\mu _0,\theta )-\mu _{\mathrm{obs}}(z_i)]^2}{ \sigma ^2_\mu (z_i)}, $$

(46)

where $\mu _{th}$, $\mu _{\mathrm{obs}}$ and $\sigma _\mu$ are the theoretical, observed distance modulus and the uncertainty in the observed quantity respectively. Here $\theta$ represents the parameters of the model under consideration. After marginalizing $\mu _0$ and by following the reference Nesseris & Perivolaropoulos (2005), we get

$$ \chi _{\mathrm{SN}}^2(\theta )=A(\theta )-\frac{B^2(\theta )}{C(\theta )}, $$

(47)

where

$$ A(\theta ) =\sum _{i=1}^{1048} \frac{[\mu _{th}(z_i,\mu _0=0,\theta )-\mu _{\mathrm{obs}}(z_i)]^2}{ \sigma ^2_\mu (z_i)},$$

(48)

$$ B(\theta ) =\sum _{i=1}^{1048} \frac{\mu _{th}(z_i,\mu _0=0,\theta )-\mu _{\rm obs}(z_i)}{\sigma ^2_\mu (z_i)}, $$

(49)

$$ C(\theta ) =\sum _{i=1}^{1048} \frac{1}{\sigma ^2_\mu (z_i)}. $$

(50)

6.1.3 Baryon acoustic oscillations (BAO)

The Baryon acoustic oscillations (BAO), which are considered as the standard rulers of the cosmology, are frozen relics left over from the pre-decoupling universe. Here we have used the BAO data from 6dFGS, SDSS DR7 and WiggleZ at redshifts z = 0.106, 0.2, 0.35, 0.44, 0.6 and 0.73. In order to derive the BAO constraints we make use of the distance parameter $D_v(z)$ which is a function of angular diameter distance and Hubble parameter given by

$$ D_v(z) = \left[ (1+z)^2 d^2_A(z)\frac{z}{H(z)}\right] ^\frac{1}{3}. $$

(51)

Here $d_A(z)$ is the angular diameter distance. We use the measurements of acoustic parameter A(z) from Blake et al. (2011), where the theoretically predicted $A_{th}(z)$ is given by Equation (5) of Eisenstein et al. (2005)

$$ A_{th}(z) = \frac{100 D_v(z) \sqrt{\Omega _{m0}h^2}}{z}. $$

(52)

After following the procedures given in Section 5.4 of Omer Farooq (2013), one can obtain the acoustic parameter $A_{th}$ independent of the Hubble constant $H_0$. Finally after calculations the chi-squared function of BAO data (Blake et al. 2011) reads as

$$ \chi _{\mathrm{BAO}}^2(\theta )=\sum _{i=1}^{6} \frac{[A_{th}(z_i,\theta )-A_{\mathrm{obs}}(z_i)]^2}{ \sigma ^2_A(z_i)}. $$

(53)

Table 1 Priors used for the MCMC analysis of the power law potential, $V_0 a^n$.

6.2 Methodology

We used the Markov Chain Monte Carlo (MCMC) method to find the high confidence regions of the model parameters given a set of observational data. We perform a likelihood analysis to minimize the $\chi ^2$ function in Equation (42) and thereby obtain the best-fit model parameters corresponding to the minimum $\chi ^2$ value. The minimization of the $\chi ^2$ is equivalent to the maximization of the likelihood function in Equation (41). Here we constrain the parameters of the power law potential given in Section 3.1. The model parameters and their prior values considered for the MCMC analysis is given in Table 1.

Initially, we begin the MCMC analysis with the usual way where we consider a simple proposal function of the form, $\theta ^j_{i+1} = \theta ^j_i + \delta \theta ^j \eta ^j$, where j is a parameter index, $\delta ^j$ is a predefined rms step size, and $\eta ^j$ is a Gaussian stochastic variate of zero mean and unit variance. As we are dealing with a model of five parameters, most of the parameters of interest will be strongly correlated and make this choice quite inefficient. So we performed certain optimization on the MCMC chain samples, which enables us to increase the acceptance ratio and also the chain convergence. After obtaining sufficient samples from the preliminary chain, we check the autocorrelation of the Markov chain. This will give us an idea for estimating how many iterations of the Markov chain are needed for effectively independent samples. Later we perform thinning on the initial chain we had already obtained so as to get less correlated samples. This action will further reduce the total number of samples. We will then compute the covariance matrix $C_{ij} = \langle \delta \theta ^i\delta \theta ^j\rangle$ of the resulting samples. Finally, we then Cholesky-decompose this matrix, $\varvec{C} =\varvec{L L^{t}}$ where $\varvec{C}$ is the covariance matrix, $\varvec{L}$ and $\varvec{L^t}$ are the lower triangular matrix and its conjugate transpose respectively. We then redefine our proposal function to be $\theta _{i+1} = \theta _i + \alpha \varvec{L} \eta$, where $\eta$ is now a vector of Gaussian variate and $\alpha$ is an overall scale factor, typically initialized at ${\sim }0.3$. This will help us to have the proposed samples with approximately correct covariance structure, and it will also improve the sampling efficiency significantly. In order to avoid very high and very small step sizes, we also impose a constraint that the acceptance ratio must be higher than 5% and lower than 80%. One can adjust the scale factor $\alpha$ if one of these two criteria is violated.

Table 2 Best fit model for the power law potential.

7 Discussions and conclusions

The exact solutions of Einstein’s equations play a very important role in cosmology as they help in the understanding of quantitative and qualitative features of the dynamics of the universe as a whole. In this article, we discuss a method to obtain analytical expressions for the equation of state parameter, deceleration parameter and Hubble parameter in spatially flat FRW model of the universe with a perfect fluid and scalar field.

In Section 2, a method is proposed to obtain analytical expressions for the kinetic energy ($\dot{\phi}^2$) of the scalar field as a function of scale factor for different choices of the scalar field potential. Once the kinetic term ($\dot{\phi}^2$) is obtained, one can also obtain exact solutions for $\omega _{\phi }$, $\omega _{\mathrm{tot}}$, q and H(a) by simple substitution. The method proposed in this article can also be applied to inflationary phase, to obtain analytical solutions, where the scalar field dominates. The effective equation of state parameter $\omega _{\mathrm{tot}}$ and also the deceleration parameter are of great importance as they provide information about the epochs of acceleration and deceleration phases of the universe.

It is important to emphasize the importance of exact expression of H(a) (or H(z)) obtained by us in scalar field cosmology with other perfect fluid components like matter and radiation. The analytical results can be directly fitted with observations of H(z) to estimate the best-fit values of parameters of the theory. Thus our method builds an important connection between theory and observations to constrain the scalar field potential along with other cosmological parameters.

In Section 4, we consider the inverse problem of reconstructing the scalar field potential energy by assuming any general analytical expression of scalar field equation of state parameter as a function of the scale factor. By this method, we also reconstructed the scalar field potential for one of the most widely used parametrizations of dark energy called the Chevallier–Polarski–Linder (CPL) model.

Another important result that can be obtained using the results of this article, is to reconstruct the scalar field potential in terms of scalar field. In Section 5, we have discussed the method of reconstruction of $V(\phi )$ from the assumed model of V(a) and the exact analytical expressions of ${{\dot{\phi }}}(a)$, H(a) and using simple numerical integration. Thus we obtained that the potential $V(a)=V_0 a^n$ has a close resemblance to the class of quintessential tracker potentials proposed by Ratra & Peebles (1988).

Finally in Section 6, we constrained the model parameters of the power law potential with the Hubble parameter data, BAO data and the recent Panthelon Type 1a supernovae compilation. The contours showing the 68.3% and 98.5% confidence regions are depicted in Figure 2. The best-fit and the mean values are shown in Table 2. Interestingly, we observed that the $H_{0}$ value ($H_0 = 67.1\pm 1.5$ Km/S/$\hbox {M}_{\mathrm{pc}}$) we obtained with low redshift data is consistent with the high redshift CMB observations ($H_0 = 67.4\pm 0.5\,\hbox {Km/S/M}_{\mathrm{pc}}$) at one sigma (Planck Collaboration et al. 2020). We also explored the late-time evolution of the universe corresponding to the best-fit model parameters. Although, the formalism of this article is capable also for early scalar field dominated inflation, in the current work we focus on the study of the late time acceleration of the universe. For our analysis, we therefore, choose the scale factor between a = 0.1 and a = 1.2 which includes the current epoch $a_0 = 1$.⁸

Figure 2

Posterior distribution for the model parameters ($\Omega _{m0}, V_0, n, H_0$) of the power law potential. The contours shows 68.3% and 95.5% confidence regions. The quantitative results are summerised in Table 2.

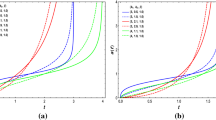
The variation of equation of state parameter $\omega _{\phi }$ and deceleration parameter q(a) for the best-fit parameters are shown in Figures 3 and 4. From the Figure 3, we can see that the present value (a = 1) of the equation of state parameter of the scalar field can go as low as $\omega _{\phi }=-0.9999$. Thus at the present epoch, the scalar field behaves just like a cosmological constant. This is because within two sigma limits the best-fit value of the power ‘n’ is consistent with zero, see Table 2, which gives a constant scalar field potential. Moreover, the transition between the deceleration to the accelerated phases of expansion occurs at $a\sim 0.6$ which is also shown in Figure 4. The Figure 5 shows the variation of energy density of the scalar field and the non-relativistic matter as a function of scale factor. We see that transition between matter and dark-energy dominated universe occurs around $a \sim 0.75$, i.e., the scalar field starts to dominate at the very late stage of the evolution of the Universe and it drives the present accelerated expansion. From the Table 2, the present density parameter of the non-relativistic matter and dark energy corresponds to $\Omega _{m0}\sim 0.29$ and $\Omega _{\phi }\sim 0.71$ respectively.

Figure 3

The variation of $\omega _{\phi }$ as a function of scale factor corresponding to the best-fit values of the power law potential.

Figure 4

The variation of deceleration parameter as a function of scale factor corresponding to the best-fit values of the power law potential.

Figure 5

The variation of energy density (log scale) of scalar field and non-relativistic matter as a function of scale factor corresponding to the best-fit values of the power law potential.

The method discussed in Section 2 is not limited to the power law form of the potential that we have considered. It can also be applied to any other forms of potentials which are not discussed here. This method helps in finding the cosmological dynamical variables in an exact form without even knowing the evolution of scale factor. For instance, the Hubble parameter, H(a) which we obtained analytically is directly observable. So the difficulty of solving coupled non-linear equations that one usually encounters while applying observational constraints in scalar field dark energy models can be alleviated.

Appendix

To derive Equation (34) using Equation (32) we first obtain

$$\begin{aligned} \frac{d{{\dot{\phi}^2}}}{da}&= 2\left[ \frac{dV}{da} \left( \frac{1+\omega _\phi }{1-\omega _\phi }\right) \right. \\&\quad \left. +\,V\left\{ \frac{1}{1-\omega _\phi }+\frac{1+\omega _\phi }{(1-\omega _\phi )^2}\right\} \frac{d\omega _\phi }{da}\right] , \end{aligned}$$

(54)

which can be simplified as

$$ \frac{d{{\dot{\phi}^2}}}{da} = \frac{2V}{(1-\omega _\phi )^2}\frac{d\omega _\phi }{da} + 2\frac{dV}{da} \left( \frac{1+\omega _\phi }{1-\omega _\phi }\right) . $$

(55)

Using Equation (55) in Equation (9) and rearranging terms we obtain

$$\begin{aligned}&\frac{dV}{da}\left[ 1 + \frac{1+\omega _\phi }{1-\omega _\phi }\right] \\&\quad + V\left[ \frac{6}{a}\frac{(1+\omega _\phi )}{(1-\omega _\phi )} + \frac{1}{( 1 - \omega _\phi )^2}\frac{d\omega _\phi }{da} \right] = 0, \end{aligned}$$

(56)

which can be easily simplified into the form of Equation (34).