1 Introduction

Functionally graded materials (FGMs) are nonhomogeneous composites that possess continuous variations in the thermomechanical properties. Due to their potential usage in high temperature applications as protective coatings and interlayers, fracture mechanics and thermal stress analyses of FGMs have been considered by many researchers in the past. Various techniques have been developed in order to study the behavior of cracks in FGMs under mechanical and thermal loading conditions. For crack problems subjected to mechanical loading, Anlas et al. [1] have evaluated SIFs in FGMs for an edge-cracked plate under uniform mechanical loading, using both the strain energy release rate and the J-contour integral. Rao and Rahman [2] present a Galerkin-based meshless method for calculating SIFs for a stationary crack in two-dimensional FGMs of arbitrary geometry. Kim and Paulino [3,4,5] extended various finite elements based approaches for fracture mechanics analysis of FGMs such as modified crack closure method, mixed-mode J-integral and interaction integral. Gu et al. [6] have proposed a finite element based method for calculating SIFs of graded materials, using the equivalent domain integral (EDI) technique. Guo et al. [7] considered mode I crack problems in a finite width graded orthotropic strip under static loading. Shojaee and Daneshmand [8] applied the extended isogeometric analysis with orthotropic approach for numerical modeling of stationary cracks in FGM plane bodies. Martinez-Paneda and Gallego [9] evaluated the performance of numerical tools in the computational assessment of cracks in FGMs by means of the well-known ABAQUS FE code. This analysis is based on computational results of fracture parameters SIFs and T-stress. Benamara et al. [10] performed mixed-mode crack propagation in FGMs subjected to mechanical loads using the finite element method (FEM) and the strain energy density (SED) approach.

For crack problems in FGMs under thermal loads, many researchers are considered using different approaches, Yildirim [11] investigated the equivalent domain integral method to evaluate the SIFs in FGM under steady-state and transient thermal loading conditions. Dag [12] developed the computational method based on the Jk-integral in order to calculate crack tip parameters for FGMs, subjected to mixed-mode thermal loading. Yildirim et al. [13] analysed the 3D surface crack problems in functionally graded coatings subjected to mode-I mechanical and transient thermal loadings. Chen et al. [14] analyzed the influence of nonhomogeneity on the standard J-integral and defines a modified J-integral for cracked FGM. Amit and Kim [15] evaluated of the non-singular T-stress and mixed-mode SIFs in FGMs under steady-state thermal loads by means of interaction integral. Rangaraj and Kokini [16] investigated the two-dimensional finite element models with a cohesive zone to study quasi-static crack extension in functionally graded thermal barrier coatings (TBC). Jin and Paulino [17] considered an edge crack in a strip of a FGM to calculate the thermal stress intensity factors (TSIFs) under transient thermal loading conditions. Dag et al. [18] introduced a computational method based on the Jk-integral for mixed-mode fracture analysis of orthotropic FGMs subjected to thermal stresses. Yildirim and Erdogan [19] have used the enriched element technique to evaluate mixed-mode SIFs under uniform thermal loading. Kosker et al. [20] investigated three dimensional FEM in order to evaluate the mixed-mode SIFs around the front of an inclined semi-elliptical crack located in an FGM coating, using the displacement correlation technique under the effect of transient thermal stresses. Dag [21] proposed a new computational method based on the equivalent domain integral for mode-I fracture analysis in orthotropic FGMs subjected to thermal stresses.

Some researchers examined the crack problems in FGMs under thermomechanical loading conditions. In this direction, Jain et al. [22] developed quasi-static stress and displacement fields for a crack in an infinite FGM medium under thermomechanical loading. Kidane et al. [23] developed the stress fields near the crack tip for mixed-mode crack propagation under thermomechanical loading in FGM. Nami and Eskandari [24] investigated 3D-FEM to evaluate the SIFS for semi-elliptical circumferential surface crack in FGM cylinder subjected to thermomechanical loading (the internal pressure and the temperature gradient). Takabi [25] presented an analytical and a numerical thermomechanical investigation of a thick-walled cylinder made of the FGMs, subjected to a pressure and a thermal load. Matthew et al. [26] developed a general domain integral method to obtain J-values along crack fronts in three-dimensional configurations of isotropic FGMs, subjected to thermomechanical loading. Moghaddam et al. [27] analyzed the mixed mode SIFs of three-dimensional curved non-planar cracks in FGMs, using the interaction energy integral. The FEM is employed to extract the SIFs along the front of a lens shaped crack in a FGM. Lee et al. [28] developed analytical expressions for dynamic crack-tip stress and displacement fields under thermo-mechanical loading in FGM. Zhang et al. [29] exploited the numerical manifold method (NMM) to study the fracture behavior of two-dimensional FGMs subjected to thermo-mechanical loadings. Firstly, the steady-state heat conduction simulation of the cracked FGMs is performed, and then the computed temperatures are input into the thermoelastic modeling. Moghaddam and Alfano [30] deployed the interaction energy integral in the finite element framework and carried out an un-coupled thermomechanical analysis to extract the mixed-mode SIFs for surface cracks in FGM hollow cylinders. Mahbadi [31] estimated SIFs of rotating solid disks in isotropic functionally graded with a radial crack subjected to a uniform tension at their outer surface and a uniform temperature change through the body. Abotula et al. [32] studied mixed-mode dynamic crack growth in FGMs under thermomechanical loading. Karimi et al. [33] has conducted numerical investigations to reduce stress concentration in a design with an interactive procedure and to identify the most important parameters of a design which called target variables.

The objective of this study is to present a numerical modeling of mixed-mode fracture in FGMs. Using the APDL code [34], the displacement extrapolation technique (DET) is used to determine numerically the SIFs for isotropic FGMs subjected to mechanical and thermal loading conditions. In this paper, four numerical examples including both mode-I and mixed-mode problems are presented to evaluate the SIFs calculated using proposed method. Comparisons have been made between the SIFs predicted by displacement extrapolation technique DET and available reference solutions in the literature.

The paper consists of four sections. Besides this introduction, Sect. 2 presents the numerical evaluation of SIFs using displacement extrapolation method. In Sect. 3, we present several numerical examples to examine the accuracy and performance of the displacement extrapolation technique in evaluating mixed-mode SIFs for isotropic FGMs subjected to thermal and mechanical loading conditions. Finally, the major conclusions are summarized in Sect. 4.

2 Numerical evaluation of SIFs

Among the computational methods developed to study fracture mechanics of FGMs, we can mention mixed-mode J-integral Kim and Paulino [4], modified crack closure method Kim and Paulino [3], interaction integral Kim and Paulino [5], equivalent domain integral Dag [21] and continuum shape sensitivity method Rao and Rahman [35]. In this work, the displacement extrapolation technique DET proposed for homogeneous materials is modified to calculate the SIFs for isotropic FGMs, as follows Benamara et al. [36]:

$$ K_{I} = \frac{{E_{tip} }}{{3{\kern 1pt} \left( {1 + \nu_{tip} } \right){\kern 1pt} {\kern 1pt} \left( {1 + k_{tip} } \right)}}{\kern 1pt} \sqrt {\frac{2\pi }{L}} \left[ {4\left( {v_{b} - v_{d} } \right) - \frac{{\left( {v_{c} - v_{e} } \right)}}{2}} \right] $$
(1)
$$ K_{II} = \frac{{E_{tip} }}{{3{\kern 1pt} \left( {1 + \nu_{tip} } \right){\kern 1pt} \;{\kern 1pt} \left( {1 + k_{tip} } \right)}}{\kern 1pt} \sqrt {\frac{2\pi }{L}} {\kern 1pt} {\kern 1pt} \left[ {4\left( {u_{b} - u_{d} } \right) - \frac{{\left( {u_{c} - u_{e} } \right)}}{2}} \right] $$
(2)

where Etip and νtip are the Young’s modulus and the Poisson’s ratio given at the crack-tip. ktip= (3 − νtip)/(1 + νtip) for plane stress and ktip= (3 − 4νtip) for plane strain. L is the length of the singular element side. un (n = b, c, d and e) are the nodal displacements at nodes b, c, d and e in the x and y directions, respectively.

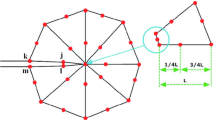
In this work, the special quarter point finite elements proposed by Barsoum [37] are used to obtain a better approximation of the field around the crack-tip (Fig. 1), where the mid-side node of the element connected to the crack-tip is moved to 1/4 of the length of this element.

Fig. 1
figure 1

Singular element used for present study

Full size image

3 Numerical results and discussion

The performance of the extrapolation technique for SIFs evaluation in isotropic FGMs subjected to mechanical and thermal loading conditions is examined by means of numerical examples. The following examples are presented:

  1. (1)

    Three-point bending specimen with crack parallel to material gradation, subjected to mechanical loading.

  2. (2)

    FGM disk with an inclined center crack, subjected to mechanical loading.

  3. (3)

    An edge crack in a FGM plate, subjected to thermal loading.

  4. (4)

    Crack in functionally graded thermal barrier coating.

3.1 Example 1: Three-point bending specimen with crack parallel to material gradation

In this example, three-point bend specimen are considered with length L = 54 units, depth 2H = 10 units, and thickness t = 1 unit. A crack of length (a) is assumed to initiate parallel to the material gradation as shown in Fig. 2.

Fig. 2
figure 2

Three-point bend specimen with crack parallel to material gradation [2]

Full size image

A concentrated load P = 1 unit was applied at the middle of the beam and two supports were symmetrically placed with respect to an edge crack of length a. The three-point bend specimen consists of 2 h units deep FGM sandwiched between two distinct homogeneous materials, each of which has depth H–h.

The variation of Young’s modulus in the material gradient region is linear, is expressed by:

$$ E\left( {x_{2} } \right) = Ax_{2} + B $$
(3)

where

$$ A = \frac{{\left( {E_{2} - E_{1} } \right)}}{2h} $$
(4)
$$ B = \frac{{\left( {E_{2} + E_{1} } \right)}}{2} $$
(5)

The Poisson’s ratio (ν) is assumed to be constant.

Where E1, E2 and 2h are material parameters. The following data were used in the present analysis:

2h = 1 unit, E1 = 1 unit, and \( {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }} \) = 0.05, 0.1, 0.2, 0.5, 1, 2, 5, 10, and 20.

For each \( {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }} \) ratio, three different crack lengths with \( {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0pt} {2H}} \) = 0.45, 0.5 and 0.55 were examined such that the crack tips were either at the middle of the FGM layer (\( {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0pt} {2H}} \) = 0.5) or at the material interfaces (\( {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0pt} {2H}} \) = 0.45 or 0.55), as shown in Fig. 3a, b.

Fig. 3
figure 3

FE mesh for three-point bending specimen: a global FE mesh, b detail of the mesh refinement around the crack tip for different crack positions

Full size image

The structure considered is meshed by quadratic elements with 8 nodes and particularly, special elements were used to characterize the singularity around the crack-tip. The number of element used in this analysis is 841 elements with 2248 nodes (for \( {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0pt} {2H}} \) = 0.45).

The determination of stress intensity factors \( K_{I} \) for three crack sizes (a = 4.5, 5 and 5.5 units) is performed under plane stress condition.

Table 1 compare the normalized mode-I SIF \( \left( {\frac{{K_{I} \sqrt H }}{P}} \right) \) obtained by present method for various combinations of \( {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }} \) and \( {a \mathord{\left/ {\vphantom {a {2H}}} \right. \kern-0pt} {2H}} \), with the FEM results of Kim and Paulino [38] using J*-Integral method and the results obtained by Rao and Rahman [2] using modified interaction integrals based on element-free Galerkin method (EFGM). The results obtained is in good agreement with that reported by Kim and Paulino [38] and by Rao and Rahman [2].

Table 1 Normalized SIF for three-Point bending specimen
Full size table

3.2 Example 2 FGM disk with an inclined center crack

We consider a circular FGM disk with a center crack inclined by θ = 30° (Fig. 4a). The disc is meshed by quadratic and triangular elements, as shown in (Fig. 4b). A special mesh is used to characterize the singularity around the two crack-tips (Fig. 4c). FGM disk was meshed by 2688 elements with 6180 nodes.

Fig. 4
figure 4

a Geometry of FGM disc with a central crack, b complete mesh configuration, c detailed mesh around the two crack-tips

Full size image

The FGM Disk is considered under plane stress condition and the variation of Young’s modulus along the radial direction is given as follows:

$$ E\left( r \right) = \overline{E} e^{\beta r} $$
(6)
$$ r = \sqrt {X_{1}^{2} + X_{2}^{2} } $$
(7)

r: (disc radius); X1 and X2: (cartesian coordinates).

A point load P = ± 100 units is applied to the top and bottom of the disk, at the coordinate nodes (0, ± 10), respectively.

The displacement boundary conditions are defined as follows: (X1, X2) = (− 10, 0), (u1, u2) = (0, 0), (X1, X2) = (10, 0) and u2 = 0.

Figure 4 shows the applied boundary conditions used for this example. The determination of stress intensity factors KI is performed under plane stress condition, for following numerical values:

$$ {\text{a}} = 1,\;{\text{r}} = 10,\;\upbeta{\text{a}} = \left( { - 0. 5, \, - 0. 2 5, \, 0, \, 0. 2 5, \, 0. 5} \right),\;\bar{E} = 1,\;\nu = 0.3. $$

Table 2 presents FEM results for the mode-I SIF obtained by present approach for various values of βa, with those reported by other methods using M-integral method [5] and modified crack closure method (MCC) [3]. there is a good agreement between present evaluation of SIFs results and the other available reference in the literature.

Table 2 Mode-I SIF for an inclined center crack in a circular FGM disk
Full size table

The results obtained in examples 1 and 2 allow us to conclude that the displacement extrapolation technique modified for non-homogeneous materials, correctly described the stress–strain field around the crack-tip, for plates subjected to mechanical loading.

3.3 Example 3: An edge crack in a FGM plate

This example is selected to verify the present displacement extrapolation method for an edge crack FGM plate subjected to thermal loads. The FGM plate of dimensions H = 8 units, W = 1 unit and a crack of length a = 1 unit is illustrated in Fig. 5a.

Fig. 5
figure 5

a Geometry of cracked FGM plate, b complete mesh configuration

Full size image

The values of mode-I SIFs are calculated under plane strain and plane stress conditions, using present technique. Figure 5b illustrates the complete mesh configuration. The 2D mesh discretization consists of 2344 elements and 4889 nodes.

The elastic modulus and the thermal expansion coefficient of the FGM plate are assumed to follow an exponential gradation as given by the function:

$$ E(X_{1} ) = E_{1} e^{{(\beta X_{1} )}} $$
(8)
$$ \alpha (X_{1} ) = \alpha_{1} e^{{(\gamma X_{1} )}} $$
(9)
$$ \beta = \frac{1}{w}\ln \left( {\frac{{E_{2} }}{{E_{1} }}} \right) $$
(10)
$$ \gamma = \frac{1}{w}\ln \left( {\frac{{\alpha_{2} }}{{\alpha_{1} }}} \right) $$
(11)

\( E_{1} = 1 \) and \( E_{2} = 5\;{\text{or}}\;10 \); \( \alpha_{1} = 0.01\,(^\circ {\text{C}}^{ - 1} ) \) and \( \alpha_{2} = 0.02\,(^\circ {\text{C}}^{ - 1} ) \).

In this analysis, we considered a constant Poisson’s ratio (ν = 0.3) because it has negligible effect on fracture behavior of FGMs under pure mode-I conditions [39]. The thermal boundary conditions are defined as follows:

$$ \text{T}_{0} = 10\,(^\circ {\text{C}})\;\text{T}_{1} \;{\text{at}}\; \left( {X_{1} = 0} \right)\;\;{\text{and}}\;\;\text{T}_{2} \;{\text{at}}\;\left( {X_{1} = w} \right). $$

Two cases were considered in this study:

  • Case 1 the thermal conductivity coefficient (k) is constant.

  • Case 2 we considered:

$$ k(X_{1} ) = k_{1} e^{{(\delta X_{1} )}} $$
(12)

where

$$ \delta = \frac{1}{w}\ln \left( {\frac{{k_{2} }}{{k_{1} }}} \right) $$
(13)

\( k_{1} = 1 \) and \( k_{2} = 10 \).

$$ \theta (X_{1} ) = Ae^{{( - \delta X_{1} )}} + B $$
(14)

where the unknowns A and B are obtained from temperature boundary conditions.

Table 3 compares the present FEM results for normalized mode-I SIF in FGMs plate under various thermal loads with those reported by KC and Kim [15], Walters et al. [26], Erdogan and Wu [40], Yildirim [11] and Yildirim et al. [13]. The FEM results shows a good agreement with the reference results.

Table 3 Normalized mode-I SIF in FGMs under thermal loads
Full size table

Case 1

$$ {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }} = 5,\;\;{{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }} = 2. $$

Case 2

$$ {{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-0pt} {E_{1} }} = 10,\quad {{\alpha_{2} } \mathord{\left/ {\vphantom {{\alpha_{2} } {\alpha_{1} }}} \right. \kern-0pt} {\alpha_{1} }} = 2,\quad {{k_{2} } \mathord{\left/ {\vphantom {{k_{2} } {k_{1} }}} \right. \kern-0pt} {k_{1} }} = 10. $$

3.4 Example 4: Crack in functionally graded thermal barrier coating TBC

In the present problem, an edge crack in functionally graded thermal barrier coating under thermal loading has been modelled and analysed using present technique (DET). Figure 6 shows a functionally graded thermal barrier coating deposited on the bond coat and the metallic substrate. The FGM coating consists of 100% zirconium–yttria at X1 = 0 and 100% nickel–chromium–aluminium–zirconium (NiCrAlY) bond coat at X1 = W1. The metallic substrate is made up of a nickel-based super-alloy.

Fig. 6
figure 6

A crack in a functionally graded thermal barrier coating

Full size image

The dimensions of FGM TBC along with thermal loading and boundary conditions are shown in Fig. 6. Initially the system is assumed to be at a uniform temperature (T0 = 1000 °C).

The top and bottom edges of the TBC system are assumed to be insulated. Application of temperature boundary conditions drives the system to a steady state condition with temperature T1 = 0.2T0 and T2 = 0.5T0 at left and right edges, respectively.

Material property variations of Young’s modulus (E), Poisson’s ratio (ν) and thermal expansion coefficient (α) for the FGM coating are represented by power-law type functions, which are given as follows:

$$ E(X_{1} ) = E_{c} + (E_{bc} - E_{c} ){X_{1}}^{2} $$
(15)
$$ \nu (X_{1} ) = \nu_{c} + (\nu_{bc} - \nu_{c} )X_{1} $$
(16)
$$ \alpha (X_{1} ) = \alpha_{c} + (\alpha_{bc} - \alpha_{c} )X_{1} $$
(17)
$$ k(X_{1} ) = k_{c} + (k_{bc} - k_{c} ){X_{1}}^{2} $$
(18)

where subscript (c) denotes FGM coating and subscript (bc) symbolizes the bond coat. The thermomechanical properties of different constituents of TBC are listed in Table 4.

Table 4 Thermomechanical properties of TBC constituents [41]
Full size table

Figure 7 shows complete mesh configuration with mesh detail around the crack-tip. The representative mesh discretization consists of 1734 elements and 4749 nodes.

Fig. 7
figure 7

Complete mesh configuration in a functionally graded

Full size image

Figure 8 compares the variation of mode-I SIF for various a/W ratios in a FGM TBC using present approach with reported by Garg and Pant [41] using element-free Galerkin method (EFGM) and by Amit and Kim [15] using interaction integral method (M-integral), excellent agreement was observed between three techniques.

Fig. 8
figure 8

Variations of SIF KI along the graded region

Full size image

In Fig. 9 we have shown the temperature distribution in graded TBCs (for a/W = 0.4). It can be clearly seen that the temperature field remains unaffected by the presence of crack and the heat flux is parallel to the crack surface, along x-direction.

Fig. 9
figure 9

Temperature distributions in FGM-TBC a Garg and Pant [41]; b present study

Full size image

The temperature distribution obtained by present study was compared with that obtained by Garg and Pant [41]. A good agreement in numerical results with the EFGM solution.

4 Conclusion

In this paper, the displacement extrapolation technique used for homogeneous materials has been modified and proposed to determine numerically the SIFs for isotropic FGM. The present method is investigated to analyze the mixed mode fracture problems under mechanical and steady-state thermal loads. In order to obtain a better approximation of the field near the crack tip in graded region, the special quarter point finite elements proposed by Barsoum is used.

This paper presents various numerical examples in which the accuracy of the present method is verified. A comparison of SIF values predicted by FEM and available reference solutions generated numerically reveals the applicability of present technique. This approach has been successfully used in evaluating SIFs in FGMs under mechanical loading and has also been used in the evaluation of mixed-mode SIFs in FGMs under thermal loadings.

The simplicity and accuracy of this implementation show that it can be further extended to study and analyses the fracture in graded materials with multi-loading and complex geometry conditions.