Relations between Hermite and Laguerre expansions of ultradistributions over ${\varvec{\mathbb R}^d}$ and ${\varvec{\mathbb R}^d_+}$

Abstract

The aim of this paper is twofold. Firstly, to show the existence of topological isomorphism between the G-type spaces $G_\alpha ^\alpha (\mathbb {R}^d_+)$, $\alpha \ge 1$ and the subspaces of the Gelfand-Shilov spaces $\mathcal S_{\alpha /2}^{\alpha /2}(\mathbb {R}^d)$, $\alpha \ge 1$, consisting of “even” functions. The same is done for their dual spaces. Secondly, to obtain two structural theorems for the dual spaces $(G_\alpha ^\alpha (\mathbb {R}^d_+))'$, $\alpha \ge 1$.

1 Introduction

The test space $\mathcal {S}(\mathbb R_+)$ for the space of tempered distributions supported by $[0,\infty )$ is studied in [2, 15, 20]; recently, two of the authors have studied the space $\mathcal {S}(\mathbb R_+^d)$ over $[0,\infty )^d$ in [9]. We have studied in [10] G-type spaces, $G_\alpha ^\alpha (\mathbb {R}_+^d)$, $\alpha \ge 1$ and their dual spaces, i.e. the spaces of ultradistributions over $[0,\infty )^d$, in terms of their Fourier-Laguerre coefficients; cf. Durán [3] for the one-dimensional case. Actually, we extend the results of [3] and give the full topological characterisation, in all dimensions, as well as applications to pseudo-differential operators with radial symbols.

In this paper, we use the expansion of the Laguerre functions into finite sums of Hermite functions and vice versa in order to prove that there exists a topological isomorphism between $G_\alpha ^\alpha (\mathbb {R}^d_+)$, $\alpha \ge 1$ and the subspace of the Gelfand-Shilov spaces $\mathcal S_{\alpha /2}^{\alpha /2}(\mathbb {R}^d)$, $\alpha \ge 1$, consisting of “even” functions, denoted as $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$. Also, we describe their dual spaces in order to study pseudo-differential operators on the G-type spaces in our future work. As a remark (Remark 3.5), we have shown that the symbol class of pseudo-differential operators considered in [10] is in bijection with a subspace of $(\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d))'$ (i.e. closely related to the Gelfand-Shilov even ultradistributions). We refer to [5–8, 11, 19, 21] for the expansions of Gelfand-Shilov ultradistribution spaces.

Furthermore, we give two structural theorems for $(G_\alpha ^\alpha (\mathbb {R}^d_+))'$, $\alpha \ge 1$ (Theorems 4.6, 4.8). The first one states that $f\in (G_\alpha ^\alpha (\mathbb {R}^d_+))'$, $\alpha \ge 1$, if and only if it can be written as

$$\begin{aligned} f=\left( \sum _{k\in \mathbb N_0^d}c_k\left( xD^2+D-\frac{x}{4}+\frac{1}{2}\right) ^k \right) F \end{aligned}$$

with a suitable growth of the coefficients $c_k$, where $F\in L^2(\mathbb R^d_+)$ and $(xD^2+D-x/4+1/2)^k=\prod _{j=1}^d(x_jD_j^2+D_j-x_j/4+1/2)^{k_j}$, $k\in \mathbb N^d_0$. In fact, the theorem gives a stronger result: if $f\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, $\alpha \ge 1$ varies in a bounded subset, then this representation can be chosen such that the operator is the same for all the elements of the bounded subset and the function F varies in a bounded subset of $L^2(\mathbb R^d_+)$. The second one is similar to the first, but instead of using the operator $(xD^2+D-x/4+1/2)^k$, $f\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ is represented as an infinite sum of integrals of $L^2(\mathbb R^d_+)$-functions integrated against the test functions that are differentiated and then multiplied by powers of x suitable number of times. As we shall see, $G^{\alpha }_{\alpha }(\mathbb R^d_+)$, $\alpha \ge 1$ is given as an injective inductive limit of Fréchet spaces (from now on abbreviated as (F)-space). This theorem, loosely speaking, represents an element f of $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, $\alpha \ge 1$, by giving its action on each layer of the inductive limit in the following way

$$\begin{aligned} \langle f,\phi \rangle= & {} \sum _{p,k\in \mathbb N^d_0}\int _{\mathbb R^d_+}F_{A,p,k}(x)x^{(p+k)/2}D^p\phi (x)dx\\&+ \sum _{|m|\le j,\, |n|\le j}\int _{\mathbb R^d_+}\tilde{F}_{A,n,m}(x)x^mD^n\phi (x)dx, \end{aligned}$$

where the $L^2(\mathbb R^d_+)$-functions $F_{A,p,k}$ and $\tilde{F}_{A,n,m}$ depend on the layer.

We briefly describe the content. We state the notation and definitions of the basic spaces in Sect. 2. Section 3 is devoted to the topological isomorphism announced above. The structural theorems are proved in Sect. 4.

2 Preliminaries

2.1 Notations

We denote by $\mathbb N$, $\mathbb Z$, $\mathbb R$ and $\mathbb C$ the sets of positive integers, integers, real and complex numbers, respectively; $\mathbb N_0=\mathbb N\cup \{0\}$, $\mathbb R_+=(0,\infty )$, $\mathbb R^d_+=(0,\infty )^d$ and $\overline{\mathbb R^d_+}=[0,\infty )^d$. We use the standard multi-index notation. Let $x=(x_1,\ldots , x_d)\in \mathbb {R}^d$, $k=(k_1,\ldots , k_d)\in \mathbb N_0^d$. Then $|x|=\sqrt{x_1^2+\cdots +x_d^2}$, $|k|=k_1+\cdots +k_d$, $k!=k_1!\cdots k_d!$, $x^k=\prod _{i=1}^d x_i^{k_i}$, $D^k=\prod _{i=1}^d \partial ^{k_i}/\partial x_i^{k_i}$. Furthermore, if $x,\gamma \in \overline{\mathbb R^d_+}$, we also use $x^{\gamma }=\prod _{j=1}^d x_j^{\gamma _j}$. In this case, if $x_j=0$ and $\gamma _j=0$, we use the convention $0^0=1$. We define the Laguerre operator as

$$\begin{aligned} R=\prod _{j=1}^d\left( x_jD_{x_j}^2+D_{x_j}-\frac{x_j}{4}+\frac{1}{2}\right) . \end{aligned}$$

For $j\in \mathbb {N}_0$ and $\gamma >-1$, the j-th Laguerre polynomial of order $\gamma$ is defined by

$$\begin{aligned} L_j^\gamma (x)=\frac{x^{-\gamma }e^x}{j!}\frac{d^j}{dx^j}(e^{-x}x^{\gamma +j}),\;x \ge 0, \end{aligned}$$

or, equivalently,

$$\begin{aligned} L_j^\gamma (x)=\sum _{l=0}^j {{j+\gamma }\atopwithdelims (){j-l}}\frac{(-x)^l}{l!},\;x \ge 0. \end{aligned}$$

For $\gamma =(\gamma _1,\ldots ,\gamma _d)\in \mathbb R^d$ such that $\gamma _j>-1$, $j=1,\ldots ,d$ and $n\in \mathbb N^d_0$, the d-dimensional n-th Laguerre polynomial of order $\gamma$ is defined by $L^{\gamma }_n(x)=L^{\gamma _1}_{n_1}(x_1)\ldots L^{\gamma _d}_{n_d}(x_d)$. For $\gamma =0$, we write $L_n(x)$ instead of $L^0_n(x)$.

The j-th Laguerre function (of order 0) is defined by $l_j(x)=L_j(x)e^{-x/2}$, $x\ge 0$, $j\in \mathbb N_0$ and in the d-dimensional case we have $l_n(x)=l_{n_1}(x_1)\ldots l_{n_d}(x_d)$, $x\in \overline{\mathbb R^d_+}$, $n\in \mathbb N^d_0$. The Laguerre functions form an orthonormal basis for $L^2(\mathbb {R}^d_+)$ and are eigenfunctions for R i.e. $R^k l_n(x)=(-1)^{|k|}n^kl_n(x)$, $k,n\in \mathbb N_0^d$, where

$$\begin{aligned} R^k=\prod _{j=1}^d\left( x_jD_{x_j}^2+D_{x_j}-\frac{x_j}{4}+\frac{1}{2}\right) ^{k_j},\,\,\, k\in \mathbb N^d_0, \end{aligned}$$

(2.1)

where, if $k_j=0$ then we have the identity operator in the j-th variable. The Laguerre functions have a special role for the characterisation of the spaces $G^{\alpha }_{\alpha }(\mathbb R^d_+)$, $\alpha \ge 1$, considered below.

The Hermite polynomial $H_j$ and the corresponding Hermite function $h_j$ are defined by

The d-dimensional Hermite polynomials $H_n$ and Hermite functions $h_n$ are defined by

From [9], we recall that the space $\mathcal S(\mathbb {R}_+^d)$ consists of all $f\in \mathcal {C}^{\infty }(\mathbb R^d_+)$ such that all derivatives $D^pf$, $p\in \mathbb N^d_0$, extend to continuous functions on $\overline{\mathbb R^d_+}$ and

$$\begin{aligned} \sup _{x\in \mathbb {R}^d_+}x^k|D^pf(x)|<\infty \;,\forall k,p\in \mathbb {N}_0^d. \end{aligned}$$

Equipped with this system of seminorms $\mathcal S(\mathbb {R}_+^d)$ becomes an (F)-space. By s we denote the space of all complex sequences $\{a_n\}_{n\in \mathbb N^d_0}$ such that

$$\begin{aligned} \sup _{n\in \mathbb N^d_0}(|n|+1)^j|a_n|<\infty ,\,\, \forall j\in \mathbb N_0, \end{aligned}$$

(2.2)

which becomes an (F)-space when equipped with the seminorms (2.2). There is a topological isomorphism between $\mathcal S(\mathbb R^d_+)$ and s given by $f\mapsto \{\langle f,l_n\rangle \}_{n\in \mathbb N^d_0}$. Moreover, for $f\in \mathcal S(\mathbb R^d_+)$, $\sum _{n\in \mathbb N^d_0} \langle f,l_n\rangle l_n$ converges absolutely to f in $\mathcal S(\mathbb R^d_+)$ (cf. [9, Theorem 3.1]). Also, the strong dual $(\mathcal S(\mathbb R^d_+))'$ of $\mathcal S(\mathbb R^d_+)$ is topologically isomorphic to the strong dual $s'$ of s via the isomorphism $T\mapsto \{\langle T,l_n\rangle \}_{n\in \mathbb N^d_0}$ and for $T\in (\mathcal S(\mathbb R^d_+))'$, $\sum \nolimits _{n\in \mathbb N^d_0}\langle T,l_n\rangle l_n$ converges absolutely to T in $(\mathcal S(\mathbb R^d_+))'$ (cf. [9, Theorem 3.2]).

Let $\alpha \ge 1$ and $a>1$. We define $s^{\alpha ,a}$ as the space of all complex sequences $\{a_n\}_{n\in \mathbb N^d_0}$ for which $\displaystyle \Vert \{a_n\}_{n\in \mathbb N^d_0}\Vert _{s^{\alpha ,a}}= \sup \nolimits _{n\in \mathbb N^d_0}|a_n|a^{|n|^{1/\alpha }}<\infty$. Equipped with this norm $s^{\alpha ,a}$ becomes a Banach space (from now on, abbreviated as (B)-space). We define $\displaystyle s^{\alpha }=\lim \nolimits _{\begin{array}{c} \longrightarrow \\ a\rightarrow 1^+ \end{array}}s^{\alpha ,a}$. In particular, $s^{\alpha }$ is a (DFN)-space and its strong dual $(s^{\alpha })'$ is the (FN)-space of all complex valued sequences $\{b_n\}_{n\in \mathbb N^d_0}$ such that $\sum _{n\in \mathbb N^d_0} |b_n|a^{-|n|^{1/\alpha }}<\infty$, for each $a>1$.

For $\alpha ,A>0$, denote by $\mathcal S^{\alpha ,A}_{\alpha ,A}(\mathbb R^d)$ the (B)-space of all $\varphi \in \mathcal {C}^{\infty }(\mathbb R^d)$ with norm

$$\begin{aligned} \Vert \varphi \Vert _{\mathcal S^{\alpha ,A}_{\alpha ,A}}=\sup _{n,m\in \mathbb N^d_0}\frac{\left\| x^m D^n\varphi (x)\right\| _{L^2(\mathbb R^d)}}{ A^{|n|+|m|}n!^{\alpha }m!^{\alpha }}<\infty . \end{aligned}$$

The Gelfand-Shilov space $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$, $\alpha \ge 0$ (cf. [6–8] and the recent paper of J. Toft and his collaborators [5]) is defined as an inductive limit of $\mathcal S^{\alpha ,A}_{\alpha ,A}(\mathbb R^d)$ with respect to A:

$$\begin{aligned} \mathcal S^{\alpha }_{\alpha }(\mathbb R^d)= \lim _{\begin{array}{c} \longrightarrow \\ A\rightarrow \infty \end{array}} \mathcal S^{\alpha ,A}_{\alpha ,A}(\mathbb R^d). \end{aligned}$$

The space $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ is nontrivial if and only if $\alpha \ge 1/2$. In this case, we have the following dense and continuous inclusion: $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)\hookrightarrow \mathcal S(\mathbb R^d)$. We denote by $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ the strong dual of $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$. Moreover, $h_n\in \mathcal S^{1/2}_{1/2}(\mathbb R^d)$, $n\in \mathbb N^d_0$ and the space $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ can be given through the Hermite expansions when it is nontrivial. In fact, we have the following result which proof is similar to the proof of [13, Theorem 3.4 and Corollary 3.5] and we omit it.

Proposition 2.1

Let $\alpha \ge 1/2$. The map $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)\rightarrow s^{2\alpha }$, $f\mapsto \{\langle f,h_n\rangle \}_{n\in \mathbb N^d_0}$, is a topological isomorphism. For $f\in \mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$, $\sum _{n\in \mathbb N^d_0}\langle f,h_n\rangle h_n$ converges absolutely to f in $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$.

The map $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'\rightarrow (s^{2\alpha })'$, $T\mapsto \{\langle T,h_n\rangle \}_{n\in \mathbb N^d_0}$, is a topological isomorphism. For $T\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$, $\sum _{n\in \mathbb N^d_0}\langle T,h_n\rangle h_n$ converges absolutely to T in $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$.

We will be particularly interested in the subspace $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ of $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ consisting of all “even” functions in $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$, i.e. of all $\psi \in \mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ such that

$$\begin{aligned} \psi (x_1,\ldots ,x_{j-1},-x_j,x_{j+1},\ldots ,x_d)=\psi (x), \end{aligned}$$

(2.3)

for all $x=(x_1,\ldots ,x_d)\in \mathbb R^d,\, j=1,\ldots ,d.$

Proposition 2.2

The space $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ is a closed subspace of $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$. In particular, it is a (DFS)-space. Moreover, $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ consists of those $\psi \in \mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ which can be represented as $\psi =\sum _{n\in \mathbb N^d_0} a_{2n}h_{2n}$ where $\{a_{2n}\}_{n\in \mathbb N^d_0}\in s^{2\alpha }$.

Remark 2.3

Before we give the proof of this proposition, we want to explain the meaning of $\{a_{2n}\}_{n\in \mathbb N^d_0}\in s^{2\alpha }$. It should be understood as the sequence $\{b_k\}_{k\in \mathbb N^d_0}\in s^{2\alpha }$ such that the elements with indexes $k=2n$, $n\in \mathbb N^d_0$, are equal to $a_{2n}$ and all the rest are equal to 0. In the sequel, whenever we use this notation, it will have this exact meaning.

Proof

The fact that $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ is a closed subspace of $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ is trivial. It is a (DFS)-space as a closed subspace of a (DFS)-space. If $\psi =\sum _{n\in \mathbb N^d_0}a_nh_n\in \mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$, then $a_n=\int _{\mathbb R^d}\psi (x)h_n(x)dx$ and $\{a_n\}_{n\in \mathbb N^d_0}\in s^{2\alpha }$ (cf. Proposition 2.1). Since $h_j(t)$ is even when j is even and is odd when j is odd, the last assertion in the proposition follows. $\square$

For the moment, we denote by X the subspace of $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ consisting of all $T\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ such that $T=\sum _{n\in \mathbb N^d_0}a_{2n}h_{2n}$, for some $\{a_{2n}\}_{n\in \mathbb N^d_0}\in (s^{2\alpha })'$. Of course, these are exactly the “even” tempered ultradistributions, i.e. the elements of $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ which remain unchanged under the antipode mappings in each coordinate (cf. (2.3)). It is easy to verify that X is a closed subspace of $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ and consequently, an (FS)-space.

Proposition 2.4

The strong dual of $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ is topologically isomorphic to X.

Proof

By Proposition 2.2, $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ is a (DFS)-space which is a closed subspace of the (DFS)-space $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$. Hence [14, Theorem A.6.5., p. 255] implies that the strong dual $(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d))'$ of $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$ is topologically isomorphic to the (FS)-space $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}} (\mathbb R^d))^{\perp }$, where

$$\begin{aligned} (\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d))^{\perp }= \{T\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'|\, \langle T,\psi \rangle =0,\, \forall \psi \in \mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)\} \end{aligned}$$

is the orthogonal space to $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$. By $\hat{T}\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\, \mathrm {even}}(\mathbb R^d))^{\perp }$ we denote the coset of $T\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$. We define the mapping $I: X\rightarrow (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}} (\mathbb R^d))^{\perp }$, $I(T)=\hat{T}$. It is easy to verify that I is injective. For $\hat{T}\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}} (\mathbb R^d))^{\perp }$, let $T=\sum _n b_n h_n$. Then, $T_1=\sum _n b_{2n}h_{2n}\in X$ and $T-T_1\in (\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d))^{\perp }$. Hence $I(T_1)=\hat{T}$, which proves the surjectivity of I. Moreover, I is continuous since it decomposes as $X\rightarrow (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'\rightarrow (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}} (\mathbb R^d))^{\perp }$, where the first mapping is the canonical injection and the second is the natural mapping. Since X and $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'/(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}} (\mathbb R^d))^{\perp }$ are (F)-spaces, the open mapping theorem proves that I is a topological isomorphism. $\square$

Remark 2.5

From now on, we will identify $(\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d))'$ (the strong dual of $\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$) with X. It follows directly from the proof of the previous proposition that each $T\in (\mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d))'$ can be represented as $\sum _{n\in \mathbb N^d_0}b_{2n}h_{2n}$, where $\{b_{2n}\}_{n\in \mathbb N^d_0}\in (s^{2\alpha })'$ and for $\varphi =\sum _{n\in \mathbb N^d_0}a_{2n}h_{2n} \in \mathcal S^{\alpha }_{\alpha ,\,\mathrm {even}}(\mathbb R^d)$, we have $\langle T,\varphi \rangle =\sum _{n\in \mathbb N^d_0}a_{2n}b_{2n}$.

2.2 Test spaces

In this subsection we give the definition of the space $G^{\alpha }_{\alpha }(\mathbb R^d_+)$, $\alpha \ge 1$, and its basic properties (for details we refer to [10]). Let $A>0$. We denote by $G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ the space of all $\phi \in \mathcal S(\mathbb R^d_+)$ such that

$$\begin{aligned} \sup _{p,k\in \mathbb N^d_0}\frac{\Vert x^{(p+k)/2}D^p\phi (x)\Vert _{L^2(\mathbb R^d_+)}}{A^{|p+k|}k^{(\alpha /2)k}p^{(\alpha /2)p}}<\infty . \end{aligned}$$

Equipped with the seminorms

$$\begin{aligned} \sigma _{A,j}(\phi )=\sup _{p,k\in \mathbb N^d_0}\frac{\Vert x^{(p+k)/2}D^p\phi (x)\Vert _{L^2(\mathbb R^d_+)}}{A^{|p+k|}k^{(\alpha /2)k}p^{(\alpha /2)p}}+\sup _{\begin{array}{c} |p|\le j\\ |k|\le j \end{array}} \sup _{x\in \mathbb R^d_+}|x^k D^p\phi (x)|,\; j\in \mathbb N_0, \end{aligned}$$

$G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ becomes an (F)-space. (The extra term in $\sigma _{A,j}$ forces all derivatives of $\phi \in G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ to be continuously extendable to the closure of $\mathbb R^d_+$ and $\phi$ to be well defined element of $\mathcal S(\mathbb R^d_+)$.) When $A_1<A_2$, $G^{\alpha ,A_1}_{\alpha ,A_1}(\mathbb R^d_+)$ is continuously injected into $G^{\alpha ,A_2}_{\alpha ,A_2}(\mathbb R^d_+)$. As a locally convex space (from now on abbreviated as l.c.s.), we define $\displaystyle G^{\alpha }_{\alpha }(\mathbb R^d_+)= \lim \nolimits _{\begin{array}{c} \longrightarrow \\ A\rightarrow \infty \end{array}} G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d)$. The space $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is continuously and densely injected into $\mathcal S(\mathbb R^d_+)$ and the Laguerre functions are in $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ (cf. [10, Section 3]).

Theorem 2.6

([10, Theorem 5.7]) Let $\alpha \ge 1$. Let $f\in L^2(\mathbb {R}^d_+)$ and $a_n=\int _{\mathbb {R}^d_+}f(t)l_n(t)dt$, $n\in \mathbb {N}^d_0$. Then $f\in G_\alpha ^\alpha (\mathbb {R}^d_+)$ if and only if there exist $c>0$ and $a>1$ such that $|a_n|\le ca^{-|n|^{1/\alpha }}$.

Moreover, since $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is isomorphic (as a l.c.s.) to $s^{\alpha }$, important topological properties of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and its strong dual $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ follow.

Theorem 2.7

([10, Theorem 6.1]) Let $\alpha \ge 1$. The mapping $\iota : G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow s^{\alpha }$, $\iota (f)=\{\langle f,l_n\rangle \}_{n\in \mathbb N^d_0}$, is a topological isomorphism between $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $s^{\alpha }$. In particular, $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is a (DFN)-space and $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ is an (FN)-space.

For each $f\in G^{\alpha }_{\alpha }(\mathbb R^d_+)$, $\sum _{n\in \mathbb N^d_0}\langle f,l_n\rangle l_n$ is summable to f in $G^{\alpha }_{\alpha }(\mathbb R^d_+)$.

Theorem 2.8

([10, Theorem 6.2]) Let $\alpha \ge 1$. The mapping $\tilde{\iota }: (G^{\alpha }_{\alpha }(\mathbb R^d_+))'\rightarrow (s^{\alpha })'$, $\tilde{\iota }(T)=\{\langle T,l_n\rangle \}_{n\in \mathbb N^d_0}$, is a topological isomorphism.

Moreover, $\sum _{n\in \mathbb N^d_0}\langle T,l_n\rangle l_n$ is summable to T in $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$.

The last three results are crucial and we will often tacitly apply them throughout the rest of this article.

Remark 2.9

In the sequel, we will use the following estimate

$$\begin{aligned} \sum _{j=0}^\infty \frac{s^j}{j!^\alpha }\le e^{\alpha s^{1/\alpha }},\,\, s\ge 0,\, \alpha \ge 1. \end{aligned}$$

(2.4)

Moreover,

$$\begin{aligned} \sup _{j\in \mathbb N_0}\frac{s^j}{j!^\alpha }= & {} \left( \sup _{j\in \mathbb N_0}\frac{s^{j/\alpha }}{j!}\right) ^{\alpha }\ge \left( \frac{1}{2}\sum _{j=0}^{\infty }\frac{(s^{1/\alpha })^j}{2^jj!}\right) ^{\alpha }\\= & {} 2^{-\alpha }e^{(\alpha /2) s^{1/\alpha }},\,\, s\ge 0,\, \alpha \ge 1, \end{aligned}$$

i.e. there exists $c>0$ such that

$$\begin{aligned} \sup _{j\in \mathbb N_0}\frac{s^j}{j!^\alpha }\ge ce^{cs^{1/\alpha }},\,\, s\ge 0,\, \alpha \ge 1. \end{aligned}$$

(2.5)

3 Topological isomorphism between $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$

From now on, we fix $\alpha \ge 1$. The goal of this section is to give the explicit topological isomorphism between $G_\alpha ^\alpha (\mathbb {R}^d_+)$ and $\mathcal S_{\alpha /2,\,\mathrm {even}}^{\alpha /2}(\mathbb {R}^d)$.

Throughout this section, we denote by v and w the following mappings:

For $\gamma =(\gamma _1,\ldots ,\gamma _d)\in \mathbb R^d$ such that $-\gamma _j\not \in \mathbb N$, $j=1,\ldots ,d$ and $m\in \mathbb N^d_0$, we use the abbreviation

$$\begin{aligned} {\gamma \atopwithdelims ()m}=\prod _{j=1}^d {\gamma _j\atopwithdelims ()m_j}. \end{aligned}$$

Moreover, we introduce the following notation $\mathbf {1/2}=(1/2,\ldots , 1/2)\in \mathbb R^d_+$ and $\mathbf {3/2}=(3/2,\ldots , 3/2)\in \mathbb R^d_+$.

Proposition 3.1

Let $\phi =\sum _{n\in \mathbb N^d_0} a_nl_n$ be an element of $G_\alpha ^\alpha (\mathbb {R}^d_+)$. Then $\phi \circ v$ is in $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$ and

$$\begin{aligned} \phi \circ v=\sum _{n\in \mathbb N^d_0} b_{2n}h_{2n}, \end{aligned}$$

where $\{b_{2n}\}_{n\in \mathbb N^d_0}\in s^{\alpha }$ is given by

$$\begin{aligned} b_{2n}=\frac{(-1)^{|n|}\pi ^{d/4}\sqrt{(2n)!}}{2^{|n|} n!}\sum _{k\in \mathbb N^d_0}a_{k+n}{{k-\mathbf {1/2}}\atopwithdelims ()k},\,\, n\in \mathbb N^d_0. \end{aligned}$$

(3.1)

Moreover, the mapping $\phi \mapsto \phi \circ v$, $G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow \mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$, is a continuous injection.

Proof

By [4, (39), p. 192], for $n\in \mathbb N^d_0$ we have

$$\begin{aligned} L_n(x)=\sum _{m\le n} {{m-\mathbf {1/2}}\atopwithdelims ()m}L_{n-m}^{-\mathbf {1/2}} (x),\, x\in \overline{\mathbb R^d_+}. \end{aligned}$$

Recall, [4, (2), p. 193]

$$\begin{aligned} L_j^{-1/2}(t^2)=\frac{(-1)^j}{2^{2j} j!}H_{2j}(t),\,\, t\in \mathbb R,\, j\in \mathbb N_0. \end{aligned}$$

Thus, for $x\in \mathbb R^d$, $n\in \mathbb N^d_0$,

$$\begin{aligned} l_n(v(x))= & {} \pi ^{d/4}\sum _{m\le n}{{m-\mathbf {1/2}}\atopwithdelims ()m}\frac{(-1)^{|n-m|}\sqrt{(2n-2m)!}}{2^{|n-m|} (n-m)!}h_{2(n-m)}(x)\nonumber \\= & {} \pi ^{d/4}\sum _{m\le n}{{n-m-\mathbf {1/2}}\atopwithdelims ()n-m}\frac{(-1)^{|m|}\sqrt{(2m)!}}{2^{|m|} m!}h_{2m}(x). \end{aligned}$$

(3.2)

Let $\psi (x)=\phi (v(x))$, $x\in \mathbb R^d$. Clearly, $\psi \in \mathcal {C}(\mathbb R^d)$. Observe that,

$$\begin{aligned} \psi (x)= & {} \phi (v(x))=\sum _{n\in \mathbb N^d_0}a_nl_n(v(x))\\= & {} \pi ^{d/4}\sum _{n\in \mathbb N^d_0}a_n\sum _{m\le n}{{n-m-\mathbf {1/2}}\atopwithdelims ()n-m}\frac{(-1)^{|m|}\sqrt{(2m)!}}{2^{|m|} m!}h_{2m}(x). \end{aligned}$$

We will prove that the double series is absolutely convergent in $L^{\infty }(\mathbb R^d)$. By Cramér’s inequality [4, (19), p. 208], we have $|h_n(x)|\le 1$, for all $n\in \mathbb N^d_0$, $x\in \mathbb R^d$. For $j\in \mathbb N$, we have

$$\begin{aligned} {{j-1/2}\atopwithdelims ()j}=\frac{(2j-1)!!}{2^jj!}\le \frac{(2j)!!}{2^{j}j!}=1. \end{aligned}$$

(3.3)

This inequality trivially holds for $j=0$ since, in this case, the left hand side is equal to 1. Hence,

$$\begin{aligned} \left| a_n{{n-m-\mathbf {1/2}}\atopwithdelims ()n-m}\frac{(-1)^{|m|}\sqrt{(2m)!}}{2^{|m|} m!}h_{2m}(x)\right| \le |a_n|,\,\, x\in \mathbb R^d,\, n\ge m. \end{aligned}$$

Since $\{a_n\}_{n\in \mathbb N^d_0}$ is in $s^{\alpha }$ (cf. Theorem 2.6), the double series in the equality for $\psi (x)$ converges absolutely in $L^{\infty }(\mathbb R^d)$. Thus, we can change the order of summation in order to obtain

$$\begin{aligned} \psi (x)= & {} \pi ^{d/4}\sum _{m\in \mathbb N^d_0}\frac{(-1)^{|m|}\sqrt{(2m)!}}{2^{|m|} m!}h_{2m}(x)\sum _{n\ge m}a_n{{n-m-\mathbf {1/2}}\atopwithdelims ()n-m}\\= & {} \sum _{m\in \mathbb N^d_0}b_{2m}h_{2m}(x), \end{aligned}$$

where

$$\begin{aligned} b_{2m}=\frac{(-1)^{|m|}\pi ^{d/4}\sqrt{(2m)!}}{2^{|m|} m!}\sum _{n\in \mathbb N^d_0}a_{n+m}{{n-\mathbf {1/2}}\atopwithdelims ()n},\,\, m\in \mathbb N^d_0. \end{aligned}$$

If $\phi$ varies in a bounded subset B of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$, then the sequence $\{a_n\}_{n\in \mathbb N^d_0}$ varies in a bounded subset of $s^{\alpha }$ (cf. Theorem 2.7). Since $s^{\alpha }$ is a (DFS)-space there exist $C,a>1$ such that $|a_n|\le C a^{-|n|^{1/\alpha }}$, $\forall n\in \mathbb N^d_0$. The Cauchy-Schwarz inequality yields

$$\begin{aligned} |n|^{1/\alpha }+|m|^{1/\alpha }\le 2(|n|+|m|)^{1/\alpha },\,\, \forall n,m\in \mathbb N^d_0. \end{aligned}$$

(3.4)

Thus $a^{-|n+m|^{1/\alpha }}\le \sqrt{a}^{-|n|^{1/\alpha }}\sqrt{a}^{-|m|^{1/\alpha }}$. Hence, there exist $a',C'>1$ such that $|a_{n+m}|\le C' a'^{-|n|^{1/\alpha }}a'^{-|m|^{1/\alpha }}$. Using (3.3), we can estimate $b_{2m}$ as follows

$$\begin{aligned} |b_{2m}|\le C'a'^{-|m|^{1/\alpha }}\sum _{n\in \mathbb N^d_0}a'^{-|n|^{1/\alpha }}\le C''a''^{-|2m|^{1/\alpha }},\,\, m\in \mathbb N^d_0, \end{aligned}$$

where $a''=a'^{1/2^{1/\alpha }}$. Hence, when $\phi$ varies in B, the sequence $\{b_{2m}\}_{m\in \mathbb N^d_0}$ varies in a bounded subset of $s^{\alpha }$. Thus, the mapping $\phi \mapsto \phi \circ v$, $G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow \mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$, is well defined and it maps bounded sets into bounded sets (cf. Propositions 2.1 and 2.2). As $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is bornological, the mapping is continuous. Clearly, this mapping is injective. $\square$

Proposition 3.2

Let $\psi =\sum _{n\in \mathbb N^d_0} a_{2n}h_{2n}\in \mathcal S_{\alpha /2,\, \mathrm {even}}^{\alpha /2}(\mathbb {R}^d)$. Then, $\psi _{|\mathbb R^d_+}\circ w\in G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and

$$\begin{aligned} \psi _{|\mathbb R^d_+}\circ w=\sum _{n\in \mathbb N^d_0} b_nl_n, \end{aligned}$$

where $\{b_n\}_{n\in \mathbb N^d_0}\in s^{\alpha }$ is given by

$$\begin{aligned} b_n=\frac{(-1)^{|n|}2^{|n|}}{\pi ^{d/4}} \sum _{k\in \mathbb N^d_0}{{k-\mathbf {3/2}}\atopwithdelims ()k} \frac{(-1)^{|k|}2^{|k|}(k+n)!a_{2k+2n}}{\sqrt{(2k+2n)!}},\,\, n\in \mathbb N^d_0. \end{aligned}$$

(3.5)

Moreover, the mapping $\psi \mapsto \psi _{|\mathbb R^d_+}\circ w$, $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)\rightarrow G^{\alpha }_{\alpha }(\mathbb R^d_+)$, is a continuous injection.

Proof

We represent $h_{2n}$ as a finite Laguerre series. The equality [4, (2), p. 193] implies

$$\begin{aligned} H_{2n}(x)=(-1)^{|n|}2^{2|n|}n!L^{-\mathbf {1/2}}_n(v(x)),\,\, x\in \mathbb R^d,\, n\in \mathbb N^d_0. \end{aligned}$$

Thus, by using [4, (39), p. 192], we have

$$\begin{aligned} H_{2n}(x)= & {} (-1)^{|n|}2^{2|n|}n!\sum _{m\le n}{{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}L_m(v(x)),\,\, x\in \mathbb R^d,\, n\in \mathbb N^d_0, \end{aligned}$$

i.e.

$$\begin{aligned} h_{2n}(w(x))=\frac{(-1)^{|n|}}{\pi ^{d/4}}\sqrt{\frac{2^{2|n|}n!^2}{(2n)!}}\sum _{m\le n} {{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}l_m(x), \end{aligned}$$

(3.6)

where $x\in \overline{\mathbb R^d_+},\, n\in \mathbb N^d_0$. Let $\psi =\sum _{n\in \mathbb N^d_0}a_{2n}h_{2n}\in \mathcal S^{\alpha /2}_{\alpha /2,\, \mathrm {even}}(\mathbb R^d)$. Then $\{a_{2n}\}_{n\in \mathbb N^d_0}\in s^{\alpha }$ (cf. Proposition 2.2). Hence, there exist $C,a>1$ such that

$$\begin{aligned} |a_{2n}|\le Ca^{-|2n|^{1/\alpha }},\,\, \forall n\in \mathbb N^d_0. \end{aligned}$$

(3.7)

Let $\phi (x)=\psi (w(x))$, $x\in \overline{\mathbb R^d_+}$. Clearly, $\phi \in \mathcal {C}(\overline{\mathbb R^d_+})$. We have

$$\begin{aligned} \phi (x)=\sum _{n\in \mathbb N^d_0}\frac{(-1)^{|n|}a_{2n}}{\pi ^{d/4}} \sqrt{\frac{2^{2|n|}n!^2}{(2n)!}}\sum _{m\le n} {{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}l_m(x). \end{aligned}$$

(3.8)

By [4, (3), p. 205], $|l_n(x)|\le 1$, for all $x\in \overline{\mathbb R^d_+}$, $n\in \mathbb N^d_0$. Similarly as in (3.3), we have

$$\begin{aligned} \left| {{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}\right| \le 1,\,\, \text{ for } \text{ all }\,\, n\ge m, n,m\in \mathbb N^d. \end{aligned}$$

Since,

$$\begin{aligned} {{2j}\atopwithdelims ()j}\sim \frac{4^j}{\sqrt{j\pi }},\,\, \text{ as }\,\, j\rightarrow \infty , \end{aligned}$$

we obtain

$$\begin{aligned} \left| \frac{(-1)^{|n|}}{\pi ^{d/4}}\sqrt{\frac{2^{2|n|}n!^2}{(2n)!}} {{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}l_m(x)\right| \le C_1 (|n|+1)^{d/2}, \end{aligned}$$

(3.9)

$n,m\in \mathbb N^d_0,\, n\ge m,$ for some $C_1>1$. By (3.7), we can conclude that the series on the right hand side in (3.8) converges absolutely in $L^{\infty }(\overline{\mathbb R^d_+})$. Thus, we can change the order of summation in order to obtain $\phi (x)=\sum _{m\in \mathbb N^d_0}b_ml_m(x)$, where

$$\begin{aligned} b_m=\frac{(-1)^{|m|}2^{|m|}}{\pi ^{d/4}} \sum _{n\in \mathbb N^d_0}{{n-\mathbf {3/2}}\atopwithdelims ()n} \frac{(-1)^{|n|}2^{|n|}(n+m)!a_{2n+2m}}{\sqrt{(2n+2m)!}}. \end{aligned}$$

To estimate $b_m$ we can perform analogous technique as for (3.9). Hence, for all $m\in \mathbb N^d_0,$ we obtain

$$\begin{aligned} |b_m|\le C_2\sum _{n\in \mathbb N^d_0}(|n+m|+1)^{d/2}a^{-|2n+2m|^{1/\alpha }}\le C_3\sum _{n\in \mathbb N^d_0}a'^{-|n+m|^{1/\alpha }}, \end{aligned}$$

for some $1<a'<a$. Now, (3.4) implies that there exist $C'',a''>1$ such that $|b_m|\le C''a''^{-|m|^{1/\alpha }}$, $\forall m\in \mathbb N^d_0$, i.e. $\{b_m\}_{m\in \mathbb N^d_0}\in s^{\alpha }$. Thus, $\phi \in G^{\alpha }_{\alpha }(\mathbb R^d_+)$. If $\psi$ varies in a bounded subset B of $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$, then (3.7) holds with the same $C,a>1$ for all the sequences $\{a_{2n}\}_{n\in \mathbb N^d_0}$ generated by $\psi \in B$ (since $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$ is a subspace of the (DFS)-space $\mathcal S^{\alpha /2}_{\alpha /2}(\mathbb R^d)$). Thus, from the above proof, it follows that $\{b_m\}_{m\in \mathbb N^d_0}$ varies in a bounded subset of $s^{\alpha }$, i.e. $\phi$ varies in a bounded subset of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$. Hence, the mapping $\psi \mapsto \psi _{\mathbb R^d_+}\circ w$, $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)\rightarrow G^{\alpha }_{\alpha }(\mathbb R^d_+)$, is well defined and maps bounded sets into bounded sets. As $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$ is a (DFS)-space (cf. Proposition 2.2), it is bornological. Hence, the mapping is continuous. The proof for the injectivity is trivial. $\square$

Combining the above two propositions, we obtain the following result.

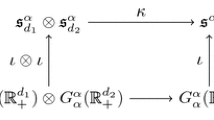
Theorem 3.3

The mapping $\phi \mapsto \phi \circ v$, $G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow \mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$ is a topological isomorphism. If $\phi =\sum _{n\in \mathbb N^d_0} a_n l_n$, then $\phi \circ v=\sum _{n\in \mathbb N^d_0} b_{2n}h_{2n}$, where $\{b_{2n}\}_{n\in \mathbb N^d_0}\in s^{\alpha }$ is given by (3.1). The inverse of this mapping is given by $\psi \mapsto \psi _{|\mathbb R^d_+}\circ w$, $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)\rightarrow G^{\alpha }_{\alpha }(\mathbb R^d_+)$. If $\psi =\sum _{n\in \mathbb N^d_0}a_{2n}h_{2n}$, then $\psi \circ w=\sum _{n\in \mathbb N^d_0}b_nl_n$, where $\{b_n\}_{n\in \mathbb N^d_0}\in s^{\alpha }$ is given by (3.5).

If we denote by $\mathfrak {I}$ the isomorphism $\psi \mapsto \psi _{|\mathbb R^d_+}\circ w$, $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)\rightarrow G^{\alpha }_{\alpha }(\mathbb R^d_+)$ with $\mathfrak {I}^{-1}:\phi \mapsto \phi \circ v$, $G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow \mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)$ being its inverse, then the transpose ${}^t\mathfrak {I}$ is an isomorphism between $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ and $(\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d))'$. By Proposition 2.4 (and the remark after), for $T=\sum _n a_nl_n\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ there exists $\{b_{2n}\}_{n\in \mathbb N^d_0}\in (s^{\alpha })'$ such that ${}^t\mathfrak {I}T=\sum _n b_{2n}h_{2n}\in (S^{\alpha }_{\alpha }(\mathbb R^d))'$. Then, (3.6) implies

$$\begin{aligned} b_{2n}=\langle {}^t\mathfrak {I}T,h_{2n}\rangle = \frac{(-1)^{|n|}2^{|n|}n!}{\pi ^{d/4}\sqrt{(2n)!}}\sum _{m\le n}{{n-m-\mathbf {3/2}}\atopwithdelims (){n-m}}a_m. \end{aligned}$$

(3.10)

Similarly, given $T=\sum _n a_{2n}h_{2n}\in (S^{\alpha }_{\alpha ,\, \mathrm {even}}(\mathbb R^d))'$, ${}^t(\mathfrak {I}^{-1})T\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Hence, ${}^t(\mathfrak {I}^{-1})T=\sum _nb_nl_n$, for some $\{b_n\}_{n\in \mathbb N^d_0}\in (s^{\alpha })'$. The equality (3.2) implies

$$\begin{aligned} b_n=\langle {}^t(\mathfrak {I}^{-1})T,l_n\rangle =\pi ^{d/4}\sum _{m\le n}{{n-m-\mathbf {1/2}}\atopwithdelims ()n-m}\frac{(-1)^{|m|}\sqrt{(2m)!}}{2^{|m|} m!}a_{2m}. \end{aligned}$$

(3.11)

Since ${}^t(\mathfrak {I}^{-1})=({}^t\mathfrak {I})^{-1}$, we proved the following theorem.

Theorem 3.4

The transpose ${}^t\mathfrak {I}$ of the isomorphism $\mathfrak {I}:\psi \mapsto \psi _{|\mathbb R^d_+}\circ w$, $\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d)\rightarrow G^{\alpha }_{\alpha }(\mathbb R^d_+)$, is a topological isomorphism ${}^t\mathfrak {I}:(G^{\alpha }_{\alpha }(\mathbb R^d_+))' \rightarrow (\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d))'$. The image of $\sum _n a_nl_n\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ under this isomorphism is $\sum _n b_{2n}h_{2n}$, where $\{b_{2n}\}_{n\in \mathbb N^d_0}\in (s^{\alpha })'$ is given by (3.10). The inverse of this isomorphism $({}^t\mathfrak {I})^{-1}$ maps $\sum _n a_{2n}h_{2n}\in (\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}}(\mathbb R^d))'$ into $\sum _n b_nl_n\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, where $\{b_n\}_{n\in \mathbb N^d_0}\in (s^{\alpha })'$ is given by (3.11).

Remark 3.5

Let $\sigma _n$, $n\in \mathbb N^d_0$, be measurable functions on $\mathbb R^d_+$ such that $\sigma _n(\rho )/(\mathbf {1}+\rho )^{n/2}\in L^2(\mathbb R^d_+)$, for all $n\in \mathbb N^d_0$ and for each $A>0$,

$$\begin{aligned} \sum _{n\in \mathbb N^d_0}\left\| \sigma _n(\rho )/(\mathbf {1}+\rho )^{n/2} \right\| _{L^2(\mathbb R^d_+)}A^{|n|}n^{\alpha n/2}<\infty . \end{aligned}$$

Then, by [10, Lemma 7.5] $\sum _{n\in \mathbb N^d_0} \sigma _n$ converges absolutely in $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ to some $\sigma$. Moreover, the same result also states that $\tilde{\sigma }_n(x,\xi )=\sigma _n(2x_1^2+2\xi _1^2,\ldots ,2x_d^2+2\xi _d^2)$ is measurable on $\mathbb R^{2d}$ and $\sum _n\tilde{\sigma }_n$ converges absolutely in $(\mathcal S^{\alpha /2}_{\alpha /2}(\mathbb R^{2d}))'$ to some $\tilde{\sigma }$. The Weyl pseudodifferential operator with symbol $\tilde{\sigma }$ is well defined and continues mapping from $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$ into $\mathcal S^{\alpha }_{\alpha }(\mathbb R^d)$, it extends to a continuous mapping from $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ into $(\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ and it is given by $W_{\tilde{\sigma }}f=\sum _k f_k\sigma _kh_k$, where $f=\sum _k f_kh_k\in (\mathcal S^{\alpha }_{\alpha }(\mathbb R^d))'$ and $\sigma _k=(2\pi )^{d/2}(-1)^{|k|}2^{-d}\langle \sigma ,l_k\rangle$ (see [10, Theorem 7.6]). By Theorem 3.4, each $\sigma$ given as above originates from a unique even tempered ultradistribution by the isomorphism $({}^t\mathfrak {I})^{-1}:(\mathcal S^{\alpha /2}_{\alpha /2,\,\mathrm {even}} (\mathbb R^d))'\rightarrow (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$.

4 Structural theorems

4.1 The first structural theorem

In order to give the first structural theorem, we need to introduce some additional terminology.

Let $\{M_p\}_{p\in \mathbb N_0}$ be a sequence of positive numbers such that satisfies the following condition (see [12]):

(M.1) $M^2_p\le M_{p-1}M_{p+1}$, $p\in \mathbb N$.

Notice that the condition (M.1) is equivalent to the assumption that the sequence $m_p=M_p/M_{p-1}$, $p\in \mathbb N$, increases monotonically. Furthermore, if the sequence $m_p=M_p/M_{p-1}$, $p\in \mathbb N$, tends to infinite, then we define the associated function of $M_p$ as (cf. [12]):

$$\begin{aligned} M(t)=\sup _{p\in \mathbb N_0}\ln \frac{t^pM_0}{M_p},\,\, t\in (0,\infty ). \end{aligned}$$

It is a monotonically increasing continuous function which vanishes for sufficiently small $t>0$ and increases more rapidly than $\ln t^p$ for any p as $t\rightarrow \infty$. We are interested only in the sequences of type $\{p!^{\alpha }\}_{p\in \mathbb N_0}$, with $\alpha \ge 1$. So, from now on, we specialise $M_p=p!^{\alpha }$, $p\in \mathbb N_0$. Thus $M(\cdot )$ will be the associated function of $\{p!^{\alpha }\}_{p\in \mathbb N_0}$. Given a sequence of positive numbers $\{r_p\}_{p\in \mathbb N}$ which monotonically increases to infinity, the sequence with zeroth term equal to $0!^{\alpha }=1$ and p-th term equal to $p!^{\alpha }\prod _{j=1}^p r_j$, $p\in \mathbb N$, also satisfies (M.1) and one can define its associated function, which we denote by $N_{r_p}(\cdot )$.

Before we state the next result, notice that the operator $R^k$, $k\in \mathbb N^d_0$, is continuous on $\mathcal S(\mathbb R^d_+)$ and on $\mathcal S'(\mathbb R^d_+)$ (recall (2.1) for the definition of $R^k$).

Lemma 4.1

For each $k\in \mathbb N^d_0$, $R^k$ acts continuously on $G^{\alpha }_{\alpha }(\mathbb R^d_+)$.

Proof

If $\phi =\sum _{n\in \mathbb N^d_0}a_n l_n$ varies in a bounded subset of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$, then $\{a_n\}_{n\in \mathbb N^d_0}$ varies in a bounded subset of $s^{\alpha }$. Since $\sum _{n\in \mathbb N^d_0}a_n l_n$ converges absolutely to $\phi$ in $\mathcal S(\mathbb R^d_+)$, we have $R^k\phi =\sum _na_n R^kl_n=\sum _n a_n(-1)^{|k|}n^k l_n$ and the series converges absolutely in $\mathcal S(\mathbb R^d_+)$. It can be easily proved that $\{a_n(-1)^{|k|}n^k\}_{n\in \mathbb N^d_0}$ is in $s^{\alpha }$ and when $\{a_n\}_{n\in \mathbb N^d_0}$ varies in a bounded subset of $s^{\alpha }$ so does $\{a_n(-1)^{|k|}n^k\}_{n\in \mathbb N^d_0}$. Hence, $R^k$ is well defined as a mapping from $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ into itself and it maps bounded sets into bounded sets. As $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is bornological, $R^k$ is continuous. $\square$

By duality, we can define the transpose ${}^t R^k$ of $R^k$ as a continuous operator on $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. If $T=\sum _{n\in \mathbb N^d_0} b_n l_n$, then one easily verifies that ${}^tR^kT=\sum _n b_n(-1)^{|k|}n^k l_n$ (since $\{b_n\}_{n\in \mathbb N^d_0}\in (s^{\alpha })'$, the sequence $\{b_n(-1)^{|k|}n^k\}_{n\in \mathbb N^d_0}$ also belongs to $(s^{\alpha })'$ and thus the right hand side is a well defined element of $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$). We come to the conclusion that ${}^tR^k$ coincides with $R^k$ when $T\in G^{\alpha }_{\alpha }(\mathbb R^d)\subseteq (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Hence, from now on, we will write $R^k$ instead of ${}^t R^k$.

Following Komatsu [12], we call an entire function $P:\mathbb C^d\rightarrow \mathbb C$, $P(z)=\sum _{n\in \mathbb N^d_0}c_n z^n$, an ultrapolynomial of class $\{p!^{\alpha }\}$ if for every $h>0$ there exists $C>0$ such that $|c_n|\le Ch^{|n|}/|n|!^{\alpha }$. By [12, Proposition 4.5], P is an ultrapolynomial of class $\{p!^{\alpha }\}$ if and only if for every $h>0$ there exists $C>0$ such that $|P(z)|\le Ce^{M(h|z|)}$, $\forall z\in \mathbb C^d$. Now, notice that Remark 2.9 yields that P is an ultrapolynomial of class $\{p!^{\alpha }\}$ if and only if for every $h>0$ there exists $C>0$ such that $|P(z)|\le Ce^{h|z|^{1/\alpha }}$, $\forall z\in \mathbb C^d$.

Next, for a given ultrapolynomial $P(z)=\sum _n c_n z^n$ of class $\{p!^{\alpha }\}$, we will show that the operator $\sum _n c_n R^n$, denoted by P(R),  is a well defined and continuous operator on $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. In the proof we will use the fact that $\mathcal {L}_b(G^{\alpha }_{\alpha }(\mathbb R^d_+), G^{\alpha }_{\alpha }(\mathbb R^d_+))$ and $\mathcal {L}_b((G^{\alpha }_{\alpha }(\mathbb R^d_+))',(G^{\alpha }_{\alpha }(\mathbb R^d_+))')$ are complete (cf. [18, Corollary 1, p. 344]; notice that $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ are bornological and complete spaces).

Lemma 4.2

Let $P(z)=\sum _{n\in \mathbb N^d_0}c_n z^n$ be an ultrapolynomial of class $\{p!^{\alpha }\}$. Then, $\sum _{n\in \mathbb N^d_0}c_n R^n$ converges absolutely in both $\mathcal {L}_b(G^{\alpha }_{\alpha }(\mathbb R^d_+), G^{\alpha }_{\alpha }(\mathbb R^d_+))$ and $\mathcal {L}_b((G^{\alpha }_{\alpha }(\mathbb R^d_+))',(G^{\alpha }_{\alpha }(\mathbb R^d_+))')$.

Proof

Since $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is a barrelled and complete space, its topology is given by the system of seminorms $\phi \mapsto \sup _{T\in B'}|\langle T,\phi \rangle |$, where $B'$ ranges over all bounded subsets of $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Hence, the topology of $\mathcal {L}_b(G^{\alpha }_{\alpha }(\mathbb R^d_+), G^{\alpha }_{\alpha }(\mathbb R^d_+))$ is given by the system of seminorms

$$\begin{aligned} \Phi \mapsto \sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}}|\langle T,\Phi (\phi )\rangle |, \end{aligned}$$

where B and $B'$ range over all bounded subsets of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, respectively.

To prove that $\sum _{n\in \mathbb N^d_0}c_n R^n$ converges absolutely in $\mathcal {L}_b(G^{\alpha }_{\alpha }(\mathbb R^d_+), G^{\alpha }_{\alpha }(\mathbb R^d_+))$, we have to prove that for each such B and $B'$,

$$\begin{aligned} \sum _{n\in \mathbb N^d_0}|c_n|\sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}}|\langle T, R^n\phi \rangle |<\infty . \end{aligned}$$

(4.1)

Fix such B and $B'$. Let $\phi =\sum _n a_{n,\phi }l_n$, $\phi \in B$ and $T=\sum _n b_{n,T}l_n$, $T\in B'$. Thus, $\{\{a_{n,\phi }\}_n|\, \phi \in B\}$ is bounded in $s^{\alpha }$ and $\{\{b_{n,T}\}_n|\, T\in B'\}$ is bounded in $(s^{\alpha })'$. There exist $a,C>1$ such that $|a_{n,\phi }|\le Ca^{-|n|^{1/\alpha }}$, for all $n\in \mathbb N^d_0$, $\phi \in B$. For this a, choose $1<b\le a^{1/4}$. Then, there exists $C_1>0$ such that $|b_{n,T}|\le C_1 b^{|n|^{1/\alpha }}$ for all $n\in \mathbb N^d_0$, $T\in B'$. Moreover, there exist $s,C_2>1$ such that $|m|^{|n|}\le C_2 s^{|n|}b^{|m|^{1/\alpha }}|n|!^{\alpha }$, for all $n,m\in \mathbb N^d_0$. Hence,

$$\begin{aligned} \sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}}|\langle T, R^n\phi \rangle |\le \sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}} \sum _{m\in \mathbb N^d_0}|a_{m,\phi }||b_{m,T}||m|^{|n|}\le C_3 s^{|n|}|n|!^{\alpha },\,\, \forall n\in \mathbb N^d_0. \end{aligned}$$

Since P is an ultrapolynomial of class $\{p!^{\alpha }\}$, the last inequality implies (4.1).

The topology of $\mathcal {L}_b((G^{\alpha }_{\alpha }(\mathbb R^d_+))',(G^{\alpha }_{\alpha }(\mathbb R^d_+))')$ is given by the system of seminorms

$$\begin{aligned} \Phi \mapsto \sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}}|\langle \Phi (T),\phi \rangle |, \end{aligned}$$

where B and $B'$ range over all bounded subsets of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, respectively. In $\mathcal {L}_b((G^{\alpha }_{\alpha }(\mathbb R^d_+))',(G^{\alpha }_{\alpha }(\mathbb R^d_+))')$, $\sum _{n\in \mathbb N^d_0}c_n R^n$ converges absolutely if we prove that for each such B and $B'$

$$\begin{aligned} \sum _{n\in \mathbb N^d_0}|c_n|\sup _{\begin{array}{c} T\in B'\\ \phi \in B \end{array}}|\langle R^nT, \phi \rangle |<\infty . \end{aligned}$$

This can be done by using the same technique as above. $\square$

Before we prove the main result of this subsection, we state the following three technical lemmas. The first one is proved in [17].

Lemma 4.3

([17, Lemma 2.4]) Let $g:[0,\infty )\rightarrow [0,\infty )$ be an increasing function such that satisfies the following estimate: for every $h>0$ there exists $C>0$ such that $g(t)\le M(ht)+\ln C$. Then there exists a subordinate function $\epsilon (t)$ such that $g(t)\le M(\epsilon (t))+\ln C'$, for some constant $C'>1$.

For the definition of a subordinate function see [12, Definition 3.11].

Lemma 4.4

Let B be a bounded subset of $(s^{\alpha })'$. There exist a sequence of positive numbers $\{r_p\}_{p\in \mathbb N}$ which monotonically increases to infinity and $C'>1$ such that $|b_n|\le C'e^{N_{r_p}(|n|)}$, for all $n\in \mathbb N^d_0$, $\{b_n\}_{n\in \mathbb N^d_0}\in B$.

Proof

Since B is a bounded subset of $(s^{\alpha })'$, for every $h>0$ there exists $C>1$ such that $|b_n|\le Ce^{M(h|n|)}$, for all $n\in \mathbb N^d_0$, $\{b_n\}_n\in B'$ (cf. Remark 2.9). Define $f:[0,\infty )\rightarrow [0,\infty )$ as

$$\begin{aligned} f(t)=\sup _{\begin{array}{c} |k|\le t\\ \{b_n\}_n\in B \end{array}}\ln _+|b_k|,\,\, t\in [0,\infty ). \end{aligned}$$

One easily verifies that f is a nonnegative monotonically increasing function and for every $h>0$ there exists $C>0$ such that $f(t)\le M(ht)+ C$. Thus, we can apply Lemma 4.3 to obtain the existence of a subordinate function $\epsilon :[0,\infty )\rightarrow [0,\infty )$ and $C_1>1$ such that $f(t)\le M(\epsilon (t))+C_1$, $t\in [0,\infty )$. Now, [12, Lemma 3.12] implies the existence of a sequence $N_p$, $p\in \mathbb N_0$, of positive numbers which satisfies (M.1) such that $M(\epsilon (t))\le N(t)$, $t\in (0,\infty )$ ($N(\cdot )$ is the associated function of the sequence $N_p$) and $N_pM_{p-1}/(N_{p-1}M_p)\rightarrow \infty$ as $p\rightarrow \infty$. Define $r'_p=N_pM_{p-1}/(N_{p-1}M_p)$, $p\in \mathbb N$. Since $r'_p\rightarrow \infty$, one can find a monotonically increasing sequence of positive numbers $\{r_p\}_{p\in \mathbb N}$ which tends to infinity and $r_p\le r'_p$, $p\in \mathbb N$. Then,

$$\begin{aligned} f(t)\le & {} N(t)+C_1=\sup _{p\in \mathbb N_0}\ln \frac{t^pN_0}{N_p}+C_1=\sup _{p\in \mathbb N_0} \ln \frac{t^p}{M_p\prod _{j=1}^pr'_j}+C_1\\\le & {} \sup _{p\in \mathbb N_0}\ln \frac{t^p}{M_p\prod _{j=1}^pr_j}+C_1=N_{r_p}(t)+C_1. \end{aligned}$$

By the definition of f, this readily implies the conclusion of the lemma. $\square$

The next lemma is proved in [16]; here $\mathfrak {R}$ stands for the set of all sequences of positive numbers which increase monotonically to infinity.

Lemma 4.5

([16, Lemma 2.1], Roumieu case) Let $r'\ge 1$ and $(k_p)\in \mathfrak {R}$. There exists an ultrapolynomial P(z) of class $\{M_p\}$ such that P does not vanish on $\mathbb R^{d}$ and satisfies the following estimate:

There exists $C>0$ such that for all $x\in \mathbb R^d$ and $\alpha \in \mathbb N^d,$

$$\begin{aligned} \left| D^{\alpha }\left( {1}/{P(x)}\right) \right|\le & {} C\frac{\alpha !}{r'^{|\alpha |}} e^{-N_{k_p}(|x|)}. \end{aligned}$$

As a special case, we see that for any given sequence of positive numbers $\{r_p\}_{p\in \mathbb N}$ which increases monotonically to infinity, one can find an ultrapolynomial P(z) of class $\{p!^{\alpha }\}$ and $C>0$ such that $|P(x)|\ge Ce^{N_{r_p}(|x|)}$ for all $x\in \mathbb R^d$.

Theorem 4.6

Let $B'\subseteq (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ be a bounded set. There exists an ultrapolynomial P(z) of class $\{p!^{\alpha }\}$ and a bounded set B in $L^2(\mathbb R^d_+)$ such that for each $T\in B'$ there exists $F_T\in B$ satisfying $T=P(R)F_T$ in $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$.

Conversely, given a bounded set B in $L^2(\mathbb R^d_+)$ and an ultrapolynomial P(z) of class $\{p!^{\alpha }\}$, P(R)F belongs to $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ for each $F\in B$ and the set $\{P(R)F|\, F\in B\}$ is bounded in $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$.

Proof

Let $T=\sum _{n\in \mathbb N^d_0} b_{n,T}l_n$, $T\in B'$. The set $\{\{b_{n,T}\}_{n\in \mathbb N^d_0}|\, T\in B'\}$ is bounded in $(s^{\alpha })'$. Lemma 4.4 implies that there exists a sequence of positive numbers $\{r_p\}_{p\in \mathbb N}$ which increases monotonically to infinite such that $|b_{n,T}|\le C'e^{N_{r_p}(|n|)}$, for all $n\in \mathbb N^d_0$, $T\in B'$. We define the sequence $\{r'_p\}_{p\in \mathbb N}$ by $r'_j=\min \{1, r_1\}$, $j=1,\ldots , d+1$ and $r'_j=r_{j-d-1}$, $j\ge d+2$, $j\in \mathbb N$. Then, $\{r'_p\}_{p\in \mathbb N}$ increases monotonically to infinity, $r'_p\le r_p$, $p\in \mathbb N$ and there exists $\tilde{C}_1\ge 1$ such that

$$\begin{aligned} (t^{d+1}+1)e^{N_{r_p}(t)}\le \tilde{C}_1e^{N_{r'_p}(2^{\alpha }t)}+e^{N_{r_p}(t)},\,\, t\in [0,\infty ). \end{aligned}$$

Hence, if we define $k_p=r'_p/2^{\alpha }$, $p\in \mathbb N$, the sequence $\{k_p\}_{p\in \mathbb N}$ increases monotonically to infinity and there exists $\tilde{C}_2>1$ such that

$$\begin{aligned} (t^{d+1}+1)e^{N_{r_p}(t)}\le \tilde{C}_2e^{N_{k_p}(t)},\,\, t\in [0,\infty ). \end{aligned}$$

By Lemma 4.5, we can choose an ultrapolynomial $P(z)=\sum _{n\in \mathbb N^d_0} c_nz^n$ of class $\{p!^{\alpha }\}$ such that $|P(x)|\ge C e^{N_{k_p}(|x|)}$, for all $x\in \mathbb R^d$. Lemma 4.2 verifies that P(R) acts continuously on $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ and on $(G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Observe that

$$\begin{aligned} \sum _{n\in \mathbb N^d_0}\left| \frac{b_{n,T}}{P(-n)}\right| ^2\le C_1\sum _{n\in \mathbb N^d_0}e^{2N_{r_p}(|n|)}e^{-2N_{k_p}(|n|)}\le C_2,\,\, \forall T\in B'. \end{aligned}$$

Hence, $F_T=\sum _{n\in \mathbb N^d_0}(b_{n,T}/P(-n))l_n\in L^2(\mathbb R^d_+)$ and the set $\{F_T|\, T\in B'\}$ is bounded in $L^2(\mathbb R^d_+)$. As $L^2(\mathbb R^d_+)\subseteq (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$, $P(R)F_T\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Moreover,

$$\begin{aligned} P(R)l_n=\sum _{m\in \mathbb N^d_0}c_mR^ml_n=\sum _{n\in \mathbb N^d_0}c_m(-n)^ml_n=P(-n)l_n. \end{aligned}$$

Hence,

$$\begin{aligned} P(R)F_T=\sum _{n\in \mathbb N^d_0}\frac{b_{n,T}}{P(-n)}P(R)l_n=\sum _{n\in \mathbb N^d_0}b_{n,T}l_n=T. \end{aligned}$$

The converse part of the theorem is trivial. $\square$

4.2 The second structural theorem

Before we prove the second structural theorem, we need several preliminary results. Firstly, using the Sobolev embedding theorem, we will prove that the topology of $\mathcal S(\mathbb R^d_+)$ can be defined by $L^2$-seminorms instead of supremum seminorms. We need to verify that $\mathbb R^d_+$ satisfies the strong local Lipschitz condition (cf. [1, Definition 4.9, p. 83]) in order to obtain the assertion. For the moment, denote $\mathbf {C}=\mathbb R^d_+$. On the hyperplane $x_1+\cdots +x_d=0$ take $d-1$ orthonormal vectors $\xi _1,\ldots ,\xi _{d-1}$ and let $\xi _d=(-1/\sqrt{d},\ldots ,-1/\sqrt{d})$ (given in the $x_1,\ldots ,x_d$ coordinate system). Then, $\xi _1,\ldots ,\xi _d$ is an orthonormal basis for $\mathbb R^d$. Notice that the boundary of $\mathbf {C}$ is exactly the graph, given in the $(\xi _1,\ldots ,\xi _d)$-coordinate system of a continuous piecewise linear function f in $\xi _1,\ldots ,\xi _{d-1}$ such that the domain of each piece is a polyhedral cone. Thus, this function is Lipschitz continuous on $\mathbb R^{d-1}$ and $\mathbf {C}$ is represented by the inequality $\xi _d<f(\xi _1,\ldots ,\xi _{d-1})$. This proves that $\mathbf {C}=\mathbb R^d_+$ satisfies the strong local Lipschitz condition. Thus, the Sobolev embedding theorem [1, Theorem 4.12, p. 85] is applicable on $\mathbb R^d_+$, i.e. for all $j\in \mathbb N_0$, the Sobolev space $H^{j+j_0}(\mathbb R^d_+)$ is continuously injected into $\mathcal {C}^j(\overline{\mathbb R^d_+})$, where $2j_0>d\ge 2(j_0-1)$ (here, $\mathcal {C}^j(\overline{\mathbb R^d_+})$ denotes the (B)-space of all functions which have bounded uniformly continuous derivatives up to order j; the norm is given by $\sup _{|k|\le j}\sup _{x\in \mathbb R^d_+}|D^k\varphi (x)|$). This implies that the topology on $\mathcal S(\mathbb R^d_+)$ can be given by the family of seminorms

$$\begin{aligned} \varphi \mapsto \left( \sum _{|m|\le j,\, |n|\le j} \Vert x^mD^n\varphi \Vert ^2_{L^2(\mathbb R^d_+)}\right) ^{1/2},\,\, j\in \mathbb N_0. \end{aligned}$$

Now, we can give an alternative representation (again as an inductive limit) of $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ which will enable us to prove the second structural theorem. For $A>0$, we denote by $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ the space of all $f\in \mathcal S(\mathbb R^d_+)$ such that

$$\begin{aligned} \sum _{p,k\in \mathbb N^d_0}\frac{\Vert x^{(p+k)/2}D^pf(x)\Vert ^2_{L^2(\mathbb R^d_+)}}{A^{2|p+k|}k^{\alpha k}p^{\alpha p}}<\infty . \end{aligned}$$

From the alternative definition of the topology of $\mathcal S(\mathbb R^d_+)$ given above, the space $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ with the seminorms

$$\begin{aligned} \tilde{\sigma }_{A,j}(f)= & {} \left( \sum _{p,k\in \mathbb N^d_0} \frac{\Vert x^{(p+k)/2}D^pf(x)\Vert ^2_{L^2(\mathbb R^d_+)}}{A^{2|p+k|}k^{\alpha k}p^{\alpha p}}\right. \\&\left. \quad + \sum _{|m|\le j,\, |n|\le j} \Vert x^mD^nf(x)\Vert ^2_{L^2(\mathbb R^d_+)}\right) ^{1/2},\,\, j\in \mathbb N_0, \end{aligned}$$

becomes an (F)-space. When $A_1<A_2$, $\tilde{G}^{\alpha ,A_1}_{\alpha ,A_1}(\mathbb R^d_+)$ is continuously injected into $\tilde{G}^{\alpha ,A_2}_{\alpha ,A_2}(\mathbb R^d_+)$. Clearly, $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is continuously injected into $G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ and $G^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is continuously injected into $\tilde{G}^{\alpha ,2A}_{\alpha ,2A}(\mathbb R^d_+)$. Hence, $\displaystyle G^{\alpha }_{\alpha }(\mathbb R^d_+)=\lim \nolimits _{\begin{array}{c} \longrightarrow \\ A\rightarrow \infty \end{array}} \tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ as a l.c.s.

Proposition 4.7

Let $A>0$. For each $T\in (\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))'$, there exists $j\in \mathbb N_0$ and $F_{A,p,k}\in L^2(\mathbb R^d_+)$, $p,k\in \mathbb N^d_0$ and $\tilde{F}_{A,n,m}\in L^2(\mathbb R^d_+)$, $n,m\in \mathbb N^d_0$ with $|n|\le j$, $|m|\le j$, such that

$$\begin{aligned} \sum _{p,k\in \mathbb N^d_0}A^{2|p+k|}p^{\alpha p}k^{\alpha k}\Vert F_{A,p,k}\Vert ^2_{L^2(\mathbb R^d_+)}+\sum _{|m|\le j,\, |n|\le j} \Vert \tilde{F}_{A,n,m}\Vert ^2_{L^2(\mathbb R^d_+)}<\infty \end{aligned}$$

(4.2)

and for all $\phi \in \tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$,

$$\begin{aligned} \langle T,\phi \rangle= & {} \sum _{p,k\in \mathbb N^d_0}\int _{\mathbb R^d_+}F_{A,p,k}(x)x^{(p+k)/2} D^p\phi (x)dx\nonumber \\{} & {} \,\,+ \sum _{|m|\le j,\, |n|\le j}\int _{\mathbb R^d_+}\tilde{F}_{A,n,m}(x)x^mD^n\phi (x)dx. \end{aligned}$$

(4.3)

Conversely, given $j\in \mathbb N_0$ and a set of $L^2(\mathbb R^d_+)$-functions $\{F_{A,p,k}|\,p,k\in \mathbb N^d_0\}\cup \{\tilde{F}_{A,n,k}|\, n,m\in \mathbb N^d_0,\,|n|\le j,\,|m|\le j\}$ such that (4.2) holds, there exists $T\in (\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))'$ given by (4.3).

Proof

For $j\in \mathbb N_0$, we define

$$\begin{aligned} \mathbf {U}_j=\bigsqcup _{(p,k)\in \mathbb N^{2d}_0}\mathbb R^d_{+,p,k}\,\,\bigsqcup \,\, \bigsqcup _{\begin{array}{c} (n,m)\in \mathbb N^{2d}_0\\ |n|\le j,\, |m|\le j \end{array}}\mathbb R^d_{+,n,m}, \end{aligned}$$

where, as standard, $\bigsqcup$ denotes disjoint union. Each member of this disjoint union is an exact copy of $\mathbb R^d_+$. We equip $\mathbf {U}_j$ with the disjoint union topology. Since there are countably many copies of $\mathbb R^d_+$, $\mathbf {U}_j$ is Hausdorff locally compact space and an each open set in $\mathbf {U}_j$ is $\sigma$-compact. We define a Borel measure $\mu _j$ on $\mathbf {U}_j$ by

$$\begin{aligned} \mu _j(E)= & {} \sum _{(p,k)\in \mathbb N^{2d}_0}A^{-2|p+k|}p^{-\alpha p}k^{-\alpha k}|E\cap \mathbb R^d_{+,p,k}|\\&+\sum _{\begin{array}{c} (n,m)\in \mathbb N^{2d}_0\\ |n|\le j,\, |m|\le j \end{array}}|E\cap \mathbb R^d_{+,n,m}|, \end{aligned}$$

where $|E\cap \mathbb R^d_{+,p,k}|$ and $|E\cap \mathbb R^d_{+,n,m}|$ is the Lebesgue measure of $E\cap \mathbb R^d_{+,p,k}$ and $|E\cap \mathbb R^d_{+,n,m}|$, respectively (clearly, E is a Borel set in $\mathbf {U}_j$ if and only if $E\cap \mathbb R^d_{+,p,k}$ and $E\cap \mathbb R^d_{+,n,m}$ are Borel sets in $\mathbb R^d_{+,p,k}$ and $\mathbb R^d_{+,n,m}$, respectively, for all $p,k,n,m\in \mathbb N^d_0$, $|m|\le j$, $|n|\le j$). As readily seen, $\mu _j$ is locally finite, $\sigma$-finite and $\mu _j(\mathbf {K})<\infty$ for every compact set $\mathbf {K}$ in $\mathbf {U}_j$. By the properties of $\mathbf {U}_j$, $\mu _j$ is regular (both inner and outer regular). Now, observe that, for each $j\in \mathbb N_0$, $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is continuously injected into $L^2(\mathbf {U}_j,\mu _j)$ by the mapping $\mathfrak {J}_j:\phi \mapsto \mathbf {F}$, where $\mathbf {F}$ is defined by $\mathbf {F}_{|\mathbb R^d_{+,p,k}}=x^{(p+k)/2}D^p\phi (x)$ and $\mathbf {F}_{|\mathbb R^d_{+,n,m}}=x^mD^n\phi (x)$, $p,k,n,m\in \mathbb N^d_0$, $|m|\le j$, $|n|\le j$. In fact,

$$\begin{aligned} (\tilde{\sigma }_{A,j}(\phi ))^2= & {} \sum _{p,k\in \mathbb N^d_0}\frac{\Vert x^{(p+k)/2}D^p\phi (x)\Vert ^2_{L^2(\mathbb R^d_+)}}{A^{2|p+k|}k^{\alpha k}p^{\alpha p}}\nonumber \\&\quad +\sum _{|m|\le j,\, |n|\le j} \Vert x^mD^n\phi (x)\Vert ^2_{L^2(\mathbb R^d_+)}\nonumber \\= & {} \int _{\mathbf {U}_j}|\mathbf {F}|^2d\mu _j= \Vert \mathbf {F}\Vert ^2_{L^2(\mathbf {U}_j,\mu _j)}. \end{aligned}$$

(4.4)

If $T\in (\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))$, there exist $j\in \mathbb N_0$ and $C>0$ such that $|\langle T,\phi \rangle |\le C\tilde{\sigma }_{A,j}(\phi )$. From (4.4), T induces a continuous functional on $\mathfrak {J}_j(\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))$ when this space is equipped with the topology induced by $L^2(\mathbf {U}_j,\mu _j)$. By the Hahn-Banach theorem, we can extend T to a continuous functional $\mathbf {T}$ on the whole $L^2(\mathbf {U}_j,\mu _j)$ and hence $\mathbf {T}\in L^2(\mathbf {U}_j,\mu _j)$. Denote

$$\begin{aligned} F_{A,p,k}=A^{-2|p+k|}p^{-\alpha p} k^{-\alpha k}\mathbf {T}_{|\mathbb R^d_{+,p,k}},\, \tilde{F}_{A,n,m}=\mathbf {T}_{|\mathbb R^d_{+,n,m}}, \end{aligned}$$

where $p,k,n,m\in \mathbb N^d_0$, $|m|\le j$, $|n|\le j.$ Then, $F_{A,p,k},\tilde{F}_{A,n,m}\in L^2(\mathbb R^d_+)$, for all $p,k,n,m\in \mathbb N^d_0$, $|m|\le j$, $|n|\le j$ and (4.2) holds since this is exactly $\Vert \mathbf {T}\Vert ^2_{L^2(\mathbf {U}_j,\mu _j)}$. For $\phi \in \tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$, we have

$$\begin{aligned} \langle T,\phi \rangle= & {} \mathbf {T}(\mathfrak {J}_j(\phi ))= \int _{\mathbf {U}_j}\mathfrak {J}_j(\phi )\mathbf {T}d\mu _j\\= & {} \sum _{p,k\in \mathbb N^d_0}\int _{\mathbb R^d_+}F_{A,p,k}(x)x^{(p+k)/2}D^p\phi (x)dx\\&+\sum _{|m|\le j,\, |n|\le j}\int _{\mathbb R^d_+}\tilde{F}_{A,n,m}(x)x^mD^n\phi (x)dx. \end{aligned}$$

The converse part follows trivially. $\square$

Theorem 4.8

Let $T\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$. Then, for each $A>0$ there exist $j=j(A)\in \mathbb N_0$ and a set of $L^2(\mathbb R^d_+)$-functions

$$\begin{aligned} \{F_{A,p,k}|\,p,k\in \mathbb N^d_0\}\cup \{\tilde{F}_{A,n,m}|\, n,m\in \mathbb N^d_0,\,|n|\le j,\,|m|\le j\} \end{aligned}$$

(4.5)

such that (4.2) holds and the restriction of T to each $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is given by (4.3).

If for each $A>0$, there exist $j=j(A)\in \mathbb N_0$ and a set of $L^2(\mathbb R^d_+)$-functions (4.5) such that (4.2) holds, then for each $A>0$ there exists $T_A\in (\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))'$ given by (4.3). Furthermore, if for each $A_1<A_2$, the restriction of $T_{A_2}$ to $\tilde{G}^{\alpha ,A_1}_{\alpha ,A_1}(\mathbb R^d_+)$ coincides with $T_{A_1}$, then there exists $T\in (G^{\alpha }_{\alpha }(\mathbb R^d_+))'$ such that for each $A>0$ the restriction of T to $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is $T_A$, i.e. for $\phi \in \tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$, $\langle T,\phi \rangle$ is given by (4.3).

Proof

The first part follows directly from Proposition 4.7, since the restriction of T to each $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$, $A>0$, is continuous. For the second part, observe that the existence of $T_A\in (\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+))'$, for each $A>0$, given by (4.3) is verified by Proposition 4.7. Furthermore, if $T_A$, $A>0$, satisfies that for each $A_1<A_2$ the restriction of $T_{A_2}$ to $\tilde{G}^{\alpha ,A_1}_{\alpha ,A_1}(\mathbb R^d_+)$ coincides with $T_{A_1}$, then one can define a linear functional $T:G^{\alpha }_{\alpha }(\mathbb R^d_+)\rightarrow \mathbb C$ by $\langle T,\phi \rangle =\langle T_A,\phi \rangle$ when $\phi \in \tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$. Because of this condition, this is indeed a well defined linear mapping into $\mathbb C$. The continuity of T follows from the fact that each restriction of T to $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ is $T_A$, $A>0$, which is continuous as a mapping from $\tilde{G}^{\alpha ,A}_{\alpha ,A}$ onto $\mathbb C$ and the fact that $G^{\alpha }_{\alpha }(\mathbb R^d_+)$ is the inductive limit of $\tilde{G}^{\alpha ,A}_{\alpha ,A}(\mathbb R^d_+)$ as $A\rightarrow \infty$. $\square$