Teaching calculus with infinitesimals and differentials

Abstract

Several new approaches to calculus in the U.S. have been studied recently that are grounded in infinitesimals or differentials rather than limits. These approaches seek to restore to differential notation the direct referential power it had during the first century after calculus was developed. In these approaches, a differential equation like dy = 2x·dx is a relationship between increments of x and y, making dy/dx an actual quotient rather than code language for $\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f(x)}{h}$. An integral ${\int }_{a}^{b}2x dx$ is a sum of pieces of the form 2x·dx, not the limit of a sequence of Riemann sums. One goal is for students to develop understandings of calculus notation that are imbued with more direct referential meaning, enabling them to better interpret and model situations by means of this notation. In this article I motivate and describe some key elements of differentials-based calculus courses, and I summarize research indicating that students in such courses develop robust quantitative meanings for notations in single- and multi-variable calculus.

1 Introduction

Long before there was The Calculus, there were the “differential calculus,” the “integral calculus,” and “the infinitesimal calculus,” several among many calculuses that emerged in the seventeenth and eighteenth centuries (Hutton 1795). The fundamental notations for these calculi, which are still the main notations of calculus today, were invented by Leibniz in the mid-1670s. He used the differential (e.g., dx) to denote an infinitesimal difference, and the integral ∫ (big S for summa) to denote an infinite sum of such infinitesimal quantities. Isaac Newton, of course, independently developed similar foundational ideas although his notations are less commonly used today. During the first century in the life of what is now calculus, mathematicians on the continent used Leibniz’ notation, treating the differential calculus and infinitesimal calculus as being fundamentally about (unsurprisingly) differentials and infinitesimals. What exactly these continental mathematicians imagined “infinitesimals” to be is a matter of scholarly debate,¹ but nonetheless two things are clear enough about their views:

• 1. The fundamental object of the differential calculus was the differential, not the derivative, and certainly not the limit.

• 2. A differential represented an infinitesimal difference between two values of a variable.

By the end of the nineteenth century, various calculuses had become The Calculus. The differential was no longer the primary object, nor did it any longer refer to an infinitesimal. By the mid-twentieth century, the story had become about how infinitesimals were jettisoned due to their lack of rigor. Bertrand Russell sums up this oft-told tale succinctly in his History of Western Philosophy (1946):

The great mathematicians of the seventeenth century were optimistic and anxious for quick results; consequently they left the foundations of analytical geometry and the infinitesimal calculus insecure. Leibniz believed in actual infinitesimals, but although this belief suited his metaphysics it had no sound basis in mathematics. Weierstrass, soon after the middle of the nineteenth century, showed how to establish the calculus without infinitesimals, and thus at last made it logically secure (Russell 1946, p. 857).

With this narrative in mind, by the early twentieth century the foundational concept for the calculus had become the limit. This replacement was done not because infinitesimals were difficult for students to learn but only because they were seen as insufficiently rigorous (Thompson 1914). Differential notation remained omnipresent in twentieth century calculus texts, but as vestiges of older usage, no longer directly referring to infinitesimal differences. For well over a century now, calculus textbooks have not used the differential dx to directly denote an increment of x. A differential typically cannot be written meaningfully by itself. It has meaning only when it is amalgamated with other notations. Thus “dy/dx” is not directly a quotient of two quantities but is code language for $\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f(x)}{h}$. An expression like ${\int }_{a}^{b}3{x}^{4}dx$ does not mean a sum, but is shorthand for the limit of a sequence of finite Riemann sums.

Differentials are not taken seriously in the overwhelming majority of calculus classrooms and curricula, to borrow a phrase from Dray and Manogue (2010). By this I mean that (a) differentials are not a primary object of study and (b) that they do not refer directly to quantities. Yet this fact is in tension with the actual practice of calculus-users, because differentials are such a common shorthand for scratch-work in the margins. For example, to evaluate an integral such as ${\int }_{1}^{4}t\sqrt{{t}^{2}-1}dt$, students are taught to use substitution: First set $u={t}^{2}-1$, then “derive” $du=2tdt$, then reduce to $t dt=du/2$ in order to replace the leftovers inside the integral. This is a strange state of affairs: students are not supposed to believe that differentials are quantities, yet sometimes they are supposed to manipulate them as though they are. What are the equations $du=2tdt$ and $t dt=du/2$ supposed to mean for these students? Perhaps students know better than to ask such a question. At any rate, it is perfectly reliable to manipulate differentials algebraically as though they were quantities, a fact that is no secret to engineers and scientists, nor to several centuries of practitioners of the differential calculus.

If working with differentials as objects in their own right is reliable, sometimes even indispensable, then why not take them seriously? In this paper I discuss two objections to doing so. One objection was that differentials rely on infinitesimals, which cannot be rigorously grounded. But this objection was definitively refuted in the 1960s with Abraham Robinson’s development of nonstandard analysis. As I describe in Sect. 2, Robinson’s hyperreal numbers provide a rigorous development of infinitesimals, which allows differentials to once again directly refer to quantities without sacrificing rigor. Yet more than 50 years later, almost no textbooks and classes take differentials seriously or use an approach based on infinitesimals. The reason for this is probably the second objection: teaching calculus with limits is working fine, so why upset the apple cart by introducing a new approach that is less familiar to instructors? The answer to this objection is that teaching calculus with limits is, by and large, not working fine. As I discuss in Sect. 4, studies show that students often do not emerge from standard calculus classes with a robust quantitatively-based understanding of calculus concepts and notation that would allow them to meaningfully interpret and model situations with calculus. The goal of current approaches to calculus that take differentials seriously is to remedy this situation. In this paper I describe such approaches, particularly those that treat differentials as representing infinitesimal quantities. I also provide rationale for such approaches and summarize some findings about the kinds of reasoning students develop in such classrooms.

2 What are differentials and infinitesimals?

2.1 What are differentials?

I know of two ways to mathematically define differentials such as dx for students that allow this notation to meaningfully represent an increment of x. Both ways allow the notation dx to directly represent quantities, not just shorthands, in expressions such as “dy/dx”, “${\int }_{a}^{b}f\left(x\right)dx$”, and “$2xdx+2ydy=0$”. Both of these ways can be made mathematically precise:

• 1. An infinitesimal increment of x: In keeping with Leibniz’ usage, a differential can be defined as an infinitesimal quantity, which itself can be formalized as a type of hyperreal number. This way of defining infinitesimals is discussed in the next section.

• 2. An arbitrarily small change in x: The differential dx is an increment of x that can be made arbitrarily small. To clarify the difference between “∆x” and “dx”, some treat dx as a quantity that varies continuously within any interval of fixed size ∆x (e.g., Thompson and Ashbrook 2019).

Either interpretation allows differentials to be used as the grounding notational idea of calculus, and thus can be the basis for a differentials-based calculus courses (detailed in Sect. 4). In addition to these two ways of defining differentials, there are others that can be used that are mathematically coherent but that do not as easily allow for differentials to be the central notational idea of calculus. These include:

• 3. A differential form: For instance, the differential dx is a one-dimensional density that allows for integration over an oriented manifold (see, for instance, Flanders 1963).

• 4. A shorthand for limits: The differential dx is not defined independently, but has mathematical meaning only in conjunction with other symbols. For instance, dy/dx means $\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f(x)}{h}$ (for y = f(x)).

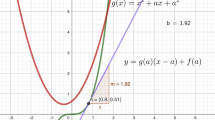
• 5. A linear approximation: The differential dx is defined to be a small finite increment of x, equal to ∆x. If y = f(x) is not linear, then the differential dy serves as an approximation for ∆y, but is not equal to it. Thus dy is a function of two variables x and dx. This definition is illustrated in Fig. 1.

Fig. 1

The linear approximation definition of the differentials dx and dy (Dray and Manogue 2010)

Definition 5, the linear approximation definition of differentials, appears in most standard American calculus textbooks. It is worth noting that this definition could easily be a source of confusion for students, particularly since there is no obvious reason to refer to the approximate change of y as dy instead of as ∆y. Dray and Manogue (2010) point out that there is no need to use differentials at all when discussing linear approximations; the equation of the tangent line could quite sensibly be written as $\Delta y={f}^{{\prime}}\left(x\right)\Delta x$. Yet if ∆ notation could adequately serve this purpose, why did differentials ever come to be used as linear approximations? These authors suggest that the reason is because this usage, which only became common in the mid-1900s, effectively prevents using differentials for any other purpose, such as to describe infinitesimals:

It thus appears that differential notation was appropriated for linear approximation only within the last 60 years, and that one of the motivations for doing so was to “clarify” that infinitesimals are meaningless. This claim was convincingly rebutted by Robinson barely 10 years later, yet little effort has been made to restore the original role of differentials in calculus (Dray and Manogue 2010, p. 97).

Just as differentials can be mathematically defined in various ways, students also develop a variety of ways to interpret them, even when they have taken standard calculus courses instead of differentials-based ones. For instance, David Tall surveyed students entering Warwick University if they had seen the notation $\frac{dy}{dx} = \lim \limits_ {\delta x \to 0} \frac{\delta y}{\delta x}$ (1980). He categorized the responses of the 60 students who completed the survey according to Fig. 2, counting “½” when students gave multiple answers. It can be seen that well more than 25% of the students viewed dy as a small or infinitesimal quantity, even if it is unclear how they imagine ‘infinitesimal’ (or what is meant by the response “dy is the differential of y”).

Fig. 2

Undergraduate interpretations of differential notation (Tall 1980)

2.2 What are infinitesimals?

One interpretation of a differential is as an infinitesimal increment of a variable quantity. This raises the question: what exactly is an infinitesimal increment?

The mathematical machinery of the 1600s did not allow infinitesimals to be formally defined in a manner that would satisfy current standards for mathematical rigor. Here I summarize two broad ways in which seventeenth century ideas of infinitesimal transformed and became formalized over time. One of these, which Bair et al. (2013) call the “A-track”, begins with Newtonian infinitesimals. Newton often used dynamic language, and described infinitesimals as “evanescent” or vanishing quantities whose values are achieved at the moment when they disappear (Bell 2005). This is the imagery that led Berkeley to famously mock infinitesimals as being “ghosts of departed quantities” (1734). Yet this imagery can be seen as anticipating the idea of the limit: a finite variable quantity approaching zero. In this way, Newtonian infinitesimals can be seen as ultimately formalized along the A-track by the epsilontic limit definition fully developed in the nineteenth century by Weierstrass.

Leibniz’ accounts of infinitesimals are typically more static than Newton’s. In the 1670s, Leibniz developed techniques for calculating with and comparing various orders of infinitesimal and infinite quantities. Formalization of this imagery for infinitesimal occurred along the “B-track” (Bair et al. 2013), through Abraham Robinson’s development of the hyperreal numbers and nonstandard analysis in the early 1960s (e.g., Robinson 1961). In particular, historians have pointed out how operations in the hyperreal numbers capture and reflect the heuristics Leibniz and his immediate continental colleagues used in the infinitesimal calculus, particularly Leibniz’ Law of Continuity and its implications (e.g., Bos 1974; Katz and Sherry 2013). It is a formalization of infinitesimals in the sense that it develops and grounds them in the normal ZFC axiomatization of modern mathematics. Robinson’s Transfer Principle proved that any first-order logical statement in standard analysis is true if and only if the “same” statement is true in nonstandard analysis (“sameness” here means that there exist interpretations for the statement in both models). This means that standard analysis and nonstandard analysis are equivalent in power, consistency, and scope—calculus can be done in either.

The hyperreals are a field including all real numbers, their infinitesimal neighbors, and their infinite cousins. An infinitesimal is a nonnegative number that is smaller than every finite real number. A positive number is infinite when it is larger than every positive real number.

Each finite hyperreal number p is infinitely close to exactly one real number r. This real r is often called the shadow of p (sh(p)), or standard part of p (st(p)). Likewise, each real number r has a cloud or monad² of infinitely many hyperreal numbers that are infinitesimally close to it. We notate if two hyperreals a and b are infinitesimally close to one another by a ≈ b. So p ≈ sh(p). Likewise, if a is real and ε is infinitesimal, then a + ε ≈ a. The monad of hyperreals around the real number p formalizes the concept image that an infinitesimal only becomes visible when you zoom in infinitely on the continuum at a particular point.

If it possible to zoom infinitely on a point p at a scale factor of ε to reveal a monad of hyperreals infinitely close to p, it is also possible to imagine zooming in again at scale factor ε on any of these points to reveal yet another neighborhood of second-order infinitesimals. This process could be repeated, and Leibniz discussed such a hierarchy of infinitely many orders of infinitesimal and infinite numbers. He also developed heuristics for rounding away higher-order infinitesimals when deriving differential equations and derivatives. These heuristics can be formalized in the hyperreals. For instance, consider the function y = x³ in the hyperreals. For any infinitesimal non-zero increment dx of x, we might seek to find the magnitude of the corresponding increment dy of y:

$$dy={(x+dx)}^{3}-{(x)}^{3}$$

$$dy={{x}^{3}+3{x}^{2}dx+3xdx}^{2}+{dx}^{3}-{x}^{3}$$

At this point Leibniz would use heuristics to dismiss the higher-ordered infinitesimal terms on the right as being negligible at this scale, ending up with the differential equation

$$dy={3x}^{2}dx$$

In the hyperreals, if we wanted to define a derivative function, we could divide both sides by the infinitesimal dx (the hyperreals are a field, allowing this division by a non-zero number):

$$\frac{dy}{dx}=3{x}^{2}+3dx+{dx}^{2}$$

This allows us to define ${f}^{{\prime}}\left(x\right)=\mathrm{sh}\left(\frac{dy}{dx}\right)=\mathrm{sh}\left(3{x}^{2}+3dx+{dx}^{2}\right)=3{x}^{2}$. This is an example of transfering between the hyperreals and reals by looking at hyperreals’ shadows. Such a process often does the same work as taking a limit does in standard analysis.

I have been answering the question ‘What are infinitesimals?’ by summarizing how infinitesimals can be mathematically defined. A different kind of answer to this question is to view the concept imagery involved when imagining infinitesimals as being more fundamental than the mathematical definitions that seek to formalize that imagery. The foundational image, one which is appealed to in every treatment of infinitesimals I have seen, is that of the infinite zoom. Figure 3 illustrates how imagining zooming infinitely much on the number line reveals how points in the shadow of c are distinct, when they were indistinguishable at the finite scale (Tall 2001). Thus the foundational image of infinitesimal uses scaling-continuous variational reasoning, by which one generalizes the properties of the continuum to different scales by imagining repeated zooming (Ellis et al. in press). Tall describes a similar mental act: “Infinitesimal concepts are natural products of the human imagination derived through combining potentially infinite repetition and the recognition of its repeating properties” (Tall 2009, p. 3).

Fig. 3

Infinite magnification of the number line reveals that c-ε, c, and c + ε are different (Tall 2001)

This zooming imagery also supports other images and heuristics that students develop for comparing and operating with infinitesimal quantities, even when they were not taught these ideas themselves. For instance, I studied a student who developed coherent heuristics for comparing infinitesimals to finite numbers, for squaring infinitesimals, and for other operations; all of them paralleled Leibniz’ heuristics, even though she had never been taught them (Ely 2010). Further imagery of student ideas of infinitesimals is described in Sect. 4 below, in the context of student reasoning that arises in differentials-based calculus courses.

3 Calculus classes that use differentials and infinitesimals

I am aware of a variety of approaches over the last few decades for teaching first-year calculus using differentials and/or infinitesimals.³ These approaches fall roughly into two categories.

The first category includes classes that are explicitly grounded in the hyperreal numbers, using the textbooks of Keisler or of Henle and Kleinberg. Keisler’s textbook, Elementary Calculus: An Infinitesimal Approach (2011) develops calculus formally using the hyperreal numbers. It first appeared in 1976, saw widespread use during the following decade, and is still in use in various classrooms around the world. Henle and Kleinberg’s Infinitesimal Calculus (1979) is short and formal, and to my knowledge has been used mainly in some honors undergraduate courses.

Studies of student reasoning in such courses focus on how students learn formal definitions more robustly in the hyperreals than with limits. Sullivan found that students in classes using Keisler’s book were much more successful proving a particular function’s continuity using the formal nonstandard definition of continuity than were students in the standard classes using the formal δ-ε limit definition (1976). The teachers of the nonstandard classes tended to report that their students understood the course material better than in the previous times when they had used a standard approach. In another recent study, first-year calculus students at a university in Israel were taught both the formal standard epsilontic definitions and nonstandard definitions of limit, continuity, and convergence (Katz and Polev 2017). The students overwhelmingly responded that they preferred, and better understood, the nonstandard definitions. The primary results of both studies are unsurprising in light of how thorny the formal epsilontic definitions of these concepts are known to be for students (e.g., Davis and Vinner 1986; Roh 2008).

The second category includes differentials-based approaches to calculus. These approaches treat differentials as quantities and develop differential equations independently of, and before, derivatives. They use an informal approach to infinitesimals, rather than developing them formally with the hyperreals. It is courses of this kind that I profile more extensively in the following section. Examples of such courses are the ones taught and studied by Dray and Manogue (2003, 2010), by Boman and Rogers (2020), and the ones I have taught and studied (e.g., Ely 2017, 2019), as well as the approach developed by Thompson and Ashbrook (2019). Some of these courses employ a historical approach to calculus, such as the one studied by Can and Aktas (2019), in which the instructor’s perspective on teaching calculus was transformed by teaching with primary sources (notably Euler’s 1775 Foundations of Differential Calculus) that develop the subject using differentials. Finally, I note that there are plenty of researchers and instructors around the world who treat differentials as quantities in carefully chosen moments while teaching, to provide intuition of the big ideas of the subject for their students. For example, Moreno-Armella provides such reflections drawing on his experiences teaching calculus in Mexico (2014).

4 Differentials-based approach to calculus

In this section I describe in more detail the elements of differentials-based approaches to calculus. Such courses may or may not use infinitesimals, formally or informally, to define differentials. I provide rationales for these elements that is grounded in prior research about student reasoning in calculus. Along the way I also summarize research about student reasoning in differentials-based approaches, for the handful of topics for which this research has been conducted.

4.1 A grounding idea: correspondence between amount equations and differential equations

The fundamental object in a differentials-based approach to calculus is the variable quantity, not the function. It accords with Leibniz’ view that any variable can be written in terms of other related variables. Any such relationship is represented by what I will here call an “amount” equation. An amount equation is an equation with finite quantities with more than one variable—it tells how the (finite) amounts of several variable quantities relate to each other. Examples include $y=5{x}^{3}+7\mathrm{cos}t$ and ${y}^{2}-xy={x}^{2}$. At this point there is no a priori assumption that one quantity is a function of the other. This idea reflects Ransom’s proposal to treat equations, not functions, as fundamental in calculus (1951).

A differential equation tells you the relative magnitudes of infinitesimal increments (differentials) of the variable quantities in terms of each other. Examples include $dy=15{x}^{2}dx-7\mathrm{sin}tdt$ and $2y dy=x dy+y dx+2x dx$.

One broad overarching goal in differentials-based calculus is to find correspondences between amount equations and differential equations. This idea grounds the further development of derivatives and integrals. Figure 4 shows how a differential equation can be imagined as a zoomed-in version of an amount equation. Figure 5 shows how an amount equation can be imagined as a sum of infinitely many differentials in a differential equation.⁴ Most of what we want to represent, calculate, and interpret in calculus stems from the idea of this correspondence.

Fig. 4

Infinite zoom reveals a relation between differentials

Fig. 5

Amounts as sums of differentials

4.2 The chain “rule” and implicit differentiation

Methods for deriving a differential equation from an amount equation are relatively systematic, as Newton and Leibniz discovered. A differentials-based example of such a derivation is seen in Sect. 2.2 above. Standard approaches to calculus develop these methods (power rule, product rule, etc.) very similarly with limits. On the other hand, a significant difference can be seen with the chain “rule.” In standard calculus approaches, the chain rule states that the derivative of the composite function $F\left(x\right)=f(g\left(x\right))$ is $F^{\prime}\left(x\right)=f^{\prime}(g\left(x\right))\cdot g^{\prime}(x)$. This formulation can be baffling for students (Clark et al. 1997); it is not readily supported by the underlying logic of converting units, and seems purposefully designed to guarantee that students do not think about cancelling fractions. On the other hand, in a differentials-based approach where dt and dy are quantities rather than shorthands, students really are cancelling fractions. There is nothing baffling about why $dy=\frac{dy}{dt}dt$ or $\frac{dy}{dt}=\frac{dy}{du}\frac{du}{dt}$.

In some sense with differentials there really is no chain rule at all, just the recognition of the benefit of changing variables to aid with differentiating. In practice this often looks like: If $dy=p du$ and $du=q dt$, then $dy=p (q dt)$. For example, suppose you want to find the differential equation corresponding to the amount equation $y={\mathrm{sin}}^{2}\left(3{\theta }^{4}+1\right)$. Performing a few substitutions helps you stay organized:

$y={\mathrm{sin}}^{2}(3{\theta }^{4}+1)$
$d[y]=d \left[{\left(\mathrm{sin}\left(3{\theta }^{4}+1\right)\right)}^{2}\right]$	Let $u=\mathrm{sin}\left(3{\theta }^{4}+1\right)$
$dy=d[{u}^{2}]$	$d\left[u\right]=d \left[\mathrm{sin}\left(3{\theta }^{4}+1\right)\right]$	Let $v=3{\theta }^{4}+1$
$dy=2u du$	$du=d[\mathrm{sin}\left(v\right)]$	$dv=12{\theta }^{3}d\theta$
	$du=\mathrm{cos}\left(v\right)dv$
	$du=\mathrm{cos}\left(3{\theta }^{4}+1\right) \left(12{\theta }^{3}d\theta \right)$
$dy=2\mathrm{sin}\left(3{\theta }^{4}+1\right)\mathrm{cos}\left(3{\theta }^{4}+1\right) \left(12{\theta }^{3}d\theta \right)$

This flexibility with differentials also allows one to find a differential equation from an amount equation, and then to work flexibly with that equation to answer various questions about the situation at hand. Dray and Manogue (2010) illustrate this flexibility in the context of a cylinder of volume $V=\pi {r}^{2}h$. Using the product rule in the form

$$d\left[uv\right]=v du+u dv,$$

one gets the differential equation

$$dV=2\pi r h dr+\pi {r}^{2} dh.$$

Now, suppose the problem is about related rates. This equation is valid no matter what rate is sought; it does not require the student to decide from the outset whether the problem seeks the rate of change of one of these quantities with respect to radius, time, temperature, or whatever else. If they find out that they want the rate of change of radius with respect to time, then they can divide both sides of the equation by an infinitesimal time increment dt, and solve for the ratio $\frac{dr}{dt}$. If the problem is about optimization, they can set dV = 0 and solve for $\frac{dh}{dr}$ (or perhaps $\frac{dr}{dh}$).

Implicit differentiation can also be thorny for students in a standard calculus class. In a differentials-based approach the term does not even need to be used; nothing is different about it. In a standard calculus class, when students differentiate ${y}^{2}=xy+{x}^{2}$, it is a source of confusion why the ${y}^{2}$ becomes $2y y^{\prime}$ while the ${x}^{2}$ becomes just $2x$. Using differentials, this doesn’t happen. The differential of ${y}^{2}$ is $2y dy$, the differential of ${x}^{2}$ is $2x dx$, the differential of ♣² is 2♣ d♣, etc. The differential equation for

$${y}^{2}=xy+{x}^{2}$$

is thus

$$2y dy=x dy+y dx+2x dx.$$

This could be used for a variety of purposes now. For instance, if you want the slope of the tangent line to the original curve at some point (${x}_{0}, {y}_{0}),$ you can plug that point into the differential equation and divide both sides by dx to determine the slope $\frac{dy}{dx}$ at that point.

4.3 Derivatives and rates

Although the above discussion touches on the idea of rate, the development of robust student reasoning about rates in calculus goes far beyond calculating a differential equation or a derivative function. A variety of studies have explored the complexity of reasoning involved in conceptualizing rate of change among secondary and university students (e.g., Bezuidenhout 1998; Herbert and Pierce 2012; Thompson 1994). Students often understand rate of change as one experiential quantity, developed from their embodied experience, such as the speed of their own walking. Few have constructed from this a robust coordination between two covarying quantities that itself composes a new quantity (Carlson et al. 2003). Such a new composed quantity has been called a multiplicative object (Thompson and Carlson 2017); flexible student reasoning with it entails the ability to mentally decompose it as needed into its two component coordinated varying quantities (Thompson 1994). The coordination is not just between pairs of values of these two variables, but between pairs of changes or increments in the values of these two variables.

This understanding supports the abstraction of the idea of a rate of change at a moment, an image that is crucial for a meaningful understanding of derivative (Thompson and Ashbrook 2019). In a differentials-based approach to calculus, this coordination between increments over an infinitesimal (or small enough) scale is seen in two forms. In a differential equation such as dy = r(x)·dx, the rate is a factor that converts between an increment of x and an increment of y. As x changes, y changes by a proportional amount, and this proportionality factor r(x) depends on what value of x you’re at. In a derivative such as $\frac{dy}{dx}=r\left(x\right)$, the rate is a ratio of increments of the two quantities, which can also be represented as the slope of a curve over such an increment.

When differentials have quantitative meaning for a student, the students have a basis for making a robust rate-based meaning of both notations, as coordinations of changes in covarying quantities. In contrast, in standard treatments of calculus, $\frac{dy}{dx}$ is code language for $\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f(x)}{h}$, which is quickly replaced with the notation $f^{\prime}(x)$. Since dy and dx cannot be decoupled, this reinforces a monolithic student interpretation of rate. Many students develop only a vague idea of slope as “slantiness” of a curve, without seeing how this represents a rate composed of two covarying quantities (Thompson and Ashbrook 2019).

In a standard limits-based calculus course, the image that is often used to develop the understanding of derivative at a point is the slope of a secant line approaching a tangent line as two points on the curve get closer. In a differentials-based calculus course, the grounding image is that of zooming or rescaling (Fig. 4). Whether the zoom is imaged as infinite, or just as “enough,” depends on the course. In Tall’s locally-straight approach to calculus, the image of zooming was deliberately fostered to anchor the idea of derivative (1985). Zoomed in enough, the magnified graph looks like a straight line, so it is indistinguishable from its tangent line over that neighborhood. Tall notes, “by choosing a suitably small value of dx, we can see dy/dx, as the slope of the tangent, now a ‘good enough’ approximation to give a visual representation for the slope of the graph itself” (2009, p. 5). Others have further developed calculus approaches grounded in the idea of local linearity and zooming rather than in the limiting secant line (Samuels 2017). This image has been found to be helpful and flexible for developing single variable calculus ideas such as the derivative, tangent line and non-differentiability (Samuels 2012), and multivariable calculus ideas such as partial derivatives, tangent vectors, and tangent planes (Fisher and Samuels 2019).

Frid studied the student understandings of derivative that developed in three different Canadian calculus courses (1994). The first class was a standard calculus course focusing on techniques and procedures. The second was also a standard but much more conceptually-oriented course. The third used infinitesimal language and shared many features with differentials-based approaches, including the consistent imagery of zooming in. Frid found that students who used infinitesimal language were by far the most likely to demonstrate coherent interpretations of derivative at a point. Students in the first class could not explain what the limit notation for the derivative meant, while students in the third class could talk about the function as locally straight and describe its slope where the “rise and the run would be infinitesimal”.

This finding supports the idea that a differentials-based calculus class can foster student understanding of derivative as a composed quantity rather than as just a unitary slope. In such an approach, the notation $\frac{dy}{dx}$ transparently reflects a rate understanding of derivative at a point, while the notation $f^{\prime}(x)$ does not. On the other hand, with the notation $f^{\prime}(x)$ it is easier to specify whether one is talking about a derivative at a point or a derivative function—the notation $f^{\prime}(3)$ is less cumbersome than $\frac{dy}{dx}{|}_{x=3}$.

4.4 Integrals

Differentials-based approaches can also provide students with more robustly meaningful interpretations of integrals. Recently a number of studies have shown the limitations of the understandings students develop for definite integrals in standard calculus courses. Jones notes several distinct modes students use for interpreting definite integral notation ${\int }_{a}^{b}f\left(x\right)dx$:

• 1. The integral is an area of the region bounded by the x-axis and the curve y = f(x), between x = a and b—this region is taken as a whole that is not partitioned into smaller pieces.

• 2. The integral is an instruction to find the anti-derivative of f and evaluate it at x = a and b.

• 3. The integral is a sum of pieces over a specified domain (more detail about this type of interpretation follows).

Area and anti-derivative interpretations are commonly displayed by calculus students, while sum-based interpretations are rare (e.g., Orton 1983; Sealey and Oehrtman 2005; Jones 2013, 2015a, b; Wagner 2016; Fisher et al. 2016). For example, Jones et al. (2017) used two prompts to survey 150 undergraduate students who had completed first-semester university calculus. Nearly every student used an area interpretation or anti-derivative interpretation, or both, on the two prompts. Only 22% of students made even a passing reference to summation of any kind, and on each prompt less than 7% used a sum-based interpretation. Fisher et al. (2016) found that the majority of students in a standard calculus class used only the area interpretation when describing the meaning of a definite integral, and Grundmeier et al. (2006) found that only 10% of students mentioned an infinite sum when asked to define a definite integral.

This reveals a significant problem in American undergraduate calculus classes, because many studies indicate that sum-based interpretations are much more productive for supporting student reasoning than area and anti-derivative interpretations (e.g., Sealey 2014; Sealey and Oehrtman 2005; Jones 2013, 2015a, b; Jones and Dorko 2015; Wagner 2016). The area and anti-derivative interpretations have serious limitations for students modeling in various applications, particularly in physics, when the sought quantity is often difficult to imagine as the area of a region (e.g., Meredith and Marrongelle 2008; Nguyen and Rebello 2011; Jones 2015a).

In contrast, Jones (2013, 2015a) found that students who used sum-based reasoning were more successful on physics modeling tasks than students who used only area or antiderivative interpretations. The reason for this can be seen by looking more closely at the types of interpretation involved in sum-based reasoning:

• The adding up pieces (AUP) interpretation treats an integral generally as a sum ${\int }_{x=a}^{b}dA$. The domain has been broken into increments of size dx, and the summand dA is a piece of a sought quantity A that corresponds to each such increment. These pieces are summed to produce a total amount of that quantity A, from x = a to b.

• The multiplicatively-based summation (MBS) interpretation is similar but it requires multiplicative structure in the summand: dA = f(x)·dx. The f(x) is then seen as a rate at which A changes over any increment dx (terminology adapted from Jones 2015a, b; Jones and Dorko 2015; Ely 2017).

If the differential dx is viewed as an infinitesimal increment, then these sum-based interpretations view the integral directly as a sum of infinitely many infinitesimal bits, each corresponding to a distinct increment dx. In an approach without infinitesimals, an integral ${\int }_{a}^{b}f\left(x\right)dx$ is the limit of a sequence of Riemann sums of the form $\sum f\left({x}^{*}\right)\Delta x$, so the dx might be seen as a vestige of $\Delta x$.

One reason sum-based reasoning is more successful for modeling is that it focused attention on the quantities and units of the situation at hand. Jones found that students who used MBS could appeal to the multiplicative structure between the integrand and differential to explain why they had produced the correct integrand, since (revolutions per min) (mins) would cancel to the desired quantity, revolutions. This accords with Thompson’s view that a meaningful interpretation of integrals is grounded in the recognition of the multiplicative relationship between the two quantities inside the integral (1994).

Nearly all calculus books define the definite integral using Riemann sums, but this fact seems to contribute little to building sum-based reasoning for the students who use these books. When investigating this apparent pedagogical disconnect, Jones et al. (2017) found that instructors’ teaching moves lead students to perceive the limit of Riemann sums not as a conceptual basis for understanding the definite integral, but merely as a calculational procedure that allows an integral to be estimated accurately. This is one way that the limit process involved in the Riemann sum interpretation can form a didactical obstacle to building sum-based conceptions of the integral. A differentials-based approach, where the big S really is a sum, and the dx really is an infinitesimal increment of x, avoids this obstacle.

Recent evidence supports the conclusion that students in differentials-based calculus classes can develop robust sum-based interpretations of definite integral notation. In a recent case study, students used the AUP interpretation for modeling a novel volume problem using integral notation, and readily converted to the MBS interpretation when transitioning from modeling with integrals to evaluating integrals. Similar benefits of a differentials-based approach scaled up to a large lecture format. In a recent comparison study, the same eight multiple-choice items appeared on the final exam for students in a differentials-based Calculus I lecture and a standard Calculus I lecture (Ely 2019). Figure 6 shows the two items that focused on interpreting ̄notation pertaining to integrals. In the differentials-based class (n = 92), 91.3% answered Item 8 correctly (response e), while 58.6% of students in the standard class (n = 133) did. On Item 4,⁵ 65.2% of students in the differentials-based class answered correctly (response d), compared to 37.6% of students in the standard class.

Fig. 6

Sample assessment items with notation that pertains to interpreting integrals

4.5 Accumulation functions and the fundamental theorem of calculus

Differentials-based approaches also provide a way for students to make sense of the deep connection at the heart of calculus, which is reflected in the Fundamental Theorem of Calculus (FTC). Thompson and Ashbrook’s approach foregrounds this connection (2019). An accumulation function f can be notated as $f\left(x\right)={\int }_{a}^{x}{r}_{f}\left(t\right)dt$. To ground this approach, these authors define a differential dt as a variable whose value varies smoothly, repeatedly, through infinitesimal intervals (x, x + ∆x]. This treatment of differentials uses smooth covariational reasoning both at the finite real-valued scale and at the infinitesimal scale. The function f varies smoothly with t and dt: t varies smoothly through the real numbers, while dt varies smoothly at the infinitesimal scale, within infinitesimal intervals (x, x + ∆x].

One reason they define differentials in this way is that it provides a clear way to connect rate of change and accumulation, to support the Fundamental Theorem of Calculus (FTC). This connection, and how differentials figure into it, is illustrated when they define integral notation for accumulation functions:

When r_f is an exact rate of change function, any value r_f(x) is an exact rate of change of f at the moment x. The function f having an exact rate of change of r_f(x) at a value of x means that f varies at essentially a constant rate of change over a small interval containing that value of x. This means that we can, in theory, approximate the variation in f around that value of x to any degree of precision. We just need to make Δx small enough so that r_f(x)dx is essentially equal to the actual variation in f as dx varies from 0 to Δx over that Δx-interval (Thompson and Ashbrook 2019, https://patthompson.net/ThompsonCalc/section_5_3.html).

The integral ${\int }_{a}^{x}{r}_{f}\left(t\right)dt$ thus represents an accumulation over an interval from a to x of the function f that comes from this rate-of-change function r_f. A definite integral can be defined after this: it is simply an accumulation function evaluated at two specific values, like f(14) − f(4).

Many meaningful treatments of calculus ideas in classrooms around the world can be adapted to differentials with only, let’s say, infinitesimal changes. Practically speaking, working with differentials often just involves writing dx instead of ∆x and not taking a limit. For example, consider Arnold Kirsch’s discussion (2014) of Part I of the FTC. As Kirsch states the theorem, if $F\left(x\right)={\int }_{a}^{x}{f}_{a}\left(t\right)dt$, then $F^{\prime}(x)={f}_{a}(x)$ (for continuous functions r). On the one hand, the accumulation function $F\left(x\right)$ can be seen as an area bounded between the curve f and the axis, between a and x (see Fig. 7a). Then ${F}^{{\prime}}\left(x\right)=\frac{dF}{dx}$ is the rate that this area changes as x moves. Therefore $\frac{dF}{dx}\approx \frac{{\text{Area}} \, {\text{under}} \, f \, {\text{ between}} \, x \,{\text{and}} \, x \, + \, \Delta x}{\left({\text{small}}\right) \, {\text{ time}} \, {\text{interval}} \, \Delta x}\approx \frac{{\text{Area}} \, {\text{of}} \,{\text{rectangle}} \, f\left(x\right)\cdot \Delta x}{\left({\text{small}}\right) \, {\text{time}} \, {\text{interval}} \, \Delta x} \, = \, f(x)$.

Fig. 7

The FTC Part I, from Kirsch (2014)

How does this idea of area relate to the idea of the slope of the tangent line? Kirsch graphs the area accumulation function ${F}_{0}\left(x\right)$ (noting the difficulty of the idea that the changing areas on the top of Fig. 7 are being kept track of as changing heights on the bottom). The slope of F’s graph is $\frac{{F}_{a}\left(x+\Delta x\right)-{F}_{a}\left(x\right)}{\Delta x}$, which means:

• On the one hand, the average height of f in the interval [x, x + ∆x];

• On the other hand, the slope of the secant line from F_a in the interval [x, x + ∆x].

Then Kirsch describes how, as ∆x gets smaller and smaller, these become, respectively,

• The average height of f at x, and

• The slope of the tangent line of F_a at the position x.

Notice how small of a change it is to adapt this intuitive treatment of the FTC by replacing ∆x with dx and avoiding limits. The key ideas remain clear, and even become a bit more direct. The shaded region in the upper right of Fig. 7, which is ${F}_{a}\left(x+\Delta x\right)-{F}_{a}\left(x\right)$, is simply dF! Writing the rate as $\frac{dF}{dx}$ directly indicates the ratio of such an area to its width.

4.6 Multivariate and vector calculus

Taking differentials seriously makes multivariate and vector calculus more quantitatively grounded and easier to use when modeling in physics and other arenas. In particular, as the geometry gets more complex, differentials can transparently represent magnitudes and vectors, to more clearly illustrate how important identities are derived. Dray and Manogue (2003) illustrate this using as an example the question of describing the infinitesimal vector displacement $d\overrightarrow{r}$ along a curve, whose magnitude is ds and whose direction is tangent to the curve (Fig. 8a–d). Because ds can be seen as the hypotenuse of an infinitesimal right triangle (Fig. 8b), the Pythagorean theorem gives us the differential equation ${ds}^{2}={dx}^{2}+{dy}^{2}$. In rectangular vector coordinates, we have that $d\overrightarrow{r}=dx \widehat{{\varvec{i}}}+dy \widehat{{\varvec{j}}}$. Suppose we wish to describe this same displacement with polar coordinates, using as a basis $\widehat{{\varvec{r}}}$ as the unit radial vector and $\widehat{{\varvec{\phi}}}$ as the unit vector orthogonal to it, which points in the direction in which the coordinate $\phi$ increases. Reasoning with infinitesimal similar triangles allows us to see that $d\overrightarrow{r}=dr \widehat{{\varvec{r}}}+r d\phi \widehat{{\varvec{\phi}}}$. The infinitesimal rotational factor $d\phi$ has been scaled by multiplying it by r, to correspond to the distance along an arc of radius r, not of radius 1. At an infinitesimal scale, the difference is negligible between this straight vector component and the actual arc length.

Fig. 8

(From Dray and Manogue 2003, p. 285)

a Zooming in to visualize an infinitesimal vector displacement $d\overrightarrow{r}$ along a curve. b Magnitude ds of displacement as hypotenuse of an infinitesimal right triangle. c Vector version of b using rectangular basis vectors. d Vector version of 8b using polar basis vectors

It is not uncommon for standard multivariate and vector calculus classes to use differentials directly when describing vector geometry, rather than using the clumsier approach of writing these quantities in terms of$\Delta y$ or $\Delta \phi$ and then taking limits. For instance, consider the illustration of the conversion factor to polar coordinates $r dr d\phi$ for a double integral from the Stewart textbook in Fig. 9 (Stewart 2016, p. 1052). This direct use of differentials is a standard practice in STE disciplines.⁶ For example, in a recent study of how experts in various STEM disciplines reason with partial derivatives, physicists and engineers almost invariably treated derivatives and partial derivatives as ratios of small quantitative measurements (Roundy et al. 2015). They were also more comfortable than the mathematicians in approximating derivatives using small measurements, and they used language of differentials when doing so.

Fig. 9

Differential diagram from Stewart’s Calculus, 8^th edition (2016, p. 1052)

5 Limits and limitations

In calculus classes that use differentials and infinitesimals, how and when do students learn about limits?

Limits are taught in most such classes, although they appear later than in standard approaches. Limits are not needed for defining derivatives and integrals, but they are important for (a) sequences and series and (b) describing asymptotic behavior of functions and their graphs.⁷ At the end of my first-semester calculus class I teach students (c) how derivatives and integrals are defined using limits, so that they are familiar with how the majority of people see these ideas.⁸ I see no reason why this approach would hamper students’ development of a robust informal understanding of limits, although I know of no research addressing the question. More research is warranted studying how well such students can work with limits in subsequent courses. One potential benefit for delaying the introduction of the limit idea is that it avoids an antididactical inversion that commonly occurs in standard calculus classes, when limits are defined before the students have met any contexts that warrant the definition. Delaying the idea of limits may have significant pedagogical benefits, as David Bressoud notes in his foreword to Toeplitz’s (2007) The Calculus, A Genetic Approach: “Though it would have been heresy to me earlier in my career, I have come to the conclusion that most students of calculus are best served by avoiding any discussion of limits.”

This raises a more general question about using infinitesimals and differentials in calculus: How well does such an approach prepare students for later classes? The research is sparse. One arena for continued study is how such students interpret the array of calculus notations. I have argued that students develop a more robust understanding of notations such as $\frac{dy}{dt}$, ${\int }_{a}^{b}f\left(x\right)dx$, and $r dr d\phi$, but what meanings do they develop for notations that do not use differentials, such as $f^{\prime}$, ${f}^{\prime\prime}$, ${F}_{x}$, and $\dot{x}$?

There are plenty of broader institutional limitations to teaching calculus with infinitesimals and/or differentials. Students can encounter confusion and opposition from their peers and other instructors. They can find it more difficult to interact with tutors, or to learn from standard online resources. Textbooks using infinitesimals are not (yet?) supported by vast multi-million dollar publishing companies. Instructors using such approaches have reported pushback from colleagues, particularly 30 years ago when nonstandard analysis was less familiar as a rigorous grounding for infinitesimals (Pittenger 1995). These institutional factors can make teaching calculus with infinitesimals and/or differentials feel like swimming upstream, but if this was a good enough reason not do something, when would change ever occur? The benefits for student understanding of calculus, as research has been uncovering, make it worth the effort.