1 Introduction

Financial networks refer to a group of financial institutions interconnected between them through several ways, such as financial markets or infrastructures. There are multiple financial networks composed by different entities (e.g., banks, investment companies or insurance companies), which provide products and services at many different levels, such as payments or investment services. A set of banks, pension funds, trade agencies, etc., can be considered as a financial network. Financial instruments can also act as a financial network (e.g., a network of derivatives, a network of REPOs, etc.). Even the properties of a financial product can be the subject of a financial network (e.g., a network of maturities, a network of liquidity, etc.).

These institutions, instruments and features operate simultaneously at different levels in multilayer networks, i.e., networks that have layers in which their elements interact at a multidimensional level. The analysis of the factors governing the interrelationships among financial agents, instruments and properties in networks is essential to understand and control the financial system and predict financial crises (Berndsen et al. 2018). This is due to the importance of financial networks for measuring and evaluating systemic risk.

Systemic risk is the risk of transmission of financial distress from one or more agents to other agents in a financial network, with the possibility of generating a widespread crisis (Eboli 2004). Billio et al. (2012) consider that systemic risk, which affects the financial system, i.e., a collection of interconnected institutions that conduct mutually beneficial business relationships, is the risk of that illiquidity, insolvency, and losses quickly propagate during periods of financial distress. Comparing these definitions, the key factor that both authors share about systemic risk is the propagation and transmission mechanisms of negative shocks in a set of interrelated institutions. Being propagation and transmission the key components of systemic risk, it is easy to see that, systemic risk in the financial system is correlated with its degree of interconnectedness, since the latter is directly connected with the availability of a shock to propagate.

To infer the importance of systemic risk, one could start with the costs of financial crises and their propagation. Only in economic terms, the cumulative output losses due to long lasting banking crises have been estimated in the 15–20% of the annual GDP of an economy on average (Hoggarth et al. 2002). Significant welfare, social and psychological costs have to be added to the equation. In concordance, it is not surprising that as a consequence of the financial crisis of 2007–2009, the body of research around financial network models and financial stability has gained an increasing attention from both, the theoretical and the empirical perspective in the last decades (Diamond and Dybvig 1983; Allen and Gale 2000; Boss et al. 2004; Battiston et al. 2012; Battiston and Martinez-Jaramillo 2018). Frequently, financial stability models for systemic risk analysis rely on network science.

Network science can be understood as "the generation of descriptive models that explain and describe a certain system" (Berndsen et al. 2018, p. 131). These models arrived late to economics and finance compared to other disciplines (Nier et al. 2007), although much progress has been done in the last decades (Glasserman and Young 2016; Caccioli et al. 2018; Bardoscia et al. 2021), motivated, among other factors, by the financial crisis of 2007–2009 (Garcıa et al. 2022). Some of the main approaches to the analysis of systemic risk in financial networks rely on numerical simulations (Nier et al. 2007; May and Arinaminpathy 2010; Gai et al. 2011; Gai 2013), empirical analyses founded on the topological statistics of the financial network, such as its density, clustering, transitivity, connectivity, layer similarity, etc. (Minoiu and Reyes 2013; Bongini et al. 2018; Berndsen et al. 2018), optimization and algorithmic approaches (Battiston et al. 2012; Bardoscia et al. 2015; Pichler et al. 2021; Cerqueti et al. 2021) and economic and econometric models (Diebold and Yılmaz 2014; Acemoglu et al. 2015; Demirer et al. 2018). Section 2 provides a description of each approach.

In this paper, we propose an approach to conduct inference about the factors that explain interconnections in financial networks based on the so-called Exponential Random Graph Model (ERGM) (Cranmer and Desmarais 2011; Chatterjee and Diaconis 2013; van der Pol 2019; Ghafouri and Khasteh 2020). Exponential-family random graph models describe the processes governing the formation of links in networks as a result of the factors selected by a researcher (Morris et al. 2008). In a network, the response variable is the state of a pair of nodes (or dyad), usually measured by the presence or absence of a tie between them, and the predictor variables are attributes of the nodes, the dyads and the ties. In a ERGM of that network, the predictors are fuctions of the ties of the network, and at the same time, they are direct functions of the response variable. The predictors have a configuration of ties, and to determine its relevance for the model, they are hypothesized to occur more or less often than expected randomly. Thus, by applying the ERGM to a financial network, we can infer which predictors make a financial network more or less prone to be interconnected, and as a result, determine the characteristics that are relevant to explain the edge generation process (EGP) of a financial network. This is a reverse approach to numerical simulation models, which assume aprioristically the probability distribution of a financial network and accordingly conduct simulations in order to study the evolution of systemic risk. Instead, we aim to conduct inference to determine which factors are relevant for the EGP of a financial network using real financial network data.

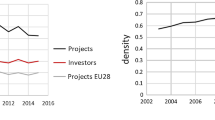
We apply our approach to study how financial concentration affects interconnectedness in a multiplex international financial network which has countries as nodes, and the total volume of financial claims between countries as edges. This network operates at various levels including institutions such as banks, Monetary and Financial Institutions (MFIs) which are not banks, central banks and governments, pension funds, investment banks, and other relevant financial institutions (see Table 11). The main objective of this paper is to inquire whether financial concentration is a relevant source of systemic risk, as both systemic risk and interconnectedness are directly correlated (Battiston et al. 2012; Allen et al. 2012; Roukny et al. 2018; Barucca et al. 2021). The focus of the application on financial concentration is motivated by the high number of banking fusions which are happening currently in many countries (see Fig. 1).

The contribution of this paper is, therefore, threefold. First, it provides a new approach to carry out statistical inference about the structure of financial networks by employing exponential random graph models (ERGMs). Second, it provides a multi-layer macro-financial network analysis by using international financial data extracted from the bank of international settlements (BIS). Third, it analyzes the effects of financial concentration over the interconnection component of systemic risk, in a scenario in which several fusions of financial institutions are taking place.

The interest of understanding the relationship between financial concentration and systemic risk is in the fact that, in the last ten years, there has been a considerable increase in banking concentration in many countries, as it is shown in Fig. 1. In the case of Europe, this increase of concentration is being articulated by fusion waves, fostered by the regulatory and supervisory institutions such as the European Central Bank. Understanding the systemic implications of financial concentration is crucial to design regulatory and supervisory policies effectively, and to prevent, detect and understand the dynamics of future shocks and crises.

Fig. 1
figure 1

5-bank asset concentration by country

Full size image

As Sect. 2.2 exposes, even though the effects of financial competition on certain factors such as economic growth, profits and financial risk have been widely studied both theoretically and empirically, the body of literature in the subject of financial concentration compared to connectiveness, contagion and systemic risk studied through network models is much smaller. Bearing this in mind, this research aims to provide results about if, and to which extent, these relationships exist.

The rest of the paper is organized as it follows. Section 2 studies the literature related to the paper. Section 3 presents the methodology and the data. Section 4 shows and analyzes the results of the study. Section 5 concludes and discusses the results through the lens of the literature.

2 Related literature

The last financial crisis constituted a turning point in the scientific literature of financial stability. Before that period, network science was not as developed in economics and finance as in other fields, such as biological sciences (Nier et al. 2007). It was in the aftermath of the crisis when the literature of financial networks started to grow in an exponential manner (Tabak et al. 2020).

Indeed, the boom of this stream of literature comes from the underestimation of systemic risk before the recent financial crisis. In effect, before this event, either there was a clear absence of financial market restrictions and financial-real interconnections in economic models, or financial systemic risks were underestimated in many cases (Blanchard 2014). On the one hand, quantitative macroeconomic models used in production remained silent about the origins of the financial crisis (Taylor et al. 2016). On the other, they did not provide any understanding about how the economic institutions could have taken any measures to mitigate its effects (and to which extend one or other kind of policy could contribute more, i.e., comparisons between policy effects) (Taylor et al. 2016). Most importantly, they did not provide any insights about the interconnections between financial systems and systemic risk, and hence on the regulatory and supervisory policies needed to avoid a crisis of this kind (Taylor et al. 2016). Furthermore, some literature focusing on unveil the quantitative dynamics of systemic risk dramatically underestimated its importance (e.g., Bartram et al. (2007)).

After those events, in the context of economic and financial modelling, and in applied network theory in finance and economics, there exists a post-crisis increasing interest in how complex systemic dynamics work in financial networks. Therefore, important concepts related to these issues have been retrieved with engagement, such as liquidity restrictions, contagion channels, credit cycles, financial accelerators, or non-linear considerations (Battiston et al. 2012; Billio et al. 2012; Taylor et al. 2016; Tabak et al. 2020; Barucca et al. 2021).

2.1 Financial networks and systemic risk

One of the main approaches to financial networks and systemic risk are numerical simulations. Numerical simulation models start with the construction of an artificial financial system, most frequently, a banking system. These models recreate the balance sheet of financial institutions that can vary in structure, detail, and depth. For example, Nier et al. (2007) divide artificial bank liabilities in net worth, deposits and borrowed. Assets are divided into two groups: external assets and lent. On the other hand, Gai et al. (2011) split the bank liabilities into: retail deposits, REPO, unsecured interbank liabilities, and capital. Assets are separated into: fixed assets, ’collateral’ assets, reverse REPO, unsecured interbank assets and liquid assets. After the definition of the balance sheets, a set of key parameters are defined, a probability distribution governing the network is assumed, and the structural dynamics of the propagation mechanism of the network are formulated. Finally, numerical simulations are ran, and resulting networks are drawn from the simulations. By tuning the parameters of interest, and observing the resulting realizations of the network, the systemic dynamics of the artificial financial network can be studied.

The work of Eboli (2004) inspired other works in this area, such as the work of Nier et al. (2007). Eboli (2004) carries out analytical research about the financial contagion mechanics based on graph theory and the notion of systemic risk provided by the works of (Dow 2000; De Bandt and Hartmann 2000). The author focuses on direct contagion (the contagion channel which arises from interbank lending and borrowing, as well as other contracts) and common exposures (a shock in the value of assets held by various institutions or in the value of assets that have a high positive correlation), and sets aside informational contagion. Authors who share the same fundamentals about network modelling follow the same approach (May and Arinaminpathy 2010; Gai and Kapadia 2010; Gai et al. 2011).

In order to increase the understanding of systemic risk dynamics, May and Arinaminpathy (2010) construct a network model that builds into the works of Nier et al. (2007; Gai and Kapadia (2010), and adds two distinctive features. These are, respectively, the employment of mean field approximations to approach the dynamical conduct of random networks of banks, and the introduction of strong and weak liquidity shocks to the model (May and Arinaminpathy 2010).

As another example of this stream of literature, Gai and Kapadia (2010) develop an analytical model based on a Poisson distributed random graph to study how the frequency and extent of contagion evolve with respect to macroeconomic or idiosyncratic shocks, variations in the balance sheet of the banks, and liquidity effects in the market. The numerical simulations of their model show that, in line with much of the literature, financial networks have a robust-yet-fragile structure. Therefore, shocks that may seem small a priory can have devastating consequences, which means that evidence about the resilience of the financial system in the past is not a sound signpost of its future robustness, as shown by the 2007–2009 financial crisis. These effects are amplified by further liquidity market restrictions and aggregated shocks to the balance sheets of banks (Gai and Kapadia 2010).

Gai et al. (2011) develop a network model of a generic financial network, which decomposes each bank balance sheet to collateral assets, REPO contracts, and unsecured interbank operations. It incorporates the multilayer approach into a numerical simulation model. With the purpose of analyzing liquidity crisis dynamics and systemic risk, they provide analytic formulation for these, and carry out six experimental numerical simulations and four policy exercises. Furthermore, in addition to employ a uniform Poisson distribution, they provide results for a more realistic geometric distribution, in which some banks are much more highly connected than others, i.e., a clustered network structure. Their results highlight how concentration and complexity can increase liquidity systemic risk, and how microprudential policy measures, such as demanding higher quality liquidity stocks to banks, and macroprudential policy ones, such as counterciclycal liquidity buffers or surcharges to key systemic players, can help reduce systemic risk by directly making the financial system less prone to systemic liquidity crisis.

In their milestone paper, Elliott et al. (2014) expand substantially the simulation framework with important advances in the field. Firstly, they explore contagions in a Core-Periphery model, implying by this studying a network conformed by a core, a small number of large organizations which are completely interconnected, and a periphery, a big number of small organizations that have only a few connections with the core. Secondly, they study contagions in a model that allows for segregation or homophily between different segments of an economy, such as countries, industries or sectors. Thirdly, they explore power law distributions, which have been advocated as more realistic for real world financial networks than regular networks (although with an on-going debate (Berndsen et al. 2018)). Fourthly, they model a network with correlated and common assets, that as the 2007–2009 financial crisis showed, is crucial to account for, due to the high number of commonly held investments and correlated payoffs that organizations hold. Finally, they illustrate their model with data of the cross-holdings of debt between six European countries. As main results of their work, the authors highlight the useful distinction between diversification and integration, and the trade-off implications of those mechanisms over contagion, which may be related to the core-periphery structure and/or segregation structure of a network.

Cinelli et al. (2021) evaluate the effect of incomplete information on the resilience of financial networks. By performing extensive cascade failure simulations with different core-periphery structures, they conclude that the incomplete network of interbank exposures retrieved from the dataset of real interconnections of the Bank of International Settlements is far from a worst case scenario. This means that the lack of information originated by the absence of these links can lead to important biases, as unobserved links can alter significantly the resiliency of the whole network. Finally, they confirm the robust-yet-fragile tendency of the network documented in previous works (Acemoglu et al. 2015; May and Arinaminpathy 2010; Gai 2013).

Other important papers in the field are, among others, (Nier et al. 2007; Luu et al. 2021; Chong and Kluppelberg 2018; Amini et al. 2016; Caccioli et al. 2014). Eventually, some efforts have been made in the literature to study financial networks employing dynamical network models. See, for example, (Georg 2013; Bargigli et al. 2015).

Empirical analyses of financial networks usually employ network statistics to expose properties of the topology, clustering, communality and other properties of the financial network that are relevant for systemic risk. For example, Barucca et al. (2021) study fire sales of commonly held assets, i.e., fire sales systemic vulnerabilities, of financial institutions from Europe and the UK, by characterizing the equity and debt portfolio overlap of the communities of the network using histograms, number of common holdings, cosine similarities, affinity matrices, eigenvector centralities, the Herfindhal–Hirschman Index, etc. Other important papers in the field are (Poledna et al. 2015; Aldasoro and Alves 2018; León et al. 2018; Bargigli et al. 2015), among others.

Optimization approaches usually apply optimization procedures to determine minimum systemic risk financial networks. This is the case of Pichler et al. (2021), who develop an optimization procedure that minimizes the systemic risk by rearranging optimal networks of overlapping portfolios, and then apply it to the exposures of the major European banks. Their results show that their procedure minimizes systemic risk up to a factor of two, with contagion probabilities that are critically reduced for the optimized network, and no individual loss to banks. On the other hand, the most common algorithmic approach is the Debt-rank algorithm, that identifies systemically important nodes by measuring the impact for the network of the distress of one of the central nodes (Battiston et al. 2012; Bardoscia et al. 2015; Battiston et al. 2016).

Economic and econometric models for financial networks differ in their approach. Some of the most relevant works in this area are the ones of Diebold and Yılmaz (2014); Demirer et al. (2018). In these works, the authors employ variance decompositions from Vector Autoregressions to build financial networks. From there, they define measures of financial connectedness to measure systemic risk. Examples of economic models applied to financial networks are the one of Acemoglu et al. (2015), who formulate an economic model of three periods (\(t= 0, 1, 2\)), a single economic good, and n risk neutral banks to study the phase transition of the financial system. Another important work is the one of Battiston et al. (2012), who use a dynamic model based on a system of stochastic differential equations with financial acceleration to study the optimal resilience of financial networks in relation with its level of risk diversification.

Other important approaches to systemic risk and financial networks are the ones of Guttal et al. (2016) and Torri et al. (2021). Torri et al. (2021) present a methodology based on conditional tail risk networks to evaluate the transmission of shocks in financial systems, and to identify the institutions that are more fragile in a financial network. Their framework is an extension of the \(\Delta CoVaR\) framework of Tobias and Brunnermeier (2016) to networks. They further compute synthetic indicators of systemic risk for each bank and for the network. By applying their procedure to a set of European banks, they find regional clusters, which are more significant in crisis periods. On the other hand, the work of Guttal et al. (2016) seeks to investigate whether a phenomenon called critical slowing down (an increasingly slow response of the financial system to shocks before a crisis), characterizes financial meltdowns. To do it, they employ two models: a mean-field model and a microeconomic agent-based model. They find that a critical slowing down is not what precedes a financial crisis, but rising stochastic variability is, with the handicap of signing potential false alarms.

2.2 Financial concentration and systemic risk

Although an a priori reasoning can lead to higher concentrated financial systems having higher profits, efficiency and competitiveness, the specialized literature points out that the general effects of further banking concentration on economic growth are negative for developed countries, but can be positive or irrelevant for developing countries. Thus, just as some scholars like (Fernandez et al. 2010; Diallo 2017) find that concentration has a negative effect on economic growth which disappears for low-quality institutional countries and is reduced in the case of countries with a high level of corporate governance. Other authors such as Abuzayed and Al-Fayoumi (2016), Levine et al. (2000) find that concentration has a positive effect on economic growth for the MENA countries and a non-negative relationship in advanced countries. Diallo (2017) finds that the relationship between financial concentration and economic growth depends on the proximity of the country to the world technology frontier. Therefore, when a country is enough financially developed, banking concentration has a negative effect on the GDP. However, prior to the turning point, economic growth depends exclusively on the financial intermediation.

In the case of the relationship between banking competition and financial stability, the theoretical views are twofold: a traditional competition-fragility pairing, in which more competition (less concentration) has a negative effect on market power, profit margins, and stimulates risk appetite via less franchise value; and an alternative competition-stability hypothesis, where concentration leads to an increased market power in the loan market, and as a result, to greater risk taking by financial institutions since they increase the interest rates of loans to clients, generating moral hazard and adverse selection (Berger et al. 2017).

On the other hand, evidence is sparse. Beck et al. (2006), Chang et al. (2008), Berger et al. (2017), Kabir and Worthington (2017) find evidence about the traditional competition-fragility hypothesis. Hakenes and Schnabel (2011) get ambiguous results with a theoretical model, and similarly Fernandez and Garza-Garcia (2015) find evidence about both hypotheses for the Mexican banking industry. IJtsmaet al. (2017) find that concentration hardly affects financial stability. Finally, Clark et al. (2018), Su et al. (2021) find evidence about the competition-stability hypothesis in the Commonwealth of Independent States (CIS) markets and in China, and Anginer et al. (2014) get similar results by analyzing the risk-taking behavior of banks.

However, the relationship between financial concentration and systemic risk has an intermediate component: the level of interconnectedness of agents in the financial system. Several studies document the robust-yet-fragile structure of the financial system because of its highly interconnected nature, meaning that high connection levels generate a low probability of big shocks to the system, but when these appear, the effects can widespread to the whole system (Gai 2013; Battiston et al. 2012; Acemoglu et al. 2015). The effect of financial concentration over the systemic risk then depends directly on its effect over the degree of interconnectedness of the financial system.

3 Data and methodology

As a methodology to investigate whether financial concentration is a driver of interconnectedness and systemic risk in the financial network that we have built, we employ the exponential random graph model, a network model from the family of the generalized random graphs (GRG). The ERGM is a technique that allows for statistical inference with network data. It can be used to model endogenous (structural) effects and exogenous (predictor or covariates) effects to the network, without needing any assumptions about the independence of of the nodes or edges (Cranmer and Desmarais 2011). Developed mainly with a focus on Markov random graphs (Frank and Strauss 1986; Frank 1991; Robins et al. 2007) and with applications in the analysis of social networks (Snijders 2002; Wasserman and Pattison 1996; Wasserman and Robins 2005), they have recently been proposed for the analysis of economic networks (van der Pol 2019). However, they have not yet been popularized for the analysis of financial networks, and, to the extent of our knowledge, this is the first application to the analysis of financial concentration and interconnectedness. Section 3.1 introduces the formulation and estimation of a generic ERGM.

3.1 Inference

To draw inferences about the EGP of our international financial network, we use the exponential random graph model (ERGM). This model is a generalizable methodology to infer structural properties of financial networks. The ERGM is a GRG model which describes, in a parsimonious way, the local selection forces which configure the structure of a network (Hunter et al. 2008; Newman 2003). Network datasets are then considered as the outputs from a regression model with a set of predictor variables which are network attributes, such as vertices or edges. Then, the insights provided by the ERGM can then be used to understand particular network relationships or to simulate random realizations of networks conserving the properties of the original network data (Hunter et al. 2008).

In essence, the ERGM is a network analogy of the logistic regression to network settings, in which the probability of a link depends on the presence of other links or node attributes of the network dataset. Thus, they are capable of accounting for the existing direct and weighted interactions in a network, to identify the probability distribution of a network, and therefore to identify which edge and node attributes impact the probability of conforming new nodes (van der Pol 2019). The application to financial networks and systemic risk is therefore immediate, as they allow to infer which factors determine the generation of new interconnections in the financial system.

Section 3.1.1 presents the mathematical derivation of the general form of the ERGM applied in Sect. 4.

3.1.1 The exponential random graph mOne of the main approachesodel (ERGM)

In general, the exponential family is a broad family of probabilistic models which covers many types of data, not precisely networks. Specifically, exponential random graph models (ERGMs) are a subfamily of the exponential family consisting in statistical methods for analyzing the graphs of networked data (Ghafouri and Khasteh 2020). Following the Hammersley–Clifford theorem (van der Pol (2019)), the probability of a graph is proportional to the probability of counts of subgraphs. Then, starting from an observed network (y), which is of replication interest, the goal is to obtain the probability that the network generated by the model (say Y) equals the observed network. Then

$$\begin{aligned} \log P(Y = y) \propto \beta \cdot v(G) \end{aligned}$$
(1)

or, equivalently,

$$\begin{aligned} P(Y = y) \propto \exp \{\beta \cdot v(G)\} \end{aligned}$$
(2)

where \(\beta \) is a vector of parameters of interest, G a network, and v(G) the vector of variables of that network.

To obtain a probability distribution, the normalization of Equation (2) is required. This is the same as normalizing a network, which means normalizing all the potential networks with the same number of nodes. Mathematically,

$$\begin{aligned} P(Y = y) = \frac{\exp \{\beta \cdot v(G)\}}{{\sum _{G \in {\mathcal {G}}}} \exp \{\beta \cdot v(G)\}} \end{aligned}$$
(3)

\(G \in {\mathcal {G}}\) being a potential network in the set of all possible networks (\({\mathcal {G}}\)) with the same number of nodes.

The most general and commonly used representation of an ERGM model is then

$$\begin{aligned} Z = \frac{1}{\omega } \exp \{ \beta \cdot v(G)\} \end{aligned}$$
(4)

where \(\omega = {\sum _{G \in {\mathcal {G}}}} \exp \{\beta \cdot v(G)\}\), i.e., the normalizing constant (a big magnitude), and \(Z = P(Y = y)\). Equation (4) is, additionally, the canonical form of the ERGM.

To get marginal effects, let \(G_{ij}\) a graph which contains the nodes i and j. If i is linked to j in the graph, we will write \(G_{ij} = 1\). Otherwise, \(G_{ij} = 0\). Thus, the odds of a link between the nodes i and j are:

$$\begin{aligned} \hbox {odds}(G_{ij} = 1) = \frac{P(G_{ij} = 1)}{P(G_{ij} = 0)} \end{aligned}$$
(5)

and the logit, which ensures a probability space between 0 and 1, is:

$$\begin{aligned} {\hbox {logit}[G_{ij} = 1] = \log [\hbox {odds}(G_{ij} = 1)]} = \log \frac{P(G_{ij} = 1)}{P(G_{ij} = 0)} \end{aligned}$$
(6)

Assume that the \(\log \) probability of the existence of this connection between i and j is determined by a set of n explanatory variables and parameters in the following way:

$$\begin{aligned} {\log P(G_{ij} = 1)} = \sum _{k=1}^{n} \beta _{n} X_{n} = \beta _{1} X_1 + \beta _{2} X_2 + \cdots + \beta _{n} X_n \end{aligned}$$
(7)

where \({\beta }:= (\beta _{1}, \beta _{2}, \dots , \beta _{n})\) is the vector of parameters of interest, and \(X:= (X_{1}, X_{2}, \dots , X_{n})\) is the vector of explanatory variables. Therefore, one has:

$$\begin{aligned} {P(G_{ij} = 1)} = \exp \left\{ \sum _{k=1}^{n} \beta _{k} X_{k}\right\} = \exp \{ \beta _{1} X_1 + \beta _{2} X_2 + \cdots + \beta _{n} X_n \} \end{aligned}$$
(8)

Equation (6) is a logit model, which supposes that the observations are i.i.d. However, the observations of networks are not independent. Therefore, the original logit equations need a modification to account for this dependence. If \(G^{o}_{ij}\) is the network without the link between i and j, then:

$$\begin{aligned} \hbox {odds}(G_{ij}=1 {| G^{o}_{ij}})) = \frac{P(G_{ij} = 1 | G^{o}_{ij})}{P(G_{ij} = 0 | G^{o}_{ij})} \end{aligned}$$
(9)

is the new odds of a link in the network, where the probabilities are now conditioned by the structure of the network without a link ij, denoted by \(G^{o}_{ij}\).

Because some features of the model may be subgraphs and these are included in the model by their accounting, the counts of those variables are not equal when the link ij is present or absent (van der Pol 2019). The model has to account for these differences. Thus, being \(v(G^{+}_{ij})\) the vector of variables when the link ij is present and \(v(G^{-}_{ij})\) when it is absent, by equations (8) and (9), one has (\({\beta }'\) is the transposed of \({\beta }\) and \({\beta }'_k\) is the transposed of \({\beta }_k\), \(k=1,2,\dots ,n\)):

$$\begin{aligned} \hbox {odds}(G_{ij}=1 {| G^{o}_{ij}}) &= {} \frac{P(G_{ij} = 1 | G^{o}_{ij})}{P(G_{ij} = 0 | G^{o}_{ij})} \nonumber \\& = {} \frac{\exp \{{\beta }' \cdot v(G^{+}_{ij})\}}{\exp \{{\beta }' \cdot v(G^{-}_{ij})\}} \nonumber \\ &= {} \exp \{{\beta }' (v(G^{+}_{ij}) - v(G^{-}_{ij}))\} \nonumber \\ &= {} \exp \{\beta '_{1} (v_{1}(G^{+}_{ij}) - v_1(G^{-}_{ij}))\} + \cdots \nonumber \\&\quad+ {} \exp \{\beta '_{n} (v_{n}(G^{+}_{ij}) - v_n(G^{-}_{ij}))\} \end{aligned}$$
(10)

where the parameters of interest of the model measure the linear dependence of the count differences of the subgraphs of the model, which is the basis of the ERGM. Observe that \(v_{k}(G^{+}_{ij}) - v_k(G^{-}_{ij})\) (\(k = 1, 2, \dots , n\)) is the difference of the count number of the network statistic k as the result of an additional link. Thus, \(v_{k}\) is the k-th change statistic.

Consider \(v_{k}(\Delta _{k}G_{ij}):= v_{k}(G^{+}_{ij}) - v_k(G^{-}_{ij})\) the change statistic for an ij link of the variable k. Then, by applying natural logarithms to remove the exponential component of Equation (10) (which gives the exponential term to the ERGM), one has:

$$\begin{aligned} \hbox {logit}[G_{ij} = 1 {| G^{o}_{ij}}]=\, & {} {\log [\hbox {odds}(G_{ij}=1 | G^{o}_{ij})]}\\=\, & {} \log \frac{\exp \{ {\beta }' \cdot v(G^{+}_{ij})\}}{\exp \{ {\beta }' \cdot v(G^{-}_{ij})\}} \\=\, & {} \beta '_{1}(v_{1}(G^{+}_{ij}) - v_1(G^{-}_{ij})) + \cdots + \beta '_{n}(v_{n}(G^{+}_{ij}) - v_n(G^{-}_{ij})) \\=\, & {} \beta '_{1} v_{1}(\Delta _1 G_{ij}) + \cdots + \beta '_{n} v_{n}(\Delta _n G_{ij}) \end{aligned}$$

So, the model predicts the logit of a tie by the impact of a change in the counts of the network statistics measured by the parameters \({\beta }'\).

3.1.2 Layer similarity

Intuitively, a multilayer network consists of a series of interrelated sub-networks, called layers, as well as links connecting each network. When the node set of every sub-network inside the multilayer network represents the same agents, then the structure is called a multiplex network. In these networks, nodes remain similar but edges change.

In this paper, we are going to consider structures with layers apart from nodes and edges. In the most general multilayer network, a node in a specific layer can be linked to any node in any layer. In other words, the edges in a multilayer network can be intralayer (the two nodes of the edge are in the same layer) and interlayer edges (which connects nodes between different layers). More precisely, a multilayer network is a triple \({\mathcal {M}} = (V,E,{\mathcal {L}})\), where V is the set of nodes, E the set of links between nodes, and \({\mathcal {L}}\) the set of layers. The set E is composed by triples (u, v, l), where \(u,v \in V\) and \(l \in {\mathcal {L}}\).

Usually, the set of layers is composed by d elementary layers (also called aspects):

$$\begin{aligned} {\mathcal {L}} = \{{\mathcal {L}}_{\alpha }\}_{\alpha =1}^{d} \end{aligned}$$

whereby the multilayer network can be defined as a quadruplet

$$\begin{aligned} {\mathcal {M}} = (V_M,E_M,V,{\mathcal {L}}) \end{aligned}$$

where V is the set of nodes, \(V_M \subseteq V \times {\mathcal {L}}_1 \times {\mathcal {L}}_2 \times \cdots \times {\mathcal {L}}_d\), \(E_M \subseteq V_M \times V_M\), and now the set of layers is defined by the Cartesian product of the elementary layers \({\mathcal {L}}_{\alpha}\).

To measure the structural similarity between layers, we are going to use the so-called Jaccard similarity:

$$\begin{aligned} {J_{ij} = \frac{\sum _{k}n_{ij}}{k_i + k_j - n_{ij}}} \end{aligned}$$
(11)

and the Cosine similarity:

$$\begin{aligned} {C_{ij}= \frac{\sum _{k}n_{ij}}{\sqrt{k_{i}k_j}}} \end{aligned}$$
(12)

where \(n_{ij} = A_{ik}A_{kj}\) is the set of interconnections between the nodes i and j, \(A_{ij}\) the adjacency matrix of the edge ij, and \(k_i\) the degree of the node i. Then

$$\begin{aligned} {0 \le J_{ij} \le 1} \end{aligned}$$

and

$$\begin{aligned} {0 \le C_{ij} \le 1}, \end{aligned}$$

where 1 denotes maximum similarity and 0 no similarity.

3.1.3 Estimation and computation

Following Hunter et al. (2008), we estimate the model by employing pseudo-likelihood methods in R, as the normalizing constant of Equation (4) is difficult and costly to estimate by using maximum likelihood methods. Hunter et al. (2008) use a local substitute approach to the estimation of the full likelihood function. This is called pseudo-likelihood estimation which mirrors the likelihood of a logistic regression. Furthermore, assuming that the elements of Y are independent, the maximum pseudo-likelihood estimator (MPLE) of an ERGM maximizes the pseudo-likelihood by employing logistic regression as a computational mechanism (Hunter et al. 2008).

3.2 Data and variables

This paper employs datasets from three sources. First, the Federal Reserve Economic Data from the Federal Reserve Bank of St. Louis (FRED), for the node covariates of Japan and the United States. Second, the Consolidated Banking Data from the European Central Bank (ECB statistics), for the node covariates of the rest of the countries: Austria, Belgium, Denmark, Finland, France, Germany, Greece, Ireland, Italy, Luxembourg, Netherlands, Portugal, Sweden and the United Kingdom. Third, the edge relational data comes from the Consolidated Banking Statistics of the Bank of International Settlements (BIS-CBS).

The data consider financial claims of all maturities between the financial sectors of the aforementioned countries for 2017, in all currencies. The relative weight of each country is then calculated for normalization purposes. These data generate a directional network. Taking advantage of the division of these data by the BIS in four categories (banks, non-banks monetary and financial institutions, official sector and private sector), as reported in Table 11, we can extend our analysis to a multilayer setting.

The node covariates are five-bank asset concentration, which is the proportion of assets of the five largest financial institutions related to the total assets of the financial system of a country, the value of the assets of the financial system, the number of monetary and financial institutions of a country in relative terms, and the debt of a country as a share of its GDP. All the data corresponds to 2017. In order to standardize the currency, the data from Japan and the United States have been converted into euros prior to the variable transformation.

The BIS provides data about every financial relationship of each country, that is, of a complete network. Because complete networks are uninformative to the ERGM, we consider cutoffs at a relative weight to obtain the most important financial relationships among countries. These cutoffs are different for the monoplex network and for each layer of the multilayer network, because the volume of financial claims varies, specially from the monoplex to the multiplex setting. The cutoffs values and edges are listed in Table 1.

Table 1 Cutoff values for the monoplex and multiplex networks that feed the ERGM
Full size table

3.3 Hypotheses

Due to the different theories and evidence about financial concentration presented in Subsection 2.2, we postulate the following hypothesis to be tested in the network models.

Hypothesis 1

(H1) Financial concentration increases financial interconnections.

Hypothesis 1 comes naturally from the ERGM estimation of an international financial network. If financial concentration is a positive factor for creating new edges of a relevant magnitude in our model, then it is immediate to infer that it is a relevant variable which increases financial interconnectedness. This is the same as accepting that a more concentrated financial system is more connected.

Hypothesis 2

(H2) Financial concentration decreases financial interconnections.

Hypothesis 2 is the alternative to hypothesis 1. As opposed to the reasoning behind hypothesis 1, if financial concentration is a negative factor for creating new edges in the model, then it is a relevant variable which decreases financial interconnectedness. This is the same as accepting that a more concentrated financial system is less connected, obviously rejecting that a more concentrated financial system is more connected.

We are going to use mathematics to state the third hypothesis in an unambiguous way. Consider a layer (\(L_i\)) in our international financial network (N) as a set of vertices (V), where each vertex represents a financial institution. Being the nature of the edges equal but the potential number interconnections (\(E_j\)) between institutions differing across layers, then our international financial network has four layers \(\{L_1, L_2, L_3, L_4\} = \{L_i: L_i \subseteq N\}\) with different edges combinations \(\{E_1, E_2, E_3, E_4\} = \{E_j: E_j \subset L_i\)} such that \(\{L_i(V, E_j) \subseteq L \subseteq N\}\). Then, we can state hypothesis 3.

Hypothesis 3

(H3) Financial concentration shares its effects across layers.

Assume linearity, that is to say, if Y is connectiveness in our network N, X is financial concentration, and \(\beta \) is a linear parameter which connects both, then:

$$\begin{aligned} Y_i = \beta _iX_i \end{aligned}$$
(13)

where \(i=1,2,3,4\) corresponds to layers, so that \(Y_i, X_i, \beta _i \subseteq L_i\). Then we assume our hypothesis to be true if there exist statistically significant parameters in each layer of the ERGM so:

$$\begin{aligned} \hbox {for every}\ L_i \in N, \quad \beta > 0, \quad \beta _q \approx \beta _k, \quad q \ne k \end{aligned}$$
(14)

or, equivalently,

$$\begin{aligned} \hbox {for every}\ L_i \in N, \quad \beta < 0, \quad \beta _q \approx \beta _k, \quad q \ne k \end{aligned}$$
(15)

where \(\beta = \beta _1, \beta _2, \beta _3, \beta _4\).

4 Results

The formulas of the models estimated for the monoplex and multiplex networks of Tables 4, 6, 7, 8 and 9 are presented in Table 2 (monoplex network), and Table 3 (multiplex network). Among all the combinations of the random variables, the models presented in Tables 2 and 3 are the ones for which the MCMC algorithm converges to a result.

Fig. 2
figure 2

International network of financial claims. The node size indicates the relative magnitude of financial concentration in the country. The edge size measures the directional volume of financial claims exchanged between two countries

Full size image
Table 2 List of all the models estimated in the monoplex network of Table 4
Full size table
Table 3 List of all the models estimated in the multiplex networks of Tables 6, 7, 8 and 9.
Full size table

4.1 Monoplex network

The ERGM estimates for the monoplex network (Fig. 2) are presented in Table 4. Both the AIC and BIC criteria select model 5 as the best fit. Model 5 has the in-degree geometrically weighted coefficient, the mutual coefficient, and the edges coefficient as statistically significant parameters. The geometrically weighted in-degree coefficient shows that the network is prone to have a lower quantity of low-degree and high-degree nodes, this is, less clustering in comparison with a random network. The mutual coefficient points out that the number of reciprocated links is higher in comparison with a random network. The edges coefficient controls for the density of the network. The remaining coefficient, the absolute difference of financial concentration, is not statistically significant. The coefficients for the random variable concentration, although small and not statistically significant, are negative in the rest of the models too, reflecting a negative impact of concentration over the generation of new edges in the network. Interestingly enough, the coefficients for the absolute difference of concentration in models 5 and 6 are both positive and of higher magnitude than ones of the variable in levels; however, they are neither statistically significant.

Table 4 ERGM estimates for the monoplex network and the model variants of Table 2
Full size table

4.2 Multiplex network

We now move on to the multiplex network, in which all the nodes are the same but the edges vary depending on the layer, this is, the financial sector considered. Table 5 presents the Jaccard and Cosine similarity indices of the different layers of the network, while Sects. 4.2.1, 4.2.2, 4.2.3 and 4.2.4 present the results of the analyses.

Table 5 Layer similarity analysis. The numbers behind (above) the diagonal are the Jaccard (Cosine) similarity values
Full size table

4.2.1 Layer 1: Banks

The first layer, the layer of banks, is the one of Figure 3. The biggest interconnections are the ones between France and the UK, and Germany and the UK. There are also substantial interconnections between France and Italy, France and Spain, France and the US, and Germany and the US. As the size of the nodes shows, the biggest interconnections in the layer of banks are between countries of relatively low financial concentration levels.

Fig. 3
figure 3

Layer 1: Links countries by their banks. Node size measures the country’s relative financial concentration and edge size measures the directional volume of financial claims between two countries

Full size image

Next, we report the ERGM results for the layer of banks in table 6. Up to 9 models were estimated, depending on the combinations that are feasible to the convergence of the MCMC algorithm. All the differences between the number of parameters and the models between the monoplex and multiplex setup, and across layers, obey to this computational aspect.

Table 6 ERGM estimates for the layer of banks and the model variants of Table 3
Full size table

According to the AIC and BIC criteria, the best model is Model 5, which incorporates the coefficients of the variables geometrically weighted out- and in-degree, mutual, edges, and the absolute difference of financial concentration. Only the coefficient of the geometrically weighted out-degree and the absolute difference of financial concentration are statistically significant, with p-values less than 0.05 and 0.1, respectively.

The geometrically weighted out-degree negative coefficient \({\hat{\beta }}=-3.25\) means that on-going clustering structures are less probable in the banks layer than in a random network. Although of different magnitudes, this coefficient is negative and statistically significant in any model.

Regarding financial concentration, the coefficient of the absolute difference of Model 5 shows a negative statistically significant effect over the formation of edges (\({\hat{\beta }}=-0.04\)). Therefore, financial concentration is associated with a \({\hat{I}}=3.92\%\) reduction in the generation of new edges in the layer of banks, and this effect is statistically significant. This effect is robust to different model specifications, as the coefficients of models 6 and 7 are also negative and statistically significant (\({\hat{\beta }}=-0.05\) and \({\hat{\beta }}=-0.06\), respectively). Moreover, the reduction in connectedness increases in those two specifications (\({\hat{I}}=4.87\%\) and \({\hat{I}}=5.82\%\)). Furthermore, the only other statistical significant co-variate is concentration in its levels form in Model 2 (\({\hat{\beta }}=-0.03\)), which further increases the robustness of these results.

Finally, the edges tend to be more reciprocated than in a random network in every model. However, only in models 1, 3, 4 and 8 these coefficients are statistically significant.

4.2.2 Layer 2: Non-bank financial and monetary institutions

The layer of non-bank monetary and financial institutions is presented in Fig. 4. At a first glance, the relative size of the volume of financial claims is smaller compared to Fig. 3. The only sizeable linkage is the one between France and the United States and vice-versa, followed by a link from Germany to the United States. The rest of links are not very big, which leads to conclude that the international transactions of the banking sector are still considerably higher in magnitude compared to other financial institutions.

Fig. 4
figure 4

Layer 2: Links countries by their non-bank MFI. Node size measures the country’s relative financial concentration and edge size measures the directional volume of financial claims between two countries

Full size image

The estimates for the layer of non-bank monetary and financial institutions is provided in Table 7. In this case, the AIC and BIC criteria diverge, as the Akaike Information Criterion chooses Model 6, but the Bayesian Information Criterion chooses Model 1. This last model has the out-degree geometrically weighted and the edges coefficients as statistically significant control variables. Then, it has concentration as a co-variate, which is statistically significant at 0.05. In this model, an increase of financial concentration is related to an \({\hat{I}}=-2.95\%\) decrease in connectiveness.

Table 7 ERGM estimates for the layer of non-bank MFI and the model variants of Table 3
Full size table

In Model 6, the same controls, with the same signs, are statistically significant. However, this model includes three co-variates in absolute differences, financial concentration, volume of assets of a financial system, and number of monetary and financial institutions of the system, but only the first and the third are statistically significant at 0.05 and 0.1, respectively. In this model the coefficient for the absolute differences of concentration is \({\hat{\beta }}=-0.08\) and the coefficient for the absolute differences of MFI is \({\hat{\beta }}=0.25\). This means that an increase of financial concentration is associated with an \({\hat{I}}=-7.68\%\) reduction in connectedness, and an increase in the number of monetary and financial institutions, with an increase of \({\hat{I}}=28.4\%\). These are the biggest impacts registered.

A horizontal analysis of the results leads to conclude that the out-degree geometrically weighted control is negative and statistically relevant in any model but the seventh, so the ERGM is pointing out again that the degree of clustering is smaller than the one of a random network. Financial concentration has a negative coefficient of statistical relevance in three of the four models in which it appears. The edges control is significant in most models, as opposed to the previous model. Assets are associated with a powerful negative effect over connectedness (Model 4: \({\hat{\beta }}=-0.14\) (\(p \le 0.1\))), specially over the number of in-going linkages (Model 9: \({\hat{\beta }}=-0.25\) (\(p \le 0.1\))). Finally, the number of monetary institutions has the most powerful positive effect over connectedness (Model 5: \({\hat{\beta }}=0.25\) (\(p \le 0.1\)) and Model 6: \({\hat{\beta }}=0.23\) (\(p \le 0.1\))).

4.2.3 Layer 3: Official sector

Fig. 5
figure 5

Layer 3: Links countries by their official sector. Node size measures the country’s relative financial concentration and edge size measures the directional volume of financial claims between two countries

Full size image

Figure 5 provides graphical representation of the official sector layer which has, by far, the biggest financial interconnections of all layers. The most important links to be highlighted are the one from the United States to Germany (the biggest) and vice-versa, the one from the United Kingdom to Germany, the one from France to the United States, the one from France to the United Kingdom, and the one from the United Kingdom to the United States and vice-versa. Overall, the sizes of these links are bigger than the size of the ones of the rest of layers, by indicating that financial claims between governments, central banks and international organizations are highly relevant.

Table 8 ERGM estimates for the layer of the official sector and the model variants of Table 3
Full size table

The ERGM estimates for the layer of the official sector are shown in Table 8. This time, the AIC and BIC criteria converge to select Model 1 where only the parameters of the concentration and the edge control co-variates are statistically significant random variables. The value of the financial concentration parameter is \({\hat{\beta }} = -0.05\) (\(p \le 0.05\)), which leads to an \({\hat{I}}=4.87\%\) decrease in financial connectedness. Furthermore, financial concentration is consistently significant in three out of the four models which include it (models 1, 2, and 3). Moreover, it is not the only variable of statistical significance in all models, but also the edges, the mutual and the geometrically weighted out-degree controls.

4.2.4 Layer 4: Private sector

Fig. 6
figure 6

Layer 4: Links countries by their private sector. Node size measures the country’s relative financial concentration and edge size measures the directional volume of financial claims between two countries

Full size image

The layer corresponding to the private sector is presented in Fig. 6. The size of the edges is much smaller than the layer of the official sector (Fig. 5). The biggest links are the ones from Germany to the United Kingdom and to the United States, from the United Kingdom to the United states, from Spain to the United Kingdom, from the United States to the United Kingdom, from Spain to the United States, from France to Italy, and from France to the United States.

Table 9 ERGM estimates for the layer of the private sector and the model variants of Table 3
Full size table

The results from the ERGM estimation for the private sector layer have been presented in Table 9. This time, both the AIC and BIC criteria converge to select Model 2, which is the best model by far, specially according to the BIC criterion. In this model, the edges control, the concentration and the asset covariates are statistically significant at 0.05. The concentration coefficient is \({\hat{\beta }} = -0.10\), with an associated impact of \({\hat{I}}=-9.51\%\) over the connectedness of the network, whilst the coefficient of the random variable assets is \({\hat{\beta }} = -0.35\), which equals an associated impact of \({\hat{I}}=-29.53\%\) in connectedness in comparison with a random network.

Whilst the control for out-degree is not significant in Model 2, it is in the majority of models. Similarly, the controls for edges and mutual roughly are in a half of models. Again, the variable concentration is significant in three out of four models, with a negative coefficient. The coefficient for the random variable assets is also negative and of a very relevant magnitude for the private sector, a result that is consistent in every model in which it appears (models 2 and 4; \({\hat{\beta }} = -0.35\ (p \le 0.05)\) and \({\hat{\beta }} = -0.34\ (p \le 0.05)\), respectively). The coefficient is even higher in the case of in-going links (Model 6: \({\hat{\beta }} = -0.46\ (p \le 0.1)\)). Finally, in Model 6, the absolute difference of concentration is also negative and statistically significant, with a value \({\hat{\beta }} = -0.04\ (p \le 0.1)\)).

4.3 Analysis of the results

The comparison between Tables from 6, 7, 89 and Table 4 shows substantial differences between the monoplex network and the multiplex network. The ERGM fit for the monoplex network has no statistically significant parameters and a bad AIC and BIC fit. However, when disaggregating the full picture into different layers conformed by different financial sectors, we find that the fit is four times better, and a lot of relevant factors are statistically significant.

Table 10 Summary of the statistically significant estimates and impacts of the layers of the multiplex financial network
Full size table

As shown in Table 10, the main factor explaining financial interconnectedness in our international financial network is financial concentration, which is statistically significant in all layers. In layer 2, financial concentration is significant in all the models in which it appears with the exception of one. Overall, the impact of financial concentration over the connectedness of the financial network is \({\bar{I}}=-5.60\%\), with an average coefficient of \({\bar{\beta }}=-0.058\). When in absolute differences, the impact increases to \({\bar{I}}=-6.39\%\), with an average coefficient of \({\bar{\beta }}=-0.066\). As a consequence of these results, we fail to accept Hypothesis 1, and we accept Hypothesis 2. Additionally, we find enough evidence to accept Hypothesis 3, as financial concentration has a negative impact on any model of the multiplex network in which it appears, its statistically significant in most of models, and has an economic and financial significant impact on the connections of our multiplex network.

Finally, we find that the volume of assets of a financial system, also has a negative effect on the quantity of its financial interconnections. This impact is even bigger in magnitude than the one of concentration (but it has less statistically significant coefficients), with an average coefficient of \({\bar{\beta }}=-0.345\), and an average effect of \({\bar{I}}=-29.18\%\). This effect is concentrated around in-going links (with a coefficient of \({\bar{\beta }}=-0.355\) and an impact \({\bar{I}}=-29.88 \%\)). However, this effect appears only in the non-bank MFI layer and the private sector, therefore, in a smaller way than concentration. Eventually, the number of monetary and financial institutions of a country has a relevant positive financial and statistical outcome on financial connectedness in the non-bank MFI layer. Here, increasing the number of MFI increases connectedness in \({\bar{I}}=21.34\%\), with a coefficient of \({\bar{\beta }}=0.24\).

Regarding layer similarity, we find a high degree of it. This is specially true for the Jaccard similarity index, and it is in concordance with other works of the literature of multiplex financial networks, such as the one of Aldasoro and Alves (2018) for maturities and types of European financial instruments. However, the values reported by Bargigli et al. (2015) for the Italian interbank market and by Poledna et al. (2015) for the Mexican interbank system are lower.

Eventually, the degree distributions of the financial network are showed in Figs. 7 and 8 in the Appendix. From Fig. 7 it is possible to see that the degrees from one to six accumulate a high probability, which descends drastically when considering a degree beyond six (for a degree of eight, the probability is around 0.3). When considering a degree of more than ten, the probability is very low. The in-degree distribution reflected in Fig. 8 concentrates the probability around a degree of two, and decreases dramatically from there to reach a low probability of a degree beyond four (around 0.2). The probability remains stable until reaching a degree of ten, when the probability reaches zero. On the other hand, the probabilities of the out-degree distribution are much more densely concentrated, as they are ranged between degrees one and six. Furthermore, the probability of having a degree of three or less is of 0.9, while in the case of the in-degree distribution, it is of 0.6. The in and out degree distributions behave quite differently.

4.4 A note on financial concentration, asset accumulation and the interconnectedness of the financial system

Proceeding inductively, the results of the econometric analysis carried out in this paper can be interpreted as it follows.

When the financial institutions of a country concentrate a substantial share of assets in the system, the country tends to be less connected with the rest of the financial system at an international level. Thus, when in a financial market there are financial institutions which are in a competitive situation instead of having big entities which concentrate most of the assets around them, its financial institutions are more prone to connect with other agents in other countries and vice-versa. This mechanism is highly potentiated by asset accumulation.

Specifically, a country with a high quantity of assets connects much less with other agents in the international financial system, that is, it is more financially self-sufficient. Specifically, it tends to have less in-going linkages. That is, it exports financial claims, but it reduces its imports. This effect is specially relevant for the private sector.

A priory, one may think that from this it can be concluded that, as financial concentration and asset accumulation decrease the number of financial interconnections of the international financial system, it reduces the widespread potential of financial crises, and therefore, it decreases systemic risk. Although this reasoning is not completely false and supports the robust-yet-fragile argument, it is not completely true. To understand the full effects of financial concentration and asset accumulation on systemic risk, other factors such as too-big-to-fail risks must be considered.

Finally, the more monetary and financial institutions of a country, the more the interconnections with the financial system. As financial institutions go to international money markets, primary and secondary financial markets, foreign exchange markets, capital markets and so on in order to conduct their financial operations, when the number of financial institutions of a country increases, so do its chances to be connected with the financial system at an international level.

5 Conclusion and discussion

In this study, we have proposed the usage of the Exponential Random Graph Model to inquiry some of the characteristics that influence the level of interconnection between agents in a financial network. This approach has been proposed by van der Pol (2019) in economic networks; however, it is new to the literature of financial networks. We believe that the ERGM is a generalizable methodology to inquire the determinants of new interconnections in financial networks. As interconnectedness is one of the key drivers of systemic risk, (Gai et al. 2011; Battiston et al. 2012; Acemoglu et al. 2015; Roukny et al. 2018) knowing its determinant factors is essential for researchers, practitioners and policy-makers involved in finance, and particularly in financial stability.

We have applied the model to a international country-wise financial network connecting the countries by their financial claims, at a monoplex and multiplex level. We have mainly centered our study over the effects of financial concentration on connectiveness and systemic risk, due to a current wave of fusions between financial institutions, specially Europe (see Figure 1). Additionally, we study the impact of asset accumulation, the number of monetary and financial institutions, and the number of public debt of a country on the degree of interconnection of our financial network. Our main conclusions can be summarized as it follows:

  1. 1.

    In concordance with the literature (Poledna et al. 2015; Battiston and Martinez-Jaramillo 2018; Aldasoro and Alves 2018), we have found that the results of the monoplex network differ substantially from the multiplex network. However, the layers of the multiplex network are highly correlated as in Aldasoro and Alves (2018), and the estimates are robust to layers. Furthermore, the effects of the variables, when present in various layers, are always of the same sign, and centered around the same magnitude.

  2. 2.

    Financial concentration decreases the number of interconnections in the financial network. Overall, an increase in financial concentration causes a reduction of the \(-5.60\%\) in the edge generation process of new interconnections.

  3. 3.

    Asset accumulation highly decreases the number of interconnections in the financial network. On average, this effect is of the \(-29.18\%\), but it increases to the \(-29.88\%\) in the case of in-going connections, and it is specially relevant for the private sector of the financial system (see Table reftab:layeragents).

  4. 4.

    The number of monetary and financial institutions of a country increases, overall, in a \(21.34\%\) the generation of new connections. This effect affects monetary and financial institutions which are not banks.

Smaga (2014); Cifuentes et al. (2003) argue that, as the financial system becomes more concentrated, systemic risk increases. Our model suggests that this increase of systemic risk may be due to correlated or commonly held assets (Barucca et al. 2021) or too-big-to-fail risks (Haldane and May 2011), not due to connectedness.

Although our model provides important results about the impact of financial concentration (and other variables) on the generation of new connections in a financial network, it is important to distinguish it from the total effect of financial concentration and systemic risk, specially for policy design and implementation. When talking about systemic risk, other factors such as too-big-to-fail risks must be taken into consideration. Therefore, it is not directly arguable that financial concentration reduces systemic risk overall. Furthermore, luckily the understanding of the effects of financial concentration on interconnectedness are going to be contrasted, revised and augmented in further studies related to the topic.

Future research can be done in estimating the rest of the factors of the concentration-systemic risk binomial, specially in a dynamic setting. A systematical report of the probability distributions of a wide number of financial networks to feed numerical simulations models is an important matter, due to the variety of them that may exist according to the results of this and other researches. Finally, we propose employing the ERGM as a methodology to uncover new relationships in financial networks.