Introduction

Reduced-order, low-computational cost, process-structure-property (PSP) linkages play a central role in the efforts related to the design of materials for targeted combinations of effective properties or performance characteristics.1,2,3,4,5 This is because the materials design space (comprising a broad range of potential chemistries and available options in processing) is typically too large to explore with the computationally expensive physics-based materials modeling toolsets (e.g., micromechanical finite element models, phase-field models). The formulation and use of high fidelity, reduced-order, surrogate PSP linkages offer one of the most promising research avenues for realizing the goals of accelerated materials innovation targeted by the US Materials Genome Initiative.6 In addition to facilitating rapid exploration of the vast materials design spaces, the low computational cost PSP linkages play an important role in the objective calibration of the multiscale physics-based models to the available, often limited, experimental data.7,8,9 This is because the calibration of parameters present in multiscale models is inherently an inverse problem that also demands many executions of the forward models.

Establishing high-fidelity surrogate PSP linkages requires a suitable framework for the rigorous quantification of the material internal structure (i.e., the quantification of ‘S’ in the PSP linkages).10 This is because the material internal structure often spans a hierarchy of material length scales, from the subatomic to the macroscale, with each scale exhibiting a rich variety of defects and/or disorder. Consequently, the rigorous quantification of the material internal structure needs a versatile framework that can address the diverse features observed in the material structure at the different length scales in the different material systems. A second challenge comes from the fact that any rigorous quantification of the material internal structure is likely to produce a large number of statistical measures of the microstructure. The number of microstructure measures constitutes the dimensionality of the material structure representation for the present discussion (i.e., each microstructure measure corresponds to one dimension). Our goal of formulating low computational cost PSP linkages demands that we seek high-value, but low-dimensional, representations of the material structure. In recent years, our research group has advanced a systematic framework called Materials Knowledge Systems (MKS)2 for extracting data-driven reduced-order PSP linkages from materials datasets aggregated from either multiscale simulations or multiscale experiments. At the core of MKS lies an approach for high-value, low-dimensional representation of the material internal structure by bringing together the concepts of n-point spatial correlations11,12,13 and principal component analysis (PCA).14,15 The efficacy of the MKS framework in producing high-fidelity reduced-order PSP linkages has been demonstrated in prior work.16,17,18

There exist many opportunities for the further development of the MKS framework. Of particular relevance to this work are the approaches used to build the reduced-order models after the feature engineering step (i.e., after the low-dimensional representations of the material structure are obtained employing n-point spatial correlations and PCA). In most of the prior work,16,17,19,20 surrogate models were built using standard regression techniques. These techniques are indeed ideally suited when there is a reasonably large dataset available, and there is already evidence (or physical insights) suggesting a specific model form for capturing the governing physics of the problem. In many practical applications of the MKS framework for a broad range of multiscale materials phenomena, one or both of these requirements are not met. There is therefore a critical need to expand beyond the standard regression techniques. In the present work, we specifically explore the utility and benefits of employing modern machine learning (ML) tools, specifically Gaussian process regression (GPR),21 in establishing the desired surrogate PSP linkages.

Several benefits are anticipated from the use of GPR in the MKS framework for extracting PSP linkages from materials data. Unlike standard regression, GPR does not demand the aggregation of a sufficiently large dataset before building the surrogate model. In other words, one can start with a very small number of data points and gradually build the desired PSP linkages as more data become available. Furthermore, since GPR provides a rigorous assessment of the uncertainty (i.e., variance) in the predictions made from the surrogate model, it can provide objective guidance on where one should generate new training data points. This is particularly important when the data are being generated using expensive computations or experiments. In the basic regression techniques, one usually aims to spread the data points uniformly in the input domain. Such a simple strategy is unlikely to be optimal in terms of maximizing the predictive accuracy of the extracted surrogate model. Using GPR, one can select inputs for generating new training data based on systematically minimizing the uncertainty of the model predictions over the entire input domain of interest. One can therefore implement a dynamic selection process that leads to autonomous (without the need for human intervention) and economical workflows for the extraction of robust surrogate models for any selected physics-based multiscale materials model. A second major advantage of using GPR is that that there is no need for a priori selection of a specific parametric model form. GPR employs specialized kernels22,23 on the training data that serve as efficient interpolators. These kernels have hyperparameters that are optimized to produce the most reliable surrogate models from the available training data.

GPR has already been used successfully to address a limited set of materials problems. Bélisle et al.24 presented a scalable GPR approach for predictions of martensite start temperature and electrical conductivity. Tapia et al.25 used GPR to predict porosity in stainless steel parts fabricated in an additive manufacturing process, and to predict the melt pool depth.26 GPR was used by Hoang et al.27 to predict the compressive strength of concrete samples based on composition and process variables. Yabansu et al.18 used GPR models to predict the microstructural evolution of Ni-based superalloys in a thermal aging process. Tallman et al.28 used a GPR-based approach to drive data collection for a homogenization model in order to study deformation of α-Ti. Hashemi et al.29 used an autoregressive GPR model to predict the time evolution of structure in FCC metals during static recrystallization processes. This work is specifically aimed at using GPR for the autonomous extraction of PSP linkages.

The main goal of this study is to develop and demonstrate GPR-based MKS protocols for autonomous and economical extraction of reduced-order PSP models for the bulk (effective) plastic response of multiphase materials. Specifically, our focus will be on two-phase composites, where each phase exhibits an isotropic plastic response. This specific case study was selected because the viability of the standard MKS regression techniques for this problem has already been established.19 Therefore, it offers an opportunity to evaluate critically the computational cost of training the new GPR-based MKS models and their predictive accuracy compared to the previously established models based on standard regression methods.

Methods

Mean-Field Theory Approximations for Plastic Response of Composites

Mean-field theories approximate the effective response of composites by assuming uniform stress and/or strain fields within the constituents.30,31 The specific approach employed in this work builds on the approach described initially by Stringfellow et al.,32,33 and more recently by Latypov et al.19 The problem of interest here is the homogenized equivalent stress–equivalent plastic strain response of a composite material made of two isotropic constituents (i.e., thermodynamic phases), both following a J2-based associated flow rule34 with distinct hardening responses. The composite microstructure is assumed to be adequately captured in a voxelized 3-D representative volume element (RVE).34,35 The main state variable of interest in these models is the resistance to plastic deformation, henceforth referred to as strength, and denoted by g. During any imposed deformation, the evolution of strength (due to strain hardening) at any material point in the RVE can be expressed as:

$$ \dot{g} = h\dot{\epsilon }, $$
(1)

where \(\dot{\epsilon } = \sqrt {\frac{2}{3}{\mathbf{D}} \cdot {\mathbf{D}}}\) is the equivalent plastic strain rate, and h represents a hardening law expressed typically as a nonlinear function of the strength, i.e., \(h = h\left( g \right)\). In the present application, we expect the two phases present in the composite to exhibit two distinct hardening laws denoted as \(h_{1} \left( g \right)\) and \(h_{2} \left( g \right)\), where the subscripts index the different phases present in the composite.

Prior work employing mean-field approaches32,33 has demonstrated the remarkable utility of simplified approaches for predicting the overall response of the composite by tracking only the volume averaged values of the plastic strain rates and strengths for each phase. Following the prior work of Stringfellow and Parks33, we assume here that Eq. 1 can be applied to phase–volume averaged quantities as (no summation is implied on the repeated index):

$$ \dot{g}_{k} = h_{k} \left( g \right)\dot{\epsilon }_{k} $$
(2)

where \(g_{k}\) and \(\dot{\epsilon }_{k}\) now denote the volume averaged strength and the volume averaged equivalent plastic strain rate, respectively, for the kth phase. With this simplifying assumption, the problem of predicting the overall response of the composite can be addressed by partitioning the overall imposed deformation into the phase–volume averaged quantities, \(\dot{\epsilon }_{k}\). The phase–volume averaged strengths in each phase, \(g_{k}\), are updated using Eq. 2, and the effective (composite) strength, \(\overline{g}\), is computed. Stringfellow and Parks33 addressed these challenges using the self-consistent approach based on the Eshelby solution for a spherical inclusion in a homogeneous effective medium. Although the approach yields a simple model, it only incorporates highly simplified information on the material microstructure, i.e., volume fractions of the constituents.

In the recent work of Latypov et al.,19 the approach of Stringfellow and Parks33 was extended to include the higher-order details of the material microstructure. This was accomplished by extending the MKS framework2 as shown schematically in Fig. 1. In this new strategy, calibrated MKS models are established to predict the strain rate partitioning ratios for the soft and hard phases (denoted as \(\chi_{1}\) and \(\chi_{2}\), respectively). The ratios are defined through \(\dot{\epsilon }_{k} = \chi_{k} \dot{\overline{\epsilon }}\), where \(\dot{\overline{\epsilon }}\) denotes the macroscopically imposed equivalent plastic strain rate on the RVE. The inputs for these models are the microstructure’s reduced-order representation (PC scores) and strength contrast, \(\eta = g_{2} /g_{1}\). A key underlying assumption in this approach is that the changes in morphology of the microstructure are minimal for the small plastic strains imposed; therefore, the PC scores are kept constant for each prediction of the stress–plastic strain response. Once the volume-averaged strain rates \(\dot{\epsilon }_{k}\) are computed, the strain hardening in each phase is computed using Eq. 2, and the strengths of each phase are updated as \(g_{k} \left( \tau \right) = g_{k} \left( t \right) + \dot{g}_{k} \Delta t\), where \(\Delta t = \left( {\tau - t} \right)\) is the time increment. The value of the strength contrast η is then updated and used in a different MKS model developed specifically to predict the effective yield strength of the composite \((\overline{g})\). This MKS model takes the PC scores of the microstructure and the strength contrast, η, as inputs. Repeating the computations described above, one can then predict the equivalent stress–equivalent plastic strain curve for the RVE with high fidelity and very low computational cost. The PC scores used as inputs to the effective yield strength MKS model are the same PC scores used as inputs by the other two MKS models described above. The only difference is that the value of η used as input to the yield strength MKS model is the updated value after the prediction of the strain rate partitioning ratios. The viability of this approach was demonstrated in prior work.19

Fig. 1
figure 1

The MKS plasticity framework applies a velocity gradient tensor to the RVE. Predictions are then made for the strain partitioning ratios (via MKS Models I and II) and then for effective yield strength (via MKS Model III). The phase-averaged strain rates are utilized in updating the yield strengths of each constituent phase. Adapted from.19

Full size image

Full Field Numerical Evaluation of Micromechanical Responses

Datasets are needed to train and subsequently test the GPR models built in this study. These were generated using finite element (FE) micromechanical simulations on digitally generated 3-D RVEs.19,36,37 The results from the micromechanical FE simulations are treated as the ground-truth for building the GPR models. The protocols used for generating the datasets are essentially the same as those used in prior work,19 and are briefly described next.

Commercial FE software Abaqus38 was used for generating the datasets. Each voxel of the 3-D RVE was converted into a C3D8 element in the FE model. A J2 rate-independent plasticity model based on the von Mises yield criterion was selected for this study. Each RVE was subjected to a velocity gradient tensor (\(\overline{L}\)), defined as \(\overline{L}_{11} = 10^{ - 3} \,{\text{s}}^{ - 1}\) and \(\overline{L}_{22} = \overline{L}_{33} = - \overline{L}_{11} /2\), with all off-diagonal components set to zero. These are imposed as periodic velocity boundary conditions on the RVE. To minimize the effects of elasticity, the elastic modulus of each phase was selected to be 106 times larger than its yield strength.

The MKS models identified in Fig. 1 take only the microstructure and the strength contrast as inputs and output the strain rate partitioning ratios and the effective strength. The data needed to train these models only require FE simulations performed to small strain levels. Specifically, digitally generated microstructures were deformed to an equivalent strain of 0.002. The constituent phases were assigned strength values without hardening to enforce the desired strength contrast ratio (one of the inputs to the MKS models to be built).

Test datasets were also generated the critical evaluation of the GPR-based framework depicted in Fig. 1. For this purpose, FE simulations were conducted on selected digitally created microstructures to an equivalent strain of 0.1. The hardening laws for both constituent phases were described by a power law as:

$$ \begin{array}{*{20}c} {\dot{g}_{k} = h_{k}^{0} \left( {1 - \frac{{g_{k} }}{{g_{k}^{\infty } }}} \right)^{{a_{k} }} \dot{\epsilon }_{k} } \\ \end{array} $$
(3)

where \(h_{k}^{0}\), \(g_{k}^{\infty }\), and \(a_{k}\) denote hardening parameters for the phase \(k\). These parameters were selected to correspond to literature values reported for ferrite and martensite,39 and are summarized in Table I.

Table I Values of quantities used for strain hardening law calculations.
Full size table

Following the Hill–Mandel principle,40,41 the macroscopic stress was computed as the volume-averaged stress tensor over the RVE. The equivalent stress was then computed using the von Mises definition, which is the same as effective strength in the rate-independent plastic theory used in this study. The equivalent plastic strain rate is computed at each integration point in the FE mesh, and the strain rate partitioning ratios, \(\chi_{k}\), are obtained by dividing the average equivalent strain rate in the kth phase by the macroscopically imposed equivalent strain rate.

Generation of Three-Dimensional (3-D) Digital Microstructure Volumes

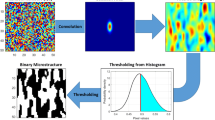
Voxelized 3-D RVEs reflecting a diverse range of morphological features were generated to serve as the training and test data, where each voxel is assigned to either the soft phase or the hard phase. The RVE size was selected to be 27 × 27 × 27, which produced good results in previous work.19 Two specific methods were used in this study for the generation of a large ensemble of diverse RVEs for the present study. The first technique generated RVEs through the use of a Gaussian filter,42 where each voxel is assigned a value drawn randomly from a uniform distribution over the range (0,1). A 3-D Gaussian filter with diagonal covariance matrix, Σ, is applied to the random field via circular convolution to obtain a smooth (locally averaged) field. Thresholding is then applied to assign label 1 or 2 (denoting a soft or hard phase, respectively) to each voxel; this process results in a two-phase 3-D RVE. The thresholding value determines the phase volume fractions, while the diagonal values of Σ control the average phase size and shape. By suitably changing the diagonal values of Σ, one can generate a diverse range of morphologies ranging between equiaxed morphologies to plate-like morphologies to rod-like morphologies, with volume fractions in the range (0,1). A total of 512 RVEs were generated using this strategy. The top row of Fig. 2 shows example RVEs generated using the Gaussian filter approach.

Fig. 2.
figure 2

(Top) Example RVEs generated with the Gaussian filter method. (Bottom) Example RVEs generated with the UMGF method. For both methods, the ensemble was generated to target different hard phase volume fractions (f2) and morphologies.

Full size image

The Universal Microstructure Generation Framework (UMGF) developed recently43 was used as a second approach for generating the digital RVEs used in the present study. This approach utilizes a user-specified cost function to identify the optimal placement of objects in the microstructure. Objects to be used in the microstructure may be called from a library or defined by the user, allowing for tremendous morphological flexibility. This method is also computationally efficient, because it uses convolution filters for carrying out many of the computations involved. The UMGF approach used in this work systematically controls object overlap; this feature allows it to generate morphologies that are unobtainable using the Gaussian filter approach. A total of 286 RVEs were generated using the UMGF approach. Examples are presented in the bottom row of Fig. 2, where D represents the sizes of objects used in the generation.

For each RVE, 10 different values of η, corresponding to integers between 1 and 10, were assigned. As a result, the total number of distinct inputs generated for the models was 7980.

Microstructure Quantification

Voxelized microstructures can be conveniently represented by the array, \(m_{{\varvec{s}}}^{k}\), which reflects the volume fraction of local state, k, in voxels, s.10 Since each voxel is assigned entirely to a single phase, the values of \(m_{{\varvec{s}}}^{k}\) are either 0 or 1 for the RVEs studied. These microstructures can be featurized using two-point spatial correlations and PCA.14,15 For two-phase microstructures, the autocorrelation of a single local state provides an adequate set of spatial correlations.44,45 These are mathematically defined as:

$$ \begin{array}{*{20}c} {f_{{\varvec{t}}}^{kk} = \frac{1}{{\left| {\varvec{S}} \right|}} \mathop \sum \limits_{{\varvec{s}}}^{{\varvec{S}}} m_{{\varvec{s}}}^{k} m_{{{\varvec{s}} + {\varvec{t}}}}^{k} } \\ \end{array} $$
(4)

where \(f_{t}^{kk}\) is the probability of finding local state, \(k,\) in spatial bins separated by a specified discretized vector, \({\varvec{t}}\).46 For this study, \(k = 1\) was selected; this has no consequence on the results.47 Fast Fourier transform algorithms allow highly efficient computation of the autocorrelations.46 Figure 3 shows four example RVEs exhibiting different phase volume fractions and morphologies. The figure also presents three orthogonal sections of the corresponding 3-D autocorrelations. The value at the origin of the 3-D autocorrelations reflects the phase volume fraction, and the averaged inclusion size and shape is reflected in the contours surrounding the central peak. The first set of 3-D autocorrelations in Fig. 3 shows a very small central peak because its corresponding RVE has very small inclusions. The second set of 3-D autocorrelations in Fig. 3 clearly show a vertical fiber as the central peak, reflecting the dominant morphology of its RVE. Furthermore, the spacings between the vertical bands in this set of autocorrelations reflect the distributions of spacings between vertical fibers in the RVE. The third and fourth sets of autocorrelations reflect coarse equiaxed features in their corresponding RVEs.

Fig. 3
figure 3

Example RVEs (top row) and their autocorrelations of the soft phase (bottom row). Only three orthogonal sections of the 3-D autocorrelations are shown. The autocorrelations contain information such as the hard phase volume fraction (value at the origin), morphology, and spacing.

Full size image

Although two-point correlations provide rigorous statistical descriptions for the microstructure, they result in high dimensional representations (each value of \(f_{{\varvec{t}}}^{kk}\) is treated as a dimension). In the present application, the dimensionality of the autocorrelations is 19,683, which is the number of voxels in the generated RVEs. As a result, dimensionality reduction becomes essential for the development of ML models. In the MKS framework, dimensionality reduction is achieved performing PCA on the full ensemble of microstructures. The autocorrelations of the nth microstructure (the superscripts on the two-point statistics have been dropped since we selected \(k = 1\)) can then be expressed as:

$$ \begin{array}{*{20}c} {f_{{\varvec{t}}}^{\left( n \right)} \approx \mathop \sum \limits_{j = 1}^{{R^{*} }} \alpha_{j}^{\left( n \right)} \varphi_{{j{\varvec{t}}}} + \overline{{f_{{\varvec{t}}} }} } \\ \end{array} $$
(5)

where \(\alpha_{j}^{\left( n \right)}\) denote PC scores, \(\varphi_{{j{\varvec{t}}}}\) describes the basis vectors of the PC space, \(\overline{{f_{{\varvec{t}}} }}\) denotes the ensemble mean, and \(R^{*}\) denotes the truncation level (i.e., the reduced dimensionality of the microstructure representation). Several prior applications of MKS have shown that a small number of PCs (typically 3–8) are adequate for capturing PSP linkages with high fidelity.17,20,36,37

The PC space representation of the 798 digital microstructures generated for this study is presented in Fig. 4 in multiple subspaces. It is noted that the two microstructure generation methods produced microstructures occupying different regions, even in the 3-D PC subspace. Each PC score reflects the strength of the corresponding PC basis (\(\varphi_{{j{\varvec{t}}}}\) in Eq. 5). Each PC basis essentially reflects a normalized and weighted set of autocorrelations. Figure 4 also presents the basis maps for the first two PC scores, along with example RVEs corresponding to selected locations, from which it is clear that an increase in the value of PC1 results in an increase in the phase volume fraction, while a decrease in the value of PC2 results in the phase regions being elongated in the y-axis while also becoming coarser. While some of the microstructural features represented in the PC scores may be readily interpreted from their PC basis maps, there will be many other features in the high-dimensional (19,683 for the present case) PC basis that are not easily interpreted.

Fig. 4
figure 4

Projections of the microstructure ensemble in PC space: (Top left) PC1-PC2 projection, (Top Middle) PC1-PC3 projection, (Top right) PC2-PC3 projection. (Bottom left) 3-D basis vectors for first two PC scores. (Bottom right) Illustration of RVEs on the PC1-PC2 projection of the PC space. It may be observed that PC1 strongly correlates with soft phase volume fraction, while PC2 strongly correlates with elongation of soft phase domains along the y-axis.

Full size image

A general practice is to use a truncated set of PC scores in the model building effort. Percent variance capture is a useful measure for selecting the number of PC scores, since it quantifies the differences between microstructures. However, this is not necessarily the only criterion: some of the PC scores contributing to only a small fraction of variance can exhibit a strong correlation to the effective property of interest. Based on the prior study,19 we have decided to use the first 10 PC scores in this study. These 10 PCs account for over 99.9% of the variance between the elements of the microstructure ensemble utilized for this study.

Gaussian Process Regression (GPR)

GPR is a nonparametric ML approach to building surrogate models. A Gaussian process21 is completely defined by specifying its mean and covariance. Therefore, the target, \(y\), can be expressed as

$$ \begin{array}{*{20}c} {y = \hat{y} + \epsilon ,\hat{y} \sim N\left( {\mu \left( {\varvec{x}} \right){, }{\varvec{K}}\left( {{\varvec{x}},\user2{x^{\prime}}} \right)} \right)} \\ \end{array} $$
(6)

where \(\hat{y}\) denotes the predicted value, \(\varepsilon\) is the residual, \({\varvec{x}}\) is the vector of inputs, and \({\mathcal{N}}\left( {\mu {, }{\varvec{K}}} \right)\) is a multivariate Gaussian distribution with a mean \(\mu\) and a covariance \({\varvec{K}}\). Generally, the mean of a Gaussian process is assumed to be zero. The covariance is generally estimated using a kernel function designed for efficient interpolation between the training data points. An automatic relevance determination squared exponential (ARD-SE) kernel21, 22 is used in this study, and is expressed as:

$$ \begin{array}{*{20}c} {k\left( {{\varvec{x}},\user2{x^{\prime}}} \right) = \sigma_{f}^{2} \exp \left( { - \frac{1}{2}\mathop \sum \limits_{d = 1}^{D} \frac{{\left( {x_{d} - x_{d}^{^{\prime}} } \right)^{2} }}{{l_{d}^{2} }}} \right) + \sigma_{n}^{2} \delta_{{\user2{xx^{\prime}}}} } \\ \end{array} $$
(7)

where \(\sigma_{f} ,l_{d}\), and \(\sigma_{n}\) serve as hyperparameters controlling the accuracy of the predictions; \(\sigma_{f}\) scales the variance associated with the predictions, with increasing the value of \(\sigma_{f}\) increasing the probability of capturing outlier values, but also increasing the prediction noise; \(l_{d}\) is an interpolation hyperparameter, where low values of \(l_{d}\) imply short-range interpolations (and noisier predictions); and \(\sigma_{n}\) controls the homoscedastic Gaussian noise applied to predictions. The central feature of the ARD-SE kernel is that it allows different interpolation parameters for the different input variables. This feature allows the model to capture the different levels of contributions of the different inputs to the accuracy of the prediction, improving its fidelity and interpretability. The main task in building a reliable GPR model reduces to the estimation of the values of the hyperparameters in Eq. 7. This task is generally approached as an optimization problem based on the maximization of the joint log marginal likelihood of the hyperparameters, given the training dataset. In this work, a quasi-Newton method, known as the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm48,49,50 is used to optimize the hyperparameters in Eq. 7.

Once the optimized hyperparameters have been established, the mean (\({\varvec{\mu}}^{\user2{*}}\)) and covariance (\({\varvec{\varSigma}}^{\user2{*}}\)) of the Gaussian predictive distribution for test inputs \({\varvec{x}}^{\user2{*}}\) are computed as:

$$ \begin{array}{*{20}c} {{\varvec{\mu}}^{\user2{*}} = {\varvec{k}}^{{\user2{*}T}} {\varvec{K}}^{ - 1} y} \\ \end{array} $$
(8)
$$ \begin{array}{*{20}c} {{\varvec{\varSigma}}^{\user2{*}} = \user2{ K}^{\user2{*}} - {\varvec{k}}^{{\user2{*}T}} {\varvec{K}}^{ - 1} {\varvec{k}}^{\user2{*}} } \\ \end{array} $$
(9)

where \({\varvec{k}}^{\user2{*}}\) is the covariance between the training inputs x and the test inputs \({\varvec{x}}^{\user2{*}}\), \({\varvec{K}}\) is the covariance within the training inputs, and \({\varvec{y}}\) denotes the target responses for the training inputs. Superscript T denotes the transpose operation.

Dynamic Selection Methods

As already discussed, our main focus is on optimal generation of the training data for establishing surrogate PSP models from expensive physics-based micromechanical FE models. This will be accomplished through dynamic sequential selection of the next input to the physics-based simulations. Specifically, we will employ a relatively simple approach based on the highest predictive variance, known as the mean squared error (MSE) approach.51,52,53,54 In this approach, a single sample point is added in each selection cycle in a sequential manner,52 and may be interpreted as seeking the maximization of information added to the surrogate model.

Autonomous Protocols for Formulation of the MKS Models

The present application requires the establishment of three different surrogate models, identified in Fig. 1 as MKS Models I, II, and III. In prior work,19,36 these were calibrated using all of the available RVEs and their corresponding micromechanical responses, without considering the order in which new data should be added to the training set. By contrast, this work seeks to develop protocols for the autonomous generation of training data that optimally improve the surrogate models being built. This is accomplished using a variant of the MSE approach described in “Dynamic Selection Methods” section, where we identify one new set of inputs for each model being built. In other words, in each cycle of training data generation, we have identified three different sets of inputs: each set is expected to maximize the information gain for each of the MKS Models I, II, and III, respectively. Additionally, when a candidate input is selected, it is removed from the candidate set so that it cannot be selected again in future data generation cycles. Note that the input set for all three MKS models comprises the same set of variables, which include the first 10 PC scores of the microstructure (see “Microstructure Quantification” section) and the strength contrast value, η. A total of 7980 distinct inputs were established in “Generation of Three-Dimensional (3-D) Digital Microstructure Volumes” section for this purpose. Before applying GPR, each input variable was scaled to exhibit a unit standard deviation over the complete set of inputs; this is to improve the optimization of the hyperparameters in Eq. 7. A subset of 500 inputs from the total set of 7980 inputs were set aside as the test set. The test inputs were selected such that they uniformly covered the eleven-dimensional input space. Therefore, we were left with 7480 inputs as the candidate training set for the present work.

Figure 5 provides a schematic of the autonomous workflow developed and implemented in this work to build the desired surrogate models. This workflow was comprised of the following steps:

  1. 1.

    An initial training dataset was created by selecting 10 inputs from the set of 7480 candidate inputs. FE simulations were conducted for these, and the results were used to train the initial GPR-based MKS Models I, II, and III.

  2. 2.

    The single-point MSE approach was used to select three new inputs (each aimed at maximizing the fidelity of each MKS model) from the remaining candidate set.

  3. 3.

    FE simulations were performed for the three new inputs, and the results were added to the training dataset.

  4. 4.

    All three GPR models were updated using the enhanced training set.

  5. 5.

    Steps 2–4 were repeated until the model exhibited the desired predictive accuracy on the test set (not included in the training set).

Fig. 5
figure 5

Schematic describing the autonomous workflow for the development of GPR-based MKS Models identified in Fig. 1. The workflow involves three main steps: (1) establishing the candidate set of inputs that may be selected for FE evaluation, (2) identifying the next set of inputs to be evaluated using FE models, and (3) performing the FE simulations and adding them as new training data. This cycle of steps is repeated as many times as needed until the models exhibit the desired predictive accuracies.

Full size image

Figure 6 demonstrates the improvement in the GPR-based MKS models with each model update, as measured by the errors on the test set. It is seen that the proposed workflow is quite efficient in systematically improving the MKS models. For comparison, Fig. 6 also shows the model improvement with random selection of training points. It can be seen that the single-point MSE approach used in this work significantly outperforms the random selections (repeated 10 times). In terms of error, there are only a very few times in which the random selection outperforms the single-point MSE selection; even in these rare cases, the advantage is not seen in all three models simultaneously, and the benefit is often lost in the next few updates of the model. There is a clear benefit to the sequential design approach in the selection of training points. The models appear to learn quickly, displaying a roughly asymptotic behavior. The training in the present work was stopped after using 190 training points. For all models, the dynamic selection outperformed the random selection after this number of training points.

Fig. 6
figure 6

Model learning efficiency of max uncertainty versus random selection approaches for a test set of 500 inputs. The max uncertainty selection scheme shows faster error convergence compared to random selection for all models generated in this study.

Full size image

The final model errors were found to be 3.3%, 7.5%, and 6.1% for \(\overline{g}\), \(\chi_{1}\), and \(\chi_{2}\), respectively. These errors are higher than those obtained in prior work,19 where errors of 0.6%, 5.0%, and 4.7%, respectively, were reported after using 1140 training points and 380 test points. However, the RVEs used in the test set for that work covered a much smaller range in PC space compared to the test set used for the present work. Even with much fewer training points and a test set covering a larger range PC space, the \(\chi_{1}\) and \(\chi_{2}\) errors are only slightly higher for this work compared to those obtained previously. Clearly, the dynamic selection approach utilized in this work produced significant economy in the training effort (only 190 training points were used in the present work). Figure 6 also shows that the model error does not always decrease in subsequent cycles of model improvement. This is mainly because of the simplicity of the single-point MSE approach. Other approaches based on maximization of information gain are likely to improve on this aspect.

If one aims to improve the model accuracy, one might try to include more PC scores (10 PC scores were used in this work) or explore other feature engineering approaches (PCA on two-point statistics was used in this work) combined with other surrogate model building approaches (GPR was used in this work).

Prediction of the Stress–Strain Responses with Uncertainty Quantification

Prior work,19 based on simple polynomial-based regression approaches for establishing the three MKS models, made predictions only for the expected stress–strain responses of new microstructures, without quantifying their prediction uncertainty. Replacing the polynomial regression models with GP-based models not only allows for a richer representation of the underlying model form but also allows for the quantification of the prediction uncertainty.

The overall workflow for the prediction of the equivalent stress–equivalent plastic strain response follows the workflow shown in Fig. 1, and was summarized in “Mean-Field Theory Approximations for Plastic Response of Composites” section. The stress–strain response is computed by performing 200 increments, with each increment corresponding to an increase of 5 × 10−3 in the equivalent plastic strain. For each strain step, the expected value of the equivalent stress is obtained using the GPR-based MKS models I, II, and III following the workflow described earlier. The main changes in the workflow are related to the computation of the prediction uncertainty and its propagation throughout the sequential strain increments in the predicted stress–strain response.

In the workflow employed in this work, the prediction uncertainty is propagated to the stress–strain response by sampling the variables of interest. At the beginning of each strain step, variables \(\chi_{k}\) are sampled from their respective distributions and evolved to the end of the time step, providing a distribution of stress values at the end of the time step. Standard deviation in the predicted stress value is then computed from the sampled values. In the first time step, the phase strengths are assumed to be known with zero variance. For all subsequent strain steps, the GPR models provide the information on the variances for both \(\chi_{k}\), which are used to compute the phase strengths. It was found adequate to represent each distribution at each strain step using 10 samples (i.e., a higher number of samples did not significantly influence the computed variance on the predicted stress value). Sampling from the normal distributions was performed using built-in functions in the Numpy module55 of Python. A total of 1000 samples are obtained from each of the 10\(\overline{g}\) values computed in each step, yielding a population of 10,000\(\overline{g}\) samples. The mean and variance of this population are computed to establish the prediction mean and its uncertainty.

The accuracy of the predicted stress-strain responses was validated using multiple RVEs that were not in the training set. Three examples of these RVEs are shown in Fig. 7, exhibiting hard phase volume fractions of 0.25, 0.35, and 0.75. The phases were assigned the hardening parameters in Table 1, corresponding to dual-phase steels. Note that the initial strength contrast for these examples is 3.42 (= 974.4/285), which is distinct from the values used in the training set. Figure 7 shows the predicted equivalent stress–equivalent plastic strain responses using the protocols developed in this work. These predictions not only include the expected values but also their associated uncertainties (depicted using ± 2 standard deviations). The predictions are compared with corresponding results from FE simulations (considered as ground-truth).

Fig. 7
figure 7

Comparison of the predicted equivalent stress–equivalent plastic strain responses for three different microstructures. The mean prediction is shown by the center line, the ± 2 SD (4 standard deviations in total) showing prediction uncertainty are shown by the outer lines, and the FE simulation results (i.e., ground-truth) are shown as circles.

Full size image

The GPR-MKS framework developed in this work shows good agreement with the FE-predicted stress–strain responses for the very different microstructures shown in Fig. 7. Note that the modeling framework developed here is applicable to virtually any two-phase microstructure 3D RVE with arbitrary assignment of hardening laws for each phase. Most importantly, the GPR-MKS framework is able to generate the full stress-strain curve prediction in under 3 s on a personal laptop with an Intel i5 processor, compared to approximately 4 h required for the FE simulation, executed on the PACE computing cluster at Georgia Tech. Therefore, it is clear that the proposed GPR-MKS framework provides remarkable savings in computational cost, while retaining a high degree of accuracy in its predictions.

Summary

This work has demonstrated the benefits of GPR approaches for the development of low computational cost MKS surrogate models for the prediction of the equivalent stress–equivalent plastic strain responses of arbitrary (user-specified) 3D RVEs of two (isotropic)-phase microstructures. It has been shown that the use of GPR approaches allows for optimal training of the surrogate models with a minimal number of training data points. This is particularly useful for building surrogate models calibrated to computationally expensive physics-based simulation data. In this work, this was accomplished using a simple single-point maximum variance-based approach. It has been shown that the dynamic selection strategy significantly outperforms the random selection of the training data, especially when large-dimensional input domains are involved.