Temperature Profile, Bead Geometry, and Elemental Evaporation in Laser Powder Bed Fusion Additive Manufacturing Process

Abstract

Powder bed fusion processes have been a focus of research in recent years. Computational models of this process have been extensively investigated. In most cases, the distribution of heat intensity over the powder bed during the laser–powder interaction is assumed to follow a Gaussian beam pattern. However, the heat distribution over the surface is a complicated process that depends on several factors such as beam quality factor, laser wavelength, etc. and must be considered to present the laser–material interaction in a way that represents the actual beam. This work presents a process in which a non-Gaussian laser beam model is used to model the temperature profile, bead geometry, and elemental evaporation in the powder bed process. The results are compared against those of a Gaussian beam model and also an experiment using Inconel 718 alloy. The model offers good predictions of the temperature, bead shape, and concentration of alloying elements.

Introduction

The powder bed fusion (PBF) process for metal additive manufacturing is gaining increasingly widespread recognition for its ability to produce components with complex geometry. Three-dimensional parts can be produced using this process in a layer-by-layer manner which involves rapid heating, melting, fluid flow, remelting of the previous layer, and cooling during the process. Metallic powders are first spread over a substrate, then a laser or electron beam is used to selectively melt them. Many researchers have concentrated on the powder bed process, motivated by its potential to produce high-quality parts.1,2,3,4,5,6,7,8,9,^–10

This process is conducted using either a laser or electron beam power source, which have different operating principles. A laser works optically (thus mainly following the physics of optics, where its reflection, absorption, and transmission are dictated by the corresponding coefficients), while high-speed electrons interact with the powder when using an electron beam. This study deals with the selective laser melting (SLM) process, in which powder particles are fully melted when they interact with the laser beam, as opposed to selective laser sintering (SLS), where the powders are partially melted.

Due to the complications associated with the powder bed fusion process, researchers have followed different modeling approaches to understand the underlying physics of the process. Roberts et al.11 presented a simulation technique called element birth and death to model the multiple layers during the process, where all the elements are present from the beginning but do not contribute to the overall matrix. Each layer is activated after the previous layer is built. Dong et al.12 used variable material properties such as thermal conductivity, density, etc. during different steps of the simulation. However, heat transfer through the bottom of the powder bed was not considered, which is not representative, as heat must be transferred to the build plate to precisely model the process. Michaleris13 provided a “quiet” and “inactive” method of simulation. The “quiet” method takes into account all the elements but allocates properties to the quiet elements such that their presence is ignored until they are activated. In the “inactive” method, elements are not taken into account until the associated material is included. He also proposed a “hybrid quiet–inactive” method, where elements are inactive initially and then assigned to the quiet mode for each layer when they are activated. Lee et al.14 constructed a computational model of a single layer with two overlapping tracks, assuming a preheating temperature of 573 K. In most of the literature, the laser–powder interaction is modeled based on a Gaussian beam, where the laser intensity decreases as one moves outward from the center of the beam. However, Horak et al.15 conducted an experiment to observe the laser–material interaction with the help of a high-quality camera and found that the beam profile was actually different from the Gaussian beam, showing lower intensity. It is therefore important to model the laser in such a way that it represents the actual laser.

Accurately modeling the fluid flow in the melt pool due to Marangoni and buoyancy effects is of great importance as it affects the heat distribution as well as the melt pool shape. Marangoni flow, which takes place at the surface of the molten metal due to the variation of the surface tension caused by the temperature gradient, is one of the major forces for fluid flow within the melt pool.16 Many researchers17^,18 have completely ignored the Marangoni flow in their models. Romano et al.3 came up with an effective conduction coefficient approach that accounted for the thermal convection due to fluid flow inside the melt pool. However, the fluid flow around the melt pool was not modeled. Andreotta et al.4 included mass and moment equations to take into account the Marangoni flow.

The geometry of the melt pool is an important parameter in additive manufacturing, Influencing the dimensional accuracy of the build as well as its surface roughness. The melt pool geometry impacts the residual stress in several different ways. The depth of the melt pool determines how many previous layers are melted in each cycle. This remelting and solidification not only impact the microstructure and grain size and orientation, but also the residual stress, as the solidification causes shrinkage in each pass. The melt pool dimensions also impact the temperature gradient and the rate at which the material is heated and cooled, which causes the thermal strain within the material to vary, resulting in mechanical deformation and strain. The fluid flow around the melt pool has a large impact on the temperature profile during solidification. This in turn affects the residual stress, which causes distortion in the built part.19 Fu et al.20 generated a three-dimensional model for the SLM process and concluded that the depth and volume of melt pool increase for higher laser power and lower scan speed. It was observed that, for a given combination of laser power and scan speed, the melt pool dimension increases towards the upper layers of the build.9 Considering the effect of the melt pool geometry on the properties of the final build, it is of utmost importance to develop a well-tested model that can predict the melt pool geometry for various laser power–scan speed combinations.

Because SLM and e-beam melting use a concentrated power source on a very small region, the temperatures in the process can easily exceed the melting temperature of the materials significantly. It is very feasible to even exceed the vaporization temperature of some of the alloying elements during the process, locally. Exceeding the vaporization temperature can cause evaporation of some of alloying elements. Evaporation of elements can change the composition of the final build. If the change in composition exceeds the permissible limit, it can adversely affect the properties (i.e., tensile strength, hardness, etc.).21 Mukherjee et al.21 developed an analytical model using the Langmuir equation for direct energy deposition and observed that chromium experiences the greatest amount of evaporation when processing Inconel 625. Khan et al.22 collected the condensate of vaporized elements using a quartz tube and examined the samples by x-ray analysis. They found out that manganese, iron, and chromium were the most volatile alloying elements during laser welding of AISI 202 stainless steels. Liu et al. predicted the vaporization rate of the Knudsen layer in laser keyhole welding using an analytical model and found out that the concentration of manganese changed significantly for stainless steel. Although the compositional change in laser welding is more pronounced because of the low welding speed and high laser power involved, the importance of determining the evaporation in SLM cannot be ignored, as higher laser powers and lower-melting materials have been used in this process lately.

The current study was conducted using Inconel 718 alloy, whose chemical composition consists of nickel (50–55%), chromium (17–21%), niobium (4.75–5.50%), molybdenum (2.80–3.30%), titanium (0.65–1.15%), aluminum (0.20–0.80%), cobalt (1.00%), carbon (0.08%), manganese (0.35%), silicon (0.35%), copper (0.30%), and iron (balance). Chromium and nickel have high vapor pressure at elevated temperatures. They also have high weight percentage in the alloy, thus making them more susceptible to evaporation compared with the other elements. A significant amount of work has been done on evaporation in laser welding, but the literature on the effect of evaporation in powder bed additive manufacturing is not adequate.

The temperature profile created during the interaction of the laser and powder bed is of great significance, as it impacts the melt pool geometry, which dictates the microstructure of the build. The majority of the literature characterizes the laser by a Gaussian beam, where the intensity of the laser is maximum at the center and decays exponentially as one goes radially outward. To model the process appropriately, the behavior of the laser must be implemented in such a way that its properties such as the beam quality factor, wavelength, and waist radius can be considered appropriately. The aim of this work is to present the laser–material interaction in such a way that the generated beam profile represents the actual beam in a more appropriate way. Marangoni flow was simulated with COMSOL multiphysics, where both heat transfer and computational fluid dynamics were combined. The temperature profile, melt pool size, and elemental evaporation were obtained from the simulation results. The temperature profile obtained from the simulation was compared with that of Gaussian beam profile. The bead geometry, which dictates the dimensional accuracy of the final build, was obtained using a level set method, then compared with experimental results. The evaporation rate of different alloying elements was also determined using the same temperature profile for different laser power–scan speed combinations.

Laser Heat Source

Most literature on modeling the laser beam melting process models the laser as a heat source on the surface of the material. The intensity of the heat source is typically considered to follow a Gaussian distribution, where the heat intensity is maximum at the middle of the beam and decreases exponentially as one goes radially outward. The aim of this work is to approach the laser–powder interaction equation in a way that represents the actual laser profile in a more comprehensible way. A Gaussian distributed laser beam is defined as follows23:

$$ I\left( {x,y,z} \right) = \frac{2P}{{\pi \times w\left( z \right)^{2} }} \times \exp \left[ { - \frac{{2 \times \left( {x - vt)^{2} + y^{2} } \right)}}{{w\left( z \right)^{2} }}} \right], $$

(1)

$$ w\left( z \right) = w_{0} \times {\text{sqrt}}\left[ {1 + \left( {\frac{\lambda \times z}{{\pi \times \left( {w_{0} } \right)^{2} }}} \right)^{2} } \right], $$

(2)

where w(z) is the beam radius at a depth z, w₀ is the beam waist radius, t is the laser scan time, and $\lambda$ is the laser wavelength. The beam waist is the location at which the radius of the beam is minimum. In most literature, the beam radius is assumed to be equal to $w_{0}$. A beam that follows a Gaussian profile is highly concentrated towards the focus of the beam, thus creating a very high temperature at that point. However, it was observed that the actual beam is not as highly focused as a Gaussian beam,24 making the temperature profile lower than the Gaussian one. For lasers with low power, the beam profile can be similar to a Gaussian beam, but the eccentricity of the beam profile increases with increasing laser power. To differentiate between a Gaussian or ideal beam and a non-Gaussian beam, a new parameter called the beam quality factor is used, denoted by M². The value of M² for an ideal or Gaussian beam is equal to 1, while it is more than 1 for a non-Gaussian beam. For high laser power, this value can reach up to 10 or more.25 With the introduction of this quality factor, the laser can be modeled in a more appropriate manner. The beam quality factor is defined as26

$$ M^{2} = {\text{BPP}} \times \frac{\pi }{\lambda }, $$

(3)

where BPP is the beam parameter product, viz. the product of the beam radius (w₀) and beam divergence (θ). A Yb fiber laser with a wavelength of 1064 nm is considered. Including the factor M², Eq. 2 can be rearranged as25

$$ w\left( z \right) = w_{0} \times {\text{sqrt}}\left[ {1 + \left( {\frac{{\lambda \times z \times M^{2} }}{{\pi \times \left( {w_{0} } \right)^{2} }}} \right)^{2} } \right]. $$

(4)

This equation is used herein to model the laser–powder interaction.

Modeling Technique

The modeling strategy consists of two sets of models. A three-dimensional finite element model is utilized to determine the temperature history through thermal modeling combined with fluid dynamic modeling inside the melt pool region. The second model is two dimensional, considering a cross-section of the material as the laser crosses a region. This 2D model is used to obtain the geometry and shape of the bead. The temperature history extracted from the 3D model is applied to the 2D model as the thermal load. The 2D model utilizes the level set method to obtain the bead geometry of the solidified part.

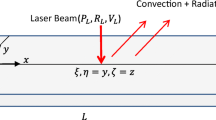
The 3D model and meshing are presented in Fig. 1a. As can be seen from this figure, there are three distinct regions in the model: the substrate made of stainless steel with thickness of 1 mm, upon which the process is completed, a 0.9-mm solid portion in the middle, which is melted and subsequently solidified, and 0.04 mm of freshly spread powder on the top, which is to be melted by the laser. The domains each have length of 9 mm and width of 3 mm. Symmetry in the Y direction is used to save computational time, so half of the model is built along that direction. Radiative boundary conditions are applied to the powder surface

$$ q = \varepsilon \times \sigma \times \left( {T^{\text{amb}} - T^{4} } \right), $$

(5)

where $\varepsilon$ = 0.87 is the surface emissivity,27$\sigma = 5.67 \times 10^{ - 8}$ W/m² K⁴ is called the Stefan–Boltzmann constant, $q$ is the heat flux, and $T^{\text{amb}}$ is the temperature of the surrounding atmosphere.

Fig. 1

(a) 3D model setup, boundary conditions, dimensions, and mesh to model temperature profile. (b) 2D model setup, boundary conditions, and mesh to model bead geometry

Adiabatic boundary conditions are applied to the bottom of the build plate and side domains.

The governing equations for energy, mass, and moment balance are respectively

$$ \rho C_{p} \frac{\partial T}{\partial t} + \rho C_{p} \varvec{u} \cdot \nabla T + \nabla \cdot q = Q, $$

(6)

$$ \rho \frac{\partial u}{\partial t} + \rho \left( {u \cdot \nabla } \right)u = \nabla \cdot \left[ { - pI + \mu \left( {\nabla {\text{u}} + \left( {\nabla {\text{u}}} \right)^{T} } \right)} \right] + F, $$

(7)

$$ p\nabla \left( u \right) = 0, $$

(8)

where u is the velocity field, Q is the heat source, T is the temperature field, $\rho$ is the density, C_p is the heat capacity, q is the heat flux, $\mu$ is the dynamic viscosity, p is the pressure, and F is the force due to fluid flow. The heat transport is associated with the energy equation, while the mass and moment account for the fluid flow in the molten region. In this work, the calculated Reynolds number around the melt pool varied from 0.00054 (lowest, 150 W/1200 mm/s) to 52.6 (highest, 300 W/200 mm/s) for different laser power–scan speed combinations. As the Reynolds number marking the transition from the laminar to turbulent region is Re = 600,28 a laminar model was used in the simulation. The Marangoni flow, which is caused by the variation of the surface tension within the melt pool, contributes significantly to the melt pool dynamics. The variation of the surface tension is caused by the temperature gradient within the melt pool. The Marangoni number is given by29

$$ {\text{Ma}} = \left( {\frac{\partial \gamma }{\partial T}} \right) \cdot \frac{{L \cdot\Delta T}}{\mu \cdot \alpha }, $$

(9)

where $\gamma$ is the surface tension, α is the thermal diffusivity, L is the length scale of the melt pool, and $\mu$ is the dynamic viscosity. The Marangoni number varied from 48.38 (lowest, 150 W/1200 mm/s) to 1.03 × 10⁴ (highest, 300 W/200 mm/s) for different laser power–scan speed combinations.

The final mesh had 170,630 elements and 292,856 number of degrees of freedom in total. Small cubic elements were used around the laser scanning path to conduct a good analysis of that part. Mesh sensitivity analysis was performed to ensure that high-quality results are obtained. A Core i7-7700 processor was used with memory of 32 GB. The parameters used in the simulation are laser power of 100 W, 150 W, 200 W, and 300 W; Scan speed of 200 mm/s, 700 mm/s, and 1200 mm/s; beam waist radius of 100 $\mu$m; and penetration depth of 140 $\mu$m.

Bead Geometry

A second model (Fig. 1b) was built to obtain the bead geometry of the build. The model was two dimensional, consisting of the melt pool, whose location was extracted from the first model, where the temperature was maximum and the outside nitrogen atmosphere. The interface between the melt pool and atmosphere was traced using a process called the level set method. The process started as soon as melting started and finished when the melt pool solidified under the effect of surface tension and gravity.

The level set method uses the following equations:

$$ \nabla GI \cdot \nabla GI + \gamma \cdot GI\left( {\nabla \cdot \nabla GI} \right) = \left( {1 + 2\sigma_{w} } \right)GI^{4} , $$

(10)

$$ \frac{\partial \emptyset }{\partial t} + \nabla \cdot \left( {u\emptyset } \right) = \lambda \nabla \cdot \left( { \in_{ls} \nabla \emptyset - \emptyset \left( {1 - \emptyset } \right)\frac{\nabla \emptyset }{{\left| {\nabla \emptyset } \right|}}} \right), $$

(11)

where GI is the reciprocal interface distance, $\gamma$ is the surface tension, $u$ is the velocity field, λ is the reinitialization parameter, $\in_{ls}$ is the parameter controlling the interface thickness, and $\emptyset$ is the level set variable. At the beginning of the level set method, $\emptyset$ is 0 for the molten region and 1 in the atmosphere, which gradually changes. The properties, i.e., viscosity and density, are different for the molten pool and atmosphere. Therefore, when the interface is crossed, there is an abrupt change in these properties, which means that there is a sudden change in $\emptyset$. This sudden change causes numerical instability in the simulation. To avoid this effect, the coding is done such that this property change takes place smoothly across a finite width in the interface region. This width is denoted by $\in_{ls}$. Reinitialization is used in the level set method to avoid numerical deterioration of the interface. As time progresses, there,may be some discontinuity in the zero-level set function $\emptyset$. To avoid this, $\emptyset$ is updated (reinitialized) after a certain number of iterations. λ determines the required amount of reinitialization or stabilization. If λ is too small, there might be oscillation in $\emptyset$, while too large a value of $\emptyset$ may make the interface move incorrectly with time. Hence, an optimized value of λ has to be used. The parameters used in this work are $\gamma_{m}$ = 0.018 N/m at melting temperature, λ = 0.4 m/s, and $\in_{ls}$ = 0.005 mm.30

Material Properties

Inconel 718 was used in this simulation, in the form of powder, molten metal, and solid metal. As the temperature changes, the properties are updated and changed as the phases of the material change. Powder is one of the most difficult materials to model. The properties of metallic powders are not readily available in literature; For example, the thermal conductivity of metallic powders is typically modeled using analytical or numerical models. However, most of these theoretical models are functions of many parameters. To avoid the variability of these models and model the powder materials realistically, actual thermal conductivity properties were obtained experimentally for this study. The experiments were conducted using an instrument called a transient plane source (TPS-2200). The TPS-2200 can quickly and accurately measure the thermal conductivity of a metallic powder through a nondestructive process. The thermal conductivity values obtained for a packing density of 5.46 g/cm³ were chosen for the present study. The temperature-dependent thermal conductivity of solid Inconel 718 and steel was taken from the work of Mills.31

The equation used to calculate the dynamic viscosity was taken from literature32

$$ \mu \,\left( {{\text{mPa}} \times {\text{s}}} \right) = 0.196{\text{e}}^{{\frac{5848}{T}}} . $$

(12)

The temperature-dependent specific heat and density values were imported from the work of Mills.31 The density of powder was chosen to be 5.46 g/cm³ with porosity of 0.3.

The surface tension was obtained from Ref. 14 as

$$ \gamma \left( T \right) = \gamma_{\text{m}} + {\text{d}}\gamma /{\text{d}}T \times \left( {T - T_{\text{m}} } \right). $$

(13)

The temperature-dependent absorptivity of Inconel 718 alloy was taken from literature, varying from 0.3 to 0.55.33

Modeling Elemental Evaporation

The vaporization flux of elements from an alloy is determined by the Langmuir equation34:

$$ J_{i} = \frac{{P_{i} }}{{\left( {2 \times\Pi \times R \times M_{i} \times T} \right)^{{\frac{1}{2}}} }} , $$

(14)

where $P_{i}$ is the vapor pressure of each element in the alloy, R = 8.314 J/mol K is the universal gas constant, $M_{i}$ is the molecular weight of element i, and T is the maximum temperature generated during the laser–material interaction. It was observed experimentally that the Langmuir equation overpredicts the vapor flux by 5–20%,34 as it does not take into account the mass that condenses back onto the surface. To remove this error, J_i is multiplied by $\beta =$ 0.05,21 a fractional value considering the condensation:

$$ J_{i} = \frac{{\beta \times P_{i} }}{{\left( {2 \times \varPi \times R \times M_{i} \times T} \right)^{{\frac{1}{2}}} }}. $$

(15)

The vapor pressure $P_{i}$ is obtained from the following equation35:

$$ \log \left( P \right) = A + \frac{B}{T} + C\log T + \frac{D}{{T^{3} }}, $$

(16)

where the constants A, B, C, and D are different for each element. It can be seen that the vapor pressure is heavily influenced by the melt pool temperature. The mass of the vaporized elements is

$$ \Delta m_{i} = J_{i} \times A_{s} \times t, $$

(17)

where $A_{\text{s}}$ is the area of the melt pool, as determined by COMSOL, and t is the laser scanning time.

The final concentration of the elements is21

$$ W_{f} = \frac{{V \times \rho \times W_{i} -\Delta m_{i} }}{{V \times \rho - \sum\Delta m_{i} }}, $$

(18)

where V is the volume of deposited material, $\rho$ is the density, and $W_{i}$ is the initial concentration of the element. The volume was determined by multiplying the cross-sectional area of the melt pool by the length of the track.

Results and Discussion

Temperature Profile

Figure 2a shows the temperature profile of non-Gaussian and Gaussian beams. The Gaussian beam generates a more localized temperature profile, which causes a higher temperature build-up at the center of the melt pool, as is evident from this figure. A comparatively more uniform distribution of heat, away from the center of the beam, is observed with the introduction of a beam quality factor, since it reduces the beam focus. As the quality factor distorts the behavior of an ideal Gaussian beam, the heat is no longer highly concentrated at the focus of the beam. With further increase of the quality factor (M²), deterioration of the beam quality is observed, which represents a more realistic beam nature. This emphasizes the fact that incorporating the M² factor is important to model the true interactive behavior of the material and laser.

Fig. 2

(a) Melt pool and temperature distribution for (i) Gaussian and (ii) non-Gaussian beam, (b) comparison of temperature profile for Gaussian and non-Gaussian beam versus experiment, (c) variation of temperature profile for various speeds and powers comparing Gaussian and non-Gaussian beam profiles

To validate the temperature profile, an alternate geometry was modeled with length of 60 mm, width of 5 mm, and height of 25 mm. The experiment was conducted with laser power of 180 W and scan speed of 600 mm/s.36 An MCS 640 thermal imager was used to measure the temperature at the laser–powder interaction zone. Figure 2b shows a comparison between the non-Gaussian and Gaussian beam model versus the experimental result. The profile obtained with the non- Gaussian beam was more similar to the experimental temperature profile, with a lower maximum temperature than the Gaussian beam. The spikes in the experimental data in the lower temperature range are due to the inability of the camera to measure temperature in the lower range. The laser profile could not be obtained from this specific literature. However, as the temperature profile of the non-Gaussian beam was similar to the experimental result, it can be expected that the laser profiles would agree as well.

Figure 2c presents the temperature profile of both the non-Gaussian and Gaussian beam for different laser power–scan speed combinations; all of them show a lower temperature profile for the non-Gaussian beam. Due to the high concentration, both the temperature and intensity are higher at the focus for the Gaussian model for all three combinations. For the 150 W/700 mm/s combination, the high speed allows a shorter time span of interaction between the laser and powder, which results in a lower intensity and temperature profile. On the other hand, the maximum temperature is higher for the 300 W/700 mm/s combination than 100 W/200 mm/s, due to the considerably higher power in the former combination despite the latter having a lower scan speed; this indicates that power plays the dominant role over scan speed for all combinations. The temperature exceeds 1443 K, the assumed melting point of Inconel 718, for all the laser power–scan speed combinations.

Bead Geometry

Figure 3a presents a graphical comparison between the bead geometry of the model and experiment. The experiment5 was conducted using an EOSINT M 280 machine. Twenty-four square Inconel 718 specimens having block dimensions of 25.4 mm × 25.4 mm × 4.0 mm were manufactured. Each specimen was fabricated using different sets of combinations of laser power and scan speed. The laser scanned 10 equally spaced lines to analyze the variations of the process parameters. Images of the cross-sectional area were taken to investigate the melt pool geometries.

Fig. 3

(a) Simulated and experimentally obtained bead cross-sections for laser power of 100 W and scan speed of 200 mm/s, (b) melt pool width comparison at scan speed of 1200 mm/s, and (c) bead height comparison at scan speed of 200 mm/s

The following paragraphs compare the bead geometry for the non-Gaussian beam with the M² factor, the Gaussian beam,4 and experimental results.

Table I presents a comparison of the width of the melt pool between the non-Gaussian and Gaussian beam models versus experimentally observed data. These results show that the results obtained with the non-Gaussian beam were more accurate than those obtained with the Gaussian beam. The temperature was lower around the melt pool for the non-Gaussian model, decreasing the width of the melt pool. The results obtained with the higher scan speed provided more accurate results for both models.

Table I Melt pool width

Bead heights could be obtained only for those experiments conducted at a scan speed of 200 mm/s. At higher scan speeds, the shape was partially distorted due to the balling effect. The comparison with experiment showed that the non-Gaussian beam model performed better than the Gaussian beam model in predicting the bead height; it is expected that the same trend would be observed in case of higher scan speed as well. It is observed that there is a considerable difference between the experimental and simulation results for the bead height for the scan speed of 200 mm/s. The experimentally measured values for the bead height at this speed are significantly greater than the layer thickness (40 µm), which leads this researcher to believe that some errors occurred when measuring the bead height and that the simulated results are reasonable (Table II).

Table II Bead height

Figure 3b and c show a comparison of the melt pool width and bead height at scan speed of 1200 mm/s and 200 mm/s, respectively, for the Gaussian model, non-Gaussian model, and experimental data.

For the melt pool depth, the results obtained using the Gaussian beams were slightly better than those obtained using the non-Gaussian beam (Table III).

Table III Melt pool depth

Composition Change

Figure 4a shows the concentration change for different elements for a constant power of 300 W and three different scan speeds, viz. 200 mm/s, 700 mm/s, and 1200 mm/s. It is evident that, for lower scan speeds, the composition change is the highest as the temperature is high for such combinations of laser power and scan speed. Consequently, the vapor pressure also increases considerably, which helps to evaporate the metals. In contrast, the laser does not have much time to interact with the surface in case of higher scan speed, resulting in very low concentration changes. The concentration change for chromium is highest, with a change of 0.2255%.

Fig. 4

Change in concentration of elements for (a) varying scan speed, (b) varying power

Figure 4b shows the concentration changes for the different elements for different powers at a scan speed of 200 mm/s. As the power is increased, the concentration change becomes more evident. Chromium and nickel undergo the maximum change in concentration. It can also be observed that only aluminum and iron exceed by a small amount the permissible limit set by ASTM for the 300 W/200 mm/s process parameter combination,37 while the results for the other elements lie well within the permissible range.

The calculated and experimental values for the final concentration are listed in Table IV. EDX was used to obtain the final concentrations experimentally. When the electron beam hits the sample, x-rays are generated, consisting of photons. Silicon/drift detectors were used to measure the energy of these photons. Data generated in this way consist of spectra with peaks corresponding to different elements. The heights of the peaks indicate the concentration of each element. The measured intensity for each element of the sample is affected by the composition of the whole sample. EDX software applies the ZAF (Z, atomic number; A, absorption; F, fluorescence) correction method to convert the raw intensity data to true intensity to calculate the elemental composition. Area mapping was conducted on different regions of the sample, and the average value was taken.

Table IV Comparison between experimental and calculated concentration

The calculated and experimental values of the final concentrations showed reasonable agreement except for aluminum. EDS does not provide good analysis of elements with low atomic number, so this inaccuracy for Al is reasonable. The errors for the other elements may be subject to several factors. The EDX mapping could be conducted on a wider range of areas to get a better result. Also, the detector could be placed at a different optimum angle with the sample to obtain accurate peaks from the sample. For the analytical calculation, a different value of $\beta = 0.05{-}0.2$ could have offered a better outcome, as the Langmuir equation overpredicts the vapor flux by 5–20%.

Conclusion

Two finite-element thermofluid models were generated to determine the temperature profile and melt pool geometry of a non-Gaussian beam. A non-Gaussian beam model was proposed to model the laser–material interaction accurately. The temperature profile obtained with the thermal model showed that the maximum temperature was lower for a non-Gaussian beam. The bead geometry was generated from the second model using the level set method. The melt pool width and bead height showed better correlation when using the non-Gaussian than Gaussian beam versus experimental values. The elemental evaporation was also determined using the temperature profile obtained from the 3D model. The concentration changes for the alloying elements were found to be more significant at higher laser power and lower scan speed. For lower powers and higher scan speeds, the change was insignificant. Chromium exhibited the maximum concentration change due to its higher vapor pressure at elevated temperature.