High-Resolution Viscous Terms Discretization and ILW Solid Wall Boundary Treatment for the Navier–Stokes Equations

Abstract

Robust numerical methods for CFD applications, such as WENO schemes, quickly evolved in the past few decades. Together with the Inverse Lax–Wendroff (ILW) procedure, WENO ideas were also applied in the boundary treatment. Those methods are known for their high-resolution property, i.e., good representation of nonlinear phenomena, which is an important property in solving challenging engineering problems. In light of that, the objective of this work is to present a review of well-established high-resolution numerical methods to solve the Euler equations and adapt the Navier–Stokes viscous terms discretization and boundary treatment. To test the modifications, we employed the positivity-preserving Lax–Friedrichs splitting, multi-resolution WENO scheme, third-order strong stability preserving Runge–Kutta time discretization, and ILW boundary treatment. The first problems were simple flows with analytical solutions for accuracy tests. We also tested the accuracy with nontrivial phenomena in the vortex flow. Oblique shock and complicated flow structures were captured in the Rayleigh–Taylor instability and flow past a cylinder. We showed the discretization and boundary treatment can handle non-constant viscosity, are high-order, high-resolution, and behave similarly to the well-established numerical methods. Furthermore, the methods discussed here can preserve symmetry and no approximations regarding the boundary layer were made. Therefore, the discretization and boundary treatment can be considered when solving direct numerical simulations.

1 Introduction

High-order and high-resolution numerical methods quickly evolved in the past few decades, either in the interior scheme or at the boundaries [1,2,3,4,5]. WENO is a robust class of schemes known for their high-resolution property and is popular for solving CFD problems with nonlinear phenomena and complex flow structures [3, 6,7,8]. Stall in aerodynamic profiles or turbomachinery blades, flow separation, side loads, mixing, combustion, and detonation are examples of challenging engineering problems that demand robust numerical solvers [9,10,11,12,13,14,15,16]. Moreover, LES and DNS computations are becoming more feasible and require restricted time and space scales, which can be attained through high-resolution methods [17,18,19].

Depending on the phenomena, one may need three-dimensional discretization, compressibility and viscous effects, small grid sizes, and small time steps [13, 17, 18]. The Euler equations can be used, e.g., to solve compressible fluid flows containing shock waves. However, it will not be able to model the boundary layer and related phenomena. By adding viscous terms to the Euler equations, one reaches the so-called Navier–Stokes equations, which are capable of modeling challenging engineering problems.

When solving the Navier–Stokes equations, a boundary layer will develop near solid walls. The boundary layer or the turbulent flow near the wall has a great impact in academical and industrial applications [20]. To maintain the interior scheme high-resolution, the boundary conditions shall be properly imposed at the walls. Among the boundary imposition strategies, the Inverse Lax–Wendroff (ILW) is distinguished by its ability to be applied to rectangular meshes on arbitrary domains, easing the mesh construction and spatial discretization [2, 5, 21, 22].

While reviewing well-established numerical methods to solve the Euler equations, we will present modifications to add the viscous contribution and we will introduce a new way of discretizing the first-order derivatives of the viscous terms using already-available information from the inviscid fluxes. Taking advantage of mixed discretization for the convective and viscous terms has already been considered for, e.g., finite element methods [23, 24]. Moreover, we will show how to adapt the ILW boundary treatment at solid walls without using rotation, something that has not been experimented before in the literature for the Navier–Stokes equations. This is found in Sect. 2.2.

To assess these modifications, in Sect. 3 we will solve simple 2D flows, as well as the vortex flow, the Rayleigh–Taylor instability, and the supersonic flow past a cylinder. To do that, we will employ the positivity-preserving Lax–Friedrichs splitting [1], multi-resloution central WENO [8], WENO-type extrapolation [21], and ILW boundary treatment [2, 5, 21, 22].

2 Numerical Methods

2.1 Discretization

In this paper, we are interested in the following set of equations

$$\begin{aligned} {\varvec{U}}_t+{\varvec{F}}({\varvec{U}})_x+{\varvec{G}} ({\varvec{U}})_y=\varvec{S_1}_x+\varvec{S_2}_y+{\varvec{S}} ({\varvec{U}}), \end{aligned}$$

(1)

where

$$\begin{aligned} {\varvec{U}}= & {} \begin{bmatrix} \rho \\ \rho u\\ \rho v\\ E \end{bmatrix}, \; {\varvec{F}}({\varvec{U}}) = \begin{bmatrix} \rho u\\ \rho u^2+p\\ \rho u v\\ u(E+p) \end{bmatrix},\end{aligned}$$

(2)

$$\begin{aligned} {\varvec{G}}({\varvec{U}})= & {} \begin{bmatrix} \rho v\\ \rho u v\\ \rho v^2+p\\ v(E+p) \end{bmatrix}, \varvec{S_1} = \begin{bmatrix} 0\\ \tau _{xx}\\ \tau _{xy}\\ {\epsilon _v}_x+\dfrac{\mu }{Pr(\gamma -1)}\dfrac{\partial (a^2)}{\partial x} \end{bmatrix},\end{aligned}$$

(3)

$$\begin{aligned} \varvec{S_2}= & {} \begin{bmatrix} 0\\ \tau _{xy}\\ \tau _{yy}\\ {\epsilon _v}_y+\dfrac{\mu }{Pr(\gamma -1)}\dfrac{\partial (a^2)}{\partial y} \end{bmatrix}, \end{aligned}$$

(4)

the source term ${\varvec{S}}({\varvec{U}})$ depends on the problem, and $\rho$, $u$, $v$, and $p$ are the density, $x$ and $y$ velocities, and pressure. $E$, $\varvec{\tau }$, $\varvec{\epsilon _v}$, and $a$ are the the total energy per unit of volume, viscous tensor, viscous dissipation rate, and speed of sound, given as

$$\begin{aligned} E= & {} \frac{p}{\gamma -1}+\frac{\rho }{2}(u^2+v^2), \; \tau _{xx}=\mu \left( \frac{4}{3}\frac{\partial u}{\partial x}-\frac{2}{3}\frac{\partial v}{\partial y}\right) \end{aligned}$$

(5)

$$\begin{aligned} \tau _{xy}= & {} \mu \left( \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right) , \; \tau _{yy}=\mu \left( \frac{4}{3}\frac{\partial v}{\partial y}-\frac{2}{3}\frac{\partial u}{\partial x}\right) \end{aligned}$$

(6)

$$\begin{aligned} {\epsilon _v}_x= & {} u\tau _{xx}+v\tau _{xy}, \; {\epsilon _v}_y=u\tau _{xy}+v\tau _{yy}, \; a=\sqrt{\frac{\gamma p}{\rho }}, \end{aligned}$$

(7)

where $\gamma =1.4$, $\mu =5E-5\ Pa\cdot s$, and $Pr=0.7$ are the specific heat ratio, absolute viscosity, and the Prandtl number for the air. Unless explicitly stated, these properties will be used in the test problems.

We discretize the fluxes ${\varvec{F}}$ and ${\varvec{G}}$ with the following conservative finite difference scheme [25]:

$$\begin{aligned} \begin{aligned} \frac{d{\varvec{U}}_{i,j}(t)}{dt}=-\frac{1}{\Delta x}\left( \hat{{\varvec{F}}}_{i+1/2,j}-\hat{{\varvec{F}}}_{i-1/2,j}\right) -\\ \frac{1}{\Delta y}\left( \hat{{\varvec{G}}}_{i,j+1/2}-\hat{{\varvec{G}}}_{i,j-1/2}\right) , \end{aligned} \end{aligned}$$

(8)

where $\Delta x=\Delta y=\text {constant}$ is the mesh size.

To compute the numerical flux, we use the positivity-preserving Lax–Friedrichs splitting [1]

$$\begin{aligned} {\varvec{F}}^{\pm }({\varvec{U}}_{i,j})=\frac{1}{2} \left( {\varvec{U}}_{i,j}\pm \frac{{\varvec{F}} ({\varvec{U}}_{i,j})}{\alpha _x}\right) , \end{aligned}$$

(9)

where $\alpha _x=\underset{{\varvec{U}}}{\max }\ \underset{m}{\max }|\lambda _m({\varvec{U}})|$ is computed for the whole domain [25], $\lambda _m$ are the eigenvalues of the Jacobian, and $m=1,\dots ,4$ is the $m$-th vector component.

Through a local characteristic decomposition, we have

$$\begin{aligned} {\varvec{H}}_{\pm }={\varvec{L}} \left( {\varvec{U}}_{i+1/2,j}\right) {\varvec{F}}^\pm \left( {\varvec{U}}_{i,j}\right) , \end{aligned}$$

(10)

where ${\varvec{U}}_{i+1/2,j}=\left( {\varvec{U}}_{i,j}+{\varvec{U}}_{i+1,j}\right) /2$ is an average state and ${\varvec{L}}$ are the left eigenvectors.

As in [1], we approximate $({\varvec{H}}_+)_{i+1/2,j}^{\pm }$ with ${\varvec{H}}_+$ and a multi-resolution WENO reconstruction. The same is valid for $({\varvec{H}}_-)_{i+1/2,j}^{\pm }$ with ${\varvec{H}}_-$. Then, we transform back with the right eigenvectors, ${\varvec{R}}$,

$$\begin{aligned} \begin{aligned} \left( {\varvec{F}}_+\right) _{i+1/2,j}^-={\varvec{R}} \left( {\varvec{U}}_{i+1/2,j}\right) ({\varvec{H}}_+)_{i+1/2}^-,\\ \left( {\varvec{F}}_-\right) _{i+1/2,j}^+={\varvec{R}} \left( {\varvec{U}}_{i+1/2,j}\right) ({\varvec{H}}_-)_{i+1/2}^+, \end{aligned} \end{aligned}$$

(11)

and form the numerical flux [1]

$$\begin{aligned} \hat{{\varvec{F}}}_{i+1/2,j}=\alpha _x\left[ \left( {\varvec{F}}_+\right) _{i+1/2,j}^-- \left( {\varvec{F}}_-\right) _{i+1/2,j}^+\right] . \end{aligned}$$

(12)

We remark that the procedure is analogous for the ${\varvec{G}}$ flux. Among other choices, the multi-resolution WENO of [4, 8] can reach machine error for steady non-smooth problems and preserve symmetry. Symmetry breaking issues are addressed, e.g., in [3, 26]. We compute the reconstruction polynomials for a fixed $j$ with $r=-s,\dots ,s$, $s=1,\dots ,2$, [4, 25]

$$\begin{aligned} q_1(\xi )=h_{i,j}, \end{aligned}$$

(13)

and

$$\begin{aligned} \int _r^{r+1}q_{s+1}(\xi )\,d\xi =h_{i+r,j}. \end{aligned}$$

(14)

Next, we obtain equivalent expressions for the reconstruction polynomials [4]

$$\begin{aligned} p_1(\xi )=q_1(\xi ), \quad p_{r}(\xi )=\frac{q_{r}(\xi )}{\Gamma _{r,r}}-\sum _{s=1}^{r-1}\frac{\Gamma _{s,r}}{\Gamma _{r,r}}p_{s}(\xi ), \end{aligned}$$

(15)

with $s=1,\dots ,r$, $r=2,\dots ,3$, and

$$\begin{aligned} \Gamma _{s,r}=\frac{{\overline{\Gamma }}_{s,r}}{\sum _{l=1}^{r}{\overline{\Gamma }}_{l,r}}, \quad {\overline{\Gamma }}_{s,r}=10^{s-1}. \end{aligned}$$

(16)

The smoothness indicators are obtained through [4, 8]:

$$\begin{aligned} \beta _{r}= & {} \sum _{\alpha =1}^{2(r-1)}\int _0^1\left[ \frac{d^\alpha p_r(\xi )}{d\xi ^\alpha }\right] ^2\,d\xi ,\quad r=2,\dots ,3, \end{aligned}$$

(17)

$$\begin{aligned} \varsigma _0= & {} (h_{i,j}-h_{i-1,j})^2,\quad \varsigma _1=(h_{i+1,j}-h_{i,j})^2, \end{aligned}$$

(18)

$$\begin{aligned}&\begin{aligned} {\overline{\Gamma }}_{0,1} = {\left\{ \begin{array}{ll} 1 &{} \varsigma _0\ge \varsigma _1 \\ 10, &{} \text {otherwise} \end{array}\right. },\quad {\overline{\Gamma }}_{1,1}=11-{\overline{\Gamma }}_{0,1}, \\ \Gamma _{0,1}=\frac{{\overline{\Gamma }}_{0,1}}{{\overline{\Gamma }}_{0,1} +{\overline{\Gamma }}_{1,1}},\quad \Gamma _{1,1}=1-\Gamma _{0,1}, \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned}&\begin{aligned} \sigma _0=\Gamma _{0,1}\left( 1+\frac{|\varsigma _0-\varsigma _1|^2}{\varsigma _0 +\epsilon }\right) ,\\ \sigma _1=\Gamma _{1,1}\left( 1+\frac{|\varsigma _0-\varsigma _1|^2}{\varsigma _1 +\epsilon }\right) , \sigma =\sigma _0+\sigma _1, \end{aligned} \end{aligned}$$

(20)

$$\begin{aligned} \beta _1= & {} \frac{1}{\sigma ^2}\big [\sigma _0(h_{i,j}-h_{i-1,j}) +\sigma _1(h_{i+1,j}-h_{i,j})\big ]^2, \end{aligned}$$

(21)

where $\epsilon =1E-06$.

The nonlinear weights are [4, 7]:

$$\begin{aligned} \omega _r= & {} \frac{\alpha _r}{\sum _{s=1}^3\alpha _{s}}, \end{aligned}$$

(22)

$$\begin{aligned} \alpha _{r}= & {} \Gamma _{r,3}\left[ 1+\left( \frac{\tau }{\beta _{r}+\epsilon }\right) \right] , \end{aligned}$$

(23)

$$\begin{aligned} \tau= & {} \left( \frac{\sum _{s=1}^{2}\left| \beta _{3}-\beta _{s}\right| }{2}\right) ^{2}. \end{aligned}$$

(24)

Finally, the multi-resolution WENO reconstruction is

$$\begin{aligned} h_{i+1/2,j}^-=\sum _{r=1}^3\omega _{r} \, p_r(1). \end{aligned}$$

(25)

The reconstruction for a fixed $i$ is analogous. For the viscous terms, $\varvec{S_1}$ and $\varvec{S_2}$, we have the advantage of $\left( {\varvec{F}}_{\pm }\right) _{i+1/2,j}^{\pm }$ being already computed. Therefore, we use the numerical flux approximation regarding the flux splitting (9),

$$\begin{aligned} \hat{{\varvec{U}}}_{i+1/2,j}=\left( {\varvec{F}}_+\right) _{i+1/2,j}^- +\left( {\varvec{F}}_-\right) _{i+1/2,j}^+. \end{aligned}$$

(26)

Then,

$$\begin{aligned}&({\varvec{U}}_x)_{i,j}=\frac{1}{\Delta x}\left( \hat{{\varvec{U}}}_{i+1/2,j} -\hat{{\varvec{U}}}_{i-1/2,j}\right) , \nonumber \\&\quad \frac{\partial {\varvec{W}}}{\partial {\varvec{U}}} = \begin{bmatrix} 1 &{} 0 &{} 0 &{} 0 \\ -u/\rho &{} 1/\rho &{} 0 &{} 0 \\ -v/\rho &{} 0 &{} 1/\rho &{} 0 \\ \frac{1}{2}(\gamma -1)(u^2+v^2) &{} (1-\gamma )u &{} (1-\gamma )v &{} \gamma -1 \\ \end{bmatrix}, \end{aligned}$$

(27)

$$\begin{aligned}&({\varvec{W}}_x)_{i,j}=\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}({\varvec{U}}_x)_{i,j}. \end{aligned}$$

(28)

Using the same procedure for the $y$-direction derivatives, we can compute $\varvec{S_1}$ and $\varvec{S_2}$. The viscous terms derivatives are then approximated with a central fourth-order discretization, e.g.,

$$\begin{aligned} (\varvec{S_1}_x)_{i,j}=\frac{\varvec{S_1}_{i-2,j}-8 \varvec{S_1}_{i-1,j}+8\varvec{S_1}_{i+1,j}-\varvec{S_1}_{i+2,j}}{12\Delta x}. \end{aligned}$$

(29)

One should notice that this will demand approximations to $\varvec{S_1}$ and $\varvec{S_2}$ at the ghost points.

Once the spatial approximation, $L({\varvec{U}})$, is computed for all interior points, we use the third-order SSP Runge–Kutta to integrate from time step $n$ to $n+1$ [25]:

$$\begin{aligned}&{U_m}^{(1)}={U_m}^n+\Delta t L({U_m}^n), \end{aligned}$$

(30)

$$\begin{aligned}&{U_m}^{(2)}=\frac{3}{4}{U_m}^n+\frac{1}{4}{U_m}^{(1)}+\frac{1}{4} \Delta t L({U_m}^{(1)}), \end{aligned}$$

(31)

$$\begin{aligned}&{U_m}^{n+1}=\frac{1}{3}{U_m}^n+\frac{2}{3}{U_m}^{(2)}+\frac{2}{3}\Delta t L({U_m}^{(2)}). \end{aligned}$$

(32)

The time step, $\Delta t$, can be computed as [2] ($\Delta ={\min \left( {\Delta x},{\Delta y}\right) }$):

$$\begin{aligned} \Delta t=\min \!\left[ \frac{CFL}{\frac{\alpha _x}{\Delta x}+\frac{\alpha _y}{\Delta y}+\frac{6\alpha _d({\Delta x}^2+{\Delta y}^2)}{{\Delta x}^2{\Delta y}^2}}, \, \Delta ^{5/3}\right] , \end{aligned}$$

(33)

where $\alpha _x$ and $\alpha _y$ are the same as in (9) for the $x$- and $y$-direction, and $\alpha _d$ is the absolute largest eigenvalue for the diffusive terms.

2.2 Boundary Conditions

The boundary conditions will be handled with the ILW procedure regarding [2, 5, 21, 22]. We use the 1D WENO-type extrapolation of [21]. Here, we present a generic coordinate, $\eta$, and construct polynomial approximations, $p(\eta )$, for each one of the five candidate substencils

$$\begin{aligned} S_r=\{\eta _0,\dots ,\eta _r\},\quad r=0,\dots ,4. \end{aligned}$$

(34)

The nonlinear weights are [6, 21]:

$$\begin{aligned} \omega _r=\frac{\alpha _r}{\sum _{s=0}^4\alpha _s},\quad \alpha _r=\frac{d_r}{(\epsilon +\beta _r)},\quad r=0,\dots ,4, \end{aligned}$$

(35)

with

$$\begin{aligned} d_r={\Delta \eta }^{4-r},\quad \text {for}\quad r=0,\dots ,3,\quad d_4=1-\sum _{r=0}^3d_r, \end{aligned}$$

(36)

where $\Delta \eta$ is the generic coordinate mesh size. For instance, it is equal to $\Delta y$ when extrapolating in the $y$-direction.

The smoothness indicators are computed with $r=1,\dots ,4$, [5]:

$$\begin{aligned} \beta _0&= {\Delta \eta }^2, \end{aligned}$$

(37)

$$\begin{aligned} \beta _r&= \sum _{l=1}^r\Delta \eta ^{2l-1}\int _{\eta _0-\Delta \eta /2}^{\eta _0+\Delta \eta /2} \left( \frac{d^l}{d\eta ^l}p_r(\eta )\right) ^2\,d\eta . \end{aligned}$$

(38)

The 1D WENO-type extrapolation is then given by

$$\begin{aligned} \Big \{\partial _\eta ^{(l)}p(\eta )\Big \}_{l=0}^4=\sum _{r=0}^4\omega _r \frac{d^l}{d\eta ^l}p_r(\eta ). \end{aligned}$$

(39)

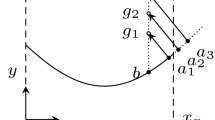
Now, suppose we want to impose boundary conditions at $\eta _0 = (x_0,y_0)$ at the wall, presented in Fig. 1. For the Navier–Stokes equations, we are interested in two situations: known wall temperature and heat flux. At the wall, the normal velocity component is zero and, because of the non-slip condition, the tangent velocity component will match the wall velocity.

Fig. 1

Region near a wall

2.2.1 Known Wall Temperature

For a known wall temperature, we can write

$$\begin{aligned} p=\rho RT_\text {wall},\quad v=v_\text {wall},\quad u=u_\text {wall}, \end{aligned}$$

(40)

where $R$ is the gas constant.

We now adapt the ILW procedure of [5] to impose the boundary conditions regarding [2, 22]. We let the detailed algebra for the Appendix and rewrite (1) as

$$\begin{aligned} \begin{aligned}&{\varvec{U}}_t + {\varvec{F}}({\varvec{U}})_x + {\varvec{G}}'({\varvec{U}}){\varvec{U}}_y = \varvec{\Psi _1}{\varvec{U}}_{xx}\\&\quad + \varvec{\Psi _2}{\varvec{U}}_{yy} + \varvec{\Psi _3} {\varvec{U}}_{xy} + {\varvec{N}}. \end{aligned} \end{aligned}$$

(41)

It is advisable to consider the general convection-diffusion case because it is a combination of both phenomena. For that, we use a convex combination where each contribution can be adjusted via previously defined parameters [2]. We diagonalize the matrices in front of the first and second $y$-direction derivatives and write

$$\begin{aligned}&{\varvec{V}}={\varvec{L}}{\varvec{U}},\quad \varvec{\Lambda }=\text {diag}{\left( v-a,v,v,v+a\right) }, \end{aligned}$$

(42)

$$\begin{aligned}&{\varvec{V}}_d={\varvec{L}}_d{\varvec{U}},\quad \varvec{\Lambda }_d=\text {diag}{\left( 0,\frac{\mu }{\rho },\frac{4\mu }{3\rho }, \frac{\gamma \mu }{Pr\rho }\right) }, \end{aligned}$$

(43)

where the subscript $d$ denotes “diffusive”. One may refer to the Appendix for the diffusive eigenvectors.

If we use (43) to rewrite (41) we will also be able to get a scalar hyperbolic equation and a parabolic system, as in [2]. Therefore, the same conclusions apply. As in [2], we can write

$$\begin{aligned} {\varvec{B}} = {\varvec{L}}_d{\varvec{G}}'({\varvec{U}}){\varvec{R}}_d = \begin{bmatrix} v &{} 0 &{} \displaystyle -\frac{a}{\gamma } &{} 0\\ 0 &{} v &{} 0 &{} 0\\ -a &{} 0 &{} v &{} -a\\ 0 &{} 0 &{} \displaystyle -\frac{a}{\gamma }(\gamma -1) &{} v \\ \end{bmatrix}. \end{aligned}$$

(44)

We also define [2]

$$\begin{aligned} b_1= & {} (B_{11}^2+B_{12}^2+B_{13}^2+B_{14}^2){\Delta y}^2,\nonumber \\ \epsilon _1= & {} 3({\lambda _d}_2^2+{\lambda _d}_3^2+{\lambda _d}_4^2), \alpha _1=\frac{b_1}{b_1+\epsilon _1} \end{aligned}$$

(45)

$$\begin{aligned} b_2= & {} \frac{1}{3}\left( b_1+b_3+b_4\right) ,\nonumber \\ \epsilon _2= & {} 9{\lambda _d}_2^2, \alpha _2=\frac{b_2}{b_2+\epsilon _2}, \end{aligned}$$

(46)

$$\begin{aligned} b_3= & {} (B_{31}^2+B_{32}^2+B_{33}^2+B_{34}^2){\Delta y}^2,\nonumber \\ \epsilon _3= & {} 9{\lambda _d}_3^2, \alpha _3=\frac{b_3}{b_3+\epsilon _3}, \end{aligned}$$

(47)

$$\begin{aligned} b_4= & {} (B_{41}^2+B_{42}^2+B_{43}^2+B_{44}^2){\Delta y}^2,\nonumber \\ \epsilon _4= & {} 9{\lambda _d}_4^2, \alpha _4=\frac{b_4}{b_4+\epsilon _4}. \end{aligned}$$

(48)

With $\alpha _m$, $m=1,\dots ,4$, and $k=0,\dots ,4$, we have the following convex combination of convection and diffusion terms [2]

$$\begin{aligned} \partial _y^{(k)}(V_m)_{cc}=\alpha _m\partial _y^{(k)}(V_m)_c+(1-\alpha _m) \partial _y^{(k)}(V_m)_d. \end{aligned}$$

(49)

We now discuss how convection and diffusion terms are obtained. Starting with $\partial _y^{(k)}{\varvec{V}}_c$, we assess the eigenvalues signs and the direction. Regarding Fig. 1, $\lambda _1<0$, $\lambda _{2,3}\approx 0$, and $\lambda _4>0$. Therefore, we must impose the boundary conditions on the fourth characteristic variable. To form the eigensystem, $\partial _y^{(0)}U_1$ is approximated at the boundary with the WENO-type extrapolation and

$$\begin{aligned} \begin{aligned} (U_1)_{\eta _0}=\partial _y^{(0)}U_1,\quad (U_2)_{\eta _0}=u_\text {wall}\partial _y^{(0)}U_1,\\ (U_3)_{\eta _0}=v_\text {wall}\partial _y^{(0)}U_1,\\ (U_4)_{\eta _0}=\frac{\partial _y^{(0)}U_1RT_\text {wall}}{\gamma -1} +\frac{\partial _y^{(0)}U_1}{2}(u_\text {wall}^2+v_\text {wall}^2). \end{aligned} \end{aligned}$$

(50)

With ${\varvec{U}}_{\eta _0}$, we compute ${\varvec{R}}$, $\varvec{\Lambda }$, and ${\varvec{L}}$. Next, we do a local characteristic decomposition on $S_a=\{\eta _1,\eta _2,\eta _3,\eta _4,\eta _5\}$

$$\begin{aligned} {\varvec{V}}={\varvec{L}}{\varvec{U}}, \end{aligned}$$

(51)

and use the WENO-type extrapolation to obtain $\{\partial _y^{(l)}{\varvec{V}}\}_{l=0}^{4}$ at the boundary.

We remark that if the $S_a$ points are outside the computational domain, one can use the least squares strategy with WENO-type extrapolation to approximate them. Details of this strategy will be presented next.

We first update $\partial _y^{(0)}(U_1)$ with

$$\begin{aligned} \begin{aligned}&\partial _y^{(0)}(V_1)=\partial _y^{(0)}(U_1)\Bigg [l_{11}+u_\mathrm {wall}l_{12}\\&+ v_\mathrm {wall}l_{13}+l_{14}\left( \frac{RT_\mathrm {wall}}{\gamma -1} +\dfrac{u_\mathrm {wall}^2+v_\mathrm {wall}^2}{2}\right) \Bigg ]. \end{aligned} \end{aligned}$$

(52)

Then,

$$\begin{aligned} \begin{aligned}&\partial _y^{(0)}(U_2)=u_\mathrm {wall}\partial _y^{(0)}(U_1),\quad \partial _y^{(0)} (U_3)=v_\mathrm {wall}\partial _y^{(0)}(U_1),\\&\quad \partial _y^{(0)}(U_4)=\frac{\partial _y^{(0)}(U_1)RT_\mathrm {wall}}{\gamma -1} +\frac{\partial _y^{(0)}(U_1)}{2}(u_\mathrm {wall}^2+v_\mathrm {wall}^2). \end{aligned} \end{aligned}$$

(53)

With the ILW, we update

$$\begin{aligned} \begin{aligned}&\partial _y^{(1)}V_4=\frac{-(U_1)_t-(F_1)_x+({{S_1}}_1)_x+ \partial _y^{(1)}{S_2}_1}{r_{14}(v_\mathrm {wall}+a)}\\&\quad -\frac{r_{11}(v_\mathrm {wall}-a)\partial _y^{(1)} V_1+r_{12}v_\mathrm {wall}\partial _y^{(1)}V_2+r_{13}v_\mathrm {wall} \partial _y^{(1)}V_3}{r_{14}(v_\mathrm {wall}+a)}. \end{aligned} \end{aligned}$$

(54)

With $\partial _y^{(k)}{\varvec{V}}$, the conservative variable derivatives are

$$\begin{aligned} \{\partial _y^{(l)}{\varvec{U}}\}_{l=1}^4={\varvec{R}}\{\partial _y^{(l)} {\varvec{V}}\}_{l=1}^4. \end{aligned}$$

(55)

Then,

$$\begin{aligned} \{\partial _y^{(l)}{\varvec{V}}_c\}_{l=0}^4={\varvec{L}}_d\{\partial _y^{(l)} {\varvec{U}}\}_{l=0}^4, \end{aligned}$$

(56)

where ${\varvec{R}}_d$, $\varvec{\Lambda }_d$, and ${\varvec{L}}_d$ are also obtained with ${\varvec{U}}_{\eta _0}$.

As one can see in (54), approximations to the $x$-direction inviscid flux and viscous terms first derivatives are needed. We now address how to obtain high-order approximations to the derivatives, matrices, nonlinear terms, fluxes, and viscous terms. We remark that ${\varvec{U}}_t$ are part of the known boundary conditions, which in this work are zero because the flows are steady.

We have ${\varvec{U}}$ in the vicinity of $\eta _0$ and we use it to obtain 2D least square polynomials, $P_r$, with $r=1,\ldots ,4$. One should notice that the polynomial must be obtained for each ${\varvec{U}}$ component separately. To compute $P_r$, we follow the procedure of [22], i.e., we start with the nearest $(r+1)^2$ interior points to $\eta _0$ and add points if the matrix rank is deficient. After obtaining the polynomials, we approximate ${\varvec{U}}_x$, ${\varvec{U}}_y$, and ${\varvec{U}}_{xx}$ on $S_a$ in different substencils [5].

For instance, for one ${\varvec{U}}_x$ component

$$\begin{aligned} S_0= & {} \{0\}, \quad S_1 = \{P_1(\eta _1)_x,P_1(\eta _2)_x\}, \end{aligned}$$

(57)

$$\begin{aligned} S_2= & {} \{P_2(\eta _1)_x,P_2(\eta _2)_x,P_2(\eta _3)_x\}, \end{aligned}$$

(58)

$$\begin{aligned} S_3= & {} \{P_3(\eta _1)_x,P_3(\eta _2)_x,P_3(\eta _3)_x,P_3(\eta _4)_x\}, \end{aligned}$$

(59)

$$\begin{aligned} S_4= & {} \{P_4(\eta _1)_x,P_4(\eta _2)_x,P_4(\eta _3)_x,P_4(\eta _4)_x,P_4(\eta _5)_x\}. \end{aligned}$$

(60)

With ${\varvec{U}}$ and ${\varvec{U}}_x$, we compute ${\varvec{F}}({\varvec{U}})_x$ on those different substencils. Then, we use the WENO-type extrapolation to approximate $\partial _y^{(0)}{\varvec{F}}({\varvec{U}})_x$ at $\eta _0$. For the $y$-direction flux, we compute ${\varvec{G}}({\varvec{U}})$ on $S_a$ and approximate $\{\partial _y^{(l)}{\varvec{G}}({\varvec{U}})\}_{l=0}^4$ with the WENO-type extrapolation. With similar ideas, $\{\partial _y^{(l)}{\varvec{U}}_x\}_{l=0}^1$ and $\partial _y^{(0)}{\varvec{U}}_{xx}$ are also approximated at $\eta _0$.

$\varvec{\Psi }_1$, $\varvec{\Psi }_2$, $\varvec{\Psi }_3$, and other matrices for the diffusive terms are obtained with the approximated derivatives and $\partial _y^{(0)}{\varvec{U}}$, i.e., with WENO-type extrapolation. The nonlinear terms can now be computed with the Appendix formulae. Then,

$$\begin{aligned} \varvec{S_1}_x=\varvec{\psi _1}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(1)}{\varvec{U}}_x+\varvec{\psi _2}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(0)}{\varvec{U}}_{xx}+\varvec{N_1}. \end{aligned}$$

(61)

Finally, we compute $\varvec{S_2}$ on $S_a$ with

$$\begin{aligned} {\varvec{W}}_x=\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_x,\quad {\varvec{W}}_y=\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_y, \end{aligned}$$

(62)

and approximate $\{\partial _y^{(l)}\varvec{S_2}\}_{l=0}^4$ at $\eta _0$ with the WENO-type extrapolation.

For the diffusive terms, we also perform a decomposition on $S_a$

$$\begin{aligned} {\varvec{V}}_d={\varvec{L}}_d{\varvec{U}}, \end{aligned}$$

(63)

and use the WENO-type extrapolation to obtain $\{\partial _y^{(l)}{\varvec{V}}_d\}_{l=0}^{4}$ at the boundary.

As stated in [2], the number of boundary conditions depends on the normal velocity sign and the coordinate direction. In our case, a positive velocity $v$ is oriented towards the computational domain. Therefore, for $v>0$ we shall impose four boundary conditions and three for $v\le 0$.

Particularly, if the wall is not moving both velocities are zero $(u_\mathrm {wall}=v_\mathrm {wall}=0)$ regardless of its inclination. Therefore, we only need to impose three boundary conditions and the local coordinate system and transformation of the equations are not required. This is advantageous because the number of least squares approximations is reduced, as discussed in [22]. Then, the conservative variables at the boundary can be updated with

$$\begin{aligned} \begin{aligned}&\partial _y^{(0)}(V_1)_d=\partial _y^{(0)}(U_1)_d\Bigg [{l_d}_{11}+u_\mathrm {wall}{l_d}_{12}\\&\quad +v_\mathrm {wall}{l_d}_{13}+{l_d}_{14}\left( \dfrac{RT_\mathrm {wall}}{\gamma -1} +\dfrac{u_\mathrm {wall}^2+v_\mathrm {wall}^2}{2}\right) \Bigg ],\\&\quad \partial _y^{(0)}(U_2)_d=\partial _y^{(0)}(U_1)_du_\mathrm {wall},\\&\quad \partial _y^{(0)}(U_3)_d=\partial _y^{(0)}(U_1)_dv_\mathrm {wall},\\&\quad \partial _y^{(0)}(U_4)_d=\partial _y^{(0)}(U_1)_d\left( \frac{RT_\mathrm {wall}}{\gamma -1}+\frac{u_\mathrm {wall}^2+v_\mathrm {wall}^2}{2}\right) . \end{aligned} \end{aligned}$$

(64)

For stability, we compute

$$\begin{aligned} \begin{aligned}&\partial _y^{(0)}(V_m)_d = {l_d}_{m1}\partial _y^{(0)}U_1+{l_d}_{m2}\partial _y^{(0)}U_2+{}\\&\quad {l_d}_{m3}\partial _y^{(0)}U_3+{l_d}_{m4}\partial _y^{(0)}U_4, \quad m=2,3,4. \end{aligned} \end{aligned}$$

(65)

Then, we perform slightly modifications on the WENO-type extrapolation and its polynomials, and use the stencil $S_b=\{\eta _0,\eta _1,\eta _2,\eta _3,\eta _4\}$ to compute $\{\partial _y^{(l)}(V_d)_m\}_{l=1}^{4}$ for $m=2,3,4$ at the boundary. One should notice that $S_b$ have four substencils and the first one have two points, $\eta _0$ and $\eta _1$. Now, $d_r={\Delta x}^{4-r}$ for $r=0,\dots ,2$, $d_3=1-\sum _{r=0}^2d_r$, and the formulae should be adjusted accordingly.

As in [2], we compute

$$\begin{aligned} \begin{aligned}&{{\varvec{l}}_d}_1\partial _y^{(2)}{\varvec{U}}_d = \partial _y^{(2)}{V_1}_d, \\&\quad {\Psi _2}_m\partial _y^{(2)}{\varvec{U}}_d = (U_m)_t+F_m({\varvec{U}})_x+\partial _y^{(1)}G_m({\varvec{U}})\\&\quad - {\Psi _1}_m{\varvec{U}}_{xx}-{\Psi _3}_m{\varvec{U}}_{xy}-N_m, \quad m=2,3,4, \end{aligned} \end{aligned}$$

(66)

which forms a $4\times 4$ linear system with $\partial _y^{(2)}{\varvec{U}}_d$ as unknowns.

Then, we update

$$\begin{aligned} \partial _y^{(2)}{\varvec{V}}_d={\varvec{L}}_d\partial _y^{(2)} {\varvec{U}}_d, \end{aligned}$$

(67)

and the computation of diffusive terms is finished.

We now return to the convex combination. $\alpha _m$ is computed with ${\varvec{U}}_{\eta _0}$ and $\{\partial _y^{(l)}(V_m)_{cc}\}_{l=0}^{l=4}$ is obtained with (49). Then,

$$\begin{aligned} \{\partial _y^{(l)}{\varvec{U}}\}_{l=0}^{4}={\varvec{R}}_d\{\partial _y^{(l)}{\varvec{V}}_{cc}\}_{l=0}^{4}. \end{aligned}$$

(68)

We update the convective flux with

$$\begin{aligned}&\partial _y^{(0)}{\varvec{G}}({\varvec{U}})={\varvec{G}} (\partial _y^{(0)}{\varvec{U}}),\end{aligned}$$

(69)

$$\begin{aligned}&\partial _y^{(1)}{\varvec{G}}({\varvec{U}})={\varvec{G}}' ({\varvec{U}})\partial _y^{(1)}{\varvec{U}},\end{aligned}$$

(70)

$$\begin{aligned}&\partial _y^{(2)}{\varvec{G}}({\varvec{U}})=\frac{\partial ^2}{\partial y^2}{\varvec{G}}({\varvec{U}}). \end{aligned}$$

(71)

We also update $\partial _y^{(0)}\varvec{S_2}$ with

$$\begin{aligned} {\varvec{W}}_x=\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(0)}{\varvec{U}}_x,\quad {\varvec{W}}_y=\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(1)}{\varvec{U}}, \end{aligned}$$

(72)

and then we update $\varvec{\psi _3}$, $\varvec{\psi _4}$, $\varvec{N_2}$ using (A.7), (A.8), and (A.16) (see the Appendix). Then, we get

$$\begin{aligned} \partial _y^{(1)}\varvec{S_2}=\varvec{\psi _3}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(1)}{\varvec{U}}_{x}+\varvec{\psi _4}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}\partial _y^{(2)}{\varvec{U}}+\varvec{N_2}. \end{aligned}$$

(73)

At the ghost points, the interior scheme requires ${\varvec{U}}$, ${\varvec{G}}({\varvec{U}})$, and $\varvec{S_2}$. Therefore we use Taylor expansion to approximate them, e.g.,

$$\begin{aligned} {\varvec{U}}_j=\sum _{l=0}^{4}\frac{(y_j-y_0)^l}{l!} \partial _y^{(l)}{\varvec{U}}. \end{aligned}$$

(74)

2.2.2 Known Heat Flux

Regarding $y$ is the normal direction in Fig. 1, we now show how to handle a known heat flux at the wall. We change how the WENO-type extrapolation polynomials are obtained, now they must satisfy $p_r(\eta _j)=T(\eta _j)$ for $j=1\dots ,r$, and

$$\begin{aligned} \left. \frac{dp_r(y)}{dy}\right| _{\eta _0}=\left. \frac{\partial T}{\partial y}\right| _{\eta _0}\quad r=1,\dots ,4. \end{aligned}$$

(75)

With $T_\mathrm {wall}$, we use the procedure for known temperature of Sect. 2.2.1.

3 Numerical Problems

3.1 Simple 2D Flows

For the first simple 2D flow, we propose an analytical solution with non-constant viscosity similar to the Example 6 of [2]

$$\begin{aligned} \begin{aligned} \rho (x,y)=\exp \!\big (\!\sin (x)\sin (y)\big ),\\ u(x,y)=2+0.02(x^2-\pi ^2),\\ v(x,y)=1+0.01(y^2-\pi ^2),\quad p(x,y)=5. \end{aligned} \end{aligned}$$

(76)

In CFD, it is common to model the viscosity with temperature, e.g., Shutherland law. Since pressure is constant in this flow, we use

$$\begin{aligned} \mu =\frac{5\times 10^{-5}}{\rho }. \end{aligned}$$

(77)

By inserting the analytical solution into the Euler ($\varvec{S_1}=\varvec{S_2}={\varvec{0}}$) or Navier–Stokes equations, we compute the source terms, ${\varvec{S}}({\varvec{U}})$, so the equations are analytically satisfied. We use $[-\pi ,\pi ]\times [-\pi ,\pi ]$ as domain and the analytical solution to compute the ghost points.

Our principal goal in solving this simple 2D flow is to test the methodology for Euler and Navier–Stokes equations. The observed accuracy orders of the Euler and Navier–Stokes solutions were similar; as such, for brevity we only present the accuracy results for the Navier–Stokes in Table 1, where one can see that fifth order is being reached.

Table 1 Density accuracy results for the Navier–Stokes simple 2D flow

We now change the analytical solution to test the Navier–Stokes wall boundary treatment. As in [17], a compressible Couette flow is set with

$$\begin{aligned} \begin{aligned} & u=\frac{u_u}{A}y,\quad v=0,\quad p=5,\\ & e=e_l+\frac{y}{A}(e_u-e_l) +\frac{u_u^2Pr}{2\gamma }\frac{y}{A}\left( 1-\frac{y}{A}\right) ,\\ &\rho =\frac{p}{e(\gamma -1)},\quad \rho _u=1,\quad \rho _l=1.25,\quad M_u=0.3, \end{aligned} \end{aligned}$$

(78)

where $M=\sqrt{u^2+v^2}/a$ is the Mach number, the subscripts $u$ and $l$ means upper and lower, the domain is $[0,2]\times [0,A]$, and the height $A$ is set to $1$ for simplicity.

One should notice that $v$ is zero everywhere, $u=0$ at the lower boundary, and $u\ne 0$ at the upper boundary. Therefore, we can approximate fixed and moving walls at those boundaries. Since the analytical solution is available, we use it at the left and right ghost points and focus on known wall temperature and heat flux boundary treatments. The accuracy tests are shown in Tables 2 and 3, where each situation is tested separately.

Table 2 Density accuracy results for the Navier–Stokes wall boundary treatment with known temperature

Table 3 Density accuracy results for the Navier–Stokes wall boundary treatment with known heat flux

Despite being nonrealistic, the simple 2D flows are useful to show that the Navier–Stokes wall boundary treatment is high-order. We remark that the convex combination parameter suggest a convective dominant problem, $\underset{m}{\min }(\alpha _m) > 0.999$ for the most refined mesh.

We now arbitrarily set $Pr=0.1$ and $\mu =0.01$ to test the convex combination in an idealized mixed convective-diffusive problem, in which we only consider that the temperature is known at the lower boundary. The accuracy tests are shown in Table 4, where we can see that the Navier–Stokes wall boundary treatment is high-order.

Table 4 Density accuracy results for the mixed problem Navier–Stokes wall boundary treatment

3.2 Vortex Flow

We now start to test the methodology in idealized flows with nontrivial phenomena. For the vortex flow, we use (1) with ${\varvec{S}}={\varvec{0}}$. We consider a stationary version of the idealized and isentropic vortex of [25]. Starting with $\rho =p=1$ and $u=v=0$, we add perturbations in $(u,v)$ and in the temperature, $T=p/\rho$, [25]

$$\begin{aligned} \begin{aligned} (\delta u,\delta v)=\frac{\epsilon }{2\pi }e^{0.5(1-r^2)} \left( -{\overline{y}},{\overline{x}}\right) ,\\ \delta T=-\frac{(\gamma -1)\epsilon ^2}{8\gamma \pi ^2}e^{1-r^2}, \quad \delta s=0, \end{aligned} \end{aligned}$$

(79)

where $\left( {\overline{x}},{\overline{y}}\right) =\left( x-5,y-5\right)$, $r^2={\overline{x}}^2+{\overline{y}}^2$, the vortex strength is $\epsilon =5$, and the entropy, $s=p/\rho ^\gamma$, remains undisturbed. We use the perturbed solution as the exact solution, $\left[ 0,10\right] \times \left[ 0,10\right]$ as domain, and periodic boundary conditions [25].

Although isentropic, the Euler vortex flow models recirculation, which is an important phenomenon that occurs in more complicated flows that do lack an analytical or exact solution. As stated in [27], care must be taken when solving the Euler vortex flow. For example, when using periodic boundary conditions one may have an infinite array of coupled interacting vortices [27]. We again are interested in accuracy tests, which are shown in Table 5.

Table 5 Density accuracy results for the Euler vortex flow and $t=1$

For the Navier–Stokes vortex flow, the diffusion will prevent us to do the same accuracy tests. We present the Mach number color map for the Euler and Navier–Stokes in Fig. 2, where we can see that they are visually similar.

Fig. 2

Mach number color map for the vortex flow and $160\times 160$ mesh

3.3 Rayleigh–Taylor Instability

The next problem is the Rayleigh–Taylor instability, in which we use (1) with ${\varvec{S}}({\varvec{U}})=(0,0,U_1,U_3)^T$ and as initial condition [7]

$$\begin{aligned}&\left( \rho _0,p_0\right) ={\left\{ \begin{array}{ll} (2,2y+1), &{} y < 1/2,\\ (1,y+3/2), &{} y \ge 1/2, \end{array}\right. } \end{aligned}$$

(80)

$$\begin{aligned}&u_0=0,\quad v_0=-0.025a\cos {(8\pi x)}. \end{aligned}$$

(81)

The computational domain is $\left[ 0,0.25\right] \times \left[ 0,1\right]$, $t=1.95$, and $\gamma =5/3$ for this case only. We use constant values on the upper and lower boundaries, reflective boundary conditions on the left and right for the convective variables and inviscid fluxes [7], and periodic boundary conditions on the left and right for the viscous terms.

The Rayleigh–Taylor instability has a simple setup, and it is a shock-dominated problem with complicated flow structures. Although the exact solution is not available, it is a good test for symmetry. We present a color map for the density, and the $160\times 640$ points mesh in Fig. 3, where we can see a good representation of flow features for both Euler and Navier–Stokes, and that the latter seems to be more smooth, as expected. The $L^1$, $L^2$, and $L^\infty$ norms of the difference of both sides of the symmetry line ($x=0.125$) are presented in Table 6 for the $160\times 640$ points mesh, where we can see an excellent hold of symmetry.

Table 6 $L^1$, $L^2$, and $L^\infty$ norms of the difference of both sides of the symmetry line for the $160\times 640$ points mesh

Fig. 3

Density color map for the Rayleigh–Taylor instability and $160\times 640$ mesh with equally spaced contour lines from 0.85 to 2.25

3.4 Flow Past a Cylinder

We now turn our attention to the supersonic flow past a cylinder which radius is one and is centered at the origin. Similar to Example 7 of [2], we use as initial conditions

$$\begin{aligned} M(x,y)= & {} {\left\{ \begin{array}{ll} x^2+y^2-1, &{} \text {if}\ 1 < x^2+y^2 \le 4,\\ 3, &{} \text {otherwise}, \\ \end{array}\right. } \end{aligned}$$

(82)

$$\begin{aligned} \rho(x,y)= & \,\rho _0\left( 1+\frac{\gamma -1}{2}M^2\right) ^{-1/(\gamma -1)}, \end{aligned}$$

(83)

$$\begin{aligned} p(x,y)= & \, p_0\left( 1+\frac{\gamma -1}{2}M^2\right) ^{-\gamma /(\gamma -1)}, \end{aligned}$$

(84)

$$\begin{aligned} u(x,y)= & \, Ma,\quad v(x,y)=0, \end{aligned}$$

(85)

with $\rho _0$ and $p_0$ computed with free-stream data $(\rho ,u,v,p)=(1.4,3,0,1)$.

For simplicity, we take $[-3,6]\times [0,6]$ as the domain and use the free-stream data at the upper, left, and right ghost points of the domain. At $y=0$ we use the symmetry condition and, at the walls, the ILW solid wall boundary treatment for the Navier–Stokes equations. The wall is fixed, $u_\mathrm {wall}=v_\mathrm {wall}=0$, and $T_\mathrm {wall}=T_0=2$.

The flow past a cylinder has an oblique shock near its walls, providing a good test case for the wall boundary treatment. We show the pressure color map and contours in Figure 4, where we can see that the oblique shock is being captured. We show six pressure profiles along constant $y$ lines in Figure 5. Therefore, we conclude that the post-shock behavior is due to the contour lines generation.

Fig. 4

Pressure color map for the flow past a cylinder and mesh with $\Delta x=\Delta y=1/40$ and equally spaced contour lines from 2 to 15

Fig. 5

Pressure profiles along constant $y$ lines

For comparison, we also present the pressure profile along the center line for our results and the pressure profiles of [2] in Figure 6, where we can see that our result behaves similarly.

Fig. 6

Pressure profiles along the center line for the flow past a cylinder and meshes with $\Delta x=\Delta y=1/40$ of [2] and this work

4 Concluding Remarks

Challenging engineering problems such as stall in aerodynamic profiles or turbomachinery blades, flow separation, side loads, mixing, combustion, detonation, and turbulence demands robust numerical methods. To properly capture the flow phenomena, the Navier–Stokes equations are required.

We reviewed the well-established methods to solve the Euler equations and added the Navier–Stokes viscous terms discretization. Since the conservative variables first derivatives are available from the inviscid flux discretization, we computed the viscous terms, $\varvec{S_1}$ and $\varvec{S_2}$, and employed a central fourth-order scheme to approximate its derivatives and finish the spatial discretization. To maintain the high-resolution of the interior scheme, we adapted the ILW boundary treatment of [2] regarding [5, 22].

We showed that the proposed discretization can handle non-constant viscosity, has an excellent hold of symmetry, and, with the boundary treatment, is high-order and high-resolution. We remark that no approximations regarding the boundary layer were made, i.e., the methodology presented here could be considered for direct numerical simulations.

Appendix. Matrices and Vectors for the Rewritten Navier–Stokes Equations

To rewrite the Navier–Stokes equations, we start expanding $\varvec{S_1}$ and $\varvec{S_2}$

$$\begin{aligned}&\begin{aligned} & ({S_1}_x)_1=0,\\ &({S_1}_x)_2=\mu _x\left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) +\mu \left( \frac{4}{3}u_{xx}-\frac{2}{3}v_{xy}\right) ,\\ & ({S_1}_x)_3=\mu _x\left( u_y+v_x\right) +\mu \left( u_{xy}+v_{xx}\right) ,\\ & ({S_1}_x)_4=u_x\mu \left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) +v_x\mu \left( u_y+v_x\right) \\ &+\left( \frac{\mu \gamma }{Pr(\gamma -1)}\right) _x\left( \frac{p}{\rho }\right) _x+ u\mu _x\left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) \\ &+ u\mu \left( \frac{4}{3}u_{xx}-\frac{2}{3}v_{xy}\right) +v\mu _x\left( u_y+v_x\right) +v\mu \left( u_{xy}+v_{xx}\right) \\ & +\frac{\mu \gamma }{Pr(\gamma -1)}\left( \frac{p_{xx}}{\rho }+\frac{2p\rho _x^2}{\rho ^3}-\frac{2p_x\rho _x}{\rho ^2}-\frac{p\rho _{xx}}{\rho ^2}\right) , \\ \end{aligned} \end{aligned}$$

(A.1)

$$\begin{aligned}& \begin{aligned} & ({S_2}_y)_1=0,\\ &({S_2}_y)_2=\mu _y\left( u_y+v_x\right) +\mu \left( u_{yy}+v_{xy}\right) ,\\ & ({S_2}_y)_3=\mu _y\left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) +\mu \left( \frac{4}{3}v_{yy}-\frac{2}{3}u_{xy}\right) ,\\ & ({S_2}_y)_4=u_y\mu \left( u_y+v_x\right) +v_y\mu \left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) \\ & + \left( \frac{\mu \gamma }{Pr(\gamma -1)}\right) _y\left( \frac{p}{\rho }\right) _y+u\mu _y\left( u_y+v_x\right) \\ &+ u\mu \left( u_{yy}+v_{xy}\right) +v\mu _y\left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) +v\mu \left( \frac{4}{3}v_{yy}-\frac{2}{3}u_{xy}\right) \\ &+ \frac{\mu \gamma }{Pr(\gamma -1)}\left( \frac{p_{yy}}{\rho }+\frac{2p\rho _y^2}{\rho ^3}-\frac{2p_y\rho _y}{\rho ^2}-\frac{p\rho _{yy}}{\rho ^2}\right) . \end{aligned} \end{aligned}$$

(A.2)

One should notice that we did not consider $\mu$ and $Pr$ as constants nor remove any terms. We now group terms containing first and second derivatives to the primitive variables, and nonlinear terms separately

$$\begin{aligned} \varvec{S_1}_x= & {} \varvec{\psi _1}{\varvec{W}}_{xy} +\varvec{\psi _2}{\varvec{W}}_{xx}+\varvec{N_{w1}},\end{aligned}$$

(A.3)

$$\begin{aligned} \varvec{S_2}_y= & {} \varvec{\psi _3}{\varvec{W}}_{xy} +\varvec{\psi _4}{\varvec{W}}_{yy}+\varvec{N_{w2}}, \end{aligned}$$

(A.4)

where

$$\begin{aligned} \varvec{\psi _1}= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} -2\mu /3 &{} 0\\ 0 &{} \mu &{} 0 &{} 0\\ 0 &{} \mu v &{} -2\mu u/3 &{} 0\\ \end{bmatrix},\end{aligned}$$

(A.5)

$$\begin{aligned} \varvec{\psi _2}= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 4\mu /3 &{} 0 &{} 0\\ 0 &{} 0 &{} \mu &{} 0\\ -\mu a^2/[\rho Pr(\gamma -1)] &{} 4\mu u/3 &{} \mu v &{} \mu \gamma /[\rho Pr(\gamma -1)] \end{bmatrix},\end{aligned}$$

(A.6)

$$\begin{aligned} \varvec{\psi _3}= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} \mu &{} 0\\ 0 &{} -2\mu /3 &{} 0 &{} 0\\ 0 &{} -2\mu v/3 &{} \mu u &{} 0\\ \end{bmatrix},\end{aligned}$$

(A.7)

$$\begin{aligned} \varvec{\psi _4}= & {} \begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \mu &{} 0 &{} 0\\ 0 &{} 0 &{} 4\mu /3 &{} 0\\ -\mu a^2/[\rho Pr(\gamma -1)] &{} \mu u &{} 4\mu v/3 &{} \mu \gamma /[\rho Pr(\gamma -1)] \end{bmatrix},\end{aligned}$$

(A.8)

$$\begin{aligned}&\begin{aligned} &(N_{w1})_1=0,\\ &(N_{w1})_2=\mu _x\left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) ,\\ &(N_{w1})_3=\mu _x\left( u_y+v_x\right) ,\\ & (N_{w1})_4=u_x\mu \left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) +v_x\mu \left( u_y+v_x\right) \\ &+\left( \frac{\mu \gamma }{Pr(\gamma -1)}\right) _x\left( \frac{p}{\rho }\right) _x+u\mu _x\left( \frac{4}{3}u_x-\frac{2}{3}v_y\right) \\ & + v\mu _x\left( u_y+v_x\right) +\frac{\mu \gamma }{Pr(\gamma -1)}\left( \frac{2p\rho _x^2}{\rho ^3}-\frac{2p_x\rho _x}{\rho ^2}\right) ,\\ \end{aligned}\end{aligned}$$

(A.9)

$$\begin{aligned}&\begin{aligned} & (N_{w2})_1=0,\\ &(N_{w2})_2=\mu _y\left( u_y+v_x\right) ,\\ &(N_{w2})_3=\mu _y\left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) ,\\ &(N_{w2})_4=u_y\mu \left( u_y+v_x\right) +v_y\mu \left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) \\ &+\left( \frac{\mu \gamma }{Pr(\gamma -1)}\right) _y\left( \frac{p}{\rho }\right) _y+u\mu _y\left( u_y+v_x\right) \\& + v\mu _y\left( \frac{4}{3}v_y-\frac{2}{3}u_x\right) +\frac{\mu \gamma }{Pr(\gamma -1)}\left( \frac{2p\rho _y^2}{\rho ^3}-\frac{2p_y\rho _y}{\rho ^2}\right) . \end{aligned} \end{aligned}$$

(A.10)

The boundary treatment is based on conservative variables, we then transform to the latter with

$$\begin{aligned}&\begin{aligned} \varvec{S_1}_x & =\varvec{\psi _1}\left[ {\varvec{M}}{\varvec{U}}_y+\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xy}\right] \\ & \quad +\varvec{\psi _2}\left[ {\varvec{M}}{\varvec{U}}_x+\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xx}\right] +\varvec{N_{w1}}, \end{aligned}\end{aligned}$$

(A.11)

$$\begin{aligned}&\begin{aligned} \varvec{S_2}_y & =\varvec{\psi _3}\left[ {\varvec{O}}{\varvec{U}}_x+\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xy}\right] \\ &\quad +\varvec{\psi _4}\left[ {\varvec{O}}{\varvec{U}}_y+\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{yy}\right] +\varvec{N_{w2}}, \end{aligned}\end{aligned}$$

(A.12)

$$\begin{aligned}&\begin{aligned} {\varvec{M}}=\begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ \displaystyle \frac{\rho _x u-\rho u_x}{\rho ^2} &{} \displaystyle -\frac{\rho _x}{\rho ^2} &{} 0 &{} 0 \\ \displaystyle \frac{\rho _x v-\rho v_x}{\rho ^2} &{} 0 &{} \displaystyle -\frac{\rho _x}{\rho ^2} &{} 0 \\ \left( uu_x+vv_x\right) (\gamma -1) &{} -u_x(\gamma -1) &{} -v_x(\gamma -1) &{} 0 \\ \end{bmatrix},\\ {\varvec{O}}=\begin{bmatrix} 0 &{} 0 &{} 0 &{} 0\\ \frac{\rho _y u-\rho u_y}{\rho ^2} &{} \displaystyle -\frac{\rho _y}{\rho ^2} &{} 0 &{} 0 \\ \frac{\rho _y v-\rho v_y}{\rho ^2} &{} 0 &{} \displaystyle -\frac{\rho _y}{\rho ^2} &{} 0 \\ \left( uu_y+vv_y\right) (\gamma -1) &{} -u_y(\gamma -1) &{} -v_y(\gamma -1) &{} 0 \\ \end{bmatrix}. \end{aligned} \end{aligned}$$

(A.13)

We finally write the viscous terms as

$$\begin{aligned} \varvec{S_1}_x= & \, \varvec{\psi _1}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xy} +\varvec{\psi _2}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xx}+\varvec{N_{1}}, \end{aligned}$$

(A.14)

$$\begin{aligned} \varvec{S_2}_y= & \, \varvec{\psi _3}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{xy} +\varvec{\psi _4}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}{\varvec{U}}_{yy}+\varvec{N_{2}}, \end{aligned}$$

(A.15)

with

$$\begin{aligned} \varvec{N_1}= & \, \varvec{\psi _1}{\varvec{M}}{\varvec{U}}_y+\varvec{\psi _2}{\varvec{M}}{\varvec{U}}_x+\varvec{N_{w1}}, \nonumber \\ \varvec{N_2}= & {} \varvec{\psi _3}{\varvec{O}}{\varvec{U}}_x+\varvec{\psi _4}{\varvec{O}}{\varvec{U}}_y+\varvec{N_{w2}} . \end{aligned}$$

(A.16)

Introducing four new terms, we write

$$\begin{aligned} \varvec{S_1}_x+\varvec{S_2}_y= \, \varvec{\Psi _1}{\varvec{U}}_{xx} +\varvec{\Psi _2}{\varvec{U}}_{yy}+\varvec{\Psi _3}{\varvec{U}}_{xy} +{\varvec{N}} \end{aligned}$$

(A.17)

with

$$\begin{aligned} \varvec{\Psi _1}= & \, \varvec{\psi _2}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}, \end{aligned}$$

(A.18)

$$\begin{aligned} \varvec{\Psi _2}= & \, \varvec{\psi _4}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}, \end{aligned}$$

(A.19)

$$\begin{aligned} \varvec{\Psi _3}= & \, \varvec{\psi _1}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}} +\varvec{\psi _3}\frac{\partial {\varvec{W}}}{\partial {\varvec{U}}}, \end{aligned}$$

(A.20)

$$\begin{aligned} {\varvec{N}}= & \, \varvec{N_1}+\varvec{N_2}. \end{aligned}$$

(A.21)

To apply the wall boundary treatment, we need to diagonalize the matrix $\varvec{\Psi _2}$. We choose the scaling factors in a way that the resulting eigenvectors are similar to those employed in [2], i.e.,

$$\begin{aligned} {\varvec{L}}_d= & {} \begin{bmatrix} \dfrac{1}{2\gamma } &{} 0 &{} 0 &{} 0 \\ -u &{} 1 &{} 0 &{} 0 \\ \dfrac{v}{2a} &{} 0 &{} -\dfrac{1}{2a} &{} 0 \\ \dfrac{q(\gamma -1)}{2a^2}-\dfrac{1}{2\gamma } &{} -\dfrac{u\left( \gamma -1\right) }{2a^2} &{} -\dfrac{v\left( \gamma -1\right) }{2a^2} &{} \dfrac{\gamma -1}{2a^2} \\ \end{bmatrix},\end{aligned}$$

(A.22)

$$\begin{aligned} {\varvec{R}}_d= & {} \begin{bmatrix} 2\gamma &{} 0 &{} 0 &{} 0\\ 2u\gamma &{} 1 &{} 0 &{} 0\\ 2v\gamma &{} 0 &{} -2a &{} 0\\ 2q\gamma +\dfrac{2a^2}{\gamma -1} &{} u &{} -2av &{} \dfrac{2a^2}{\gamma -1}\\ \end{bmatrix}, \end{aligned}$$

(A.23)

with $q=(u^2+v^2)/2$.