1 Introduction

“Now however I recognise the FVM/FEM dichotomy as being comparable with those between Protestant and Catholic, or Sunni and Shia. That is to say that it promotes needless conflict; and expense; and loss of opportunity.” [1] With these words, Brian Spalding highlighted the, at times, unproductive nature of the debate around the relative merits of the finite volume (FVM) and finite element (FEM) methods. Although accepted in the computational fluid dynamics (CFD) field, there remains a reluctance and general confusion around the application of the finite volume method to solid mechanics. The aim of this article is to clarify this confusion, by: providing an overview of the significant developments within the field; linking variants of the finite volume method for solid mechanics analyses; comparing finite volume methods with standard finite element methods; and, finally, identifying future directions for the field.

Building on the foundations of the finite difference method, the finite volume method is a generalisation in terms of geometry and topology: simple finite volume schemes reduce to finite difference schemes. Whereas the finite difference method is based on nodal relations for differential equations, the finite volume method balances forces acting on control volumes, directly discretising the integral form of the conservation laws. A number of prior developments within CFD provided the foundation for the earliest paper on the cell-centred finite volume method for solid mechanics by Demirdžić et al. [2]. In the subsequent three decades the finite volume method for solid mechanics has developed in a number of directions, differing in terms of discretisation, solution methodology and overall philosophy. The varied approaches may be classified in a number of ways, including, for example:

  • Grid arrangement: cell-centred [2, 3] vs. vertex-centred [4,5,6,7,8,9,10,11,12] vs. staggered-grid [13,14,15,16,17,18,19], as well as more recently face-centred [20, 21] and meshless [22, 23];

  • Solution algorithm: implicit [3, 24, 25] vs. explicit (matrix-free) [26,27,28];

  • Stabilisation approach: Rhie–Chow [29, 30] vs. Jameson–Schmidt–Turkel [31] vs. Godunov two-sided upwinding [27, 32].

There are countless other ways to classify the approaches, for example, based on force discretisation at the control volume face, however, the current article will base its discussion primarily around the three classification types above.

The essential characteristic of a finite volume method is the integration of the governing conservation equation over finite control volumes. In this sense, the cell-centred vs. vertex-centred vs. staggered-grid approaches primarily differ in how these control volumes are constructed. Cell-centred approaches use the primary mesh control volumes, whereas vertex-centred approaches construct a dual mesh with control volumes surrounding the vertices of the primary mesh. On the other hand, staggered-grid approaches create multiple secondary meshes, one for each scalar component of the primary solution vector, constructed about the primary mesh faces. Despite their close relationship, as explored further in Sect. 3, approaches based on differing grid arrangements often differ greatly in terms of philosophy: as noted by Baliga and Atabaki [33], the cell-centred method is often thought of as a control-volume finite difference method, combining ideas borrowed from finite volume and finite difference methods; whereas, the vertex-centred approach is viewed as a control-volume finite element method, formulated by amalgamating concepts native to finite volume and finite element methods.

Regardless of the chosen grid arrangement, spatio-temporal integration of the governing equations may adopt an implicit or explicit solution algorithm. Implicit algorithms are characterised by the solution of a linear system of equations and are unconditionally stable with respect to the time increment size. In contrast, explicit or matrix-free algorithms avoid the need to construct such a system of linear equations but the time increment size is restricted by the classic Courant–Friedrichs–Lewy constraint [34]. The choice of solution algorithm often depends on the problems of interest, with implicit methods favoured for elliptic and parabolic cases (steady-state and quasi-steady-state) and explicit methods for hyperbolic (high rates, wave propagation). Once the grid arrangement and solution algorithm are selected, care must be taken in the construction of a stable discretisation that does not suffer from unphysical instabilities in the solution field. To this end, a variety of stabilisation approaches have been proposed. Generally, each approach can be viewed upon as adding some form of diffusion to the surface force discretisation with the purpose of quelling high-frequency oscillations. Rhie–Chow-style stabilisation is common in the implicit approaches originating from the work of Demirdžić and Muzaferija [29], while Godunov upwinding and Jameson–Schmidt–Turkel approaches are more commonly seen in the explicit approaches, rooted in the solution of compressible gas flow Euler equations.

From afar, each of these main variants of finite volume method can seem quite distinct; however, upon closer inspective, they share many similarities in terms of discretisation and solution algorithm. Nevertheless, the fragmented nature of the finite volume solid mechanics community is evident from many recent publications in the area, where authors, reviewers and editors tend to be unaware of developments within the field, for example, see [35]. In addition, and more generally, there is a lack of awareness in the computational mechanics community around the capabilities of the finite volume method for solid mechanics. Accordingly, a comparative and critical review of the finite volume method for solid mechanics is timely, relevant and essential for the future progress of the field. Within this domain, there are a number of open questions: What are the strengths and weaknesses of the various approaches? Which approaches show the greatest potential and widest applicability? Are there possibilities for the various methods to be combined to produce superior methods? How do the finite volume approaches relate to finite element methods? Are there directions of development which are missing? This article will attempt to provide answers to these questions, as well as providing a unifying framework for the discussion of finite volume methods for solid mechanics, and their relationship with finite element methods. Given the scale of the field, it is outside the scope of the article to provide an exhaustive review of all formulations; instead, the article aims to provide detailed analysis on the main variants of approach common in the literature. The primary novel contributions of the current article are twofold: (i) The first detailed review of the finite volume solid mechanics field is presented; and (ii) The first analysis of similarities and differences between all main variants of the finite volume method for solid mechanics is detailed.

The remainder of the article is constructed as follows: Sect. 2 provides a chronological overview of the prominent finite volume developments for solid mechanics. Section 3 compares and contrasts the three main flavours of the finite volume method for solid mechanics. In Sect. 4, the finite volume method for solid mechanics is compared to the “standard” continuous Bubnov–Galerkin finite element method, highlighting similarities and differences in terms of discretisation, solution methodology and overall philosophy. Section 5 reviews the variety of structural applications to which the finite volume method has been applied in its thirty year history. The penultimate section briefly reviews software that use, or have previously used, the finite volume method for solid mechanics simulations. Finally, Sect. 7 summaries the main conclusions of the article and considers the current challenges facing the field.

2 History of the Finite Volume Method for Computational Solid Mechanics

The development of the finite volume method for solid mechanics has occurred independently in a number of forms, with finite difference methods, computational fluid mechanics algorithms, and finite element methods providing much of the inspiration. This section gives an overview of the historical development of these finite volume methods. The treatise is primarily partitioned based on the grid arrangement, where comments regarding the solution algorithm and stabilisation scheme are given where appropriate. In-depth dissections of the technical details are left to Sect. 3. While the field is small and fragmented, there are a number of notable reviews worth mentioning, including those of Maneeratana [36], Vaz Jr. et al. [37] and Cavalcante et al. [38].

Before delving into details of influential publications, it is insightful to first consider the literature landscape as a whole. To this end, Fig. 1 presents a histogram of the publications in the area to-date, separated into journal articles, conferences, Ph.D. theses, Masters theses and books. Of course, exact records of each publication type are difficult to track and consequently the data should be taken as indicative. To complement this, Fig. 2 lists the most popular international journals for publishing finite volume solid mechanics articles; only journals with greater than five articles have been included. Furthermore, a table of the most cited articles related to the finite volume method for solid mechanics can be found in “Appendix 1”.

Fig. 1
figure 1

Histogram of the finite volume method for solid mechanics publications to-date. (Color figure online)

Full size image
Fig. 2
figure 2

Number of publications per journal related to computational solid mechanics using the finite volume method, based on the cited references, where only journals with greater than five articles have been counted. (Color figure online)

Full size image

A perspective on the literature landscape is gained from the co-authorship network presented in Fig. 3, which has been generated using the VOSviewer software [39]. A co-authorship network is a visual method to assess research collaborations within a field, as well as observe detached regions of research. Referring to Fig. 3, the three larger sub-networks broadly correspond to: implicit cell-centred approaches indicated by the red sub-network centred on demirdžić and ivanković; implicit vertex-centred approaches indicated by the green sub-network centred on cross, bailey and fallah; and a specialised form of finite volume method for microstructural analysis indicated by the blue sub-network centred on aboudi, pindera and cavalcante. Although the co-authorship graph is not a direct measure of contribution to the field, it does provide insight into the collaboration between authors and subdivisions within the domain. In the graph, individual authors are represented by filled circles, and a co-authored publication between two individual authors is symbolised by a line connecting the two filled circles; the line thickness increases with increasing number of co-authored publications; the size of an author’s filled circle is directly proportional to the number of their related publications. To maintain interpretability, only authors with five or more related publications have been included in the network, and only peer-reviewed publications have been incorporated.

Fig. 3
figure 3

Co-authorship network of the finite volume method for solid mechanics, generated using the VOSviewer software [39]. To maintain interpretability, only authors with five or more related peer-reviewed publications have been included in the network. The network provides insight into collaborations within the field but is not a direct measure of contribution. (Color figure online)

Full size image

Finally, before considering individual contributions, we will clarify the meaning of a number of terms in the current context to avoid any confusion. For the domain spatial discretisation, this will be referred to interchangeably as the “mesh” or “grid”; each sub-domain in a finite volume mesh will be equivalently referred to as a “control volume”, a “cell”, or even an “element”; similarly, each sub-domain in the finite element mesh will be referred to as an “element” or “cell’. The term “node” indicates the mesh location where the solution variable is stored, which could be a vertex, face-centre or cell-centre depending on the method.

2.1 Cell-Centred Approaches

Thirty years ago, Demirdžić et al. [2] proposed the first application of the cell-centred finite volume method in its modern form to solid mechanics. Subsequently, cell-centred developments have primarily focussed on two relatively disconnected approaches:

  • Implicit cell-centred approaches based on the original approach of Demirdžić et al. [2], and

  • Explicit Godunov-type cell-centred approaches stemming from the work of Trangenstein and Colella [40].

The cell-centred approach takes its name from the dependent variable(s) residing at the cell centres (control volume centroids); equivalently, the approach has been termed the colocated, co-located or collocated finite volume method, as the dependent variables share their location at the cell centres/centroids.

2.1.1 Implicit Cell-Centred Methods

Considering first the implicit methods: in the original approach of Demirdžić et al. [2], a structured rectangular 2-D method was applied to the simulation of thermal deformations in welded workpieces (Fig. 4a). The displacement was assumed to vary linearly between computational nodes, and the small strain material behaviour was described by the Duhamel–Neumann form of Hooke’s law. A distinguishing feature of the proposed solution algorithm was the partitioning of the surface force term into a compact-stencil implicit term and a larger stencil explicit term. As a result, the linear momentum vector equation was temporarily decoupled into three scalar component equations that were independently solved, where outer fixed-point/Gauss–Seidel/Picard iterations provided the required coupling. This form of solution methodology is termed a segregated approach, as the governing conservation of linear momentum equation is segregated into three scalar equations during solution. This style of implicit segregated solution algorithm was inspired by the methods adopted in similar CFD procedures, where the restrictive computer memory sizes available at the time necessitated memory efficient procedures.

Fig. 4
figure 4

Original 2-D structured quadrilateral mesh of Demirdžić et al. [2] (left) and the subsequent generalisation to 3-D unstructured convex polyhedra [41] (right). (Color figure online)

Full size image

The original 2-D method was later generalised to 3-D convex polyhedral cells by Demirdžić and Muzaferija [41] (Fig. 4b). This form of the cell-centred approach has since been extended to deal with a wide variety of solid and multi-physics phenomena, including:

Of particular note are the developments of Weller et al. [193] and Jasak and Weller [194], where the same implicit cell-centred form has been demonstrated to be well-suited to running on distributed-memory supercomputers. The domain decomposition method was used where the solution domain is decomposed into a number of sub-domains, each solved on a separate central processing unit (CPU) core; necessary coupling between the sub-domains is performed using a message-passing protocol, initially parallel virtual machine, but message passing interface in later publications. The Weller et al. [193] and Jasak and Weller [194] implementations form a component of the popular open-source C++ library OpenFOAM, formerly commercial software FOAM. Many of the subsequent developments in the implicit cell-centred field have been based on the OpenFOAM platform, for example, [25, 30, 77, 78, 83, 88, 90, 104, 112, 113, 131, 195]. It should, however, be noted that the explicit Godunov-type approaches have also been implemented in OpenFOAM [28, 196].

The essence of the implicit cell-centre finite volume method has been the use of a displacement approach combined with a segregated algorithm; however, alternative solution methodologies have also been developed, including geometric multi-grid procedures [86, 120, 142, 143, 197], block-coupled algorithms [30, 188, 189, 198, 199], hybrid/mixed pressure–displacement formulations [46, 95, 97, 100, 138, 139, 200, 201], Aitken acceleration [78, 160, 199], and curvilinear formulations [43, 202]. In addition, fourth-order accuracy variants have been proposed [203] as well as novel gradient and tractions calculation methods [25, 157, 160, 199, 204,205,206,207,208]. Apart from the standard continuum approaches, a number of authors have proposed implicit cell-centred finite volume methods for beams, plates and shells [59, 89, 145, 146, 150, 167, 173, 174, 181, 185, 186, 209, 210].

2.1.2 Explicit Cell-Centred Methods

Explicit Godunov-type finite volume methods were first proposed for the solution of hyperbolic problems characterised by waves and shocks [32, 211, 212], and have been popularised for the solution of Euler compressible gas flow equations. The typical approach, which casts the conservation laws as a system of first-order hyperbolic equations, is characterised by the solution of a Riemann problem (propagation of a solution discontinuity) at the control volume faces to determine forces. The resulting discretisation evaluates the force at a control volume face as a weighted average of the force evaluated at each side of the face. Godunov-type methods were first applied to structural problems by Trangenstein and Colella, when they modelled the 1-D propagation of waves in elasto-plastic solids [40, 213, 214]; in their approach, the primitive conservation variables were the linear momentum vector and the deformation gradient (or displacement gradient) tensor. Subsequently, the method has been extended to unstructured 3-D grids in a variety of forms, differing in terms of discretisations and primitive variables [20, 21, 26,27,28, 32, 196, 215,216,217,218,219,220,221,222,223,224,225,226,227,228,229,230,231,232,233,234,235,236], for example, see Fig. 5. Although cell-centred formulations are the most common form of Godunov-type method, vertex-centred [31, 237] and, recently, face-centred approaches [20, 21] have also been explored.

Fig. 5
figure 5

Forms of mesh employed by Kluth and Després [26] and Aguirre et al. [237]. (Color figure online)

Full size image

To-date, Godunov-type approaches have been used to model a wide range of physical mechanisms:

A distinctive characteristic of Godunov-type methods is the adoption of fully explicit solution algorithms, where the time increment size is restricted by the standard Courant–Friedrichs–Lewy constraint [34].

From an implementation and philosophy perspective, the implicit approaches stemming from Demirdžić et al. [2] differ greatly from the explicit approaches deriving from Trangenstein and Colella [40]. The most obvious difference is the need of the implicit approach to form and solve a linear system of equations, and the time increment size restriction for explicit methods. In addition to this, the implicit methods have typically assumed a smooth variation of the primitive variable within each cell (or across cell faces); in contrast, the explicit approaches have aimed to directly approximate the propagation of solution discontinuities. Many of these technical distinctions are discussed further in Sect. 3. It should be noted that explicit cell-centred approaches that do not adopt a Godunov approach are also possible, for example, as developed by Selim et al. [238, 239].

2.2 Vertex-Centred Approaches

2.2.1 Implicit Vertex-Centred Methods

Fryer et al. [5] was the first to propose a vertex-centred finite volume method for solid mechanics. The approach, initially termed a control volume-unstructured mesh procedure, could analyse complex 2-D geometry using both quadrilateral and triangular cells (Fig. 6a). The method of Fryer et al. [5] followed closely the approach of Baliga and Patankar [240] from a decade earlier, who developed a so-called control-volume-based finite element method for convection–diffusion equations on unstructured triangular grids.

Fig. 6
figure 6

Vertex-based finite volume formulation of Fryer et al. [5] (left) showing the construction of control volumes around a mesh vertex for quadrilateral and triangular 2-D cells, and of Taylor et al. [241] showing the extension to 3-D cells. (Color figure online)

Full size image

In addition to the designation vertex-based finite volume method, the formulation is referred to by a number of other names, including vertex-centred finite volume method, cell-vertex finite volume method, control volume procedure, control-volume finite element method, control-volume-based finite-element method, and element-based finite volume method.

In contrast to cell-centred and staggered-grid approaches, vertex-centred approaches store the primary unknowns at the primary mesh vertices and integrate the governing equation over secondary/dual mesh control volumes surrounding each primary mesh vertex.

The original 2-D approach of Fryer et al. [5] was subsequently extended to three dimensions by Bailey and Cross [24] (Fig. 6b) and has since been applied to a wide range of physical phenomena:

Alternative solution methodologies have been examined, including mixed displacement-rotation approaches [300,301,302], and addressing parallelisation on distributed memory supercomputers [303, 304]. Also of note are the developments of Maitre et al. [305] and Souhail [306], who proposed a higher order extension of the vertex-based approach.

It is important to note the distinction between overlapping and non-overlapping vertex-centred methods: the more common approach involves non-overlapping control volumes, where the control volumes about each primary mesh vertex do not overlap with the control volumes of neighbouring primary mesh vertices. In the less popular overlapping control volumes approaches, for example, as discussed by Oñate et al. [12], primary mesh vertices partly share control volumes with primary mesh neighbouring vertices, resulting in the governing equations being integrated more than once over regions of the domain; this overlapping local integration domain approach is more similar to the finite element method. Additionally, Tsui et al. [249] proposed a variation on the common approach to construct the control volumes: the primary mesh cell centres are joined together to make the control volumes, rather than joining the cell-centres to the face-centres as per the classic vertex-based method.

2.2.2 Explicit Vertex-Centred Methods

Similar to cell-centred methods, both implicit and explicit solution algorithms have been developed, although explicit vertex-centred methods have seen less development. Within the category of explicit vertex-centred methods, there exists a variety of sub-classes, including: so-called dual-time-stepping explicit methods, where the solution is calculated in an explicit manner and a linear system is not directly formed [248, 249, 277, 279, 297]; Godunov-type approaches [31, 237] similar to those seen in cell-centred approaches, as noted in Sect. 2.1; and the so-called grid method [307,308,309,310,311,312]. Regarding the grid-method, the originators of the method, Zhang and Liu [307], argue for the distinction between the grid method and the vertex-based finite volume method, however, the authors of the current article believe this distinction is unwarranted: like other finite volume methods, the grid method starts from the governing momentum equation in strong integral form and approximates the forces over the boundaries of the control volumes; although there are minor differences in the techniques used to approximate the surface forces, for example, comparing Dormy and Tarantola [313] and Zhang and Liu [308], the grid method still remains a form of vertex-centred finite volume method.

2.3 Staggered-Grid Approaches

In staggered-grid approaches, as originally proposed for CFD by Harlow and Welch [314], the components of the primary solution variable, for example, the x and y components of displacement, are stored at different locations. In addition, different sets of control volumes are used when integrating the discretised governing equation in each Cartesian direction. For example, the x-momentum component equation employs a different grid to the y-momentum component equation. The primary motivation for such staggered-grid approaches is the avoidance of solution instabilities, namely the “checker-boarding” phenomenon, where high frequency variations appear in the solution variables that are unobservable to the discretisation. Consequently, staggered-grid approaches do not need to explicitly included a stabilisation term, as is common in cell-centred methods. The extension of staggered-grid approaches to general unstructured 3-D meshes is, however, not trivial; and consequently, this major limitation has resulted in declining popularity for such approaches in solid mechanics.

The first application of a staggered-grid formulation to solid mechanics was by Beale and Elias [13, 14], who showed how the finite volume CFD code PHOENICS could be applied to stress analysis problems. In their method, Beale and Elias used the analogy between the stream functions in creeping-fluid-flow and the Airy stress functions in solid mechanics, where the stress components were the primary unknowns. This method was later generalised by Spalding et al. [15, 17, 315,316,317,318,319,320,321], where a displacement, rather than a force analogy, was adopted, having the major advantage of being more general in three dimensions. Spalding noted that a CFD solution procedure designed for computing velocities is suitable for computing displacements if the convection terms are set to zero and the volume/dilatation stress term is introduced by inclusion of a pressure- and temperature-dependent source term. As a consequence, the resulting solution method used an implicit SIMPLE algorithm [322, 323], still popular in modern CFD codes. The employed primitive variables were displacement and pressure, as opposed to velocity and pressure in standard fluid flow analyses.

The use of mixed displacement-pressure approaches, however, is not a requirement of staggered-grid approaches. Hattel, Hansen and collaborators [16, 18, 19, 324,325,326,327,328,329,330,331,332,333,334,335,336] demonstrated a staggered-grid approach where the sole primary variable was displacement. Hattel and Hansen [16] initially proposed their staggered-grid approach for the analysis of thermally induced stresses in casting problems, and subsequently extended it for a variety of thermo-elasto-plasticity problems. They termed their approach “a control volume based finite difference method”, further indicating the close-relationship with finite difference methods. The authors noted that their method resulted in an elegant formulation for non-constant material properties, a benefit of the staggered grid approach.

In addition to the displacement and displacement-pressure approaches, a number of alternative staggered grid formulations have also been proposed: Spalding [319] proposed a staggered formulation where rotation and displacement were the primitive variables; Spalding surmised that the rotation-based method may provide a more efficient solution algorithm in certain situations. The approach is described in documentation from an early version of the PHOENICS software; however, issues with boundary conditions are noted and no further articles appear on the formulation. A similar idea was subsequently proposed by Wenke et al. [300,301,302] in the framework of vertex-based finite volume methods, where both displacements and rotations are considered the primitive variables. More recently, Wang and Melnik [337] put forward a staggered finite volume approach for analysis of shape memory alloys, defined on 2-D structured rectangular grids. In contrast to the majority of staggered grid approaches, which employ implicit solution algorithms, Rajagopal et al. [338] proposed a one-step explicit staggered grid finite volume approach to investigate the response of a layered viscoelastic plate.

2.4 Other Approaches

Across the spectrum of finite volume methods for solid mechanics, not all procedures align with the previously discussed divisions.

2.4.1 Approaches for Periodic Heterogenous Microstructures

Although arguably not a fundamental class of finite volume method, there has been significant development related to specialised versions of the finite volume method for periodic microstructures. Depending on the formulation, the related methods can be referred to by a number of names, including: the higher-order theory for functionally graded material (HOTFGM) [339], the high-fidelity generalised method of cells (HFGMC) [340,341,342,343], the finite volume direct averaging micromechanics (FVDAM) theory [344, 345], or some variant thereof. Although there is some disagreement over the naming convention [342, 343, 345], these methods have a common origin in the method of cells and the generalised method of cells developed by Aboudi and Paley [346,347,348]. Recent discussions around the development of these methods can be found in Haj-Ali and Aboudi [343], Cavalcante et al. [38], Gong et al. [291], and Cavalcante and Pindera [349], along with reviews of the high fidelity generalised method of cells approaches by Aboudi [350] and of microstructural analysis approaches by Pindera et al. [351] and Charalambakis and Murat [352]. Reviews of the application of such methods can be found in Aboudi et al. [353] and Aboudi [354]. A brief overview of the discretisation used in HOTFGM/HFGMC/FVDAM approaches is given in “Appendix 2”.

2.4.2 Meshless Finite Volume Approaches

Meshless methods have been proposed to overcome the drawbacks of mesh-based finite element and finite volume methods, particularly related to large deformations and cracking. Atluri and Shen [355] were the first to propose a meshless finite volume formulation, based on the earlier generalised Meshless Local Petrov–Galerkin (MLPG) method by Atluri and Zhu [356]. The approach has subsequently been extended and applied to a variety of problems in elasto-statics, elasto-dynamics and fracture mechanics [357,358,359,360,361,362,363,364,365,366,367,368,369,370,371,372,373,374]. Based on the initial development of Atluri and Shen [355], Moosavi and Khelil [366] proposed a novel meshless form of the finite volume method for elasto-static analysis, that combined the finite volume concept with the meshless local Petrov–Galerkin approach with moving least squares interpolation. Moosavi and co-workers have since extended the method to elasto-dynamics, beams, plates, shells and crack problems [367,368,369, 373, 374], where the method has been named the orthogonal meshless finite volume method. Whereas the Atluri and Shen [355] approach uses overlapping control volumes, the meshless finite volume method developed by Ebrahimnejad et al. [22, 375, 376] employs non-overlapping control volumes. The method has been applied to 2-D elasticity with adaptive mesh refinement, and was later extended to problems with material discontinuities [23, 377], to free vibration analysis of laminated composite plates [378, 379], and to fractures in orthotropic media [380].

2.4.3 Eulerian Approaches

There are many solid mechanics problems which can be equivalently considered from the fluid mechanics perspective, for example, in the analysis of extrusion and drawing. Eulerian “fluid” approaches are often used to solve such problems, for example, [46, 48, 50,51,52, 54, 286, 287, 381,382,383,384,385,386,387,388,389,390,391,392,393]. These methods are more closely related to CFD procedures and are not discussed further here.

2.4.4 Miscellaneous

Teng et al. [394] and Chen et al. [395] developed a finite volume method to simulate the draping of woven fabrics, where the governing nonlinear equations were solved using a single-step full Newton–Raphson method. Martin and Pascal [396, 397] proposed a novel discrete duality finite volume method for solving linear elasticity problems on unstructured meshes; the main characteristic of the discretisation is the integration of the governing equations over two meshes: the given primal mesh and also over a dual mesh built from the primal one. Pietro et al. [398] proposed a novel discretisation scheme for linear elasticity with only one degree of freedom per control-volume face, corresponding to the normal component of the displacement.

3 Comparing Variants of the Finite Volume Method for Computational Solid Mechanics

The finite volume method, like other related numerical approaches, consists of the following main components:

  1. (a)

    Discretisation of space and time;

  2. (b)

    Discretisation of the mathematical model equations;

  3. (c)

    Solution algorithm.

To facilitate comparison between the major variants, three popular formulations will be considered here:

  • Implicit cell-centred approach originating from the work of Demirdžić et al. [2];

  • Implicit vertex-centred approach of Fryer et al. [5] and Bailey and Cross [24];

  • Explicit cell-centred approach emanating from Trangenstein and Colella [40].

Analysis and insight into the similarities and differences between these variants is provided.

3.1 Mathematical Model for Dynamic Linear Elasticity

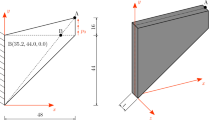
To allow a clear comparison of the methods, the dynamic behaviour of a body with volume \(\Omega\) and surface \(\Gamma\) is analysed (Fig. 7), where part of its boundary is subjected to a specified displacement, \(\varvec{u}_b\), and the remainder is subjected to a specified traction, \(\varvec{T}_b\).

Fig. 7
figure 7

Generic solid body, with volume \(\Omega\) and surface \(\Gamma\), subjected to boundary displacements, \(\varvec{u}_b\), and boundary tractions, \(\varvec{T}_b\). (Color figure online)

Full size image

Assuming the relationship between stress and strain to be described by Hooke’s law, the governing conservation of linear momentum equation, a generalisation of Newton’s second law, can be given in strong integral form as:

$$\begin{aligned} \underbrace{ \int _\Omega \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}\;\text {d}\Omega }_{\text {Inertia forces}}= & {} \underbrace{ \oint _\Gamma \varvec{n} \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;\text {d}\Gamma }_{\text {Surface forces}} \nonumber \\&\quad + \underbrace{ \int _\Omega \rho \varvec{f}_b \;\text {d}\Omega }_{\text {Body forces}} \end{aligned}$$
(1)

Small deformations are assumed i.e. no distinction is made between the initial and deformed configurations; \(\rho\) is the initial density, \(\varvec{u}\) is the unknown total displacement vector, \(\varvec{n}\) is the outward-pointing surface unit normal vector, \(\varvec{\nabla }\) is the del operator, \(\lambda\) is the first Lamé parameter, \(\mu\) is the second Lamé parameter, synonymous with the shear modulus, \(\mathbf{I}\) is the second-order identity tensor, and \(\varvec{f}_b\) is a body force acceleration. To avoid unnecessary complexity, the material properties (\(\rho\), \(\mu\) and \(\lambda\)) are assumed to be uniform and isotropic; however, this assumption is not required. It should be noted that the finite volume method directly discretises this strong integral form of the governing equation, without requiring weighting functions, the weak form of the equation or the use of the Gauss divergence theorem.

3.2 Implicit Cell-Centred Approach

In this sub-section, the implicit cell-centred approach stemming from Demirdžić et al. [2] is described.

3.2.1 Discretisation of Time

For all described variants of the finite volume method, discretisation of the solution domain comprises time discretisation and space discretisation. The total specified simulation time is divided into a finite number of time increments, \(\Delta t\), and the discretised governing equations are solved in a time-marching manner.

3.2.2 Discretisation of Space

For the implicit cell-centred approach, the spatial domain is divided into a finite number of contiguous convex polyhedral cells bounded by polygonal faces that do not overlap and fill the space completely. A typical control volume is shown in Fig. 8, with the computational node P located at the cell centre/centroid, and the cell volume is \(\Omega _P\); \(N_{f}\) is the centroid of a neighbouring control volume, which shares face f with the current control volume; \(\varvec{\Gamma }_{f}\) is the area vector of face f, vector \(\varvec{d}_{f}\) joins P to \(N_f\), and \(\varvec{x}\) is a positional vector. No distinction is made between different cell volume shapes, as all general convex polyhedra are discretised in the same fashion.

Fig. 8
figure 8

Adapted from [25, 29, 155]. (Color figure online)

General convex polyhedral control volume.

Full size image

3.2.3 Discretisation of the Mathematical Model Equations

The governing conservation law (Eq. 1) is applied to each polyhedral cell in the mesh. The discretisation of each of the three terms (inertia, surface forces, body forces) within the equation is now discussed in turn.

Considering first the spatial discretisation of the inertia term in Eq. (1). The term can be approximated by making an assumption about the variation of the displacement vector \(\varvec{u}\) over the cell; typically in the implicit cell-centred approach a linear variation is assumed. This linear variation can be expressed in terms of a truncated Taylor series expansion about the cell centre:

$$\begin{aligned} \varvec{u}(\varvec{x}) = \varvec{u}_P + (\varvec{x} - \varvec{x}_P) \cdot (\varvec{\nabla } \varvec{u})_P \end{aligned}$$
(2)

This expression says that the displacement \(\varvec{u}(\varvec{x})\) at any point in the cell can be calculated using the cell-centre displacement \(\varvec{u}_P\) and the constant gradient of displacement within the cell \((\varvec{\nabla } \varvec{u})_P\). This approximation is second-order order in space i.e. as the mesh spacing is reduced, the error in this approximation reduces at second-order rate. In principle, any other distribution could be used; for example, Demirdžić [203] extended the approach to use a fourth-order cubic distribution.

Using the approximation in Eq. (2), the inertia term can be calculated using the midpoint rule as a function of the cell-centred values:

$$\begin{aligned} \int _\Omega \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}\;\text {d}\Omega\,\approx & {} \,\rho \left( \frac{\partial ^2 \varvec{u}}{\partial t^2}\right) _P \Omega _P \end{aligned}$$
(3)

where the subscript P on the density has been dropped as a uniform density field is assumed i.e. \(\rho _P = \rho\).

The acceleration \(\partial ^2 \varvec{u}/\partial t^2\) may be discretised in time using any appropriate finite difference scheme; in the original cell-centred approach of Demirdžić et al. [2], the bounded first-order backward Euler method was used:

$$\begin{aligned} \left( \frac{\partial ^2 \varvec{u}}{\partial t^2}\right) _P\approx & {}\, \frac{\varvec{u}_P - 2\varvec{u}_P^{[m-1]} + \varvec{u}_P^{[m-2]}}{\Delta t^2} \end{aligned}$$
(4)

where m is the time-step counter; the superscript on the unknown current time value of displacement has been dropped for brevity. Here it is assumed that the time-step size \(\Delta t\) is constant; however, the method can be generalised to variable time-step sizes. There are numerous other temporal discretisations that may be used; for example, the unbounded second-order backward Euler scheme [194], the second-order trapezoidal rule [199], or the second-order Newmark schemes that are popular with the finite element method.

The final discretised inertia term is:

$$\begin{aligned} \int _\Omega \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}\;\text {d}\Omega\,\approx & {} \,\rho \; \frac{\varvec{u}_P - 2\varvec{u}_P^{[m-1]} + \varvec{u}_P^{[m-2]}}{\Delta t^2} \; \Omega _P \end{aligned}$$
(5)

In a similar fashion, the body force term (second term on the right-hand side of Eq. (1)) is approximated by assuming \(\varvec{f}_b\) to vary over the cell according to Eq. (2). Consequently, the term can be approximated in terms of the cell-centre values using the midpoint rule as:

$$\begin{aligned} \int _\Omega \rho \varvec{f}_b \;\text {d}\Omega\,\approx & {}\, \rho \varvec{f}_{b_P} \Omega _P \end{aligned}$$
(6)

Towards the discretisation of the surface force term, the closed surface integral in Eq. (1) is converted into a sum of surface integrals over each polygonal face:

$$\begin{aligned}&\oint _\Gamma \varvec{n} \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;\text {d}\Gamma \nonumber \\&\quad = \sum ^{nFaces}_{f=1} \int _{\Gamma _f} \varvec{n} \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;\text {d}\Gamma \end{aligned}$$
(7)

where nFaces is the number of faces in the cell. This form represents a force balance for the cell. To approximate the stress term \([\mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} ]\) at each cell face, the assumed variation of displacement in Eq. (2) is once again used; accordingly, the stress can be calculated in terms of the displacement gradient values at the face centre (centroid):

$$\begin{aligned}&\sum ^{nFaces}_{f=1} \int _{\Gamma _f} \varvec{n} \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;\text {d}\Gamma \nonumber \\&\quad \approx \sum ^{nFaces}_{f=1} \varvec{n}_{f} \cdot \left[ \mu (\varvec{\nabla } \varvec{u})_{f} + \mu (\varvec{\nabla } \varvec{u})^T_{f} + \lambda \; \text {tr}\left[ (\varvec{\nabla } \varvec{u})_{f} \right] \mathbf{I} \right] |\varvec{\Gamma }_{f}| \end{aligned}$$
(8)

where subscript f indicates a quantity at a face centre, for example, \((\varvec{\nabla } \varvec{u})_{f}\) is the gradient of displacement tensor at the centre of face f. The approach used to approximate this face displacement gradient is one of the principal differences between variants of the finite volume method. In addition, polygonal faces may not be flat and approaches have been examined to accommodate this; for example, Tuković et al. [208] proposed decomposing all faces into triangles before evaluating the forces.

As a consequence of the assumed variation (Eq. 2), the gradient of displacement \(\varvec{\nabla } \varvec{u}\) is constant within each cell and so the displacement gradient at a face, between two cells, is discontinuous; to resolve this, the standard cell-centred approach expresses the displacement gradient at a face \((\varvec{\nabla } \varvec{u})_{f}\) as a weighted mean of the displacement gradient at the two adjacent cell-centres:

$$\begin{aligned} (\varvec{\nabla } \varvec{u})_{f}\,\approx & {} \;\gamma _{f} (\varvec{\nabla } \varvec{u})_P + (1 - \gamma _{f}) (\varvec{\nabla } \varvec{u})_{N_{f}} \end{aligned}$$
(9)

where subscript P indicates a quantity at the current cell-centre, subscript \(N_f\) indicates a quantity at the neighbour cell-centre adjacent to face f, and \(0< \gamma _{f} < 1\) is the interpolation weight. Typically, the interpolation weight is calculated using an inverse distance method:

$$\begin{aligned} \gamma _{f} \,= \frac{|\varvec{x}_{N_f} - \varvec{x}_{f}|}{|(\varvec{x}_{f} - \varvec{x}_P) + (\varvec{x}_{N_f} - \varvec{x}_{f})|} \end{aligned}$$
(10)

In addition to the standard cell-centred method for approximating the face centre displacement gradient given in Eq. (9), a number of alternative methods have also been examined, for example, temporary elements with isoparametric formulations [204] or using a compact stencil for the normal gradient as in the original discretisation of Demirdžić et al. [2]; in this compact stencil form, the normal component is calculated using central differencing:

$$\begin{aligned} (\varvec{\nabla } \varvec{u})_{f}&\approx \underbrace{ \varvec{n}_f \left[ \frac{|\varvec{\Delta }_{f}|}{|\varvec{\Gamma}_{f}|} \frac{\varvec{u}_{N_{f}} - \varvec{u}_P}{|\varvec{d}_{f}|} + \frac{\varvec{\Gamma }_{f} - \varvec{\Delta }_{f}}{|\varvec{\Gamma}_{f}|} \cdot (\varvec{\nabla } \varvec{u})_{f} \right] }_{\text {normal component}} \nonumber \\&\quad + \underbrace{ (\mathbf{I} - \varvec{n}_f \varvec{n}_f) \cdot \left[ \gamma _{f} (\varvec{\nabla } \varvec{u})_P + (1 - \gamma _{f}) (\varvec{\nabla } \varvec{u})_{N_{f}} \right] }_{\text {tangential component}} \end{aligned}$$
(11)

where \(\varvec{n}_f = \varvec{\Gamma }_{f}/|\varvec{\Gamma }_{f}|\) are the face unit normals, and:

$$\begin{aligned} \varvec{\Delta }_{f} = \frac{\varvec{d}_{f}}{\varvec{d}_{f} \cdot \varvec{n}_{f}} |\varvec{\Gamma }_{f}| \end{aligned}$$
(12)

At this point, it is worth noting the locally conservative nature of the discretisation: adjacent cells share integration points at the face centres, resulting in the force at cell faces being locally and hence globally conserved. This is a characteristic shared by all finite volume methods.

To complete the discretisation of the surface force in terms of displacement \(\varvec{u}\), the cell-centred displacement gradients need to be expressed in terms of the cell-centred displacements. For its accuracy on unstructured grids and ease of implementation, the least-squares method is the most popular:

$$\begin{aligned} (\varvec{\nabla } \varvec{u})_P\approx & {} \left[ \sum _{f=1}^{nFaces} w_{f}^2 \varvec{d}_{f} \varvec{d}_{f} \right] ^{-1} \cdot \sum _{f=1}^{nFaces} \left[ w_{f}^2 \varvec{d}_{f} \left( \varvec{u}_{N_{f}} - \varvec{u}_P \right) \right] \end{aligned}$$
(13)

As shown previously in Fig. 8, vector \(\varvec{d}_{f}\) joins cell-centre P to the neighbour cell-centre \(N_f\). The scalar weighting function can be taken as unity (\(w_{f} = 1\)) [29] or as the inverse distance (\(w_{f} = \nicefrac {1}{|\varvec{d}_{f}|}\)) [194]. Alternative gradient calculation methods, such as the Gauss divergence method or point Gauss divergence method [208] have also been proposed. With respect to the Gauss divergence method of gradient calculation, this approach stems from the Lawrence Livermore Laboratory ‘hydrocodes’ of the 1960s developed by Wilkins [399, 400]. Zienkiewicz and Oñate [6, 12] claimed this Gauss divergence cell-gradient method to be “an early attempt to use FV concepts in CSM”; this link is, however, tenuous; the Gauss divergence cell-gradient calculation is not a core postulate of the finite volume method and is in fact not required. For descriptions of subsequent finite difference developments based on the original Wilkins [399] approach, the interested reader is referred to [401, 402].

Although the discretisation of the surface force in terms of displacement \(\varvec{u}\) is complete, the presented discretisation is unstable and known to suffer from so-called checker-boarding errors. Without an appropriate stabilisation term, oscillations in the displacement field, which are twice the period of the cell size, will go unnoticed. These unstable oscillations are analogous to the spurious singular modes that appear in reduced-integration finite element discretisations, also known as zero-energy modes or hourglassing. Typically the implicit cell-centred approach adds the so-called Rhie–Chow stabilisation term to the discretised divergence of stress (Eq. 8), as introduced to solid mechanics by Demirdžić and Muzaferija [29]:

(14)

This third-order diffusion term corresponds to the difference between two ways of calculating the normal gradient of displacement at a face, resulting in an ability to ‘sense’ high-frequency oscillations in \(\varvec{u}\). The approach was first proposed by Rhie and Chow [403] in the context of cell-centred finite volume methods for incompressible fluid flow, and is commonly used in cell-centred finite volume fluid formulations. The \(K_{f}\) coefficient controls the magnitude of the smoothing effect and is typically taken as \(K_{f} = \mu\) [29], \(K_{f} = \mu + \lambda\) [194] or \(K_{f} = 2\mu + \lambda\) [30]. The third-order diffusion term also serves a purpose towards choice of implicit components within the segregated solution algorithm: this is discussed further below. Alternative forms of diffusion/smoothing terms have been also been proposed, for example, the fourth-order Jameson–Schmidt–Turkel [404] term employed in Godunov-type approaches [31, 237], which takes the form of a Laplacian of a Laplacian:

(15)

The scalar coefficient \(K_{\text {JST}}\) gives the correct dimension to the dissipation as well as controlling its magnitude.

The final discretised form of the governing momentum equation, employing the Rhie–Chow form of stabilisation and \(K_f = 2\mu + \lambda\), is expressed as:

$$\begin{aligned}&\rho \, \frac{\varvec{u}_P - 2\varvec{u}_P^{[m-1]} + \varvec{u}_P^{[m-2]}}{\Delta t^2} \, \Omega _P \nonumber \\&\quad = \sum ^{nFaces}_{f=1} \varvec{n}_{f} \cdot \left[ \mu (\varvec{\nabla } \varvec{u})_{f} + \mu (\varvec{\nabla } \varvec{u})^T_{f} + \lambda \; \text {tr}\left[ (\varvec{\nabla } \varvec{u})_{f} \right] \mathbf{I} \right] |\varvec{\Gamma }_{f}| \nonumber \\&\qquad \;+\; \sum ^{nFaces}_{f=1} (2\mu + \lambda ) \left[ |\varvec{\Delta }_{f}| \frac{\varvec{u}_{N_{f}} - \varvec{u}_P}{|\varvec{d}_{f}|} - \varvec{\Delta }_{f} \cdot (\varvec{\nabla } \varvec{u})_{f} \right] \nonumber \\&\qquad \;+\; \rho \varvec{f}_{b_P} \Omega _P \end{aligned}$$
(16)

where the face displacement gradients \((\varvec{\nabla } \varvec{u})_{f}\) are calculated using Eqs. (9), (10) and (13). The primitive unknown variables are the cell-centre displacement vectors \(\varvec{u}_P\) at time t (time index [m]).

Boundary conditions are incorporated through appropriate modification of the surface force term discretisation at faces coinciding with the boundary of the solution domain. In the case of a displacement condition \(\varvec{u}_b\) (Dirichlet boundary condition), the face displacement gradients are calculated at the face, while in the case of a traction condition \(\varvec{T}_b\) (Neumann boundary condition), the specified traction directly replaces the surface stress expression. Initial conditions, in the form of the displacement field at \(t = 0\), \(t = -\Delta t\), and \(t = -2\Delta t\), must also be specified.

3.2.4 Solution Algorithm

In order to solve the discretised governing equation (Eq. 16) for the unknown displacement vector, the typical cell-centre approach uses a segregated solution procedure, where the central-differencing component in Eq. (16), \((2\mu + \lambda ) |\varvec{\Delta }_{f}| (\varvec{u}_{N_{f}} - \varvec{u}_P)/|\varvec{d}_{f}|\), and \(\rho \left( \varvec{u}_P/\Delta t^2 \right) \Omega _P\) within the inertia term are treated implicitly; all other terms are calculated explicitly using the latest available displacement field. The purpose of the segregated approach is to temporarily decouple/segregate the three scalar components of the vector momentum equation so that they can be solved sequentially; outer fixed-point/Gauss–Seidel/Picard iterations provide the necessary coupling, where the displacement gradient terms are explicitly updated each outer iteration using the latest available displacement field. Employing this implicit–explicit split, the discretised equation for each cell can be written in the form of a linear algebraic equation:

$$\begin{aligned} a_P \; \varvec{u}_P \; - \sum _{f=1}^{nFaces} a_{N_{f}} \varvec{u}_{N_{f}}= \;\;& {} \varvec{b}_P \end{aligned}$$
(17)

where

$$\begin{aligned} a_P= \;& {} \frac{\rho \Omega _P}{\Delta t^2} + \sum _{f=1}^{nFaces} a_{N_{f}} \end{aligned}$$
(18)
$$\begin{aligned} a_{N_{f}}= \;& {} (2\mu + \lambda ) \frac{|\varvec{\Delta }_{f}|}{|\varvec{d}_{f}|} \end{aligned}$$
(19)
$$\begin{aligned} \varvec{b}_P= \;& {} \;\rho \, \frac{2\varvec{u}_P^{[m-1]} - \varvec{u}_P^{[m-2]}}{\Delta t^2} \, \Omega _P \nonumber \\&+ \sum ^{nFaces}_{f=1} \varvec{n}_{f} \cdot \left\{ \mu (\varvec{\nabla } \varvec{u})_{f} + \mu (\varvec{\nabla } \varvec{u})^T_{f} + \lambda \; \text {tr}\left[ (\varvec{\nabla } \varvec{u})_{f} \right] \mathbf{I} \right\} |\varvec{\Gamma }_{f}| \nonumber \\&- \sum ^{nFaces}_{f=1} (2\mu + \lambda ) \varvec{\Delta }_{f} \cdot (\varvec{\nabla } \varvec{u})_{f} \;\;+\;\; \rho \varvec{f}_{b_P} \Omega _P \end{aligned}$$
(20)

In contrast, typical implicit vertex-centred and implicit finite element solution algorithms treat the entire divergence of stress term implicitly within the linear system matrix, or a linearisation of it when nonlinearities are present. This so-called block-coupled approach has also been proposed for the cell-centred approach [25, 59]: in this case, \(a_P\) and \(a_{N_{f}}\) in Eq. (17) are second-order tensors.

The algebraic equations (Eq. 17) can be assembled for all M cells in the domain into the form of three decoupled linear systems:

$$\begin{aligned} \left[ \varvec{K} \right] \left[ \varvec{U} \right] = \left[ \varvec{F} \right] \end{aligned}$$
(21)

where \(\left[ \varvec{K} \right]\) is a \(M \times M\) sparse matrix with diagonal coefficients \(a_P\) and off-diagonal coefficients \(a_{N_{f}}\), \(\left[ \varvec{U} \right]\) is a vector of the unknown cell-centre displacement vectors, and \(\left[ \varvec{F} \right]\) is the source vector containing contributions from \(\varvec{b}_P\). In finite element parlance, \(\left[ \varvec{K} \right]\) is the global stiffness matrix and \(\left[ \varvec{F} \right]\) is the global force vector. The segregated cell-centred discretisation ensures that matrix \(\left[ \varvec{K} \right]\) has the following properties [29]:

  • It is sparse with the number of non-zero elements in each row equal to the number of nearest neighbours cells (those sharing a face with the cell) plus one;

  • It is symmetric;

  • It is positive definite;

  • It is diagonally dominant (\(|a_P| \ge \sum _{f=1}^{nFaces} |a_{N_{f}}|\)), which makes the linear system efficiently solved by a number of iterative methods, which retain the sparsity of matrix \(\left[ \varvec{K} \right]\): this results in significantly lower memory requirements than equivalent direct linear solvers, for example, see [25]. The most common iterative method used is the conjugate gradient method with incomplete Cholesky preconditioning [405].

It is worth noting that the segregated solution algorithm has been shown to suffer from slow convergence for slender geometry undergoing bending [25]; in that case, a block-coupled algorithm is significantly faster [25] and \(\left[ \varvec{K} \right]\) is a \(M \times M\) sparse matrix, where each coefficient is a second-order tensor.

For the segregated approach, the linear system (Eq. 21) need not be solved to a tight tolerance as coefficients and source terms are approximated from the previous outer iteration; instead, a reduction in the residuals of one order of magnitude is typically sufficient. Outer iterations are performed until the predefined solution tolerance has been achieved. Under-relaxation of the displacement field and/or the linear system may improve convergence, depending on the boundary conditions and mesh. Acceleration of the approach can be achieved through geometric multi-grid procedures [86, 120, 197], block-coupled algorithms [30, 188, 189, 199], Aitken acceleration [78, 160, 199], and/or parallelisation on distributed memory clusters [88, 194]. A favourable characteristic of the solution procedure is the straightforward extension to nonlinearity: nonlinear terms (material, geometric or boundary conditions) are resolved on the fly; after each outer iteration the coefficients and the source terms are updated and the procedure continues as in the linear case, for example, compare the linear elasticity approach of Jasak and Weller [194] with the finite strain elasto-plastic frictional contact procedure of Cardiff et al. [30].

In addition to the displacement-based approach described above, alternative solution algorithms, where pressure and displacement are the primary variables, have been proposed by Bijelonja et al. [95, 97, 100] and Fowler and Yee [200]; the benefit of such approaches is their ability to deal with incompressible and quasi-incompressible solids in a straightforward manner, while avoiding pressure instabilities.

3.3 Implicit Vertex-Centred Approach

3.3.1 Discretisation of Space

Like the other approaches, the vertex-centred approach divides the spatial domain into a finite number of contiguous cells that do not overlap and fill the space completely. When compared with the typical cell-centred approach, there are two key differences related to the mesh arrangement:

  • The vertex-centred approach integrates the governing equations over cells in a secondary-grid, with cells that are typically constructed around the vertices/points in the primary grid (Fig. 9). The resulting secondary grid cells may not preserve convexity;

  • The primitive unknowns are stored at the vertices/points of the primary grid, corresponding to the approximate, but not necessarily exact, centre of the secondary-grid cells.

However, in essence vertex-centred approaches can be viewed as a form of cell-centred method integrated over a secondary mesh.

Fig. 9
figure 9

Figure adapted from Hassan [406]. (Color figure online)

2-D vertex-centred grid showing the (a) primary mesh, (b) secondary-grid used to integrate the governing equations.

Full size image

In principal, the primary mesh can consist of arbitrary convex polyhedral cells; however, depending on the chosen discretisation (for example, if shape functions are used), the method may be limited to triangular/quadrilateral meshes in 2-D and tetrahedral/hexahedral meshes in 3-D; in fact, no vertex-centred solid mechanics examples using polyhedral meshes were found when preparing this article.

In addition to this form of the vertex-centred approach, a variant exists where the primary mesh cells around a vertex are used to perform the integration, for example, as discussed by Oñate et al. [12]; this produces overlapping regions of integration, where neighbouring vertices share part of their integrated volume. Secondary-grid cells can also be created by joining the mesh cell centres together [249], rather than joining the cell-centres to the face-centres as per the classic vertex-based method.

3.3.2 Discretisation of the Mathematical Model Equations

The vertex-centred approach starts from the strong integral form of the governing momentum equation (Eq. 1), which is integrated over a secondary-grid [5]. The vertex-centred approach discretises each term of the governing equation over the cells in the secondary-grid. An example secondary-grid cell is shown in Fig. 10, where each vertex i in the primary grid is uniquely associated with a cell in the secondary-grid.

Fig. 10
figure 10

Figure adapted from Bailey and Cross [24]. (Color figure online)

A typical control volume constructed around vertex i, with a volume \(\Omega _i\). The solid lines show the primary grid and the dashed lines show the secondary-grid. When calculating the momentum balance for a secondary-grid cell (shaded), the displacement gradient is calculated at the boundary edge centres (boundary face centres in 3-D) of the secondary-grid cell (marked by “x”).

Full size image

As with the cell-centred variant, the discretisation of each of the three terms (inertia, surface forces, body forces) in the governing conservation law (Eq. 1) will now be discussed in turn.

To approximate the volume integral temporal term, the displacement \(\varvec{u}\) within each secondary-grid cell is assumed to be constant [24, 240, 273]. Consequently, for a volume about vertex i, the term may be approximated in terms of the acceleration at vertex i and the secondary-grid cell volume \(\Omega _i\) about vertex i:

$$\begin{aligned} \int _\Omega \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}\;\text {d}\Omega\,\approx & {} \,\rho \left( \frac{\partial ^2 \varvec{u}}{\partial t^2}\right) _i \Omega _i \end{aligned}$$
(22)

As with other finite volume approaches, the acceleration term \(\partial ^2 \varvec{u}/\partial t^2\) may be discretised in time using any appropriate finite difference scheme. For example, Slone et al. [273] employed the Newmark finite difference scheme, which is popular in the finite element community. For ease of comparison with the cell-centred approach (Eq. 5), a first-order Euler scheme is assumed here, giving the final discretised term as:

$$\begin{aligned} \int _\Omega \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}\;\text {d}\Omega\,\approx & {} \,\rho \; \frac{\varvec{u}_i - 2\varvec{u}_i^{[m-1]} + \varvec{u}_i^{[m-2]}}{\Delta t^2} \; \Omega _i \end{aligned}$$
(23)

Comparing this expression with the equivalent cell-centred expression (Eq. 5), the only difference is the mesh location where the unknown displacement is stored. A conceptual difference comes from the fact that vertex i is not in general situated at the centre of the secondary-grid cell volume \(\Omega _i\); consequently, in the approximation of the inertia term, the cell-centred approach allows a local linear displacement distribution, whereas the vertex-centred approach requires a constant displacement distribution.

The volume integral body force term is discretised in a similar manner to the temporal term, where the body force \(\varvec{f}_b\) is assumed to be constant within each secondary-grid cell and equal to the value at vertex i:

$$\begin{aligned} \int _\Omega \rho \varvec{f}_b \;\text {d}\Omega\,\approx & {}\, \rho \varvec{f}_{b_i} \Omega _i \end{aligned}$$
(24)

Once again the discretised term differs from the the equivalent cell-centred term in that a constant rather than a linear local variation is assumed. In the case that vertex i does lie at the centroid of the control volume, then the vertex-centred and cell-centred terms are the same.

To discretise the surface force term, the closed surface integral in Eq. (1) is converted into a sum of surface integrals over the faces of the secondary-grid cell, taking the same form as Eq. (7). Approximation of the stress term at each face requires an assumption about the local displacement distribution. In contrast to the standard cell-centred approach, most vertex-centred approaches explicitly use shape functions to describe the local displacement field variation. Following the standard finite element notation, these shape (or interpolation) functions refer to the displacement within each cell of the primary mesh:

$$\begin{aligned} \varvec{u}(\varvec{x}) = \sum _{i=1}^{nVertices} N_i (\varvec{x}) \varvec{u}_i = \left[ \varvec{N} \right] \left[ \varvec{u} \right] \end{aligned}$$
(25)

where nVertices is the number of vertices in the primary mesh cell of interest, \(N_i (\varvec{x})\) is the shape function associated with vertex i within the cell, \(\varvec{u}_i\) is the displacement at vertex i, and \(\left[ \varvec{N} \right]\) and \(\left[ \varvec{u} \right]\) represent a vector of all shape functions and nodal displacements within the cell respectively. It should be emphasised that these shape functions refer to the vertices and cells of the primary mesh, as opposed to of the secondary mesh cells.

As is standard in the conventional continuous Bubnov–Galerkin finite element method, the shape functions, which are defined in the reference domain and mapped to the physical domain, approximate the displacement field as a continuous piecewise distribution. As the shape functions describe the displacement distribution between the vertices on the primary mesh, this allows convenient calculation of the displacement gradients at the secondary-grid cell boundaries when applying the momentum balance (Fig. 10). Although shape functions are a key characteristic of the vertex-centred approaches presented in literature, they are not essential. As shown by Tsui et al. [249], it is possible to develop a vertex-centred finite volume approach that does not directly use shape functions; similar to many cell-centred approaches, Tsui et al. [249] applied the Gauss divergence theorem to calculate secondary-grid cell displacement gradients; these gradients were then interpolated to secondary-grid cell faces. In the cell-centred approach, the truncated Taylor series expansion about the cell centres (Eq. 2) fulfills the role of shape functions. As shape functions are specific to the cell geometry (e.g. triangle, quadrilateral, tetrahedral), shape function based approaches are limited in their choice of element shape, whereas all convex polyhedral meshes are valid for cell-centred approaches.

To approximate the stress at the faces of a secondary-grid cell, the gradient of displacement must be calculated. The use of shape functions allows this spatial gradient of displacement to be conveniently calculated as:

$$\begin{aligned} \varvec{\nabla } \varvec{u} \approx \sum _{i=1}^{nVertices} \varvec{\nabla } N_i (\varvec{x}) \varvec{u}_i = \left[ \varvec{B} \right] \left[ \varvec{u} \right] \end{aligned}$$
(26)

where \(\left[ \varvec{B} \right]\) is a vector of the shape functions gradients. Substituting Eq. (26) into Eq. (7) allows the surface force term to be expressed in terms of the unknown displacements at the primary mesh vertices:

$$\begin{aligned} &\sum ^{nFaces}_{f=1} \int _{\Gamma _i} \varvec{n} \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;\text {d}\Gamma \nonumber \\ &\quad\approx\sum _{f=1}^{nFaces} \sum _{v=1}^{nVertices} \varvec{n}_f \cdot \left[ \mu \varvec{\nabla } N_{vf} \varvec{u}_v + \mu \varvec{u}_v \varvec{\nabla } N_{vf} + \lambda \; \text {tr}(\varvec{\nabla } N_{vf} \varvec{u}_v ) \mathbf{I} \right] \end{aligned}$$
(27)

where nVertices refers to the number of vertices in the primary-grid cell in which the secondary-grid face f is situated; \(N_{vf}\) refers to the corresponding shape function for vertex v within the primary-gird cell. Consequently, the surface force term for a secondary-grid cell surrounding vertex v will be a function of the displacement at vertex v as well as the displacement at all vertices that share a primary-grid cell with vertex v. For example, for the secondary-grid cell shown in Fig. 10, the surface force term will be a function of the displacements at all vertices shown except for the vertex in the top-right.

The final discretised form of the governing momentum equation for the vertex-centred approach is expressed for a secondary-grid cell as:

$$\begin{aligned}&\rho \, \frac{\varvec{u}_i - 2\varvec{u}_i^{[m-1]} + \varvec{u}_i^{[m-2]}}{\Delta t^2} \, \Omega _i \nonumber \\&\quad =\sum _{f=1}^{nFaces} \sum _{v=1}^{nVertices} \varvec{n}_f \nonumber \\&\qquad \cdot \left[ \mu \varvec{\nabla } N_{vf} \varvec{u}_v + \mu \varvec{u}_v \varvec{\nabla } N_{vf} + \lambda \; \text {tr}(\varvec{\nabla } N_{vf} \varvec{u}_v ) \mathbf{I} \right] \nonumber \\&\qquad +\rho \varvec{f}_{b_v} \Omega _v \end{aligned}$$
(28)

As with the other finite volume approaches, boundary conditions are incorporated through appropriate modification of the surface force term, and initial conditions must be specified for dynamic cases.

3.3.3 Solution Algorithm

The discretised equation for each secondary-grid cell can be written in the form of an algebraic equation:

$$\begin{aligned} \varvec{A}_i \cdot \varvec{u}_i \; - \sum _{v=1}^{nVertices} \varvec{A}_{v} \cdot \varvec{u}_{v}= & {} \;\varvec{b}_i \end{aligned}$$
(29)

where \(\varvec{u}_i\) is the displacement at the primary-grid vertex associated with the secondary-grid cell, and nVertices indicates all vertices which share a primary-grid cell with vertex i. \(\varvec{A}_i\) and \(\varvec{A}_{v}\) are the corresponding block coefficients (second-order tensors in 3-D).

In earlier publications [5], the vertex-centred approach followed a similar solution algorithm to the standard cell-centred approach, where the surface force term was partitioned into implicit and explicit components and a segregated solution algorithm was employed. In later publications [24], a block-coupled solution procedure is used, where the entire surface force term is discretised implicitly. As noted previously, similar coupled solution algorithms were later proposed for the cell-centred variant by Das et al. [188] and Cardiff et al. [25].

Following the block-coupled approach, the algebraic equations (Eq. 29) can be assembled for all M secondary-grid cells (primary-grid vertices) in the domain to form a system of linear equations:

$$\begin{aligned} \left[ \varvec{K} \right] \left[ \varvec{U} \right] = \left[ \varvec{F} \right] \end{aligned}$$
(30)

where the \(M \times M\) global stiffness matrix \(\left[ \varvec{K} \right]\) is sparse with block diagonal coefficients \(\varvec{A}_i\) and off-diagonal block coefficients \(\varvec{A}_{v}\), \(\left[ \varvec{U} \right]\) is a vector of the unknown primary-grid vertex displacement vectors, and the global force source vector \(\left[ \varvec{F} \right]\) contains contributions from \(\varvec{b}_i\).

This linear system can then be solved using direct or iterative linear solvers, where iterative conjugate gradient solvers with diagonal/Jacobi scaling have been favoured in literature, for example, [5, 24]. Parallelisation on distributed memory supercomputers has been addressed by McManus et al. [303, 304], and mixed displacement-rotation approaches have also been employed [300,301,302].

3.4 Explicit Cell-Centred Godunov-Type Approach

Godunov-type procedures are specialised approaches for analysis of problems that involve wave propagation, shocks and solution discontinuities. Features that distinguish this variant of finite volume approach from the others are the use of acoustic Riemann solvers, solution reconstruction procedures, slope limiters for gradient calculations, occasionally nodal integration, as well as representing the governing equations as a coupled system of first-order equations; in addition, explicit time marching solution algorithms are employed.

3.4.1 Discretisation of Space

The majority of Godunov-type approaches are spatially discretised using cell-centred approaches, for example, [26,27,28, 196, 220, 222, 223, 225,226,227,228,229, 231,232,233,234,235,236]; consequently, this section will focus on such approaches; however, Godunov-type approaches have also used vertex-centred [31, 237], staggered grid [224, 228] and face-centred [20, 21] formulations. To-date, many of the developments have been limited to one and two dimensions, but in general the procedures can be extended to three dimensions. Like the implicit cell-centred approach described in Sect. 3.2, the solution spatial domain is divided into a finite number of contiguous convex polyhedral cells bounded by polygonal faces that do not overlap and fill the space completely.

3.4.2 Discretisation of the Mathematical Model Equations

In a notable deviation from the other finite volume variants, Godunov-type approaches portray the second-order governing momentum equation (Eq. 1) as a coupled system of first-order equations:

$$\begin{aligned} \int _\Omega \rho \frac{\partial \varvec{v}}{\partial t}\;\text {d}\Omega= & {} \oint _\Gamma \varvec{n} \cdot \varvec{\sigma } \;\text {d}\varvec{\Gamma } \;+\; \int _\Omega \rho \varvec{f}_b \;\text {d}\Omega \end{aligned}$$
(31)
$$\begin{aligned} \int _\Omega \frac{\partial \varvec{F}}{\partial t}\;\text {d}\Omega= & {} \oint _\Gamma \varvec{v} \varvec{n} \;\text {d}\varvec{\Gamma } \end{aligned}$$
(32)

where \(\varvec{v}\) is the velocity vector and the deformation gradient, \(\varvec{F}\), defines the local deformation as:

$$\begin{aligned} \varvec{F} = \mathbf{I} + (\varvec{\nabla } \varvec{u})^T \end{aligned}$$
(33)

Equation (32) is obtained by taking the time-derivative of Eq. (33) and employing the Gauss divergence theorem.

To ensure the compatibility conditions are satisfied, the deformation gradient at the initial time should be curl free:

$$\begin{aligned} \varvec{\nabla } \times \varvec{F}^{[m = 0]} = \varvec{0} \end{aligned}$$
(34)

In addition, the discrete evolution of \(\varvec{F}\) (or \(\varvec{\nabla } \varvec{u}\)) should not allow curl errors to escalate. For further discussion of this point, see [27, 28, 40, 214, 225]. It is also possible to employ the evolution of the displacement gradient \(\varvec{\nabla } \varvec{u}\) directly rather than the deformation gradient, as shown by Trangenstein and Colella [40]; however, this is less popular in literature.

The governing system of coupled first-order equations (Eqs. 31, 32) can be expressed concisely as:

$$\begin{aligned} \int _\Omega \frac{\partial \varvec{\mathcal {U}}}{\partial t} \;\text {d}\Omega = \oint _\Gamma \varvec{\mathcal {F}}_n \;\text {d}\varvec{\Gamma } + \int _\Omega \varvec{\mathcal {S}} \;\text {d}\Omega \end{aligned}$$
(35)

where \(\varvec{\mathcal {U}}\) is the primary unknown vector, \(\varvec{\mathcal {F}}_n\) is the flux vector, and \(\varvec{\mathcal {S}}\) is the source vector, given as:

$$\begin{aligned} \varvec{\mathcal {U}} = \begin{pmatrix} \varvec{v} \\ \varvec{F} \end{pmatrix}, \quad \varvec{\mathcal {F}}_n = \begin{pmatrix} \nicefrac {\varvec{t}}{\rho } \\ \varvec{v}\varvec{n} \end{pmatrix}, \quad \varvec{\mathcal {S}} = \begin{pmatrix} \varvec{f}_b \\ \varvec{0} \end{pmatrix} \end{aligned}$$
(36)

and the traction vector, \(\varvec{t}\), gives the stress on a plane as \(\varvec{t} = \varvec{n} \cdot \varvec{\sigma }\). To close the system, we give the constitutive relation (Hooke’s law) in terms of the deformation gradient:

$$\begin{aligned} \varvec{\sigma } = \mu \varvec{F}^T + \mu \varvec{F} + \lambda \; \text {tr} \left( \varvec{F} \right) \mathbf{I} - (2\mu + 3 \lambda )\mathbf{I} \end{aligned}$$
(37)

We next describe the discretisation of the three terms in Eq. (35): the time derivative term, the diffusion term and the body force term.

Assuming the primary unknowns (\(\varvec{v}\) and \(\varvec{F}\)) vary linearly within each cell according to Eq. (2), the volume integrals can be expressed in terms of the cell-centre values (subscript P) and the surface integral becomes a sum over the face-centre values (subscript f); consequently, Eq. (35) becomes:

$$\begin{aligned} \frac{\partial \varvec{\mathcal {U}}_P}{\partial t} \Omega _P = \sum _{f=1}^{nFaces} \varvec{\mathcal {F}}_{n_f} |\varvec{\Gamma }_f| \; \; + \; \; \varvec{\mathcal {S}}_P \Omega _P \end{aligned}$$
(38)

Similar to the other approaches, discretisation of the time-rate term can be achieved using a variety of finite difference methods. Here we assume a first-order forward Euler discretisation to allow straight-forward comparison with the other methods:

$$\begin{aligned} \frac{\varvec{\mathcal {U}}_P - \varvec{\mathcal {U}}_P^{[m-1]}}{\Delta t} \Omega _P = \sum _{f=1}^{nFaces} \varvec{\mathcal {F}}_{n_f}^{[m-1]} |\varvec{\Gamma }_f| \; \; + \; \; \varvec{\mathcal {S}}_P \Omega _P \end{aligned}$$
(39)

where, as before, m is the time-step counter, which for brevity has been dropped on the unknown current time value. Of course, as an explicit time-marching solution algorithm will be employed, the time step size is limited by the Courant–Friedrichs–Lewy constraint [34]; this condition is necessary for stability but is not sufficient. It is also necessary that the time integrator avoids the creation of new local extrema, known as the total variation diminishing property or the local maximum principle; the first-order forward Euler approach is one such method that obeys this condition.

Alternatively, the flux calculation in Eq. (39), which sums over the cell faces, can be expressed as a sum over the cell points/vertices according to:

$$\begin{aligned} \frac{\varvec{\mathcal {U}}_P - \varvec{\mathcal {U}}_P^{[m-1]}}{\Delta t} \Omega _P = \sum _{v=1}^{nVertices} \varvec{\mathcal {F}}_{n_v}^{[m-1]} |\varvec{C}_v| \; \; + \; \; \varvec{\mathcal {S}}_P \Omega _P \end{aligned}$$
(40)

where the calculation of the point/vertex/nodal area vector, \(\varvec{C}_v\), is given in Carré et al. [221] and Kluth and Després [26] or equivalently in Maire et al. [222].

Up to this point, the presented discretisation coincides with the cell-centred approach described in Sect. 3.2, apart from the introduction of a system of first-order conservation equation and the use of the forward Euler method as opposed to the backward Euler method; however, in the discretisation of the face flux, \(\varvec{\mathcal {F}}_n\), Godunov-type methods deviate from the other approaches. As a result of the assumed piecewise linear distribution (Eq. 2), there is a discontinuity at the cell internal faces. A distinguishing characteristic of Godunov-type methods is the acknowledgement of this discontinuity in the solution field, known as a Riemann problem, and the development of appropriate methods (Riemann solvers) to deal with the propagation of this discontinuity. Accordingly, the face flux, \(\varvec{\mathcal {F}}_n\), is defined as a function of the solution variable at either side of the interface:

$$\begin{aligned} \varvec{\mathcal {F}}_{n_f} = f(\varvec{\mathcal {U}}_{Pf}, \varvec{\mathcal {U}}_{Nf}) \end{aligned}$$
(41)

The solution at either side of the interface (\(\varvec{\mathcal {U}}_{P_f}\) and \(\varvec{\mathcal {U}}_{N_f}\)) is determined via extrapolation from the adjacent cell centres:

$$\begin{aligned} \varvec{\mathcal {U}}_{P_f}= & {}\; \varvec{\mathcal {U}}_{P} + \varvec{G}_P \cdot (\varvec{x}_f - \varvec{x}_P) \nonumber \\ \varvec{\mathcal {U}}_{N_f}= & {} \;\varvec{\mathcal {U}}_{N} + \varvec{G}_N \cdot (\varvec{x}_f - \varvec{x}_N) \end{aligned}$$
(42)

where \(\varvec{G}_P\) is the gradient of \(\varvec{\mathcal {U}}\) within cell P, and \(\varvec{G}_N\) is the gradient within cell N. A critical component of Godunov-type methods is the definition of this solution reconstruction, such that the local maximum principle is preserved i.e. the value of \(\varvec{\mathcal {U}}\) at face f should not be greater than the value at adjacent cell centres P and N. There are a number of ways to define such discrete gradients; here, as a typical example, the monotone upstream scheme for conservation law (MUSCL) scheme is described [27]. The MUSCL approach consists of two steps: first, the gradient is predicted based on local neighbouring values, then this gradient is corrected/limited to respect the local maximum principle.

To predict the gradient, the second-order least-squares method described in Sect. 3.2 can be used; this approach does not prohibit overshoots and undershoots at the faces, and hence does not satisfy the local maximum principle. To remedy this, a so-called slope limiter is used to restrict the value of the gradient, \(\varvec{G}\). The slope limiter is included through modification of the reconstruction expression (Eq. 42):

$$\begin{aligned} \varvec{\mathcal {U}}_{P_f}= & {} \;\varvec{\mathcal {U}}_{P} + \phi _P \varvec{G}_P \cdot (\varvec{x}_f - \varvec{x}_P) \nonumber \\ \varvec{\mathcal {U}}_{N_f}= & {}\; \varvec{\mathcal {U}}_{N} + \phi _N \varvec{G}_N \cdot (\varvec{x}_f - \varvec{x}_N) \end{aligned}$$
(43)

where \(0 \le \phi \le 1\) is a scalar slope limiter. When \(\phi = 1\), no limiting is applied, whereas when \(\phi = 0\), full limiting is applied and the value near the face is assumed equal to the cell-centre value. Choosing the value of \(\phi\) is a balance between stability (lower value of \(\phi\)) and accuracy (higher value of \(\phi\)). For the MUSCL procedure, \(\phi\) is determined as described by Lee et al. [27]:

  1. 1.

    Find the smallest and largest values among the current and adjacent cells:

    $$\begin{aligned} \varvec{\mathcal {U}}^{\text {min}} = \text {min}(\varvec{\mathcal {U}}_P, \varvec{\mathcal {U}}_{Ni}), \quad \varvec{\mathcal {U}}^{\text {max}} = \text {max}(\varvec{\mathcal {U}}_P, \varvec{\mathcal {U}}_{Ni}) \end{aligned}$$
    (44)

    where \(\varvec{\mathcal {U}}_{Ni}\) represents the values at neighbour cells, which share an internal face with cell P.

  2. 2.

    Calculate the un-restricted reconstructed value \(\varvec{\mathcal {U}}_{Pf}\) with \(\phi _P = 1\) at each internal face within cell P.

  3. 3.

    Find the maximum allowable value of \(\phi _{Pf}\) for each face in cell P:

    $$\begin{aligned} \phi _{Pf} = {\left\{ \begin{array}{ll} \text {min}\left( 1, \frac{\varvec{\mathcal {U}}^{\text {max}} - \varvec{\mathcal {U}}_P}{\varvec{\mathcal {U}}_{P_f} - \varvec{\mathcal {U}}_P} \right) , &{} \text {if} \quad \varvec{\mathcal {U}}_{P_f} - \varvec{\mathcal {U}}_{P} > 0 \\ \text {min}\left( 1, \frac{\varvec{\mathcal {U}}^{\text {min}} - \varvec{\mathcal {U}}_P}{\varvec{\mathcal {U}}_{P_f} - \varvec{\mathcal {U}}_P} \right) , &{} \text {if} \quad \varvec{\mathcal {U}}_{P_f} - \varvec{\mathcal {U}}_{P} < 0 \\ 1, &{} \text {if} \quad \varvec{\mathcal {U}}_{P_f} - \varvec{\mathcal {U}}_{P} = 0 \end{array}\right. } \end{aligned}$$
  4. 4.

    Select \(\phi _P = \text {min}_f(\phi _{Pf})\)

  5. 5.

    Calculate the reconstructed value at each internal face using \(\phi _P\) determined in step 4 and Eq. 43.

To complete the discretisation, all that remains is to express the flux vector, \(\varvec{\mathcal {F}}_{n_f}\), in terms of the solution vector, \(\varvec{\mathcal {U}}\). To achieve this, the Rankine–Hugoniot jump conditions [32] are employed. These jump conditions describe the relationship between the states on both sides of a shock wave. The jump conditions corresponding to Eqs. 31 and 32 are [27]:

$$\begin{aligned} U \llbracket \varvec{v}\rrbracket&= -\left( \nicefrac {1}{\rho }\right) \varvec{n} \cdot \llbracket \varvec{\sigma }\rrbracket \end{aligned}$$
(45)
$$\begin{aligned} U\llbracket \varvec{F}\rrbracket&= -\llbracket \varvec{v}\rrbracket \varvec{n} \end{aligned}$$
(46)

where the operator \(\llbracket \cdot \rrbracket\) represents the jump across the shock, for example, \(\llbracket \varvec{\mathcal {U}}_f\rrbracket = \varvec{\mathcal {U}}_{N_f} - \varvec{\mathcal {U}}_{P_f}\). The wave speed is indicated by U. Using Eqs. (45) and (46) and assuming a constant wave speed, the face flux can be expressed as the sum of an average flux and a stabilisation flux [27, 28]:

$$\begin{aligned} \varvec{\mathcal {F}}_{n_f} = \varvec{\mathcal {F}}_{n_f}^{\text {average}} + \varvec{\mathcal {F}}_{n_f}^{\text {stab}} \end{aligned}$$
(47)

where the average flux is:

$$\begin{aligned} \varvec{\mathcal {F}}_{n_f}^{\text {average}} = \frac{1}{2} \left[ \varvec{\mathcal {F}}_n(\varvec{\mathcal {U}}_{P_f}) + \varvec{\mathcal {F}}_n(\varvec{\mathcal {U}}_{N_f}) \right] \end{aligned}$$
(48)

and the so-called upwinding stabilisation term is:

$$\begin{aligned} \varvec{\mathcal {F}}_{n_f}^{\text {stab}}&= \begin{bmatrix} \frac{\rho }{2} \left[ c_s \mathbf{I} + (c_p - c_s) \varvec{n}_f \varvec{n}_f \right] \cdot \left( \varvec{v}_{N_f} - \varvec{v}_{P_f} \right) \\ \frac{1}{2} \left[ \frac{1}{c_s}{} \mathbf{I} + \left(\frac{1}{c_p} - \frac{1}{c_s}\right)\varvec{n}_f \varvec{n}_f \right] \cdot \left( \varvec{n}_f \cdot \left[ \varvec{\sigma }_{N_f} - \varvec{\sigma }_{P_f} \right] \right) \end{bmatrix} \end{aligned}$$
(49)

The volumetric and shear wave speeds are indicated by \(c_p\) and \(c_s\). Jameson–Schmidt–Turkel stabilisation has been used as an alternative to this upwinding stabilisation, and in principle Rhie–Chow stabilisation could also be used.

The final discretised governing equations, given in terms of unknowns \(\varvec{v}^{[m]}_P\) and \(\varvec{F}^{[m]}_P\) at time-step m, are expressed as:

$$\begin{aligned}&\frac{\varvec{v}_P^{[m]} - \varvec{v}_P}{\Delta t} \Omega _P\nonumber \\&\quad = \sum _{f=1}^{nFaces} \frac{1}{2\rho } \varvec{n}_f \cdot \left[ \mu \varvec{F}_{P_f}^T + \mu \varvec{F}_{P_f} + \lambda \; \text {tr} \left( \varvec{F}_{P_f} \right) \mathbf{I} - (2\mu + 3 \lambda )\mathbf{I} \right] |\Gamma _f| \nonumber \\&\qquad \;+\; \sum _{f=1}^{nFaces} \frac{1}{2\rho } \varvec{n}_f \cdot \left[ \mu \varvec{F}_{N_f}^T + \mu \varvec{F}_{N_f} + \lambda \; \text {tr} \left( \varvec{F}_{N_f} \right) \mathbf{I} - (2\mu + 3 \lambda )\mathbf{I} \right] |\Gamma _f| \nonumber \\&\qquad \;+\; \sum _{f=1}^{nFaces} \frac{1}{2} \left[ c_s \mathbf{I} + (c_p - c_s) \varvec{n}_f \varvec{n}_f \right] \cdot \left( \varvec{v}_{N_f} - \varvec{v}_{P_f} \right) |\Gamma _f| \nonumber \\&\qquad \;+ \; \varvec{f}_{b_P} \; \Omega _P \end{aligned}$$
(50)
$$\begin{aligned}&\frac{\varvec{F}_P^{[m]} - \varvec{F}_P}{\Delta t} \Omega _P\nonumber \\&\quad = \sum _{f=1}^{nFaces} \frac{1}{2} \left( \varvec{v}_{P_f} \varvec{n}_f + \varvec{v}_{N_f} \varvec{n}_f \right) |\Gamma _f| \nonumber \\&\qquad \;+\; \sum _{f=1}^{nFaces} \frac{1}{2} \left[ \frac{1}{c_s}{} \mathbf{I} + (\frac{1}{c_p} - \frac{1}{c_s})\varvec{n}_f \varvec{n}_f \right] \cdot \left[ \varvec{n}_f \cdot \left( \varvec{\sigma }_{N_f} - \varvec{\sigma }_{P_f} \right) \right] |\Gamma _f| \end{aligned}$$
(51)

where the \(m - 1\) time index on \(\varvec{F}\) and \(\varvec{v}\) has been omitted for brevity i.e. \(\varvec{F} \equiv \varvec{F}^{[m-1]}\) and \(\varvec{v} \equiv \varvec{v}^{[m-1]}\). The stress either side of a face is calculated according to Eq. (37).

3.4.3 Solution Algorithm

The solution of the governing discretised equations (Eqs. 50, 51) proceeds in an explicit manner as follows:

  1. 1.

    Increase the total time by \(\Delta t = \alpha _{\text {CFL}} \frac{h_{\text {min}}}{c_p}\), according to the Courant–Friedrichs–Lewy [34] condition, where \(h_{\text {min}}\) is the shortest length within the mesh and \(\alpha _{\text {CFL}}\) is typically chosen to be less than \(\nicefrac {1}{2}\)

  2. 2.

    Store the old-time solution values: \(\varvec{v}^{[m - 1]} \leftarrow \varvec{v}^{[m]}\) and \(\varvec{F}^{[m - 1]} \leftarrow \varvec{F}^{[m]}\)

  3. 3.

    Calculate the reconstructed solution values, \(\varvec{v}_{N_f}\), \(\varvec{v}_{P_f}\), \(\varvec{F}_{N_f}\) and \(\varvec{F}_{P_f}\), at each cell face according to Eq. (43)

  4. 4.

    Solve Eq. (50) for \(\varvec{v}^{[m]}\)

  5. 5.

    Solve Eq. (51) for \(\varvec{F}^{[m]}\)

  6. 6.

    Repeat steps 1–5 until the end time has been reached

Like all explicit methods, this approach does not require the solution of an implicit linear system of equations and hence each time-step can be evaluated more rapidly than in the previously discussed implicit methods; however, the time-step size limit essentially restricts explicit methods to hyperbolic-style problems. Finally, the explicit nature of the algorithm allows straight-forward and efficient parallelisation on distributed memory supercomputers.

3.5 Discussion

The field of finite volume solid mechanics comprises more approaches than those presented above, however, the selected three variants capture the primary differences in the approaches. It can be seen that the distinction between the variants can be narrowed down to four components:

  1. 1.

    Control volume construction;

  2. 2.

    Face gradient calculation;

  3. 3.

    Stabilisation approach;

  4. 4.

    Solution methodology.

Each of these components is briefly reviewed below, followed by the natural definition of a unified approach linking all variants.

3.5.1 Control Volume Construction

There are predominantly four ways to construct control volumes (Fig. 11): (1) cell-centred, (2) vertex-centred with non-overlapping volumes; (3) vertex-centred with overlapping control volumes, (4) and a staggered-grid. In terms of the relative merits of the different approaches, a number of observations can be made:

  1. 1.

    The staggered-grid is restricted to structured quadrilateral/hexahedral meshes in 2-D/3-D;

  2. 2.

    The vertex-centred approach with non-overlapping control volumes requires the construction and storage of a second mesh;

  3. 3.

    The vertex-centred approach has nodes on the boundary, whereas the cell-centre approach typically does not;

  4. 4.

    The cell-centred approach allows convenient approximation of the face normal gradients but requires interpolation to approximate the tangential gradients;

  5. 5.

    In contrast, the vertex-centred approach with overlapping volumes allows convenient approximation of the tangential gradients but requires interpolation to approximate the normal gradients.

Fig. 11
figure 11

Illustration of the four ways to construct control volumes on a primary mesh: (1) cell-centred (green); (2) vertex-centred with non-overlapping control volumes (blue); (3) vertex-centred with overlapping control volumes (red); and (4) staggered-grid (purple). The nodal locations are indicated by filled circles. (Color figure online)

Full size image

3.5.2 Face Gradient Calculation

Once the control volume is constructed, all approaches must approximate the traction at each control volume face. To achieve this, the gradient of displacement at the face \((\varvec{\nabla } \varvec{u})_f\) is approximated in terms of the nodal displacement values. Neglecting any additional stabilisation terms (addressed in the next section), the most common approaches are:

  1. 1.

    Interpolate the gradient from the adjacent cell-centres:

    $$\begin{aligned} (\varvec{\nabla } \varvec{u})_f&= \frac{ |\varvec{d}_{Pf}| (\varvec{\nabla } \varvec{u})_P + |\varvec{d}_{Nf}| (\varvec{\nabla } \varvec{u})_N }{|\varvec{d}_f|} \end{aligned}$$
    (52)

    where \(\varvec{d}_f\) is the vector from the centre of cell P to the centre of cell N, \(\varvec{d}_{Pf}\) is the vector from the centre of cell P to the centre of face f, and \(\varvec{d}_{Nf}\) is the vector from the centre of cell N to the centre of face f. These interpolation weights may differ depending on the specific approach.

  2. 2.

    Calculate the normal gradient using central-differencing, and interpolate the tangential gradient from the adjacent cell-centres:

    $$\begin{aligned} (\varvec{\nabla } \varvec{u})_f&= \varvec{n}_f \frac{\varvec{u}_N - \varvec{u}_P}{|\varvec{d}_f|} \;+\; \nonumber \\&\quad \left( \mathbf{I} - \varvec{n}_f \varvec{n}_f \right) \cdot \, \frac{ |\varvec{d}_{Pf}| (\varvec{\nabla } \varvec{u})_P + |\varvec{d}_{Nf}| (\varvec{\nabla } \varvec{u})_N }{|\varvec{d}_f|} \end{aligned}$$
    (53)
  3. 3.

    Calculate the normal gradient using central-differencing, and calculate the tangential gradient using the point or edge values. In the case of a staggered-grid, these point or edge values correspond to nodes and no interpolation is necessary. For the cell-centred approach, these point or edge values are interpolated from the cell-centred nodes, and an appropriate face tangential gradient calculation method used; for example, the face-Gauss method [25, 208] is a generalisation of the approach used in the original Demirdžić et al. [2] approach:

    $$\begin{aligned} (\varvec{\nabla } \varvec{u})_f&= \varvec{n}_f \frac{\varvec{u}_N - \varvec{u}_P}{|\varvec{d}|_f} \;+\; \sum _{e=1}^{nEdges} \varvec{m}_e \, \varvec{u}_e \, L_e \end{aligned}$$
    (54)

    where \(\varvec{m}_e\) is the outward-facing bi-normal at edge e, \(L_e\) is the length of edge e, and \(\varvec{u}_e\) is the displacement at the centre of edge e, which has been interpolated from adjacent cell-centres.

  4. 4.

    Extrapolate the gradient from each adjacent cell-centre, and take the average:

    $$\begin{aligned} (\varvec{\nabla } \varvec{u})_f&= \frac{ (\varvec{\nabla } \varvec{u})_P + \varvec{d}_{Pf} \cdot \varvec{\nabla }(\varvec{\nabla } \varvec{u})_P + (\varvec{\nabla } \varvec{u})_N + \varvec{d}_{Nf} \cdot \varvec{\nabla } (\varvec{\nabla } \varvec{u})_N }{2} \end{aligned}$$
    (55)
  5. 5.

    For each of the previous face gradient calculation methods, a limiter can be applied to preserve the local maximum principle, as discussed in Sect. 3.4.

  6. 6.

    Use shape functions to evaluate the face gradient. As an example, taking a vertex-based method and a 2-D triangular grid with linear shape functions, the face gradient is given in Voigt notation as:

    $$\begin{aligned}&\begin{bmatrix} (\varvec{\nabla } \varvec{u})_f \end{bmatrix} = \begin{bmatrix} \partial u_x/\partial x \\ \partial u_y/\partial y \\ \partial u_x/\partial y \\ \partial u_y/\partial x \end{bmatrix}\nonumber \\&\quad = \underbrace{ \frac{1}{x_{13} y_{23} - x_{23} y_{13}} \begin{bmatrix} y_{23} &{} 0 &{} y_{31} &{} 0 &{} y_{12} &{} 0 \\ 0 &{} x_{32} &{} 0 &{} x_{13} &{} 0 &{} x_{21} \\ x_{32} &{} 0 &{} x_{13} &{} 0 &{} x_{21} &{} 0 \\ 0 &{} y_{23} &{} 0 &{} y_{31} &{} 0 &{} y_{12} \end{bmatrix} }_{\text {Derivative of shape functions}} \cdot \begin{bmatrix} u_{x_1} \\ u_{y_1} \\ u_{x_2} \\ u_{y_2} \\ u_{x_3} \\ u_{y_3} \end{bmatrix} \end{aligned}$$
    (56)

    where subscripts 1, 2 and 3 refer to the three nodes in the triangle, and the relative coordinates are given as \(x_{ab} = x_a - x_b\). Here we are referring to the vertex-centred method, however, shape functions could in principle be used with any control volume construction.

  7. 7.

    Use a higher-order approach, for example, the fourth-order approach proposed by Demirdžić [203].

Fig. 12
figure 12

Local integration domain (shaded orange) and computational stencil (white-filled dots) for a node (black-filled dot) in a 2-D quadrilateral mesh. All methods include close neighbours (white-filled dots with black border) within their stencil, while method 1 additionally includes distant neighbours (white-filled dots with orange border). (Color figure online)

Full size image

To provide additional insight, let us consider the face gradient calculations on a simple grid. Taking a uniform quadrilateral mesh (Fig. 12), we will calculate the gradient at a face using the most popular of the methods above. The discretised governing equation for the cell in Fig. 12 can be written in the form of a tensor algebraic equation:

$$\begin{aligned} \sum _{i=1}^{i=13}\varvec{A}_i \cdot \varvec{u}_i = \varvec{0} \end{aligned}$$
(57)

which corresponds to a block row in the resulting stiffness matrix, assuming a block-coupled solution methodology is used. It is possible to present the coefficients \(\varvec{A}_i\) of this equation graphically to allow direct comparison between the different face gradient calculation approaches: Fig. 13 compares the resulting coefficients from using methods 1, 2, 3 and 6, neglecting any stabilisation terms. Noting that boundary conditions have not been considered, a number of observations can be made:

  • Methods 2, 3 and 6 employ the same compact computational stencil, whereas method 1 (interpolated gradient) uses a larger stencil, including second face-neighbours;

  • All coefficients are symmetric;

  • All methods show geometric symmetries, for example, the top-right coefficient is equal to the bottom-left coefficient; this is a consequence of the momentum/force being conserved between nodes;

  • In methods 1, 2, and 3, the normal forces are calculated entirely from the central cell displacement as well as the left, right, top and bottom cell displacements (far-left/right/top/bottom cells in the case of method 1). Similarly, the shear forces are calculated entirely from the top-left, top-right, bottom-left and bottom-right cell displacements;

  • Methods 2 (interpolated tangential gradient) and 3 (tangential gradient calculated at the face) are equivalent for this simple grid. For meshes including skewness and non-orthogonality, this may not be the case;

  • Method 1 differs from methods 2 and 3 in only one way: the left, right, top and bottom cell coefficients have been moved to a more distant neighbour and scaled in magnitude; in addition, the central coefficient has been scaled in magnitude. This corresponds to the normal component being calculated using a larger stencil (interpolated gradient) in method 1 vs. methods 2 and 3 (central differencing at the face);

  • Method 6 (shape functions) requires the force to be integrated over 8 faces compared with 4 faces for methods 1, 2 and 3; this comes from the way in which the mesh is constructed from a primary mesh;

  • Half the components of the corner coefficients are zero for methods 1, 2 and 3, while they are all non-zero for method 6.

Fig. 13
figure 13

A comparison of the block coefficients in the stiffness matrix for the centre node/cell, where different face gradient calculation methods are employed. A unit thickness is assumed and stabilisation terms have been disregarded. (Color figure online)

Full size image
Fig. 14
figure 14

Stiffness matrix coefficients for methods 2 and 3 when a segregated solution algorithm is used; the inter-component coupling terms are included via the source vector in a deferred correction manner. (Color figure online)

Full size image

It should be noted that the coefficients that appear in the linear system matrix depend on the chosen solution algorithm; for block-coupled approaches, the coefficients will be as shown, whereas for segregated approaches, the coefficients will be more sparse and will not contain inter-component couplings (the off-diagonal components of the coefficients will be zero). For example, the matrix coefficients corresponding to method 2 (and equivalently method 3) are given for the segregated approach in Fig. 14. In contrast to the coefficients given in Fig. 13b, the segregated coefficients (Fig. 14) differ in the following ways:

  • As noted, all inter-component coupling is zero i.e. all block off-diagonal coefficients are zero; this allows the two scalar displacement equations to be solved separately;

  • The matrix has greater sparsity that the other approaches, leading to reduced memory requirements;

  • The coefficients produce a matrix which is weakly diagonally dominant: the magnitude of the centre node coefficient is equal to the sum of the magnitudes of the other nodes. Such a weakly diagonally dominant system (which becomes strongly diagonally dominant with the inclusion of Dirichlet/essential boundary conditions) promotes the convergence of iterative linear solvers.

3.5.3 Stabilisation Approach

For the discretisations that require stabilisation, three distinct forms of stabilisation term can be found; these can be expressed as a stabilisation traction \(\varvec{t}^{\text {stab}}\) applied at the control volume face:

$$\begin{aligned} \varvec{t}^{\text {stab}} = {\left\{ \begin{array}{ll} \alpha ^{\text {stab}} K_f \left( \dfrac{\varvec{u}_N - \varvec{u}_P}{|\varvec{d}_{f}|} \;- \; \varvec{n}_f \cdot \dfrac{ |\varvec{d}_{Nf}| \varvec{\nabla }\varvec{u}_N + |\varvec{d}_{Pf}| \varvec{\nabla }\varvec{u}_P}{|\varvec{d}_{f}|} \right) \, |\varvec{\Gamma }_f| &{} \text {Rhie}{-}\text {Chow} \\ -\alpha ^{\text {stab}} \rho \, c_p \, |\varvec{d}_{f}|^2 \left( \varvec{\nabla }^2 \varvec{v}_N - \varvec{\nabla }^2 \varvec{v}_P \right) \, |\varvec{\Gamma }_f| &{} \text {Jameson}{-}\text {Schmidt}{-}\text {Turkel} \\ \rho \left[ c_s \mathbf{I} + (c_p - c_s) \varvec{n}_f\varvec{n}_f \right] \cdot \dfrac{ \varvec{v}_{N} + \varvec{d}_{Nf} \cdot \varvec{\nabla } \varvec{v}_N - \varvec{v}_{P} - \varvec{d}_{Pf} \cdot \varvec{\nabla } \varvec{v}_P }{2} \,|\varvec{\Gamma }_f| &{} \text {Godunov upwinding} \end{array}\right. } \end{aligned}$$
(58)

where \(\alpha ^{\text {stab}}\) is a user-defined scaling factor, the pressure wave speed of sound is \(c_p = \sqrt{\frac{2\mu + \lambda }{\rho }}\), and the shear wave speed of sound is \(c_s = \sqrt{\frac{\mu }{\rho }}\).

In Eq. (58), Jameson–Schmidt–Turkel and Godunov-upwinding terms are given in a form that is only suitable for dynamic problems; however, it is possible to define similar stabilisation terms for quasi-static analyses:

$$\begin{aligned} \varvec{t}^{\text {stab}} = {\left\{ \begin{array}{ll} \alpha ^{\text {stab}} K_f \left( \dfrac{\varvec{u}_N - \varvec{u}_P}{|\varvec{d}_{f}|} \;-\; \varvec{n}_f \cdot \dfrac{ |\varvec{d}_{Nf}|\varvec{\nabla }\varvec{u}_N + |\varvec{d}_{Pf}| \varvec{\nabla }\varvec{u}_P}{|\varvec{d}_{f}|} \right) \, |\varvec{\Gamma }_f| &{} \text {Rhie}{-}\text {Chow} \\ -\alpha ^{\text {stab}} K_f \, |\varvec{d}_{f}| \left( \varvec{\nabla }^2 \varvec{u}_N - \varvec{\nabla }^2 \varvec{u}_P \right) \, |\varvec{\Gamma }_f| &{} \text {Jameson}{-}\text {Schmidt}{-}\text {Turkel} \\ \alpha ^{\text {stab}} \dfrac{ K_f}{2} \dfrac{ \varvec{u}_{N} + \varvec{d}_{Nf} \cdot \varvec{\nabla } \varvec{u}_N - \varvec{u}_{P} - \varvec{d}_{Pf} \cdot \varvec{\nabla } \varvec{u}_P }{|\varvec{d}_{f}|} \,|\varvec{\Gamma }_f| &{} \text {Godunov upwinding} \end{array}\right. } \end{aligned}$$
(59)

where the Rhie–Chow term is given for comparison. A user-defined scaling factor \(\alpha ^{\text {stab}}\) is added to the Godunov-type term in 59, as this form of the term does not have the same physical significance as the dynamic term in Eq. (58). After some algebraic manipulation, where we include the \((\nicefrac {1}{2})\) factor in \(\alpha ^{\text {stab}}\) and note that \(\varvec{d}_{Nf} = -|\varvec{d}_{Nf}|\varvec{n}_{f}\), the Godunov upwinding-type stabilisation term is seen to be identical to Rhie–Chow stabilisation. This shows that even in its original dynamic form (Eq. 58), it is in fact just a scaled version of Rhie–Chow stabilisation, and is equivalent for a specific choice of scaling parameters.

Using the 2-D square grid (Fig. 12) as before, the computational stencil and coefficients resulting from the Rhie–Chow and Jameson–Schmidt–Turkel stabilisation terms can be graphed (Fig. 15). Scale factors of \(\alpha ^{\text {stab}} = (1/4)\) for the Jameson–Schmidt–Turkel term and \(\alpha ^{\text {stab}} = 1\) for the Rhie–Chow term are chosen so that the magnitude of the terms are similar. For this grid, both approaches produce similar coefficients, however, the Jameson–Schmidt–Turkel approach differs in that it includes additional coupling in the corner coefficients. It can also be seen that both approaches require a large computational stencil, in that second face-neighbours are needed. When either of these stabilisation approaches are combined with one of the face gradient calculations methods discussed above, the stencil of coefficients are summed. For example, the computational stencil and coefficients from face gradient calculation method 1 with Rhie–Chow stabilisation are shown in Fig. 16a, and from face gradient calculation method 2 with Jameson–Schmidt–Turkel stabilisation in Fig. 16b.

Fig. 15
figure 15

A comparison of the block coefficients in the stiffness matrix for the centre node/cell for two styles of stabilisation term: Rhie–Chow and Jameson–Schmidt–Turkel. (Color figure online)

Full size image
Fig. 16
figure 16

The effect on the stiffness matrix coefficients by including stabilisation terms. (Color figure online)

Full size image

Within literature, a number of authors have described stabilisation techniques, however, stability analysis of finite volume discretisations for solid mechanics is not common. Of course, the stability of a formulation quickly becomes apparent in use, however, we can also take inspiration from finite element approaches [407] and analyse the stiffness matrix eigenvalues. Taking a single unconstrained finite element, the number of zero eigenvalues of the stiffness matrix indicates the number of zero energy modes. For a stable formulation, the number of zero valued eigenvalues is equal to the number of rigid degrees of freedom; in 3-D, there are three rigid translations and three rigid rotations, whereas in 2-D there are two rigid translations and one rigid rotation. For an unstable formulation, there will be additional zero valued eigenvalues, where the corresponding eigenvector indicates the unstable mode. For the finite volume method, an equivalent analysis of an individual cell/element is less obvious. One such approach is to consider a periodic patch of finite volume cells, containing a central cell and all neighbour cells within its computational stencil (Fig. 17), and analyse the eigenvalues of its (block-coupled) global stiffness matrix. In this case, as there are 9 cells, each with 2 degrees of freedom, the global stiffness matrix is \(18 \times 18\). As each cell contains all eight other cells in their stencil (due to the periodic conditions), the stiffness matrix is fully dense (no zero block entries). In this case, using face gradient calculation method 2, the stiffness matrix contains 2 zero eigenvalues, corresponding to the two rigid translation directions; the periodic conditions prohibit rigid rotation; this indicates that the discretisation is stable in this configuration. In addition to analysing a periodic patch of internal cells, it may also be necessary to examine a patch of cells adjacent to a boundary. The discretisation at boundary faces is typically different than at internal faces, and so boundaries may quell or excite spatial instabilities.

Fig. 17
figure 17

A periodic patch of finite volume cells, containing a central cell (cell 5) and all neighbour cells within its computational stencil. The periodic/cyclic neighbours are indicated as cells in grey numbering. (Color figure online)

Full size image

3.5.4 Solution Methodology

Like other popular numerical methods, the finite volume method can employ implicit or explicit solution algorithms. The relative merits of implicit vs explicit approaches are independent of the finite volume method; the interested reader can find numerous textbooks addressing this topic, for example, [407,408,409].

3.5.5 A Generalised Finite Volume Method for Solid Mechanics

Based on these four components, it is possible to describe a generalised approach encompassing all individual variants, as shown in Fig. 18. Common approaches are indicated by the coloured lines: implicit cell-centred (green), implicit vertex-centred (blue), explicit Godunov-type (red), and staggered-grid (purple). This figure allows the relationship between the variants to be concisely expressed. What is also apparent from this figure is that there are avenues that have yet to be fully explored.

Fig. 18
figure 18

Generalisation of the finite volume method for solid mechanics, allowing the creation of any scheme through appropriate selection of four key components: (1) control volume construction method, (2) face gradient calculation approach, (3) stabilisation technique, and (4) solution methodology. Common approaches are indicated by the coloured lines: implicit cell-centred (green), implicit vertex-centred (blue), explicit Godunov-type (red), and staggered-grid (purple). (Color figure online)

Full size image

4 Comparing of the Finite Volume Method for Computational Solid Mechanics with the Finite Element Method

Within this section, the finite volume method for solids mechanics is compared with the “standard” continuous Bubnov–Galerkin finite element method, for example, as described by Bathe [408], Zienkiewicz and Taylor [410], and Belytschko et al. [407]. Following the approach taken in the previous section, the finite element method will be compared to the finite volume method in terms of: (a) discretisation of space and time; (b) discretisation of the mathematical model equations; and (c) solution algorithm.

4.1 Discretisation of Time and Space

Like the finite volume method, the finite element method follows the standard time-marching temporal discretisation approach. Similarly, the solution domain space is divided into a finite number of convex cells (or elements) that do not overlap and fill the space completely. With regard to the mesh, the following differences can be noted between the finite element method and each of the finite volume variants:

  • The cell-centred approach and vertex-centred approaches which do not use shape functions are applicable to general convex polyhedra in 3-D and general polygons in 2-D, whereas the standard finite element method is limited to standard element shapes, such as hexahedra/tetrahedra in 3-D and quadrilaterals/triangles in 2-D. A consequence of this it that ‘hanging nodes’ (Fig. 19) are common in finite volume analyses but not directly possible with the standard finite element method;

  • The vertex-centred (and hypothetically cell-centred) approaches which do use shape function are limited to the same types of meshes used by the standard finite element method.

Fig. 19
figure 19

2-D quadrilateral mesh of a beam, where ‘hanging nodes’ are shown as black dots. (Color figure online)

Full size image

4.2 Discretisation of the Mathematical Model Equations

In Sect. 3.1, the conservation of linear momentum in strong integral form (Eq. 1) was taken as the starting point for the finite volume discretisation. In contrast, the finite element method requires the weak form of the governing equation, and hence begins with the strong differential form:

$$\begin{aligned} \rho \frac{\partial ^2 \varvec{u}}{\partial t^2}= & {} \,\varvec{\nabla } \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;+\; \rho \varvec{f}_b \end{aligned}$$
(60)

This form is then multiplied by an arbitrary continuous weighting function \(\varvec{\omega }\) and integrated over the material volume to give the conservation of momentum in weak form:

$$\begin{aligned} \int _\Omega \varvec{\omega } \cdot \left\{ \rho \frac{\partial ^2 \varvec{u}}{\partial t^2} \;-\; \varvec{\nabla } \cdot \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] \;-\; \rho \varvec{f}_b \right\} \;\text {d}\Omega= & {} \,\varvec{0} \end{aligned}$$
(61)

Unsurprisingly a finite volume method is recovered if the weighting functions \(\varvec{\omega }\) are taken as unity within the control volumes and zero elsewhere.

To derive the finite element method, the weak form (Eq. 61) is rearranged using integration by parts combined with the Gauss divergence theorem:

$$\begin{aligned} \int _\Omega \rho \varvec{\omega } \cdot \frac{\partial ^2 \varvec{u}}{\partial t^2} \;\text {d}\Omega \;+\; \int _\Omega \varvec{\nabla } \varvec{\omega } : \overbrace{ \left[ \mu \varvec{\nabla } \varvec{u} + \mu (\varvec{\nabla } \varvec{u})^T + \lambda \; \text {tr}(\varvec{\nabla } \varvec{u}) \mathbf{I} \right] }^{\varvec{\sigma }} \;\text {d}\Omega= & {} \nonumber \\ \oint _{\Gamma _T} \varvec{\omega } \cdot \varvec{T}_\Gamma \;\text {d}\Gamma \;+\; \int _\Omega \rho \varvec{\omega } \cdot \varvec{f}_b \;\text {d}\Omega \end{aligned}$$
(62)

where \(\Gamma _T\) is the region of the domain boundary where tractions \(\varvec{T}_\Gamma\) are applied. In the second term on the left-hand side of Eq. (62), the differential operator now acts on the weighting function \(\varvec{\omega }\), in contrast to Eq.  (1) where it acts on the stress tensor \(\varvec{\sigma }\). It is assumed that the weighting functions, also known as test functions, satisfy the following requirements [407]:

  • They are not functions of time;

  • They are \(C^0\) continuous;

  • They vanish on displacement boundaries.

Interpreting the weighting functions \(\varvec{\omega }\) as virtual displacements allows Eq. (62) to be viewed as the principle of virtual work. In this way, the original problem of trying to find a displacement field which satisfies the conservation of linear momentum can be reinterpreted as trying to find a displacement field which minimises the total energy.

The finite element method then assumes the displacement \(\varvec{u}\) within each mesh element to vary according to shape functions, as presented previously in Eq. (25). The standard Bubnov–Galerkin form of the finite element method is achieved by assuming that the weighting functions \(\varvec{\omega }\) in Eq. (62) are approximated using the same shape functions as the displacement field:

$$\begin{aligned} \varvec{\omega } = \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \end{aligned}$$
(63)

where \(\varvec{\bar{\omega }}_A\) represents the discrete weighting function value at vertex A; uppercase letter A is used as an index for vertices to avoid confusion with index notation i, j and k.

Combining Eqs. 25 (displacement shape functions), 63 and 62, the finite element equations are expressed as [411]:

$$\begin{aligned}&\underbrace{ \int _\Omega \rho \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \; \cdot \; \sum _{B=1}^{nVertices} N_B \frac{\partial ^2 \varvec{u}_B}{\partial t^2} \;\text {d}\Omega }_{\text {Inertial force term}} \nonumber \\&\quad \;+\; \underbrace{ \int _\Omega \sum _{A=1}^{nVertices} \varvec{\nabla } N_A \varvec{\bar{\omega }}_A \; : \; \left[ \mu \sum _{B=1}^{nVertices} \varvec{\nabla } N_B \varvec{u}_B + \mu \sum _{B=1}^{nVertices} \varvec{u}_B \varvec{\nabla } N_B + \lambda \; \text {tr}\left( \sum _{B=1}^{nVertices} \varvec{\nabla } N_B \varvec{u}_B \right) \mathbf{I} \right] \;\text {d}\Omega }_{\text {Internal force term}} \nonumber \\&\quad \;=\; \underbrace{ \oint _{\Gamma _T} \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \; \cdot \; \varvec{T}_\Gamma \;\text {d}\Gamma }_{\text {External (surface) force term}} \;+\; \underbrace{ \int _\Omega \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \;\cdot \; \rho \varvec{f}_b \;\text {d}\Omega }_{\text {External (body) force term}} \end{aligned}$$
(64)

To proceed, we will switch to index notation, not referring to spatial directions i and j or nodes A and B, but instead to the degrees of freedom [411]. For this, the index for a global degree of freedom P can be given uniquely in terms of the spatial index and node index:

$$\begin{aligned} P = f\left( i, A\right) \end{aligned}$$
(65)

Examining Eq. (64) term by term and using both index notation and degree of freedom notation, the inertial force term can be expanded as:

$$\begin{aligned}&\int _\Omega \rho \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \; \cdot \sum _{B=1}^{nVertices} N_B \frac{\partial ^2 \varvec{u}_B}{\partial t^2} \;\text {d}\Omega \nonumber \\&\quad = \sum _{A=1}^{nVertices} \sum _{i=1}^{nDims} \int _\Omega \rho N_A \bar{\omega }_{iA} \sum _{B=1}^{nVertices} N_B \frac{\partial ^2 U_{iB}}{\partial t^2} \;\text {d}\Omega \nonumber \\&\quad = \sum _{A=1}^{nVertices} \sum _{i=1}^{nDims} \bar{\omega }_{iA} \sum _{B=1}^{nVertices} \sum _{j=1}^{nDims} \int _\Omega \rho N_A \delta _{ij} N_B \frac{\partial ^2 U_{iB}}{\partial t^2} \;\text {d}\Omega \nonumber \\&\quad = \sum _{P=1}^{nDoF} \bar{\omega }_{P} \sum _{Q=1}^{nDoF} M_{PQ} \frac{\partial ^2 U_{Q}}{\partial t^2} \;\text {d}\Omega \end{aligned}$$
(66)

where nDims is the number of spatial dimensions, \(\delta _{ij}\) is the Kronecker delta, and \(nDoF = nDims \times nVertices\) is the number of global degrees of freedom. Matrix \(M_{PQ}\) is known as the mass matrix and is given as:

$$\begin{aligned} M_{PQ} = \int _\Omega \rho N_A \delta _{ij} N_B \;\text {d}\Omega \end{aligned}$$
(67)

The volume integral can be calculated (or approximated) using Gaussian/numerical quadrature:

$$\begin{aligned} M_{PQ} \approx \sum _{p=1}^{nQuadPoints} w_p\, \rho (\xi _p)\, N_A(\xi _p)\, \delta _{ij}\, N_B(\xi _p) \end{aligned}$$
(68)

where nQuadPoints is the number of quadrature points, w is the quadrature weight, and \(\xi\) is the quadrature location within the element. For example, using one-point quadrature, the quadrature locations are situated at the centroids of the elements; in that case, the density and the derivative of the shape functions are evaluated at element centroids.

Unlike finite volume approaches, the resulting mass matrix will not in general be diagonal; however, diagonalisation or lumping of the mass matrix is common, although often ad hoc [407]; for example, the row-sum technique calculates the diagonal elements as the sum of the coefficients for that row.

The internal force term in Eq. (64) can be simplified as:

$$\begin{aligned}&\int _\Omega \sum _{A=1}^{nVertices} \varvec{\nabla } N_A \varvec{\bar{\omega }}_A \; : \; \left[ \mu \sum _{B=1}^{nVertices} \varvec{\nabla } N_B \varvec{u}_B + \mu \sum _{B=1}^{nVertices} \varvec{u}_B \varvec{\nabla } N_B + \lambda \; \text {tr}\left( \sum _{B=1}^{nVertices} \varvec{\nabla } N_B \varvec{u}_B \right) \mathbf{I} \right] \;\text {d}\Omega \nonumber \\&\quad = \int _\Omega \sum _{A=1}^{nVertices} \sum _{i=1}^{nDims} \sum _{j=1}^{nDims} N_{A,j} \bar{\omega }_{iA} \left( \mu N_{B,j} U_{iB} + \mu N_{B,i} U_{jB} + \lambda N_{B,k} U_{kB} \delta _{ij} \right) \;\text {d}\Omega \nonumber \\&\quad = \sum _{P=1}^{nDoF} \bar{\omega }_{P} K_{PQ} U_{Q} \end{aligned}$$
(69)

where matrix \(K_{PQ}\) is known as the stiffness matrix:

$$\begin{aligned} K_{PQ} = \int _\Omega \sum _{j=1}^{nDims} N_{A,j} \left[ \mu N_{B,j} + \mu N_{B,i} + \lambda N_{B,i} \delta _{ij} \right] \;\text {d}\Omega \end{aligned}$$
(70)

The integral can once again be evaluated using Gaussian/numerical quadrature:

$$\begin{aligned} K_{PQ} \approx \sum _{p=1}^{nQuadPoints} \sum _{j=1}^{nDims} w_p\, N_{A,j}(\xi _p)\, \left[ \mu (\xi _p)\, N_{B,j}(\xi _p)\, + \mu (\xi _p)\, N_{B,i}(\xi _p)\, + \lambda (\xi _p)\, N_{B,i}(\xi _p)\, \delta _{ij} \right] \end{aligned}$$
(71)

Evaluating this integral exactly (using sufficient quadrature points) would naively appear to be the best approach; however, formulations that use full integration tend to suffer from locking [407], which can be described as an overly stiff behaviour in bending. Consequently, reduced integration is often favoured, where the local field is under-integrated. This reduced integration has the benefit of relieving this locking phenomena as well as reducing the computational time, due to the lower number of integration points.

A downside of reduced integration is the introduction of spatial instabilities into the discretisation. In essence, the element is capable of deforming in certain modes which offer no resistance. These spurious singular or zero energy modes produce an accordion-like deformation pattern known as hourglassing. Similar to the finite volume method, a stabilisation term is included in the formulation to suppress such spatial instabilities. For the finite element method, this hourglass stabilisation is incorporated through the inclusion of a stabilisation stiffness within the element stiffness matrix, or a viscous stabilisation term for dynamic problems [407]. For static problems a variety of stabilisation methods have been proposed, but typically a stabilisation stiffness term \(K_{PQ}^{\text {stab}}\) is added to the element stiffness matrix of the form [407, 412]:

$$\begin{aligned} K_{PQ}^{\text {stab}} = \alpha _{\text {stab}} \, \mu \, N_{A,j}^{\text {stab}} \, N_{B,j}^{\text {stab}} \, \Omega \end{aligned}$$
(72)

where \(N_{A/B,j}^{\text {stab}}\) represents the gradient interpolators used to define the hourglass deformation modes. The \(\alpha _{\text {stab}}\) is a scaling factor typically set between 0.005 and 0.1 [407, 412], depending on the form of \(N_{A,j}^{\text {stab}}\). For volumetric spatial instabilities, \(\mu\) is replaced by the bulk modulus, \(\kappa = (2/3)\mu + \lambda\), and \(N_{A,j}^{\text {stab}}\) represents the gradient interpolators for the volumetric/pressure hourglass mode.

Finally, the two external force terms in Eq. (64) are expressed as:

$$\begin{aligned} \oint _{\Gamma _T} \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \; \cdot \; \varvec{T}_\Gamma \;\text {d}\Gamma \;+\; \int _\Omega \sum _{A=1}^{nVertices} N_A \varvec{\bar{\omega }}_A \;\cdot \; \rho \varvec{f}_b \;\text {d}\Omega \; = \; \sum _{P=1}^{nDoF} \bar{\omega }_{P} F_P \end{aligned}$$
(73)

where vector \(F_P\) is known as the global force vector:

$$\begin{aligned} F_P = \oint _{\Gamma _T} \sum _{A=1}^{nVertices} N_A T_{i\Gamma } \;\text {d}\Gamma \;+\; \int _\Omega \sum _{A=1}^{nVertices} \rho N_A f_{ib} \;\text {d}\Omega \end{aligned}$$
(74)

and once again the integrals are evaluated using quadrature.

Equation (64) can now be expressed as:

$$\begin{aligned} \varvec{\bar{\omega }}^T \left( \varvec{M} \frac{\partial ^2 \varvec{U}}{\partial t^2} + \varvec{K} \varvec{U} - \varvec{F} \right) = \varvec{0} \end{aligned}$$
(75)

where the global vectors of dimension \(nDoF \times 1\) are:

$$\begin{aligned} \varvec{\bar{\omega }} = [\bar{\omega }_P], \quad \varvec{U} = [U_P], \quad \varvec{F} = [F_P] \end{aligned}$$
(76)

and global matrices of dimension \(nDoF \times nDoF\) are:

$$\begin{aligned} \varvec{M} = [M_P], \quad \varvec{K} = [K_P] \end{aligned}$$
(77)

As Eq. (75) is satisfied for all values of \(\varvec{\bar{\omega }}\), this requires that the bracketed term is equal to zero. This gives the semi-discrete form (discrete in space, not in time) of the finite element equations:

$$\begin{aligned} \varvec{M} \frac{\partial ^2 \varvec{U}}{\partial t^2} + \varvec{K} \varvec{U}&= \varvec{F} \end{aligned}$$
(78)

To complete the discretisation, the acceleration term \(\frac{\partial ^2 \varvec{U}}{\partial t^2}\) is discretised using a finite difference scheme. Similar to the finite volume approaches, many finite difference schemes can be used, where Newmark schemes are popular. The simple Euler backward scheme is given here for comparative purposes:

$$\begin{aligned} \varvec{M} \; \frac{\varvec{U} - 2 \varvec{U}^{[m-1]} + \varvec{U}^{[m-2]}}{\Delta t^2} + \varvec{K} \varvec{U} = \varvec{F} \end{aligned}$$
(79)

Boundary tractions/forces have already been included in \(\varvec{F}\) via the external (surface) force term in Eq. (64). For the incorporation of displacement conditions, this signifies that some of the degrees of freedom in \(\varvec{U}\) are known; these equations can hence be disregarded. As in the case with the finite volume methods, initial conditions, in the form of the displacement field at \(t = 0\), \(t = -\Delta t\), and \(t = -2\Delta t\), must also be specified.

4.3 Solution Algorithm

Once known degrees of freedom have been incorporated, Eq. (79) represents a system of \(nDoF - nKnownDof\) linear algebraic equations, where nKnownDof is the number of known degrees of freedom. Similar to the analogous matrices in the finite volume method, the mass matrix is a function of the density and element geometry; the stiffness matrix is a function of the mechanical properties and element geometry; and the force vector \(\varvec{F}\) contains surface and body force contributions as well as inertial terms and non-zero known degree of freedom contributions. Like the finite volume approaches, this system of algebraic equations can be solved using either an implicit or explicit time marching procedure.

For implicit approaches, Eq. (79) can be rearranged and solved for \(\varvec{U}\):

$$\begin{aligned} \left( \frac{1}{\Delta t^2} \varvec{M} + \varvec{K} \right) \varvec{U} = \varvec{F} + \varvec{M} \; \frac{2 \varvec{U}^{[m-1]} - \varvec{U}^{[m-2]}}{\Delta t^2} \end{aligned}$$
(80)

Assuming a stable discretisation, the matrix of the linear system \(\left( \frac{1}{\Delta t^2} \varvec{M} + \varvec{K} \right)\) (or \(\varvec{K}\) for quasi-static) has the following properties:

  • It is sparse with the number of non-zero elements in each row equal to the number of vertices which share an element with the current vertex, plus one;

  • It is symmetric;

  • It is positive definite;

  • In general, unlike for the cell-centred finite volume approaches where a segregated algorithm is used, it is not diagonally dominant; however, finite volume discretisations that employed block-coupled solution methodologies will produce a similar non-diagonally dominant matrix.

To solve Eq. (80), typically a direct linear solver is employed, for example, Gaussian elimination, LU decomposition or multi-frontal methods; however, iterative methods such as preconditioned conjugate gradient are also possible [408].

4.4 Discussion

4.4.1 Overview

Given the close relationship between the finite volume and finite element methods, it is not surprising that both have been compared previously: some notable dissections include those from Oñate, Zienkiewicz, Idelsohn [6, 8, 11, 12, 413,414,415,416], Lahrmann [417], Perré and Passard [293], Harrild and Henriquez [418], Zarrabi and Basu [55], Fang et al. [419], Yamamoto et al. [420], Jacquemet and Henriquez [421, 422], Vaz Jr. et al. [37], Filippini et al. [423], and recently Demirdžić [424]. The general consensus is that both methods share the same data structure and general strategy to assemble the corresponding characteristic matrices, with the main conceptual difference being in the local integration domain and local integration method. Although a number of authors have claimed superior accuracy of one method over the other [37, 417, 418], the majority of authors have found both methods to produce similar predictions with no significant differences [293, 419, 420, 422].

One generally accepted appeal of the finite volume method is the ease with which it can be followed and implemented: the finite volume method is simply based on balancing forces acting on a volume, requiring no knowledge of advanced mathematical frameworks. Comparing the derivations in Sects. 3.2 and 4.2, the finite element approach would appear to be more mathematically involved; however, proponents of the finite element method claim that the principle of virtual work and energy minimisation techniques are as equally interpretable as the balance equation form.

4.4.2 Weak Vs. Strong Forms of the Conservation Law and the Implications

As discussed, finite volume and finite element methods differ is their philosophy: where the finite volume method deals with the strong balance form of the governing law, the finite element method deals with the equivalent weak virtual energy form. One consequence of this is the manner in which local conservation is enforced. As finite volume approaches discretise surface integrals at the (typically non-overlapping) control volume boundaries, strong local conservation is achieved: forces are equal and opposite at cell boundaries. As a consequence of this local conservation, global conservation within the domain is automatically achieved. In contrast, finite element methods discretise the surface force term as a volume integral using locally overlapping integration domains: this results in local conservation in an average sense, rather than directly for each element. Global conservation is ensured in an average sense, assuming there are sufficient numbers of elements. An additional consequence of these contrasting approaches is how each method treats Neumann/natural boundary conditions: considering traction conditions, finite volume methods satisfy these conditions exactly regardless of the mesh density; whereas finite element approaches satisfy them in an approximate sense, and as the mesh is refined strong enforcement is approached.

As noted by a number of authors, for example, [11, 12, 24], by choosing unity weighting functions in the weak form of the governing equation (Eq. 62), it is possible to recover the finite volume method. Spalding [321] alludes to this point by referring to finite volume approaches as unity-weighting function methods and to finite element approaches as non-unity weighting function methods.

4.4.3 Geometric Flexibility

As standard finite element methods use shape functions to define a continuous displacement distribution, this limits their application to meshes containing standard element shapes. Concretely, only standard shapes such as triangles and quadrilaterals are allowed in 2-D, and tetrahedra and hexahedra in 3-D. Similarly, finite volume approaches that explicitly use shape functions are constrained in the same way. More commonly finite volume methods describe the local solution distribution using a truncated Taylor expansion, resulting in discontinuous jumps at the cell interfaces. An outcome of this is the ability of finite volume approaches to deal with general convex polyhedral meshes. In this way, finite volume approaches are more flexible in terms of mesh generation and dynamic remeshing. In addition to hanging nodes, typical finite volume discretisations can deal with overset/chimera and immersed boundary meshes in a straight-forward manner.

4.4.4 Mass Matrix and Stiffness Matrix Properties

A desirable property of final volume methods for explicit implementation and parallelisation is that the mass matrix is automatically diagonal. For finite element methods, the lack of a diagonal consistent mass matrix results in the use of so-called mass lumping approaches, which are often ad-hoc, as noted previously. The stiffness matrix, however, bares many similarities between the methods.

To allow direct comparison, let us consider finite volume and finite element discretisations on a uniform equilateral-triangular grid (Fig. 20). We will consider a typical domain of integration around a node, where a node represents a vertex in the finite element method and a cell-centre in the finite volume method. For ease of comparison, the dual mesh is used for the finite volume method. In the finite element case (Fig. 20a), the local integration domain (shaded in orange) consists of all elements adjacent to the centre node (black-filled dot). Consequently, the computational stencil for the centre vertex consists of the six neighbouring vertices (indicated by white-filled dots), which share an element with the centre node. In the finite volume case (Fig. 20b), the local integration domain (shaded in orange) is the cell itself containing the node at its centre (black-filled dot); the computational stencil includes all neighbouring cell-centres (white-filled dots). In this case, as both methods share the same computational stencil, the resulting stiffness matrices will share the same structure and sparsity, assuming that the same solution strategy is used, for example, block-coupled or segregated. For a triangular grid, either the nodal locations or the orientation of the local integration domains can be aligned between the methods, but not both; as such, the comparison of coefficients from both methods is not entirely direct, however, it does still provide insight. Here it was chosen to align the nodal locations rather than the local integration domains: the finite volume cell can be seen to be rotated \(90^{\circ }\) relative to the finite element cell, as well as being one third the area.

Fig. 20
figure 20

Uniform 2-D triangular grid showing the local integration domains and computational stencils for the finite element and finite volume methods. The centre node is shown as a black dot and all neighbouring nodes are shown as white-filled dots, where nodes are vertices in the finite element method, and are cell-centres in the finite volume method. (Color figure online)

Full size image

It is important to mention that the size and shape of the computational stencil in the finite volume method depend on the approach used to calculate the displacement gradients at the cell faces. Here face gradient calculation method 2 in Sect. 3.5 has been employed. Alternative face gradient calculation methods can result in the second cell-neighbours being included in the stencil; in contrast, a characteristic of the finite element method is that the integration domain is fixed regardless of local discretisation.

An additional observation is that the local integration domains overlap in the finite element method, but do not in the typical finite volume method i.e. integration domains for neighbouring finite element nodes overlap. An overlapping version of the vertex-centred finite volume method has been considered by Oñate et al. [12] but has not received significant attention.

Referring to the node numbering given in Fig. 20, the block row for the centre node in the global mass matrix is given for the finite element method [407], consistent and lumped, as well as the finite volume method in Fig. 21. The finite element mass-lumped approach can be seen to coincide with the finite volume approach; from this, we can see that the finite element lumped approach is essentially assigning the mass of the hexagon surrounding a node to the node itself, corresponding with the integration domain of the finite volume approach.

Fig. 21
figure 21

Block coefficients for a row in the mass matrix corresponding to the centre node, where \(L_\Delta\) is the triangle side-length, a unit thickness is assumed, and \(\frac{\sqrt{3}}{4} L_\Delta ^2\) is the area of a triangular element. The area of the hexagonal finite volume cell is equal to \(\frac{\sqrt{3}}{2} L_\Delta ^2\). (Color figure online)

Full size image
Fig. 22
figure 22

Block coefficients for a row in the stiffness matrix corresponding to the centre node, where \(L_\Delta\) is the triangle side-length and a unit thickness is assumed. (Color figure online)

Full size image

Considering next the stiffness matrix. Once again taking the same uniform 2-D triangular grid given in Fig. 20, the block row for the centre node in the global stiffness matrix for the finite element method [407] is compared with the equivalent row from the finite volume method in Fig. 22. For the finite volume method, the matrix using a block-coupled solution algorithm is given, as well as for the segregated approach. Examining the general structure of the coefficients for all three methods (Fig. 22a–c), the following observations can be made:

  • All three methods employ the same computational stencil;

  • The coefficients are symmetric in all three cases, albeit the effect of boundary conditions has not been considered here;

  • As expected, all three methods show geometric symmetries, for example, the top-right coefficient is equal to the bottom-left coefficient;

  • The finite element and coupled finite volume approaches show the same sparsity structure i.e. there are zeros in the same locations; in addition, the coefficients have the same signs and show similar magnitudes, but do not have the same value, apart from for the central node;

  • The segregated finite volume approach differs from the others by removing all inter-component coupling from the coefficients, as discussed in Sect. 3.5;

  • The segregated finite volume approach produces a row of coefficients which is weakly diagonally dominant, also discussed in Sect. 3.5;

  • The momentum/force between nodes is conserved for all three methods (based on the symmetry of the coefficients), however, conservation of momentum/force between elements/cells is not directly enforced for the finite element method, whereas it is for the finite volume method.

4.4.5 Discretisation Stabilisation

As described in Sect. 4.2, finite element formulations which under-integrate the local domain require the inclusion of a stabilisation term, in the same way one is required in many finite volume formulations. In the finite element method, these spurious singular, zero energy modes produce an accordion-like deformation pattern known as hourglassing (Fig. 23a), named due to its visual similarity to an hourglass timing device. These spatial instabilities are equivalent to checkerboarding instabilities that occur in finite volume formulations (Fig. 23b); these checkerboarding pressure-type instabilities are also possible in finite element formulations. The origin of these spatial instabilities in both finite element and finite volume formulations is a rank deficiency in their respective stiffness matrices. Essentially, a stable discretisation should not support any deformation modes which do not offer resistance, apart from rigid body translations and rotations. More precisely, rank deficiency refers to the fact that the discretised stiffness matrix has zero-valued eigenvalues which are not related to rigid body motions (as discussed in Sect. 3.5). For example, considering a 3-D element/cell, the stiffness matrix for a full rank formulation has six zero valued eigenvalues: three rigid translations and three rigid rotations; for a rank deficient formulation, additional zero valued eigenvalues are present corresponding to zero energy instability modes.

Fig. 23
figure 23

The equivalence of spatial instabilities in finite element and finite volume formulations. (Color figure online)

Full size image

To address these spatial instabilities, both finite element and finite volume approaches add a stabilisation term to the discretised governing equations. In both cases, there are two primary constraints on the form of this stabilisation term [407]:

  • It should not significantly affect the accuracy of the discretisation, and

  • It should not affect the linear completeness of the discretisation; in other terms, the discretisation should still be able capable of describing a linear solution field exactly after the inclusion of the stabilisation term.

For both methods, a variety of techniques exist and the stabilisation force often takes a similar form:

$$\begin{aligned} \begin{aligned}{l} \varvec{f}^{\text {stab}} = \\ \\ f^{\text {stab}}_P = \end{aligned} \begin{aligned}{l}&\alpha ^{\text {stab}} C^{\text {stab}} \Omega \, \left( \varvec{\nabla }^2 \varvec{u} - \varvec{\nabla } \cdot \varvec{\nabla } \varvec{u} \right) \\&-\alpha ^{\text {stab}} C^{\text {stab}} \Omega \, \varvec{\nabla }^2 \left( \varvec{\nabla }^2 \varvec{u} \right) \\&\alpha ^{\text {stab}} C^{\text {stab}} \Omega \, N_{A,j} \, N_{B,j} U_Q \end{aligned} \begin{aligned}{l}&\qquad \text {Rhie}{-}\text {Chow stabilisation} \\&\qquad \text {Jameson}{-}\text {Schmidt}{-}\text {Turkel}\,\mathrm{stabilisation} \\&\qquad \text {Hourglass stabilisation} \end{aligned} \end{aligned}$$
(81)

where \(C^{\text {stab}}\) is some measure of mechanical property that gives an appropriate dimension to the dissipation, such as \(\mu\), \(2\mu + \lambda\), \(\mu + \lambda\), or \(\kappa\), for quasi-static analyses, or a function of the speed of sound for dynamic analyses. The \(\alpha ^{\text {stab}}\) factor allows the magnitude of the stabilisation to be scaled.

4.4.6 Performance of the Methods

The differences in local integration domain and local integration method between the finite volume and finite element methods has consequences for the robustness, accuracy and efficiency of the resulting methods. Particularly for nonlinear analysis, the ideal discretisation is unclear due to a variety of numerical challenges which are yet to be fully resolved, including [425]: (1) spurious hourglassing and pressure checker-boarding, (2) bending difficulties, (3) shear and volumetric locking, (4) high frequency noise in the vicinity of shocks, (5) lower order of convergence for strains and stresses in comparison with displacements, and (6) sensitivity to mesh distortions. It is these challenges that finite volume discretisations can potentially solve in a novel way.

Apart from this, a major motivation for finite volume solid mechanics schemes is the challenge of multi-physics problems. As long as the finite volume method is prominent in the world of computational fluid mechanics, there will be a demand for straight-forward finite volume solid mechanics implementations. These solid mechanics implementations can share the same computational framework, discretisation and solution methodologies as their fluid counterparts and can be integrated seamlessly into the code base.

Regarding accuracy and overly stiff behaviour, finite volume methods have not shown the same locking behaviour typical in fully integrated finite element methods. Given their similarity with reduced integrated finite elements, it is perhaps not surprising that this is the case; however, like finite elements, the absolute accuracy depends on the details of the formulation. Concerning order of accuracy, an attractive property of most finite volume methods is that the error in the strain and stress reduces at a second-order rate, like the displacement [37, 208]; this may not be the case for many finite element schemes, where the error in the strain and stress reduce at a rate closer to first order.

As models become larger and the availability of supercomputers and cloud computing increases, code parallelisation is becoming critical. Due to the widespread use of iterative linear solvers, finite volume methods (fluid and solid) commonly exploit hundreds or thousands of CPU cores, for example, the OpenFOAM software. In contrast, as direct linear solvers have often been the chosen solution approach for finite element schemes, parallel efficiency is inherently limited (relative to iterative solvers) and the use of large numbers of CPU cores has been less common; however, there are a number of projects focussed on the application of finite element methods to supercomputers using iterative solvers, for example, ParaFEM [426]. Apart from the choice between direct and iterative linear solver, cell-centred finite volume approaches possess a convenient advantage over vertex-centred methods (such as the finite element method) when it comes to domain decomposition parallelisation: each node (cell-centre) is uniquely located on one CPU core domain. As a result, duplication of nodal data at processor-to-processor boundaries is not required. In contrast, in the finite element method, nodes (vertices) that lie on a processor-to-processor boundary are present on at least two processor domains, requiring the use of ghost elements or similar data duplication techniques. A final point related to parallelisation is the debate around open-source vs. commercial software, which equally affects both finite volume and finite element methods. For many, the current per-CPU-core pricing of some well known commercial codes may in fact be the greatest practical obstacle to parallel efficiency.

4.4.7 Higher Order Discretisations

Apart from the size of the finite element solid mechanics community, arguably the next greatest advantage of the finite element method over the finite volume method is its straight-forward extension to higher-order discretisation. A key feature of the finite element method is that an element is completely characterised by the coordinates and degrees of freedom associated with its nodes/vertices [411]. This compact computational stencil allows uncomplicated inclusion of higher-order local distributions. As noted previously, higher-order finite volume approaches have been developed for solid mechanics [203], however, as the order increases, so does the size of the computational stencil; this introduces significant challenges for unstructured polyhedral grids, and as such, higher-order schemes are not as common as in the finite element field.

For linear analyses, the power of higher-order schemes is undeniable, notwithstanding challenges with locking behaviour, however, for nonlinear analysis such higher order schemes are not commonly used in practice. For example, considering an elasto-plastic analysis, as noted by Belytschko et al. [407], the stress may have discontinuous derivatives at the surface separating elastic and plastic material. In this case, the errors in Gaussian quadrature of an element that contains an elastic–plastic interface are likely to be large; higher-order quadrature is not a solution as it often leads to stiff behaviour or locking. Additionally, finite element users are typically recommended to use lower order formulations for problems that include either contact, large strains or plasticity [412].

4.4.8 Discontinuous Galerkin Methods

The standard continuous Bubnov–Galerkin finite element method, as presented above, assumes a continuous distribution of the displacement between elements. In contrast, as shown in Fig. 24, the finite volume method typically assumes discontinuous jumps in the displacement field at the interfaces between cells (although it does not have to). There is, however, a class of finite element approaches known as discontinuous Galerkin methods, introduced by Reed and Hill [427], which assume similar jumps in the solution field across element boundaries. In this way, the local integration method adopted by the discontinuous Galerkin method combines features of the finite volume and finite element methods. In particular, discontinuous Galerkin schemes bare the following desirable finite volume properties [428]:

  • They produce mass matrices that are block-diagonal;

  • They easily handle irregular meshes with hanging nodes;

  • They are locally conservative, which is a critical property for computational fluid dynamics.

In addition, a potential advantage of discontinuous Galerkin schemes over finite volume schemes is their ease of extension to higher orders, and the mixing of lower and higher order elements.

Discontinuous Galerkin methods are, however, typically implemented using explicit solution algorithms. The reason they are less suitable for implicit implementations (and analysis of quasi-static type problems) is they possess large numbers of globally-coupled degrees of freedom. To overcome this disadvantage, the so-called hybridisable discontinuous Galerkin (HDG) method was introduced by Cockburn et al. [429]. The key characteristic of the hybridisable form was defining traces of field variables as single values at cell interfaces, allowing a significant reduction in the number of global unknowns. Detailed analysis of the HDG method is outside the scope of the current article and readers are referred to recent articles on the application of HDG to solid mechanics [430,431,432,433].

Fig. 24
figure 24

Adapted from Lee et al. [27]. (Color figure online)

A comparison between the representation of the displacement field in the finite volume method (and discontinuous Galerkin finite element method) and the finite element method.

Full size image

5 Applications of the Finite Volume Method for Computational Solid Mechanics

Some of the main areas where finite volume methods have been applied to solid mechanics are summarised below, including example images.

5.1 Fluid–Solid Interaction

Example cases are shown in Fig. 25, and examples references include: [29, 94, 96, 98, 99, 113, 120, 121, 138,139,140, 142,143,144,145, 147, 149, 152,153,154,155,156,157,158,159,160, 162, 164, 199, 208, 216, 239, 249, 268, 271, 272, 274,275,276,277, 277,278,279,280, 309, 434,435,436,437,438,439,440,441,442,443,444,445,446,447,448,449,450,451,452,453,454,455,456,457,458,459,460,461,462,463,464,465,466,467].

Fig. 25
figure 25

Fluid–solid interaction examples. (Color figure online)

Full size image

5.2 Fracture and Adhesive Joints

Example cases are shown in Fig. 26, and examples references include: [84, 119,120,121,122,123,124,125,126,127,128,129,130,131,132, 140, 380, 446, 457, 468,469,470,471,472,473,474,475,476,477,478,479,480,481,482,483,484,485,486,487,488,489,490,491,492,493,494,495,496,497,498,499,500].

Fig. 26
figure 26

Fracture and adhesive joint examples. (Color figure online)

Full size image

5.3 Microstructure Analysis

Example cases are shown in Fig. 27, and examples references include: [38, 49, 339,340,341,342,343,344,345, 347,348,349,350,351,352,353,354, 492,493,494, 496, 497, 501,502,503,504,505,506,507,508,509,510,511,512,513,514,515,516,517,518,519,520,521,522,523,524,525,526,527,528,529,530,531,532,533,534,535,536,537,538,539,540,541,542,543,544,545,546,547,548,549,550,551,552,553,554,555,556,557,558].

Fig. 27
figure 27

Microstructure analysis examples. (Color figure online)

Full size image

5.4 Metal Forming and Casting

Example cases are shown in Fig. 28, and examples references include: [30, 44, 46, 47, 50, 51, 51,52,53,54, 110, 135,136,137, 276, 281, 285,286,287, 331, 334, 336, 385, 386, 388, 389, 391, 559,560,561,562,563,564,565,566,567].

Fig. 28
figure 28

Metal forming and casting examples. (Color figure online)

Full size image

5.5 Biomechanics

Example cases are shown in Fig. 29, and examples references include: [60, 102, 105, 138, 156, 158, 196, 259, 278, 337, 418, 421, 455, 458, 464, 465, 568,569,570,571,572,573,574,575,576,577,578,579,580,581,582,583,584,585,586,587].

Fig. 29
figure 29

Biomechanics examples. (Color figure online)

Full size image

5.6 Screw Compressors

Example cases are shown in Fig. 30, and examples references include: [147, 148, 151,152,153, 161, 588,589,590,591,592,593,594];

Fig. 30
figure 30

Screw compressor examples. (Color figure online)

Full size image

5.7 Geomechanics and Poroelasticity

Example cases are shown in Fig. 31, and examples references include: [78, 80,81,82, 84, 149, 307,308,309,310,311,312,313, 595].

Fig. 31
figure 31

Geomechanics and poroelasticity examples. (Color figure online)

Full size image

6 Softwares Employing the Finite Volume Method for Solid Mechanics

A number of software have, or previously have, implemented versions of the finite volume method for solid mechanics; these software, in alphabetical order, include:

7 Conclusions and Challenges

The various finite volume approaches to solid mechanics can be seen to share many similarities, and in fact can all be described in a general unified manner (Sect. 3.5). When comparing the finite volume approach with the finite element approach, the likenesses are clear: both approaches adopt the same general strategy to discretise space into cells/elements, both use similar data storage structures, and both follow similar approaches to assemble their corresponding characteristic matrices. The main differences lie in how the local integration domains are constructed, how the local integration is performed, and their fundamental philosophy: finite volume approaches are rooted in balance laws, where the governing equation is enforced by summing forces/fluxes acting on a control volume; in contrast, finite element methods adopt a more mathematical approach, based on variational methods, where the weak form of the governing equation is imposed in a volumetrically-averaged sense.

To end this article, we state three main challenges we see for the development of finite volume solid mechanics, such that its strengths and weaknesses may be rigorously explored in the context of solid mechanics, and its merits, relative to other similar approaches, may become clear to the computational solid mechanics community at large:

  1. 1.

    Awareness:

    • Three decades after the first contributions to the field, there is still a general lack of awareness around the capabilities of the finite volume method in the sphere of solid mechanics; consequently, in the worst case, prestigious journals inadvertently assign inappropriate reviewers, reviewers who, having only limited knowledge of the area, accept poor or reject good articles, for example, see [35], and authors are unaware of major developments in the field when surveying the literature.

  2. 2.

    Benchmarking:

    • As should be clear from this review, numerous differing finite volume formulations are possible; although some variants have been developed specifically for specialised applications, the comparison of the differing approaches on standard benchmarks is rare. Without such comparisons, in terms of efficiency, accuracy and robustness, it will not be possible to determine which approaches are optimal for certain classes of problems. Furthermore, given the trends in modern computing, the suitability of proposed approaches for execution on large-scale distributed memory clusters (> 1000 s CPU cores) should be further explored. Simulations using hundreds of millions of cells are commonplace at CFD conferences: clearly finite volume-based solid mechanics procedures have great potential. Similarly, finite volume variants should be benchmarked against alternative approaches, such as the finite element method, to determine relative merits, not just on academic standard cases but on complex industrial cases to test robustness. Processes such as round robin benchmarking series, for example [608], may offer one solution.

  3. 3.

    Code dissemination:

    • Where possible, code for published procedures should be shared for academic scrutiny: such distribution has the potential to: (a) accelerate academic progress, as others learn from and build on methods, as well as aiding in the discovery and resolution of errors; (b) facilitate ease of understanding and ease of implementation; (c) allow direct comparison of methods; (d) provide insight into the algorithm intricacies that may not be clear from academic articles; and (e) allow faster integration into commercial software and industrial use.