1 Introduction

Image segmentation is regarded as one of the most important issues for image processing, and its main characteristic is that an image is divided into a certain number of regions according to the static and dynamic properties of the images. When image segmentation results are given by appropriate segmentation algorithms, we can further extract related features, and conduct the identification and classification of objects.

In the past decades, Eckhorn et al.’s [1,2,3,4] bio-inspired neural network based on cat visual cortex, can synchronously release pulses for similar neuron inputs. Johnson et al. [5,6,7,8,9,10] developed the above model and proposed a pulse coupled neural network (PCNN). Subsequently, Ranganath and Kinser et al. [11,12,13,14,15] presented modified PCNN models and further exploited image processing capacities of the PCNN.

PCNN has broad applications in image processing field, such as image fusion, image segmentation, image denoising, image enhancement, feature extraction. In recent years, PCNN have significant potentials for evolving image segmentation algorithms, due to its synchronous dynamic properties of the neuronal activity, including synchronous pulse release, capture behavior, nonlinear modulation and automatic wave. Further, in contrast to other prevalent segmentation methods, PCNN has low computational complexity and high segmentation accuracy, which becomes quite suitable for image segmentation. Thus, PCNN can obtain good segmentation application effects in natural images, medical images and other types of images.

In this paper, we provide basic and classical PCNN models to introduce fundamental properties of the PCNN, then explain internal segmentation behaviors of the PCNN according to three main aspects: dynamic properties, parameter setting and complex PCNN. We also give image segmentation applications of the PCNN as possible in subsequent section. The flowchart of the whole framework in this paper is shown as Fig. 1.

Fig. 1
figure 1

The whole framework of the paper

Full size image

The rest of paper is organized as follows. Section 2 introduces the basic model and classical modified models of the PCNN. Section 3 elaborates the dynamic properties of the PCNN for image segmentation. Section 4 deduces main parameter setting methods of the prevalent PCNN models. Section 5 explains complex PCNN models by analyzing heterogeneous PCNN and multi-channel PCNN. Section 6 reviews image segmentation applications of the PCNN. Section 7 makes a conclusion for the paper.

2 The PCNN Models

2.1 Basic PCNN Model

A neuron is regarded as a basic unit for constructing neural networks, and is also an electrically excitable cell which can transmit and receive information via chemical and electrical signals. A typical neuron comprises a cell body, an axon and dendrites. Most neurons transmit and receive one particular type of signal by the axon and the dendrites, respectively. The majority of neurons belong to central nervous system that is simulated as artificial neural networks to analyze and solve practical problems.

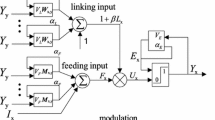
Different from traditional artificial neural networks, PCNN only has a single layer of laterally linked pulse coupled neurons, which main includes four crucial components: the dendritic tree, the membrane potential, the action potential and the dynamic threshold potential.

On the dendritic tree, the feeding synapses receive the external stimulus which is main input signal, and the action potential of the neighboring neurons. Moreover, the linking synapses are only associated with their adjacent neurons. The interaction of the above two synapses produces the membrane potential of the neuron, which is compared with the dynamic threshold potential to judge whether the action potential generates or not.

Lindblad and Kinser et al. [13] developed pulse-coupled neural network and presented its discrete model. The model in the position (i,j) for neuron Nij has five main parts: feeding input Fij[n], linking input Lij[n], internal activity Uij[n], dynamic threshold Eij[n] and pulse output Yij[n]. Hereinto, feeding input Fij[n] and linking input Lij[n] are given as follows:

$$F_{\text{ij}} [n] = e^{{ - \alpha_{\text{f}} }} F_{\text{ij}} [n - 1] + V_{\text{F}} \sum\limits_{\text{kl}} {M_{\text{ijkl}} Y_{\text{kl}} } [n - 1] + S_{\text{ij}}$$
(1)
$$L_{\text{ij}} [n] = e^{{ - \alpha_{\text{l}} }} L_{\text{ij}} [n - 1] + V_{\text{L}} \sum\limits_{\text{kl}} {W_{\text{ijkl}} Y_{\text{kl}} } [n - 1]$$
(2)

In (1) and (2), e−αf and e−αl denote the exponential decay factors recording previous input states, VF and VL are the weighing factors modulating the action potentials of surrounding neurons. Additionally, Mijkl and Wijkl denote the feeding and linking synaptic weights, respectively. Sij is external feeding input stimulus which has a great influence for pulse-coupled synaptic modulation.

The decrease of numerical values for the first terms in (1) and (2) is with the increase of iteration times, moreover, corresponding values of the second terms in the above equations are always larger than zero owing to neighboring neurons firing. The third term in (1) denotes an external input stimulus with a nonzero positive number. Obviously, if the decay values of the first term in (1) surpass the sum of the second and third terms, the values of the feeding input Fij[n] will be smaller than the previous iteration Fij[n − ]. Similarly, Lij[n] and Lij[n − 1] can also acquire a comparison result after comparing with the values of two input terms in (2).

According to the computational mechanisms of pulse-coupled neural network, the non-linear modulation between feeding and linking inputs produces internal activity Uij[n] to deduce the coupling result of the membrane potential. The corresponding equation is given by:

$$U_{\text{ij}} [n] = F_{\text{ij}} [n](1 + \beta L_{\text{ij}} [n])$$
(3)

where β denotes the linking strength, which directly determines the contribution of the linking input Lij[n] in internal activity Uij[n]. The above formula shows the modulatory coupling to the neuronal inputs. Obviously, the feeding input Fij[n] plays a most significant role in coupling modulating because of its weighing assignment, while the linking input Lij[n] has a secondary influence from neighboring neurons. Based on the comparison result between internal activity Uij[n] and dynamic threshold Eij[n], the neuronal firing condition and the dynamic threshold Eij[n] are described as follows:

$$Y_{\text{ij}} [n] = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad {\text{if}}\quad U_{\text{ij}} [n] > E_{\text{ij}} [n]} \hfill \\ {0,} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(4)
$$E_{\text{ij}} [n] = e^{{ - \alpha_{\text{e}} }} E_{\text{ij}} [n - 1] + V_{\text{E}} Y_{\text{ij}} [n]$$
(5)

In (4), if internal activity Uij[n] of a neuron is more than its dynamic threshold Eij[n], it will instantaneously fire and generate an output pulse (Yij[n] = 1); otherwise, the neuron will continue to keep quiet (Yij[n] = 0) until the above firing condition is ultimately satisfied.

In (5), αe is an exponential decay factor. The smaller its value, the more obviously dynamic threshold is affected from previous iteration. VE is the amplitude of dynamic threshold which generates an obvious influence only after previous neuron firing. The structure of basic PCNN model is shown in Fig. 2.

Fig. 2
figure 2

The structure of basic PCNN model

Full size image

2.2 Classical PCNN-Modified Models

For image segmentation, there are four classical modified PCNN models: the intersecting cortical model (ICM) [14], the region growing PCNN model (RG-PCNN) [16], the spiking cortical model (SCM) [17], Simplified PCNN model (SPCNN) [18]. Most modified or simplified PCNN models derive from the above models because of high segmentation accuracy and low computational complexity.

2.2.1 Icm

Ekblad et al. [14] presented the ICM to extract image features without obvious boundaries. This PCNN structure simplifies the feeding and linking inputs, and remains the characteristics of the basic PCNN. Corresponding equations are given as

$$F_{\text{ij}} [n + 1] = fF_{\text{ij}} [n] + S_{\text{ij}} + W_{\text{ij}} \{ Y[n]\}$$
(6)
$$Y_{\text{ij}} [n + 1] = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad {\text{if}}\quad F_{\text{ij}} [n] > E_{\text{ij}} [n]} \hfill \\ {0,} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(7)
$$E_{\text{ij}} [n + 1] = gE_{\text{ij}} [n] + hY_{\text{ij}} [n + 1]$$
(8)

where f and g are decay constants of internal activity Fij[n] and dynamic threshold Eij[n], respectively. h is the amplitude of the dynamic threshold.

2.2.2 RG-pcnn

Stewart et al. [16] proposed the RG-PCNN to achieve region growing based on seed points, and avoided over-segmentation or under-segmentation of pixel regions. This is the first time that the PCNN combines basic region growing algorithm to segment interesting regions. The model is formulated as

$$U_{\text{ij}} [n] = F_{\text{ij}} [n]\left\{ {1 + \beta \left[ {\sum\limits_{{N_{\text{ij}} }} {Y_{\text{ij}} (n) - d} } \right]} \right\}$$
(9)
$$Y_{\text{ij}} [n] = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad {\text{if}}\quad U_{\text{ij}} [n] > E_{\text{ij}} [n]} \hfill \\ {0,} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(10)
$$T_{\text{ij}} [n] = \left\{ {\begin{array}{*{20}l} {n,} \hfill & {\quad Y_{\text{ij}} [n] = 1} \hfill \\ {T_{\text{ij}} [n - 1],} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(11)
$$E_{\text{ij}} [n] = \left\{ {\begin{array}{*{20}l} {\omega [n],} \hfill & {\quad {\text{if}}\quad T_{\text{ij}} [n - 1] = 0} \hfill \\ {\varOmega ,} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(12)

In (9)–(12), Fij[n] is feeding input corresponding the pixel intensity at the n-th iteration. Tij[n] is firing time matrix which records neuronal firing states at each iteration. d is an inhibition term to limit the linking input and improve the smoothness of the segmented image. The parameters ω and \(\varOmega\) are fixed thresholdings at each iteration.

2.2.3 SCM

Referring to the literature of [7], the SCM is reasonably presented for image processing [17]. its equations are given by

$$U_{\text{ij}} (n) = fU_{\text{ij}} (n - 1) + S_{\text{ij}} \beta V_{\text{L}} \sum\limits_{kl} {W_{\text{kl}} Y_{\text{kl}} (n - 1) + S_{\text{ij}} }$$
(13)
$$E_{\text{ij}} (n) = gE_{\text{ij}} (n - 1) + V_{\text{E}} Y_{\text{ij}} (n - 1)$$
(14)
$$Y_{\text{ij}} [n] = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad {\text{if}}\quad U_{\text{ij}} [n] > E_{\text{ij}} [n]} \hfill \\ {0,} \hfill & {\quad {\text{else}}} \hfill \\ \end{array} } \right.$$
(15)

In (13)–(15), f and g denote exponential decay factors. VL and VE are the amplitudes of internal activity and dynamic threshold, respectively.β is the linking strength. Obviously, the SCM retains main characteristics of the basic PCNN, and reduces setting parameters from seven to five. Additionally, the negative time matrix of the SCM can associate human subjective perception with objective input stimulus of the PCNN.

2.2.4 SPCNN

Based on Zhan et al.′s. SCM model, Chen et al. [18] proposed a SPCNN model with an automatic parameter setting method to segment assigned objects. The setting parameters of the former are obtained from empirical image attribution values, while those of the latter can be automatically determined according to static and dynamic properties of the PCNN. Hereinto, the setting parameters of SPCNN are formulated as

$$W_{\text{ijkl}} = \left[ {\begin{array}{*{20}c} {0.5} & 1 & {0.5} \\ 1 & 0 & 1 \\ {0.5} & 1 & {0.5} \\ \end{array} } \right]$$
(16)
$$\alpha_{\text{f}} = \log \left( {\frac{1}{\sigma (S)}} \right)$$
(17)
$$\beta = \frac{{(S_{\hbox{max} } /S^{\prime } ) - 1}}{{6V_{L} }}$$
(18)
$$V_{E} = e^{{ - \alpha_{\text{f}} }} + 1 + 6\beta V_{L}$$
(19)
$$V_{L} = 1$$
(20)
$$\alpha_{\text{e}} = \ln \left( {\frac{{\frac{{V_{E} }}{{S^{\prime } }}}}{{\frac{{1 - e^{{ - 3\alpha_{\text{f}} }} }}{{1 - e^{{ - \alpha_{\text{f}} }} }} + 6\beta V_{\text{L}} e^{{ - \alpha_{\text{f}} }} }}} \right)$$
(21)

Subsequently, two segmentation examples of the SPCNN taken from Berkeley Segmentation Dataset [19], are given as shown in Fig. 3. Obviously, the SPCNN can generates good segmentation results with high contrast as shown in Fig. 3a–e, and bad results with low contrast as shown in Fig. 3f–j, due to automatic setting method of the above parameters.

Fig. 3
figure 3

The segmentation process of the SPCNN from Berkeley Segmentation Dataset: Images in the first column represent natural gray images; images in the second, third and fourth column represent the segmentation results of the SPCNN with iteration times 1–3; images in the fifth column represent the final segmentation results of the SPCNN with iteration times 3–6 (blue regions, cyan regions, red regions and yellow regions denote the third, fourth, fifth and sixth iteration results, respectively). (Color figure online)

Full size image

3 Dynamic Properties

3.1 Feeding Input F

The feeding input Fij[n] of a neuron in (1) always includes three terms, and its expression can be rewritten as

$$F_{\text{ij}} [n]^{1} = F1 + F2 + F3$$
(22)

Hereinto, the first term F1 denotes previous feeding input state based on an exponential decay factor e−αf. The second term F2 shows action potential outputs of the neighboring neurons with the weighing factor VF. The third term F3 is an external input stimulus Sij. A neuron changes its own previous state by adjusting the parameter e−αf in F1, and is always affected by its neighboring neurons according to F2. The neuron also receives external stimuli based on F3. Since F1 and F2 have similar input expressions and practical influences in contrast to traditional linking input in (2), simplified feeding inputs tend to be defined as F3, such as Refs. [20, 21], and its mathematical equation is expressed as

$$F_{\text{ij}} [n]^{2} = S_{\text{ij}}$$
(23)

The input stimulus Sij is always defined as image attribution values, such as pixel intensities and pixel gradient values. In Addition, there are still little literatures that the feeding input is composed of last two items in (22), like Cheng et al. [22]. The literature adopted a simplified feeding input to strongly associate central neurons with neighboring neurons to detect the existence of the cracks. The simplified feeding input is given as

$$F_{\text{ij}} [n]^{3} = S_{\text{ij}} + V_{\text{F}} \sum {M_{\text{ijkl}} } Y_{\text{kl}} [n - 1]$$
(24)

In (24), the first and second items actually derive from F2 and F3 in (22). Referring to [22], subsequent feeding input of basic PCNN can be divided into any combination of F1, F2 and F3 to solve practical image segmentation problems.

3.2 Linking Input L

The linking input Lij[n] of a neuron in (2) has two terms, and its equation can be also simplified as

$$L_{\text{ij}} [n]^{1} = L1 + L2$$
(25)

Hereinto, the first term L1 denotes previous linking input state from an exponential decay factor e−αl analogous to the above parameter e−αf in (1). The second term L2 gives action potential outputs of the neighboring neurons. However, the above two terms would be difficult to distinguish from previous two terms of the feeding input in (22). In order to build a clear corresponding relationship between the feeding and the linking inputs, most simplified PCNN models mainly retain the second term L2 of the linking input in (25). Further, the linking inputs mainly focus on real influences of neighboring firing neurons to exhibit the connectivity and the interoperability between neurons. Most simplified linking input is written as

$$L_{\text{ij}} [n]^{2} = V_{\text{L}} \sum\limits_{\text{kl}} {W_{\text{ijkl}} Y_{\text{kl}} } [n - 1]$$
(26)

Additionally, the simplified linking input Lij[n] can also increase a positive constant d as an inhibition term to improve the smoothness of neuronal firing regions, especially when the whole image has a smaller difference for pixel intensities [16]. The linking input Lij[n] is rewritten as

$$L_{\text{ij}} [n]^{3} = \sum\limits_{\text{kl}} {W_{\text{ijkl}} Y_{\text{kl}} } [n - 1] - d$$
(27)

In (27), the distribution range of the parameter d is 1 ≥ d > 0. The larger the values of the parameter d, the smoother the segmented image obtains final segmenting region. Neighboring firing neurons can also directly affect the linking input. It is obvious that the modified expression of the linking input always depends on the inhibition term d and neighboring action potentials Ykl[n − 1].

3.3 Internal Activity U

The internal activity Uij[n] in (3) derives from the coupled results between the feeding input and the linking input with linking strength β. The increase of Uij[n] is with the increase of the above two inputs. In recent years, there are several significantly improved expressions of the internal activity from the SPCNN [18], the enhanced PCN [23], the pulse coupled neural filter [24].

In the SPCNN, the internal activity Uij[n]1 includes its previous neuron state and the coupled result in (3). Its mathematical expression is given as

$$\begin{aligned} U_{\text{ij}} [n]^{1} & = e^{{ - \alpha_{\text{f}} }} U_{\text{ij}} [n - 1] + F_{\text{ij}} [n](1 + \beta L_{\text{ij}} [n]) \\ & = e^{{ - \alpha_{\text{f}} }} U_{\text{ij}} [n - 1] + S_{\text{ij}} \left( {\left. {1 + \beta V_{\text{L}} \sum\limits_{\text{kl}} {W_{\text{ijkl}} Y_{\text{kl}} } [n - 1]} \right)} \right. \\ \end{aligned}$$
(28)

where the parameter αf is the exponential decay factor based on the internal activity. Comparing with most simplified PCNN models, the internal activity Uij[n] of the SPCNN provides the neuronal modulation results more reasonably.

The enhanced PCN is a two-layer recurrent PCNN whose internal activity Uij(t)2 in each layer increases an inhibition term γLij(t) modulated by the linking strength γ. The internal activity terms of the enhanced PCN are shown as

$$U_{\text{ij}} (t)_{1}^{2} = F_{\text{ij}} (t)(1 + \beta_{1} L_{\text{ij}} (t)_{11} - \gamma_{1} L_{\text{ij}} (t)_{12} )$$
(29)
$$U_{\text{ij}} (t)_{2}^{2} = F_{\text{ij}} (t)(1 + \beta_{2} L_{\text{ij}} (t)_{21} - \gamma_{2} L_{\text{ij}} (t)_{22} )$$
(30)

In (29) and (30), the inhibition terms readjust the firing times of corresponding neurons than basic PCNN. What is more, neurons firing speed of two-layer network is faster than single-burst PCNN.

For the pulse coupled neural filter, traditional coupled modulation is changed for avoiding direct influence of zero-valued pixels, and new internal activity is given as follows:

$$U_{\text{ij}} (t)^{3} = F_{\text{ij}} (t) + \beta L_{\text{ij}} (t).$$
(31)

3.4 Action Potential Y

For basic PCNN in (4), the generation of action potential Y derives from the comparisons of internal activity Uij[n] and dynamic threshold Eij[n]. If Uij[n] > Eij[n], neuron Nij outputs a pulse (Yij[n] = 1); otherwise, it does not fire (Yij[n] = 0). Additionally, output values of action potential Y can occasionally be set by logical operation rules [25]. Certainly, referring to the SCM model [17], action potential Y can also be described as

$$Y_{\text{ij}} [n]^{1} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\quad \frac{1}{{1 + e^{{( - \gamma (U_{\text{ij}} (n) - E_{\text{ij}} (n)))}} }} > 0.5} \hfill \\ {0,} \hfill & {\quad {\text{otherwise}}} \hfill \\ \end{array} } \right.$$
(32)

In (32), action potential Yij[n]1 adopts the sigmoid function with the parameter γ. This indicates that the action potential can generate various types of pulse outputs, which is analogous to traditional action potential Yij[n] in (4).

Besides the above sigmoid function, the action potential can also adopt the radial-basis function [26]. Its equation is described as

$$Y_{\text{ij}} [n]^{2} = e^{{ - ((U_{\text{ij}} (n) - E_{\text{ij}} (n))^{2} )}}$$
(33)

Additionally, The action potential can generate other output values except ‘0’ or ‘1’, such as [27], and its equation is given as

$$\left\{ {\begin{array}{*{20}l} {\xi (n) = U_{\text{ij}} (n) - E_{\text{ij}} (n)} \hfill \\ {G_{\text{ij}} = \sum\nolimits_{r} {\sum\nolimits_{t} {|\xi_{\text{ij}} (n) - \xi_{\text{i + r,j + t}} (n)|} } } \hfill \\ {Y_{\text{ij}} (n)^{3} = \left\lceil {\frac{{\xi_{\text{ij}} (n)}}{\hbox{max} \xi (n)} \times k} \right\rceil } \hfill \\ \end{array} } \right.$$
(34)

Where ξij(n) is initial output results based on the comparisons between internal activity and dynamic threshold. Gij denotes the difference between the parameter ξij(n) and neighboring thresholdings. Yij(n)3 and k are final action potential and the hierarchy parameter, respectively. The above action potential setting method merge more related image information based on spatial adjacency proximity into the expression of the action potential.

3.5 Dynamic Threshold E

Dynamic threshold Eij[n] influenced by the exponential decay factor αe and the amplitude parameter VE, plays an important role for PCNN segmentation. In (4), the comparison results between internal activity Uij[n] and dynamic threshold Eij[n] can directly judge whether a neuron fire or not. This indicates that the calculation results of dynamic threshold Eij[n] obviously affect final firing results. The smaller the values of dynamic threshold Eij[n], the greater the number of firing neuron at the iteration is. Based on the dynamic threshold of basic PCNN, we will give several main improved equations and analyze their image segmentation characters.

Firstly, Gao et al. [20] adopted a regularized Heaviside function Hε including the cluster center m2[n] of the object to modify the dynamic threshold as

$$E_{\text{ij}} [n]^{1} = m_{2} [n]H_{\varepsilon } \left\{ {m_{2} [n] - I_{\text{ij}} } \right\}$$
(35)

In (35), the dynamic threshold cannot form periodic oscillation because of the uses of the parameters Hε and m2[n]. Further, if the internal activity of a neuron is lower than m2[n], it will be prevented from firing.

Secondly, Cheng et al. [22] introduced a decay constant λ to control the changing rate of firing signal inputs and normalized pixel intensity Sij. The new dynamic threshold is described as

$$E_{\text{ij}} [n]^{2} = \lambda \sum\limits_{kl} {\left\{ {Y_{kl} [n - 1]S_{\text{ij}} } \right\}}$$
(36)

In (36), the dynamic threshold is gradually growing with the increase of the number of neighboring firing neurons before the new threshold satisfies the terminate condition of the whole cycle. Here, the setting method of the dynamic threshold focuses on the influences of neighboring pixels and normalized pixel intensity rather than dynamic threshold itself.

Thirdly, Xiang et al. [28] used five proper parameters to form a new dynamic threshold rather than the parameters αe and VE of basic PCNN. The dynamic threshold can be given by

$$E_{\text{ij}} [n]^{3} = T^{ + } - n \times N\;\;\;\;\;n \le M$$
(37)

where

$$M = \frac{K}{N}$$
(38)

In (37) and (38), N is the length of the attenuation step. T+ and K are the upper limit and the width of the variation range for dynamic thresholds, respectively. n denotes iteration number and M is maximum number of iterations. As the parameters T+, N, M and K are set to constant values, the change of dynamic threshold depends only on the parameter n. This setting method provides a new thinking that the dynamic threshold is determined by iteration times of the PCNN.

3.6 Feature Expression

3.6.1 Entropy Sequence

Ma et al. [29] proposed an automatic image segmentation method based on the maximum entropy to choose optimal segmentation result after n iterations. They also gave an entropy sequence to extract feature values of testing images. For entropy sequence, information entropy is firstly calculated at each iteration

$$H(P) = - \,P_{1} \log (P_{1} ) - P_{0} \log (P_{0} )$$
(39)

where H(P) denotes the information entropy of a binary image. P1 and P0 are the occurring probabilities of ‘1’ and ‘0’, respectively. Secondly, all information entropies are combined into one sequence, which is regarded as an entropy sequence. It has invariant texture features in rotation, translation and scale. Significantly, most images always generate a unique entropy sequence by setting suitable PCNN parameters.

3.6.2 Time Sequence and Time Matrix

Time sequence is given by the sum of firing neurons at each iteration [16, 17]. Its expression is given as follow:

$$T^{1} [n] = \sum\limits_{x,y} {Y_{\text{ij}} [n]}$$
(40)

Obviously, time sequence can save neuronal firing information of the whole image, and further accomplish a feature conversion between multi-dimensional and one-dimensional information. Further, related mathematical definitions of time matrix are also given to determine its final expression [26]. Their corresponding equations are described as

$$T_{\text{ij}}^{2} [n] = \log_{g} \frac{{U_{\text{ij}} \{ T_{\text{ij}}^{2} [n]\} }}{{\theta_{\text{ij}} (0)}}$$
(41)
$$T_{\text{ij}}^{3} [n] = T_{\text{ij}}^{3} [n - 1] + nY_{\text{ij}} [n]$$
(42)

In (41), the parameters g and θij(0) are the decay coefficient, and the amplitude of the dynamic threshold, respectively. As T 2ij [n] is an implicit function and cannot obtain the calculating result, we get reasonable time matrix by calculating the formula (42).

3.6.3 Neighboring Firing Matrix

We adopt a neighboring firing matrix to record the number of neighboring firing neurons at each iteration [30]. The mathematical equation of the firing matrix for four neighboring neurons is given as

$$Q_{ (i ,j )} [n] = Y_{{ (i{ + 1,}j )}} [n - 1] + Y_{{ (i{ - 1,}j )}} [n - 1] + Y_{{ (i ,j{ + 1)}}} [n - 1] + Y_{{ (i ,j{ - 1)}}} [n - 1]$$
(43)

Neighboring firing matrix based on human visual system (HVS) can improve the image description capacity of edge regions, which easily generate a more reasonable input stimulus for the PCNN.

3.6.4 Sub-intensity Ranges of Neurons Firing

The sub-intensity ranges exhibit corresponding pixel intensities of firing neurons at each iteration [18, 29]. Thus, it is significant to calculate and analyze the sub-intensity ranges of neurons firing for PCNN. Subsequently, we give two examples about the sub-intensity ranges of the SPCNN in Fig. 4a, b to clearly illustrate the change of pixel intensities at each iteration.

Fig. 4
figure 4

Intensity ranges using SPCNN within the first pulsing cycle for Fig. 3: a intensity ranges of SPCNN with iteration times 1-6 in Fig. 3a–e; b intensity ranges of SPCNN with iteration times 1–5 in Fig. 3f–j

Full size image

4 Parameter Setting

4.1 Input Stimulus

For traditional PCNN, input stimulus Sij is usually defined as a normalized pixel intensity, which directly affects computational results of the feeding inputs. Since more and more researchers pay attention to HVS, subsequent modified strategies are proposed to associate input stimuli of the PCNN with HVS. Based on Weber-Fechner law, Ref. [31] used a new input stimuli to simulate human vision perception, and the expression is defined by

$$S_{\text{ij}}^{1} = K\ln B + K_{0}$$
(44)

where B and S 1ij denote objective and subjective pixel intensities, respectively. K and K0 denote two modulated constants. Referring to [31], Huang et al. [21] adopted a more reasonable external stimulus analogous to human eyes inputs

$$S_{\text{ij}}^{2} = K\left[ {\alpha_{\text{E}} - \alpha_{\text{E}} T_{\text{ij}} + \ln \left( {\frac{{V_{\text{E}} }}{C}} \right)} \right] + r$$
(45)

where K, C and r are three empirical constants. Tij records corresponding iteration times from firing neurons. The above formula builds the relationship between the time matrix Tij and subjective visual brightness. Ref. [30] also used the new expression of the input stimulus as follow:

$$S_{\text{ij}}^{3} = \ln \left[ {1 + Sori_{\text{ij}} + \frac{{4S^{\prime 3} }}{{Q_{\text{ij}} + (4 - Q_{\text{ij}} )S^{\prime } }}} \right]$$
(46)

where Soriij is a normalized pixel intensity in position (i,j) from an original image. S′denotes a normalized Otsu thresholding of the original image. Qij denotes the corresponding value of neighboring firing matrix Q in position (i,j). In (46), neighboring firing matrix and Otsu thresholding determine the input stimulus of modified PCNN model.

4.2 Exponential Decay Factor

4.2.1 Exponential Decay Factors α f and α l

For image segmentation, the exponential decay factors αf in (1) and αl in (2) are always set to empirical values under a complex scene. In order to satisfy desired requirements for identifying complex objects, several self-adaptive parameter setting methods, such as the SPCNN [18] and the PA-PCNN [32], are proposed.

In the SPCNN, the parameters αf and αl are merging into one parameter α 1f , the equation of which is given as

$$\alpha_{\text{f}}^{1} = \log \left( {\frac{1}{\sigma }} \right)$$
(47)

Based on the SPCNN, the parameter α 2f in the PA-PCNN adopts normalized Otsu thresholding S′ and its mathematical equation is written as

$$\alpha_{\text{f}}^{2} = \log \left( {\frac{1}{{S^{\prime } }}} \right)$$
(48)

Comparing with the PA-PCNN, the parameter α 1f in the SPCNN is easy to generate more obviously exponent decay.

4.2.2 Exponential Decay Factor α e

Exponential decay factor αe has several expression approaches proposed by Refs. [18, 25, 31,32,33]. Chen et al. [18] adopted an adaptive-parameter expression and its equation is formulated by

$$\alpha_{e}^{1} = \ln \left( {\frac{{\frac{{V_{E} }}{{S^{\prime } }}}}{{\frac{{1 - e^{{ - 3\alpha_{f} }} }}{{1 - e^{{ - \alpha_{f} }} }} + 6\beta V_{L} e^{{ - \alpha_{f} }} }}} \right)$$
(49)

In (49), S′ denotes the normalized Otsu thresholding of the whole image. What is more, Zhou et al. [25] used the cluster mean m2(n) from the fired region at previous iteration to build the relationship between the parameters m2(n) and α 2e

$$\alpha_{\text{e}}^{2} = - \ln \left( {\frac{{m_{2} (n)}}{{m_{2} (n - 1)}}} \right)$$
(50)

In addition, the parameter α 3e in Wei et al. [31] and Helmy et al. [33] adopted the average gray level μ and an adjustable constant C as follows:

$$\alpha_{\text{e}}^{3} = \frac{C}{\mu }$$
(51)

Based on the above equations, Ref. [32] also provided a simplified expression of the parameter α 4e as

$$\alpha_{\text{e}}^{4} = \frac{1}{{S^{\prime } }}.$$
(52)

4.3 Input Amplitudes

4.3.1 Feeding Input Amplitude V F and Linking Input Amplitude V L

The parameters VF and VL in basic PCNN denote the amplitudes of the sum of output values from neighboring neurons at previous iteration for the feeding input and the linking input, respectively. In most prevalent modified models, the above two parameters are often eliminated to reduce computational complexity. Meanwhile, several important PCNN models only retain the parameter VL, which is empirically set to 1 [17, 18].

4.3.2 Dynamic Threshold Amplitude V E

The parameter VE is reasonably evolved from the experience data to the adaptive results. Significantly, several adaptive setting methods, such as the SPCNN and the MSPCNN, should be introduced due to their practical roles on image segmentation [18, 30].

For the SPCNN, the parameter V 1E is set to an adaptive value by reasonable formula derivation as follows:

$$V_{\text{E}}^{1} = e^{{ - \alpha_{\text{f}} }} + 1 + 6\beta V_{\text{L}}$$
(53)

Referring to the SPCNN, the parameter V 2E in the MSPCNN decreases the number of the setting parameters and its formula is written as

$$V_{\text{E}}^{2} = 1 + S^{\prime 2} - S^{\prime 8}$$
(54)

In (54), the parameter S′ denotes normalized Otsu thresholding and the parameter S′8 is an offset value.

4.4 Linking Strength

Kuntimad and Ranganath calculated the range of the linking strength β, and built the relationship between the linking strength and the linking input by acquiring neuronal capture ranges [34]. If the intensity range of object regions is [I4, I3], and the intensity range of background regions is [I2, I1] (I4 > I2 > I3 > I1), the capture results of the whole image can be given by

$$I_{3} (1 + \beta L_{\hbox{min} 1} (T_{1} )) \ge I_{4}$$
(55)
$$I_{1} (1 + \beta L_{\hbox{min} 2} (T_{2} )) \ge I_{2}$$
(56)
$$I_{2} (1 + \beta L_{\hbox{max} 2} (T_{2} )) < I_{4}$$
(57)

In (55)–(57), Lmin1(T1) and Lmin2(T2) are minimum linking inputs of the object and the background, respectively. According to the above three formulae, the range of the parameter β can be given as

$$[\hbox{max} \{ (I_{4} /I_{3} - 1) /L_{\hbox{min} 1} ,(I_{2} /I_{1} - 1) /L_{\hbox{min} 2} \} ,(I_{4} /I_{2} - 1) /L_{\hbox{max} 2} ]$$
(58)

Refs. [20, 23] also adopted the above method to determine the range of the parameter β. Refs. [16, 35, 36] gave the parameters βini and Δβ to redefine β. Hereinto, the parameter βini contains the minimum distance diffmin and the neuronal pulsing seed input inputseed. The parameter Δβ is a constant. Obviously, the value of β is gradually added by the parameter Δβ at each iteration until the statistical termination is met. Refs. [37, 38] set the value of the parameter β by calculating the distance between the neighboring pixels and the central pixel for a fixed region. Ref. [39] proposed the setting method of the parameter β, and can evidently improve neuron firing speed. Ref. [40] supplied a new expression based on the mean and variance of the pixel intensity. Ref. [22] gave a 3 × 3 matrix to obtain the linking strength β, which can decrease the influences of the bed pixels.

Besides the above semi-automatic setting method through calculating the empirical values and the constant values, several automatic parameter setting methods of the linking strength β are also presented, such as the SPCNN and the PA-PCNN. The SPCNN gives the expression of the parameter β1 as

$$\beta^{1} = \frac{{(S_{\hbox{max} } /S^{\prime } ) - 1}}{{6V_{\text{L}} }}$$
(59)

Based on simplified parameter β1, the parameter β2 in the PA-PCNN is given as

$$\beta^{2} = \frac{1 - S'}{6S'}$$
(60)

In (59) and (60), Smax denotes the maximum normalized intensity of the whole image. S′ denotes the normalized Otsu thresholding.

4.5 Synaptic Weight

The parameters Mijkl and Wijkl in basic PCNN represent synaptic weights that are the sum of neighboring neuron outputs. Ranganath et al. [12] firstly adopted the inverse of the Euclidean distance to describe Mijkl and Wijkl as follows:

$$M_{\text{ijkl}} ,W_{\text{ijkl}} = \frac{1}{{(i - k)^{2} + (j - l)^{2} }}$$
(61)

In (61), synaptic weights for neuron Nij in position (i, j) have many linking values by calculating the distances between neurons. Hereinto, the Euclidean distances of four and eight neighboring neurons are shown in Fig. 5.

Fig. 5
figure 5

The Euclidean distances of neighboring neurons: a the Euclidean distance of four neighboring neurons; b the Euclidean distance of eight neighboring neurons

Full size image

References [28, 39, 41] adjusted synaptic weights based on the exponential function. Hereinto, Ref. [39] used a synaptic weight Mijkl with Gaussian distribution and its mathematical equation is defined as

$$M_{\text{ijkl}} = C_{\sigma } e^{{\frac{{(i - k)^{2} + (j - l)^{2} }}{{2\sigma^{2} }}}}$$
(62)

where the parameter C is the normalized coefficient, and the parameter represents the smoothness of neighboring regions. For most modified models, the parameter Mijkl is removed and the parameter Wijkl is retained to reduce parameters number. Refs. [18, 30] expressed the synaptic weights by the matrices with constant values as follows:

$$W_{\text{ijkl}} = \left[ {\begin{array}{*{20}c} {0.5} & 1 & {0.5} \\ 1 & 0 & 1 \\ {0.5} & 1 & {0.5} \\ \end{array} } \right]$$
(63)
$$W_{\text{ijkl}} = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \\ \end{array} } \right]$$
(64)

Besides the constant values, the synaptic weight Wijkl also contains fixed parameter values such as [42].

5 Complex PCNN

5.1 Heterogeneous PCNN

Ref. [21] presented a heterogeneous PCNN model that is more suitable for human to observe. Based on the above PCNN, Ref. [43] proposed a heterogeneous SPCNN, including SPCNN 1, SPCNN 2 and SPCNN 3 for image segmentation. There are three types of the SPCNN models to produce the heterogeneous structure of the SPCNN. The above SPCNN models have different internal activities, linking strengths and synaptic weights, while they have same other setting parameters. They can be also connected via the linking parameter L12 linking the SPCNN 1 and the SPCNN 2, and the linking parameter L23 linking the SPCNN 2 and the SPCNN 3. Hereinto, the changes of internal activities directly influence final segmentation results, and three types of internal activities are given by

$$U_{1} [n] = e^{ - \alpha f} U_{1} [n - 1] + S_{ij} \left\{ {1 + \beta_{1} V_{L} \sum\limits_{kl} {W_{ijkl} (1)Y_{1kl} [n - 1]} } \right\}$$
(65)
$$U_{ 2} [n] = e^{ - \alpha f} U_{ 2} [n - 1] + S_{\text{ij}} \left\{ {1 + \beta_{2} V_{\text{L}} \sum\limits_{kl} {W_{\text{ijkl}} (2)Y_{{ 2 {\text{kl}}}} [n - 1] + L{}_{12}} } \right\}$$
(66)
$$U_{ 3} [n] = e^{ - \alpha f} U_{ 3} [n - 1] + S_{\text{ij}} \left\{ {1 + \beta_{3} V_{\text{L}} \sum\limits_{kl} {W_{\text{ijkl}} (3)Y_{{ 3 {\text{kl}}}} [n - 1] + L_{23} } } \right\}$$
(67)

In (65)–(67), the heterogeneous SPCNN can acquire three different values for the internal activities at each iteration, meanwhile, it also gives the comparison results between the dynamic thresholds and the above internal activities to produce three different outputs as follows:

$$Y_{{ 1 {\text{ij}}}} [n] = \left\{ {\begin{array}{*{20}l} {a_{1} } \hfill & {\quad if\quad U_{{ 1 {\text{ij}}}} [n] > E_{{ 1 {\text{ij}}}} [n - 1]} \hfill \\ 0 \hfill & {\quad if\quad U_{{ 1 {\text{ij}}}} [n] \le E_{{ 1 {\text{ij}}}} [n - 1]} \hfill \\ \end{array} } \right.$$
(68)
$$Y_{{ 2 {\text{ij}}}} [n] = \left\{ {\begin{array}{*{20}l} {a_{2} } \hfill & {\quad if\quad U_{{ 2 {\text{ij}}}} [n] > E_{{ 2 {\text{ij}}}} [n - 1]} \hfill \\ 0 \hfill & {\quad if\quad U_{{ 2 {\text{ij}}}} [n] \le E_{{ 2 {\text{ij}}}} [n - 1]} \hfill \\ \end{array} } \right.$$
(69)
$$\begin{aligned} \hfill \\ Y_{{ 3 {\text{ij}}}} [n] = \left\{ {\begin{array}{*{20}l} {a_{3} } \hfill & {\quad if\quad U_{{ 3 {\text{ij}}}} [n] > E_{{ 3 {\text{ij}}}} [n - 1]} \hfill \\ 0 \hfill & {\quad if\quad U_{{ 3 {\text{ij}}}} [n] \le E_{{ 3 {\text{ij}}}} [n - 1]} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(70)

In (68)–(70), a1, a2 and a3 are final output values of SPCNN 1, SPCNN 2 and SPCNN 3, respectively. Their parameter values are set to 0.3, 0.5 and 0.2 (the sum of the parameter values is 1). The above three outputs Y1ij[n], Y2ij[n] and Y3ij[n] can be combined to one output Yij[n], corresponding values of which have ‘0’, ‘0.2’, ‘0.3’, ‘0.5’, ‘0.7’, ‘0.8’ and ‘1’ rather than ‘0’ or ‘1’. This indicates that the heterogeneous SPCNN has more clearly segmentation levels, which easily generate more reasonable segmentation results. The structure flowchart of heterogeneous SPCNN is shown in Fig. 6. The segmentation results of the heterogeneous PCNN from two examples of Berkeley Segmentation Dataset are given in Fig. 7.

Fig. 6
figure 6

The structure of heterogeneous PCNN

Full size image
Fig. 7
figure 7

The segmentation results of the heterogeneous PCNN: a, d original images from Berkeley Segmentation Dataset; b, e the histograms of original images; c, f the segmentation results of the heterogenous PCNN

Full size image

5.2 Multi-channel PCNN

For color image segmentation, single-channel PCNN is difficult to provide reasonable segmentation results, because of corresponding color spaces of normalized Red Green Blue (RGB). Therefore, multi-channel PCNN with appropriate setting parameters has a significant meaning for further conducting color image segmentation.

Ref. [44] gave a reasonable segmentation strategy and identified objects in complex real-world scenes. Significantly, the achievement of multi-channel PCNN mainly depends on normalized expressions of different channels in color spaces. The resulting images based on RGB color spaces are shown as follows:

$$\left( {\begin{array}{*{20}c} r \\ g \\ b \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{R}{R + G + B}} \\ {\frac{G}{R + G + B}} \\ {\frac{B}{R + G + B}} \\ \end{array} } \right)$$
(71)
$$\left( {\begin{array}{*{20}c} {O_{1} } \\ {O_{2} } \\ {O_{3} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\frac{r - g}{\sqrt 2 }} \\ {\frac{r + g - 2b}{\sqrt 6 }} \\ {\frac{r + g + b}{\sqrt 3 }} \\ \end{array} } \right)$$
(72)
$$O_{4} = - \,O_{1}$$
(73)
$$O_{5} = - \,O_{2}$$
(74)

In (71)–(74), R, G and B denote pixel intensities of Red, Green and Blue in color space channels, respectively. r, g and b are the normalized expressions of different channels in RGB color models. O1, O2, O3, O4 and O5 denote five channels of transformed color images. For multi-channel PCNN, we first analyze transformed color channels, and then adopt modified PCNN models to acquire the result of each channel and integrate all the above results into final results for achieving the segmentation goal of multi-channel PCNN.

6 Related Applications of PCNN for Image Segmentation

6.1 Natural Image Segmentation

Stewart et al. [16] proposed a seeded region growing (SRG) algorithm that uses the inhibition term d to control the amplitude of the linking input in the PCNN and designs the fixed threshold Tx[t] to take the place of the dynamic threshold. Refs. [45,46,47] gave the termination conditions and the increment step Δβ of the linking strength to deduce fine segmentation steps of the modified region growing algorithms. Xu et al. [35] proposed a color region growing PCNN (CRG-PCNN) model, converting RGB color space into LAB and assessing the color distance between the neurons of feeding inputs. Zhou et al. [48] presented an extended PCNN based on a decision tree, which builds a direct relation between the adjustable parameters and the image characteristics. Zhao et al. [49]. designed a gradient-coupled spiking cortex model for further smoothing the pixels of same regions and enhancing the pixels of the contours from different regions.

Xiao et al. [50] modified the expression of dynamic thresholds for PCNN, and used fuzzy mutual information as the criterion of optimal segmentation results. Nie et al. [51, 52] merged Unit-Linking PCNN, maximum Shannon entropy rule, minimum cross-entropy rule and pre-processing strategies into image segmentation schemes. Ma et al. [53] gave the evaluation criterion of maximum information-entropy to find suitable iteration times for PCNN to obtain reasonable segmentation results. Zhou et al. [39] changed the expressions of the synaptic weights, the linking strength and the dynamic threshold to improve the automatic segmentation control ability of the PCNN. Zhan et al. [54] showed a fast-linking SCM model that can achieve the optimal thresholding selection and make better homogeneous objects as soon as possible. Li et al. [55] found a parameter optimal method of simplified PCNN based on immune algorithm for adjusting setting parameters automatically. Jiao et al. [56, 57] combined the SPCNN and the gbest led gravitational search (GLGSA) into a novel image segmentation method that is applied to 23 standard benchmark function. Guo et al. [58] first defined adaptive-semi-local feature contrast as the input stimulus of the original images, and then introduce saliency motivated improved simplified pulse coupled neural network based on HVS to locate interest regions.

There are still other modified algorithm based the PCNN, which are suitable for image segmentation, such as, oscillatory correlation PCNN [59], automatic design PCNN [60], clustering threshold PCNN [61], simplified parameters PCNN [62], unsupervised texture multi-PCNN [63], genetic PCNN [64], bidirectional search PCNN [65] and sine–cosine oscillation heterogeneous PCNN [66].

6.2 Medical Image Segmentation

For medical images, the lesions tend to be determined by appropriate segmentation steps, together including pre-processing, regions segmentation and post-processing. Hereinto, most modified PCNN models has a good potential for finding the locations of the lesions rapidly and accurately for different types of diseases.

Micro-calcification detection methods in digitized mammograms are separately proposed, including contourlet transform and simplified pulse coupled neural network, to extract micro-calcification clusters [67, 68]. PCNN-based level set also supplies a reasonable segmentation strategy with PCNN coarse segmentation and level set refined segmentation [69]. A PCNN-based segmentation algorithm in breast MR images can identify corresponding interest regions and detect the boundary of the breast regions [70]. An evolutionary PCNN is proposed to segment and detect breast lesions in ultrasound images [42]. Basic PCNN model is adopted to improve segmentation accuracy rate of potential masses based on digitized mammograms [71]. Moreover, MSPCNN [30] and PA-PCNN [32], simplifying adaptive parameters than traditional PCNN, are proposed to achieve initial segmentation of mass regions for digitized mammograms. Hereinto, the segmentation results of the MSPCNN based on Digital Database for Screening Mammography (DDSM) and Mammographic Image Analysis Society (MIAS) database [72, 73], are shown in Fig. 8.

Fig. 8
figure 8

The segmentation results of the MSPCNN: a an original image from the DDSM database; b the segmentation result of the MSPCNN for a; c an original image from the MIAS database; d the segmentation result of the MSPCNN for c

Full size image

Besides breast images, several modified PCNN is gradually used to segment the lesions of other common diseases. A biologically-inspired spiking neural network with median filter can reasonably detect the boundary of the prostate in ultrasound images [74]. A modified SPCNN obtains a reliable stone segmentation result in the ultrasound images of the gallbladder [75]. A spatial pulse coupled neural network with the statistical expectation maximization is proposed in brain MR images [76]. A PCNN-based segmentation algorithm can obtain the segmentation results of rat brain volumes in MR images [77]. A segmentation method combining the PCNN and Selective Binary and Gaussian Filtering Regularized Level Set (GFRLS) is adopted to segment and classify teeth based on anatomical structure in MicroCT slices [27]. A modified PCNN derived from Zhan et al.’s [78]. SCM model acquires nuclei in reflectance confocal images of epithelial tissue. A self-adaptive PCNN model with any colony optimization (ACO) obtains reasonable segmentation results of the lesion in MR medical images [79]. A Tandem Pulse Coupled Neural Network (TPCNN) with Contrast Limited Adaptive Histogram Equalization (CLAHE) and Deep Learning Based Support Vector Machine (DLBSVM) is proposed to acquire segmentation results of retinal blood vessels in ophthalmologic diabetic retinopathy images [80]. A memristive pulse coupled neural network (M-PCNN) based on hardware implementation, is applied to medical image edge extraction [81].

Other PCNN segmentation methods of medical images also provide reasonable segmentation frameworks, such as, the SCM-motivated enhanced CV [82, 83], the SPCNN-based segmentation approaches [84,85,86,87], the particle-swarm optimization PCNN [88].

6.3 Image Segmentation Based on HVS

Image segmentation algorithms based on HVS for PCNN can achieve desired segmentation goal, where the segmentation results are much closer to human vision classification than other prevalent algorithms. Huang et al. [21, 89] introduced the Web–Fechner law to build the relationship between objective image brightness and subjective human perception. Its equation is given as

$$I_{\text{ij}}^{1} = K\ln S_{\text{ij}} + r$$
(75)

Meanwhile, PCNN time matrix was also given to associate adjustable PCNN parameters with image brightness values as follows:

$$T_{\text{ij}} [n] = 1 + \frac{1}{{\alpha_{\text{E}} }}\ln \frac{{V_{\text{E}} }}{{cS_{\text{ij}} }}$$
(76)

In (75), K and r denote setting constants. S and I represent objective image brightness values and subjective perception values, respectively. In (76), Tij[n] is time matrix of PCNN at the nth iteration. c denotes a constant. VE and αE denote the amplitudes of dynamic threshold and the exponential decay factor, respectively. According to the above two equations, final expression of subjective human perception based on PCNN can be written as

$$I_{\text{ij}}^{2} = K\ln S_{\text{ij}} + r = K[\alpha_{\text{E}} - \alpha_{\text{E}} T_{\text{ij}} + \ln (V_{\text{E}} /c)] + r$$
(77)

Based on (77), an objective expression with neighboring firing matrix based on HVS is described to provide a new input stimulus of the feeding input [30]. Its final equation is given in (46). Corresponding experimental results show segmentation performances analogous to human visual perception. The flowchart is given in Fig. 9.

Fig. 9
figure 9

The flowchart of feeding inputs based on HVS for MPCNN

Full size image

6.4 Other Applications

PCNN also has broad applications in other aspects based on image segmentation, such as satellite image analysis [33, 90,91,92,93], visual saliency detection [58, 94, 95], plant recognition [28, 53, 96,97,98], iris feature extraction [99, 100], infrared human segmentation [101], palmprint verification [102], crack detection [22], power line detection [24], catenary fault detection [37], fabric defection [103], constrained ZIP code segmentation [104], vehicle recognition [38], aquatic feeding detection [105], heterogeneous material segmentation [106], fingerprint orientation field estimation [107], character recognition [108], feature extraction and object detection based on color images [44, 109,110,111]. Other segmentation applications can also be elaborated by the corresponding reviews [112,113,114,115].

7 Conclusion

PCNN plays important roles for image segmentation. In this paper, we give a comprehensive review to analyze PCNN segmentation properties and show related applications. There are three main steps. We first provide basic PCNN model and classical modified PCNN models, then introduce dynamic properties, parameter setting and multi-channel PCNN. In addition, we also provide main image segmentation applications of the PCNN. In the future, the PCNN merging semantic segmentation and deep learning will probably generate new image segmentation frameworks and bring a rapid progress than state-of-the-art algorithms.