Abstract
In this work we develop a new class of high order accurate Arbitrary-Lagrangian–Eulerian (ALE) one-step finite volume schemes for the solution of nonlinear systems of conservative and non-conservative hyperbolic partial differential equations. The numerical algorithm is designed for two and three space dimensions, considering moving unstructured triangular and tetrahedral meshes, respectively. As usual for finite volume schemes, data are represented within each control volume by piecewise constant values that evolve in time, hence implying the use of some strategies to improve the order of accuracy of the algorithm. In our approach high order of accuracy in space is obtained by adopting a WENO reconstruction technique, which produces piecewise polynomials of higher degree starting from the known cell averages. Such spatial high order accurate reconstruction is then employed to achieve high order of accuracy also in time using an element-local space–time finite element predictor, which performs a one-step time discretization. Specifically, we adopt a discontinuous Galerkin predictor which can handle stiff source terms that might produce jumps in the local space–time solution. Since we are dealing with moving meshes the elements deform while the solution is evolving in time, hence making the use of a reference system very convenient. Therefore, within the space–time predictor, the physical element is mapped onto a reference element using a high order isoparametric approach, where the space–time basis and test functions are given by the Lagrange interpolation polynomials passing through a predefined set of space–time nodes. The computational mesh continuously changes its configuration in time, following as closely as possible the flow motion. The entire mesh motion procedure is composed by three main steps, namely the Lagrangian step, the rezoning step and the relaxation step. In order to obtain a continuous mesh configuration at any time level, the mesh motion is evaluated by assigning each node of the computational mesh with a unique velocity vector at each timestep. The nodal solver algorithm preforms the Lagrangian stage, while we rely on a rezoning algorithm to improve the mesh quality when the flow motion becomes very complex, hence producing highly deformed computational elements. A so-called relaxation algorithm is finally employed to partially recover the optimal Lagrangian accuracy where the computational elements are not distorted too much. We underline that our scheme is supposed to be an ALE algorithm, where the local mesh velocity can be chosen independently from the local fluid velocity. Once the vertex velocity and thus the new node location has been determined, the old element configuration at time \(t^n\) is connected with the new one at time \(t^{n+1}\) with straight edges to represent the local mesh motion, in order to maintain algorithmic simplicity. The final ALE finite volume scheme is based directly on a space–time conservation formulation of the governing system of hyperbolic balance laws. The nonlinear system is reformulated more compactly using a space–time divergence operator and is then integrated on a moving space–time control volume. We adopt a linear parametrization of the space–time element boundaries and Gaussian quadrature rules of suitable order of accuracy to compute the integrals. We apply the new high order direct ALE finite volume schemes to several hyperbolic systems, namely the multidimensional Euler equations of compressible gas dynamics, the ideal classical magneto-hydrodynamics equations and the non-conservative seven-equation Baer–Nunziato model of compressible multi-phase flows with stiff relaxation source terms. Numerical convergence studies as well as several classical test problems will be shown to assess the accuracy and the robustness of our schemes. Finally we briefly present some variants of the algorithm that aim at improving the overall computational efficiency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many real world processes are modeled using time-dependent partial differential equations (PDE), which are based on the conservation of some physical quantities. Therefore these mathematical and physical models are typically addressed as conservation laws and they cover a wide range of phenomena, such as environmental and meteorological flows, hydrodynamic and thermodynamic problems, plasma flows as well as the dynamics of many industrial and mechanical processes.
In general any conservation law assumes that the modeled medium is a continuum and describes the evolution of the conserved quantity \(u(\mathbf {x},t)\) in the control volume \(\omega\), which can be chosen arbitrarily. The conserved quantity depends both on space (\(\mathbf {x}\)) and time (t) and any change of u, i.e. the time evolution of u, is assumed to be due to some fluxes F(u) across the boundary \(\partial \omega\) of the control volume and, in some cases, also to a so-called source term S(u) that may affect the evolution of u by either increasing or decreasing the conserved quantity. A very general formulation for a conservation law reads
where \(\overline{n}\) represents the outward pointing unit normal vector on the boundary \(\partial \omega\). The above expression must be valid for any control volume, hence leading to the following partial differential equation:
where Gauss’ theorem has been used to rewrite the boundary integral as the volume integral of the divergence of the fluxes \(\nabla \cdot F(u)\).
The quantity u might also be a vector, hence involving more conserved quantities. For instance, fluid dynamics is governed by conservation laws which describe the evolution of three conserved quantities, namely mass, momentum and total energy. As a consequence we obtain a system of conservation laws, whenever the quantity u is given by a vector. In this case a system matrix \(\mathbf {A}\) can be defined as
and the system is considered hyperbolic if for all \(\overline{n}\) all eigenvalues of matrix \(\mathbf {A}\) are real and if a complete set of eigenvectors exists.
In any case the governing equations (2) can generally be solved using either an Eulerian or a Lagrangian approach. In the first case the evolution of the conserved quantity u is observed and computed in a fixed reference system, while in the latter case the reference system is moving together with the local velocity of the medium.
This work focuses on the solution of hyperbolic systems of conservation laws of the form (2), considering a Lagrangian-like approach, where the control volume \(\omega (t)\) is moving and therefore is time-dependent. Specifically, our task is to design high order accurate finite volume schemes for the solution of hyperbolic systems adopting an Arbitrary-Lagrangian–Eulerian approach. In the following, Sect. 1.1 provides a general overview of high order numerical methods for the solution of hyperbolic PDEs in the Eulerian framework, while Sect. 1.2 presents a literature review of the state-of-the-art in the field of Lagrangian numerical schemes. Finally, Sect. 1.3 gives the introduction to this work.
1.1 High Order Finite Volume Methods on Fixed Grids
The Eulerian approach implies the introduction of nonlinear convective terms in the governing equations because the flow is observed in a fixed reference system, which does not neither change nor move in time. These terms are considered within the flux term F(u) of the conservation law (2). A lot of research has been carried out in the past decades in order to solve conservation laws of the form (2) numerically, starting from the one-dimensional case. A very famous and widespread approach is given by Godunov-type finite volume methods [93, 180], where the discrete solution is stored as constant data within each control volume of the computational mesh and is evolved in time by using the integral form of the conservation law (1). Since the discrete solution in general exhibits jumps at the element interfaces, the introduction of numerical fluxes across the discontinuities of each cell is necessary. Godunov suggested to obtain these numerical fluxes by solving Riemann problems at each interface. Early work regarded the exact solution of the Riemann problem [52, 93], that was followed by the development of approximate Riemann solvers, such as the linearized Riemann solver of Roe [146], the HLL and HLLE Riemann solvers [82, 96] and the local Lax–Friedrichs (LLF) solver proposed by Rusanov [147], which can be reinterpreted as an HLL-type flux with a particular choice of the signal speeds. While the above-mentioned HLL schemes are very robust, they smear out contact discontinuities. An improvement was made by Einfeldt and Munz [83] with the introduction of the HLLEM Riemann solver, where the intermediate state was assumed piecewise linear instead of piecewise constant. Another well-known improvement of the original HLL scheme is due to Toro et al. [175] with the design of the HLLC Riemann solvers that use an enhanced wave model that is able to capture also the intermediate contact wave. Osher et al. [137] introduced a class of approximate Riemann solvers based on path integrals, where the paths were obtained by an approximation of the solution of the Riemann problem by rarefaction fans. A simpler and more general version of the Osher flux has recently been forwarded by Dumbser and Toro [78, 79]. All those one-dimensional Riemann solvers can be used even in two- and three-dimensional problems, where the discontinuities are resolved at each boundary of the control volume along the normal direction.
In order to design high order accurate finite volume numerical schemes, a high order reconstruction operator in space is needed as well as a time evolution of the conserved quantities that allows the method to achieve high order of accuracy even in time. Since linear monotone schemes are at most of order one, as stated by the Godunov theorem [94], a first contribution for the improvement of the order of accuracy has been provided by the class of second order accurate TVD schemes, which adopts a linear reconstruction in space and time, like the MUSCL scheme of van Leer [180] and the second order method of Barth and Jespersen on unstructured meshes [14]. Later on nonlinear ENO reconstructions on unstructured grids have been introduced [1, 163] as well as WENO reconstructions [91, 100, 161]. Once the high order spatial reconstruction is available, a suitable time stepping technique has to be used to guarantee the final order of accuracy. Runge–Kutta (RK) methods perform a multi-stage time-integration to evolve the numerical solution from the current time level \(t^n\) to the next time level \(t^{n+1}\). The higher is the order of accuracy, the higher is the number of substages which are needed. Furthermore, the reconstruction operator must be recomputed at each substage, hence drastically decreasing the efficiency of the algorithm. For this reason RK methods are at most of order four, because of the so-called Butcher barriers [34], which cause the number of intermediate RK substages to become larger than the formal order of accuracy.
In recent years a valid alternative was proposed by Toro et al., who developed the ADER approach [12, 38, 68, 72, 129, 166, 167]. ADER is the abbreviation for “Arbitrary high order schemes using DERivatives” and the basic idea is to use the high order reconstructed states, which are available from the reconstruction operator, to evaluate the numerical fluxes at element interfaces. In this way the initial data for the local Riemann problems occurring at element boundaries are given by high order piecewise polynomials, instead of piecewise constants as in the original formulation of Godunov [94]. The first ADER algorithms [106, 129, 157, 158, 166, 167, 176, 177] follow the concept of Ben-Artzi and Falcovitz [15] based on the solution of the generalized Riemann problem (GRP) at zone boundaries. The time evolution is carried out by using repeatedly the governing conservation law in differential form to replace time derivatives by space derivatives, which is the so-called Cauchy–Kovalewski or Lax–Wendroff procedure. The idea behind the GRP approach is a temporal Taylor series expansion of the state at the interface. However, problems arise when the solution is discontinuous. Since in general jumps are admitted at element boundaries, conventional homogeneous Riemann problems for the state and all space derivatives have first to be solved at the interface, then the obtained results are plugged into the Cauchy–Kovalewski procedure to obtain high order accurate time derivatives. The resulting ADER schemes are one-step fully discrete and of arbitrary order of accuracy in space and time, and have been successfully used in the framework of both finite volume (FV) and discontinuous Galerkin (DG) methods, see [75–77, 157, 158]. An efficient quadrature-free approach for the numerical flux integration has been proposed in [76].
The most recent ADER methods [11, 12, 68, 72] evolve the spatially high order accurate reconstruction polynomial locally in time using a weak integral formulation of the conservation law in space–time, hence obtaining a space–time accurate representation of the solution within a cell. This most recent version of the ADER schemes is more similar to the original ENO scheme proposed by Harten et al. [95], since it first evolves the data in each element by solving a local Cauchy problem in the small, i.e. without accounting for the neighbor cells, and then solves the interactions at the zone boundaries. The main advantages of this time evolution are: (i) the cumbersome Cauchy–Kovalewski procedure is no more needed, and (ii) the resulting technique can handle very general and different hyperbolic systems of conservation laws. Furthermore stiff sources are also treated properly, as highlighted in [73, 98].
1.2 Lagrangian Methods on Moving Meshes
Any Lagrangian method aims at following the fluid motion as closely as possible, with a computational mesh that is moving with the local fluid velocity. In the Lagrangian description of the fluid the nonlinear convective terms disappear and Lagrangian schemes exhibit virtually no numerical dissipation at contact waves and material interfaces. Therefore the Lagrangian approach allows such discontinuities to be precisely located and tracked during the computation, achieving a much more accurate resolution of these waves compared to classical Eulerian methods on fixed grids. For this reason a lot of efforts has been made in the last decades in order to develop Lagrangian methods. Already John von Neumann and Richtmyer were working on Lagrangian schemes in the 1950s [184], using a formulation of the governing equations in primitive variables, which was also used later in [16, 35]. However, most of the modern Lagrangian finite volume schemes use the conservation form of the equations based on the physically conserved quantities like mass, momentum and total energy in order to compute shock waves properly, see e.g. [37, 126, 132, 162]. Lagrangian schemes can be also classified according to the location of the physical variables on the mesh: when all variables are defined on a collocated grid the so-called cell-centered approach is adopted [50, 125–127, 148], while in the staggered mesh approach [121, 122] the velocity is defined at the cell interfaces and the other variables at the cell center.
Cell-centered Lagrangian Godunov-type schemes of the Roe-type and of the HLL-type for the Euler equations of compressible gas dynamics have first been considered by Munz [132]. A cell-centered Godunov-type scheme has also been introduced by Carré et al. [37], who developed a Lagrangian finite volume algorithm on general multidimensional unstructured meshes. The resulting finite volume scheme is node based and compatible with the mesh displacement. In the work of Després et al. [56, 57] the physical part of the system of equations is coupled and evolved together with the geometrical part, hence obtaining a weakly hyperbolic system of conservation laws that is solved using a node-based finite volume scheme. Furthermore they presented a cell-centered Lagrangian method [50] that is translation invariant and suitable for curved meshes. Maire [123–125] proposed first and second order accurate cell-centered Lagrangian schemes in two- and three- space dimensions on general polygonal grids, where the time derivatives of the fluxes are obtained using a node-centered solver that may be considered as a multidimensional extension of the Generalized Riemann problem methodology introduced by Ben-Artzi and Falcovitz [15], Le Floch et al. [32, 113] and Titarev and Toro [166, 168, 171]. Cell-centered discontinuous Galerkin methods for solving the Lagrangian equations of gas dynamics have been considered in [116, 181–183]. Since Lagrangian schemes may lead to severe mesh deformation after a finite time, it is necessary to remesh (or at least to rezone) the computational grid from time to time. A very popular approach consists therefore in Lagrangian remesh and remap schemes, such as the family of cell-centered ALE remap algorithms introduced by Shashkov et al. and Maire et al. in [17, 19, 109, 110, 117, 148]. In [33, 90, 149, 185] purely Lagrangian and Arbitrary-Lagrangian–Eulerian (ALE) numerical schemes with remapping for multi-phase and multi-material flows are discussed. All the Lagrangian schemes listed so far are at most second order accurate in space and time.
Higher order of accuracy in space was first achieved in [45–47, 118] by Cheng and Shu, who introduced a third order accurate essentially non-oscillatory (ENO) reconstruction operator into Godunov-type Lagrangian finite volume schemes. High order of accuracy in time was guaranteed either by the use of a Runge–Kutta or by a Lax–Wendroff-type time stepping. The mesh velocity is simply computed as the arithmetic average of the corner-extrapolated values in the cells adjacent to a mesh vertex. Such a nodal solver algorithm is very simple and general and can be easily applied to different complicated nonlinear systems of hyperbolic PDE in multiple space dimensions. Cheng and Toro [48] also investigated Lagrangian ADER-WENO schemes in one space dimension. In the finite element framework high order Lagrangian schemes have been developed for example by Scovazzi et al. [119, 160] and also by Dobrev et al. [60–62], who solved the equations for Lagrangian hydrodynamics using high order curvilinear finite element methods.
In the literature there are also other methods using a Lagrangian approach and these schemes are at least briefly mentioned in the following. For example, also meshless particle schemes, such as the smooth particle hydrodynamics (SPH) method, belong to the category of fully Lagrangian schemes, see e.g. [86–89, 130]. SPH is generally used to follow the fluid motion in very complex deforming domains. Since it is a particle method, no rezoning or remeshing has to be applied. Furthermore, also semi-Lagrangian methods should be mentioned. They are typically adopted to solve transport equations [97, 145]. Although these schemes use a fixed mesh, as in the classical Eulerian approach, the Lagrangian trajectories of the fluid are followed backward in time in order to compute the numerical solution at the the new time level, see for example [28, 42, 43, 101, 115, 143]. There is also the class of Arbitrary-Lagrangian–Eulerian (ALE) methods [44, 64, 84, 85, 99, 140, 162], where the mesh moves with a velocity that does not necessarily have to coincide with the local fluid velocity. This method is often used for fluid-structure interaction (FSI) problems, but it is also used together with Lagrangian remap schemes.
1.3 Towards High Order ALE ADER-WENO Schemes
The aim of this work is to design a new family of high order accurate Arbitrary-Lagrangian–Eulerian (ALE) one-step ADER-WENO finite volume schemes for the solution of nonlinear systems of conservative and non-conservative hyperbolic partial differential equations.
The work is based on the already existing high order ADER finite volume solver [68, 72] mentioned in Sect. 1.1, which is used here as a starting point for the development of the new Lagrangian algorithms. From Sect. 1.2 we know that no better than third order accurate non-oscillatory finite volume Lagrangian schemes have ever been proposed on unstructured meshes in two and three space dimensions, hence leading to a challenging task that matches the research frontier of numerical methods on moving mesh. Furthermore, the new algorithm emerging from this work will be so general that it will be applicable to a wide range of scientific fields, since it is based on a very general formulation of the governing PDE, which many hyperbolic systems can be cast into.
The first contribution to this new class of numerical methods, which will be addressed as direct ALE ADER-WENO schemes, has been presented by Dumbser et al. [80], where the authors proposed the first one-dimensional high order ALE ADER-WENO finite volume schemes for hyperbolic balance laws with stiff source terms. In this case high order of accuracy in time was achieved by using the local space–time Galerkin predictor method introduced in [72, 98] for the Eulerian case, whereas a high order WENO reconstruction algorithm was used to obtain high order of accuracy in space.
Then, this paper contains all the contributions for ALE ADER-WENO methods that have been done in the last three years of research. In [22, 70] Boscheri and Dumbser extended the one-dimensional algorithm [80] to unstructured triangular meshes for conservative and non-conservative hyperbolic systems with stiff source terms. In [26] three different nodal solver techniques have been applied to the Euler equations of compressible gas dynamics as well as to the equations for magnetohydrodynamics and have been compared with each other. The multidimensional HLL Riemann solver presented in [63] for the Eulerian framework on fixed grids has been used as a nodal solver for the computation of the mesh velocity in [26] and for the computation of the space–time fluxes of a high order Lagrangian-like finite volume scheme in [21]. In the latter reference it has been shown that the adoption of a multidimensional Riemann solver allows the use of larger time steps in multiple space dimensions and therefore leads to a computationally more efficient scheme compared to a method based on classical one-dimensional Riemann solvers. In [23] the ALE ADER-WENO finite volume schemes have been applied to conservative and non-conservative hyperbolic systems on unstructured tetrahedral moving meshes, while in [24] Boscheri and Dumbser introduce a quadrature-free formulation for the numerical flux computation in the ALE context. In order to reduce the computational efforts, which is typically higher for Lagrangian schemes than for Eulerian methods, in [29, 67] the first high order time-accurate local time stepping ALE ADER-WENO schemes have been presented in one and two space dimensions, while in [31] the expensive WENO reconstruction procedure has been replaced with the very recently developed MOOD paradigm [49, 58, 59, 120], which requires the use of only one central reconstruction stencil because the limiting procedure is carried out a posteriori instead of a priori, as done in the WENO formulation. Finally, in [27] the ALE ADER-WENO method is applied to the unified first order hyperbolic Godunov–Peshkov–Romenski [141] (GPR) model of continuum mechanics, while in [25] we have extended the presented algorithm to high order curvilinear elements.
The rest of the work is structured as follows. In Sect. 2 we describe in detail the new high order ALE ADER-WENO finite volume schemes, considering what has been done in [22, 23, 70]. The algorithm will be presented in a very general way, treating both conservative and non-conservative hyperbolic systems as well as the presence of algebraic source terms which are allowed to become stiff. Next, Sect. 2.3 focuses on the techniques used to carry out the mesh motion, i.e. the numerical strategies adopted to evaluate the mesh velocity and consequently to compute the new node location. Section 3 contains numerical convergence studies up to sixth order of accuracy in space and time together with numerical results for several classical test problems applied to different hyperbolic balance laws. In Sect. 4 we give an overview of some modifications introduced in our algorithm to improve the computational efficiency. Finally, in Sect. 5 we discuss some concluding remarks and we provide an outlook to future research and developments.
For a more detailed discussion about any of the topics illustrated and described within this work, we refer the reader to the above mentioned references. For the sake of generality, the new family of high order direct ALE ADER-WENO finite volume schemes presented in this paper adopts an ALE approach, so that the local mesh velocity can in principle be chosen independently from the local fluid velocity. As a consequence the method in general allows a mass flux and even when the mesh velocity is set to be equal to the fluid velocity the proposed scheme is not meant to be a pure Lagrangian method in sensu stricto. In this sense, our scheme falls into the category of direct ALE methods.
2 Finite Volume Framework on Moving Unstructured Meshes
In this work we consider nonlinear systems of hyperbolic balance laws which may also contain non-conservative products and stiff source terms. In our approach we rely on a very general formulation of the governing equations which can be applied to several hyperbolic systems. This gives our algorithm the possibility to cover a wide range of physical phenomena, namely all the ones that are governed by equations which can be cast into the following form:
where \(\mathbf {Q}=(q_1,q_2,\ldots ,q_\nu )\) denotes the vector of conserved variables, \({\mathsf {\mathbf {F}}} = (\mathbf {f}, \mathbf {g}, \mathbf {h})\) is the conservative nonlinear flux tensor, \({\mathsf {\mathbf {B}}}=(\mathbf {B}_1,\mathbf {B}_2,\mathbf {B}_3)\) contains the purely non-conservative part of the system written in block-matrix notation and \(\mathbf {S}(\mathbf {Q})\) represents a nonlinear algebraic source term that is allowed to be stiff. We furthermore introduce the abbreviation \(\mathbf {P}= \mathbf {P}(\mathbf {Q},\nabla \mathbf {Q}) = \mathbf {B}(\mathbf {Q}) \cdot \nabla \mathbf {Q}\) to make notation easier. The balance law (4) is defined in the multidimensional physical computational domain \(\varOmega\), where \(d \in [2,3]\) denotes the number of space dimensions and \(\mathbf {x}=(x,y,z)\) is the position vector. In the following we present the algorithm for \(d=3\), since for the two-dimensional case the method can be easily derived setting to zero the third spatial coordinate, i.e. \(z=0\), as well as all its related quantities.
In a Lagrangian framework the computational domain \(\varOmega (t) \subset \mathbb {R}^d\) is time-dependent and is discretized at the current time \(t^n\) by a set of non-overlapping control volumes \(T^n_i\) that can be either triangles (\(d=2\)) or tetrahedra (\(d=3\)). \(N_E\) denotes the total number of elements contained in the domain and the union of all elements is called the current mesh configuration \(\mathcal {T}^n_{\varOmega }\) of the domain
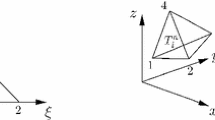
Since we are dealing with a moving computational domain where the mesh configuration continuously changes in time, it is more convenient to map the physical element \(T^n_i\) to a reference element \(T_E\) via a local reference coordinate system \(\xi -\eta -\zeta\). The spatial reference element \(T_E\) is the unit tetrahedron (or the unit triangle in 2D) shown in Fig. 1 and is defined by the nodes \(\varvec{\xi }_{e,1}=(\xi _{e,1},\eta _{e,1},\zeta _{e,1})=(0,0,0)\), \(\varvec{\xi }_{e,2}=(\xi _{e,2},\eta _{e,2},\zeta _{e,2})=(1,0,0)\), \(\varvec{\xi }_{e,3}=(\xi _{e,3},\eta _{e,3},\zeta _{e,3})=(0,1,0)\) and \(\varvec{\xi }_{e,4}=(\xi _{e,4},\eta _{e,4},\zeta _{e,4})=(0,0,1)\), where \(\varvec{\xi } = (\xi , \eta , \zeta )\) is the vector of the spatial coordinates in the reference system, while the position vector \(\mathbf {x}=(x,y,z)\) is defined in the physical system. Let furthermore \(\mathbf {X}^n_{k,i} = (X^n_{k,i},Y^n_{k,i},Z^n_{k,i})\) be the vector of physical spatial coordinates of the k-th vertex of element \(T^n_i\). Then the linear mapping from \(T^n_i\) to \(T_E\) is given by
When \(d=2\) the same transformation applies for the coordinates x and y, setting \(\zeta =0\). The vertices of \(T^n_i\) are given a connectivity \(\mathcal {C}\) with a counterclockwise convention, as illustrated in Fig. 1, hence
Spatial mapping from the physical element \(T^n_i\) defined with \(\mathbf {x}\) to the unit reference element \(T_E\) in \(\varvec{\xi }\) for triangles (top) and tetrahedra (bottom). Vertices are numbered according to the local connectivity \(\mathcal {C}\) given by (7)
The finite volume approach is based on the integral formulation of the conservation law (4), hence providing discrete evolution equations for integral cell averages. As a consequence, data are represented and stored as cell averages which are evolved in time. The main advantage of working in the context of finite volume schemes is that the integral formulation of the governing equations must hold for arbitrary control volumes, hence yielding almost no restrictions in the discretization of the computational domain \(\varOmega\). The piecewise constant cell averages are defined at each time level \(t^n\) within the control volume \(T^n_i\) as
with \(|T_i^n|\) denoting the volume of element \(T_i^n\). The key point of any finite volume schemes is the so-called numerical flux function, which computes the fluxes across the boundaries of the control volume \(T_i^n\). According to Godunov’s idea [94], the numerical flux function can be defined by solving local Riemann problems at the interfaces of the control volumes. If we limit us to use only the values given by (8) to evaluate the numerical fluxes, we obtain a first order accurate numerical scheme. In order to construct higher order finite volume schemes we need to improve the order of accuracy of the solution employed for the computation of the numerical flux function. In the next Sect. 2.1 a WENO reconstruction technique is described and used to obtain piecewise higher order polynomials \(\mathbf {w}_h(\mathbf {x},t^n)\) from the known cell averages \(\mathbf {Q}_i^n\). High order of accuracy in time is achieved later in Sect. 2.2 by applying a local space–time Galerkin predictor method to the reconstruction polynomials \(\mathbf {w}_h(\mathbf {x},t^n)\).
2.1 Polynomial WENO Reconstruction
The WENO reconstruction operator produces piecewise polynomials \(\mathbf {w}_h(\mathbf {x},t^n)\) of degree M. The \(\mathbf {w}_h(\mathbf {x},t^n)\) are computed for each control volume \(T^n_i\) from the known cell averages within a so-called reconstruction stencil \(\mathcal {S}_i^s\), which is composed of an appropriate neighborhood of element \(T^n_i\) and contains a prescribed total number \(n_e\) of elements which depends on the order M of the polynomial. We do not use the original pointwise WENO method first introduced by Shu et al. [100, 102, 188], but we adopt the polynomial formulation proposed in [74, 75, 91, 106] and also used in [169, 179], which is relatively simple to code and which allows the scheme to reach very high order of accuracy even on unstructured tetrahedral meshes in three space dimensions.
In [13, 106, 135] it has been shown that the total number of elements \(n_e\) must be greater than the smallest number \(\mathcal {M}\) needed to reach the formal order of accuracy \(M+1\). As suggested in [74, 75] we normally take \(n_e=d \cdot \mathcal {M}\), with
According to [75] we always use seven \((1 \le s \le 7)\) and nine \((1 \le s \le 9)\) reconstruction stencils in two and three space dimensions, respectively. Specifically, \(s=1\) denotes the central stencil, while one half of the remaining stencils are the so-called forward stencils and the others are the backward reconstruction stencils, as depicted in Figs. 2 and 3. For reconstruction, each element \(T_i^n\) and its surrounding elements are first mapped to the reference coordinate system \(\xi -\eta -\zeta\) using the mapping (6) in order to avoid ill-conditioned reconstruction matrices, see [1]. The three types of stencils (central, forward and backward) are then obtained by a recursive algorithm which adds recursively neighbor elements to the stencil until the prescribed number \(n_e\) is reached. Therefore:
-
for the central stencil (\(s=1\)), we first add the Neumann neighbors of \(T_i^n\) (i.e. the direct side neighbors surrounding element \(T_i^n\)) to the stencil, and then recursively continue adding the neighbors of these neighbors, until the desired total number of elements in the stencil \(n_e\) is reached;
-
each of the forward stencils (\(2\le s \le 4\) in 2D and \(2\le s \le 5\) in 3D) is filled with elements using the same recursive algorithm, but adding only those elements whose barycenters are located in the corresponding forward sector. On triangular meshes (\(d=2\)) the three forward sectors are spanned by a vertex of the triangle and the pair of vectors connecting this vertex with the two vertices of the opposite edge, while for tetrahedra (\(d=3\)) the four forward stencils are defined by a vertex k of the tetrahedron \(T_i^n\) and the triplet of vectors connecting k to the three vertices of the opposite face;
-
the backward stencils (\(5 \le s \le 7\) in 2D and \(6 \le s \le 9\) in 3D) are constructed in the same way as the forward stencils. The associated backward sectors cover the remaining part of \(\mathbb {R}^d\) that has not been covered by the forward stencils and are spanned by the negative vectors of the forward stencils and the opposite edge or face barycenter in two and three space dimensions, respectively.
For the central stencil we use a simple Neumann-type neighbor search algorithm that recursively adds direct face neighbors to the stencil, until the desired number \(n_e\) is reached. For the remaining one-sided stencils we use a Voronoi-type search algorithm, which fills the stencil starting from the vertex neighborhood of the control volume and then using recursively vertex neighbors of stencil elements. Figures 2 and 3 show the stencils used for the WENO reconstruction technique on triangular and tetrahedral meshes, respectively.
Two-dimensional WENO reconstruction stencils in the physical (top row) and in the reference (bottom row) coordinate system for \(M=2\), hence \(n_e=12\): one central stencil (left), three forward stencils (center) and three backward stencils (right)
Three-dimensional WENO reconstruction stencils in the physical (top row) and in the reference (bottom row) coordinate system for \(M=2\), hence \(n_e=30\): one central stencil (left), four forward stencils (center) and four backward stencils (right)
Once the stencil search procedure has been carried out, each stencil contains a total number of elements \(n_e\) that depends on the reconstruction degree M given by (9), hence
where \(1 \le j \le n_e\) is a local index which progressively counts the elements in the stencil number s and m(j) represents a mapping from the local index j to the global index of the element in \(\mathcal {T}^n_{\varOmega }\).
The high order reconstruction polynomial for each candidate stencil \(\mathcal {S}_i^s\) for element \(T_i^n\) is written in terms of the orthogonal Dubiner-type basis functions \(\psi _l(\xi ,\eta ,\zeta )\) [51, 65, 105] on the reference element \(T_e\), i.e.
where the mapping to the reference coordinate system is given by (6) and \(\hat{\mathbf {w}}^{n,s}_{l,i}\) denote the unknown degrees of freedom (expansion coefficients) of the reconstruction polynomial on stencil \(\mathcal {S}_i^s\) for element \(T_i^n\) at time \(t^n\). In the rest of this manuscript we will use classical tensor index notation based on the Einstein summation convention, which implies summation over two equal indices.
Integral conservation is required for the reconstruction on each element \(T_j^n\) of the stencil \(\mathcal {S}_i^s\), yielding
Inserting the transformation (6) into the above expression (12), an analytical integration formula can be obtained that is a function of the physical vertex coordinates \(\mathbf {X}^n_{k,j}\) of the element. The resulting algebraic expressions of the integrals appearing in (12) can be obtained for example at the aid of a symbolic computer algebra system like MAPLE. Up to \(M=3\) we use the aforementioned analytical integration, while for higher reconstruction degrees the integrals in (12) are simply evaluated using Gaussian quadrature formulae of suitable order, see [164] for details, since the analytical expressions become too cumbersome. The reconstruction matrix, which is given by the integrals of the linear system (12), depends on the geometry of the control volumes in stencil \(\mathcal {S}_i^s\). Therefore, since in the Lagrangian framework the mesh is moving in time, the reconstruction matrix can not be inverted and stored once and for all during a pre-processing stage, like in the Eulerian case. As a consequence, we assemble and solve the small reconstruction system (12) for each element \(T^n_i\) directly at the beginning of each time step \(t^n\) using optimized LAPACK subroutines. This makes the ALE WENO reconstruction computationally more expensive but at the same time also much less memory consuming compared to the original Eulerian WENO algorithm presented in [74, 75], since no reconstruction matrices are stored.
While the mesh is moving in time, we always assume that the connectivity of the mesh and therefore also the topology of each reconstruction stencil remains constant in time. Therefore, the definition of the stencils \(\mathcal {S}_i^s\) does not need to be updated during the simulation. This is a very important simplification, since the stencil search may be quite time consuming in multiple space dimensions on unstructured meshes.
Since each stencil \(\mathcal {S}_i^s\) is filled with a total number of \(n_e=d \cdot \mathcal {M}\) elements, system (12) results in an overdetermined linear system that has to be solved properly by either using a constrained least-squares technique (LSQ), see [75], or a more sophisticated singular value decomposition (SVD) algorithm. The use of the reference coordinate system ensures the matrix of the linear system (12) to be reasonably well conditioned.
As stated by the Godunov theorem [94], linear monotone schemes are at most of order one and if the scheme is required to be higher order accurate and non-oscillatory, it must be nonlinear. Therefore a nonlinear formulation has to be used for the final WENO reconstruction polynomial. We first measure the smoothness of each reconstruction polynomial obtained on stencil \(\mathcal {S}_i^s\) by a so-called oscillation indicator \(\varvec{\sigma }_s\) [102],
which is computed on the reference element using the (universal) oscillation indicator matrix \(\varSigma _{lm}\), which, according to [75], is given by
In two space dimensions the above expression holds with \(\zeta =0\) and \(\gamma =0\). The nonlinearity is then introduced into the scheme by the WENO weights \(\varvec{\omega }_s\), which read
with the parameters \(r=8\) and \(\epsilon =10^{-14}\). According to [75] the linear weights are chosen as \(\lambda _1=10^5\) for the central stencil and \(\lambda _s=1\) for the remaining one-sided stencils. Formula (15) is intended to be read componentwise. For a WENO reconstruction based on characteristic variables see [74]. A weighted nonlinear combination of the reconstruction polynomials obtained on each candidate stencil \(\mathcal {S}_i^s\) yields the final WENO reconstruction polynomial and its coefficients:
2.2 Local Space–Time Galerkin Predictor on Moving Curved Meshes
The reconstructed polynomials \(\mathbf {w}_h(\mathbf {x},t^n)\) computed at the current time \(t^n\) are then evolved during one time step, i.e. up to time \(t^{n+1}\), locally within each element \(T_i(t)\) without requiring any neighbor information. As a result, one obtains piecewise space–time polynomials of degree M, denoted by \(\mathbf {q}_h(\mathbf {x},t)\). This allows the scheme to achieve also high order of accuracy in time. Such an element-local time-evolution procedure has also been used within the MUSCL scheme of van Leer [180] and the original ENO scheme of Harten et al. [95], who called this element-local predictor with initial data \(\mathbf {w}_h(\mathbf {x},t^n)\) the solution of a Cauchy problem in the small, since no information from neighbor elements is used. The coupling with the neighbor elements occurs only later in the final one-step finite volume scheme (see Sect. 2.4). While the original ENO scheme of Harten et al. uses a higher order Taylor series in time together with the strong differential form of the PDE to substitute time-derivatives with space derivatives (the so-called Cauchy–Kovalewski or Lax–Wendroff procedure [112]), here a weak formulation of the governing PDE (4) in space–time is derived (see Eq. 31 below). The resulting method does not require the computation of higher order derivatives, but just pointwise evaluations of the fluxes, source terms and non-conservative products appearing in the PDE. This approach has first been developed for the Eulerian framework on fixed grids in [69, 72, 73, 98] and here we extend it to moving unstructured meshes in multiple space dimensions.
Let \(\mathbf {x}=(x,y,z)\) and \(\varvec{\xi }=(\xi ,\eta ,\zeta )\) be the spatial coordinate vectors defined in the physical and in the reference system, respectively, and let \(\tilde{\mathbf {x}}=(x,y,z,t)\) and \(\tilde{\varvec{\xi }}=(\xi ,\eta ,\zeta ,\tau )\) be the corresponding space–time coordinate vectors. Let furthermore \(\theta _l=\theta _l(\tilde{\varvec{\xi }})=\theta _l(\xi ,\eta ,\zeta ,\tau )\) be a space–time basis function defined by the Lagrange interpolation polynomials passing through a set of space–time nodes \(\tilde{\varvec{\xi }}_m=(\xi _m,\eta _m,\zeta _m,\tau _m)\) which are defined by the tensor product of the nodes of classical conforming high order finite elements in space and the Gauss–Legendre quadrature points in time. The two-dimensional reference and physical space–time element configuration as well as the associated space–time nodes for the case \(M=2\) are depicted in Fig. 4.
Since the Lagrange interpolation polynomials define a nodal basis, the functions \(\theta _l\) satisfy the following interpolation property:
where \(\delta _{lm}\) denotes the usual Kronecker symbol. Following [69] the local solution \(\mathbf {q}_h\), the fluxes \(\mathbf {F}_h = (\mathbf {f}_{h}, \mathbf {g}_h, \mathbf {h}_h)\), the source term \(\mathbf {S}_h\) and the non-conservative product \(\mathbf {P}_h = \mathbf {B}(\mathbf {q}_h) \cdot \nabla \mathbf {q}_h\) are approximated within the space–time element \(T_i(t) \times [t^n;t^{n+1}]\) with
Because of the interpolation property (17) we evaluate the degrees of freedom for \(\mathbf {F}_h\), \(\mathbf {S}_h\) and \(\mathbf {P}_h\) in a pointwise manner from \(\mathbf {q}_h\) as
The degrees of freedom \(\nabla \widehat{\mathbf {q}}_{l,i}\) represent the gradient of \(\mathbf {q}_h\) in node \(\tilde{\varvec{\xi }}_l\).
An isoparametric approach is used, where the mapping between the physical space–time coordinate vector \(\tilde{\mathbf {x}}\) and the reference space–time coordinate vector \(\tilde{\varvec{\xi }}\) is represented by the same basis functions \(\theta _l\) used for the discrete solution \(\mathbf {q}_h\) itself. Therefore
where \(\widehat{\mathbf {x}}_{l,i} = (\widehat{x}_{l,i},\widehat{y}_{l,i},\widehat{z}_{l,i})\) are the degrees of freedom of the spatial physical coordinates of the moving space–time control volume, which are unknown, while \(\widehat{t}_l\) denote the known degrees of freedom of the physical time at each space–time node \(\tilde{\mathbf {x}}_{l,i} = (\widehat{x}_{l,i}, \widehat{y}_{l,i}, \widehat{z}_{l,i}, \widehat{t}_l)\). The mapping in time is linear and simply reads
where \(t^n\) represents the current time and \(\Delta t\) is the current time step, which is computed under a classical Courant–Friedrichs–Levy number (CFL) stability condition, i.e.
with \(d_i\) denoting the insphere or incircle diameter of element \(T_i^n\) and \(|\lambda _{\max ,i}|\) corresponding to the maximum absolute value of the eigenvalues computed from the solution \(\mathbf {Q}_i^n\) in \(T_i^n\). In multiple space dimensions, the CFL condition must satisfy the inequality \(\text {CFL} \le \frac{1}{d}\) if one-dimensional Riemann solvers are used, see [173].
The Jacobian of the transformation from the physical space–time element to the reference space–time element reads
and its inverse is given by
We point out that in the Jacobian matrix \(t_\xi = t_\eta = t_\zeta = 0\) and \(t_\tau = \Delta t\), as can be easily derived from the time mapping (21).
In the following we introduce the notation adopted for the nabla operator \(\nabla\) in the reference space \(\varvec{\xi }=(\xi ,\eta ,\zeta )\) and in the physical space \(\mathbf {x}=(x,y,z)\):
Furthermore let us introduce the two integral operators
that denote the scalar products of two functions f and g over the spatial reference element \(T_E\) at time \(\tau\) and over the space–time reference element \(T_E\times \left[ 0,1\right]\), respectively.
The governing PDE (4) is then reformulated in the reference coordinate system \((\xi ,\eta ,\zeta )\) using the inverse of the associated Jacobian matrix (24) with \(\tau _x = \tau _y = 0\) and \(\tau _t = \frac{1}{\varDelta t}\) according to (21) and adopting the gradient notation illustrated in (25) above:
Note that the Lagrangian nature of the scheme, i.e. the moving space–time control volume, leads to the term \(\frac{\partial \mathbf {Q}}{\partial \varvec{\xi }} \cdot \frac{\partial \varvec{\xi }}{\partial t}\), which is not present in the Eulerian case introduced in [69]. Relying on the following abbreviation
Eqn. (27) simplifies to
The numerical approximation of \(\mathbf {H}\) is computed by the same isoparametric approach used in (18) for the solution and the flux representation, i.e.
Inserting (18) and (30) into (27), then multiplying Eqn. (27) with the space–time test functions \(\theta _k(\varvec{\xi })\) and integrating the resulting equation over the space–time reference element \(T_E \times [0,1]\), one obtains a weak formulation of the governing PDE (4):
Since the mesh is moving, we also have to evolve in time the geometry of the space–time control volume, i.e. the vertex coordinates of element \(T^n_i\), together with the predictor solution \(\mathbf {q}_h(\mathbf {x},t)\). The mesh motion is simply described by the ODE system
with \(\mathbf {V}=\mathbf {V}(\mathbf {Q},\mathbf {x},t)\) denoting the local mesh velocity. In this work we are developing an Arbitrary-Lagrangian–Eulerian (ALE) method, which allows the mesh velocity to be chosen independently from the local fluid velocity, so that the scheme may reduce either to a pure Eulerian approach in the case where \(\mathbf {V}=0\) or to a more Lagrangian-type algorithm if \(\mathbf {V}\) coincides with the local fluid velocity \(\mathbf {v}\). Any other choice for the mesh velocity is possible. The velocity inside element \(T_i(t)\) is also expressed in terms of the space–time basis functions \(\theta _{l}\) as
with \(\widehat{\mathbf {V}}_{l,i} = \mathbf {V}(\widehat{{\mathbf {q}}}_{l,i}, \widehat{{\mathbf {x}}}_{l,i}, \widehat{t}_l)\).
The weak formulation (31), which gives the local evolution of the solution, and the ODE system (32), which governs the element motion, constitute a coupled set of equations that has to be solved simultaneously with an iterative procedure, until the residuals of the predicted solution \({\hat{\mathbf {q}}}_{l,i}\) and the new vertex position \(\hat{\mathbf {x}}_{l,i}\) at iteration r are less than a prescribed tolerance, typically set to \(10^{-12}\).
Such a local finite element predictor, called Discontinuous Galerkin (DG) predictor, has been designed also for the treatment of stiff source terms [72, 81, 98] in the governing equations (4), which might lead to a local time discontinuity of the solution. Therefore the term on the left hand side of the weak formulation (31) is integrated by parts in time, which also allows to introduce the initial condition of the local Cauchy problem in a weak form as follows:
Adopting the following matrix-vector notation
the system (34) is reformulated as
Eqn. (36) constitutes an element-local nonlinear algebraic equation system for the unknown space–time expansion coefficients \(\widehat{\mathbf {q}}_{l,i}\) which can be solved using an iterative scheme as
where r denotes the iteration number. In case of stiff algebraic source terms, the discretization of \(\mathbf {S}\) must be implicit, see [72, 80, 81, 98]. For an efficient initial guess of this iterative procedure we refer the reader to [98].
The system (32), which governs the local mesh motion, can be conveniently solved for the unknown coordinate vector \(\widehat{\mathbf {x}}_{l,i}=(x_{l,i},y_{l,i},z_{l,i})\) using the same approach, hence
where \(\mathbf {x}(\varvec{\xi },t^n)\) is given by the mapping (6) based on the known vertex coordinates of element \(T_i^n\) at time \(t^n\). The iterative procedure stops when the prescribed tolerance has been reached for both the residuals of (37) and (38).
Iso-parametric mapping with \(M=2\) of the space–time reference element (left) to the physical space–time element (right) used within the local space–time Discontinuous Galerkin (DG) predictor for a triangular control volume
For the sake of clarity the element-local predictor strategy on moving meshes can be summarized by the following steps:
-
first we compute the local mesh velocity with (33), usually by choosing the local fluid velocity, hence obtaining \(\widehat{\mathbf {V}}_{l,i} = \mathbf {V}(\widehat{{\mathbf {q}}}_{l,i}, \widehat{{\mathbf {x}}}_{l,i}, \widehat{t}_l)\);
-
knowing the mesh velocity, the geometry is updated locally within the predictor stage, i.e. obtaining the element-local space–time coordinates \(\widehat{\mathbf {x}}_{l,i}\);
-
the Jacobian matrix and its inverse are then evaluated by using (23)–(24);
-
finally we compute the term \(\mathbf {H}\) according to (27) and the new solution is evolved according to (31);
-
we measure the residuals and if they are below the prescribed tolerance we exit the loop, otherwise the new solution at the iterative step r is used to start a new step of the predictor algorithm.
Once we have carried out the above procedure for all the elements of the computational domain, we end up with an element-local predictor for the numerical solution \(\mathbf {q}_h\), for the fluxes \(\mathbf {F}_h=(\mathbf {f}_h,\mathbf {g}_h,\mathbf {h}_h)\), for the source term \(\mathbf {S}_h\) and also for the mesh velocity \(\mathbf {V}_h\).
2.3 Mesh Motion
Lagrangian schemes have been designed and developed in order to compute the flow variables by moving together with the fluid. As a consequence, the computational mesh continuously changes its configuration in time, following as closely as possible the flow motion.
Once the local predictor procedure has been carried out, at each vertex k different velocity vectors \(\mathbf {V}_{k,j}^n\) are defined, depending on the number of elements \(T_j^n\) that belong to the Voronoi neighborhood \(\mathcal {V}_k\) of node k, as depicted in Fig. 5. In order to obtain a continuous mesh configuration at the new time level \(t^{n+1}\), one has to fix a unique time-averaged node velocity \({\mathbf {V}}_k^n\) using a nodal solver algorithm. Moreover, the flow motion may become very complex, hence highly deforming the computational elements, that are compressed, twisted or even tangled. Therefore a suitable rezoning algorithm is typically used to improve the mesh quality together with a so-called relaxation algorithm to partially recover the optimal Lagrangian accuracy where the computational elements are not distorted too much.
Indeed, the entire mesh motion is composed by three main steps, namely the Lagrangian step, the rezoning step and the relaxation step.
Geometrical notation for the arithmetic nodal solver: k is the local node, \(T_j^n\) denotes one element of the neighborhood \(\mathcal {V}_k\) and \({\mathbf {V}}_{k,j}^n\) is the local velocity contribution of element \(T_j^n\) given by (41)
2.3.1 The Lagrangian Step
Here we only provide a very simple and straightforward solution to determine a unique mesh velocity for each node k of the mesh, that follows from the work proposed by Cheng and Shu [45]. In such a very general approach the node velocity is chosen to be the arithmetic average velocity among all the contributions coming from the neighbor elements, hence yielding an arithmetic nodal solver. Since the mesh might be locally highly deformed, we propose to modify this algorithm by taking a mass weighted average velocity among the Voronoi neighborhood \(\mathcal {V}_k\) of node k, i.e.
with
The local weights \(\mu _{k,j}\), which are the masses of the elements \(T_j^n\), are defined multiplying the cell averaged value of density \(\rho ^n_j\) with the cell volume \(|T_j^n|\), while the local velocity contributions \({\mathbf {V}}_{k,j}^n\) are computed integrating in time the high order vertex-extrapolated velocity at node k as
where m(k) denotes a mapping from the global node number k defined in the mesh configuration \(\mathcal {T}^n_{\varOmega }\) to the local vertex number in element \(T_j^n\), according to the local connectivity \(\mathcal {C}\) given by (7). If \(d=2\) we simply set \(\zeta ^e_{m(k)}=0\) and the space–time basis functions \(\theta _l\) are defined on the reference triangle \(T_E\) with the mappings (6)–(21).
As a result of the nodal solver, we obtain a unique high order accurate time-averaged vertex velocity \({\mathbf {V}}_k^n\) for each vertex k, that is used to evaluate the Lagrangian node position \(\mathbf {X}_k^{Lag}\) of node k at time \(t^{n+1}\) as
where \(\mathbf {X}^{n}_{k}\) denotes the coordinates of node k at the current time level \(t^n\).
We should mention that a lot of efforts have been put in the design and development of nodal solvers [21, 26, 37, 63, 123–125]. Even though the approaches are different, the aim is always to fix a unique velocity vector for each vertex of the computational mesh, i.e. computing \({\mathbf {V}}_k^n\).
2.3.2 The Rezoning Step
The Lagrangian step allows the nodes to follow the fluid motion as closely as possible. However, this may lead to bad quality elements, where the Jacobians become very small or even negative. This either drastically decreases the admissible timestep, according to (22), or even leads to a failure of the computation. Therefore, also a rezoned position should be computed for each node k in order to improve the local mesh quality without taking into account any physical information. We use a different treatment for internal nodes and boundary nodes. Specifically, the rezoning algorithm presented in [92, 108] is adopted for inner nodes, while a variant of the feasible set method proposed by Berndt et al. [18] is used for the boundary nodes.
The rezoning algorithm aims at improving the mesh quality locally, i.e. in the Voronoi neighborhood \(\mathcal {V}_k\) of node k, considering all the neighbor elements \(T_j^{n+1}\), which for sake of simplicity will be addressed by j. The starting point is the Lagrangian coordinate vector \(\mathbf {X}^{Lag}_{k}\) obtained at the end of the Lagrangian step. The rezoning procedure consists in optimizing a goal function \(\mathcal {K}_k\) that has to be defined for each node k as
where \(\kappa _j\) is the condition number of the Jacobian matrix \(\mathbf {J}_{j}\) of the mapping from the reference element to the physical element j:
In (44), considering \(\mathbf {J}^{3D}_{j}=\mathbf {J}_{j}\), the coordinate vector \(\mathbf {x}_{j,l}=(x_{j,l},y_{j,l},z_{j,l})\) represents the four nodes \(l=1,2,3,4\) of the neighbor tetrahedron \(T_j^{n+1}\), which are counterclockwise ordered in such a way that node k corresponds to \(l=1\). Note that this is a local connectivity related to node k, hence it may be different from the standard connectivity given by (7). Then, the condition number of matrix \(\mathbf {J}_{j}\) is given by
The goal function \(\mathcal {K}_k\) is computed according to [108] as the sum of the local condition numbers of the neighbors, see Eq. (43), and its minimization leads to a locally optimal position of the free node k. As proposed in [92], the optimized rezoned coordinates \(\mathbf {x}_k^{Rez}\) for vertex k are computed using the first step of a Newton algorithm, hence
where \(\mathbf {H}_k\) and \(\nabla \mathcal {K}_k\) represent the Hessian and the gradient of the goal function \(\mathcal {K}_k\), respectively:
For the boundary nodes we present a simplified but very efficient version of the feasible set method proposed in [18] for two-dimensional unstructured meshes. The original feasible set method has been designed in order to find the convex polygon on which a vertex can lie without invalid elements in its neighborhood. In three space dimensions such an algorithm becomes very complex and highly demanding in terms of computational efforts. In our simplified procedure the rezoned coordinates \(\mathbf {x}_k^{Rez,b}\) of the boundary node k are evaluated as a volume weighted average among the barycenter coordinates \(\mathbf {x}_{c,j}^{Lag}\) of each neighbor element j, which have been projected onto the boundary face. Hence,
with the weights
and the barycenter defined as usual as
2.3.3 The Relaxation Step
Since our ALE scheme is supposed to be as Lagrangian as possible, we do not want to rezone the mesh nodes where it is not strictly necessary in order to carry on the computation. Therefore the final node position \(\mathbf {X}_k^{n+1}\) is obtained applying the relaxation algorithm of Galera et al. [92], that performs a convex combination between the Lagrangian position and the rezoned position of node k, hence
where \(\omega _k\) is a node-based coefficient associated to the deformation of the Lagrangian grid over the time step \(\varDelta t\). The values for \(\omega _k\) are bounded in the interval [0, 1], so that when \(\omega _k=0\) a fully Lagrangian mesh motion occurs, while if \(\omega _k=1\) the new node location is defined by the pure rezoned coordinates \(\mathbf {X}_k^{Rez}\). We point out that the coefficient \(\omega _k\) is designed to result in \(\omega _k=0\) for rigid body motion, namely rigid translation and rigid rotation, where no element deformation occurs. Further details about the computation of \(\omega _k\) can be found in [92].
2.4 High Order ALE Finite Volume Schemes
Since finite volume schemes are based on the integral formulation of the conservation law, we first have to clearly define the control volumes where integration will be carried out. For each element \(T_i\) the new vertex coordinates \(\mathbf {X}_k^{n+1}\) are connected to the old coordinates \(\mathbf {X}_k^{n}\) with straight line segments, yielding a multidimensional space–time control volume \(C^n_i = T_i(t) \times \left[ t^{n}; t^{n+1}\right]\), that involves overall five space–time sub-surfaces in 2D or six sub-volumes in 3D, as depicted in Fig. 6. Specifically, the space–time volume \(C^n_i\) is bounded on the bottom and on the top by the element configuration at the current time level \(T_i^{n}\) and at the new time level \(T_i^{n+1}\), respectively, while it is closed with a total number of \(\mathcal {N}_i=(d+1)\) lateral sub-volumes \(\partial C^n_{ij} = \partial T_{ij}(t) \times [t^n;t^{n+1}]\) that are given by the evolution of each face \(\partial T_{ij}(t)\) of element \(T_i\) within the timestep \(\varDelta t=(t^{n+1}-t^n)\). Therefore the space–time volume \(C^n_i\) is bounded by its surface \(\partial C^n_i\) which is given by
For the sake of clarity from now on we will present the finite volume scheme for the three-dimensional case, hence addressing the sub-volumes with \(\partial C^n_{ij}\) and the faces with \(\partial T_{ij}(t)\). If \(d=2\) then volumes reduce to surfaces, while surfaces reduce to segments and the algorithm formulation can be easily derived by setting the z-aligned coordinate to zero as well as all its related physical quantities.
Space–time evolution of element \(T_i\) within one timestep \(\varDelta t\) in two (a) and three (b) space dimensions. The dashed red lines denote the evolution in time of the faces \(\partial C^n_{ij}\) of the control volume \(T_i\), whose configuration at the current time level \(t^n\) and at the new time level \(t^{n+1}\) is depicted in black and blue, respectively. (Color figure online)
In order to develop a Lagrangian-type finite volume schemes on moving unstructured meshes, we rely on a space–time divergence operator \({\tilde{\nabla }}\) that allows the governing PDE (4) to be reformulated more compactly as
where the space–time flux tensor \(\tilde{\mathbf {F}}\) and the system matrix \(\tilde{\mathbf {B}}\) explicitly read
For the computation of the state vector at the new time level \(\mathbf {Q}^{n+1}\), the balance law (53) is integrated over a four-dimensional space–time control volume \(\mathcal {C}^n_i = T_i(t) \times \left[ t^{n}; t^{n+1}\right]\), i.e.
Application of the theorem of Gauss yields
where the space–time volume integral on the left of (55) has been rewritten as the sum of the fluxes computed over the three-dimensional space–time volume \(\partial \mathcal {C}^n_i\), given by the evolution of each face of element \(T_i(t)\) within the timestep \(\varDelta t\), as depicted in Fig. 6. The symbol \(\tilde{\mathbf {n}} = ({\tilde{n}}_x,{\tilde{n}}_y,{\tilde{n}}_z,{\tilde{n}}_t)\) denotes the outward pointing space–time unit normal vector on the space–time surface \(\partial C^n_i\).
In order to simplify the integral computation, each of the space–time sub-volumes is mapped to a reference element. For the configurations at the current and at the new time level, \(T_i^{n}\) and \(T_i^{n+1}\), we use the mapping (6) with \((\xi ,\eta ,\zeta ) \in \left[ 0;1\right]\). The space–time unit normal vectors simply read \(\tilde{\mathbf {n}} = (0,0,0,-1)\) for \(T_i^{n}\) and \(\tilde{\mathbf {n}} = (0,0,0,1)\) for \(T_i^{n+1}\), since these volumes are orthogonal to the time coordinate. For the lateral sub-volumes \(\partial C^n_{ij}\) we adopt a linear parametrization to map the physical volume to a three-dimensional space–time reference prism, as shown in Fig. 7. Starting from the old vertex coordinates \(\mathbf {X}_{ik}^n\) and the new ones \(\mathbf {X}_{ik}^{n+1}\), that are known from the mesh motion algorithm described in Sect. 2.3, the lateral sub-volumes are parametrized using a set of linear basis functions \(\beta _k(\chi _1,\chi _2,\tau )\) that are defined on a local reference system \((\chi _1,\chi _2,\tau )\) which is oriented orthogonally w.r.t. the face \(\partial T_{ij}(t)\) of element \(T_i^n\), e.g. the reference time coordinate \(\tau\) is orthogonal to the reference space coordinates \((\chi _1,\chi _2)\) that lie on \(\partial T_{ij}(t)\). The temporal mapping is simply given by \(t = t^n + \tau \, \varDelta t\), hence \(t_{\chi _1} = t_{\chi _2} = 0\) and \(t_\tau = \varDelta t\). The lateral space–time sub-volume \(\partial C_{ij}^n\) is defined by a total number \(N_k\) of vertices of physical coordinates \(\tilde{\mathbf {X}}_{ij,k}^n\), namely \(N_k=4\) or \(N_k=6\) in two or three space dimensions, respectively. The first three vectors \((\mathbf {X}^n_{ij,1},\mathbf {X}^n_{ij,2},\mathbf {X}^n_{ij,3})\) are the nodes defining the common face \(\partial T_{ij}(t^n)\) at time \(t^n\), while the same procedure applies at the new time level \(t^{n+1}\). Therefore the six vectors \(\tilde{\mathbf {X}}_{ij,k}^n\) are given by
and the parametrization for \(\partial C_{ij}^n\) reads
with \(0 \le \chi _1 \le 1\), \(0 \le \chi _2 \le 1-\chi _1\) and \(0 \le \tau \le 1\). The basis functions \(\beta _k(\chi _1,\chi _2,\tau )\) for the reference space–time element in 3D are given by
The corresponding basis functions for the two dimensional case can be easily obtained by setting \(\chi _2=0\), since the space–time reference element is defined in the reference system \((\chi _1,\tau )\), as shown in Fig. 7.
Physical space–time element (a) and parametrization of the lateral space–time sub-volume \(\partial C_{ij}^n\) (b) for triangles (top) and tetrahedra (bottom). The dashed red lines denote the evolution in time of the faces of the element, whose configuration at the current time level \(t^n\) and at the new time level \(t^{n+1}\) is depicted in black and blue, respectively. (Color figure online)
The coordinate transformation is associated with a matrix \(\mathcal {T}\) that reads
with \(\hat{\mathbf {e}}=(\hat{\mathbf {e}}_1,\hat{\mathbf {e}}_2,\hat{\mathbf {e}}_3,\hat{\mathbf {e}}_4)\) and where \(\hat{\mathbf {e}}_p\) represents the unit vector aligned with the p-th axis of the physical coordinate system (x, y, z, t). In the following \(\tilde{x}_q\) denotes the q-th component of vector \(\tilde{\mathbf {x}}\). The determinant of \(\mathcal {T}\) produces at the same time the space–time volume \(| \partial C_{ij}^n|\) of the space–time sub-volume \(\partial C_{ij}^n\) and the associated space–time normal vector \(\tilde{\mathbf {n}}_{ij}\), as
where the Levi-Civita symbol has been used according to the usual definition
and with
We now need to discretize the integral form (56) to obtain an evolution equation of the cell averages of the state vector \(\mathbf {Q}\). The non-conservative term \(\tilde{\mathbf {B}}(\mathbf {Q}) \cdot {\tilde{\nabla }} \mathbf {Q}\) appearing in (56) is integrated by using a path-conservative approach [39, 40, 71, 73, 79, 131, 138, 139, 144, 178], which follows the theory of Dal Maso–Le Floch and Murat [53] and defines the non-conservative term as a Borel measure. For a more detailed discussion on the known limitations and problems associated with path-conservative schemes see [3, 41]. One thus obtains
where a new term \(\tilde{\mathbf {D}}\) has been introduced in order to take into account potential jumps of the solution \(\mathbf {Q}\) on the space–time element boundaries \(\partial \mathcal {C}^n_i\). This term is computed by the path integral
The integration path \(\varvec{\varPsi }\) in (65) is chosen to be a simple straight-line segment [40, 73, 79, 138], although other choices are possible. Therefore it reads
and the jump term (65) simply reduces to
with \(\left( \mathbf {Q}^-,\mathbf {Q}^+\right)\) representing the two vectors of conserved variables within element \(T_i^n\) and its direct neighbor \(T_j^n\), respectively.
The final one-step ALE finite volume scheme for non-conservative hyperbolic systems takes the following form:
where the term \(\tilde{\mathbf {G}}_{ij}\) contains the Arbitrary-Lagrangian–Eulerian numerical flux function as well as the path-conservative jump term, hence allowing the discontinuity of the predictor solution \(\mathbf {q}_h\) that occurs at the space–time sub-volume \(\partial C_{ij}^n\) to be properly resolved. The volume and surface integrals appearing in (68) are approximated using multidimensional Gaussian quadrature rules, see [164] for details. The term \(\tilde{\mathbf {G}}_{ij}\) can be evaluated using a simple ALE Rusanov-type scheme [80] as
where \(\mathbf {q}_h^-\) and \(\mathbf {q}_h^+\) are the local space–time predictor solution inside element \(T_i(t)\) and the neighbor \(T_j(t)\), respectively, and \(|\lambda _{\max }|\) denotes the maximum absolute value of the eigenvalues of the matrix \(\tilde{\mathbf {A}} \cdot \tilde{\mathbf {n}}\) in space–time normal direction. Using the normal mesh velocity \(\mathbf {V} \cdot \mathbf {n}\), matrix \(\tilde{\mathbf {A}}_{\tilde{\mathbf {n}}}\) reads
with \(\mathbf {I}\) denoting the \(\nu \times \nu\) identity matrix, \(\mathbf {A}= \partial \mathbf {F}/ \partial \mathbf {Q}+ \mathbf {B}\) representing the classical Eulerian system matrix and \(\mathbf {n}\) being the spatial unit normal vector given by
The numerical flux term \(\tilde{\mathbf {G}}_{ij}\) can be also computed relying on a more sophisticated Osher-type scheme [136], introduced in the Eulerian framework for conservative and non-conservative hyperbolic systems in [78, 79]. It reads
where the matrix absolute value operator is computed as usual as
with the right eigenvector matrix \(\mathbf {R}\) and its inverse \(\mathbf {R}^{-1}\). According to [78, 79] Gaussian quadrature formulae of sufficient accuracy are adopted to evaluate the path integral present in (72).
Finally, let us underline that the integration over a closed space–time control volume, as done in (56), automatically satisfies the so-called geometric conservation law (GCL), since application of Gauss’ theorem yields
Note that (74) is the time-integrated (fully discrete) version of the classical GCL relation typically used in the Lagrangian community, as fully detailed in [23]. For all the applications and the test problems shown later in Sect. 3 the integral appearing in (74) has been evaluated for each element and at each timestep using Gaussian quadrature rules of sufficient accuracy. We could verify that condition (74) has been always satisfied on the discrete level up to machine precision.
Last but not least, we would like to state clearly that within the family of high order one-step direct ALE methods proposed in this work the choices of the Riemann solver, the reconstruction technique and the mesh velocity are deliberately independent from each other, hence the method in general allows a mass flux. This means that even for \(\mathbf {V}=\mathbf {v}\) the proposed scheme is not meant to be a pure Lagrangian method in sensu stricto. However, the family of schemes presented in this framework is able to resolve material interfaces and contact waves very well, much better than traditional high order Eulerian methods on fixed meshes.
3 Numerical Results
In order to validate the unstructured multidimensional direct ALE ADER-WENO schemes presented in this work, we solve a wide set of benchmark test problems using different hyperbolic systems of governing equations that can all be cast into form (4). We apply our new schemes to different conservation laws, namely the multidimensional Euler equations of compressible gas dynamics, the ideal classical magneto-hydrodynamics (MHD) equations and the non-conservative seven-equation Baer–Nunziato model of compressible multi-phase flows with stiff relaxation source terms.
Since the aim of this work is to design almost Lagrangian-like algorithms with our direct ALE formulation, for each of the test cases we choose the local mesh velocity as the local fluid velocity, hence
Furthermore, for each simulation, we explicitly write the numerical flux that has been adopted as well as the order of accuracy of the scheme and the mesh size.
3.1 The Euler Equations of Compressible Gas Dynamics
The first set of equations considered within this work are the so-called Euler equations of compressible gas dynamics, also known as hydrodynamics equations. They constitute a conservative system of hyperbolic conservation laws with no sources and they govern the fluid flow in case of neutral, i.e. non-charged, fluids.
Let \(\mathbf {Q}=(\rho , \rho u, \rho v, \rho w, \rho E)\) be the vector of conserved variables with \(\rho\) denoting the fluid density, \(\mathbf {v}=(u,v,w)\) representing the velocity vector and \(\rho E\) being the total energy density. Let furthermore p be the fluid pressure and \(\gamma\) the ratio of specific heats of the ideal gas, so that the speed of sound is \(c=\sqrt{\frac{\gamma p}{\rho }}\). The three-dimensional Euler equations of compressible gas dynamics can be cast into form (4), with the state vector \(\mathbf {Q}\) previously defined and the flux tensor \({\mathsf {\mathbf {F}}}=(\mathbf {f},\mathbf {g},\mathbf {h})\) given by
The term \({\mathsf {\mathbf {B}}}\) appearing in (4) is zero for this hyperbolic conservation law, because the system does not involve any non-conservative product. The system is then closed by the equation of state for an ideal gas, which reads
Moreover we define the specific internal energy \(\varepsilon ^*\) as
3.1.1 Numerical Convergence Studies
The convergence studies of our direct ALE ADER-WENO finite volume schemes for the Euler equations of compressible gas dynamics (76) are carried out considering the solution of a smooth convected isentropic vortex first proposed on unstructured meshes by Hu and Shu [100] in two space dimensions. The initial computational domain for the three-dimensional case is the box \(\varOmega (0)=[0;10]\times [0;10]\times [0;5]\) with periodic boundary conditions imposed on each face. The domain reduces to the square \(\varOmega (0)=[0;10]\times [0;10]\) if \(d=2\). The initial condition is the same given in [100], where we set to zero the \(z-\)aligned velocity component w, and it is given as a linear superposition of a homogeneous background field and some perturbations \(\delta\):
The perturbation of the velocity vector \(\mathbf {v}=(u,v,w)\) as well as the perturbation of temperature T read
where the radius of the vortex has been defined on the \(x-y\) plane as \(r^2=(x-5)^2+(y-5)^2\), the vortex strength is \(\epsilon =5\) and the ratio of specific heats is set to \(\gamma =1.4\). The entropy perturbation is assumed to be zero, i.e. \(S=\frac{p}{\rho ^\gamma }=0\), while the perturbations for density and pressure are given by
The vortex is furthermore convected with constant velocity \(\mathbf {v}_c=(1,1,0)\). The final time of the simulation is chosen to be \(t_f=1.0\), otherwise the deformations occurring in the mesh due to the Lagrangian motion would stretch and twist the control volumes so highly that a rezoning stage would be necessary. Here we want the convergence studies to be done with an almost pure Lagrangian motion, hence no rezoning procedure is admitted and the final time \(t_f\) has been set to a sufficiently small value. The exact solution \(\mathbf {Q}_e\) can be simply computed as the time-shifted initial condition, e.g. \(\mathbf {Q}_e(\mathbf {x},t_f)=\mathbf {Q}(\mathbf {x}-\mathbf {v}_c t_f,0)\), with the convective mean velocity \(\mathbf {v}_c\) previously defined. The error is measured at time \(t_f\) using the continuous \(L_2\) norm with the high order reconstructed solution \(\mathbf {w}_h(\mathbf {x},t_f)\), hence
where \(h(\varOmega (t_f))\) represents the mesh size which is taken to be the maximum diameter of the circumspheres or the circumcircles of the elements in the final domain configuration \(\varOmega (t_f)\).
Figures 8 and 9 show some of the successively refined meshes used for this test case. Convergence rates up to sixth order of accuracy are reported in Tables 1 and 2.
Sequence of triangular meshes used for the numerical convergence studies for the two-dimensional Euler equations of compressible gas dynamics at different time outputs: \(t=0\) (top row), \(t=1\) (middle row) and \(t=2\) (bottom row). The total number of elements \(N_E\) is increasing from the left grid (\(N_E=320\)), passing through the middle one (\(N_E=1298\)), to the right one (\(N_E=5180\))
Sequence of tetrahedral meshes at the initial time \(t=0\) used for the numerical convergence studies for the three-dimensional Euler equations of compressible gas dynamics. The total number of elements \(N_E\) is increasing from the left grid (\(N_E=60157\)), passing through the middle one (\(N_E=227231\)), to the right one (\(N_E=801385\))
3.1.2 The Sedov Problem
A classical test case for hydrodynamics is the Sedov problem. We consider the spherical symmetric Sedov problem, which describes the evolution of a blast wave generated at the origin \(\mathbf {O}=(x,y,z)=(0,0,0)\) of the initial cubic computational domain \(\varOmega (0)=[0;1.2]\times [0;1.2]\times [0;1.2]\). It is a well-known test case for Lagrangian schemes [122, 123, 128] that becomes very challenging in the three-dimensional case. An analytical solution which is based on self-similarity arguments is furthermore available from the work of Kamm et al. [103]. The computational domain is first discretized with cubic elements, then each cube is split into five tetrahedra. The computational domain is filled with a prefect gas with \(\gamma =1.4\), which is initially at rest and is assigned with a uniform density \(\rho _0=1\). The total energy \(E_{tot}\) is concentrated only in the cell \(c_{or}\) containing the origin \(\mathbf {O}\), therefore the initial pressure is given by
where \(V_{or}\) is the volume of the cell \(c_{or}\), which is composed by five tetrahedra, and the factor \(\frac{1}{8}\) takes into account the spherical symmetry, since the computational domain \(\varOmega (0)\) is only the eighth part of the entire domain, which would have to be considered if we did not assume the spherical symmetry. According to [122] we set \(E_{tot}=0.851072\), while in the rest of the domain the initial pressure is \(p_0=10^{-6}\). At the final time of the simulation \(t_f=1.0\) the exact solution is a symmetric spherical shock wave located at radius \(r=1\) with a density peak of \(\rho =6\).
As done in [122] we consider two different meshes, the first one \(m_1\) is composed by \(20\times 20 \times 20\) cubes, while the second one \(m_2\) involves \(40\times 40 \times 40\) elements. We use the third order accurate version of the ALE ADER-WENO schemes together with the Rusanov-type numerical flux (70) and the numerical solution for the Sedov problem has been computed on both meshes \(m_1\) and \(m_2\). Figure 10 shows the solution for density at the final time of the simulation as well as the mesh configuration and a comparison between the numerical and the exact density distribution along the radial direction.
Third order results for the Sedov problem with ALE ADER-WENO schemes on the coarse grid \(m_1\) (left column) and on the fine grid \(m_2\) (right column). From top to bottom: solution for density at the final time of the simulation (top row), mesh configuration at the final time \(t_f=1.0\) (middle row) and comparison between analytical and numerical density distribution along the diagonal straight line that crosses the cubic computational domain (bottom row)
3.1.3 The Noh Problem
In [134] proposed this test case in order to validate Lagrangian schemes in the regime of strong shock waves. The initial computational domain is given by \(\varOmega (0)=[0;1]^d\) and the initial mesh is composed either by squares or by cubes, that are split into either two right triangles (in 2D) or five right tetrahedra (in 3D). A gas with \(\gamma =\frac{5}{3}\) is initially assigned with a unit density \(\rho _0=1\) and a unit radial velocity which is moving the gas towards the origin of the domain \(O=(0,0,0)\). Hence, the velocity components are initialized with
and the initial pressure is \(p=10^{-6}\) everywhere. The generic radial position is given as usual as \(r=\sqrt{x^2+y^2+z^2}\). As time advances, an outward moving cylindrical or spherical shock wave is generated which travels with velocity \(v_{sh}=\frac{1}{3}\) in radial direction. According to [123, 128, 134], the final time is chosen to be \(t_f=0.6\), therefore the shock wave is located at radius \(R=0.2\) and the maximum density value is either \(\rho _f=16\) (\(d=2\)) or \(\rho _f=64\) (\(d=3\)), which occurs on the plateau behind the shock wave. Since the problem is set up in order to take into account cylindrical or spherical symmetry, we impose no-slip wall boundary conditions on the logically internal faces of the domain, while moving boundaries have been used on the remaining sides.
We use a fifth order accurate simulation of the Noh problem with the Rusanov-type numerical flux (70). The computational mesh is constructed with \(N^3=40^3\) hexahedra which are further split into 5 tetrahedra leading to a total number of elements \(N_E=32\times 10^4\). For this difficult problem we observe that the solution is slightly perturbed by parasitical phenomenon mostly arising from the no-slip boundary conditions. Nevertheless the spherical shock wave is well located (Fig. 11).
Noh problem in 3D at \(t_f=0.6\) with ALE ADER-WENO schemes. Left final mesh configuration. Right comparison between density as a function of cell radius for all cells and the exact solution
For the two-dimensional case the domain is discretized with a total number \(N_E=5000\) of triangles and we use from second up to fourth order accurate finite volume schemes. Figure 12 shows the initial and the final mesh configuration and a comparison between the exact solution and three high order accurate numerical results obtained with the ALE ADER-WENO finite volume schemes presented in this paper. One can notice that the quality of the solution becomes the better as the order of accuracy of the scheme increases.
Top mesh configuration for the Noh problem at the initial time \(t=0\) and at the final time \(t_f=0.6\). Bottom fourth order accurate density distribution at the final time and comparison between the exact solution (solid line) and three different high order accurate numerical results, i.e. 2nd, 3rd and 4th order ALE ADER-WENO finite volume schemes
3.1.4 The Saltzman Problem
The Saltzman problem involves a strong shock wave that is caused by the motion of a piston traveling along the main direction of a rectangular box. This test case was first proposed in [66] for a two-dimensional Cartesian grid that has been skewed and it represents a very challenging test problem that allows the robustness of any Lagrangian scheme to be validated, because the mesh is not aligned with the fluid motion. According to [128], we consider the three-dimensional extension of the original problem [36, 66], hence the initial computational domain is the box \(\varOmega (0)=[0;1]\times [0;0.1]\times [0;0.1]\). The computational mesh is obtained as follows:
-
the domain is initially meshed with a uniform Cartesian grid composed by \(100 \times 10 \times 10\) cubic elements, as done in [128];
-
each cube is then split into five tetrahedra;
-
finally we use the mapping given in [36, 128] to transform the uniform grid, defined by the coordinate vector \(\mathbf {x}=(x,y,z)\), to the skewed configuration \(\mathbf {x}'=(x',y',z')\):
$$\begin{aligned} x&'= x + \left( 0.1 - z \right) \left( 1 - 20y \right) \sin (\pi x) \quad {\text{for}} \quad 0 \le y \le 0.05 \nonumber , \\ x'&= x + z\left( 20y - 1 \right) \sin (\pi x) \quad {\text {for}} \quad 0.05 < y \le 0.1 \nonumber , \\ y'&= y \nonumber , \\ z'&= z. \end{aligned}$$(85)
In 2D we consider the computational domain \(\varOmega (0)=[0;1]\times [0;0.1]\) and the computational mesh is composed of \(200 \times 20\) triangular elements, obtained as follows:
-
first we build a Cartesian mesh with \(100 \times 10\) square elements, as done in [118, 123];
-
each square element is then split into two right triangles;
-
finally the uniform grid, defined by the coordinate vector \(\mathbf {x}=(x,y)\), is skewed with the mapping
$$\begin{aligned} x'&= x + \left( 0.1 - y \right) \sin (\pi x) \nonumber , \\ y'&= y, \end{aligned}$$(86)
where \(x'\) and \(y'\) denote the deformed coordinates, respectively.
The initial mesh configuration as well as the final mesh configuration for \(d\in [2,3]\) are depicted in Fig. 13.
Initial and final mesh configuration for the Saltzman problem in 2D (top) and in 3D (bottom)
According to [118], the computational domain is filled with a perfect gas with the initial state \(\mathbf {Q}_{0}\) given by
The ratio of specific heats is taken to be \(\gamma = \frac{5}{3}\), \(\epsilon = 10^{-4}\) and the final time is set to \(t_f=0.6\). The piston is traveling from the left to the right side of the domain with velocity \(\mathbf {v}_p = (u_p,v_p,w_p) = (1,0,0)\) and it starts moving at the initial time while the gas is at rest. In the initial time steps the scheme must obey a geometric \(\text {CFL}\) condition, i.e. the piston must not move more than one element per time step. Sliding wall boundary conditions have been set everywhere, except for the piston, which has been assigned with moving slip wall boundary condition.
The exact solution \(\mathbf {Q}_{ex}(\mathbf {x},t_f)\) is a one-dimensional infinite strength shock wave and it can be computed by solving the Riemann problem given in Table 3. The details of the algorithm that computes the exact solution of the Riemann problem are given in the book of Toro [173]. The exact solution has then to be shifted by a certain quantity d to the right, corresponding to the movement of the piston during the time of the simulation \(t_f\), i.e.
It reads
where \(x_f=0.8\) is the shock location at time \(t_f = 0.6\).
Figure 14 shows the evolution of the density solution obtained using the third order accurate version of the two-dimensional ALE ADER-WENO algorithm, while Fig. 15 plots a comparison between analytical and numerical solution in 3D for density and velocity. A good agreement with the exact solution can be noticed regarding both density and velocity distribution at the final time \(t_f=0.6\). The decrease of density near the piston, which affects all computations, is due to the well known wall-heating problem, see [172].
Evolution of the density solution for the Saltzman problem at output times \(t=0\), \(t=0.2\), \(t=0.4\) and \(t=0.6\)
Third order numerical results with ALE ADER-WENO schemes for the Saltzman problem: density (left) and velocity (right) distribution and comparison with analytical solution at time \(t=0.6\)
3.1.5 The Kidder Problem
Kidder [107] proposed this test problem, which has become a benchmark for Lagrangian schemes [37, 123]. It consists in an isentropic compression of a portion of a shell filled with a prefect gas which is assigned with the following initial condition:
where \(r=\sqrt{x^2+y^2+z^2}\) represents the general radial coordinate, \(\left( r_i(t),r_e(t)\right)\) are the time-dependent internal and external frontier that delimit the shell, \(\rho _{i,0}=1\) and \(\rho _{e,0}=2\) are the corresponding initial values of density and \(\gamma =2\) or \(\gamma =\frac{5}{3}\) is the ratio of specific heats in two and three space dimensions, respectively. Furthermore \(s_0\) denotes the initial entropy distribution, that is assumed to be uniform, i.e. \(s_0= \frac{p_0}{\rho _0^\gamma } = 1\). If \(d=2\) we set \(z=0\), as usual.
The initial computational domain \(\varOmega (0)\) is either one fourth (in 2D) or one eighth (in 3D) of the entire shell and is depicted in Fig. 16. Sliding wall boundary conditions are imposed on the lateral faces and on the bottom, while on the internal and on the external frontier a space–time dependent state is assigned according to the exact analytical solution R(r, t) [107], which is defined at the general time t for a fluid particle initially located at radius r as a function of the radius and the homothety rate h(t), i.e.
where \(\tau\) is the focalisation time
with \(c_{i,e}=\sqrt{\gamma \frac{p_{i,e}}{\rho _{i,e}}}\) representing the internal and external sound speeds. As done in [37, 123], the final time of the simulation is chosen in such a way that the compression rate is \(h(t_f)=0.5\), hence \(t_f=\frac{\sqrt{3}}{2}\tau\) and the the exact location of the shell is bounded within \(0.45 \le R \le 0.5\).
Position and mesh configuration of the shell at times \(t=0\) and at \(t=t_f\) in two (left) and three (right) space dimensions
The Osher-type flux (72) is adopted to perform the simulation of the Kidder problem, in order to precisely identified the location of the internal and external frontier. In the simulations of the Kidder problem we also measure the associated absolute error |err|, that can be evaluated as the difference between the analytical and the numerical location of the internal and external radius at the final time \(t_f\).
The two-dimensional computational domain is discretized with a characteristic mesh size of \(h=1/100\) for a total number of \(N_E=3180\). Figure 17 displays the fourth order numerical results obtained. The evolution of the density distribution has been plotted as well as the time-dependent location of the internal and the external frontier, which has been compared against the exact solution of Kidder previously described.
Density distribution for the Kidder problem at output times \(t=0.00\), \(t=0.05\), \(t=0.10\), \(t=0.15\) and \(t=t_{f}\) (from top left to bottom left). Evolution of the internal and external radius of the shell and comparison between analytical and numerical solution (bottom right)
In three space dimensions a total number of \(N_E=111534\) tetrahedra has been used to discretize the computational domain. We use again the fourth order version of our ALE ADER-WENO scheme together with the Osher-type flux (72). Figure 18 shows the initial and the final density distribution of the shell as well as the evolution of the internal and external frontier location during the simulation.
Left density distribution of the shell at times \(t=0\) and at \(t=t_f\). Right evolution of the internal and external radius of the shell and comparison between analytical and numerical solution for the three-dimensional ALE ADER-WENO scheme
The absolute error |err| associated to the internal and external frontier evolution for both simulations is reported in Table 4, where one can appreciate that our direct ALE algorithm able to follow the shell compression very closely and precisely.
3.2 The Ideal Magnetohydrodynamics (MHD) Equations
The equations of ideal classical magnetohydrodynamics (MHD) are used to describe the motion of charged fluids like plasma fluids. They constitute a more complicated hyperbolic conservation law compared to the Euler equations presented in Sect. 3.1, especially because this system introduces an additional constraint regarding the divergence of the magnetic field that must remain zero in time, i.e.
If the magnetic field \(\mathbf {B}\) is initialized with data that are guaranteed to be divergence-free, then Eq. (93) is always satisfied for the exact solution. The difficulty appears at the discrete level, where the numerical divergence-free constraint has to be carefully taken into account and properly treated. To overcome this problem, we adopt the hyperbolic version of the generalized Lagrangian multiplier (GLM) divergence cleaning approach proposed by Dedner et al. [54], hence adding to the MHD system one more variable \(\Psi\) as well as one more linear scalar PDE that aims at transporting the divergence errors out of the computational domain with an artificial divergence cleaning speed \(c_h\). The augmented MHD system can be cast into form (4) and reads
The non-conservative part of the ideal MHD system is zero, the velocity vector is denoted by \(\mathbf {v}=v_i=(u,v,w)\) and similarly the vector of the magnetic field is addressed with \(\mathbf {B}=B_i=(B_x,B_y,B_z)\). The system is then closed by the equation of state
with \(\gamma\) representing the ratio of specific heats and the total pressure being defined as \(p_{tot} = p + \frac{1}{8 \pi } \mathbf {B}^2\).
3.2.1 The MHD Rotor Problem
The first test case for the ideal classical MHD equations is the MHD rotor problem proposed by Balsara et al. [10]. It consists in a fluid of high density that is rotating very quickly, surrounded by a fluid at rest with low density. The initial computational domain \(\varOmega (0)\) is a sphere of radius \(R_0=0.5\) and transmissive boundary conditions are imposed at the external boundary. The generic radial position is denoted by \(r=\sqrt{x^2+y^2+z^2}\) and at radius \(R=0.1\) the inner region with the high density fluid is separated by the outer region. Therefore the initial density distribution is \(\rho =10\) for \(0 \le r \le R\) and \(\rho =1\) in the rest of the domain, while the angular velocity \(\omega\) of the rotor is assumed to be constant and it is chosen in such a way that at \(r=R\) the toroidal velocity is \(v_t=\omega \cdot R =1\). The initial discontinuity for density and velocity occurring at the frontier \(r=R\) is smeared out according to [10], where a linear taper bounded by \(0.1 \le r \le 0.13\) is applied in such a way that the internal values for density and velocity match exactly those ones of the outer region. The pressure is \(p=1\) in the whole computational domain and a constant magnetic field \(\mathbf {B}=(2.5,0,0)^T\) is imposed everywhere. The divergence cleaning velocity is taken to be \(c_h=2\), while the ratio of specific heats is set to \(\gamma =1.4\) and the final time is \(t_f=0.25\). In two space dimensions the computational domain reduces to a circle and the z coordinate as well as all its related quantities disappear.
We use a computational grid with a characteristic mesh size of \(h=1/200\) to run the two-dimensional MHD rotor problem. Numerical results obtained with a fourth order ALE ADER-WENO scheme with the Rusanov-type flux (70) are depicted in Fig. 19. We can notice a good agreement with the solution presented in [10], although the mesh used for the simulation is coarser than the one adopted by Balsara and Spicer.
Numerical results for the two-dimensional ideal MHD rotor problem: density, pressure, magnetic pressure and a coarse mesh configuration at time \(t=0.25\). A 4th order direct ALE ADER-WENO scheme has been used
In three space dimensions the computational domain is discretized with a total number of tetrahedra of \(N_E=1089071\). The numerical results for the three-dimensional MHD rotor problem have been obtained using a third order scheme with the Rusanov-type flux (70) and they are depicted in Fig. 20. The rezoning procedure described in Sect. 2.3 allows the mesh to be reasonably well shaped, even with the strong deformations produced by the velocity field of the rotor. Figure 21 shows the initial and the final mesh configuration and the corresponding density distribution.
Third order ALE ADER-WENO numerical results for the ideal MHD rotor problem at time \(t=0.25\). Top density and pressure. Bottom magnitude of the magnetic field and Mach number
Mesh configuration and density distribution for the three-dimensional MHD rotor problem at the initial time \(t=0.0\) (top) and at the final time \(t=0.25\) (bottom)
3.2.2 The MHD Blast Wave Problem
The blast wave problem constitutes a benchmark in magnetohydrodynamics. A strong circular fast magnetosonic shock wave is traveling from the center to the boundaries of the initial computational domain \(\varOmega (0)\), which is a sphere (in 3D) or a circle (in 2D) of radius \(R_0=0.5\). The frontier delimited by radius \(R=0.1\) splits the domain into two parts, hence defining an inner state \({\mathbf {U}}_i\) and an outer state \({\mathbf {U}}_o\), that are initially assigned in terms of primitive variables \({\mathbf {U}}=(\rho ,u,v,w,p,B_x,B_y,B_z,\psi )\) as
where \(r=\sqrt{x^2+y^2+z^2}\). We set transmissive boundary conditions at the external boundary. The final time of the computation is \(t_f=0.01\) and the ratio of specific heats is taken to be \(\gamma =1.4\). For the MHD blast wave problem we use the same mesh adopted for the MHD rotor problem described in the previous section both in two and in three space dimensions.
The numerical results depicted in Fig. 22 have been computed using a third order accurate ALE ADER-WENO finite volume scheme with the Rusanov-type flux (70). We plot the logarithm of density and pressure, as well as the magnitude of both the velocity and the magnetic field, and the solution looks very similar to the results given in [9].
Numerical results for the two-dimensional MHD blast wave problem at time \(t=0.01\) obtained with a third order accurate ALE ADER-WENO scheme. Top logarithm (base 10) of the density and logarithm (base 10) of the pressure. Bottom magnitude of the velocity and the magnetic field
Due to the very strong shock wave, the velocity of the flow is quite high and the fluid is pushed by the magnetic field towards the boundary of the computational domain. Therefore we use the rezoning algorithm which allows the mesh elements to recover a more regular shape in order to carry on the simulation until the final time \(t_f\). Figure 23 shows a comparison between the fully Lagrangian mesh configuration and the rezoned mesh configuration at time \(t=0.004\).
Mesh configurations for the MHD blast wave problem in 2D at time \(t=0.004\). Left fully Lagrangian mesh motion. Right Lagrangian mesh motion with the rezoning stage (Sect. 2.3)
The numerical solution in 3D is depicted in Fig. 24 and is in qualitative agreement with the results shown previously for \(d=2\) in Fig. 22, where the two-dimensional version of our Lagrangian-like WENO algorithm has been used to run this test case. The tetrahedral mesh at the final time \(t=0.01\) is depicted in Fig. 25.
Third order ALE ADER-WENO numerical results for the three-dimensional Blast problem at time \(t=0.01\). Top logarithm (base 10) of the density and logarithm (base 10) of the pressure. Bottom magnitude of the velocity field and the magnetic field
View of the unstructured tetrahedral grid at time \(t=0.01\) for the 3D MHD blast wave problem
3.3 The Baer–Nunziato Model of Compressible Two-Phase Flows
Multi-phase flow problems, such as liquid-vapor and solid-gas flows are encountered in numerous natural processes, such as avalanches, meteorological flows with cloud formation, volcano explosions, sediment transport in rivers and on the coast, granular flows in landslides, etc., as well as in many industrial applications, e.g., in aerospace engineering, automotive industry, petroleum and chemical process engineering, nuclear reactor safety, paper and food manufacturing and renewable energy production. Most of the industrial applications are concerned with compressible multi-phase flows as they appear for example in combustion processes of liquid and solid fuels in car, aircraft and rocket engines, but also in solid bio-mass combustion processes. Already the mathematical description of such flows is quite complex and up to now there is no universally agreed model for such flows. One wide-spread model is the Baer–Nunziato model for compressible two-phase flow, which has been developed by Baer and Nunziato [8] for describing detonation waves in solid-gas combustion processes. High resolution shock capturing finite volume schemes combined with a stiff relaxation approach have been successfully applied to this system by Saurel and Abgrall [5, 150]. In this work we will use the original choice of Baer–Nunziato, which has also been adopted in several papers about the exact solution of the Riemann-problem of the Baer–Nunziato model, see [7, 55, 159]. A reduced five-equation model has been proposed in [104], for the solution of which a Godunov type scheme has been presented in [133]. Approximate Riemann solvers of Baer–Nunziato-type models of compressible multi-phase flows can be found for example in [73, 79, 165, 170]. Numerical schemes for compressible multi-phase flows on moving meshes have been considered for the one-dimensional case in [154] and an efficient Eulerian approach on fixed unstructured grids has been proposed in [4]. For further work on numerical methods for compressible multi-phase flows see, for example, [2, 6, 114, 142, 152, 153, 155, 156, 186].
The first phase is normally addressed as the solid phase, while the second one as the gas phase and in the following we will use the subscripts 1 and 2 to define them. We will write equivalently also the subscripts s and g to denote the solid and the gas phase. Let \(k=1,2\) be the phase number and \(\phi _k\) be the volume fraction of phase k with the condition \(\phi _1 + \phi _2 = 1\), while \(\rho _k\) and \(p_k\) represent the corresponding density and pressure, respectively. Let furthermore the velocity vector of each phase be addressed with \(\mathbf{u }_k=(u_k,v_k,w_k)\). The full seven-equation Baer–Nunziato model with relaxation source terms results in a non-conservative system of nonlinear hyperbolic PDE that can be written as
where only strongly simplified interphase drag and pressure relaxation source terms are considered. Further details on the choice and the formulation of such terms can be found in [104]. The so-called stiffened gas equation of state is then used for each of the two phases to close the system:
The specific total energy of each phase is \(E_k = e_k + \frac{1}{2}{\mathbf {u}}_{\mathbf {k}}^2\) with \(e_k\) denoting the corresponding internal energy, while in system (97) \(\mu\) is a parameter which characterizes pressure relaxation and \(\lambda\) is related to the friction between the phases. According to [8, 104] the velocity at the interface I is taken to be the solid velocity, while for the interface pressure we choose the gas pressure, hence
Other choices are possible, see [150, 151] for a detailed discussion.
Since this physical model involves two phases, namely the solid phase and the gas phase, we decide to move the mesh with the solid phase velocity, hence
which coincides with the interface velocity, according to our assumptions
The resolution of material interfaces, which are given by jumps in the volume fraction \(\phi _k\), is a challenging task for the numerical methods applied to the Baer–Nunziato model (97). We stress that the present approach is a so-called diffuse interface approach, which may not be suitable for all situations occurring in the simulation of multi-fluid and multi-material problems. For so-called sharp interface approaches, the reader is referred to aforementioned references.
3.3.1 Riemann Problems
The high order ALE ADER-WENO finite volume schemes proposed in this work are validated by applying them to 1D Riemann problems that are solved in a 2D and 3D geometry on unstructured triangular and tetrahedral meshes. The exact solution for these 1D Riemann problems can be found in [7, 55, 159]. From the above mentioned articles we have chosen a subset of four Riemann problems, whose initial conditions are listed in Table 5. Some of the test cases use the stiffened gas EOS, some of them consider just a mixture of two ideal gases.
The initial computational domain is given either by \(\varOmega (0)=[-0.5;0.5] \times [-0.05; 0.05]\) if \(d=2\) or \(\varOmega (0)=[-0.5;0.5]\times [-0.05;0.05]\times [-0.05;0.05]\) if \(d=3\). The domain is discretized using a characteristic mesh size of \(h=1/200\), corresponding to an equivalent one-dimensional resolution of 200 cells. The initial discontinuity is located at \(x=0\) and the final simulation times are listed in Table 5. In x-direction we use transmissive boundaries, while periodic boundary conditions are imposed along the remaining directions.
Friction and pressure relaxation are neglected in the first three Riemann problems RP1, RP2 and RP4, while for RP5 we use a moderately stiff interphase drag \(\lambda =10^3\) and pressure relaxation \(\mu =10^2\). RP5 involves two almost pure ideal gases that differ in their value of \(\gamma\). As done in [70, 73] the exact solution for RP5 is computed using the exact Riemann solver for the Euler equations of compressible gas dynamics [173] with two different values of \(\gamma\) on the left and on the right of the contact discontinuity, respectively. In this test problem the algebraic source term in the full Baer–Nunziato system (97) becomes stiff, but it can be properly treated by the local space–time predictor presented in Sect. 2.2.
The numerical results are shown in Figs. 26, 27, 28 and 29 and are compared with the exact solution. RP1 and RP4 have been run in 2D, while for RP2 and RP5 the three-dimensional results are displayed. On the top left of each figure a sketch of the mesh is depicted, while the other sub figures contain a one-dimensional cut through the reconstructed numerical solution \(\mathbf {w}_h\) along the x-axis, evaluated at the final time on 200 equidistant sample points. Due to the Lagrangian-like formulation of the method, the solid contact is resolved in a very sharp manner in all cases, which was actually the main aim in the design of a high order ALE scheme for the compressible Baer–Nunziato model. Also for the other waves we can note in general a very good agreement between our numerical results and the exact reference solutions given in [7, 55, 159].
Results for Riemann problem RP1 of the seven-equation Baer–Nunziato model in 2D at time \(t=0.1\)
Results for Riemann problem RP2 of the seven-equation Baer–Nunziato model in 3D at time \(t=0.1\)
Results for Riemann problem RP4 of the seven-equation Baer–Nunziato model in 2D at time \(t=0.15\)
Results for Riemann problem RP5 of the seven-equation Baer–Nunziato model in 3D with drag and pressure relaxation (\(\lambda =10^3, \mu =10^2\)) at time \(t=0.2\) and comparison with the exact solution
3.3.2 Explosion Problems
We use the same initial condition given for the Riemann problems in Table 5 to solve the compressible Baer–Nunziato equations either on a circular or a spherical computational domain \(\varOmega (t)\) with initial radius \(R=1.0\) in 2D and \(R=0.9\) in 3D. In all cases the initial state \(\mathbf {Q}(\mathbf {x},0)\) is assigned taking
with \(r_c=0.5\) representing the location of the initial discontinuity. The left state reported in Table 5 is assumed to be the inner state \(\mathbf {Q}_i\), while the right state represents here the outer state \(\mathbf {Q}_o\). In particular, the first explosion problem EP1 uses the initial condition of RP1, EP2 corresponds to RP2 and EP3 to RP4, respectively. In the fourth explosion problem EP4 we use again the initial values of RP2 and we set \(\lambda =10^5\) and \(\mu =0\), hence adopting a stiff interphase drag. The reference solution is obtained by solving an equivalent non-conservative one-dimensional PDE in radial direction with geometric reaction source terms, for details see [173] for the Euler equations and [174] for the Baer–Nunziato model. In our case here the reference solution has been obtained by using a path-conservative second order TVD scheme [79] on a very fine (fixed) 1D mesh consisting of 10,000 cells.
In two space dimensions the initial mesh spacing is of characteristic size \(h=1/250\), leading to a total number of \(N_E=\) 431,224 triangular elements used to discretize \(\varOmega (t)\), while in 3D we use a characteristic mesh size of \(h=1/100\) for \(r \le r_c\) and \(h=1/50\) for \(r > r_c\) for a total number of tetrahedra of \(N_E=\) 2,632,305. Numerical results for EP1 and EP3 have been collected using the two-dimensional version of the algorithm, whereas we perform a three-dimensional computation for EP2 and EP4. The numerical results are compared with the 1D reference solution in Figs. 30, 31, 32 and 33. On the top left of each figure a 3D visualization of either the solid or the gas density is shown, in order to verify that either the cylindrical or the spherical symmetry is reasonably maintained on the unstructured meshes used here. The other sub figures show a one-dimensional cut through the reconstructed numerical solution \(\mathbf {w}_h\) on 100 equidistant sample points along the x-axis. We use the path-conservative Osher-type method (72) since it is less dissipative than the Rusanov-type scheme (69), hence a better resolution of the material contact can be achieved. Since the mesh is moving with the interface velocity \({\mathbf {u}}_{\mathbf {I}}\), i.e. \(\mathbf {V}={\mathbf {u}}_{\mathbf {I}}=\mathbf {u}_1\), the contact discontinuity of the first phase \(\phi _1\) is very well resolved in all cases. The quality of the three-dimensional results is lower towards the external boundary of the computational domain because a coarser grid with \(h=1/50\) has been used there. This was necessary to reduce the amount of computational resources needed to carry on the computation.
Results obtained for the cylindrical explosion problem EP1 of the seven-equation Baer–Nunziato model in 2D at time \(t=0.15\) and comparison with the reference solution
Results obtained for the cylindrical explosion problem EP2 of the seven-equation Baer–Nunziato model in 3D at time \(t=0.15\) and comparison with the reference solution
Results obtained for the cylindrical explosion problem EP3 of the seven-equation Baer–Nunziato model in 2D at time \(t=0.15\) and comparison with the reference solution
Results obtained for the cylindrical explosion problem EP4 of the seven-equation Baer–Nunziato model in 2D with \(\lambda =10^5\) at time \(t=0.18\) and comparison with the reference solution
3.3.3 Two-Dimensional Riemann Problems
Kurganov and Tadmor [111] have collected a very nice set of numerical solutions for two-dimensional Riemann problems of the compressible Euler equations [187]. Here, we propose two 2D Riemann problems for the compressible Baer–Nunziato model, however, without following the guidelines laid out in [111, 187], which lead to exactly one elementary wave at each interface, but we just simply take as initial data some of the data used for the 1D Riemann problems before, see Table 5. The initial computational domain is the square \(\varOmega (0)=[-0.5;0.5] \times [-0.5;0.5]\) and reflective wall boundaries are applied everywhere. The initial condition is given by four piecewise constant states defined in each quadrant of the two-dimensional coordinate system:
The initial conditions for the two configurations presented in this work are listed in Table 6.
The computational domain is discretized using an unstructured triangular mesh composed of \(N_E=\) 90,080 elements with an initial characteristic mesh spacing of \(h=1/200\). The reference solution is computed with a high order Eulerian one-step scheme as presented in [79, 174], using a very fine mesh composed of \(N_E=\) 2,277,668 triangles with characteristic mesh spacing \(h=1/1000\). The obtained results together with the Eulerian reference solution are depicted in Figs. 35 and 36, where we can observe a very good qualitative agreement of the Lagrangian-like solution with the Eulerian fine-grid reference solution. For the first test problem, the initial and the final mesh are depicted in Fig. 34.
Mesh for configuration C1 at times \(t=0\) (left) and \(t=0.15\) (right)
Results obtained with the two-dimensional third order direct ALE ADER-WENO scheme for the 2D Riemann problem C1 at time \(t=0.15\) (left column). The reference solution computed with an Eulerian method on a very fine mesh is also shown (right column). 30 equidistant contour lines are shown for the solid density \(\rho _s\) (top row), the gas density \(\rho _g\) (middle row) and the solid volume fraction \(\phi _s\) (bottom row). In this test problem stiff relaxation source terms are used setting \(\lambda =10^5\) and \(\mu =10^2\)
Results obtained with the two-dimensional third order direct ALE ADER-WENO scheme for the 2D Riemann problem C2 at time \(t=0.15\) (left column). The reference solution computed with an Eulerian method on a very fine mesh is also shown (right column). 30 equidistant contour lines are shown for the solid density \(\rho _s\) (top row), the gas density \(\rho _g\) (middle row) and the solid volume fraction \(\phi _s\) (bottom row)
4 Algorithm Efficiency Improvements
In this paper we have designed and presented a new family of Arbitrary-Lagrangian–Eulerian (ALE) finite volume schemes, called direct ALE ADER-WENO schemes, where high order of accuracy in time is obtained by using a local space–time Galerkin predictor on moving curved meshes, while a high order accurate nonlinear WENO method is adopted to produce high order essentially non-oscillatory reconstruction polynomials in space. The mesh is moved at each time step according to the solution of a nodal solver algorithm that assigns a unique velocity vector to each node of the mesh. A rezoning procedure can also be applied when mesh distortions and deformations become too severe. The space–time mesh is then constructed by straight edges connecting the vertex positions at the old time level \(t^n\) with the new ones at the next time level \(t^{n+1}\), yielding closed space–time control volumes, on the boundary of which the numerical flux must be integrated.
The entire algorithm can be divided into three main parts, namely the WENO reconstruction, the local space–time predictor and the numerical flux evaluation. In order to investigate the efficiency of our numerical method, we perform the simulation of a very simple test problem, i.e. the three-dimensional smooth isentropic vortex described in Sect. 3.1.1. We run the second, third and fourth order accurate version of the numerical scheme and we measure the computational cost of each part of the algorithm, which is reported in Table 7.
The most expensive part of the algorithm is the flux evaluation, since in the Lagrangian framework no quadrature-free approach is in principle possible, due to the continuous evolution of the geometry configuration that does not allow the flux computation to be treated as done for the Eulerian case in [74], where the space–time basis used for the flux integrals in (68) are integrated on the reference space–time element in a pre-processing step and stored only once. As the order of accuracy increases the relative cost of the WENO reconstruction procedure also increases because the reconstruction stencils become larger, while the local space–time predictor step is the least expensive part of the whole algorithm.
In the following we will briefly mention and present some modifications of the direct ALE ADER-WENO algorithm that have been designed starting from the analysis and the data highlighted in Table 7. Specifically, the following strategies have been investigated in order to improve the overall algorithm efficiency:
-
In [29] we propose a local time stepping (LTS) algorithm for moving unstructured triangular meshes, where each element of the mesh has to obey only a less restrictive local CFL stability condition, hence using its own optimal local timestep to reach the final time of the simulation. The new algorithm is based on a non-conforming mesh in time, with hanging nodes that are continuously moving and in principle never match the same time level, unless either an intermediate output time or the final time of the simulation is reached. As a consequence, the reconstruction is carried out locally, i.e. within each control volume, computing a virtual geometry and a virtual set of cell averages of the surrounding elements that are both evaluated using the high order space–time predictor solution;
-
In [21] we employ the genuinely multidimensional HLL Riemann solvers developed by Balsara et al. [63] as a building block for genuinely multidimensional numerical flux evaluation that allows the scheme to run with larger time steps compared to conventional finite volume schemes that use classical one-dimensional Riemann solvers in normal direction. The space–time flux integral computation is carried out at the boundaries of each triangular space–time control volume using the Simpson quadrature rule in space and Gauss–Legendre quadrature in time. In this approach the multidimensional HLL Riemann solver is also employed as nodal solver;
-
A new and efficient quadrature-free approach for the numerical flux integration is presented in [24]. The space–time boundaries of the space–time control volumes are split into simplex sub-elements, i.e. either triangles in 2D or tetrahedra in 3D, hence leading to space–time normal vectors as well as Jacobian matrices that are constant within each sub-element. Within the space–time Galerkin predictor stage (see Sect. 2.2) that solves the Cauchy problem inside each element in the small, the discrete solution and the flux tensor are approximated using a nodal space–time basis. Since these space–time basis functions are defined on a reference element and do not change, their integrals over the simplex sub-surfaces of the space–time reference control volume can be integrated once and for all analytically during a pre-processing step. The resulting integrals are then used together with the space–time degrees of freedom of the predictor in order to compute the numerical flux that is needed in the finite volume scheme;
-
The work proposed in [30, 31] is devoted to the improvement of the reconstruction part of the algorithm. The expensive WENO approach on moving meshes, used to obtain high order of accuracy in space, is replaced by the very recent a posteriori MOOD paradigm [49, 58, 59, 120] which is shown to be less expensive but still as accurate. This a posteriori MOOD strategy ensures the numerical solution in each cell at any discrete time level to fulfill a set of user-defined detection criteria. If one cell value is not satisfying the detection criteria, then the solution is locally re-computed by progressively decrementing the order of the polynomial reconstructions, following the so-called cascade of schemes. A very robust scheme is employed as a last resort for genuinely problematic cells. The cascade of schemes defines how the decrementing process is carried out, i.e. how many schemes are tried and which orders are adopted for the polynomial reconstructions. Furthermore the iterative MOOD loop allows the numerical solution to maintain some interesting properties such as positivity, mesh validity, etc.
From the aforementioned improvements, in a very recent work [20] we have combined the quadrature-free flux evaluation [24] with the a posteriori MOOD stabilization technique [30, 31]. We have measured the efficiency ratio \(\beta\) of this new algorithm compared to the original formulation of the ALE ADER-WENO methods discussed in this paper. Table 8 reports the outputs in 2D, while Table 9 refers to the three-dimensional case: \(N_E\) denotes the total number of elements of the computational mesh, N represents the number of time steps needed to carry on the simulation until the final time and \(\tau _E=\frac{t_{CPU}}{N_E \cdot N}\) gives the time used per element update. Also the total computational time of the simulation (\(t_{CPU}\)) is provided as well as the final efficiency ratio computed as
where the ALE ADER-WENO scheme is referred to as “WGQ” (WENO Gaussian Quadrature) and the new more efficient algorithm is addressed with “MQF” (MOOD Quadrature-Free).
The simulations have been run with our MPI parallel code “PDESol” on 64 threads in 2D on the AMD Opteron cluster STiMulUs in Trento (Italy), while we have used 2048 threads in 3D on the SuperMUC supercomputer based in Munich (Germany).
5 Conclusions
In this work we have developed a new family of high order Arbitrary-Lagrangian–Eulerian one-step ADER-WENO finite volume schemes on unstructured triangular and tetrahedral meshes [22, 23, 70]. The algorithm is formulated in a very general manner so that it can be applied to both conservative and non-conservative hyperbolic systems of balance laws, with and without stiff source terms. A WENO reconstruction technique is used to achieve high order of accuracy in space, while an element-local space–time Galerkin finite element predictor on moving curved meshes is employed to obtain a high order accurate one-step time discretization. To the knowledge of the author, this is the first better than second order accurate Lagrangian-type finite volume scheme ever presented on unstructured tetrahedral meshes. The final ALE finite volume scheme belongs to the category of direct ALE methods, because an additional remapping stage, which is typically used in the context of indirect ALE and pure Lagrangian schemes, is unnecessary in our case. This is possible because the new class of ALE algorithms proposed within this work is based directly on a space–time conservation formulation of the governing PDE system, which furthermore allows the geometric conservation law (GCL) to be satisfied by the scheme by construction (see [23] for details). The mesh motion procedure has been described in details, considering all the steps needed to move the mesh, namely the Lagrangian step, the rezoning step and the relaxation step. In order to improve the overall algorithm efficiency several variants of the original scheme have been mentioned and briefly presented in Sect. 4. Numerical convergence studies up to sixth order of accuracy in space and time have been shown and the new family of direct ALE ADER-WENO schemes have been applied to different hyperbolic systems of conservation laws, namely the multidimensional Euler equations of compressible gas dynamics, the ideal classical magnetohydrodynamics (MHD) equations and the non-conservative seven-equation Baer–Nunziato model of compressible multi-phase flows with stiff relaxation source terms. Several classical test problems have been run for each system of PDEs in order to assess the robustness of the new schemes. The obtained numerical results have been carefully compared with exact or other numerical reference solutions.
In [25] we have extended the presented algorithm to curvilinear unstructured meshes, thus the space–time control volumes involved in the finite volume scheme are no longer defined by linear basis functions but by a high order isoparametric approximation. We plan to investigate pure Lagrangian algorithms, i.e. numerical methods with zero mass flux across element interfaces, in the context of ADER schemes and the extension to high order Discontinuous Galerkin schemes is also left for the future. Furthermore the use of curvilinear meshes will allow the first better than third order pure Lagrangian finite volume schemes to be developed on unstructured meshes, using the already existing framework presented in this paper.
Last but not least, another important topic will be the application of the present scheme to more realistic real world simulations in engineering and physics.
References
Abgrall R (1994) On essentially non-oscillatory schemes on unstructured meshes: analysis and implementation. J Comput Phys 144:45–58
Abgrall R, Karni S (2001) Computations of compressible multifluids. J Comput Phys 169:594–623
Abgrall R, Karni S (2010) A comment on the computation of non-conservative products. J Comput Phys 229:2759–2763
Abgrall R, Nkonga B, Saurel R (2003) Efficient numerical approximation of compressible multi-material flow for unstructured meshes. Comput Fluids 32:571–605
Abgrall R, Saurel R (2003) Discrete equations for physical and numerical compressible multiphase mixtures. J Comput Phys 186:361–396
Andrianov N, Saurel R, Warnecke G (2003) A simple method for compressible multiphase mixtures and interfaces. Int J Numer Methods Fluids 41:109–131
Andrianov N, Warnecke G (2004) The Riemann problem for the Baer–Nunziato two-phase flow model. J Comput Phys 212:434–464
Baer MR, Nunziato JW (1986) A two-phase mixture theory for the deflagration-to-detonation transition (DDT) in reactive granular materials. J Multiph Flow 12:861–889
Balsara D (2004) Second-order accurate schemes for magnetohydrodynamics with divergence-free reconstruction. Astrophys J Suppl Ser 151:149–184
Balsara D, Spicer D (1999) A staggered mesh algorithm using high order Godunov fluxes to ensure solenoidal magnetic fields in magnetohydrodynamic simulations. J Comput Phys 149:270–292
Balsara DS, Meyer C, Dumbser M, Du H, Xu Z (2013) Efficient implementation of ader schemes for euler and magnetohydrodynamical flows on structured meshes speed comparisons with Runge–Kutta methods. J Comput Phys 235:934–969
Balsara DS, Rumpf T, Dumbser M, Munz CD (2009) Efficient, high accuracy ADER-WENO schemes for hydrodynamics and divergence-free magnetohydrodynamics. J Comput Phys 228:2480–2516
Barth TJ, Frederickson PO (1990) Higher order solution of the Euler equations on unstructured grids using quadratic reconstruction. In: 28th aerospace sciences meeting. AIAA Paper No. 90-0013
Barth TJ, Jespersen DC (1989) The design and application of upwind schemes on unstructured meshes. AIAA Paper 89-0366, pp 1–12
Ben-Artzi M, Falcovitz J (1984) A second-order Godunov-type scheme for compressible fluid dynamics. J Comput Phys 55:1–32
Benson DJ (1992) Computational methods in Lagrangian and Eulerian hydrocodes. Comput Methods Appl Mech Eng 99:235–394
Berndt M, Breil J, Galera S, Kucharik M, Maire PH, Shashkov M (2011) Two-step hybrid conservative remapping for multimaterial arbitrary Lagrangian–Eulerian methods. J Comput Phys 230:6664–6687
Berndt M, Kucharik M, Shashkov MJ (2010) Using the feasible set method for rezoning in ALE. Proc Comput Sci 1:1879–1886
Bochev P, Ridzal D, Shashkov MJ (2013) Fast optimization-based conservative remap of scalar fields through aggregate mass transfer. J Comput Phys 246:37–57
Boscheri W (2016) An efficient high order direct ALE ADER finite volume scheme with a posteriori limiting for hydrodynamics and magnetohydrodynamics. Int J Numer Methods Fluids (Submitted)
Boscheri W, Balsara DS, Dumbser M (2014) Lagrangian ADER-WENO finite volume schemes on unstructured triangular meshes based on genuinely multidimensional HLL Riemann solvers. J Comput Phys 267:112–138
Boscheri W, Dumbser M (2013) Arbitrary-Lagrangian–Eulerian one-step WENO finite volume schemes on unstructured triangular meshes. Commun Comput Phys 14:1174–1206
Boscheri W, Dumbser M (2014) A direct arbitrary-Lagrangian–Eulerian ADER-WENO finite volume scheme on unstructured tetrahedral meshes for conservative and nonconservative hyperbolic systems in 3D. J Comput Phys 275:484–523
Boscheri W, Dumbser M (2016) An efficient quadrature-free formulation for high order arbitrary-Lagrangian–Eulerian ADER-WENO finite volume schemes on unstructured meshes. J Sci Comput 66:240–274
Boscheri W, Dumbser M (2016) High order accurate direct Arbitrary-Lagrangian–Eulerian ADER-WENO finite volume schemes on moving curvilinear unstructured meshes. Comput Fluids 136:48–66
Boscheri W, Dumbser M, Balsara DS (2014) High order Lagrangian ADER-WENO schemes on unstructured meshes—application of several node solvers to hydrodynamics and magnetohydrodynamics. Int J Numer Methods Fluids 76:737–778
Boscheri W, Dumbser M, Loubère R (2016) Cell centered direct Arbitrary-Lagrangian–Eulerian ADER-WENO finite volume schemes for nonlinear hyperelasticity. Comput Fluids 134–135:111–129
Boscheri W, Dumbser M, Righetti M (2013) A semi-implicit scheme for 3D free surface flows with high order velocity reconstruction on unstructured Voronoi meshes. Int J Numer Methods Fluids 72:607–631
Boscheri W, Dumbser M, Zanotti O (2014) High order cell-centered Lagrangian-type finite volume schemes with time-accurate local time stepping on unstructured triangular meshes. J Comput Phys 291:120–150
Boscheri W, Loubère R (2016) High order accurate direct Arbitrary-Lagrangian–Eulerian ADER-MOOD finite volume schemes for non-conservative hyperbolic systems with stiff source terms. Commun Comput Phys (Accepted)
Boscheri W, Loubère R, Dumbser M (2015) Direct Arbitrary-Lagrangian–Eulerian ADER-MOOD finite volume schemes for multidimensional hyperbolic conservation laws. J Comput Phys 292:56–87
Bourgeade A, LeFloch P, Raviart PA (1989) An asymptotic expansion for the solution of the generalized riemann problem. Part II: application to the gas dynamics equations. Annales de l’institut Henri Poincaré (C) Analyse non linéaire 6:437–480
Breil J, Harribey T, Maire PH, Shashkov MJ (2013) A multi-material ReALE method with MOF interface reconstruction. Comput Fluids 83:115–125
Butcher JC (1987) The numerical analysis of ordinary differential equations: Runge–Kutta and general linear methods. Wiley, New York
Caramana EJ, Burton DE, Shashkov MJ, Whalen PP (1998) The construction of compatible hydrodynamics algorithms utilizing conservation of total energy. J Comput Phys 146:227–262
Caramana EJ, Rousculp CL, Burton DE (2000) A compatible, energy and symmetry preserving Lagrangian hydrodynamics algorithm in three-dimensional cartesian geometry. J Comput Phys 157:89–119
Carré G, Del Pino S, Després B, Labourasse E (2009) A cell-centered Lagrangian hydrodynamics scheme on general unstructured meshes in arbitrary dimension. J Comput Phys 228:5160–5183
Castro CC, Toro EF (2008) Solvers for the high-order Riemann problem for hyperbolic balance laws. J Comput Phys 227:2481–2513
Castro MJ, Gallardo JM, López JA, Parés C (2008) Well-balanced high order extensions of Godunov’s method for semilinear balance laws. SIAM J Numer Anal 46:1012–1039
Castro MJ, Gallardo JM, Parés C (2006) High-order finite volume schemes based on reconstruction of states for solving hyperbolic systems with nonconservative products. Applications to shallow-water systems. Math Comput 75:1103–1134
Castro MJ, LeFloch PG, Muñoz-Ruiz ML, Parés C (2008) Why many theories of shock waves are necessary: convergence error in formally path-consistent schemes. J Comput Phys 227:8107–8129
Casulli V (1990) Semi-implicit finite difference methods for the two-dimensional shallow water equations. J Comput Phys 86:56–74
Casulli V, Cheng RT (1992) Semi-implicit finite difference methods for three-dimensional shallow water flow. Int J Numer Methods Fluids 15:629–648
Cesenek J, Feistauer M, Horacek J, Kucera V, Prokopova J (2013) Simulation of compressible viscous flow in time-dependent domains. Appl Math Comput 219:7139–7150
Cheng J, Shu CW (2007) A high order ENO conservative Lagrangian type scheme for the compressible Euler equations. J Comput Phys 227:1567–1596
Cheng J, Shu CW (2010) A cell-centered Lagrangian scheme with the preservation of symmetry and conservation properties for compressible fluid flows in two-dimensional cylindrical geometry. J Comput Phys 229:7191–7206
Cheng J, Shu CW (2012) Improvement on spherical symmetry in two-dimensional cylindrical coordinates for a class of control volume Lagrangian schemes. Commun Comput Phys 11:1144–1168
Cheng J, Toro EF (2013) A 1D conservative Lagrangian ADER scheme. Chin J Comput Phys 30:501–508
Clain S, Diot S, Loubère R (2011) A high-order finite volume method for systems of conservation laws—Multi-dimensional Optimal Order Detection (MOOD). J Comput Phys 230:4028–4050
Claisse A, Després B, Labourasse E, Ledoux F (2012) A new exceptional points method with application to cell-centered Lagrangian schemes and curved meshes. J Comput Phys 231:4324–4354
Cockburn B, Karniadakis GE, Shu CW (2000) Discontinuous Galerkin methods. In: Lecture notes in computational science and engineering. Springer, Berlin
Colella P (1985) A direct Eulerian muscl scheme for gas dynamics. SIAM J Sci Stat Comput 6:104–117
Dal Maso G, LeFloch PG, Murat F (1995) Definition and weak stability of nonconservative products. J Math Pures Appl 74:483–548
Dedner A, Kemm F, Kröner D, Munz C-D, Schnitzer T, Wesenberg M (2002) Hyperbolic divergence cleaning for the MHD equations. J Comput Phys 175:645–673
Deledicque V, Papalexandris MV (2007) An exact Riemann solver for compressible two-phase flow models containing non-conservative products. J Comput Phys 222:217–245
Després B, Mazeran C (2003) Symmetrization of Lagrangian gas dynamic in dimension two and multimdimensional solvers. C R Mec 331:475–480
Després B, Mazeran C (2005) Lagrangian gas dynamics in two-dimensions and Lagrangian systems. Arch Ration Mech Anal 178:327–372
Diot S, Clain S, Loubère R (2012) Improved detection criteria for the Multi-dimensional Optimal Order Detection (MOOD) on unstructured meshes with very high-order polynomials. Comput Fluids 64:43–63
Diot S, Loubère R, Clain S (2013) The MOOD method in the three-dimensional case: very high-order finite volume method for hyperbolic systems. Int J Numer Methods Fluids 73:362–392
Dobrev VA, Ellis TE, Kolev Tz V, Rieben RN (2011) Curvilinear finite elements for Lagrangian hydrodynamics. Int J Numer Methods Fluids 65:1295–1310
Dobrev VA, Ellis TE, Kolev TzV, Rieben RN (2012) High order curvilinear finite elements for Lagrangian hydrodynamics. SIAM J Sci Comput 34:606–641
Dobrev VA, Ellis TE, Kolev Tz V, Rieben RN (2013) High order curvilinear finite elements for axisymmetric Lagrangian hydrodynamics. Comput Fluids 83:58–69
Dumbser M, Balsara DS, Abgrall R (2014) Multidimensional HLLC Riemann solver for unstructured meshes—with application to Euler and MHD flows. J Comput Phys 261:172–208
Dubcova L, Feistauer M, Horacek J, Svacek P (2009) Numerical simulation of interaction between turbulent flow and a vibrating airfoil. Comput Vis Sci 12:207–225
Dubiner M (1991) Spectral methods on triangles and other domains. J Sci Comput 6:345–390
Dukovicz JK, Meltz B (1992) Vorticity errors in multidimensional Lagrangian codes. J Comput Phys 99:115–134
Dumbser M (2014) Arbitrary-Lagrangian–Eulerian ADER-WENO finite volume schemes with time-accurate local time stepping for hyperbolic conservation laws. Comput Methods Appl Mech Eng 280:57–83
Dumbser M, Balsara D, Toro EF, Munz CD (2008) A unified framework for the construction of one-step finite-volume and discontinuous Galerkin schemes. J Comput Phys 227:8209–8253
Dumbser M, Balsara DS, Toro EF, Munz C-D (2008) A unified framework for the construction of one-step finite volume and discontinuous Galerkin schemes on unstructured meshes. J Comput Phys 227:8209–8253
Dumbser M, Boscheri W (2013) High-order unstructured Lagrangian one-step WENO finite volume schemes for non-conservative hyperbolic systems: applications to compressible multi-phase flows. Comput Fluids 86:405–432
Dumbser M, Castro M, Parés C, Toro EF (2009) ADER schemes on unstructured meshes for non-conservative hyperbolic systems: applications to geophysical flows. Comput Fluids 38:1731–1748
Dumbser M, Enaux C, Toro EF (2008) Finite volume schemes of very high order of accuracy for stiff hyperbolic balance laws. J Comput Phys 227:3971–4001
Dumbser M, Hidalgo A, Castro M, Parés C, Toro EF (2010) FORCE schemes on unstructured meshes II: non-conservative hyperbolic systems. Comput Methods Appl Mech Eng 199:625–647
Dumbser M, Kaeser M, Titarev VA, Toro EF (2007) Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems. J Comput Phys 226:204–243
Dumbser M, Käser M (2007) Arbitrary high order non-oscillatory finite volume schemes on unstructured meshes for linear hyperbolic systems. J Comput Phys 221:693–723
Dumbser M, Käser M, Titarev VA, Toro EF (2007) Quadrature-free non-oscillatory finite volume schemes on unstructured meshes for nonlinear hyperbolic systems. J Comput Phys 226:204–243
Dumbser M, Munz CD (2006) Building blocks for arbitrary high order discontinuous Galerkin schemes. J Sci Comput 27:215–230
Dumbser M, Toro EF (2011) On universal Osher-type schemes for general nonlinear hyperbolic conservation laws. Commun Comput Phys 10:635–671
Dumbser M, Toro EF (2011) A simple extension of the Osher Riemann solver to non-conservative hyperbolic systems. J Sci Comput 48:70–88
Dumbser M, Uuriintsetseg A, Zanotti O (2013) On Arbitrary-Lagrangian–Eulerian one-step WENO schemes for stiff hyperbolic balance laws. Commun Comput Phys 14:301–327
Dumbser M, Zanotti O (2009) Very high order PNPM schemes on unstructured meshes for the resistive relativistic MHD equations. J Comput Phys 228:6991–7006
Einfeldt B (1988) On Godunov-type methods for gas dynamics. SIAM J Numer Anal 25:294–318
Einfeldt B, Munz CD, Roe PL, Sjögreen B (1991) On Godunov-type methods near low densities. J Comput Phys 92:273–295
Feistauer M, Horacek J, Ruzicka M, Svacek P (2011) Numerical analysis of flow-induced nonlinear vibrations of an airfoil with three degrees of freedom. Comput Fluids 49:110–127
Feistauer M, Kucera V, Prokopova J, Horacek J (2010) The ALE discontinuous Galerkin method for the simulation of air flow through pulsating human vocal folds. AIP Conf Proc 1281:83–86
Ferrari A (2010) SPH simulation of free surface flow over a sharp-crested weir. Adv Water Resour 33:270–276
Ferrari A, Dumbser M, Toro EF, Armanini A (2008) A new stable version of the SPH method in Lagrangian coordinates. Commun Comput Phys 4:378–404
Ferrari A, Dumbser M, Toro EF, Armanini A (2009) A new 3D parallel SPH scheme for free surface flows. Comput Fluids 38:1203–1217
Ferrari A, Fraccarollo L, Dumbser M, Toro EF, Armanini A (2010) Three-dimensional flow evolution after a dambreak. J Fluid Mech 663:456–477
Francois MM, Shashkov MJ, Masser TO, Dendy ED (2013) A comparative study of multimaterial Lagrangian and Eulerian methods with pressure relaxation. Comput Fluids 83:126–136
Friedrich O (1998) Weighted essentially non-oscillatory schemes for the interpolation of mean values on unstructured grids. J Comput Phys 144:194–212
Galera S, Maire PH, Breil J (2010) A two-dimensional unstructured cell-centered multi-material ALE scheme using VOF interface reconstruction. J Comput Phys 229:5755–5787
Godunov SK (1959) Finite difference methods for the computation of discontinuous solutions of the equations of fluid dynamics. Math USSR 47:271–306
Godunov SK (1959) Finite difference methods for the computation of discontinuous solutions of the equations of fluid dynamics. Math USSR Sb 47:271–306
Harten A, Engquist B, Osher S, Chakravarthy S (1987) Uniformly high order essentially non-oscillatory schemes, III. J Comput Phys 71:231–303
Harten A, Lax PD, van Leer B (1983) On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev 25:289–315
Healy RW, Russel TF (1998) Solution of the advection–dispersion equation in two dimensions by a finite-volume Eulerian–Lagrangian localized adjoint method. Adv Water Resour 21:11–26
Hidalgo A, Dumbser M (2011) ADER schemes for nonlinear systems of stiff advection–diffusion–reaction equations. J Sci Comput 48:173–189
Hirt C, Amsden A, Cook J (1974) An arbitrary Lagrangian–Eulerian computing method for all flow speeds. J Comput Phys 14:227–253
Hu C, Shu CW (1999) Weighted essentially non-oscillatory schemes on triangular meshes. J Comput Phys 150:97–127
Huang CS, Arbogast T, Qiu J (2012) An Eulerian–Lagrangian WENO finite volume scheme for advection problems. J Comput Phys 231:4028–4052
Jiang GS, Shu CW (1996) Efficient implementation of weighted ENO schemes. J Comput Phys 126:202–228
Kamm JR, Timmes FX (2007) On efficient generation of numerically robust sedov solutions. Technical Report LA-UR-07-2849, LANL
Kapila AK, Menikoff R, Bdzil JB, Son SF, Stewart DS (2001) Two-phase modelling of DDT in granular materials: reduced equations. Phys Fluids 13:3002–3024
Karniadakis GE, Sherwin SJ (1999) Spectral/hp element methods in CFD. Oxford University Press, Oxford
Käser M, Iske A (2005) ADER schemes on adaptive triangular meshes for scalar conservation laws. J Comput Phys 205:486–508
Kidder RE (1976) Laser-driven compression of hollow shells: power requirements and stability limitations. Nucl Fusion 1:3–14
Knupp PM (2000) Achieving finite element mesh quality via optimization of the jacobian matrix norm and associated quantities. part ii - a framework for volume mesh optimization and the condition number of the Jacobian matrix. Int J Numer Methods Eng 48:1165–1185
Kucharik M, Breil J, Galera S, Maire PH, Berndt M, Shashkov MJ (2011) Hybrid remap for multi-material ALE. Comput Fluids 46:293–297
Kucharik M, Shashkov MJ (2012) One-step hybrid remapping algorithm for multi-material arbitrary Lagrangian–Eulerian methods. J Comput Phys 231:2851–2864
Kurganov A, Tadmor E (2002) Solution of two-dimensional Riemann problems for gas dynamics without Riemann problem solvers. Numer Methods Partial Differ Equ 18:584–608
Lax PD, Wendroff B (1960) Systems of conservation laws. Commun Pure Appl Math 13:217–237
Le Floch P, Raviart PA (1988) An asymptotic expansion for the solution of the generalized Riemann problem. Part I: general theory. Annales de l’institut Henri Poincaré (C) Analyse non linéaire 5:179–207
Le Métayer O, Massoni J, Saurel R (2005) Modelling evaporation fronts with reactive Riemann solvers. J Comput Phys 205:567–610
Lentine M, Grétarsson JT, Fedkiw R (2011) An unconditionally stable fully conservative semi-Lagrangian method. J Comput Phys 230:2857–2879
Li Z, Yu X, Jia Z (2014) The cell-centered discontinuous Galerkin method for Lagrangian compressible Euler equations in two dimensions. Comput Fluids 96:152–164
Liska R, Shashkov MJ, Váchal P, Wendroff B (2011) Synchronized flux corrected remapping for ALE methods. Comput Fluids 46:312–317
Liu W, Cheng J, Shu CW (2009) High order conservative Lagrangian schemes with Lax–Wendroff type time discretization for the compressible Euler equations. J Comput Phys 228:8872–8891
López Ortega A, Scovazzi G (2011) A geometrically-conservative, synchronized, flux-corrected remap for arbitrary Lagrangian–Eulerian computations with nodal finite elements. J Comput Phys 230:6709–6741
Loubère R, Dumbser M, Diot S (2014) A new family of high order unstructured MOOD and ADER finite volume schemes for multidimensional systems of hyperbolic conservation laws. Commun Comput Phys 16:718–763
Loubère R, Maire PH, Váchal P (2010) A second-order compatible staggered Lagrangian hydrodynamics scheme using a cell-centered multidimensional approximate Riemann solver. Proc Comput Sci 1:1931–1939
Loubère R, Maire PH, Váchal P (2013) 3D staggered Lagrangian hydrodynamics scheme with cell-centered Riemann solver-based artificial viscosity. Int J Numer Methods Fluids 72:22–42
Maire PH (2009) A high-order cell-centered Lagrangian scheme for two-dimensional compressible fluid flows on unstructured meshes. J Comput Phys 228:2391–2425
Maire PH (2011) A high-order one-step sub-cell force-based discretization for cell-centered Lagrangian hydrodynamics on polygonal grids. Comput Fluids 46(1):341–347
Maire PH (2011) A unified sub-cell force-based discretization for cell-centered Lagrangian hydrodynamics on polygonal grids. Int J Numer Methods Fluids 65:1281–1294
Maire PH, Abgrall R, Breil J, Ovadia J (2007) A cell-centered Lagrangian scheme for two-dimensional compressible flow problems. SIAM J Sci Comput 29:1781–1824
Maire PH, Breil J (2007) A second-order cell-centered Lagrangian scheme for two-dimensional compressible flow problems. Int J Numer Methods Fluids 56:1417–1423
Maire PH, Nkonga B (2009) Multi-scale Godunov-type method for cell-centered discrete Lagrangian hydrodynamics. J Comput Phys 228:799–821
Millington RC, Toro EF, Nejad LAM (1999) Arbitrary high order methods for conservation laws I: the one dimensional scalar case. PhD thesis, Manchester Metropolitan University, Department of Computing and Mathematics
Monaghan JJ (1994) Simulating free surface flows with SPH. J Comput Phys 110:399–406
Muñoz ML, Parés C (2007) Godunov method for nonconservative hyperbolic systems. Math Model Numer Anal 41:169–185
Munz CD (1994) On Godunov-type schemes for Lagrangian gas dynamics. SIAM J Numer Anal 31:17–42
Murrone A, Guillard H (2005) A five equation reduced model for compressible two phase flow problems. J Comput Phys 202:664–698
Noh WF (1987) Errors for calculations of strong shocks using artificial viscosity and an artificial heat flux. J Comput Phys 72:78–120
Olliver-Gooch C, Van Altena M (2002) A high-order-accurate unstructured mesh finite-volume scheme for the advection–diffusion equation. J Comput Phys 181:729–752
Osher S, Solomon F (1982) Upwind difference schemes for hyperbolic conservation laws. Math Comput 38:339–374
Osher S, Solomon F (1982) Upwind difference schemes for hyperbolic systems of conservation laws. Math Comput 38:339–374
Parés C (2006) Numerical methods for nonconservative hyperbolic systems: a theoretical framework. SIAM J Numer Anal 44:300–321
Parés C, Castro MJ (2004) On the well-balance property of Roe’s method for nonconservative hyperbolic systems. applications to shallow-water systems. Math Model Numer Anal 38:821–852
Peery JS, Carroll DE (2000) Multi-material ALE methods in unstructured grids. Comput Methods Appl Mech Eng 187:591–619
Peshkov I, Romenski E (2016) A hyperbolic model for viscous Newtonian flows. Contin Mech Thermodyn 28:85–104
Petitpas F, Massoni J, Saurel R, Lapebie E, Munier L (2009) Diffuse interface model for high speed cavitating underwater systems. Int J Multiph Flow 35:747–759
Qiu JM, Shu CW (2011) Conservative high order semi-Lagrangian finite difference WENO methods for advection in incompressible flow. J Comput Phys 230:863–889
Rhebergen S, Bokhove O, van der Vegt JJW (2008) Discontinuous Galerkin finite element methods for hyperbolic nonconservative partial differential equations. J Comput Phys 227:1887–1922
Riemslagh K, Vierendeels J, Dick E (2000) An arbitrary Lagrangian–Eulerian finite-volume method for the simulation of rotary displacement pump flow. Appl Numer Math 32:419–433
Roe PL (1981) Approximate Riemann solvers, parameter vectors, and difference schemes. J Comput Phys 43:357–372
Rusanov VV (1961) Calculation of interaction of non-steady shock waves with obstacles. J Comput Math Phys USSR 1:267–305
Sambasivan SK, Shashkov MJ, Burton DE (2013) A finite volume cell-centered Lagrangian hydrodynamics approach for solids in general unstructured grids. Int J Numer Methods Fluids 72:770–810
Sambasivan SK, Shashkov MJ, Burton DE (2013) Exploration of new limiter schemes for stress tensors in Lagrangian and ALE hydrocodes. Comput Fluids 83:98–114
Saurel R, Abgrall R (1999) A multiphase Godunov method for compressible multifluid and multiphase flows. J Comput Phys 150:425–467
Saurel R, Gavrilyuk S, Renaud F (2003) A multiphase model with internal degrees of freedom: application to shock–bubble interaction. J Fluid Mech 495:283–321
Saurel R, Larini M, Loraud JC (1994) Exact and approximate Riemann solvers for real gases. J Comput Phys 112:126–137
Saurel R, Le Métayer O, Massoni J (2005) Modelling evaporation fronts with reactive Riemann solvers. J Comput Phys 205:567–610
Saurel R, Massoni J, Renaud F (2007) A numerical method for one-dimensional compressible multiphase flows on moving meshes. Int J Numer Methods Fluids 54:1425–1450
Saurel R, Petitpas F, Abgrall R (2008) Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J Fluid Mech 607:313–350
Saurel R, Petitpas F, Berry RA (2009) Simple and efficient relaxation methods for interfaces separating compressible fluids, cavitating flows and shocks in multiphase mixtures. J Comput Phys 228:1678–1712
Schwartzkopff T, Dumbser M, Munz CD (2003) Fast high order ADER schemes for linear hyperbolic equations and their numerical dissipation and dispersion. Technical Report 2003/35, Preprint series of SFB404, Stuttgart University
Schwartzkopff T, Munz CD, Toro EF (2002) ADER: a high order approach for linear hyperbolic systems in 2D. J Sci Comput 17(1–4):231–240
Schwendeman DW, Wahle CW, Kapila AK (2006) The Riemann problem and a high-resolution Godunov method for a model of compressible two-phase flow. J Comput Phys 212:490–526
Scovazzi G (2012) Lagrangian shock hydrodynamics on tetrahedral meshes: a stable and accurate variational multiscale approach. J Comput Phys 231:8029–8069
Shi J, Hu C, Shu CW (2002) A technique of treating negative weights in WENO schemes. J Comput Phys 175:108–127
Smith RW (1999) AUSM(ALE): a geometrically conservative arbitrary Lagrangian–Eulerian flux splitting scheme. J Comput Phys 150:268–286
Sonar T (1997) On the construction of essentially non-oscillatory finite volume approximations to hyperbolic conservation laws on general triangulations: polynomial recovery, accuracy and stencil selection. Comput Methods Appl Mech Eng 140:157–181
Stroud AH (1971) Approximate calculation of multiple integrals. Prentice-Hall Inc., Englewood Cliffs
Tian B, Toro EF, Castro CE (2011) A path-conservative method for a five-equation model of two-phase flow with an HLLC-type Riemann solver. Comput Fluids 46:122–132
Titarev VA, Toro EF (2002) ADER: arbitrary high order Godunov approach. J Sci Comput 17(1–4):609–618
Titarev VA, Toro EF (2003) ADER schemes for three-dimensional nonlinear hyperbolic systems. Isaac Newton Institute for Mathematical Sciences, Cambridge (Preprint series)
Titarev VA, Toro EF (2005) ADER schemes for three-dimensional nonlinear hyperbolic systems. J Comput Phys 204:715–736
Titarev VA, Tsoutsanis P, Drikakis D (2010) WENO schemes for mixed-element unstructured meshes. Commun Comput Phys 8:585–609
Tokareva SA, Toro EF (2010) HLLC-type Riemann solver for the Baer–Nunziato equations of compressible two-phase flow. J Comput Phys 229:3573–3604
Toro EF, Titarev VA (2006) Derivative Riemann solvers for systems of conservation laws and ADER methods. J Comput Phys 212(1):150–165
Toro EF (2002) Anomalies of conservative methods: analysis, numerical evidence and possible cures. Int J Comput Fluid Dyn 11:128–143
Toro EF (2009) Riemann solvers and numerical methods for fluid dynamics: a practical introduction. Springer, Berlin
Toro EF, Hidalgo A, Dumbser M (2009) FORCE schemes on unstructured meshes I: conservative hyperbolic systems. J Comput Phys 228:3368–3389
Toro EF, Spruce M, Speares W (1994) Restoration of contact surface in the HLL Riemann solver. Shock Waves 4:25–34
Toro EF, Titarev VA (2002) Solution of the generalized Riemann problem for advection–reaction equations. Proc R Soc Lond Ser A 458(2018):271–281
Toro EF, Titarev VA (2003) ADER schemes for scalar hyperbolic conservation laws in three space dimensions. Isaac Newton Institute for Mathematical Sciences, Cambridge (Preprint series)
Toumi I (1992) A weak formulation of Roe’s approximate Riemann solver. J Comput Phys 102:360–373
Tsoutsanis P, Titarev VA, Drikakis D (2011) WENO schemes on arbitrary mixed-element unstructured meshes in three space dimensions. J Comput Phys 230:1585–1601
van Leer B (1979) Towards the ultimate conservative difference scheme V. A. second order sequel to Godunov’s method. J Comput Phys 32:101–136
Vilar F (2012) Cell-centered discontinuous Galerkin discretization for two-dimensional Lagrangian hydrodynamics. Comput Fluids 64:64–73
Vilar F, Maire PH, Abgrall R (2014) A discontinuous Galerkin discretization for solving the two-dimensional gas dynamics equations written under total Lagrangian formulation on general unstructured grids. INRIA Research Report N 8483. Available at http://hal.inria.fr/docs/00/95/07/82/PDF/RR-8483.pdf
Vilar F, Maire PH, Abgrall R (2010) Cell-centered discontinuous Galerkin discretizations for two-dimensional scalar conservation laws on unstructured grids and for one-dimensional Lagrangian hydrodynamics. Comput Fluids 46(1):498–604
von Neumann J, Richtmyer RD (1950) A method for the calculation of hydrodynamics shocks. J Appl Phys 21:232–237
Yanilkin YV, Goncharov EA, Kolobyanin VY, Sadchikov VV, Kamm JR, Shashkov MJ, Rider WJ (2013) Multi-material pressure relaxation methods for Lagrangian hydrodynamics. Comput Fluids 83:137–143
Zein A, Hantke M, Warnecke G (2010) Modeling phase transition for compressible two-phase flows applied to metastable liquids. J Comput Phys 229:2964–2998
Zhang T, Zheng Y (1990) Conjecture on the structure of solutions of the Riemann problem for two-dimensional gas dynamics systems. SIAM J Math Anal 21:593–630
Zhang YT, Shu CW (2009) Third order WENO scheme on three dimensional tetrahedral meshes. Commun Comput Phys 5:836–848
Acknowledgments
The work discussed in this paper has been developed and carried out under the supervision of Prof. Michael Dumbser, who is warmly thanked by the author. The author would like to acknowledge PRACE for awarding access to the SuperMUC supercomputer based in Munich, Germany at the Leibniz Rechenzentrum (LRZ).
Funding
This study was funded by the European Research Council (ERC) under the European Union’s Seventh Framework Programme (FP7/2007-2013) with the research project STiMulUs, ERC Grant Agreement No. 278267
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors declare that they have no conflict of interest.
Rights and permissions
About this article
Cite this article
Boscheri, W. High Order Direct Arbitrary-Lagrangian–Eulerian (ALE) Finite Volume Schemes for Hyperbolic Systems on Unstructured Meshes. Arch Computat Methods Eng 24, 751–801 (2017). https://doi.org/10.1007/s11831-016-9188-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-016-9188-x