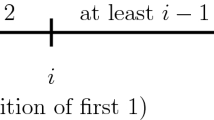The Depth of Compositions

Abstract

In this paper we consider compositions of n as bargraphs. The depth of a cell inside this graphical representation is the minimum number of horizontal and/or vertical unit steps that are needed to exit to the outside. The depth of the composition is the maximum depth over all cells of the composition. We use finite automata to study the generating function for the number of compositions having a depth of at least r.

1 Introduction

A composition $\sigma =\sigma _1\cdots \sigma _m$ of $n\in \mathbb {N}$ is an ordered collection of one or more positive integers whose sum is $|\sigma |=\sigma _1+\cdots +\sigma _m=n$. For instance, the compositions of 3 are 3, 21, 12 and 111. The number of summands, namely m, is called the number of parts of the composition and n is called the weight of $\sigma$. It is well known that the number of compositions of n is given by $2^{n-1}$ and the number of compositions of n with m parts is given by $\left( {\begin{array}{c}n-1\\ m-1\end{array}}\right)$. Compositions have been studied extensively in recent years (for example, see [4]).

Compositions can be represented as bargraphs where the lower edge lies on a horizontal axis (for instance, see [6, 10, 11]). They are drawn on a regular planar lattice grid and are made up of square cells. So a composition is uniquely defined by the size of each part. The size of the composition is the total number of cells in the representing bargraph. We will study the depth of compositions, which are presented as bargraphs. Let $\sigma$ be any composition and let c be any cell of $\sigma$. The depth of the cell c, denoted by depth(c), is the minimum number of horizontal or vertical steps to exit $\sigma$ starting from c. The depth of $\sigma$ is defined as $depth(\sigma )=\max _c depth(c)$, where the maximum is over all cells c of $\sigma$. For example, the cell that is indicated by x in Fig. 1 of the composition $\sigma =34543$, needs three steps to exit $\sigma$. Moreover, $depth(\sigma )=3$ since all other cells require fewer than three steps to exit. An alternative conception of the depth of a composition is given by the size of its Durfee square, see [2].

Fig. 1

The composition 34,543

Equivalently, the depth of a composition can be understood as the number of times the inner site-perimeter can be recursively removed or “peeled” from the composition until nothing remains, as shown below. The inner site-perimeter is defined as all cells in the composition whose depth is one, see [3, 7]. Each successive inner site-perimeter is coloured in Fig. 2.

Fig. 2

The 3 consecutive “peelings” of the inner site-perimeter of the composition 34543

The aim of this paper is to study the generating function for the number of compositions having a depth of at least r. To achieve our goals, we use finite automata technique (for such technique in enumerative combinatorics, for instance, we refer the reader to [1, 5, 8, 9, 12]).

2 Main results

We say that the composition $\sigma =\sigma _1\sigma _2\cdots \sigma _s$ contains the composition $\tau =\tau _1\tau _2\cdots \tau _m$ if there exist j such that $0\le j\le s-m$ and $\sigma _{j+i}\ge \tau _i$ for all $i=1,2,\ldots ,m$. For instance, the composition 4534 contains 234 but does not contain 144. For all $r\ge 2$, define

$$\begin{aligned} \tau ^{(r)}:=r(r+1)\cdots (2r-2)(2r-1)(2r-2)\cdots (r+1)r. \end{aligned}$$

In Fig. 1, the illustration is for $r=3$.

From the definitions, we can state the following fact.

Proposition 1

A composition $\sigma$ satisfies $depth(\sigma )\ge r$ if and only if it contains $\tau ^{(r)}$.

In order to enumerate the compositions that avoid (i.e., do not contain) $\tau ^{(r)}$, we need the following notation and definitions. A prefix of a composition $\sigma$ is a sub-composition $\sigma '$ (possible empty) such that there exists a nonempty sub-composition $\sigma ''$ with $\sigma =\sigma '\sigma ''$. Let $\mathcal {V}_r$ be the set of all prefixes of $\tau ^{(r)}$. For example, $\mathcal {V}_3=\{\epsilon , 3,34,345,3454\}$ when $\tau ^{(3)}=34543$ and $\epsilon$ is the empty composition.

For given $\sigma =\sigma _1\sigma _2\cdots \sigma _{m}$ and $k\in \mathbb {N}$, we define the reduction $red(\sigma k)$ of $\sigma k$ to be $\sigma '=\sigma '_1\sigma '_2\cdots \sigma '_{m'}$ if $\sigma '\in \mathcal {V}_r$, $m'$ is maximal and $\sigma _{m+1-m'+j}\ge \sigma '_j$ for all $j=1,2,\ldots ,m'$, where $\sigma _{m+1}=k$. Otherwise, we say the reduction of $\sigma k$ is not defined. For instance, if $r=3$ then $red(245)=34$ and $red(613445)=345$.

Now let us define a directed graph (finite automata, for example, see [1, 5]) $G_r$ on the vertices $\mathcal {V}_r$ with edges between $\sigma =\sigma _1\sigma _2\cdots \sigma _m\in \mathcal {V}_r$ and $red(\sigma k)$ with weight $x^{|\sigma k|-|red(\sigma k)|}$, where $red(\sigma k)$ is defined. For simplicity, if there are two edges between $\sigma$ and $\sigma '$ with weights $w,w'$ then we just write as one edge with weight $w+w'$.

Example 1

Let $r=2$ ($\tau ^{(2)}=232$). The graph $G_r$ has three vertices $\epsilon ,2,23$. Note that

• $red(\epsilon k)=\epsilon$ for $k=1$ and $red(\epsilon k)=2$ for all $k\ge 2$. Thus, there is an edge between $\epsilon$ and $\epsilon$ with weight x and there is an edge between $\epsilon$ and 2 with weight $x^2+x^3+\cdots =\frac{x^2}{1-x}$. This corresponds to the generating function for adding a part k of size 2 or more.

• $red(21)=\epsilon$, $red(22)=2$ and $red(2k)=23$ for all $k\ge 3$. So there is an edge between 2 and $\epsilon$ with weight x, there is an edge between 2 and 2 with weight $x^2$, and there is an edge between 2 and 23 with weight $x^3/(1-x)$.

• $red(231)=\epsilon$ and for $k>1$red(23k) is not defined. So there is an edge between 23 and $\epsilon$ with weight x.

Summarizing this information, we obtain the graph $G_2$ as presented in Fig. 3.

Fig. 3

The graph $G_2$

Example 2

Let $r=3$ ($\tau ^{(2)}=34543$). The graph $G_r$ on its five vertices $\epsilon ,3,34,345,3454$ is presented in Fig. 4.

Fig. 4

The graph $G_3$

To state our next observation, we define a weight of a path in the graph $G_r$ to be the product of the weights of all the edges. For example, the weight of the path $\epsilon ,3,3,34,345,\epsilon ,3$ is

$$\begin{aligned} \frac{x^3}{1-x}\cdot x^3\cdot \frac{x^4}{1-x}\cdot \frac{x^5}{1-x}\cdot (x+x^2)\cdot \frac{x^3}{1-x}= \frac{x^{19}(1+x)}{(1-x)^4}. \end{aligned}$$

Proposition 2

Set $r\ge 2$. Then the generating function for the number of compositions of n with exactly m parts that avoid $\tau ^{(r)}$ is given by the total weight of all paths of length m starting from $\epsilon$ in $G_r$.

Proof

Let $\sigma =\sigma _1\sigma _2\cdots \sigma _m$ be any composition that avoids $\tau ^{(r)}$ with exactly m parts. From the definition of red, we find that the path corresponding to $\sigma$ in $G_r$ is given by

$$\begin{aligned} \epsilon {\,}_{\overrightarrow{\sigma _1}}\sigma ^{(1)}{\,}_{\overrightarrow{\sigma _2}}\sigma ^{(2)} \cdots {\,}_{\overrightarrow{\sigma _m}}\sigma ^{(m)}, \end{aligned}$$

where $\sigma ^{(j)}=red(\sigma ^{(j-1)}\sigma _j)$ with $\sigma ^{(0)}=\epsilon$. On the other hand, for each $\sigma ^{(j)}$, $j=0,1,\ldots ,m$, we can use the graph $G_r$ and the above path to define unique elements $\sigma _j$, $j=1,2,\ldots ,m$ such that $\sigma ^{(j)}=red(\sigma ^{(j-1)}\sigma _j)$. Thus if $\sigma$ follows from a path (as described above), then $\sigma$ is a composition that avoids $\tau ^{(r)}$ with m parts. Thus, for each composition that avoids $\tau ^{(r)}$ there exists a unique path in $G_r$ with weight $x^{|\sigma |}$. $\square$

Let $\mathbf{A}_r$ be the adjacency matrix of the directed graph $G_r$. By Proposition 2, we have that the generating function for the number of compositions with exactly m parts that avoid $\tau ^{(r)}$ is given by $w^T\mathbf{A}_r^mv$, where $w=(1,0,0,\ldots ,0)^T$ and $v=(1,1,\ldots ,1)^T$ are vectors with $|\mathcal {V}_r|=2r-1$ coordinates. Thus, the generating function for the number of compositions that avoid $\tau ^{(r)}$ is given by, see [4]

$$\begin{aligned} \sum _{m\ge 0}w^T\mathbf{A}_r^mv=w^T(I-\mathbf{A}_r)^{-1}v. \end{aligned}$$

Hence, we obtain our main result,

Theorem 1

Let $r\ge 2$, the generating function for the number of compositions of n that avoid $\tau ^{(r)}$ is given by $w^T(I-\mathbf{A}_r)^{-1}v$, where I is the unit matrix and $w= (1,0,\ldots ,0)^T$ and $v = (1,1,\ldots ,1)^T$ are vectors of $2r-1$ coordinates. Moreover, this generating function is a rational function in x.

Example 3

From Examples 1 and 2, we obtain

$$\begin{aligned} \mathbf{A}_2=\left( \begin{array}{lll} x&{}\quad \frac{x^2}{1-x}&{}\quad 0\\ x&{}\quad x^2&{}\quad \frac{x^3}{1-x}\\ x&{}\quad 0&{}\quad 0\end{array}\right) \quad \text{ and } \quad \mathbf{A}_3=\left( \begin{array}{lllll} x+x^2&{}\quad \frac{x^3}{1-x}&{}\quad 0&{}\quad 0&{}\quad 0\\ x+x^2&{}\quad x^3&{}\quad \frac{x^4}{1-x}&{}\quad 0&{}\quad 0\\ x+x^2&{}\quad x^3&{}\quad x^4&{}\quad \frac{x^5}{1-x}&{}\quad 0\\ x+x^2&{}\quad x^3&{}\quad 0&{}\quad 0&{}\quad \frac{x^4}{1-x}\\ x+x^2&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0\end{array}\right) . \end{aligned}$$

Hence, the generating function for the number of compositions of n that avoid $\tau ^{(2)}=232$ is given by

$$\begin{aligned} \frac{(1-x)^2+x^3(1-x)+x^5}{(1-2x)(1-x)+x^3(1-2x)+x^5-x^6}, \end{aligned}$$

and the generating function for the number of compositions of n that avoid $\tau ^{(3)}=34{,}543$ is given by

$$\begin{aligned} \frac{(1-x)^4+x^5(1-x)^3+x^9(1-x)^2+x^{13}-x^{14}+x^{16}}{(1-2x)(1-x)^3+x^5(1-2x)(1-x)^2+x^9(1-2x)(1-x)+x^{13}(1-2x)+x^{16}-x^{17}-x^{18}}. \end{aligned}$$

Actually, from the definition of the graph $G_r$, we can state an explicit formula for the matrix $\mathbf{A}_r$.

Proposition 3

Let $r\ge 2$ and $\mathbf{A}_r=(a_{ij})_{1\le i,j\le 2r-1}$. Then

$$\begin{aligned} a_{ij}=\left\{ \begin{array}{ll} \sum \nolimits _{k=1}^{r-1}x^k,&{}\quad j=1,\\ \frac{x^{r-1+i}}{1-x},&{}\quad j=i+1,i=1,2,\ldots ,r,\\ \frac{x^{3r-1-i}}{1-x},&{}\quad j=i+1,i=r+1,r+2,\ldots ,2r-2,\\ x^{r-2+j},&{}\quad 2\le j\le r,j\le i\le 2r-j,\\ 0,&{}\quad \text{ otherwise. } \end{array}\right. \end{aligned}$$

Define $f_s=x+x^2+\cdots +x^s$ and define $\delta _X$ to be 1 if X holds and 0 otherwise. Let $\mathbf{L}_r=(\ell _{ij})_{1\le i,j\le 2r-1}$ be a lower triangular matrix and $\mathbf{U}_r=(u_{ij})_{1\le i,j\le 2r-1}$ be a upper triangular matrix such that $\ell _{11}=\cdots =\ell _{(2r-1)(2r-1)}=1$, $u_{11}=1-f_{r-1}$, $u_{ij}=0$ for all $j\ge i+2$, and

$$\begin{aligned} \ell _{ij}&=-\frac{f_{r-1}}{1-f_{r-1}}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r\\ 2\end{array}}\right) }}{(1-x)^{j-1}\prod _{s=2}^{j}u_{ss}} -\sum _{k=0}^{j-2}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-2-k\\ 2\end{array}}\right) }\delta _{i\le 2r-j+k}}{(1-x)^k\prod _{s=j-k}^{j}u_{ss}},\nonumber \\ {}&\quad \text{ for } j+1\le i\le 2r-1,\,2\le j\le r+1,\end{aligned}$$

(2.1)

$$\begin{aligned} \ell _{ij}&=\frac{x^{\left( {\begin{array}{c}2r-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}3r-j\\ 2\end{array}}\right) }}{(1-x)^{j-r-1}\prod _{k=r+2}^ju_{kk}}\ell _{i(r+1)}, \quad \text{ for } j+1\le i\le 2r-1,\,r+2\le j\le 2r-2,\end{aligned}$$

(2.2)

$$\begin{aligned} u_{i(i+1)}&=\left\{ \begin{array}{ll} -\frac{x^{r-1+i}}{1-x},&{}\quad i=1,2,\ldots ,r,\\ -\frac{x^{3r-1-i}}{1-x},&{}\quad i=r+1,r+2,\ldots ,2r-2. \end{array}\right. \end{aligned}$$

(2.3)

$$\begin{aligned} u_{ii}&=\left\{ \begin{array}{ll} 1-x^{r-2+i}+\ell _{i(i-1)}\frac{x^{r-2+i}}{1-x},&{}\quad i=2,3,\ldots ,r,\\ 1+\ell _{i(i-1)}\frac{x^{3r-i}}{1-x},&{}\quad i=r+1,\ldots ,2r-1. \end{array}\right. \end{aligned}$$

(2.4)

For instance,

$$\begin{aligned} \mathbf{L}_2= \left( \begin{array}{ccc} 1&{}\quad 0&{}\quad 0\\ -\frac{x}{1-x}&{}\quad 1&{}\quad 0\\ {-\frac{x}{1-x}}&{}\quad {\frac{{x}^{3}}{{x}^{4}-{ x}^{3}+2\,x-1}}&{}\quad 1\end{array} \right) \end{aligned}$$

and

$$\begin{aligned} \mathbf{U}_2= \left( \begin{array}{ccc} 1-x&{}\quad {-\frac{{x}^{2}}{1-x}}&{}\quad 0\\ 0&{}\quad {\frac{-{x}^{4}+{x}^{3}-2\,x+1}{ \left( 1-x \right) ^{2}}}&{}\quad {-\frac{{x}^{3}}{1-x}}\\ 0&{}\quad 0&{}\quad \frac{-{x}^{6}+{x}^{5}-2\,{x}^{4}+{x}^{3}+2\,{x}^{2}-3\,x+1}{ \left( -{ x}^{4}+{x}^{3}-2\,x+1 \right) \left( 1-x \right) } \end{array} \right) . \end{aligned}$$

Theorem 2

For all $r\ge 2$, $I-\mathbf{A}_r=\mathbf{L}_r\mathbf{U}_r$, where I is the unit matrix.

Proof

Define $b_{ij}=\sum _{k=1}^{2r-1}\ell _{ik}u_{kj}$. By Proposition 3, we have to show that $b_{ij}=\delta _{i=j}-a_{ij}$. Clearly, by (2.1)–(2.4), we have $b_{11}=\ell _{11}u_{11}=1-f_{r-1}=1-a_{11}$, $b_{12}=\ell _{11}u_{12}=-a_{12}$, and $b_{1j}=\ell _{11}u_{1j}=0=a_{1j}$ for all $j=3,4,\ldots ,2r-1$. Moreover, $b_{i1}=\ell _{i1}u_{11}=-f_{r-1}=-a_{i1}$, for all $i=2,3,\ldots ,2r-1$.

Now let us show that $b_{ii}=1-a_{ii}$: note that $b_{ii}=u_{ii}+\ell _{i(i-1)}u_{(i-1)i}$, so by (2.1)–(2.4), we have $b_{ii}=1-a_{ii}$, as required.

Now we show that $b_{ij}=-a_{ij}$ for all $2\le i<j\le 2r-1$: note that $b_{ij}=\ell _{i(j-1)}u_{(j-1)j}+\ell _{ij}u_{jj}$, so by (2.1)–(2.4), we have $b_{i(i+1)}=u_{i(i+1)}=-a_{i(i+1)}$ and $b_{ij}=0=-a_{ij}$ for all $j\ge i+2$.

Thus, it remains to show that $b_{ij}=-a_{ij}$ for all $2\le j<i\le 2r-1$. We show only the cases $2\le j\le r$ and $j+1\le i\le 2r-1$ since the other cases are similar. By (2.1)–(2.4) and $b_{ij}=\ell _{i(j-1)}u_{(j-1)j}+\ell _{ij}u_{jj}$, we see that

$$\begin{aligned} b_{ij}&=\left( \frac{f_{r-1}}{1-f_{r-1}}\frac{x^{\left( {\begin{array}{c}r+j-2\\ 2\end{array}}\right) -\left( {\begin{array}{c}r\\ 2\end{array}}\right) }}{(1-x)^{j-2}\prod _{s=2}^{j-1}u_{ss}} +\sum _{k=0}^{j-3}\frac{x^{\left( {\begin{array}{c}r+j-2\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-3-k\\ 2\end{array}}\right) }\delta _{i\le 2r-j+k+1}}{(1-x)^k\prod _{s=j-1-k}^{j-1}u_{ss}}\right) \frac{x^{r+j-2}}{1-x}\\&\quad -\,\left( \frac{f_{r-1}}{1-f_{r-1}}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) +\left( {\begin{array}{c}r\\ 2\end{array}}\right) }}{(1-x)^{j-1}\prod _{s=2}^{j}u_{ss}} +\sum _{k=0}^{j-2}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-2-k\\ 2\end{array}}\right) }\delta _{i\le 2r-j+k}}{(1-x)^k\prod _{s=j-k}^{j}u_{ss}}\right) u_{jj}\\&=\frac{f_{r-1}}{1-f_{r-1}}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r\\ 2\end{array}}\right) }}{(1-x)^{j-1}\prod _{s=2}^{j-1}u_{ss}} +\sum _{k=1}^{j-2}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-2-k\\ 2\end{array}}\right) }\delta _{i\le 2r-j+k}}{(1-x)^k\prod _{s=j-k}^{j-1}u_{ss}}\\&\quad -\,\frac{f_{r-1}}{1-f_{r-1}}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) +\left( {\begin{array}{c}r\\ 2\end{array}}\right) }}{(1-x)^{j-1}\prod _{s=2}^{j-1}u_{ss}} -\sum _{k=0}^{j-2}\frac{x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-2-k\\ 2\end{array}}\right) }\delta _{i\le 2r-j+k}}{(1-x)^k\prod _{s=j-k}^{j-1}u_{ss}}\\&=-x^{\left( {\begin{array}{c}r+j-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+j-2\\ 2\end{array}}\right) }=-x^{r+j-2}=-a_{ij}, \end{aligned}$$

as required. $\square$

Moreover, by using similar techniques (but more complicated) as in the Proof of Theorem 2, we can state the following explicit formulas for $u_{ss}$ and $\ell _{s(s-1)}$.

Proposition 4

Let $r\ge 2$. Then $u_{jj}=\frac{\alpha _{j+1}}{(1-x)\alpha _j}$ for all $j=1,2,\ldots ,2r-1$, where

$$\begin{aligned} \alpha _i&=x^{\left( {\begin{array}{c}r+i-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+1\\ 2\end{array}}\right) }(1-f_{r-1})\\&\quad +\,\sum _{k=0}^{i-3}x^{\left( {\begin{array}{c}r+i-1\\ 2\end{array}}\right) -\left( {\begin{array}{c}r+i-1-k\\ 2\end{array}}\right) }(1-2x)(1-x)^{i-3-k},\quad 2\le i\le r+1,\\ \alpha _{r+i}&=(1-2x)(1-x)^{r+i-3}+\sum _{k=1}^ix^{2r(2k-1)-k^2-k+1}(1-2x)(1-x)^{r+i-2k-2}\\&\quad +\,\sum _{k=1}^{i-1}x^{4rk-k^2-2k}(1-2x)(1-x)^{r+i-2k-3}\\&\quad +\,\sum _{k=1}^{r-i-2}x^{2r(2i-1+k)-i(i+1+k)-k(k+1)/2-1} (1-2x)(1-x)^{r-2-i-k}\\&\quad +\,x^{r(3r+4i-7)/2+1-i(i+1)/2}(1-f_{r-1}),\quad r+2\le i\le 2r. \end{aligned}$$

Moreover,

$$\begin{aligned} \ell _{i(i-1)}&=\left( \frac{\alpha _{i+1}}{(1-x)\alpha _i}-1+x^{r-2+i}\right) \frac{1-x}{x^{r-2+i}},\quad 2\le i\le r,\\ \ell _{i(i-1)}&=\left( \frac{\alpha _{i+1}}{(1-x)\alpha _i}-1\right) \frac{1-x}{x^{3r-i}},\quad r+1\le i\le 2r-1. \end{aligned}$$

Theorem 3

Set $r\ge 2$. Let $x=(x_1,\ldots ,x_{2r-1})^T$ and $w=(1,1,\ldots ,1)^T$ be two vectors with $2r-1$ coordinates. The solution of the system of equation $(I-\mathbf{A}_r)x=w$ is given by

$$\begin{aligned} x_i=(1-x)\sum _{k=i}^{2r-1}\frac{y_k\alpha _i}{\alpha _{k+1}} \prod _{s=i}^{k-1}\left( x^{r-1+s}\delta _{s\le r}+x^{3r-1-s}\delta _{s\ge r+1}\right) , \end{aligned}$$

where $y_i=1-\sum _{j=1}^{i-1}\ell _{ij}y_j$ for all $i=1,2,\ldots ,2r-1$.

Proof

By Theorem 2, we have that $I-\mathbf{A}_r=\mathbf{L}_r\mathbf{U}_r$. Let $\mathbf{L}_ry=w$ and $\mathbf{U}_rx=y$. Then, for all $i=1,2,\ldots ,2r-1$, we have $y_i=1-\sum _{j=1}^{i-1}\ell _{ij}y_j$ and $x_i=\frac{y_i}{u_{ii}}-\frac{u_{i(i+1)}}{u_{ii}}x_{i+1}$ with $z_{2r}=0$. Thus, by induction on i, we see that

$$\begin{aligned} x_i=\sum _{k=i}^{2r-1}(-1)^{k-i}y_k\frac{\prod _{s=i}^{k-1}u_{s(s+1)}}{\prod _{s=i}^ku_{ss}}, \end{aligned}$$

which, by Proposition 4 and (2.3), completes the proof. $\square$

By Theorems 1–3 and the fact that $(1-x)\alpha _1=1$, we obtain the following result.

Theorem 4

The generating function for the number of compositions of n that avoid $\tau ^{(r)}$ is given by

$$\begin{aligned} \sum _{k=1}^{2r-1}\frac{y_k}{\alpha _{k+1}} \prod _{s=1}^{k-1}\left( x^{r-1+s}\delta _{s\le r}+x^{3r-1-s}\delta _{s\ge r+1}\right) , \end{aligned}$$

where $y_i=1-\sum _{j=1}^{i-1}\ell _{ij}y_j$ for all $i=1,2,\ldots ,2r-1$ and $\ell _{ij}$ and $u_{ij}$ are given by (2.1)–(2.4).

Theorem 4 has already been illustrated for $r=2$ and 3 in Example 3. Here we illustrate Theorem 4 for $r=4$ and 5.

Example 4

The generating function for the number of compositions that avoid $\tau ^{(4)}=4{,}567{,}654$ is $\frac{s(x)}{t(x)}$ where

$$\begin{aligned} s(x)&=1-6x+15x^2-20x^3+15x^4-6x^5+x^6+x^7-5x^8+10x^9-10x^{10}\\&\quad +\,5x^{11}-x^{12}+x^{13}-4x^{14}+6x^{15}-4x^{16}+x^{17}+x^{19}-3x^{20}+3x^{21}\\&\quad -\,x^{22}+x^{24}-2x^{25}+x^{26}+x^{29}-x^{30}+x^{33}, \end{aligned}$$

and

$$\begin{aligned} t(x)&=1-7x+20x^2-30x^3+25x^4-11x^5+2x^6+x^7-6x^8+14x^9-16x^{10}\\&\quad +\,9x^{11}-2x^{12}+x^{13}-5x^{14}+9x^{15}-7x^{16}+2x^{17}+x^{19}-4x^{20}+5x^{21}\\&\quad -\,2x^{22}+x^{24}-3x^{25}+2x^{26}+x^{29}-2x^{30}+x^{33}-x^{34}-x^{35}-x^{36}, \end{aligned}$$

Thus as a series expansion, the generating function for the number of compositions of depth $r\ge 4$ is

$$\begin{aligned} \frac{1-x}{1-2x}-\frac{s(x)}{t(x)}=x^{37}+9x^{38}+47x^{39}+187x^{40}+\cdots \,. \end{aligned}$$

For example the nine compositions of 38 that contain 4,567,654 are: 14,567,654, 5,567,654, 4,667,654, 4,577,654, 4,567,754, 4,568,654, 4,567,664, 4,567,655 and 45,676,541. Similarly:

Example 5

For $r=5$, the generating function for the number of compositions that avoid $\tau ^{(5)}=5{,}678{,}765$ is $\frac{u(x)}{v(x)}$ where

$$\begin{aligned} u(x)&=1-8x+28x^2-56x^3+70x^4-56x^5+28x^6-8x^7+x^8+x^9-7x^{10}+21x^{11}\\&\quad -\,35x^{12}+35x^{13}-21x^{14}+7x^{15}-x^{16}+x^{17}-6x^{18}+15x^{19}-20x^{20}+15x^{21}\\&\quad -\,6x^{22}+x^{23}+x^{25}-5x^{26}+10x^{27}-10x^{28}+5x^{29}-x^{30}+x^{32}-4x^{33}+6x^{34}\\&\quad -\,4x^{35}+x^{36}+x^{39}-3x^{40}+3x^{41}-x^{42}+x^{45}-2x^{46}+x^{47}+x^{51}-x^{52}+x^{56}, \end{aligned}$$

and

$$\begin{aligned} v(x)&=1-9x+35x^2-77x^3+105x^4-91x^5+49x^6-15x^7+2x^8+x^9-8x^{10}+27x^{11}\\&\quad -\,50x^{12}+55x^{13}-36x^{14}+13x^{15}-2x^{16}+x^{17}-7x^{18}+20x^{19}-30x^{20}+25x^{21}\\&\quad -\,11x^{22}+2x^{23}+x^{25}-6x^{26}+14x^{27}-16x^{28}+9x^{29}-2x^{30}+x^{32}-5x^{33}+9x^{34}\\&\quad -\,7x^{35}+2x^{36}+x^{39}-4x^{40}+5x^{41}-2x^{42}+x^{45}-3x^{46}+2x^{47}+x^{51}-2x^{52}+x^{56}\\&\quad -\,x^{57}-x^{58}-x^{59}-x^{60}. \end{aligned}$$

As before the series expansion for generating function for the number of compositions of depth $r\ge 5$ is

$$\begin{aligned} \frac{1-x}{1-2x}-\frac{u(x)}{v(x)}=x^{61}+11x^{62}+68x^{63}+312x^{64}+1186x^{65}+\cdots \,. \end{aligned}$$