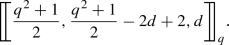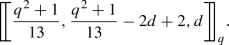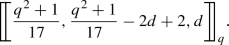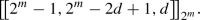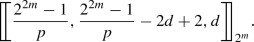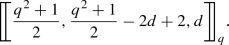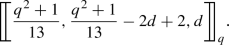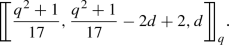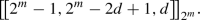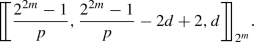A Different Construction for Some Classes of Quantum MDS Codes

Abstract

Constructing quantum codes with large minimum distance plays a significant role in quantum computation and communication. Quantum maximum-distance separable (MDS) codes have important place among quantum codes since they are optimal with regard to the maximality of their minimum distances. In this paper, by making use of constacyclic codes over $F_{q^2}$ and Hermitian construction for quantum codes, we give different constructions for some classes of quantum MDS codes.

1 Introduction

Quantum codes have been intensively studied by researchers to detect and correct the errors occurring in quantum channels during quantum information transfer since the discovery of the first quantum code, introduced by Shor in [22], showing the possibility of dealing with the decoherence destroying the information of qubits having a superposition. A q-ary quantum code of length n is a subspace of $q^n$-dimensional Hilbert space $H = \underbrace{{C^q} \otimes {C^q} \otimes \cdots \otimes {C^q}}_{n\,\,times}$ where $C^q$ is the q-dimensional complex vector space and the bar $\otimes$ denotes the tensor product. The notation denotes a quantum code having the parameters length n, dimension $q^k$ and minimum distance d, where the parameter d indicates the error detecting and correcting capability, i.e., a quantum code with minimum distance d can detect up to $d-1$ errors and correct up to $\left\lfloor {\frac{{d - 1}}{2}} \right\rfloor$ errors. One of the main problems in quantum error-correction is to construct quantum codes having large minimum distance. At the same time, it is also important for a quantum code to have large dimension. However, the following bound, which is called the quantum Singleton bound, gives a restriction on the dimension and minimum distance for a fixed length.

Proposition 1

(Quantum Singleton bound) [1, 15] For an quantum code, $k \le n-2d+2$.

An quantum code is called quantum maximum-distance separable (MDS) code if it meets the quantum Singleton bound. Recently, the constructions of quantum MDS codes have had much attention [3,4,5,6,7,8,9,10,11,12,13,14, 17,18,19,20,21, 23, 25,26,27]. In [17], La Guardia constructed a family of quantum MDS codes with parameters where $q = {2^t}$, $t \ge 1$ and $3 \le d \le q + 1$. In [3], Chen et al. constructed four classes of quantum MDS codes for odd prime power q.

Moreover, they tabulated the parameters of quantum MDS codes which had been derived by that time. In [23], Wang et al. derived two classes of quantum MDS codes for odd prime power q; for $2 \le d \le \frac{{q - 1+2\lambda }}{2}$ and $q + 1 = \lambda r$, r even, and for $2 \le d \le \frac{{q - 1 + \lambda }}{2}$ and $q + 1 = \lambda r$, r odd, . More recently, in [21], Qian et al. developed two families of quantum MDS codes, , $q = {2^t}$, where $2 \le d \le \frac{{q - 1}}{3}$ if $3|q + 2$ and $2 \le d \le \frac{{2q - 1}}{3}$ if $3|q + 1$; and , $q = 10m + 7$ where $3 \le d \le 4m + 1$. They also improved the construction given by Chen et al. in [3]. In this paper, by using the same construction and ideas as the construction in [12] and [14], we construct the following families of quantum MDS codes in different ways.

• 1. For $3 \le d(odd) \le q$,

  

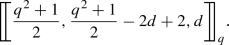  (1)

• 2. For $2 \le d\left( {even} \right) \le 5m + 2$ if $q=13m+5$ and $2 \le d\left( {even} \right) \le 5m + 3$ if $q=13m+8$,

  

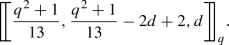  (2)

• 3. For $2 \le d\left( {even} \right) \le 5m + 1$ if $q=17m+4$ and $2 \le d\left( {even} \right) \le 5m + 4$ if $q=17m+1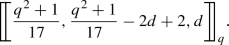3$,

  

  (3)

• 4. Let $m \ge 2$. If $2^m+1$ is a prime, then for $2 \le d \le {2^{m - 1}}$,

  

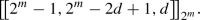  (4)

• 5. Let $m \ge 2$. If $2^m+1$ is not a prime, then for each prime p dividing $2^m+1$ and $2 \le d \le \frac{{2^m - 1}}{2} + \frac{{2^m + 1}}{{2p}}$,

  

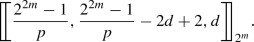  (5)

The parameters given in (1) were also obtained by Kai et al. in [13]. The parameters in (2) and (3) were further derived by Jin et al. in [10]. The family of quantum MDS codes in (4) were also gotten by Grassl et al. in [5]. The parameters of quantum MDS codes obtained in (5) were further by He et al. in [7].

The organization of this paper is as follows: In Sect. 2, we present the fundamental concepts which are needed in the rest of the paper. In Sect. 3, we construct some families of quantum codes from constacyclic codes over $F_{q^2}$. In Sect. 4, by summarizing our findings, we conclude this paper.

2 Preliminaries

In this section, we give some basic notions and results regarding constacyclic codes and quantum codes. Let $F_{q^2}$ be a finite field of $q^2$ elements where q is a prime power and let $F_{q^2}^n$ be n-dimensional vector space of n-tuples on $F_{q^2}$. A subspace of the vector space $F_{q^2}^n$ is a linear code of length n over $F_{q^2}$. The Hamming distance $d\left( {x,y} \right)$ between two vectors $x = \left( {{x_1}, \ldots ,{x_n}} \right)$ and $y = \left( {{y_1}, \ldots ,{y_n}} \right)$ is the number of their distinct components. The elements of a linear code are called codewords. The smallest Hamming distance of distinct elements in a linear code is the minimum distance of that linear code, denoted by d. A linear code of length n and minimum distance d over $F_{q^2}$ is denoted by ${\left[ {n,k,d} \right] _{q^2}}$, where k is the dimension of the linear code over $F_{q^2}$ and n, k and d are called the parameters of the linear code.

One of the most important linear code families is constacyclic codes. Denote $F_{{q^2}}^ \times$ as the multiplicative group of $F_{q^2}$ and let $\alpha \in F_{{q^2}}^ \times$. A linear code of length n over $F_{q^2}$ is an $\alpha$-constacyclic code of length n over $F_{q^2}$ if $\left( {\alpha {c_{n - 1}},{c_0}, \ldots ,{c_{n - 2}}} \right)$ is a codeword whenever $\left( {{c_0},{c_1}, \ldots ,{c_{n - 1}}} \right)$ is also a codeword. It is well-known fact that an $\alpha$-constacyclic code of length n over $F_{q^2}$ can be viewed as an ideal in the quotient ring $\frac{{{F_{{q^2}}}\left[ x \right] }}{{\left\langle {{x^n} - \alpha } \right\rangle }}$ since there is a one-to-one correspondence between $\alpha$-constacyclic codes of length n over $F_{q^2}$ and the ideals of $\frac{{{F_{{q^2}}}\left[ x \right] }}{{\left\langle {{x^n} - \alpha } \right\rangle }}$. This enables us to describe an $\alpha$-constacyclic code of length n over $F_{q^2}$ by a monic divisor $g\left( x \right)$ of ${{x^n} - \alpha }$, i.e., an $\alpha$-constacyclic code of length n over $F_{q^2}$ is an ideal generated by $g\left( x \right)$ in $\frac{{{F_{{q^2}}}\left[ x \right] }}{{\left\langle {{x^n} - \alpha } \right\rangle }}$, where $g\left( x \right)$ is called the generator polynomial. Let r be the multiplicative order of $\alpha$ in $F_{{q^2}}^ \times$. If $\left( {n,q} \right) = 1$, then there exists an $rn^{th}$ root $\beta$ of unity over $F_{q^2}$ such that $\beta ^n=\alpha$ and so all roots of ${{x^n} - \alpha }$ over $F_{q^2}$ are $\beta$, $\beta ^{1+r}$, ..., $\beta ^{1+r(n-1)}$. Set ${O_{r,n}} = \left\{ {1 + rj,\,\,0 \le j \le n - 1} \right\}$. Let $\left( {n,q} \right) = 1$. Since ${{x^n} - \alpha }$ divides ${{x^{rn}} - 1 }$, the $q^2$-cyclotomic coset modulo rn containing $1 + rj$ is given as ${C_{1 + rj}} = \left\{ {\left( {1 + rj} \right) {q^{2i}}\bmod \left( {rn} \right) ,\,i \in N} \right\}$. Then, the union of some $q^2$-cyclotomic cosets gives the set $O_{r,n}$. The defining set of an $\alpha$-constacyclic code generated by $g\left( x \right)$ is a subset Z of $O_{r,n}$ satisfying $g\left( x \right) = \prod \nolimits _{j \in Z} {\left( {x - {\beta ^j}} \right) }$. Note that the dimension of an $\alpha$-constacyclic code of length n over $F_{q^2}$ with the defining set Z is $n-\left| Z \right|$. The following bound is a useful tool to determine the minimum distance of some classes of constacyclic codes, which has been proven in [2] and [16].

Theorem 1

(BCH bound for constacyclic codes) [2, 16] Let $\left( {n,q} \right) = 1$. Let $\beta$ be an rnth root of unity with $\beta ^n=\alpha$ where $\alpha \in F_{{q^2}}^ \times$ and r is the multiplicative order of $\alpha$ in $F_{{q^2}}^ \times$. Then, the minimum distance of an $\alpha$-constacyclic code of length n over $F_{{q^2}}$ with the defining set including the set $\left\{ {1 + rj,\,l \le j \le l + d - 2} \right\}$ is at least d.

The following bound is a well-known upper bound for the dimension of linear codes, which is called the Singleton bound.

Proposition 2

(Singleton bound) If there exists a linear code with the parameters ${\left[ {n,k,d} \right] _{q^2}}$, then k is at most $n-d+1$.

A linear code with the parameters ${\left[ {n,k,d} \right] _{q^2}}$ satisfying the Singleton bound, i.e. $k=n-d+1$, is called maximum-distance separable (MDS) code. By Theorem 1, an $\alpha$-constacyclic code of length n over $F_{{q^2}}$ with the defining set $Z = \left\{ {1 + rj,\,l \le j \le l + d - 2} \right\}$ has minimum distance at least d. Hence, since such an $\alpha$-constacyclic code has the dimension $n-d+1$, by Proposition 2, this $\alpha$-constacyclic code is an MDS code having the parameters ${\left[ {n,n - d + 1,d} \right] _{{q^2}}}$.

The Hermitian inner product ${\left\langle {x,y} \right\rangle _h}$ of the vectors $x = \left( {{x_0}, \ldots ,{x_{n-1}}} \right)$ and $y = \left( {{y_0}, \ldots ,{y_{n-1}}} \right)$ in $F_{q^2}^n$ is ${\left\langle {x,y} \right\rangle _h}: = \sum \nolimits _{i = 0}^{n - 1} {{x_i}y_i^q}$. Given a linear code C over $F_{q^2}$, the Hermitian dual ${C^{{ \bot _h}}}$ of C is the set ${C^{{ \bot _h}}} = \left\{ {y \in F_{{q^2}}^n:{{\left\langle {x,y} \right\rangle }_h} = 0,\,\forall x \in C} \right\}$. The following lemma characterizes the Hermitian dual of an $\alpha$-constacyclic code of length n over $F_{{q^2}}$.

Lemma 1

[24] The Hermitian dual of an $\alpha$-constacyclic code of length n over $F_{{q^2}}$ with the generator polynomial $g\left( x \right)$ is an ${\alpha ^{ - q}}$-constacyclic code of length n over $F_{{q^2}}$ with the generator polynomial ${g^{{ \bot _h}}}\left( x \right) = \sum \nolimits _{i = 0}^k {h_i^qh_0^{ - q}{x^{k - i}}}$.

Lemma 1 implies that ${C^{{ \bot _h}}}$ is an ${\alpha ^{ - q}}$-constacyclic code over $F_{{q^2}}$ with the defining set $- q\left( {O_{r,n}-Z} \right)$ if C is an $\alpha$-constacyclic code over $F_{{q^2}}$ with the defining set Z.

It is given in [3] that if an $\alpha$-constacyclic code over $F_{{q^2}}$ contains its Hermitian dual, then $\left. r \right| q + 1$. A necessary and sufficient condition for an $\alpha$-constacyclic code to contain its Hermitian dual is given in [14] as:

Lemma 2

[14] Let $\alpha \in F_{{q^2}}^ \times$. Then, an $\alpha$-constacyclic code with the defining set Z contains its Hermitian dual if and only if $Z \cap - qZ = \emptyset$.

One of the considerable applications of linear codes over finite fields is to be used to construct quantum codes in an efficient way. The following method is mostly used to construct quantum codes from linear codes over $F_{q^2}$ containing their Hermitian dual.

Theorem 2

[1, 15] If there exists an ${\left[ {n,k,d} \right] _{{q^2}}}$ linear code C such that ${C^{{ \bot _h}}} \subseteq C$, then there exists an quantum code.

Note that if a linear code over $F_{q^2}$ containing its Hermitian dual is MDS according to Proposition 2, then the quantum code obtained from this linear code by using Theorem 2 is also MDS with respect to Proposition 1.

3 Some Classes of Quantum MDS Codes

We devote this section for deriving some families of quantum MDS codes from constacyclic codes over $F_{q^2}$. We focus on how the defining sets of an $\alpha$-constacyclic code of certain length should be so that it contains its Hermitian dual. The trick is as follows: These defining sets consist of consecutive terms as mentioned in Theorem 1 and so these constacyclic codes become MDS. Hence, we give the parameters of quantum MDS codes obtained from these constacyclic codes via Theorem 2. We begin with the length $n = \frac{{{q^2} + 1}}{p}$.

3.1 Quantum MDS Codes of Length $n=\frac{{{q^2} + 1}}{p}$

Let q be an odd prime power with $\left. p \right| {q^2} + 1$, where p is an arbitrary prime and let $r=q+1$. Then, $\alpha$ is a primitive ${\left( {q + 1} \right) ^{st}}$ root of unity over $F_{q^2}$. Let $n = \frac{{{q^2} + 1}}{p}$. It is easy to see that the multiplicative order of $q^2$ modulo rn is at most 2. Note that $q^2+1=2t$, $2\not |t$ for any odd prime power q. Hence we divide this subsection into two cases: $p=2$ and $p>2$.

3.1.1 The Case $p=2$

Let $p=2$, that is, $n=\frac{{{q^2} + 1}}{2}$. Then, n is odd and the multiplicative order of $q^2$ modulo rn is 2 since $q^2 < rn$. We characterize all $q^2$-cyclotomic cosets modulo rn in the following lemma.

Lemma 3

All $q^2$-cyclotomic cosets modulo rn containing $1+rj$ are as follows:

• 1. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) j,\,1 + \left( {q + 1} \right) \left( {q - 1 - j} \right) } \right\}$ for $0 \le j < \frac{{q - 1}}{2}$.

• 2. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) \frac{{q - 1}}{2}} \right\}$ for $j = \frac{{q - 1}}{2}$.

• 3. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) j,\,1 + \left( {q + 1} \right) \left( {n + q - 1 - j} \right) } \right\}$ for $q - 1 < j \le \frac{{q - 1}}{2} + \frac{{n - 1}}{2}$.

Proof

Let $0 \le j < \frac{{q - 1}}{2}$. Since $\left( {q + 1} \right) {q^2} \equiv - \left( {q + 1} \right) \bmod rn$, we have that ${q^2}\left( {1 + \left( {q + 1} \right) j} \right) \equiv q^2-\left( {q + 1} \right) j \equiv 1 + \left( {q + 1} \right) \left( {q - 1 - j} \right) \bmod rn$.

Let $j = \frac{{q - 1}}{2}$. Then, $q^2\left( 1 + \left( {q + 1} \right) j \right) ={q^2}\frac{{{q^2} + 1}}{2} = \frac{{{q^2} + 1}}{2}\left( {{q^2} - 1} \right) + \frac{{{q^2} + 1}}{2} \equiv \frac{{{q^2} + 1}}{2}\bmod rn$.

Let $q - 1 < j \le \frac{{q - 1}}{2} + \frac{{n - 1}}{2}$. Then, $q-1-j < 0$ and so ${q^2}\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) \left( {n + q - 1 - j} \right) \bmod rn$.

It is easy to see that the union of the cyclotomic cosets presented here gives the set $O_{r,n}$ and so proof is completed. $\square$

Set $t = \frac{{q - 1}}{2} + \frac{{n - 1}}{2}$ and $\delta = \frac{{q - 1}}{2} - 1$. Define the subset Z of $O_{r,n}$ to be $Z = \bigcup \nolimits _{j = t - \delta }^t {{C_{1 + \left( {q + 1} \right) j}}}$. Since ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) j,\,1 + \left( {q + 1} \right) \left( {n + q - 1 - j} \right) } \right\}$ for $t - \delta \le j \le t$, by Lemma 3, we have $Z = \bigcup \nolimits _{j = t - \delta }^{t + \delta + 1} {\left\{ {1 + \left( {q + 1} \right) j} \right\} }$, that is, Z comprises exactly $q-1$ consecutive terms. We need the following to derive a class of MDS $\alpha$-constacyclic codes and quantum MDS codes of length $n=\frac{{{q^2} + 1}}{2}$.

Lemma 4

$Z \cap - qZ = \emptyset$.

Proof

Suppose $Z \cap - qZ \ne \emptyset$. Then, there exists some $t - \delta \le j,k \le t + \delta + 1$ such that $- q\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) k\bmod rn$. This implies $1 + k + qj \equiv 0\bmod n$. Since $t - \delta = \frac{{n + 1}}{2}$ and $t + \delta + 1 = \frac{{n + 1}}{2} + q - 2$, it follows from $t - \delta \le j,k \le t + \delta + 1$ that $\frac{{q + 1}}{2}\left( {n + 1} \right) + 1 \le 1 + k + qj \le \frac{{q + 1}}{2}\left( {n + 1} \right) + \left( {q + 1} \right) \left( {q - 2} \right) + 1$. Since $\frac{q+1}{2}+\left( {q + 1} \right) \left( {q - 2} \right) +1 < 2n$ and $1 + k + qj \equiv 0\bmod n$, we get $1 + k + qj = \frac{{q + 3}}{2}n$. Since $1 + k\not \equiv \frac{{n + 1}}{2}\bmod q$ for all $t - \delta \le k \le t + \delta + 1$, there is no solution of the equation $1 + k + qj = \left( {q + 1} \right) \frac{{n + 1}}{2} + lq$ for any integer l and $t - \delta \le j,k \le t + \delta + 1$. Since $\frac{{q + 3}}{2}n = \left( {q + 1} \right) \frac{{n + 1}}{2} + \frac{{q - 1}}{2}q$, i.e. $l = \frac{{q - 1}}{2}$, we get $1 + k + qj \ne \frac{{q + 3}}{2}n$ for all $t - \delta \le j,k \le t + \delta + 1$. This is a contradiction. $\square$

Theorem 3

Suppose that q is an odd prime power. Then, there exists a family of MDS $\alpha$-constacyclic codes containing their Hermitian duals and having the parameters ${\left[ {\frac{{{q^2} + 1}}{2},\frac{{{q^2} + 1}}{2} - d + 1,d} \right] _{{q^2}}}$, where $3 \le d \le q$ and d is odd.

Proof

Define the set ${S_i} = \bigcup \nolimits _{j = t - i}^t {{C_{1 + \left( {q + 1} \right) j}}}$ for each $0 \le i \le \delta$. Then, $S_i$ is a subset of Z containing $2i+2$ consecutive terms and $\left| {{S_i}} \right| = 2i$. Let $C_i$ be an $\alpha$-constacyclic code having the defining set $S_i$. Theorem 1 and Proposition 2 imply that $C_i$ is an MDS code with the desired parameters. Since $S_i$ is a subset of Z, by Lemma 4$- qS_i \cap S_i = \emptyset$. Therefore, ${C_i^{{ \bot _h}}} \subseteq C_i$ by Lemma 2. $\square$

We now construct a family of quantum MDS codes with length $\frac{{{q^2} + 1}}{2}$ which was also proved by Kai et al. in [13].

Theorem 4

Suppose that q is an odd prime power. Then, there exists a family of quantum MDS codes with the parameters , where $3 \le d \le q$ and d is odd.

Proof

Using Theorem 2, one can derive the quantum codes with the desired parameters from MDS $\alpha$-constacyclic codes given in Theorem 3. By Proposition 1, these quantum codes are MDS. $\square$

3.1.2 The Case $p>2$

Let p be an odd prime dividing $q^2+1$. In this case, $n=\frac{{{q^2} + 1}}{p}$ is even since $q^2+1=2t$ and p is odd. We investigate the case $q^2 < rn$. It follows that $p < q$ and the multiplicative order of $q^2$ modulo rn is 2. The following lemma determines all $q^2$-cyclotomic cosets modulo rn.

Lemma 5

All $q^2$-cyclotomic cosets modulo rn containing $1+rj$ are as follows:

• 1. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) j,\,1 + \left( {q + 1} \right) \left( {q - 1 - j} \right) } \right\}$ for $0 \le j < \frac{{q - 1}}{2}$.

• 2. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) \frac{{q - 1}}{2}} \right\}$ for $j = \frac{{q - 1}}{2}$.

• 3. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) j,\,1 + \left( {q + 1} \right) \left( {n + q - 1 - j} \right) } \right\}$ for $q - 1< j < \frac{{q - 1}}{2} + \frac{{n}}{2}$.

• 4. ${C_{1 + \left( {q + 1} \right) j}} = \left\{ {1 + \left( {q + 1} \right) \left( {\frac{{q - 1}}{2} + \frac{{n - 1}}{2}} \right) } \right\}$ for $j = \frac{{q - 1}}{2} + \frac{{n}}{2}$.

Proof

It is enough to prove just (4) since the others are similar to Lemma 3. Let $j = \frac{{q - 1}}{2} + \frac{n}{2}$. It is seen by a simple computation that ${q^2}\left( {q + 1} \right) \frac{n}{2} \equiv \left( {q + 1} \right) \frac{n}{2}\bmod rn$ and ${q^2} + {q^2}\frac{{q^2 - 1}}{2} \equiv 1 + \frac{{{q^2} - 1}}{2}\bmod rn$. Hence, ${q^2}\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) j\bmod rn$. Since the union of the cyclotomic cosets presented here gives the set $O_{r,n}$, we complete the proof. $\square$

In addition to initial assumptions, let q be an odd prime power of the form $13m+5$ or $13m+8$ and let $p=13$, that is, $n = \frac{{{q^2} + 1}}{{13}}$. Then, clearly $m \ge 2$ and $q^2<rn$. Define the subset Z of the set $O_{r,n}$ to be ${Z} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - \frac{{5m}}{2}}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ if $q=13m+5$ and ${Z} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - \frac{{5m+1}}{2}}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ if $q=13m+8$. By Lemma 5, Z comprises exactly $5m+1$ consecutive terms if $q=13m+5$ and $5m+2$ consecutive terms if $q=13m+8$. We have the following for both cases.

Lemma 6

$Z \cap - qZ = \emptyset$.

Proof

Suppose that $q=13m+5$. If $Z \cap - qZ \ne \emptyset$, then there exits some $\frac{{q - 1}}{2} - \frac{{5m}}{2} = 4m + 2 \le j,k \le \frac{{q - 1}}{2} + \frac{{5m}}{2} = 9m + 2$ such that $- q\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) k\bmod rn$. This implies that $1 + k + qj \equiv 0\bmod n$. It follows from $\frac{{q - 1}}{2} - \frac{{5m}}{2} \le j,k \le \frac{{q - 1}}{2} + \frac{{5m}}{2}$ that $\frac{{{q^2} + 1}}{2} - \left( {q + 1} \right) \frac{{5m}}{2} \le 1 + qj + k \le \frac{{{q^2} + 1}}{2} + \left( {q + 1} \right) \frac{{5m}}{2}$. Since $q=13m+5$, we have $52{m^2} + 50m + 13 \le 1 + qj + k \le 117{m^2} + 80m + 13$ and $n = 13{m^2} + 10m + 2$. Since $4n< 52{m^2} + 50m + 13 < 5n$ and $8n< 117{m^2} + 80m + 13 < 9n$, possible values of $1 + qj + k$ are nz, where $5 \le z \le 8$. Since $4m+3 \le 1+k \le 9m+3 <13m+5=q$, the remainder when $1+k+qj$ is divided by q should be $1+k$. Observe that these remainders for 5n, 6n, 7n and 8n are $12m+5$, $4m+2$, $9m+4$ and $m+1$, respectively, none of which are in the interval $\left[ {4m + 3,9m + 3} \right]$. This is a contradiction.

Suppose now that $q=13m+8$. If $Z \cap - qZ \ne \emptyset$, then there exits some $\frac{{q - 1}}{2} - \frac{{5m+1}}{2} =4m + 3 \le j,k \le \frac{{q - 1}}{2} + \frac{{5m+1}}{2} =9m + 4$ such that $- q\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) k\bmod rn$. This implies that $1 + k + qj \equiv 0\bmod n$. Similar to above argument, we have that possible values of $1 + qj + k$ are nz, where $5 \le z \le 8$. Since $4m+4 \le 1+k \le 9m+5 <13m+5=q$, the remainder when $1+k+qj$ is divided by q should be $1+k$. Observe that these remainders for 5n, 6n, 7n and 8n are $m+1$, $9m+6$, $4m+3$ and $12m+8$, respectively, none of which are in the interval $\left[ {4m + 4,9m + 5} \right]$. This is a contradiction. $\square$

Theorem 5

Suppose that q is an odd prime power of the form $q=13m+5$ or $q=13m+8$. Then, there exists a family of MDS $\alpha$-constacyclic codes containing their Hermitian duals and having the parameters ${\left[ {\frac{{{q^2} + 1}}{13},\frac{{{q^2} + 1}}{13} - d + 1,d} \right] _{{q^2}}}$, where $2 \le d(even) \le 5m+2$ if $q=13m+5$ and $2 \le d(even) \le 5m+3$ if $q=13m+8$.

Proof

Suppose that $q=13m+5$ and define the set ${S_i} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - i}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ for each $0 \le i \le \frac{{5m}}{2}$. Then, $S_i$ is a subset of Z containing $2i+1$ consecutive terms and $\left| {{S_i}} \right| = 2i+1$. Let $C_i$ be an $\alpha$-constacyclic code having the defining set $S_i$. Then, $C_i$ is an MDS code with the desired parameters by Theorem 1 and Proposition 2. By Lemma 6$- qS_i \cap S_i = \emptyset$ since $S_i$ is a subset of Z and so ${C_i^{{ \bot _h}}} \subseteq C_i$ by Lemma 2. The case $q=13m+8$ is similar. $\square$

We now construct a family of quantum MDS codes with length $n = \frac{{{q^2} + 1}}{13}$ which was also derived by Jin et al. in [10].

Theorem 6

Suppose that q is an odd prime power of the form $q=13m+5$ or $q=13m+8$. Then, there exists a family of quantum MDS codes with the parameters , where $2 \le d(even) \le 5m+2$ if $q=13m+5$ and $2 \le d(even) \le 5m+3$ if $q=13m+8$.

Proof

The quantum codes with the desired parameters are obtained from MDS $\alpha$-constacyclic codes derived in Theorem 5 via Theorem 2 and also are MDS by Proposition 1. $\square$

In addition to initial assumptions, now let q be an odd prime power of the form $17m+4$ or $17m+13$ and let $p=17$, that is, $n = \frac{{{q^2} + 1}}{{17}}$. Then, clearly $m \ge 2$ and $q^2<rn$. Define the subset Z of the set $O_{r,n}$ to be ${Z} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - \frac{{5m-1}}{2}}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ if $q=17m+4$ and ${Z} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - \frac{{5m+2}}{2}}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ if $q=17m+13$. By Lemma 5, Z consists of exactly 5m consecutive terms if $q=17m+4$ and $5m+3$ consecutive terms if $q=17m+13$. We also have the following for both cases.

Lemma 7

$Z \cap - qZ = \emptyset$.

Proof

Suppose that $q=17m+4$ and $Z \cap - qZ \ne \emptyset$. Then, there exists some $\frac{{q - 1}}{2} - \frac{{5m-1}}{2} = 6m + 2 \le j,k \le \frac{{q - 1}}{2} + \frac{{5m-1}}{2} = 11m + 1$ such that $- q\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) k\bmod rn$. This implies that $1 + k + qj \equiv 0\bmod n$. It follows from $\frac{{q - 1}}{2} - \frac{{5m-1}}{2} \le j,k \le \frac{{q - 1}}{2} + \frac{{5m-1}}{2}$ that $\frac{{{q^2} + 1}}{2} - \left( {q + 1} \right) \frac{{5m-1}}{2} \le 1 + qj + k \le \frac{{{q^2} + 1}}{2} + \left( {q + 1} \right) \frac{{5m-1}}{2}$. Since $q=17m+4$, we have $102{m^2} + 64m + 11 \le 1 + qj + k \le 187{m^2} + 72m + 6$ and $n = 17{m^2} + 8m + 1$. Since $6n< 102{m^2} + 64m + 11 < 7n$ and $10n< 187{m^2} + 72m + 6 < 11n$, possible values of $1 + qj + k$ are nz, where $7 \le z \le 10$. Since $6m+3 \le 1+k \le 11m+2 <17m+4=q$, the remainder when $1+k+qj$ is divided by q should be $1+k$. Observe that these remainders for 7n, 8n, 9n and 10n are $11m+3$, $15m+4$, $2m+1$ and $6m+2$, respectively, none of which are in the interval $\left[ {6m + 3,11m + 2} \right]$. This is a contradiction.

Suppose now that $q=17m+13$ and $Z \cap - qZ \ne \emptyset$. Then, there exists some $\frac{{q - 1}}{2} - \frac{{5m+2}}{2} =6m + 5 \le j,k \le \frac{{q - 1}}{2} + \frac{{5m+2}}{2} =11m + 7$ such that $- q\left( {1 + \left( {q + 1} \right) j} \right) \equiv 1 + \left( {q + 1} \right) k\bmod rn$. This implies that $1 + k + qj \equiv 0\bmod n$. Similar to above argument, we have that possible values of $1 + qj + k$ are nz, where $7 \le z \le 10$. Since $6m+6 \le 1+k \le 11m+8 <17m+13=q$, the remainder when $1+k+qj$ is divided by q should be $1+k$. Observe that these remainders for 7n, 8n, 9n and 10n are $6m+5$, $2m+2$, $15m+12$ and $11m+9$, respectively, none of which are in the interval $\left[ {6m + 6,11m + 8} \right]$. This is a contradiction. $\square$

Theorem 7

Suppose that q is an odd prime power of the form $q=17m+4$ or $q=17m+13$. Then, there exists a family of MDS $\alpha$-constacyclic codes containing their Hermitian duals and having the parameters ${\left[ {\frac{{{q^2} + 1}}{17},\frac{{{q^2} + 1}}{17} - d + 1,d} \right] _{{q^2}}}$, where $2 \le d(even) \le 5m+1$ if $q=17m+4$ and $2 \le d(even) \le 5m+4$ if $q=17m+13$.

Proof

Suppose that $q=17m+4$ and define the set ${S_i} = \bigcup \nolimits _{j = \frac{{q - 1}}{2} - i}^{\frac{{q - 1}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$ for each $0 \le i \le \frac{{5m-1}}{2}$. Then, $S_i$ is a subset of Z containing $2i+1$ consecutive terms and $\left| {{S_i}} \right| = 2i+1$. Let $C_i$ be an $\alpha$-constacyclic code having the defining set $S_i$. Then, $C_i$ is an MDS code with the desired parameters by Theorem 1 and Proposition 2. By Lemma 7$- qS_i \cap S_i = \emptyset$ since $S_i$ is a subset of Z and so ${C_i^{{ \bot _h}}} \subseteq C_i$ by Lemma 2. The case $q=17m+13$ is similar. $\square$

We now construct a class of quantum MDS codes with length $n = \frac{{{q^2} + 1}}{17}$ which was also derived by Jin et al. in [10].

Theorem 8

Suppose that q is an odd prime power of the form $q=17m+4$ or $q=17m+13$. Then, there exists a family of quantum MDS codes with the parameters , where $2 \le d(even) \le 5m+1$ if $q=17m+4$ and $2 \le d(even) \le 5m+4$ if $q=17m+13$.

Proof

The quantum codes with the desired parameters are obtained from MDS $\alpha$-constacyclic codes derived in Theorem 7 via Theorem 2 and also are MDS by Proposition 1. $\square$

3.2 Quantum MDS Codes of Length $\frac{{{q^2} - 1}}{p}$, q Even

Let $q=2^m$, $m \ge 2$ and p be a prime dividing $q+1$. Let $n=\frac{{{q^2} - 1}}{p}$ and $r=p$. Then, $rn=q^2 - 1$ and $\alpha = {\omega ^{\frac{{q + 1}}{p}}}$ where $\omega$ is a primitive ${\left( {q + 1} \right) ^{st}}$ root of unity over $F_{q^2}$. It is immediate that each $q^2$-cyclotomic coset modulo rn consists of just one element, that is, ${C_{1 + pj}} = \left\{ {1 + pj} \right\}$ for all $0 \le j \le n - 1$. We first deal with the case in which $q+1$ is a prime.

3.2.1 The Case $q+1$ is a Prime

Suppose that $q+1$ is a prime and let $r=q+1$. Then, $n=q-1$ and $\alpha = \omega$. We also have the following.

Lemma 8

For all $0 \le j \le \frac{{q - 2}}{2}$, $- q\left( {1 + rj} \right) \equiv 1 + r\left( {n - 1 - j} \right) \bmod rn$.

Proof

Since $- q \equiv 1 + r\left( {n - 1} \right) \bmod rn$, $- q\left( {1 + rj} \right) \equiv 1 + r\left( {n - 1 - qj} \right) \bmod rn$. Since $rj \equiv qrj\bmod rn$, we get $- q\left( {1 + rj} \right) \equiv 1 + r\left( {n - 1 - j} \right) \bmod rn$ for all $0 \le j \le \frac{{q - 2}}{2}$. $\square$

We define the subset Z of the set $O_{r,n}$ to be $Z = \bigcup \nolimits _{j = 0}^{\frac{{q - 4}}{2}} {{C_{1 + \left( {q + 1} \right) j}}}$. Then, Z comprises exactly $\frac{{q - 2}}{2}$ consecutive elements. The following is crucial to construct a family of quantum MDS codes of length $q-1$.

Lemma 9

$Z \cap - qZ = \emptyset$.

Proof

It follows from Lemma 8 that for all $0 \le j \le \frac{{q - 4}}{2}$, we have $\frac{q}{2} \le k \le n - 1$ when $- q{C_{1 + \left( {q + 1} \right) j}} = {C_{1 + \left( {q + 1} \right) k}}$ and so $Z \cap - qZ = \emptyset$. $\square$

We are ready to derive a class of $\omega$-constacyclic codes of length $q-1$ over $F_{q^2}$ containing their Hermitian duals and quantum MDS codes of length $q-1$.

Theorem 9

Let $q = {2^m}$, $m \ge 2$ and suppose that $q+1$ is a prime. Let $\omega$ be a primitive ${\left( {q + 1} \right) ^{st}}$ root of unity over $F_{q^2}$. Then there exists a family of MDS $\omega$-constacyclic codes containing their Hermitian duals and having the parameters ${\left[ {2^m-1,2^m - d,d} \right] _{{2^{2m}}}}$, where $2 \le d \le 2^{m-1}$.

Proof

Define the set ${S_i} = \bigcup \nolimits _{j = 0}^{i} {{C_{1 + \left( {q + 1} \right) j}}}$ for each $0 \le i \le \frac{{q - 4}}{2}$. Then, $S_i$ is a subset of Z containing $i+1$ consecutive terms. Let $C_i$ be an $\omega$-constacyclic code having the defining set $S_i$. Then, $C_i$ is an MDS code with the desired parameters by Theorem 1 and Proposition 2. By Lemma 9, $- qS_i \cap S_i = \emptyset$ since $S_i$ is a subset of Z and so ${C_i^{{ \bot _h}}} \subseteq C_i$ by Lemma 2. $\square$

We now are ready to give a construction for a class of quantum MDS codes with length $2^m-1$ that was also derived by Grassl et al. in [5].

Theorem 10

Let $m \ge 2$. If $2^m+1$ is a prime, then there exists a family of quantum MDS codes having the parameters where $2 \le d \le {2^{m - 1}}$.

Proof

Using Theorem 2, one can derive the quantum codes with the desired parameters from MDS $\omega$-constacyclic codes given in Theorem 9. By Proposition 1, these quantum codes are MDS. $\square$

3.2.2 The Case $q+1$ is Not a Prime

Suppose that $q+1$ is not a prime. Let $r = p = \frac{{q + 1}}{t}$, $t \ge 3$ and $\alpha = {\omega ^t}$. Define the subset Z of $O_{r,n}$ as $Z = \bigcup \nolimits _{j = \frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} }^{q - 2} {{C_{1 + pj}}}$. We then have the following.

Lemma 10

$Z \cap - qZ = \emptyset$.

Proof

Suppose that $Z \cap - qZ \ne \emptyset$. Then, there exists some $\frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} \le j,k \le q - 2$ such that $- q\left( {1 + pj} \right) \equiv 1 + pk\bmod rn$. Letting $q+1=pt$, we get $t + qj + k \equiv 0\bmod n$. It follows from $\frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} \le j,k \le q - 2$ that $t + \left( {q + 1} \right) \frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} \le t + qj + k \le t + \left( {q + 1} \right) \left( {q - 2} \right)$. Since $t + \left( {q + 1} \right) \left( {q - 2} \right) = \left( {p - 1} \right) n + t\left( {q - p} \right)$ and $t + \left( {q + 1} \right) \frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} = \frac{{p - 1}}{2}n + pt$, the possible values of $t + qj + k$ are nz, where $\frac{p+1}{2} \le z \le p - 1$. Note that $\frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}}< tz - 2 < q - 2$ for all $\frac{p+1}{2} \le z \le p - 1$. Observe that for all $\frac{p+1}{2} \le z \le p - 1$, $nz = t + qj + k + 1 + \left( {p - 1 - z} \right) t$, where $j = tz - 2$ and $k=q-2$. However, since $t + qj + k< t + qj + q - 1 + \left( {p - 1 - z} \right) t < t + q\left( {j + 1} \right) + \frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} \le t + q\left( j+1\right) + k$ for all $\frac{p+1}{2} \le z \le p - 1$, for $j=tz-2$ and any k with $\frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}}\le k \le q-2$, it is impossible to provide the equation $nz = t + qj + k$ for all $\frac{p+1}{2} \le z \le p - 1$ and $\frac{{\left( {p - 1} \right) \left( {q + 1} \right) }}{{2p}} \le j,k \le q - 2$. This is a contradiction. $\square$

We now derive a family of $\omega ^t$-constacyclic codes of length $\frac{{2^{2m}}-1}{p}$ over $F_{2^{2m}}$ containing their Hermitian duals, which is needed to construct quantum MDS codes of length $\frac{{2^{2m}}-1}{p}$.

Theorem 11

Let $q = {2^m}$, $m \ge 2$ and $\omega$ be a primitive ${\left( {q + 1} \right) ^{st}}$ root of unity over $F_{2^{2m}}$. Suppose that $q + 1 = pt$, where p is a prime and $t \ge 3$. There exists a family of MDS $\omega ^t$-constacyclic codes containing their Hermitian duals and having the parameters ${\left[ {\frac{{{2^{2m}} - 1}}{p},\frac{{{2^{2m}} - 1}}{p} - d + 1,d} \right] _{{2^{2m}}}}$, where $2 \le d \le \frac{{q - 1}}{2} + \frac{{q + 1}}{{2p}}$.

Proof

Define the set ${S_i} = \bigcup \nolimits _{j = q-2-i}^{q-2} {{C_{1 + pj}}}$ for each $0 \le i \le \frac{{q-5 }}{2}+\frac{{q+1 }}{2p}$. Then, $S_i$ is a subset of Z containing $i+1$ consecutive terms and $\left| {{S_i}} \right| = i+1$. Let $C_i$ be an $\omega ^t$-constacyclic code having the defining set $S_i$. Then, $C_i$ is an MDS code with the desired parameters by Theorem 1 and Proposition 2. By Lemma 10$- qS_i \cap S_i = \emptyset$ since $S_i$ is a subset of Z and so ${C_i^{{ \bot _h}}} \subseteq C_i$ by Lemma 2. $\square$

The following is a generalization of Theorem 3.3 presented by Qian et al. in [21].

Theorem 12

Let $m \ge 2$. If $2^m+1$ is not a prime, then for each prime p dividing $2^m+1$ there exists a quantum MDS code having the parameters where $2 \le d \le \frac{{q - 1}}{2} + \frac{{q + 1}}{{2p}}$.

Proof

Using Theorem 2, one can derive the quantum codes with the desired parameters from MDS $\omega ^t$-constacyclic codes given in Theorem 11. By Proposition 1, these quantum codes are MDS. $\square$

The parameters presented in Theorem 12 were obtained by He et al. in [7].

4 Conclusion and Discussion

We have given constructions of five families of quantum MDS codes and we summarize them here as follows. Note that p is an odd prime and q is an odd prime power in the first three constructions.

• 1. For $3 \le d(odd) \le q$,

  

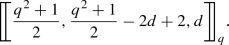  (6)

• 2. For $2 \le d\left( {even} \right) \le 5m + 2$ if $q=13m+5$ and $2 \le d\left( {even} \right) \le 5m + 3$ if $q=13m+8$,

  

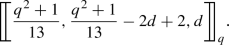  (7)

• 3. For $2 \le d\left( {even} \right) \le 5m + 1$ if $q=17m+4$ and $2 \le d\left( {even} \right) \le 5m + 4$ if $q=17m+13$,

  

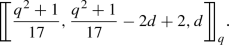  (8)

• 4. Let $m \ge 2$. If $2^m+1$ is a prime, then for $2 \le d \le {2^{m - 1}}$,

  

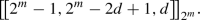  (9)

• 5. Let $m \ge 2$. If $2^m+1$ is not a prime, then for each prime p dividing $2^m+1$ and $2 \le d \le \frac{{2^m - 1}}{2} + \frac{{2^m + 1}}{{2p}}$,

  

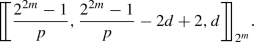  (10)