Analytical discussion for the mixed integral equations

Abstract

This paper presents a numerical method for the solution of a Volterra–Fredholm integral equation in a Banach space. Banachs fixed point theorem is used to prove the existence and uniqueness of the solution. To find the numerical solution, the integral equation is reduced to a system of linear Fredholm integral equations, which is then solved numerically using the degenerate kernel method. Normality and continuity of the integral operator are also discussed. The numerical examples in Sect. 5 illustrate the applicability of the theoretical results.

1 Introduction

Integral equation is very important in continuum mechanics, geophysics, potential theory and biology, quantum mechanics, optimal control systems, population genetics, medicine and fracture mechanics, solid mechanics, economic problems, phase transitions, electrostatics, and others [12, 19]. Many problems of mathematical physics, applied mathematics, and engineering are reduced to Volterra–Fredholm integral equations, see [1,2,3, 5, 15, 16, 20], for this, many different methods are used to solve this type of equations analytically [11,12,13, 17]. In addition, for numerical methods, see [4, 7, 8, 10, 18].

In this paper, we consider the Volterra–Fredholm integral equation of the second kind with continuous kernels with respect to time and position. We use a numerical method to transform the Volterra–Fredholm integral equation to system of linear Fredholm integral equations, where the existence and the uniqueness of the solution of the system of linear Fredholm integral equations can be discussed and proved using Picard’s method and Banach’s fixed point method.

Consider the following Volterra–Fredholm integral equation:

$$\begin{aligned} y(u,t)=g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau +\gamma \int _{0}^{t}\Psi (t,\tau )y(u,\tau )\mathrm {d}\tau , \end{aligned}$$

(1.1)

where $\gamma$ is a constant, the function y(u, t) is unknown in the Banach space $L_{2}[0,1]\times C[0,T],\,0\le T<1, [0,1]$ is the domain of integration with respect to the position and the time $t\in [0,T].$ The kernels $\Phi (t,\tau ), \Psi (t,\tau )$ are continuous in C[0, T] and the known function g(u, t) is continuous in the space $L_{2}[0,1]\times C[0,T],\,0\le t\le T.$ In addition, the kernel of position w(u, v) belongs to $C([0,1]\times [0,1])$.

2 The existence and uniqueness of solution of the Volterra–Fredholm integral equation

In this paper, we assume the following conditions:

• (i) $|w(u,v)|< C$, $\hbox {C}$ is a constant;

• (ii) $|\Phi (t,\tau )|\le A$, $|\Psi (t,\tau )|\le B$, A, B are constants

  $\forall \,t,\tau \in [0,T],\,0\le \tau \le t\le T$;

• (iii) $\Vert g(u,t)\Vert =\max \nolimits _{0<t\le T}\int _{0}^{t}\left[ \int _{0}^{1}g^{2}(u,\tau )\mathrm{d}u\right] ^{\frac{1}{2}}\mathrm {d}\tau =D$, $\hbox {D}$ is a constant.

Theorem 2.1

Let the conditions (i)–(iii) be satisfied. If the condition

$$\begin{aligned} \mid \gamma \mid <\frac{2}{T^{2}[A C+B]} \end{aligned}$$

(2.1)

is satisfied, then Eq. (1.1) has an unique solution y(u, t) in the space, $L_{2}[0,1]\times C[0,T]$.

Proof

To prove this theorem, we use the successive approximation method (Picard’s method). Therefore, we assume that the solution of Eq. (1.1) takes the form:

$$\begin{aligned} y(u,t)=\lim _{n\rightarrow \infty }y_{n}(u,t), \end{aligned}$$

where

$$\begin{aligned} y_{n}(u,t)=\sum _{i=0}^{n}G_{i}(u,t),\quad t\in [0,T],\quad n=1,2,\ldots \end{aligned}$$

(2.2)

where the functions $G_{i}(u,t),\, i=0,1,\ldots ,n$ are continuous functions of the form:

$$\begin{aligned} \left. \begin{array}{c l} G_{n}(u,t) &{}= y_{n}(u,t)-y_{n-1}(u,t),\\ G_{0}(u,t) &{}= g(u,t)\end{array} \right\} . \end{aligned}$$

(2.3)

$\square$

Now, we should prove the following lemmas:

Lemma 2.2

The series $\sum _{i=0}^{n}G_{i}(u,t)$ is uniformly convergent to a continuous solution function y(u, t).

Proof

We structure a sequence $y_{n}(u,t)$ defined by

$$\begin{aligned} y_{n}(u,t)= & {} g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)y_{n-1}(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\;\gamma \int _{0}^{t}\Psi (t,\tau )y_{n-1}(u,\tau )\mathrm {d}\tau ;\quad y_{0}(u,t) =g(u,t). \end{aligned}$$

(2.4)

Then, we get

$$\begin{aligned} y_{n}(u,t)-y_{n-1}(u,t)= & {} \gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v) [y_{n-1}(v,\tau )-y_{n-2}(v,\tau )]\mathrm{d}v\mathrm {d}\tau \nonumber \\&+\;\gamma \int _{0}^{t}\Psi (t,\tau ) [y_{n-1}(u,t)-y_{n-2}(u,\tau )]\mathrm {d}\tau . \end{aligned}$$

(2.5)

From Eq. (2.2) and using the properties of the norm, we obtain

$$\begin{aligned} \begin{aligned} \Vert G_{n}(u,t)\Vert&\le |\gamma |\left\| \int _{0}^{t}\int _{0}^{1}|\Phi (t,\tau )||w(u,v)|G_{n-1}(v,\tau )\mathrm{d}v\mathrm {d}\tau \right\| \\&\quad +|\gamma |\left\| \int _{0}^{t}|\Psi (t,\tau )|G_{n-1}(u,\tau )\mathrm {d}\tau \right\| , \end{aligned} \end{aligned}$$

(2.6)

for $n=1$, we get from formula (2.6)

$$\begin{aligned} \Vert G_{1}(u,t)\Vert&\le |\gamma |\left\| \displaystyle \int _{0}^{t}\int _{0}^{1}|\Phi (t,\tau )||w(u,v)|G_{0}(v,\tau )\mathrm{d}v\mathrm {d}\tau \right\| \nonumber \\&\quad +|\gamma |\left\| \displaystyle \int _{0}^{t}|\Psi (t,\tau )|G_{0}(u,\tau )\mathrm {d}\tau \right\| . \end{aligned}$$

(2.7)

Using conditions (i), (ii) and (iii), we have

$$\begin{aligned} \begin{aligned} \Vert G_{1}(u,t)\Vert&\le |\gamma | A C D\left\| \int _{0}^{t}\int _{0}^{1}\mathrm{d}v\mathrm {d}\tau \right\| +|\gamma | B D\left\| \int _{0}^{t}\mathrm {d}\tau \right\| ,\\&\le |\gamma | A C D\Vert t\Vert +|\gamma |B D\Vert t\Vert , \end{aligned} \end{aligned}$$

(2.8)

where

$$\begin{aligned} \Vert t\Vert =\frac{1}{2}T^{2},\quad T=\max _{0\le t\le T}|t|, \end{aligned}$$

so that Eq. (2.8) becomes

$$\begin{aligned} \Vert G_{1}(u,t)\Vert \le \frac{1}{2}|\gamma | T^{2} D [A C + B], \end{aligned}$$

(2.9)

by induction, we get

$$\begin{aligned} \Vert G_{n}(u,t)\Vert \le \eta ^{n}D ,\quad \eta =\frac{1}{2}|\gamma | T^{2}[A C + B]<1,\quad n=1,2,\ldots \end{aligned}$$

(2.10)

Since

$$\begin{aligned} |\gamma |<\frac{2}{T^{2}[AC +B]}, \end{aligned}$$

(2.11)

this leads us to say that the sequence $y_{n}(u,t)$ has a convergent solution. So that, for $n\rightarrow \infty ,$ we have

$$\begin{aligned} y(u,t)=\sum _{i=0}^{\infty }G_{i}(u,t), \end{aligned}$$

(2.12)

which represents an infinite convergent series. $\square$

Lemma 2.3

The function y(u, t) of the series (2.12) represents an unique solution of Eq. (1.1).

Proof

To show that y(u, t) is the unique solution, we assume that there exists a different continuous solution $\tilde{y}(u,t)$ of Eq. (1.1), then we obtain

$$\begin{aligned} y(u,t)-\tilde{y}(u,t)= & {} \gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)[y(v,\tau )-\tilde{y}(v,\tau )]\mathrm{d}v\mathrm {d}\tau \nonumber \\&+\gamma \int _{0}^{t}\Psi (t,\tau )[y(u,\tau )-\tilde{y}(u,\tau )]\mathrm {d}\tau . \end{aligned}$$

(2.13)

Using conditions (i) and (ii), we get

$$\begin{aligned} \Vert y(u,t)-\tilde{y}(u,t)\Vert\le & {} |\gamma |A C\int _{0}^{t}\int _{0}^{1}\Vert [y(v,\tau )-\tilde{y}(v,\tau )]\Vert \mathrm {d}v\mathrm {d}\tau \nonumber \\&+\;|\gamma |B\int _{0}^{t}\Vert [y(u,\tau )-\tilde{y}(u,\tau )]\Vert \mathrm {d}\tau , \end{aligned}$$

(2.14)

$$\begin{aligned} \Vert y(u,t)-\tilde{y}(u,t)\Vert\le & {} \eta \Vert y(u,t)-\tilde{y}(u,t)\Vert ,\quad \eta =\frac{1}{2}|\gamma | T^{2}[A C + B]<1.\nonumber \\ \end{aligned}$$

(2.15)

The formula (2.15) can be adapted as:

$$\begin{aligned} (1-\eta )\Vert y(u,t)-\tilde{y}(u,t)\Vert \le 0. \end{aligned}$$

Since $\eta <1$, so that $y(u,t)=\tilde{y}(u,t),$ that is the solution is unique. $\square$

3 The normality and continuity of the integral operator

Equation (1.1) can be written in the following integral operator form:

$$\begin{aligned} \overline{V}y=g(u,t)+Vy,\quad Vy=\Phi Wy+\Psi y, \end{aligned}$$

(3.1)

where

$$\begin{aligned} \Phi Wy=\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau ,\quad \Psi y=\gamma \int _{0}^{t}\Psi (t,\tau )y(u,\tau )\mathrm {d}\tau . \end{aligned}$$

3.1 The normality of the integral operator

For the normality, we use Eq. (3.1) to get

$$\begin{aligned} \Vert Vy\Vert&\le |\gamma |\left\| \int _{0}^{t}\int _{0}^{1}|\Phi (t,\tau )||w(u,v)|y(v,\tau )\mathrm {d}v\mathrm {d}\tau \right\| \\&\quad +|\gamma |\left\| \int _{0}^{t}|\Psi (t,\tau )| y(u,\tau )\mathrm {d}\tau \right\| . \end{aligned}$$

Using conditions (i) and (ii), we get

$$\begin{aligned} \Vert Vy\Vert \le \frac{1}{2}|\gamma | T^{2}[A C+B ]\Vert y\Vert , \end{aligned}$$

since

$$\begin{aligned} \Vert Vy(u,t)\Vert \le \eta \Vert y(u,t)\Vert ,\quad \eta =\frac{1}{2}|\gamma | T^{2}[A C+B ]<1, \end{aligned}$$

where

$$\begin{aligned} \mid \gamma \mid <\frac{2}{T^{2}[A C+B]}. \end{aligned}$$

Therefore, the integral operator V has a normality, which leads immediately after using the condition (iii) to the normality of the operator $\overline{V}$.

3.2 The continuity of the integral operator

For the continuity, we suppose the two potential functions $y_{1}(u,t)$ and $y_{2}(u,t)$ in the space $L_{2}[0,1]\times C[0,T]$ are satisfied Eq. (3.1), then

$$\begin{aligned} \overline{V}y_{1}= & {} g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)y_{1}(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\,\gamma \int _{0}^{t}\Psi (t,\tau ) y_{1}(u,\tau )\mathrm {d}\tau , \end{aligned}$$

(3.2)

$$\begin{aligned} \overline{V}y_{2}= & {} g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)y_{2}(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\,\gamma \int _{0}^{t}\Psi (t,\tau ) y_{2}(u,\tau )\mathrm {d}\tau . \end{aligned}$$

(3.3)

Using Eqs. (3.2) and (3.3), we get

$$\begin{aligned} \begin{aligned} \overline{V}[y_{1}-y_{2}] =&\; \gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w(u,v)[y_{1}(v,\tau )-y_{2}(v,\tau )]\mathrm {d}v\mathrm {d}\tau \\&+\gamma \int _{0}^{t}\Psi (t,\tau )[y_{1}(u,\tau )-y_{2}(u,\tau )]\mathrm {d}\tau . \end{aligned} \end{aligned}$$

Using conditions (i) and (ii), we get

$$\begin{aligned} \begin{aligned} \Vert \overline{V}[y_{1}-y_{2}]\Vert&\le |\gamma |A C\int _{0}^{t}\int _{0}^{1}\Vert [y_{1}(v,\tau )-y_{2}(v,\tau )]\Vert \mathrm {d}v\mathrm {d}\tau \\&\quad +\,|\gamma |B\int _{0}^{t}\Vert [y_{1}(u,\tau )-y_{2}(u,\tau )]\Vert \mathrm {d}\tau , \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \Vert t\Vert =\frac{1}{2}T^{2},\quad T=\max _{0\le t\le T}|t|, \end{aligned}$$

so that last inequality becomes

$$\begin{aligned} \Vert \overline{V}[y_{1}-y_{2}]\Vert \le \eta \Vert y_{1}-y_{2}\Vert ,\quad \eta =\frac{1}{2}|\gamma | T^{2}[A C+B ]<1, \end{aligned}$$

(3.4)

with

$$\begin{aligned} \mid \gamma \mid \,<\frac{2}{T^{2}[A C+B]}. \end{aligned}$$

Inequality (3.4) leads us to the continuity of the integral operator $\overline{V}$. So that, $\overline{V}$ is a contraction operator. Therefore by Banach’s fixed point theorem, there is an unique fixed point y(u, t), which is the solution of the linear mixed integral Eq. (1.1).

4 The reduced system of Fredholm integral equations and its solution

4.1 Quadratic numerical method [6]

We tend to use the quadratic numerical method to reduce the solution of the Eq. (1) to the system of linear Fredholm integral equations of the second kind. We divide the interval $[0,T],\,0\le t\le T,$ as $0=t_{0}<t_{1}<\cdots<t_{i}<\cdots <t_{N}=T,$ where $t=t_{i},\,i=0,1,\ldots ,N;$ to get

$$\begin{aligned} y(u,t_{i})= & {} g(u,t_{i})+\gamma \int _{0}^{t_{i}}\int _{0}^{1}\Phi (t_{i},\tau )w(u,v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\,\gamma \int _{0}^{t_{i}}\Psi (t_{i},\tau )y(u,\tau )\mathrm {d}\tau . \end{aligned}$$

(4.1)

The Volterra integral terms can be written as follows:

$$\begin{aligned}&\int _{0}^{t_{i}}\int _{0}^{1}\Phi (t_{i},\tau )w(u,v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&\quad =\sum _{j=0}^{i}\mu _{j}\Phi (t_{i},t_{j})\int _{0}^{1}w(u,v)y(v,t_{j})\mathrm {d}v +O(\hbar _{i}^{\wp _{1}+1}), \end{aligned}$$

(4.2)

$$\begin{aligned}&\int _{0}^{t_{i}}\Psi (t_{i},\tau )y(u,\tau )\mathrm {d}\tau =\sum _{j=0}^{i}\nu _{j}\Psi (t_{i},t_{j})y(u,t_{j})+O(\hbar _{i}^{\wp _{2}+1}), \end{aligned}$$

(4.3)

where

$$\begin{aligned}&(\hbar _{i}^{\wp _{1}+1}\longrightarrow 0,~\hbar _{i}^{\wp _{2}+1}\longrightarrow 0,\quad \wp _{1}>0,~\wp _{2}>0), \\&\qquad \quad \hbar _{i}=\max _{0\le j\le i}\rho _{j}\quad \hbox {and}\quad \rho _{j}=t_{j+1}-t_{j}. \end{aligned}$$

The values of the weight formula $\mu _{j},\nu _{j}$ and the constants $\wp _{1},\wp _{2}$ depend on the number of derivatives of $\Phi (t, \tau )$ and $\Psi (t, \tau )$, $\forall \tau \in [0, T],$ with respect to t.

Using Eqs. (4.2), (4.3) in Eq. (4.1), we get

$$\begin{aligned} y(u,t_{i})= & {} g(u,t_{i})+\gamma \sum _{j=0}^{i}\mu _{j}\Phi (t_{i},t_{j})\int _{0}^{1}w(u,v)y(v,t_{j})\mathrm {d}v\nonumber \\&+\;\gamma \sum _{j=0}^{i}\nu _{j}\Psi (t_{i},t_{j})y(u,t_{j}). \end{aligned}$$

(4.4)

Substituting the following notations:

$$\begin{aligned} y(u,t_{i})=y_{i}(u),\quad g(u,t_{i})=g_{i}(u),\quad \Phi (t_{i},t_{j})=\Phi _{i,j},\quad \Psi (t_{i},t_{j})=\Psi _{i,j}, \end{aligned}$$

we can rewrite Eq. (4.4) in the form

$$\begin{aligned} \delta _{i}y_{i}(u)=g_{i}(u)+\gamma \sum _{j=0}^{i}\mu _{j}\Phi _{i,j}\int _{0}^{1}w(u,v)y_{j}(v)\mathrm {d}v+\gamma \sum _{j=0}^{i-1}\nu _{j}\Psi _{i,j}~y_{j}(u), \end{aligned}$$

(4.5)

where $\delta _{i}=(1-\gamma _{i}),\quad \gamma _{i}=\gamma \nu _{i}\Psi _{i,i}.$

Equation (4.5), for $\delta _{i}\ne 0,$ represents a system of linear Fredholm integral equations of the second kind, while for $\delta _{i}=0,$ we have system of linear Fredholm integral equations of the first kind. The solution of the system (4.5), for $\delta _{i}\ne 0,$ can be obtained see [6, 14]. If we obtain, first, the value of $y_{0}(x)$, and let $i=0$ in the system (4.5), we get

$$\begin{aligned} \delta _{0}y_{0}(u)=g_{0}(u)+\gamma \mu _{0}\Phi _{0,0}\int _{0}^{1}w(u,v)y_{0}(v)\mathrm {d}v,\quad \delta _{0}=(1-\gamma \nu _{0}\Psi _{0,0}). \end{aligned}$$

(4.6)

After obtaining the solution of Eq. (4.6), we can use the mathematical induction to obtain the general solution of (4.5).

4.2 The procedure of solution using degenerate kernel method

Here, we can find that the solution of the linear algebraic integral system (4.5) by applying the degenerate kernel method [11] naturally leads one to consider replacement the given w(u, v) approximately by a degenerate kernel $w_{n}(u,v),$ that is

$$\begin{aligned} w_{n}(u,v)=\sum _{l=1}^{n}M_{l}(u)N_{l}(v), \end{aligned}$$

(4.7)

where the set of functions $\{M_{l}(u)\}$ and $\{N_{l}(v)\}$ are assumed to be linearly independent and the degenerate kernel $w_{n}(u,v)$ should satisfy the condition

$$\begin{aligned} \left\{ \int _{0}^{1}\int _{0}^{1} |w(u,v)-w_{n}(u,v)|^{2}\mathrm {d}u\mathrm {d}v\right\} ^{\frac{1}{2}}\rightarrow 0,\quad \text {as}\quad n\rightarrow \infty . \end{aligned}$$

(4.8)

Hence, the solution of Eq. (4.5) related to the degenerate kernels $w_{n}(u,v)$ takes the form:

$$\begin{aligned} \delta _{i}y_{i}^{n}(u)= & {} g_{i}(u)+\gamma \sum _{j=0}^{i}\mu _{j}\Phi _{i,j}\int _{0}^{1}w_{n}(u,v)y_{j}^{n}(v)\mathrm {d}v\nonumber \\&+\;\gamma \sum _{j=0}^{i-1}\nu _{j}\Psi _{i,j}~y_{j}^{n}(u),\quad \delta _{i}\ne 0. \end{aligned}$$

(4.9)

Using Eq. (4.7) in Eq. (4.9), we have

$$\begin{aligned} \delta _{i}y_{i}^{n}(u)=g_{i}(u)+\gamma \sum _{j=0}^{i}\sum _{l=1}^{n}\mu _{j}\Phi _{i,j}M_{l}(u)\int _{0}^{1}N_{l}(v) y_{j}^{n}(v)\mathrm {d}v +\gamma \sum _{j=0}^{i-1}\nu _{j}\Psi _{i,j}~y_{j}^{n}(u). \end{aligned}$$

(4.10)

We introduce the notations

$$\begin{aligned} \alpha _{j}^{l}=\int _{0}^{1}N_{l}(v) y_{j}^{n}(v)\mathrm {d}v, \end{aligned}$$

(4.11)

where $\alpha _{j}^{l}$ are unknown constants. Then, Eq. (4.10) takes the form:

$$\begin{aligned} \delta _{i}y_{i}^{n}(u)=g_{i}(u)+\gamma \sum _{j=0}^{i}\sum _{l=1}^{n}\mu _{j}\Phi _{i,j}M_{l}\alpha _{j}^{l}+\gamma \sum _{j=0}^{i-1}\nu _{j}\Psi _{i,j}~y_{j}^{n}(u),\qquad (\delta _{i}\ne 0). \end{aligned}$$

(4.12)

Substituting from Eq. (4.12) into Eq. (4.11), we get

$$\begin{aligned} \begin{aligned} \alpha _{j}^{r}=\int _{0}^{1}\frac{N_{r}(v)}{\delta _{j}}&\left[ g_{j}(v)+\gamma \sum _{m=0}^{j}\sum _{l=0}^{n}\mu _{m}\Phi _{j,m}M_{l}(v)\alpha _{m}^{l} +\gamma \sum _{m=0}^{j-1}\nu _{m}\Psi _{j,m}y_{m}^{n}(v)\right] \mathrm {d}v,\\&\delta _{j}\ne 0,\quad j=0,1,\dots ,i\quad r=1,2,\dots ,n. \end{aligned} \end{aligned}$$

(4.13)

Define the function

$$\begin{aligned} K_{j}^{r}(\alpha _{j}^{1},\alpha _{j}^{2},\dots ,\alpha _{j}^{n})= & {} \int _{0}^{1}\frac{N_{r}(v)}{ \delta _{j}}\left[ g_{j}(v)+\gamma \sum _{m=0}^{j}\sum _{l=1}^{n}\mu _{m}\Phi _{j,m}M_{l}(v)\alpha _{m}^{l}\right. \nonumber \\&+\left. \gamma \sum _{m=0}^{j-1}\nu _{m}\Psi _{j,m}y_{m}^{n}(v)\right] \mathrm {d}v, \end{aligned}$$

(4.14)

Equation (4.13) represents a system of linear algebraic equations which can be written in the following form [9]:

$$\begin{aligned} \left( \begin{array}{c} \alpha _{j}^{1} \\ \alpha _{j}^{2} \\ . \\ . \\ . \\ \alpha _{j}^{n} \\ \end{array} \right) =\left( \begin{array}{ccc} K_{j}^{1}(\alpha _{j}^{1},\alpha _{j}^{2},\cdots ,\alpha _{j}^{n}) \\ K_{j}^{2}(\alpha _{j}^{1},\alpha _{j}^{2},\cdots ,\alpha _{j}^{n}) \\ . \\ . \\ .\\ K_{j}^{n}(\alpha _{j}^{1},\alpha _{j}^{2},\cdots ,\alpha _{j}^{n})\\ \end{array} \right) . \end{aligned}$$

(4.15)

Formula (4.15) represents a system of linear algebraic equations and we can solve it numerically. After we get the values of $\alpha _{j}^{r}$, we can immediately determine the values of the functions $y_{i}(u)$.

Lemma 4.1

Let $w_{n}(u,v)\in C([0,1]\times [0,1])$ with the condition (4.8), then the following condition is satisfied

$$\begin{aligned} \left\{ \int _{0}^{1}\int _{0}^{1} |w_{n}(u,v)|^{2}\mathrm{d}u\mathrm {d}v\right\} ^{\frac{1}{2}}\le C,\quad \forall n>n_{0},\quad n_{0}\in N,\quad \text {s.t}\quad C\quad \text {is}\quad \text {a constant}. \end{aligned}$$

(4.16)

Proof

To prove this lemma, we use the formula

$$\begin{aligned} \left\{ \int _{0}^{1}\int _{0}^{1} |w_{n}(u,v)|^{2}\mathrm{d}u\mathrm {d}v\right\} ^{\frac{1}{2}}\le \left\{ \int _{0}^{1}\int _{0}^{1} [|w(u,v)-w_{n}(u,v)|+|w(u,v)|]^{2}\mathrm{d}u\mathrm {d}v\right\} ^{\frac{1}{2}}, \end{aligned}$$

using condition (4.8), we get

$$\begin{aligned} \forall \varepsilon>0,\quad \exists \quad n_{0}\in N:\quad \left\{ \int _{0}^{1}\int _{0}^{1} |w(u,v)-w_{n}(u,v)|^{2}\mathrm{d}u\mathrm {d}v\right\} ^{\frac{1}{2}}<\varepsilon ,\quad \forall n>n_{0}. \end{aligned}$$

Applying Minkowski’s inequality and using condition (i), we get

$$\begin{aligned} \forall \varepsilon>0,\quad \exists \quad n_{0}\in N:\quad \;\left\{ \int _{0}^{1} \int _{0}^{1} |w_{n}(u,v)|^{2}\mathrm{d}u\mathrm {d}v\right\} ^{\frac{1}{2}}<C,\quad \forall n>n_{0}. \end{aligned}$$

This completes the proof. $\square$

4.3 The existence and uniqueness of the numerical solution

In this subsection, we will present the proof of the existence and uniqueness of the numerical solution of the system under study. This aim will be achieved through the following theorems:

Theorem 4.2

The integral equation

$$\begin{aligned} y_{n}(u,t)=g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w_{n}(u,v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau +\gamma \int _{0}^{t}\Psi (t,\tau )y(u,\tau )\mathrm {d}\tau , \end{aligned}$$

(4.17)

has an unique solution $y_{n}(u,t)$ in $L_{2}[0,1]\times C[0,T],$ under the condition:

$$\begin{aligned} \mid \gamma \mid <\frac{2}{T^{2}[A C+B]}. \end{aligned}$$

Proof

Defining for each $n>n_{0},$ the integral operator

$$\begin{aligned} \overline{V}y_{n}=g(u,t)+Vy_{n}(u,t),\quad Vy_{n}=\Phi Wy_{n}+\Psi y_{n}, \end{aligned}$$

(4.18)

where

$$\begin{aligned} \Phi Wy_{n}= \gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w_{n}(u,v)y_{n}(v,\tau )\mathrm {d}v\mathrm {d}\tau ,\quad \Psi y_{n}=\gamma \int _{0}^{t}\Psi (t,\tau )y_{n}(u,\tau )\mathrm {d}\tau . \end{aligned}$$

(4.19)

Firstly, for the normality, we use Eq. (4.18) to get

$$\begin{aligned} \Vert Vy_{n}\Vert\le & {} |\gamma |\left\| \int _{0}^{t}\int _{0}^{1}|\Phi (t,\tau )||w_{n}(u,v)|y_{n}(v,\tau )\mathrm {d}v\mathrm {d}\tau \right\| \\&+ |\gamma |\left\| \int _{0}^{t}|\Psi (t,\tau )|y_{n}(u,\tau )\mathrm {d}\tau \right\| . \end{aligned}$$

Using condition (4.8), we get

$$\begin{aligned} \Vert Vy_{n}\Vert \le \frac{1}{2}|\gamma |T^{2}[A C+B ]\Vert y_{n}\Vert , \end{aligned}$$

then

$$\begin{aligned} \Vert Vy_{n}(u,t)\Vert \le \eta \Vert y_{n}(u,t)\Vert ,\quad \eta =\frac{1}{2}|\gamma |T^{2}[A C+B ]<1, \end{aligned}$$

where

$$\begin{aligned} \mid \gamma \mid <\frac{2}{T^{2}[A C+B]}. \end{aligned}$$

Therefore, the integral operator V has a normality, which leads immediately after using the condition (iii) to the normality of the operator $\overline{V}$.

Secondly, for the continuity, we assume the two functions $y_{n1}(u,t),\;y_{n2}(u,t)$ satisfy Eq. (4.19), then

$$\begin{aligned} \overline{V}y_{n1}= & {} g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w_{n}(u,v)y_{n1}(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\;\gamma \int _{0}^{t}\Psi (t,\tau ) y_{n1}(u,\tau )\mathrm {d}\tau , \end{aligned}$$

(4.20)

$$\begin{aligned} \overline{V}y_{n2}= & {} g(u,t)+\gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )w_{n}(u,v)y_{n2}(v,\tau )\mathrm {d}v\mathrm {d}\tau \nonumber \\&+\;\gamma \int _{0}^{t}\Psi (t,\tau ) y_{n2}(u,\tau )\mathrm {d}\tau . \end{aligned}$$

(4.21)

Using conditions (4.16) and (ii), we get

$$\begin{aligned} \Vert \overline{V}[y_{n1}-y_{n2}]\Vert&\le |\gamma |A C\int _{0}^{t}\int _{0}^{1}\Vert [y_{n1}(v,\tau )-y_{n2}(v,\tau )]\Vert \mathrm {d}v\mathrm {d}\tau \\&\quad +|\gamma |B\int _{0}^{t}\Vert [y_{n1}(u,\tau )-y_{n2}(u,\tau )]\Vert \mathrm {d}\tau , \end{aligned}$$

where

$$\begin{aligned} \Vert t\Vert =\frac{1}{2}T^{2},\quad T=\max _{0\le t\le T}|t|, \end{aligned}$$

so that the last inequality becomes

$$\begin{aligned} \Vert \overline{V}[y_{n1}-y_{n2}]\Vert \le \eta \Vert y_{n1}-y_{n2}\Vert ,\quad \eta =\frac{1}{2}|\gamma |T^{2}[A C+B ]<1, \end{aligned}$$

(4.22)

with

$$\begin{aligned} \mid \gamma \mid <\frac{2}{T^{2}[C A+B]}. \end{aligned}$$

Hence, $\overline{V}$ is a contraction in the space $L_{2}[0,1]\times C[0,T].$ Therefore, by Banach’s fixed point theorem, there is an unique fixed point $y_{n}(u,t)$, which is the solution of the linear V–FIE (4.17). $\square$

Theorem 4.3

Under the condition (4.8), the unique solution ${y_{n}(u,t)}$ of integral Eq. (4.17) converges to the unique solution y(u, t) of integral Eq. (1.1).

Proof

From Eqs. (1.1) and (4.17), we have

$$\begin{aligned} y(u,t)-y_{n}(u,t)= & {} \gamma \int _{0}^{t}\int _{0}^{1}\Phi (t,\tau )\left[ w(u,v)y(v,\tau )-w_{n}(u,v)y_{n}(v,\tau )\right] \mathrm {d}v\mathrm {d}\tau \nonumber \\&+\,\gamma \int _{0}^{t}\Psi (t,\tau )\left[ y(u,\tau )-y_{n}(u,\tau )\right] \mathrm {d}\tau . \end{aligned}$$

(4.23)

Using properties of the norm and condition (ii), we get

$$\begin{aligned} \Vert y(u,t)-y_{n}(u,t)\Vert\le & {} |\gamma |A\int _{0}^{t}\int _{0}^{1}\Vert w(u,v)-w_{n}(u,v)\Vert \Vert y(v,\tau )\Vert \mathrm {d}v\mathrm {d}\tau \\&+\;|\gamma |A\int _{0}^{t}\int _{0}^{1}\Vert (w_{n}(u,v)\Vert \Vert y(v,\tau )-y_{n}(v,\tau )\Vert \mathrm {d}v\mathrm {d}\tau \\&+\;|\gamma |B\int _{0}^{t}\Vert y(u,\tau )-y_{n}(u,\tau )\Vert \mathrm {d}\tau . \end{aligned}$$

Using condition (4.16), the last inequality becomes

$$\begin{aligned} \Vert y(u,t)-y_{n}(u,t)\Vert&\le |\gamma |A T\Vert w(u,v)-w_{n}(u,v)\Vert \Vert y(u,t)\Vert \\&\quad +|\gamma |T(AC+B)\Vert y(u,t)-y_{n}(u,t)\Vert . \end{aligned}$$

The last inequality can be adapted as:

$$\begin{aligned} \Vert y-y_{n}\Vert \le \frac{|\gamma |A T\Vert y\Vert }{1-\eta }\Vert w-w_{n}\Vert ,\quad \eta =\frac{1}{2}|\gamma |T^{2}(AC+B)<1, \end{aligned}$$

subsequently, if $\Vert w-w_{n}\Vert \rightarrow 0$ as $n\rightarrow \infty ,$ we have $\Vert y-y_{n}\Vert \rightarrow 0$ as $n\rightarrow \infty .$

Hence, the proof is completed. $\square$

Theorem 4.4

From Eq. (4.14) and the degenerate kernel $w_{n}(u,v),$ the linear algebraic system (4.15) has the unique solution $(\alpha _{j}^{1},\alpha _{j}^{2},\cdots ,\alpha _{j}^{n}),$ so that the Eq. (4.12) has the unique solution $y_{i}^{n}(u)$.

Proof

We use the notations $(\alpha _{j}^{1},\alpha _{j}^{2},\cdots ,\alpha _{j}^{n}),\;(\beta _{j}^{1},\beta _{j}^{2},\cdots ,\beta _{j}^{n})$ as the two different solutions of (4.15) and from Eq. (4.14), we get

$$\begin{aligned} K_{j}^{r}(\alpha _{j}^{1},\alpha _{j}^{2},\ldots ,\alpha _{j}^{n})&=\int _{0}^{1}\frac{N_{r}(v)}{ \delta _{j}} \left[ g_{j}(v)+\gamma \sum _{m=0}^{j}\sum _{l=1}^{n}\mu _{m}\Phi _{j,m}M_{l}(v)\alpha _{m}^{l}\right. \\&\quad \left. +\;\gamma \sum _{m=0}^{j-1}\nu _{m}\Psi _{j,m}y_{m}^{n}(v)\right] \mathrm {d}v, \end{aligned}$$

and

$$\begin{aligned} K_{j}^{r}(\beta _{j}^{1},\beta _{j}^{2},\ldots ,\beta _{j}^{n})&=\int _{0}^{1}\frac{N_{r}(v)}{ \delta _{j}} \left[ g_{j}(v)+\gamma \sum _{m=0}^{j}\sum _{l=1}^{n}\mu _{m}\Phi _{j,m}M_{l}(v)\beta _{m}^{l}\right. \\&\quad \left. +\;\gamma \sum _{m=0}^{j-1}\nu _{m}\Psi _{j,m}~y_{m}^{n}(v)\right] \mathrm {d}v. \end{aligned}$$

Using the properties of the norm, we obtain

$$\begin{aligned}&\Vert K_{j}^{r}(\alpha _{j}^{1},\alpha _{j}^{2},\ldots ,\alpha _{j}^{n})-K_{j}^{r}(\beta _{j}^{1},\beta _{j}^{2},\ldots ,\beta _{j}^{n})\Vert \\&\quad \le Q E\left| \frac{\gamma }{\delta _{j}}\right| \left\| \int _{0}^{1}|N_{r}(v)|\left[ \sum _{m=0}^{j}\sum _{l=1}^{n}|M_{l}(v)||(\alpha _{m}^{l}-\beta _{m}^{l})|\right] \mathrm {d}v\right\| , \end{aligned}$$

where $Q =\left\{ \sum _{m=0}^{j}|\mu _{m}|^{2}\right\} ^\frac{1}{2}\;\text {and}\; E=\left\{ \sum _{m=0}^{j}|\Phi _{j,m}|^{2}\right\} ^\frac{1}{2},$ which can be written in the vector form:

$$\begin{aligned} \Vert \overline{K_{j}}(\overline{\alpha _{j}})-\overline{K_{j}}(\overline{\beta _{j}})\Vert&\le Q E \left| \frac{\gamma }{\delta _{j}}\right| \left\{ \sum _{r=0}^{n}\int _{0}^{1}|N_{r}(v)|^{2}\mathrm {d}v\right\} ^{\frac{1}{2}}. \left\{ \sum _{l=0}^{n}\int _{0}^{1}|M_{l}(v)|^{2}\mathrm {d}v\right\} ^{\frac{1}{2}}\\&\quad .\Vert (\overline{\alpha _{m}})-(\overline{\beta _{m}})\Vert . \end{aligned}$$

So the operator $\overline{K_{j}}$ is continuous under the condition:

$$\begin{aligned} Q E\left| \frac{\gamma }{\delta _{j}}\right| \left\{ \sum _{r=0}^{n}\int _{0}^{1}|N_{r}(v)|^{2}\mathrm {d}v\right\} ^{\frac{1}{2}}. \left\{ \sum _{l=0}^{n}\int _{0}^{1}|M_{l}(v)|^{2}\mathrm {d}v\right\} ^{\frac{1}{2}}<1. \end{aligned}$$

By Banach’s fixed point theorem, $\overline{K_{j}}$ has an unique fixed point $\overline{\alpha _{j}},$ that is, of course the unique solution of the system (4.15). It is obvious, for the only solution $(\alpha _{j}^{1},\alpha _{j}^{2},\dots ,\alpha _{j}^{n}),$ there is only solution $y_{i}^{n}(u)$ of Eq. (4.12). $\square$

5 Application and numerical results

In this section, we try to apply some of the numerical methods to approximate the solution of the Volterra–Fredholm integral equation.

Example

Consider the following linear Volterra–Fredholm integral equation:

$$\begin{aligned} y(u,t)=u^{2}t^{2}-\frac{u^{2}t^{6}}{16}-\frac{u^{2}t^{7}}{5} +\int _{0}^{t}\int _{0}^{1}t^{2}\tau (u^{2}v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau +\int _{0}^{t}t^{2}\tau ^{2}y(u,\tau )\mathrm {d}\tau . \end{aligned}$$

(5.1)

If $|\gamma | < 16.075102$ (when $T = 0.6$), we find that the numerical solution quickly converges with the exact solution $y(u,t)=u^{2}t^{2}$. We divide the interval $[0,T],\,0\le T<1,$ as $0=t_{0}<t_{1}<t_{2}<t_{3}=T,$ where, $t=t_{i},\,i=0,1,2,3,$ the linear Volterra–Fredholm integral Eq. (5.1) take the form:

$$\begin{aligned} \delta _{i}y_{i}(u)=u^{2}t^{2}_{i}-\frac{u^{2}t^{6}_{i}}{16}-\frac{u^{2}t^{7}_{i}}{5}+ \sum _{j=0}^{i}\mu _{j}t_{i}^{2}t_{j}u^{2}\alpha _{j}+\sum _{j=0}^{i-1}\nu _{j}t_{i}^{2}t_{j}^{2}y_{j}(u), \end{aligned}$$

where

$$\begin{aligned} \alpha _{j}=\int _{0}^{1}\frac{v}{ \delta _{j}}\left[ v^{2}t^{2}_{ij}-\frac{v^{2}t^{6}_{j}}{16}-\frac{v^{2}t^{7}_{j}}{5}+\sum _{m=0}^{j}\mu _{m}t_{j}^{2}t_{m}v^{2} \alpha _{m}+\sum _{m=0}^{j-1}\nu _{m}t_{j}^{2}t_{m}^{2}y_{m}(v)\right] \mathrm {d}v. \end{aligned}$$

In Table 1, we presented the absolute error $|y(u,t_{i})-y_{i}(u)|,\,i=0,1,2,3$, using the introduced numerical method (degenerate kernel) with $N=3$ in the interval [0, 0.6].

Table 1 Absolute error of solution of Eq. (5.1) using the degenerate kernel with $N=3$ and $0\le t\le 0.6$

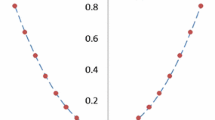
In addition, in Figs. 1, 2, 3, and 4, we presented a comparison between the exact solution and the approximate solution using the introduced numerical method with different values of $t_{i},\,i=0,1,2,3$ with $N=3$ in the interval [0, 1].

Fig. 1

The exact solution $y(u,t_{0})=u^{2} t_{0}^{2}$ and the approximate solution $y_{0}(u)$

Fig. 2

The exact solution $y(u,t_{1})=u^{2} t_{1}^{2}$ and the approximate solution $y_{1}(u)$

Fig. 3

The exact solution $y(u,t_{2})=u^{2} t_{2}^{2}$ and the approximate solution $y_{2}(u)$

Fig. 4

The exact solution $y(u,t_{3})=u^{2} t_{3}^{2}$ and the approximate solution $y_{3}(u)$

Example

Consider the following linear Volterra–Fredholm integral equation:

$$\begin{aligned} \begin{aligned} y(u,t)&=u^{2}e^{t}-\frac{u^{2}t^{5}}{3}-\frac{1}{36}t^{5}(4+3u)+\int _{0}^{t}\int _{0}^{1}t^{2}\tau (1+e^{u}v)y(v,\tau )\mathrm {d}v\mathrm {d}\tau \\&\quad +\int _{0}^{t}t^{2}\tau y(u,\tau )\mathrm {d}\tau . \end{aligned} \end{aligned}$$

(5.2)

Table 2 Absolute error of solution of Eq. (5.2) using the degenerate kernel with $N=3$ and $0\le t\le 0.6$

The numerical solution quickly converges with the exact solution $y(u,t)=u^{2}e^{t}$ if $|\gamma | < 5.451171$ (when $T = 0.6$). If we divide the interval $[0,T],0\le T<1,$ as $0=t_{0}<t_{1}<t_{2}<t_{3}=T,$ where, $t=t_{i},\,i=0,1,2,3,$ the linear Volterra–Fredholm integral Eq. (5.2) take the form:

$$\begin{aligned} \delta _{i}y_{i}(u)=u^{2}e^{t_{i}}-\frac{u^{2}t^{5}_{i}}{3}-\frac{1}{36}t^{5}_{i}(4+3u)+ \sum _{j=0}^{i}\mu _{j}t_{i}^{2}t_{j}(\alpha _{j}+e^{u}\beta _{j})+\sum _{j=0}^{i-1}\nu _{j}t_{i}^{2}t_{j}y_{j}(u), \end{aligned}$$

where

$$\begin{aligned} \alpha _{j}&=\int _{0}^{1}\frac{1}{ \delta _{j}}[v^{2}e^{t_{j}}-\frac{v^{2}t^{5}_{j}}{3}-\frac{1}{36}t^{5}_{j}(4+3v)+\sum _{m=0}^{j}\mu _{m}t_{j}^{2}t_{m}(\alpha _{m}+e^{v}\beta _{m})\\&\quad +\sum _{m=0}^{j-1}\nu _{m}t_{j}^{2}t_{m}y_{m}(v)]\mathrm {d}v,\quad j = 0,1,2,3, \end{aligned}$$

and

$$\begin{aligned} \beta _{j}&=\int _{0}^{1}\frac{v}{ \delta _{j}}[v^{2}e^{t_{j}}-\frac{v^{2}t^{5}_{j}}{3}-\frac{1}{36}t^{5}_{j}(4+3v)+\sum _{m=0}^{j}\mu _{m}t_{j}^{2}t_{m}(\alpha _{m}+e^{v}\beta _{m})\\&\quad +\sum _{m=0}^{j-1}\nu _{m}t_{j}^{2}t_{m}y_{m}(v)]\mathrm {d}v,\quad j = 0,1,2,3, \end{aligned}$$

In Table 2, we presented the absolute error $|y(u,t_{i})-y_{i}(u)|,\,i=0,1,2,3$, using the introduced numerical method (degenerate kernel) with $N=3$ in the interval [0, 0.6].

Fig. 5

The exact solution $y(u,t_{0})=u^{2} t_{0}$ and the approximate solution $y_{0}(u)$

Fig. 6

The exact solution $y(u,t_{1})=u^{2} t_{1}$ and the approximate solution $y_{1}(u)$

Fig. 7

The exact solution $y(u,t_{2})=u^{2} t_{2}$ and the approximate solution $y_{2}(u)$

Fig. 8

The exact solution $y(u,t_{3})=u^{2} t_{3}$ and the approximate solution $y_{3}(u)$

In addition, in Figs. 5, 6, 7, and 8, we presented a comparison between the exact solution and the approximate solution using the introduced numerical method with different values of $t_{i},\,i=0,1,2,3$ with $N=3$ in the interval [0, 1].

6 Conclusion and remarks

From the above results and discussion, the following may be concluded:

• 1. Equation (1.1) has a unique solution y(u, t) in the space $L_{2}[0,1]\times C^{2}[0,T]$, under some conditions.

• 2. The mixed integral equation of the second kind, in time and position, after using quadratic method leads to a system of linear Fredholm integral equations of the second kind in position.

• 3. The solution of the system of linear Fredholm integral equations is obtained using the degenerate kernel method.

• 4. The error value increases when it gets closer to the ends points $u = \pm 1$. It decreases at the middle when it gets closer to zero.