1 Introduction

Data privacy has been considered a significant issue for the past decades. The releasing data need privacy guarantee such that they cannot be re-identified back to the individuals inside. On the other hand, the very fast adoption rate for the IoT technologies even though can make people’s life more convenient, but the users’ privacy has to be protected properly [3].

The k-anonymity is one of the most widely used models for data privacy protection [15]. The model prevents the re-identification of individuals in the input datasets by employing data suppression and/or data generalization methods [18]. The suppression method protects data privacy by deleting some records from the given dataset, whereas the generalization method replaces the quasi-identifiers, attributes that can be linked with external data to re-identify the individuals [16], with a more general data. Generally, data suppression and data generalization in the k-anonymization process can affect the data utility or the usefulness of the data [17]. For ensuring both privacy and utility of the data, the k-anonymity model aims at the optimal solutions, which is protecting the data privacy and minimizing the effect of k-anonymization on the data utility.

In this paper, we focus on preserving the privacy of the IoT data, which typically the quasi-identifiers in the datasets have identical data types, so-called identical generalization hierarchy (IGH). An example IGH data from IoT devices are temperature data from the sensors, or the trajectory data and their timestamp of people from the motion detectors. Solving such special case effectively as well as efficient means that the privacy preservation of all the IoT data, which the nature of data complies to the IGH, can adopt our work. The proposed algorithm is based on the lattice of generalization traversal as in [5]; however, we take advantage of the special characteristics of an IGH data on k-anonymity model, i.e., the optimality between the nodes in different levels of generalization lattice. Our work is evaluated by experiments against well-known comparative algorithms in various aspects.

The organization of this paper is as follows. The basic background and definitions are introduced in Sect. 3. The details on the differences between an optimal k-anonymity of IGH data and non-IGH data, and our proposed optimal k-anonymity algorithms on the IGH data are presented in Sect. 4. The experimental results of the proposed algorithm with the other well-known algorithms are presented in Sect. 5. Finally, the conclusion and our future work are given in Sect. 6.

2 Related works

Privacy is one of the most important issues for IoT. The need to protect the privacy in IoT contexts is as much as in the other areas. There are a few attempts which are proposed to tackle privacy issues. For example, in [4], the privacy protection framework for IoT has been proposed, and the idea is to embed the protection mechanism into the system architecture. In [12], a security and privacy algorithm for Unicode data has been proposed for maintaining the privacy in IoT ecology. Or, in [9], the authors proposed an approach for preserving privacy based on the fault tolerance aggregation technique for the IoT people-centric sensing system.

In the past decade, several approaches have been proposed to address the optimal k-anonymity, which is one of the most prominent approaches to protect the privacy. Such optimization problem has been proven to be an NP-hard [13]. One of the most important approaches to tackle the problem was proposed by Samarati et al. in [16]. The proposed algorithm performs a binary search for the solution on a generalization lattice. Such a lattice structure is formed by combining the generalization hierarchy of each attribute of a given dataset. The authors proved that if there is no generalization of the level at height h that satisfies the k-anonymity condition, then there is no generalization in the lower level that satisfies k-anonymity either. Subsequently, a few important contributions, which adopted such an approach for reducing the computation time, have been made. For example, the Incognito algorithm [11] performs a bottom-up, breadth-first search on a generalization lattice of each subset of quasi-identifiers. Then, all subsets are evaluated for the k-anonymity condition. In [5], the Optimal Lattice Anonymization (OLA) algorithm is proposed. The general idea is to divide the generalization lattice into sublattices and determine the k-anonymity condition by searching within each sublattice. The process terminates when all sublattices have been evaluated. The Flash algorithm, proposed by Kohlmayer et al. [10], was developed to search for the optimal nodes of the lattice by building a path, and then the algorithm performs a binary search on each path. The algorithm stops when all paths are explored and evaluated and returns the optimal value.

3 Background

In this section, the basic definitions are introduced. Also, the concept of generalization based on the lattice structures which plays an important role in this paper is presented.

3.1 Basic definition

Definition 1

(Quasi-identifier) The quasi-identifier is a set of attributes \(\mathrm{QI}={Q_1, Q_2, \dots , Q_w}\) in the given dataset T that could be linked with the external data for re-identifying the individual.

Definition 2

(k-anonymity) A dataset satisfies the k-anonymity condition, where \(k > 1\), when each combination of quasi-identifiers exists at least k tuples in dataset T such that \(t[C] = t_{{i}_{1}}[C]= \dots = t_{{i}_{k-1}}[C], C \in \mathrm{QI}\).

Let us consider the dataset in Table 1(a). The quasi-identifiers in this dataset are \({\mathrm{QI} {=} {Sex, Age, Submissiondate}}\), while Disease can be considered a sensitive attribute that must be protected. For satisfying the k-anonymity condition, each tuple must not be distinguished from at least other \(k-1\) tuples. Setting the k value at 2, it is obvious that the dataset is not meeting the k-anonymity condition because each tuple does not have at least other \(k-1\) identical tuples.

Table 1 An example of a non-IGH dataset
Full size table
Table 2 An example of an IGH dataset
Full size table

To anonymize the datasets, the generalization method to replace the original value by its more general form is usually applied [16]. Such generalization can be formed as the generalization hierarchy structure.

Definition 3

(Generalization hierarchy) Let the generalization for an attribute A be a function on A, and let \(A_{0}\overset{f_{0}}{\longrightarrow }A_{1}\overset{f_{1}}{\longrightarrow }\cdots \overset{f_{n-1}}{\longrightarrow }A_{n}\) be a function generalization sequence. The generalization hierarchy for A is a set of functions \(f_{h}:h=0,1,\ldots ,n-1\) such that \(A = A_{0}\) and \(|A_{n}|=1\).

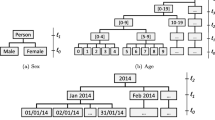
The value in the higher level of the generalization hierarchy is less specific than the value at the lower level. From the running example dataset in Table 1(a), the Age is the numeric data which could be generalized into the more general interval, Male and Female of a Sex attribute is the categorize data which can be generalized into Person, and Submission Date can be generalized from day/month/year format to only year in the highest level.

The generalization hierarchy of Sex, Age, and Submission Date is shown in Fig. 1a–c, respectively. Using the generalization hierarchies for generalizing the dataset in Table 1(a), we can obtain the generalized dataset as shown in Table 1(b) which satisfies the 2-anonymity condition or so-called a 2-anonymous dataset.

Fig. 1
figure 1

The generalization hierarchy of a non-IGH dataset

Full size image
Fig. 2
figure 2

The generalization hierarchy of an IGH dataset

Full size image

In this paper, we focus on the datasets where the attributes in the quasi-identifier have the same data type. An example dataset of such kind is shown in Table 2(a), where the quasi-identifier is the satisfaction score that users give to the taxi drivers. Obviously, the scores for taxi drivers are the same data type. Thus, the generalization hierarchy of the dataset is also identical. Hence, for privacy preservation, only one generalization hierarchy in Fig. 2 is used for generalizing this dataset. We refer to this type of dataset as an “Identical Generalization Hierarchy” or an IGH data, while other type of data is a “non-Identical Generalization Hierarchy” or a non-IGH data.

Definition 4

(Identical generalization hierarchy data) Let \(H=\{H_{1},H_{2},\ldots ,H_{m}\}\) be the set of the generalization hierarchy function of attributes \(\{A_{1},A_{2},\ldots ,A_{m}\}\) in a dataset T. A dataset T is an IGH data if and only if \(\bigcup _{i=1}^{m}H_{i} =H_{1}=H_{2}=\cdots =H_{m}\).

For privacy preservation, the IGH dataset in Table 2(a) can be generalized to satisfy the 2-anonymity condition using the generalization hierarchy in Fig. 2 into the dataset in Table 2(b).

3.2 Lattice of generalization

In order to represent the generalized dataset in the context of privacy preservation problems, the lattice of generalization [5] is commonly applied. Each node of the lattice of generalization indicates the generalization level of each quasi-identifier attribute, while the successor of each node is the direct generalization with less specific generalization. Figure 3a shows an example of the lattice of generalization from the dataset in Table 1(a) using generalization hierarchy in Fig. 1. It can be seen that the nodes in the lowest level of the generalization lattice, node<000>, are the minimal generalization node, or the original values of quasi-identifier, while the least specific generalization node, or the highest level, node<142>, indicates the highest generalization of all quasi-identifiers. We indicate the generalization nodes which satisfy the k-anonymity condition, called k-anonymous node, by the shaded nodes, e.g., node<121>. Note that on the right-hand side of lattice, we show the generalization level to be used in the next section. According to [5], the lattice of generalization has two properties as follows.

  1. 1.

    If a node is a k-anonymous node, then all its successor nodes are also k-anonymous node.

  2. 2.

    On the other hand, if a node is not a k-anonymous node, then all its predecessor nodes are also not the k-anonymous node.

Fig. 3
figure 3

The lattice of generalization

Full size image

To prevent an over-generalization to the given dataset, the information loss is measured to the k-anonymity process. For quantifying the information, the precision (Prec) is usually used [19]. The precision is a metric that relates to the height of generalization-level h of each quasi-identifier \(\mathrm{QI}\). Let the generalized version of dataset T be denoted as \(GT(A_1, A_2, \dots , A_m)\), and let height(H) be the highest generalization height of each quasi-identifier. The precision of GT is given by

$$\begin{aligned} Prec(GT)=\frac{1}{m}\cdot \sum _{i=1}^{m}\frac{h_{i}}{height(H_{i})} \end{aligned}$$
(1)

The precision of the lowest level node of the lattice of the generalization is 0, while at the highest generalization node, the precision is 1. The generalization data with higher precision metric loses more information than the lower precision. We specify the precision of each node by the red letter in generalization lattice nodes. From our running example dataset in Table 1(a) together with the generalization hierarchies in Fig. 1a–c, it can be seen that the Prec(<011>) = 0.25, while Prec(<121>) = 0.67. It can be implied that node<121> loses more information than node<011>.

3.3 Lattice of generalization on IGH

For the IGH data, the generalization hierarchies of the quasi-identifier attributes are identical, so the highest generalization height of each quasi-identifier height(H) is also identical. Thus, the precision equation of an IGH data can be transformed as in Eq. 2.

$$\begin{aligned} Prec(GT)=\frac{1}{m\cdot height(H)}\cdot \sum _{i=1}^{m}h_{i} \end{aligned}$$
(2)

From the equation, it can be seen that the precision of an IGH dataset depends on only the term \(\sum _{i=1}^{m}h_{i}\). This term is the summation of the generalization height of each quasi-identifier which is equal to the level of the generalization lattice. From the equation, the characteristics of k-anonymity of IGH data are as follows.

  1. 1.

    The precision of the nodes in the same level of generalization lattice is always identical. As the precision of an IGH data depends on the summation of the generalization height of each quasi-identifier, the precision of the nodes in the same level of generalization lattice is identical. For example, from the IGH lattice in Fig. 3b, we can see that identical values are in the same generalization levels.

  2. 2.

    The precision of the nodes in the lower level of generalization lattice is always less than the precision of the node in the higher level. According to Eq. 2, the precision of an IGH data is the generalization lattice level of each node divided by the generalization height and number of tuples. Thus, at a lower generalization lattice level, the precision of an IGH data is always lower than the precision at the higher generalization lattice level. To illustrate this observation, in 3b, the precision of an IGH data in the generalization lattice at level 3 is 0.5 which is always lower than the precision of the nodes in level 4 at 0.67. Unlike non-IGH data, the precision of the nodes in the lower generalization lattice could be greater than the precision of the nodes at the higher level. For example, in Fig. 3a, the precision of the node<102> at level 3 is greater than the precision of the node<040> at level 4.

  3. 3.

    The highest level of the generalization lattice of an IGH data generalizes all quasi-identifiers to the same level. As we can see in Fig. 3b, the highest level of the lattice generalizes the quasi-identifiers to the same hierarchy at level 2.

Note here that, for a given k value, there can exist solutions for the k-anonymization, which their precision metric is the same value. Thus, the models in this paper also apply the second metric, the discernibility metric (DM) [1] as in the previous work [20]. Discernibility metric (DM) is the information loss metric that measures the number of tuples of the equivalence class, the identical quasi-identifier group in the generalized dataset. Let E be an equivalence class of a generalized dataset GT of the original dataset T, the DM of GT can be calculated as

$$\begin{aligned} \mathrm{DM}(GT) = \sum _{\forall E s.t |E|\geqslant k}|E|^2 \end{aligned}$$
(3)

When the multiple optimal solutions determined by the precision are found, the DM will be measured to break the tie by choosing the node with the lowest DM as the single optimal solution. For example, from Fig. 3b, it is found that node<211> and node<022> are both optimal solution with the precision of 0.67. In this case, the single optimal solution is node<022> since its DM is 22, instead of node<211> which its DM is 34.

4 Optimal k-anonymity

In this section, we present our proposed algorithm to exploit the characteristics of IGH data to improve the efficiency of the optimal k-anonymization. The key idea of our algorithm is to analyze only necessary nodes, which are among the lowest generalization level found as k-anonymous nodes as compared to other algorithms in the literature that have to examine all nodes. The algorithm first finds the routes from the root node of the generalization lattice, i.e., <000> to the highest level node using pre-order traversal method. All nodes in the routes are to be determined the k-anonymity started from the node at the lowest level. The k-anonymous nodes are to be tagged, and the lowest level found k-anonymous, called k-anonymous level, is set. The algorithm continues to traverse to the other routes and visit only the nodes in the lower than the k-anonymous level until all nodes in the lower than the k-anonymous level are found and tagged.

From the characteristic of an IGH data, an optimal solution always among the lowest level found optimal nodes so-called k-anonymous level. Therefore, to make sure that the algorithm could find the optimal solution, the Optimal-IGH algorithm would traverse through the generalization lattice with the depth-first search manner until all nodes in the k-anonymous level and its one lower level are tagged. The algorithm performs the depth-first search traversal method, so the algorithm could find the optimal not only the suboptimal solution.

4.1 Optimal-IGH algorithm

4.1.1 Optimal-IGH algorithm

The main algorithm Optimal-IGH, shown in Algorithm 1, first finds the highest level of the input generalization lattice; then, the arguments would be passed to the subalgorithm FindAnonymous, illustrated in Algorithm 2. The algorithm FindAnonymous with the input, Level LV, Quasi-identifier \(\mathrm{QI}\), and Traversal method TR, is to find all routes from the root node to node in level LV using pre-order traversal method. Then, for each node in the route, the algorithm will evaluate the node using two conditions as follows:

  1. 1.

    If a node is a k-anonymous node, then such node and all its successor nodes are to be tagged as the k-anonymous node, and the current level in the lattice is set as the lowest level nLV.

  2. 2.

    If a node is not a k-anonymous node, then such node and its predecessor nodes are to be tagged as the non k-anonymous node.

After all nodes in a route are tagged, the algorithm compares the lowest level nLV and the input level LV. The algorithm breaks from the loop if nLV is less than LV. Subsequently, the algorithm recursively executes with the input level nLV until the lowest level nLV and the input level LV are equal which means that the level nLV is the lowest level found k-anonymous nodes. After that, the algorithm FindAnonymous returns all k-anonymous nodes K in the level nLV back to Optimal-IGH. Finally, the main algorithm compares the DM of each generalized dataset using the generalization of k-anonymous nodes K. Eventually, the globally optimal k-anonymity node is the node with the lowest DM.

figure a
figure b
figure c
Table 3 The study result of the traversal method on an Optimal-IGH algorithm
Full size table

4.1.2 Example of Optimal-IGH algorithm

In this section, we explain the algorithm in more detail using the running example in Table 2 and the lattice in Fig. 3b with the k value set at 2. The proposed Optimal-IGH algorithm starts with evaluating the root node of lattice, <000>. Then, the algorithm traverses to visit the other nodes using a pre-order traversal method. The nodes <100>, <200>, <210>, <220>, <221> and <222>, in the first route, are evaluated, respectively. As we can see that nodes <100>, <200>, <210> and <220> are not k-anonymous nodes. Therefore, the node <221> is a k-anonymous; then, its successor nodes are tagged as a k-anonymous node. This means that level 5 of the lattice is the current k-anonymous level. Subsequently, the next route is determined from the root node until such level 5. Until all nodes are tagged, the algorithm stops this process. Thus, the last k-anonymous level is 4 and there are 2 k-anonymous nodes in such level, i.e., node<211>, and node<022>. Finally, the algorithm compares the DM of k-anonymous nodes in level 4, in which node<022> is found the optimal k-anonymity node with the least DM.

4.1.3 Enhancement of Optimal-IGH algorithm

In general, the optimal node in the generalization lattice might be located in a different location depending on the structure of the given dataset. The Optimal-IGH algorithm traverses to the nodes in the generalization lattice to determine an optimal k-anonymity solution using the pre-order traversal method by visiting the left child first. An issue is whether the traversal method affects the performance of the algorithm. Thus, in this paper, we further study the Optimal-IGH using various traversal methods to evaluate their performance, i.e., pre-order with left child node first (pre-left), pre-order with right child node first (pre-right), pre-order with maximum degree child node first (pre-max), pre-order with minimum degree child node first (pre-min), post-order with left child node first (post-left), post-order with right child node first (post-right), post-order with maximum degree child node first (post-max) and post-order with minimum degree child node first (post-min). The evaluation is conducted on real-life IGH datasets, i.e., Jester [7] and Taxi [21]. The k-anonymity condition is set at 3, and the number of quasi-identifiers is varied from 3 to 9.

The evaluation result shows in Table 3 the number of the visited nodes on 8 traversal methods. The bold letter cell in the table indicates the lowest number of the visited nodes of each number of quasi-identifiers, which is the fastest method to find an optimal solution. From the result, the traversal method that produces the lowest number of visited nodes is diverse among the dataset. Thus, to ensure the efficiency, the traversal method should be determined and selected differently. Furthermore, we can see that the traversal method that visits the lowest number of nodes produces the same performance with regard to the number of quasi-identifiers. For instance, in Table 3(a), at the number of quasi-identifiers at 3, the traversal method that produces the lowest number of visited nodes is the post-order with the maximum degree child first (post-max). It can be seen that the number of nodes that the traversal visited is the lowest for any number of quasi-identifiers.

From the study, we further enhance the performance of our Optimal-IGH algorithm by determining the traversal method for the given dataset first. It can be done by performing the Optimal-IGH algorithm at the lower number of quasi-identifiers, i.e., 3, since it can be applicable to the other higher number of quasi-identifiers. Selecting the lower number of quasi-identifier reduces the execution time as shown in the literature [2, 6, 11].

In Algorithm 3, the Enhance-Optimal-IGH algorithm is shown. It first determines the suitable traversal method and then continues to find an optimal solution with an Optimal-IGH algorithm. For instance, the post-max and the post-min traversal is to be selected for the Jester and Taxi dataset as the result in Table 3(a) and (b) indicates, respectively.

5 Experimental evaluation

After the algorithm is proposed, this section presents the experimental results for evaluating our contribution.

5.1 Dataset

Our work is evaluated using three real-life IGH datasets from Jester [7], T-drive [21] and MovieLens [8]. The Jester dataset is the anonymous ratings from the Jester online joke recommender system. The rating score range is between \(-\,10\) and \(+\,10\) with 5000 records used in the experiments, and the number of quasi-identifiers is varied from 6 to 11. The T-drive dataset contains the GPS trajectories of taxis together with timestamp. The dataset is pre-processed to select only the trajectories with 6–11 timestamps resulting in 2500 records. The MovieLens dataset contains the rating score that users rated each movie. Basically, the attributes are the list of movies. The rating score range is between 0 and 5. For this dataset, there are 925 records, and the number of quasi-identifiers can be varied from 6 to 16.

5.2 Experimental configuration

Our proposed algorithms, i.e., Optimal-IGH and Enhance-Optimal-IGH, are to be compared with five well-known comparative algorithms including optimal k-anonymity: Samarati [16], Incognito [11], OLA [5, 14], Flash [10] and the depth-first search (DFS) algorithm. These algorithms all traverse to the lattices to find optimal solutions with different strategies as mentioned in the related work section. All algorithms are implemented based on Java SE 8. The experiments are proceeded on a 2x Intel X5670 with 24 GB memory running Linux. We average the execution time/number of visited nodes in each configuration three times to obtain stable results.

5.3 Results and discussion

5.3.1 Execution time

In the first section of experiments, we report the performance of the proposed algorithm by execution time.

Fig. 4
figure 4

Execution time per number of quasi-identifiers

Full size image
Fig. 5
figure 5

Execution time per generalization hierarchy level

Full size image
Fig. 6
figure 6

Execution time per k value

Full size image

Execution time and the number of quasi-identifiers

In the first experiment, the execution time of the proposed algorithm is reported, while the number of quasi-identifiers is varied. Note that the k value is set at 3. The result on Jester, T-drive and MovieLens datasets is reported in Fig. 4a–c, respectively. It can be seen from the results that all the algorithms perform in a similar trend, i.e., the execute time is increased exponentially when the number of quasi-identifiers is increased. At the lower number of quasi-identifiers, the Optimal-IGH algorithm uses the least execution time to determine an optimal solution followed by the Flash and Enhance-Optimal-IGH in a slight margin. The reason behind this is that the Enhance-Optimal-IGH algorithm has to evaluate the data to determine the traversal method first. Thus, at the lower number of quasi-identifiers, the Enhance-Optimal-IGH is slightly slower than the other two algorithms. At the higher number of quasi-identifiers, i.e., 10–11, 9–11 and 8–16 for the Jester, T-drive and MovieLens, respectively, the Enhance-Optimal-IGH algorithm uses the least execution time to determine an optimal k-anonymity. The second fastest algorithm is Optimal-IGH, since these two algorithms traverse to the node and evaluate the k-anonymity condition only necessarily.

Fig. 7
figure 7

Number of visited nodes per number of quasi-identifiers

Full size image

Execution time per generalization hierarchy level

In the second experiment, the effect of the level of generalization hierarchies to the execution time is investigated. The number of quasi-identifiers is set at 10, and the generalization hierarchy level is varied from 2 to 5. The result is shown in Fig. 5. Generally, it is obvious that the execution time of all the algorithm is increased exponentially when the generalization hierarchy level is increased. The number of generalization hierarchy levels also increases the number of nodes in the lattice and hence affects the execution time to traverse and evaluate the k-anonymity. However, it can be seen that the Enhance-Optimal-IGH is highly efficient for finding an optimal solution comparing with other algorithms. This can highly benefit the IoT-IGH data since the algorithm can cope with various ranges of the data from sensors or actuators which could be large and then result in a large generalization hierarchy.

Execution time and k constraint

In Fig. 6a–c, we present the result when the k constraint from the k-anonymity model is varied on Jester, T-drive and MovieLens dataset, respectively. From the result, it is clear that the execution time of each algorithm is not affected by the k value. However, it can be seen that the Enhance-Optimal-IGH algorithm is still the most efficient algorithm to find optimal solutions.

5.3.2 Node evaluated comparison

In order to evaluate the efficiency of our algorithm in detail, the number of nodes to be evaluated in the generalization lattice is reported in this section. In Fig. 7, the result is presented, the x-axis is the number of quasi-identifiers, while the y-axis is the number of nodes evaluated by the optimal k-anonymity algorithms. Note that the numbers are reported in a logarithmic scale. The label of each bar shows the percentage of node visited of each algorithm compared to the number of all nodes on the lattice. Clearly, evaluating only fewer nodes shows that an algorithm is higher efficient, and comparing our Enhance-Optimal-IGH algorithm and Optimal-IGH algorithm can show the efficiency which can be obtained from the traversal method selection. From the result, it is clear that the Enhance-Optimal-IGH algorithm is highly efficient, it evaluates the least number of nodes in all settings. For instance, at the number of quasi-identity at 7 in Fig. 7a, the Enhance-Optimal-IGH evaluated 0.173% of all nodes, while Samarati has evaluated 13.871% of all nodes. The graph also shows that our Enhance-Optimal-IGH algorithm has processed less number of nodes than the other algorithms. The node processing step is the time-consuming process, so the fewer number of nodes processed the faster find an optimal solution. The trend of a graph exponentially increases when the number of quasi-identifiers increased. Moreover, the traversal method selection aids improving the efficiency though it requires additional scans on the lattice, as we can see the comparison with the Optimal-IGH algorithm results.

6 Conclusion and future work

In summary, this paper presents a novel optimal k-anonymity algorithm for the identical generalization hierarchy (IGH) data which is the main data type in the IoT environment. The algorithms, Optimal-IGH and Enhance-Optimal-IGH, that suits for IGH data are presented. The algorithms which are highly efficient are based on the fact that the IGH data’s properties, i.e., the identical precision of the nodes in the same level of generalization lattice, and the relationship between the precision of the nodes in different levels of generalization lattice. In the case of the Enhance-Optimal-IGH algorithm, we further investigate and find that the traversal into the generalization lattice can affect the efficiency. Thus, we propose to determine the traversal method first, by evaluating a few nodes. The experimental results show that our proposed algorithm, Enhance-Optimal-IGH, can efficiently find an optimal k-anonymity solution. For our future work, we will focus on the situation where the quasi-identifier of IGH data can be updated. For example, when more sensors or actuators are added or removed from the system, coping with such a situation can help the algorithm to protect data privacy in such contexts more practically.