1 Introduction

The Kalman filter is an efficient recursive filter [1]. Because of its excellent mathematical properties and good performance, it has been widely used in many fields such as navigation systems [2], vehicle positioning [3, 4], target tracking [5], communication systems to battery management systems [6, 7].

1.1 Kalman filtering in information learning theory

KF is proposed based on the minimum mean square error (MMSE) criterion [8], whose use of the MMSE criterion minimizes the mean squared error between the estimated and true values [9, 10]. Thus, it can show good performance in a Gaussian noise environment [11]. However, the performance is severely degraded in real-world environments, which usually face the effects of impulse noise. For this reason, researchers have focused on Kalman filtering algorithms that can be applied to non-Gaussian noise environments. In information-theoretic learning (ITL), correlation entropy is used as a local similarity measure that focuses only on the local portion of the probability density in the kernel size range, making it a robust cost in signal processing and machine learning. Literature [12] proposed a maximum correlation entropy Kalman filtering algorithm (MCKF), that successfully reduces the effect of non-Gaussian noise by exploiting the insensitivity of a local metric like correlation entropy to outliers. Since then a series of Kalman filtering algorithms based on maximum correlation entropy have been proposed to improve the system’s steady state. For example, to solve the dispersion-prone property of the small kernel width state, the maximum correlation entropy Kalman filtering algorithm (m-MCKF) based on m-estimation has been proposed in the literature [13]. To find a suitable noise covariance matrix, an adaptive maximum correlation entropy Kalman filtering algorithm (AMCKF) is proposed in literature [14]. Nevertheless, MCC is usually implemented based on a Gaussian kernel function, researchers found that the performance of the algorithm can be optimized by changing the kernel function, so literature [15] proposed a maximum correlation entropy Kalman filtering algorithm based on student’s kernel (STTKF), and literature [16] proposed a Kalman filtering algorithm based on Cauchy kernel (CKKF).

However, MCC can fix the peak of the probability density function to zero, which makes the algorithm accuracy limited, for this reason, researchers take advantage of this advantage of minimum error entropy (MEE) to optimize directly for the distribution of errors and propose the Kalman filtering algorithm (MEE-KF) based on minimum error entropy in literature [17]. Although the MEE criterion reduces the uncertainty of the error variable, it does not converge the error to zero due to the translational invariance of the entropy; for this reason, a central error entropy Kalman filtering algorithm (CEEKF) has been proposed in the literature [18]. Literature [19] proposes an outlier-robust Kalman filters with mixture correntropy. To solve the problem that the shape of the kernel function of the error entropy cannot be changed freely, the researchers make use of the property that the generalized Gaussian kernel function can be adjusted to the shape freely and propose a Kalman filtering algorithm based on the generalized minimum error entropy criterion (GMEEKF) in the literature [20]. Since then to improve the robust performance of the algorithm at the expense of algorithm complexity, literature [21]-based adaptive kernel sensitive loss Kalman filtering algorithm (AKRSLKF) and various other Kalman filtering algorithms have been proposed.

1.2 Research motivation and contributions

In the course of our research, we found that compared to some other cost functions, the Softplus function has a better tolerance to outliers, which makes the model robust to handling noisy data. Furthermore, the smoothness of Softplus will enable easier finding of optimal solutions when using optimization algorithms such as gradient descent. M-estimation as a robust estimation method [22, 23], on the one hand, his score function and its derivative are bounded, so the influence function is bounded and M-estimation is robust [24,25,26]. On the other hand, the objective function of M-estimation can be freely chosen within a certain range to accommodate different needs, and the slower the objective function grows as the absolute value of the residuals increases, the more robust the estimation becomes.

Therefore, in this paper, a robust maximum correlation entropy Kalman filtering algorithm based on S-function is developed to solve the problem of insufficient robustness and convergence speed of maximum correlation entropy to deal with impulse noise. The algorithm first exploits the smooth robustness of S-shaped functions and the insensitivity of the maximum correlation entropy local measure to outliers, makes it based on the maximum correlation entropy Kalman filtering algorithm, which speeds up the convergence and enhances the robustness to a lesser extent. However, with the algorithm at large kernel widths, we find that the robust performance of the algorithm has some magnitude of degradation compared to MCKF. For that, we introduce the robustness method of Huber regression weighting so that it can better handle the effects of outliers, making the algorithm more robust here while having a faster convergence rate. Finally, the Monte Carlo simulation experiments in different impulse noise cases prove that the algorithms in this paper have faster convergence speed and better robust performance compared with KF, MCKF, STTKF and other algorithms.

1.3 Structure of the article

The structure of this paper is organized as follows: Section 2 introduces the classical Kalman filtering algorithm and the correlation entropy theory, Sect. 3 carries out the derivation of the Kalman filtering algorithm in this paper, and then the mean square error analysis and the time complexity analysis are given in Sects. 4 and 5, we carry out the simulation comparison in the Gaussian as well as non-Gaussian environments to make use of Monte Carlo experiments of the two models to illustrate the superiority of the algorithm more effectively, and finally, the conclusion is given in Sect. 6.

2 Classical Kalman filtering algorithm and correlation entropy

2.1 Classical Kalman filter algorithm

The Kalman filtering algorithm acts as an optimal estimator under the assumption of linearity and Gaussian, and the linear system is defined as the following state and measurement equations.

$$\begin{aligned} {{\textbf{x}}_k}= & {} {{\textbf{A}}_{k - 1}}{{\textbf{x}}_{k - 1}} + {{\textbf{w}}_{k - 1}} \end{aligned}$$
(1)
$$\begin{aligned} {{\textbf{y}}_k}= & {} {{\textbf{C}}_k}{{\textbf{x}}_k} + {{\textbf{v}}_k} \end{aligned}$$
(2)

where \({{\textbf{x}}_k} \in {\mathbb {R}^n}\) represents the n-dimensional state vector at moment, represents the m-dimensional observation vector at moment k, \({{\textbf{A}}_{k - 1}}\) and \({{\textbf{C}}_k}\) represent the state transfer matrix and the observation matrix, \({{\textbf{w}}_{k - 1}}\) and \({{\textbf{v}}_k}\) represent the process noise vector and the observation noise vector, which are uncorrelated and have a mean value of zero. Define the corresponding covariance matrices as \({{\textbf{Q}}_{k - 1}}\) and \({{\textbf{R}}_k}\) denoted by

$$\begin{aligned} E[{{\textbf{w}}_{k - 1}}{\textbf{w}}_{k - 1}^\textrm{T}]= & {} {{\textbf{Q}}_{k - 1}} \end{aligned}$$
(3)
$$\begin{aligned} E[{{\textbf{v}}_k}{\textbf{v}}_k^\textrm{T}]= & {} {{\textbf{R}}_k}. \end{aligned}$$
(4)

In general, the Kalman filtering algorithm can represented through two steps: prediction and update:

(1) Prediction: Obtain a priori state estimation matrix and a priori error covariance matrix

$$\begin{aligned} {{\hat{\textbf{x}}}_{k|k - 1}}= & {} {{\textbf{A}}_{k - 1}}{{\hat{\textbf{x}}}_{k - 1|k - 1}} \end{aligned}$$
(5)
$$\begin{aligned} {{\textbf{P}}_{k|k - 1}}= & {} {{\textbf{A}}_{k - 1}}{{\textbf{P}}_{k - 1|k - 1}}{\textbf{A}}_{k - 1}^\textrm{T} + {{\textbf{Q}}_{k - 1}} \end{aligned}$$
(6)

(2) Update: Obtain Kalman gain, a posteriori state estimation matrix, and a posteriori covariance matrix

$$\begin{aligned} {\textbf{K}}= & {} {{\textbf{P}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T}{({{\textbf{C}}_k}{{\textbf{P}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T} + {{\textbf{R}}_k})^{ - 1}} \end{aligned}$$
(7)
$$\begin{aligned} {{\hat{\textbf{x}}}_{k|k}}= & {} {{\hat{\textbf{x}}}_{k|k - 1}} + {\textbf{K}}({{\textbf{y}}_k} - {{\textbf{C}}_k}{{\hat{\textbf{x}}}_{k|k - 1}}) \end{aligned}$$
(8)
$$\begin{aligned} {{\textbf{P}}_{k|k}}= & {} ({\textbf{I}} - {\textbf{K}}{{\textbf{C}}_k}){{\textbf{P}}_{k|k - 1}}{({\mathbf{I - K}}{{\textbf{C}}_k})^\textrm{T}} + {\textbf{K}}{{\textbf{R}}_k}{{\textbf{K}}^\textrm{T}} \end{aligned}$$
(9)

where \({\textbf{I}} \in {\mathbb {R}^{n \times n}}\) is the unit matrix for \(n \times n\).

2.2 Correlation entropy

Define two random variables X, Y with joint probability density \({F_{XY}}(x,y)\) and correlation entropy criterion defined as

$$\begin{aligned} V(X,Y) = E[\alpha (X,Y)] = \int {\alpha (X,Y)d({F_{XY}}(x,y))} \end{aligned}$$
(10)

where \(E[ \cdot ]\) is the mathematical expectation and \(\alpha ( \cdot , \cdot )\) is the kernel function, denoted as

$$\begin{aligned} \alpha (X,Y) = {G_\sigma }(e) = \exp \left( - \frac{{{e^2}}}{{2{\sigma ^2}}}\right) \end{aligned}$$
(11)

where \(e = X - Y\), \(\sigma \) is the kernel width and \(\sigma > 0\). We can obtain the cost function of the maximum correlation entropy Kalman filtering algorithm as

$$\begin{aligned} {J_{MCC}}({{\textbf{x}}_{\textbf{k}}}) = \frac{1}{L}\sum \limits _{i = 1}^L {{G_\sigma }(e)} \end{aligned}$$
(12)

where \(L = n + m\).

3 Algorithm proposal

3.1 Enhanced models

First rewrite Eq. (1) and (2) as

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{{\hat{\textbf{x}}}}_{k|k - 1}}}\\ {{{\textbf{y}}_k}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\textbf{I}}\\ {{{\textbf{C}}_k}} \end{array}} \right] {{\textbf{x}}_k} + {o_k} \end{aligned}$$
(13)

where \({o_k} = \left[ {\begin{array}{*{20}{c}} { - \left( {{{{\hat{\textbf{x}}}}_k} - {{{\hat{\textbf{x}}}}_{k|k - 1}}} \right) }\\ {{{\textbf{v}}_k}} \end{array}} \right] \),

with

$$\begin{aligned} E\left[ {{o_k}o_k^\textrm{T}} \right]= & {} \left[ {\begin{array}{*{20}{c}} {{{\textbf{P}}_{k|k - 1}}}&{}0 \\ 0&{}{{{\textbf{R}}_k}} \end{array}} \right] \nonumber \\= & {} \left[ {\begin{array}{*{20}{c}} {{{\mathbf{\upsilon }}_{P:k|k - 1}}{\mathbf{\upsilon }}_{P:k|k - 1}^\textrm{T}}&{}0\\ 0&{}{{{\mathbf{\upsilon }}_{R:k}}{\mathbf{\upsilon }}_{R:k}^\textrm{T}} \end{array}} \right] = {{\mathbf{\upsilon }}_k}{\mathbf{\upsilon }}_k^\textrm{T} \end{aligned}$$
(14)

where \({{\mathbf{\upsilon }}_{P:k|k - 1}}\), \({{\mathbf{\upsilon }}_{R:k}}\) and \({{\mathbf{\upsilon }}_k}\) are obtained from \({{\textbf{P}}_{k|k - 1}}\), \({{\textbf{R}}_k}\) and \(E\left[ {{o_k}o_k^\textrm{T}} \right] \) by Cholesky decomposition, respectively.

Simultaneous left-multiplication of \({\mathbf{\upsilon }}_k^{ - 1}\) on both sides of Eq. (13) gives us

$$\begin{aligned} {{\textbf{D}}_k} = {{\textbf{W}}_k}{{\textbf{x}}_k} + {{\textbf{e}}_k} \end{aligned}$$
(15)

where \({{\textbf{D}}_k} = {\mathbf{\upsilon }}_k^{ - 1}\left[ {\begin{array}{*{20}{c}} {{{{\hat{\textbf{x}}}}_{k|k - 1}}}\\ {{{\textbf{y}}_k}} \end{array}} \right] \), \({{\textbf{W}}_k} = {\mathbf{\upsilon }}_k^{ - 1}\left[ {\begin{array}{*{20}{c}} {\textbf{I}}\\ {{{\textbf{C}}_k}} \end{array}} \right] \) and \({{\textbf{e}}_k} = {\mathbf{\upsilon }}_k^{ - 1}\left[ {\begin{array}{*{20}{c}} { - \left( {{{{\hat{\textbf{x}}}}_k} - {{{\hat{\textbf{x}}}}_{k|k - 1}}} \right) }\\ {{{\textbf{v}}_k}} \end{array}} \right] \). It can be further written as \({{\textbf{D}}_k} = {[{d_{1:k}},{d_{2:k}}, \cdots ,{d_{L:k}}]^\textrm{T}}\), \({{\textbf{W}}_k} = {[{{\textbf{w}}_{1:k}},{{\textbf{w}}_{2:k}}, \cdots ,{{\textbf{w}}_{L:k}}]^\textrm{T}}\) and \({{\textbf{e}}_k} = {[{e_{1:k}},{e_{2:k}}, \cdots ,{e_{L:k}}]^\textrm{T}}\). Thus

$$\begin{aligned} {e_{i:k}} = {d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k}. \end{aligned}$$
(16)

3.2 Derivation of HWSKF

To increase the convergence speed and steady state of the algorithm based on the MCKF algorithm and better adapt to the effect of impulse noise, the HWSKF algorithm presented in this section generates a new cost function framework that combines the Softplus function with the MCKF algorithm. Observe the expression for the Softplus function, which has the derivative form \(\frac{1}{{1 + {e^{ - x}}}}\), such a function is consistent with the outer manifestation of filter theory. The Softplus function expression is in logarithmic form, a feature that makes the algorithm faster to compute. On the other hand, Huber estimation is a robust statistical method designed to deal with outliers or outliers in regression analysis, while maintaining efficiency and accuracy for non-outliers. At its core is a loss function that combines the characteristics of squared loss (used in least squares) and absolute value loss (used in L1 regularization), so it can give optimal results when the noise obeys a normal distribution, and when it does not conform to a normal distribution, it can effectively address the effects of outliers and get better results than least squares.

In summary, a new Huber-weighted S-type fusion cost function is defined as

$$\begin{aligned} {J_L}({{\textbf{x}}_k}) = \frac{1}{L}\sum \limits _{i = 1}^L {{\vartheta _{i:k}}\log \left( 1 + {{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}\right) } \end{aligned}$$
(17)

where \({\vartheta _i}(x;{e_i}) = \left\{ {\begin{array}{*{20}{c}} {1,|{e_i}| \le \delta }\\ {\frac{\delta }{{|{e_i}|}},|{e_i}| > \delta } \end{array}} \right. \), \({\vartheta _i}\) is the weighting factor for the ith point. Thus, the optimal estimate of \({{\textbf{x}}_k}\) under this condition is

$$\begin{aligned} {{\hat{\textbf{x}}}_k} = \mathop {\arg }\limits _{{{\textbf{x}}_k}} \max {J_L}({{\textbf{x}}_k}) = \mathop {\arg }\limits _{{{\textbf{x}}_k}} \max {\vartheta _{i:k}}\log \left( 1 + {\exp ^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}\right) \nonumber \\ \end{aligned}$$
(18)

where \({e_i}\) is the i-th element of \({{\textbf{e}}_k}\).

Therefore, the optimal estimate \({{\textbf{x}}_k}\) can be computed as

$$\begin{aligned} \frac{{\partial {J_L}({{\textbf{x}}_k})}}{{\partial {{\textbf{x}}_k}}} {=} \sum \limits _{i = 1}^L {\left[ {{\vartheta _{i:k}}\frac{{{{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{\textbf{w}}_{_{i:k}}^\textrm{T}({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})} \right] } {=} 0 \end{aligned}$$
(19)

with

$$\begin{aligned} {{\textbf{x}}_k} = {\left( {\sum \limits _{i = 1}^L {[{\vartheta _{i:k}}\frac{{{{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{\textbf{w}}_{_{i:k}}^\textrm{T}{{\textbf{w}}_{i:k}}]} } \right) ^{ - 1}} \nonumber \\ \left( {\sum \limits _{i = 1}^L {[{\vartheta _{i:k}}\frac{{{{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}}}}{\textbf{w}}_{_{i:k}}^\textrm{T}{d_{i:k}}]} } \right) \end{aligned}$$
(20)

Equation (20) is essentially an iteration of an indefinite point that can be rewritten as

$$\begin{aligned} {{\textbf{x}}_k} = f({{\textbf{x}}_k}) \end{aligned}$$
(21)

with

$$\begin{aligned} f({{\textbf{x}}_k})= & {} {\left( {\sum \limits _{i = 1}^L {[{\vartheta _{i:k}}\frac{{{{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{\textbf{w}}_{_{i:k}}^\textrm{T}{{\textbf{w}}_{i:k}}]} } \right) ^{ - 1}}\nonumber \\{} & {} \times \left( {\sum \limits _{i = 1}^L {[{\vartheta _{i:k}}\frac{{{{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{\textbf{w}}_{_{i:k}}^\textrm{T}{d_{i:k}}]} } \right) \nonumber \\ \end{aligned}$$
(22)

An indefinite point iteration can be obtained relatively easily

$$\begin{aligned} {{\hat{\textbf{x}}}_{k:t + 1}} = f({{\hat{\textbf{x}}}_{k:t}}) \end{aligned}$$
(23)

where \({{\hat{\textbf{x}}}_{k:t + 1}}\) denotes the solution at iteration \(t + 1\) of the indefinite point.

Equation (23) can be re-expressed as

$$\begin{aligned} {{\textbf{x}}_k} = {({\textbf{W}}_{_k}^\textrm{T}{{\mathbf{\Omega }}_k}{{\textbf{W}}_k})^{ - 1}}{\textbf{W}}_{_k}^\textrm{T}{{\mathbf{\Omega }}_k}{{\textbf{D}}_k} \end{aligned}$$
(24)

where \({{\mathbf{\Omega }}_k} = \left[ {\begin{array}{*{20}{c}} {{{\mathbf{\Omega }}_{P:k}}}&{}0\\ 0&{}{{{\mathbf{\Omega }}_{R:k}}} \end{array}} \right] \), with

$$\begin{aligned} {{\mathbf{\Omega }}_{P:k}}= & {} diag({\vartheta _{1:k}}{A_{1:k}},{\vartheta _{2:k}}{A_{2:k}}, \cdots ,{\vartheta _{n:k}}{A_{n:k}}) \end{aligned}$$
(25)
$$\begin{aligned} {{\mathbf{\Omega }}_{R:k}}= & {} diag({\vartheta _{n + 1:k}}{A_{n + 1:k}},{\vartheta _{n+ 2:k}}{A_{n + 2:k}},\nonumber \\{} & {} \cdots ,{\vartheta _{n + m:k}}{A_{n + m:k}}) \end{aligned}$$
(26)

where \({A_{L:k}} = {\vartheta _{L:k}}\frac{{{{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}\).

Combining Eq. (8) and (24), by means of the matrix inversion theorem, it is obtained that

$$\begin{aligned} {\tilde{\textbf{K}}}= & {} {{\tilde{\textbf{P}}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T}{({{\textbf{C}}_k}{{\tilde{\textbf{P}}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T} + {{\tilde{\textbf{R}}}_k})^{ - 1}} \end{aligned}$$
(27)
$$\begin{aligned} {{\tilde{\textbf{P}}}_{k|k - 1}}= & {} {{\mathbf{\upsilon }}_{P:k|k - 1}}{\mathbf{\Omega }}_{_{P:k}}^{ - 1}{\mathbf{\upsilon }}_{_{P:k|k - 1}}^\textrm{T} \end{aligned}$$
(28)
$$\begin{aligned} {{\tilde{\textbf{R}}}_k}= & {} {{\mathbf{\upsilon }}_{R:k}}{\mathbf{\Omega }}_{_{R:k}}^{ - 1}{\mathbf{\upsilon }}_{_R}^\textrm{T} \end{aligned}$$
(29)

In summary, the algorithm flow of this paper is as follows

Step 0, choose a small positive number \(\iota \), set the initial state estimate \({{\textbf{x}}_{0|0}}\) and the initial error covariance matrix \({{\textbf{P}}_{0|0}}\).

Step 1, the a priori state estimation matrix \({{\hat{\textbf{x}}}_{k|k - 1}}\) and the a priori error covariance matrix \({{\textbf{P}}_{k|k - 1}}\) are obtained from Eq. (5) and (6), and \({{\mathbf{\upsilon }}_k}\) is obtained by positive definite decomposition.

Step 2, Let \(t = 1\) and \({{\hat{\textbf{x}}}_{k|k:0}} = {{\hat{\textbf{x}}}_{k|k - 1}}\), perform indefinite iteration.

Step 3, using Eqs. (30)–(38), was able to obtain \({{\hat{\textbf{x}}}_{k|k:t}}\).

$$\begin{aligned} {{\hat{\textbf{x}}}_{k|k:t}} = {{\hat{\textbf{x}}}_{k|k - 1}} + {\tilde{\textbf{K}}}({{\textbf{y}}_k} - {{\textbf{C}}_k}{{\hat{\textbf{x}}}_{k|k - 1}}) \end{aligned}$$
(30)

with

$$\begin{aligned} {\tilde{\textbf{K}}}= & {} {{\tilde{\textbf{P}}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T}{({{\textbf{C}}_k}{{\tilde{\textbf{P}}}_{k|k - 1}}{\textbf{C}}_k^\textrm{T} + {{\tilde{\textbf{R}}}_k})^{ - 1}} \end{aligned}$$
(31)
$$\begin{aligned} {{\tilde{\textbf{P}}}_{k|k - 1}}= & {} {{\mathbf{\upsilon }}_{P:k|k - 1}}{\mathbf{\Omega }}_{_{P:k}}^{ - 1}{\mathbf{\upsilon }}_{_{P:k|k - 1}}^\textrm{T} \end{aligned}$$
(32)
$$\begin{aligned} {{\tilde{\textbf{R}}}_k}= & {} {{\mathbf{\upsilon }}_{R:k}}{\mathbf{\Omega }}_{_{R:k}}^{ - 1}{\mathbf{\upsilon }}_{_R}^\textrm{T} \end{aligned}$$
(33)
$$\begin{aligned} {{\mathbf{\Omega }}_{P:k}}= & {} diag({\vartheta _{1:k}}{A_{1:k}},{\vartheta _{2:k}}{A_{2:k}}, \cdots ,{\vartheta _{n:k}}{A_{n:k}}) \end{aligned}$$
(34)
$$\begin{aligned} {{\mathbf{\Omega }}_{R:k}}= & {} diag({\vartheta _{n + 1:k}}{A_{n + 1:k}},{\vartheta _{n + 2:k}}{A_{n + 2:k}},\nonumber \\{} & {} \cdots ,{\vartheta _{n + m:k}}{A_{n + m:k}}) \end{aligned}$$
(35)
$$\begin{aligned} {A_{L:k}}= & {} {\vartheta _{L:k}}\frac{{{{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}}{{1 + {{\exp }^{ - \frac{{{{({d_{i:k}} - {{\textbf{w}}_{i:k}}{{\textbf{x}}_k})}^2}}}{{2{\sigma ^2}}}}}}} \end{aligned}$$
(36)

Step 4, Comparison utilizes Eq. (37) to compare the estimates of the current state and the previous state, if satisfied then proceed to the next step and vice versa return to Step 3.

$$\begin{aligned} \frac{{||{{{\hat{\textbf{x}}}}_{k|k:t}} - {{{\hat{\textbf{x}}}}_{k|k:t - 1}}||}}{{||{{{\hat{\textbf{x}}}}_{k|k:t}}||}} \le \iota \end{aligned}$$
(37)

Step 5, update the posterior error covariance matrix and return to Step 1.

$$\begin{aligned} {{\textbf{P}}_{k|k}} = ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{P}}_{k|k - 1}}{({I - \tilde{\textbf{K}}}{{\textbf{C}}_k})^\textrm{T}} + {\tilde{\textbf{K}}}{{\textbf{R}}_k}{{\tilde{\textbf{K}}}^\textrm{T}} \end{aligned}$$
(38)

4 Theoretical analysis

In this section, the performance of the proposed algorithm is theoretically analyzed in terms of mean square error as well as time complexity.

4.1 Mean error analysis

The estimation error of the state vector we can express in Eq. (39)

$$\begin{aligned} {{\mathbf{\gamma }}_k} = {{\textbf{x}}_k} - {{\hat{\textbf{x}}}_{k|k}}. \end{aligned}$$
(39)

It can be rewritten through Eq. (8) as

$$\begin{aligned} {{\mathbf{\gamma }}_k} = ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{A}}_k}{{\mathbf{\gamma }}_{k - 1}} + ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{w}}_k} - {\tilde{\textbf{K}}}{{\textbf{v}}_k}. \end{aligned}$$
(40)

Therefore, the statistical expectation of \({{\mathbf{\gamma }}_k}\) is

$$\begin{aligned} \begin{aligned} E[{{\mathbf {\gamma }}_k}]&= ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{A}}_k}E[{{\mathbf {\gamma }}_{k - 1}}] \\ \quad \quad \quad&= ({\textbf{I}} - {[{\tilde{\textbf{P}}}_{k|k - 1}^{ - 1} + {\textbf{C}}_k^\textrm{T}{\tilde{\textbf{R}}}_k^{ - 1}{{\textbf{C}}_k}]^{ - 1}}{\textbf{C}}_k^\textrm{T}{\tilde{\textbf{R}}}_k^{ - 1}{{\textbf{C}}_k})\\&\quad \times {{\textbf{A}}_k}E[{{\mathbf {\gamma }}_{k - 1}}] \\ \end{aligned} \end{aligned}$$
(41)

Assuming that the matrix \({{\textbf{A}}_k}\) is stable, \({{\tilde{\textbf{P}}}}_{k|k - 1}^{}\) and \({\textbf{C}}_k^\textrm{T}{{\tilde{\textbf{R}}}}_k^{ - 1}{{\textbf{C}}_k}\) are positive definite or semi-positive definite. So it can be concluded that is stable. Therefore, we can conclude that the algorithm will work unbiased when the state matrix is stable.

4.2 Mean square error analysis

Considering the errors in Eqs. (34) and (35), the covariance matrix of the error can be rewritten as

$$\begin{aligned} E[{{\mathbf{\gamma }}_k}{\mathbf{\gamma }}_k^\textrm{T}]= & {} ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{A}}_k}E[{{\mathbf{\gamma }}_{k - 1}}{\mathbf{\gamma }}_{k - 1}^\textrm{T}]{\textbf{A}}_k^\textrm{T}{({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k})^\textrm{T}}\nonumber \\{} & {} \quad + ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{Q}}_k}{({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k})^\textrm{T}} + {\tilde{\textbf{K}}}{{\textbf{R}}_k}{{{\tilde{\textbf{K}}}}^\textrm{T}} \end{aligned}$$
(42)

Suppose that \({{\textbf{C}}_k}\), \({{\textbf{A}}_k}\), \({{\textbf{Q}}_k}\), and \({{\textbf{R}}_k}\) are all time-invariant and that \(({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{Q}}_k}{({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k})^\textrm{T}} + {\tilde{\textbf{K}}}{{\textbf{R}}_k}{{\tilde{\textbf{K}}}^\textrm{T}}\) and \(({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{A}}_k}\) are time-invariant. Therefore, we can conclude that \(E[{{\mathbf{\gamma }}_k}{\mathbf{\gamma }}_k^\textrm{T}]\) converges. Furthermore, assuming that

$$\begin{aligned} \begin{array}{l} \mathop {\lim }\limits _{k \rightarrow \infty } {{\mathbf{\varsigma }}_k} = {\mathbf{\varsigma }}\\ \mathop {\lim }\limits _{k \rightarrow \infty } {{\mathbf{\psi }}_{\textbf{k}}}{\mathbf{= \psi }}\\ \mathop {\lim }\limits _{k \rightarrow \infty } {{\mathbf{\varphi }}_k} = {\mathbf{\varphi }} \end{array} \end{aligned}$$
(43)

where \({{\mathbf{\varsigma }}_k} = E[{{\mathbf{\gamma }}_k}{\mathbf{\gamma }}_k^\textrm{T}]\),\({{\mathbf{\psi }}_k} = ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{A}}_k}\) and \({{\mathbf{\varphi }}_k} = ({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k}){{\textbf{Q}}_k}{({\textbf{I}} - {\tilde{\textbf{K}}}{{\textbf{C}}_k})^\textrm{T}} + {\tilde{\textbf{K}}}{{\textbf{R}}_k}{{\tilde{\textbf{K}}}^\textrm{T}}\).

Then, we have

$$\begin{aligned} {\mathbf{\varsigma = \psi \varsigma \psi + \varphi }} \end{aligned}$$
(44)

Eventually, we can get the closed solution from Eq. (44)

$$\begin{aligned} Vec({\mathbf{\varsigma }}){\mathbf{= }}{({\textbf{I}} - {\mathbf{\psi }} \otimes {\mathbf{\psi }})^{ - 1}}Vec({\mathbf{\varphi }}) \end{aligned}$$
(45)

where \( \otimes \) is the Kronecker product.

Table 1 Time complexity analysis
Full size table

4.3 Time complexity analysis

Next, we analyze the time complexity of the algorithm in Table 1 and give the computational complexity of the basic equations.

For the classical Kalman filtering algorithm involved in Eqs. (5)–(9), the computational complexity is

$$\begin{aligned} {\tau _{KF}} = 8{n^3} + 10{n^2}m - {n^2} + 6n{m^2} - n + o({m^3}) \end{aligned}$$
(46)

And for MCKF the formulas involved are Eqs. (5), (6), (16), (30)–(33), (38) and two Gaussian kernel formulas, which define the average number of indefinite point iterations as T, so the computational complexity of MCKF is

$$\begin{aligned} {\tau _{MCKF}}= & {} (2T + 8){n^3} + (4T + 6){n^2}m + (2T - 1){n^2} \nonumber \\{} & {} + (4T + 2)n{m^2} + (3T - 1)nm + (4T - 1)n \nonumber \\{} & {} + 2T{m^3} + 2Tm + To({n^3}) + 2To({m^3}) \end{aligned}$$
(47)

The formulas involved in the algorithm of this paper are Eqs. (5), (6), (16), (30)–(35), and (38), the same as defined above the average number of indefinite point iterations as T, so the computational complexity of the algorithm of this paper is shown in Eq. (48)

$$\begin{aligned} {\tau _{HSWKF}}= & {} (2T + 8){n^3} + (4T + 6){n^2}m \nonumber \\{} & {} + (4T + 2)n{m^2} + (T + 3)nm \nonumber \\{} & {} + (4T - 1){n^2} + (6T + 1)n + 2T{m^3} + 6Tm \nonumber \\{} & {} + To({n^3}) + 2To({m^3}) \end{aligned}$$
(48)

Remark: the number of indefinite point iterations is relatively small, compared with KF, and the time complexity of this paper is moderate, but compared with MCKF, the time complexity of the algorithm in this paper is not much different.

5 Simulation experiment

To demonstrate the superiority of the proposed algorithm, over 100 Monte Carlo simulations are performed using two models, which are run on MATLAB version 2021a running on an i5-7500 CPU. We used 1000 samples in each run to measure the mean square deviation of the algorithm, which is shown in Eq. (49).

$$\begin{aligned} MSD = 20{\log _{10}}||{x_k} - {\hat{x}_{k|k}}|{|^2} \end{aligned}$$
(49)

In simulation experiments before we define the model fixed parameters, for the process noise are used Gaussian distribution of the case, and the measurement noise is divided into a Gaussian distribution \(q(k - 1) \sim N(0,0.01)\) noise and three different impulse noise two cases. The noise figure is shown in Fig. 1.

$$\begin{aligned} \left\{ \begin{array}{l} {r_1}(k) \sim N(0,0.01)\\ {r_2}(k) = M(0.9,0,0.01,10)\\ {r_3}(k) = M(0.9,0,0.01,20)\\ {r_4}(k) = M(0.9,0,0.01,30) \end{array} \right. \end{aligned}$$
(50)
Fig. 1
figure 1

Four noise maps. a Case 1 Gaussian noise map; b case 2 impulsive noise map; c case 3 impulsive noise map; d case 4 impulsive noise map

Full size image
Fig. 2
figure 2

Comparison of the algorithms under Gaussian noise in Example 1

Full size image
Fig. 3
figure 3

Comparison under impulse noise for case (2) in Example 1

Full size image
Fig. 4
figure 4

Comparison under impulse noise for case (3) in Example 1

Full size image
Fig. 5
figure 5

Comparison under impulse noise for case (4) in Example 1

Full size image
Table 2 MSDs (dB) of Example 1 under impulse noise
Full size table

5.1 Simulation 1

First, we consider a simple linear model literature [3] with the following state and observation equations

$$\begin{aligned} {{\textbf{x}}_k}= & {} \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{}{ - \sin \theta }\\ {\sin \theta }&{}{\cos \theta } \end{array}} \right] {{\textbf{x}}_{k - 1}} + {{\textbf{w}}_{k - 1}} \end{aligned}$$
(51)
$$\begin{aligned} {{\textbf{y}}_k}= & {} \left[ {\begin{array}{*{20}{c}} 1&1 \end{array}} \right] {{\textbf{x}}_k} + {{\textbf{v}}_k} \end{aligned}$$
(52)

where \({{\textbf{x}}_k}\) is a two-dimensional column vector, , the threshold is set to \(\iota = {10^{ - 4}}\), and \({{\textbf{x}}_0}\), \({{\hat{\textbf{x}}}_{0|0}}\) and \({{\textbf{P}}_{0|0}}\) are set as follows.

$$\begin{aligned} \left\{ \begin{array}{l} {{\textbf{x}}_0} \sim N(0,{{\textbf{I}}_n})\\ {{{\hat{\textbf{x}}}}_{0|0}} \sim N({{\textbf{x}}_0},{{\textbf{I}}_n})\\ {{\textbf{P}}_{0|0}} = {{\textbf{I}}_n} \end{array} \right. \end{aligned}$$
(53)

We compare the performance of this algorithm with KF, MCKF and STTKF for these four noise cases. In the MCKF algorithm, we have chosen \(\sigma = 2,3,5\) three kernel width cases for simulation. For the STTKF algorithm, we similarly choose \(\sigma = 2,3,5(v = 3)\) three identical comparison parameters for the simulation. In addition, to reflect the strong robustness of the algorithm, we compare the algorithm in this paper with the S-type maximum correlation entropy Kalman filtering algorithm without the addition of Huber’s regression weighting, which we name WSKF, and the function cost is \({J_{WSKF}}({{\textbf{x}}_k}) = \frac{1}{L}\sum \nolimits _{i = 1}^L {\log (1 + {{\exp }^{ - \frac{{{e_i}^2}}{{2{\sigma ^2}}}}})} \). The kernel widths of the WSKF are also selected for the \(\sigma = 2,3,5\) three cases.

We perform simulations under Gaussian noise and three different impulse noise shapes. The MSD plots in Gaussian noise environment we placed in Fig. 2, and the simulations in different pulse environments are shown in Figs. 3, 4 and 5, where KF-TH, MCKF-TH, STTKF-TH,WSKF-TH, and HWSKF-TH, denote the theoretical steady state errors of KF, MCKF, STTKF, WSKF, and HWSKF, respectively. We can see in Fig. 1 that KF has the lowest mean square deviation, the fastest convergence and the best performance when the system is in a Gaussian noise environment. However, when the system is under the influence of impulse noise, Figs. 2, 3 and 4 clearly show that the classical Kalman loses its original steady state properties, which are weakened with the enhancement of impulse noise. But whatever the intensity of the impulse noise environment, the proposed algorithm outperforms the classical Kalman filtering algorithm, the maximum correlation entropy Kalman filtering algorithm, and the maximum correlation entropy Kalman filtering algorithm based on the learning kernel, and has the fastest convergence speed. We list the mean square deviation values in Table 1, which show that the algorithm achieves \(-\)14.9234, \(-\)14.9234 and 15.0660 in impulse noise\((\sigma = 2)\), which are all high steady state.

5.2 Simulation 2

In this section, we investigate the effect of the parameters of the HWSKF algorithm on the performance, such as kernel width sigma and threshold \(\iota \). The conclusions obtained can also guide the selection of the parameters of the HWSKF algorithm. This part is based on the conditional simulation of model 1.

Table 3 MSD at different kernel widths sigma
Full size table
Fig. 6
figure 6

MSD maps for different core widths (case 3)

Full size image

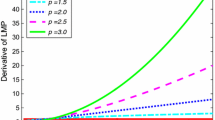
First, we investigated the effect of kernel width sigma on the performance with the kernel width set to \(sigma = 0.5,1,2,5,10\). The values of kernel width are shown in Table 3. The simulation plots for different sigma are shown in Fig. 6. It can be obtained from them that when sigma is near 0.5, the MSD of the three impulse noises reaches the optimal results of \(-\)22.0129, \(-\)22.0689, and \(-\)22.0695, respectively, when the algorithm performance reaches near the optimal.

Then, a large number of experimental analyses were conducted in this paper at different thresholds \(\iota \) (conducted in case 3), and the MSD plots and the table of MSD values at different thresholds are shown in Fig. 7 as well as in Table 4. We can see from this that the steady state performance of the algorithm increases as the threshold \(\iota \) decreases. When the threshold \(\iota \) is increased to 1e\(-\)4, the MSD reaches \(-\)14.8578 at this point, and when the threshold \(\iota \) is increased to 1e\(-\)6, the MSD decreases by only \(-\)0.0113. Therefore, we choose \(\iota = 1e\) \(-\)4 for all thresholds to reduce the computational complexity of the algorithm, while ensuring that we have a high degree of steady state.

Fig. 7
figure 7

MSD graph at different thresholds (case 2)

Full size image

5.3 Simulation 3

Consider a land navigation model whose equations of state and observation can be modeled as

$$\begin{aligned} \quad \quad {x_k}= & {} \left[ {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad t&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad t\\ 0&{}\quad 0&{}\quad 1&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad 1 \end{array}} \right] {x_{k - 1}} + {w_{k - 1}}\ \end{aligned}$$
(54)
$$\begin{aligned} {y_k}= & {} \left[ {\begin{array}{*{20}{c}} 1&{}\quad 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 1&{}\quad 0&{}\quad 0 \end{array}} \right] {x_k} + {v_k}\ \end{aligned}$$
(55)

where \(t = 0.1\) s, the process noise and observation noise are the same as in simulation (1), and Gaussian noise and three kinds of impulse noise are used for the simulation process. In the experiments, the kernel width is taken as \(\sigma = 2\) for MCKF, the parameters of STTKF are \(\sigma = 2,v = 3\), the parameters of WSKF are \(\sigma = 2\), and the choice of kernel width for HWSKF is the same as that for WSKF. The threshold is taken as \(\iota = 1\)e\(-\)4.

Fig. 8
figure 8

Position state (case 2). a Fitting plots for each algorithm at state 1; b fitting plots for each algorithm at state 2

Full size image
Fig. 9
figure 9

Comparison of case (2) in Example 2 under impulse noise

Full size image
Fig. 10
figure 10

Comparison of case (3) in Example 2 under impulse noise

Full size image
Fig. 11
figure 11

compares case (4) in Example 2 under impulse noise

Full size image
Table 4 MSD at different thresholds \(\iota \)
Full size table

We compare different algorithms for fitting one of the two positional states of the simulation model in Fig. 8a, b. We find that the algorithm proposed in this paper is closer to the real values than KF, MCKF, WSKF and STTKF, and has a better fitting effect. Similarly, Figs. 9, 10, and 11 show the performance of the algorithm in three different impulse noise environments, and the corresponding MSDs are presented in Table 5. We can clearly observe that the proposed algorithm in this paper possesses faster convergence speed and lower MSD compared to other algorithms under the influence of impulse noise, which are 8.7765, 9.1960 and 9.1960, respectively. Therefore, it can be shown that the algorithm in the second example also possesses better stationarity under the influence of impulse noise.

Table 5 MSDs (dB) of Example 1 under impulse noise
Full size table

6 Conclusion

This paper proposes a Kalman filtering algorithm that fuses the S-function with the maximum correlation entropy under Huber estimated weights, the HSWKF algorithm. The algorithm utilizes the nonlinear properties of the function and the robust estimation of the weights to solve the problem of poor robustness of algorithms such as KF and MCKF in impulse noise environments. By simulation experiments, the stability of the algorithm is verified. The simulation results show that the experimental steady state errors of the four algorithms are consistent with the theoretical values, and the HWSKF proposed in this paper has the best steady state performance, which is better than the KF, MCKF, STTKF and WSKF in the future, the algorithm can be extended to the extended Kalman filtering algorithm and the estimation of the battery’s charge state.