More accuracy approach for signal subspace-based algorithms in bistatic EMVS-MIMO radar

Abstract

This article proposed an improved signal subspace-based approach for parameter estimation in the bistatic multiple-input multiple-output radar system with an electromagnetic vector sensor (EMVS). In the proposed method, we recovered the joint transmit–receive polarization steering vector from the entire signal subspace using least squares by exploring the property of the Kronecker product and then recovered the transmit or receive polarization steering vector by position average process. We also proved that, in the recovered transmit polarization vector, the receive polarization parameters do not affect the estimation of the transmit polarization parameters. The same applies to the receive polarization vectors. Finally, the azimuth angle and polarization parameters are estimated using the ‘Vector Cross-Product’ and the least-squares strategy. The improved parameter estimation approach can realize automatic parameter pairing and have a better parameter estimation performance than the previous corresponding algorithms when it works on the subspace obtained in different ways since the proposed method uses the whole signal subspace instead of a part of the signal subspace to estimate the parameters. Simulation results verify the performance improvement of the proposed algorithm.

1 Introduction

Multiple-input multiple-output is an emerging direction estimation technology in radar systems since it has unique advantages and outstanding performance compared to the traditional phased array radar system [1,2,3]. The estimation of the direction-of-departure (DOD) and direction-of-arrival (DOA) has been extensively studied for multiple-input multiple-output radar [4,5,6,7,8]. However, the number of studies studied on two-dimensional (2D) problems, namely azimuth, elevation, 2D-DOD, and 2D-DOA estimation, is limited [9,10,11]. Chen and Zhang developed a PM-based algorithm for 2D-DOD and 2D-DOA estimation algorithms in MIMO radar with arbitrary arrays [9]. An improved ESPRIT-based algorithm was introduced for 2D-DOD and 2D-DOA estimation in MIMO radar with arbitrary arrays [12]. In [13], a new approach that combines ESPRIT and joint diagonalization technology was proposed for 2D-DOD and 2D-DOA estimation in bistatic MIMO radar with an L-shaped array. In [10], a novel tensor-ring decomposition-based method is proposed for 2D-DOA and 2D-DOD estimation, which makes full use of the multi-dimensional structure of the MIMO output and can improve estimation performance. These methods developed for 2D-DOD and 2D-DOA estimation are based on scalar sensors. A typical characteristic of [9, 12, 13] is that the antenna array is scalar sensors susceptible to external interference. As an alternative to the scalar sensor, the electromagnetic vector sensor (EMVS) brings new development space for target positioning [14]. The EMVS at a certain point in space can provide a 2D direction finding [15]. Besides, it can also provide the polarization state of the input signal, which provides new potential possibilities for detecting invisible targets.

The use of EMVS for direction finding has become a hot research topic, and various estimators have been proposed in [14,15,16,17,18,19,20,21]. In bistatic MIMO-EMVS radar, there are eight parameters used to describe the position of the target, which can better resist interference. Generally speaking, there are two types of parameter estimation methods in the bistatic MIMO-EMVS radar. The first one recovers the normalized polarization vector by exploiting the rotation invariance of the normalized polarization vector. Then, all the parameters are estimated from the recovered normalized polarization vector [20,21,22]. This type of method does not have high requirements on the shape of the array but completely ignores the spatial steering matrix. The second type of method is suitable for spatial steering matrices with rotation invariance and uses the rotation invariance of the spatial steering matrix to estimate spatial angle variables. In this paper, we discussed the last one. A general bistatic MIMO-EMVS radar with multiple transmit and receive EMVSs was introduced in [23], and an ESPRIT-like algorithm was proposed to estimate 2D-DOD, 2D-DOA, 2D transmit polarization angle (TPA) and 2D receive polarization angle(RPA). First, the signal subspace is obtained by performing eigendecomposition (EVD) on the covariance matrix of the received data. Next, a rotation matrix is obtained from the 6N or 6M rows of the signal subspace by exploiting the rotation invariance of the receive or transmit array manifold and using it to recover the receive or transmit polarization vector from these rows where N or M is the number of the receive or transmit arrays. The 2D-DOA and 2D-DOD are estimated via the ‘Vector Cross-Product’ idea using the recovered spatial response vector. Then, the 2D-TPA and 2D-RPA are calculated using the least-squares method. Finally, the orthogonality of the virtual steering vector and the noise subspace are used to pair the transmit and receive parameters. In [24], the signal subspace is obtained by performing high-order SVD on the covariance tensor, and then, all parameters are estimated using the same process as that in [23]. The HOSVD-based algorithm can improve the signal-subspace estimation accuracy to improve the parameter estimation performance, but it suffers a high computational complexity. To avoid decomposition, the signal subspace is obtained by the propagator method (PM) in [25]. Then, all parameters are estimated using the same process in [23], except the elevation angle is calculated from the rotation matrix. The above algorithms only select 6N or 6M rows of the signal subspace to estimate all parameters and do not fully utilize the entire signal subspace. Furthermore, in [26], by exploiting the rotation invariance of the virtual array manifold, the elevation angle is estimated from the entire signal subspace obtained by PM. However, the other parameters estimation process is the same as that in [23], except there is no need for the other pairing process. It is a pity that only the elevation angle estimation fully uses the entire signal subspace. We know that all algorithms based on signal subspace do not fully use the entire signal subspace to estimate all parameters through the above introduction. They only select 6N or 6M rows of the signal subspace to estimate the parameter and waste most of the signal subspace, which will cause performance degradation. Besides, as shown in [23], the parameter estimation accuracy is also affected by the position of the selected part in the signal subspace. Different positions of the selected part in the signal subspace will bring different estimation results. So, it is difficult to determine which part can get the best estimation effect. All the algorithms mentioned above, except HOSVD, do not make full use of the inherent multi-dimensional structure of the matched filters, resulting in some performance loss. The authors in [27, 28] make full use of the inherent multi-dimensional structure and introduce the trilinear decomposition to obtain the estimation of the loading matrices and use those loading matrices to realize the separate estimate of the receive and transmit parameters. At the same time, the transmit and receive parameters are automatically paired.

In this paper, we proposed an improved signal-subspace-based approach for parameter estimation in the bistatic multiple-input multiple-output radar system with an electromagnetic vector sensor (EMVS). The main contributions of this paper are as follows: (1) To make full use of the virtual array manifold of the MIMO radar and the entire signal subspace, the polarization steering vector is recovered from the joint transmit–receive spatial-polarization steering vector by exploiting the property of the Kronecker product. (2) We proposed a position average process to recover the transmit or receive polarization steering vector from the estimated joint transmit–receive polarization steering vector. We also proved that in the recovered transmit polarization vector, the receive polarization parameters do not affect the estimation of the transmit polarization parameters. The same applies to the receive polarization steering vectors; (3) the computational complexity of the proposed algorithm is analyzed. Numerical simulations are further used to verify the effectiveness of the proposed algorithm. What needs special emphasis is that although the proposed parameter estimation approach combines the ESPRIT and ‘Vector Cross-Product’ ideas to estimate the parameters, the differences from the existing algorithms are: (1) The transmit or receive elevation angle is calculated by exploiting the rotation invariance of the virtual array manifold of the MIMO radar, instead of the transmit or receive array manifold. The joint diagonalization technology is introduced to ensure the pairing estimation of the receive and transmit elevation angle, and no additional pairing process is required. (2) The transmit or receive polarization steering vector is recovered from the 36NM rows of the signal subspace instead of the 6M/6N rows. As mentioned above, all parameters are obtained from the whole signal subspace instead of the 6M or 6N rows. Therefore, when the improved approach is applied to the signal subspace obtained in different ways, a certain degree of performance improvement will be obtained compared with the original parameter estimation method.

The rest of this paper is organized as follows: The signal model for bistatic EMVS-MIMO radar is introduced in Sect. 2, and the improved signal-subspace-based parameter estimation approach is introduced in Sect. 3. The performance including complexity and CRB is derived in Sect. 4. Several numerical results are provided to indicate the effectiveness of the proposed algorithm in Sect. 5. Finally, a conclusion is drawn in Sect. 6.

Notation In this paper, we use lowercase letters, like a, to represent a variable; lowercase bold letters, like $\textbf{a}$, to represent a vector; and capital bold letters, like $\textbf{A}$, to represent a matrix. We use symbols $(\bullet )^{\textrm{T}}$,$(\bullet )^{\textrm{T}}$, $(\bullet )^{\mathrm {*}}$, $(\bullet )^{-1}$ and $(\bullet )^{\dagger }$ to represent transposition operator, conjugate operator, conjugate transposition operator, matrix inverse operator and matrix pseudo-inverse operator, respectively. $\Vert \cdot \Vert _{\textrm{F}}$ represents the Frobenius norm. $\odot$ and $\otimes$ represent the Khatri–Rao product and Kronecker product, respectively. $\textrm{angle} \{ a \}$ stands for the phase of a; The ‘Vector Cross-Product’ between ${\textbf{a}}_1 = [a_1, \, a_2, \, a_3]^{\textrm{T}}$ and ${\textbf{a}}_2 = [a_4, \, a_5, \, a_6]^{\textrm{T}}$ is defined as ${\textbf{a}}_1 \circledast {\textbf{a}}_2 = \begin{bmatrix} 0&{}-a_3&{}a_2\\ a_3&{}0&{}-a_1\\ -a_2&{}a_1&{}0 \end{bmatrix} \begin{bmatrix} a_4\\ a_5\\ a_6 \end{bmatrix}$.

Fig. 1

Illustration of the bistatic EMVS-MIMO radar

2 Signal model

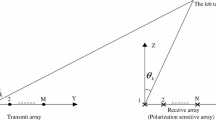
Consider the same bistatic EMVS-MIMO radar system scenario to that in Chintagunta and Palanisamy [23], which is equipped with an M-element EMVS transmit arrays and an N-element EMVS receive arrays. Both of them are uniform linear array (ULA). Suppose there are K far-field point-like targets. The 2D-DOD pair and 2D-DOA pair of the k-th target are $(\theta _{t,k}, \phi _{t,k})$ and $(\theta _{r,k}, \phi _{r,k})$, respectively, where $\theta _{t,k}$, $\theta _{r,k}$ are the elevation angles, and $\phi _{t,k}$, $\phi _{r,k}$ are the azimuth angles. The transmit and the receive steering vector of the k-th target can be expressed as [23]

$$\begin{aligned}{} & {} {\textbf{b}}_{t,k} = {\textbf{a}}_{t,k} \otimes {\textbf{c}}_{t,k} \,, \end{aligned}$$

(1a)

$$\begin{aligned}{} & {} {\textbf{b}}_{r,k} = {\textbf{a}}_{r,k} \otimes {\textbf{c}}_{r,k}, , \end{aligned}$$

(1b)

where ${\textbf{a}}_{t,k} = [1, e^{j2\pi d_t \textrm{sin}({\theta }_{t,k}) / \lambda }, \ldots , e^{j 2 \pi (M-1) d_t \textrm{sin}({\theta }_{t,k}) / \lambda } ] ^{\textrm{T}} \in {\mathbb {C}}^{M \times 1 }$ and ${\textbf{a}}_{r,k} = \big [1, e^{j 2 \pi d_r \textrm{sin}({\theta }_{r,k}) / \lambda }, \ldots , e^{j 2 \pi (N-1) d_r \textrm{sin}({\theta }_{r,k}) / \lambda } \big ] ^{\textrm{T}} \in {\mathbb {C}}^{N \times 1 }$ in which $\lambda ,d_t,d_r$ are the wavelength, the spacing of adjacent transmit array, the spacing of adjacent receive array, respectively; ${\textbf{c}}_{t,k}$ or ${\textbf{c}}_{r,k}$ stands for the polarization steering vector of transmitter or receiver. Moreover, ${\textbf{c}}_{t,k}$ and ${\textbf{c}}_{r,k}$ can be expressed in detail as

$$\begin{aligned}{} & {} {\textbf{c}}_{t,k} = {\textbf{F}}_{t,k} {\textbf{h}}_{t,k} = \left[ \underbrace{c_{t_1,k},c_{t_2,k},c_{t_3,k} }_{{\textbf{c}}^{\textrm{T}}_{t_1,k}}, \underbrace{c_{t_4,k},c_{t_5,k},c_{t_6,k} }_{{\textbf{c}}^{\textrm{T}}_{t_2,k}} \right] ^{\textrm{T}},\qquad \end{aligned}$$

(2a)

$$\begin{aligned}{} & {} {\textbf{c}}_{r,k} = {\textbf{F}}_{r,k} {\textbf{h}}_{r,k} = \left[ \underbrace{c_{r_1,k},c_{r_2,k},c_{r_3,k} }_{{\textbf{c}}^{\textrm{T}}_{r_1,k}}, \underbrace{c_{r_4,k},c_{r_5,k},c_{r_6,k} }_{{\textbf{c}}^{\textrm{T}}_{r_2,k}} \right] ^{\textrm{T}},\nonumber \\ \end{aligned}$$

(2b)

in which

$$\begin{aligned}{} & {} {\textbf{F}}_{t,k} = \begin{bmatrix} \textrm{cos}(\phi _{t,k}) \textrm{cos}(\theta _{t,k}) &{} -\textrm{sin}(\phi _{t,k})\\ \textrm{sin}(\phi _{t,k}) \textrm{cos}(\theta _{t,k}) &{} -\textrm{cos}(\phi _{t,k}) \\ -\textrm{sin}(\theta _{t,k}) &{} 0 \\ -\textrm{sin}(\phi _{t,k}) &{} -\textrm{cos}(\phi _{t,k}) \textrm{cos}(\theta _{t,k}) \\ \textrm{cos}(\phi _{t,k}) &{} -\textrm{sin}(\phi _{t,k}) \textrm{cos}(\theta _{t,k}) \\ 0 &{} \textrm{sin}(\theta _{t,k}) \end{bmatrix} \end{aligned}$$

(3a)

$$\begin{aligned}{} & {} \quad {\textbf{F}}_{r,k} = \begin{bmatrix} \textrm{cos}(\phi _{r,k}) \textrm{cos}(\theta _{r,k}) &{} -\textrm{sin}(\phi _{r,k})\\ \textrm{sin}(\phi _{r,k}) \textrm{cos}(\theta _{r,k}) &{} -\textrm{cos}(\phi _{r,k}) \\ -\textrm{sin}(\theta _{r,k}) &{} 0 \\ -\textrm{sin}(\phi _{r,k}) &{} -\textrm{cos}(\phi _{r,k}) \textrm{cos}(\theta _{r,k}) \\ \textrm{cos}(\phi _{r,k}) &{} -\textrm{sin}(\phi _{r,k}) \textrm{cos}(\theta _{r,k}) \\ 0 &{} \textrm{sin}(\theta _{r,k}) \end{bmatrix} \end{aligned}$$

(3b)

and

$$\begin{aligned}{} & {} {\textbf{h}}_{t,k} = \begin{bmatrix} \textrm{sin} (\gamma _{t,k}) e^{j \eta _{t,k}}\\ \textrm{cos}(\gamma _{t,k}) \end{bmatrix} \end{aligned}$$

(4a)

$$\begin{aligned}{} & {} \quad {\textbf{h}}_{r,k} = \begin{bmatrix} \textrm{sin} (\gamma _{r,k}) e^{j \eta _{r,k}}\\ \textrm{cos}(\gamma _{r,k}) \end{bmatrix}, \end{aligned}$$

(4b)

where $\gamma _{t,k},\gamma _{r,k} \in \left[ 0\right. \left. \pi /2 \right)$ are the polarization angles, $\eta _{t,k}, \eta _{r,k} \in \left[ -\pi \right. \left. \pi \right)$ are the polarization phase difference. Besides,

$$\begin{aligned} \left\| {\textbf{c}}_{t_1,k} \right\| _{{\textrm{F}}} = \left\| {\textbf{c}}_{t_2,k} \right\| _{{\textrm{F}}} = \left\| {\textbf{c}}_{r_1,k} \right\| _{{\textrm{F}}} = \left\| {\textbf{c}}_{r_2,k} \right\| _{{\textrm{F}}} = 1, \end{aligned}$$

(5)

and

$$\begin{aligned}{} & {} {\textbf{v}}_t = \frac{{\textbf{c}}_{t_1,k}}{ \left\| {\textbf{c}}_{t_1,k} \right\| _F } \circledast \frac{{\textbf{c}}^{*}_{t_2,k}}{ \left\| {\textbf{c}}_{t_2,k} \right\| _F } = \begin{bmatrix} \textrm{sin} (\theta _{t,k})\textrm{cos}(\phi _{t,k})\\ \textrm{sin} (\theta _{t,k})\textrm{sin}(\phi _{t,k}) \\ \textrm{cos}(\theta _{t,k}) \end{bmatrix}, \end{aligned}$$

(6a)

$$\begin{aligned}{} & {} \quad {\textbf{v}}_r = \frac{{\textbf{c}}_{r_1,k}}{ \left\| {\textbf{c}}_{r_1,k} \right\| _F } \circledast \frac{{\textbf{c}}^{*}_{r_2,k}}{ \left\| {\textbf{c}}_{r_2,k} \right\| _F } = \begin{bmatrix} \textrm{sin} (\theta _{r,k})\textrm{cos}(\phi _{r,k})\\ \textrm{sin} (\theta _{r,k})\textrm{sin}(\phi _{r,k}) \\ \textrm{cos}(\theta _{r,k}) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(6b)

Then, the received signal in the l-th snapshot can be expressed as [23]

$$\begin{aligned} {\textbf{X}}_l = {\textbf{B}}_r {\varvec{\Lambda }}_l {\textbf{B}}^{\textrm{T}}_t {\textbf{S}} + {\textbf{N}}_l, \end{aligned}$$

(7)

where ${\textbf{B}}_r = [{\textbf{b}}_{r,1}, {\textbf{b}}_{r,2},\ldots , {\textbf{b}}_{r,K}] = {\textbf{A}}_r \odot {\textbf{C}}_r \in {\mathbb {C}}^{6N \times K}$, ${\textbf{B}}_t = [{\textbf{b}}_{t,1}, {\textbf{b}}_{t,2},\ldots$, ${\textbf{b}}_{t,K}] ={\textbf{A}}_t \odot {\textbf{C}}_t \in {\mathbb {C}}^{6\,M \times K}$ are the receive and transmit array manifold, respectively, in which ${\textbf{A}}_r = [{\textbf{a}}_{r,1}, {\textbf{a}}_{r,2}, \ldots , {\textbf{a}}_{r,K} ] \in {\mathbb {C}}^{N \times K}$, ${\textbf{C}}_r = [{\textbf{c}}_{r,1}, {\textbf{c}}_{r,2}, \ldots , {\textbf{c}}_{r,K} ] \in {\mathbb {C}}^{6 \times K}$, ${\textbf{A}}_t = [{\textbf{a}}_{t,1}, {\textbf{a}}_{t,2}, \ldots , {\textbf{a}}_{t,K} ] \in {\mathbb {C}}^{M \times K}$, and ${\textbf{C}}_t = [{\textbf{c}}_{t,1}, {\textbf{c}}_{t,2}, \ldots , {\textbf{c}}_{t,K} ] \in {\mathbb {C}}^{6 \times K}$; ${\varvec{\Lambda }}_l = \textrm{diag}({\textbf{s}}^{'}_l)$, in which ${\textbf{s}}^{'}_l=[ \rho _1(l),\rho _2(l), \ldots , \rho _ K(l) ] \in {\mathbb {C}}^{K \times 1}$ and $\rho _k(l)$ stands for the reflection coefficient of the k-th target during the l-th snapshot, ${\textbf{S}} \in {\mathbb {C}}^{6\,M \times Q}$ are the orthogonal signal emitted by the transmit arrays, and ${\textbf{N}}_l \in {\mathbb {C}}^{6N \times Q}$ stands for the noise matrix. The output of matched filters can be expressed as

$$\begin{aligned} {\textbf{Y}}_l = {\textbf{X}}_l {\textbf{S}}^{\textrm{H}} \left[ {\textbf{S}}{\textbf{S}}^{\textrm{H}} \right] ^{-1} = {\textbf{B}}_r {\varvec{\Lambda }}_l {\textbf{B}}^{\textrm{T}}_t + {\textbf{N}}^{'}_l, \end{aligned}$$

(8)

where ${\textbf{N}}^{'}_l = {\textbf{N}}_l {\textbf{S}}^{\textrm{H}}({\textbf{S}}{\textbf{S}}^{\textrm{H}})^{-1}$ is the noise matrix after matched filters.

3 Parameter estimation approach

3.1 Previous signal-subspace-based algorithms

As mentioned in the introduction, the ESPRIT algorithm in [23], the HOSVD algorithm in [24], and the PM algorithm in [25] are all selecting a part of the signal subspace to estimate all parameters. The signal subspace obtained by EVD in [23], HOSVD in [24], and PM in [25] are all marked as ${\textbf{U}}_s$. When estimating the receive parameters, the selected part of the signal subspace can be expressed as

$$\begin{aligned} {\textbf{E}}_r = {\textbf{J}}_r {\textbf{U}}_s \in {\mathbb {C}}^{6N \times K}, \end{aligned}$$

(9)

where ${\textbf{J}}_r = [{\textbf{0}}_{6N \times 6pN} \, | \, I_{6N} \, | \, {\textbf{0}}_{6N \times (36NM-6(p+1)N)}]$ with $p=0, 1, \ldots , 6\,M-1$. A diagonal matrix ${\varvec{\Phi }}_r = \textrm{diag}( [e^{j \pi d_r \textrm{sin}(\theta _{r,1}) / \lambda }, e^{j \pi d_r \textrm{sin}(\theta _{r,2}) / \lambda }, \ldots , e^{j \pi d_r \textrm{sin}(\theta _{r,K}) / \lambda } ])$ related to receive elevation angle is calculated using ${\textbf{E}}_r$ by exploiting the rotation invariance of the receive array manifold. Then, the receive spatial response vector ${\textbf{c}}_{r,k}(k=1,2,\ldots , K)$ is recovered from ${\textbf{E}}_r$ using the estimated diagonal matrix ${\varvec{\Phi }}_r$. The receive elevation angle ${\theta _{r,k}}$ and azimuth angle $\phi _{r,k}$ are estimated using ‘Vector Cross-Product’ in [23, 24], and receive polarization parameters $\gamma _k$ and $\eta _k$ are estimated via LS principle. Different from the receive elevation angle estimation in [23, 24], $\theta _{r,k}$ is calculated using the estimated diagonal matrix ${\varvec{\Phi }}_r$. When estimating the transmit parameters, the selected part of the signal subspace can be expressed as

$$\begin{aligned} {\textbf{E}}_t = {\textbf{J}}_t {\textbf{U}}_s \in {\mathbb {C}}^{6M \times K}, \end{aligned}$$

(10)

where ${\textbf{J}}_t = [ {\textbf{I}}_{6\,M} \otimes {\textbf{e}}^{\textrm{T}}_{q}]$, in which ${\textbf{e}}_{q}$ is a $6N \times 1$ vector with q-th entry is one and others are zeros, and $q = 1, 2, \ldots , 6N$. Similarly, use ${\textbf{E}}_t$ to calculate the diagonal matrix ${\varvec{\Phi }}_t = \textrm{diag}([ e^{j \pi d_t \textrm{sin}(\theta _{t,1}) / \lambda }, e^{j \pi d_t \textrm{sin}(\theta _{t,2}) / \lambda }, \ldots , e^{j \pi d_t \textrm{sin}(\theta _{t,K}) / \lambda } ])$ related to the transmit elevation angle by exploiting the rotation invariance of the transmit array manifold. The transmit spatial response vector ${\textbf{c}}_{t,k}(k=1,2,\ldots , K)$ is recovered from ${\textbf{E}}_t$ using the estimated diagonal matrix ${\varvec{\Phi }}_t$. The transmit elevation angle ${\theta _{t,k}}$ and azimuth angle $\phi _{t,k}$ are estimated using ‘Vector Cross-Product’ in [23, 24], transmit polarization parameters $\gamma _k$ and $\eta _k$ are estimated via LS principle. $\theta _{t,k}$ is also estimated using the estimated diagonal matrix ${\varvec{\Phi }}_r$, and other parameters estimation is the same as that in [23, 24].

Different from the above three algorithms, the PM algorithm in [26] uses the 36NM rows of signal subspace to estimate the transmit and receive elevation angle by exploiting the rotation invariance of the joint receive–transmit array manifold, which will be introduced in the next section. But after that, the PM algorithm in [26] also selects a part of signal subspace as Eq. (9) or Eq. (10) to estimate the receive or transmit azimuth angle and polarization parameters by adopting the ‘Vector Cross-Product’ and LS ideas in [23].

It can be seen from the above analysis that all methods based on signal subspace only select 6N or 6M rows of 36NM rows in the signal subspace to estimate all transmit or receive parameters, except for the PM algorithm in [26] use the whole signal subspace to estimate the transmit and receive elevation angle. They only selected a small part of the signal subspace and wasted most of it. Besides, as shown in [23], the transmit and receive parameter estimation accuracy is also related to the value of p and q, and different values of p and q will bring different estimation results.

3.2 Proposed signal-subspace-based approach

To make full use of the entire signal subspace, we propose an improved parameters estimation approach applicable to all signal-subspace-based algorithms where all parameters are estimated by using the 36NM rows of the signal subspace instead of 6N or 6M rows of the signal subspace.

No matter which method is used to obtain the signal subspace, all of them are uniformly denoted as ${\hat{{\textbf{U}}}}_s$ for the convenience of the following expressions. From the analysis in [26], we know that ${\hat{{\textbf{U}}}}_s$ spans the same space as the joint transmit–receive spatial-polarization manifold ${\textbf{B}}_{rt}$, with $\textbf{B}_{r,t} = \textbf{B}_r \odot \textbf{B}_t$. Therefore, there excite a full-rank matrix satisfying

$$\begin{aligned} {\textbf{B}}_{r,t} = {\hat{\textbf{U}}}_s {\varvec{\Gamma }} \,. \end{aligned}$$

(11)

Define four selection matrices as

$$\begin{aligned} \left\{ \begin{aligned} {\textbf{J}}_1 =&[{\textbf{I}}_{N-1} \ {\textbf{0}}_{(N-1) \times 1}] \otimes {\textbf{I}}_{36M}\\ {\textbf{J}}_2 =&[{\textbf{0}}_{(N-1) \times 1} \ {\textbf{I}}_{N-1} ] \otimes {\textbf{I}}_{36M} \end{aligned} \right. \,, \end{aligned}$$

(12a)

$$\begin{aligned} \left\{ \begin{aligned} {\textbf{J}}_3 =&{\textbf{I}}_{36N} \otimes [{\textbf{I}}_{M-1} \ {\textbf{0}}_{(M-1) \times 1}] \\ {\textbf{J}}_4 =&{\textbf{I}}_{36N} \otimes [{\textbf{0}}_{(M-1) \times 1} \ {\textbf{I}}_{M-1} ] \end{aligned} \right. \,. \end{aligned}$$

(12b)

Then, we can find that

$$\begin{aligned}{} & {} {\textbf{J}}_{2}{\textbf{B}}_{r,t} = {\textbf{J}}_{1}{\textbf{B}}_{r,t} {\varvec{\Phi }}_r \,, \end{aligned}$$

(13a)

$$\begin{aligned}{} & {} {\textbf{J}}_{4}{\textbf{B}}_{r,t} = {\textbf{J}}_{3}{\textbf{B}}_{r,t} {\varvec{\Phi }}_t \,, \end{aligned}$$

(13b)

where ${\varvec{\Phi }}_r$ and ${\varvec{\Phi }}_t$ have been given above. Insert (11) into (13), we have

$$\begin{aligned}{} & {} {\textbf{J}}_2 {\hat{\textbf{U}}}_s {\varvec{\Gamma }} = {\textbf{J}}_1 {\hat{\textbf{U}}}_s {\varvec{\Gamma }} {\varvec{\Phi }}_r, \end{aligned}$$

(14a)

$$\begin{aligned}{} & {} {\textbf{J}}_4 {\hat{\textbf{U}}}_s {\varvec{\Gamma }} = {\textbf{J}}_3 {\hat{\textbf{U}}}_s {\varvec{\Gamma }} {\varvec{\Phi }}_t . \end{aligned}$$

(14b)

Then, we calculate

$$\begin{aligned}{} & {} {\varvec{\Psi }}_r = ({\textbf{J}}_1 {\hat{\textbf{U}}}_s )^{\dagger } {\textbf{J}}_2 {\hat{\textbf{U}}}_s = {\varvec{\Gamma }} {\varvec{\Phi }}_r {\varvec{\Gamma }}^{-1}, \end{aligned}$$

(15a)

$$\begin{aligned}{} & {} {\varvec{\Psi }}_t = ({\textbf{J}}_3 {\hat{\textbf{U}}}_s )^{\dagger } {\textbf{J}}_4 {\hat{\textbf{U}}}_s = {\varvec{\Gamma }} {\varvec{\Phi }}_t {\varvec{\Gamma }}^{-1}. \end{aligned}$$

(15b)

Perform eigenvalue decomposition on ${\varvec{\Psi }}_r$ and ${\varvec{\Psi }}_t$, respectively. Mark their eigenvalues as ${\hat{\varvec{\Phi }}}_r$ and ${\hat{\varvec{\Phi }}}_t$, respectively, and mark the corresponding eigenvectors as ${\hat{\varvec{\Gamma }}}_1$ and ${\hat{\varvec{\Gamma }}}_2$. It is easy to see that ${\hat{\varvec{\Phi }}}_r$, ${\hat{\varvec{\Phi }}}_t$, ${\hat{\varvec{\Gamma }}}_1$ and ${\hat{\varvec{\Gamma }}}_2$ are the estimates of ${\varvec{\Phi }}_r$, ${\varvec{\Phi }}_t$, ${\varvec{\Gamma }}$, respectively. Due to the non-uniqueness of eigenvalue decomposition, the position of diagonal elements of ${\hat{\varvec{\Phi }}}_r$ and ${\varvec{\Phi }}_r$ may be different, so do ${\hat{\varvec{\Phi }}}_t$ and ${\varvec{\Phi }}_t$ are. To ensure the paired estimation of the transmit and the receive elevation angle, we adopt the joint diagonalization of ${\varvec{\Psi }}_r$ and ${\varvec{\Psi }}_t$. A common approach is to perform EVD on one of the matrices and use its eigenvectors matrix to diagonalize the other matrix, i.e.,

$$\begin{aligned} {\varvec{\Psi }}_r= & {} {\hat{\varvec{\Gamma }}} {\hat{\varvec{\Phi }}}_r {\hat{\varvec{\Gamma }}}^{-1} \,, \end{aligned}$$

(16a)

$$\begin{aligned} {\hat{\varvec{\Phi }}}_r= & {} {\hat{\varvec{\Gamma }}}^{-1} {\varvec{\Psi }}_r {\hat{\varvec{\Gamma }}} . \end{aligned}$$

(16b)

where ${\hat{\varvec{\Phi }}}_r = \textrm{diag}({\hat{\lambda }}_{r,1}, {\hat{\lambda }}_{r,2}, \ldots , {\hat{\lambda }}_{r,K})$ and ${\hat{\varvec{\Phi }}}_t = \textrm{diag}({\hat{\lambda }}_{t,1}, {\hat{\lambda }}_{t,2}, \ldots , {\hat{\lambda }}_{t,K})$. The transmit and receive elevation angles can be obtained via

$$\begin{aligned} {\hat{\theta }}_{r,k}= & {} \textrm{arcsin} \{ \textrm{angle}({\hat{\lambda }}_{r,k}) \lambda /(2 d_r) \} \,, \end{aligned}$$

(17a)

$$\begin{aligned} {\hat{\theta }}_{t,k}= & {} \textrm{arcsin} \{ \textrm{angle}({\hat{\lambda }}_{t,k}) \lambda /(2 d_t) \} \,. \end{aligned}$$

(17b)

The elevation angle estimation process introduced above is all almost the same as that in [26], except the joint diagonalization process. After obtaining elevation angle estimates, we start to recover transmit and receive polarization steering vectors ${\textbf{c}}_{r,k}$ and ${\textbf{c}}_{t,k}$ from the 36NM rows of the signal subspace to estimate other parameters, instead of from the 6N or 6M rows of the signal subspace. This approach is entirely different from all previous methods based on signal subspace.

The joint transmit–receive spatial-polarization manifold can be recovered via

$$\begin{aligned} {\hat{\textbf{B}}}_{rt} = {\textbf{U}}_s {\hat{{\varvec{\Gamma }}}} \,. \end{aligned}$$

(18)

In fact, by using the property of Kronecker product, the joint transmit–receive spatial-polarization steering vector can be rewritten as

$$\begin{aligned} \begin{aligned} {\textbf{a}}_{rt,k} =&\left( {\textbf{a}}_{r,k} \otimes {\textbf{c}}_{r,k} \right) \otimes \left( {\textbf{a}}_{t,k} \otimes {\textbf{c}}_{t,k} \right) \\ =&\left[ \left( {\textbf{a}}_{r,k} \otimes {\textbf{I}}_{6} \right) {\textbf{c}}_{r,k} \right] \otimes \left[ \left( {\textbf{a}}_{t,k} \otimes {\textbf{I}}_{6} \right) {\textbf{c}}_{t,k} \right] \\ =&\left[ \left( {\textbf{a}}_{r,k} \otimes {\textbf{I}}_{6} \right) \otimes \left( {\textbf{a}}_{t,k} \otimes {\textbf{I}}_{6} \right) \right] \left( {\textbf{c}}_{r,k} \otimes {\textbf{c}}_{t,k} \right) \end{aligned} \,. \end{aligned}$$

(19)

Let ${\textbf{c}}_{rt,k} = {\textbf{c}}_{r,k} \otimes {\textbf{c}}_{t,k}$ denote the joint receive–transmit polarization steering vector of the k-th target. Since the elevation angle estimation $({\hat{\theta }}_{r,k},{\hat{\theta }}_{t,k})$ and the joint receive–transmit array manifold estimation use the same matrix ${\hat{{\varvec{\Gamma }}}}$, thus the elevation angle estimation of the k-th target and the joint receive–transmit spatial-polarization steering vector ${\hat{\textbf{B}}}_{rt}(:,k)$ are paired, in which ${\hat{\textbf{B}}}_{rt}(:,k)$ is the k-th column of matrix ${\hat{\textbf{B}}}_{rt}$. By utilizing (19), ${\textbf{c}}_{rt,k}$ can be estimated by last-squares (LS) principle via

$$\begin{aligned} {\underset{ {\textbf{c}}_{rt,k} }{\textrm{min}}} \left\| \left[ \left( {\hat{{\textbf{a}}}}_{r,k} \otimes {\textbf{I}}_{6} \right) \otimes \left( {\hat{{\textbf{a}}}}_{t,k} \otimes {\textbf{I}}_{6} \right) \right] {\textbf{c}}_{rt,k} - {\hat{\textbf{B}}}_{rt}(:,k) \right\| ^2_\textrm{F} , \end{aligned}$$

(20)

where ${\hat{\textbf{a}}}_{r,k} = [1,\, {\hat{\lambda }}_{r,k},\ldots , {\hat{\lambda }}^{N-1}_{r,k} ]^{\textrm{T}}$ and ${\hat{\textbf{a}}}_{t,k} = [1,\, {\hat{\lambda }}_{t,k},\ldots , {\hat{\lambda }}^{M-1}_{t,k} ]^{\textrm{T}}$. The LS solution for ${\textbf{c}}_{rt,k}$ is

$$\begin{aligned} {\hat{\textbf{c}}}_{rt,k} = \left( \left[ \left( {\hat{{\textbf{a}}}}_{r,k} \otimes {\textbf{I}}_{6} \right) \otimes \left( {\hat{{\textbf{a}}}}_{t,k} \otimes {\textbf{I}}_{6} \right) \right] \right) ^{\dagger } {\hat{\textbf{B}}}_{rt}(:,k) . \end{aligned}$$

(21)

Combine ${\textbf{c}}_{rt,k} = {\textbf{c}}_{r,k} \otimes {\textbf{c}}_{t,k}$, so ${\hat{\textbf{c}}}_{rt,k}$ can be rewritten as ${\hat{\textbf{c}}}_{rt,k} = {\hat{\textbf{c}}}_{r,k} \otimes {\hat{\textbf{c}}}_{t,k}$, in which ${\hat{\textbf{c}}}_{r,k} \in {\mathbb {C}}^{6\times 1}$ and ${\hat{\textbf{c}}}_{t,k} \in {\mathbb {C}}^{6\times 1}$ are the estimates of ${\textbf{c}}_{r,k}$ and ${\textbf{c}}_{t,k}$, respectively. Let ${\textbf{c}}^{'}_{r,k}$ and ${\textbf{c}}^{'}_{t,k}$ be the rough estimates of ${\hat{\textbf{c}}}_{r,k}$ and ${\hat{\textbf{c}}}_{t,k}$, respectively, and they can be calculated via

$$\begin{aligned} \begin{aligned} {\hat{\textbf{c}}}^{'}_{r,k}(j,1) =&\frac{1}{6} \sum ^{6}_{j=1} {\hat{\textbf{c}}}_{rt,k}(6j-5:6j,1) (j=1,2,\ldots ,6)\\ =&\frac{1}{6} \sum ^{6}_{j=1} {\hat{\textbf{c}}}_{t,k}(j,1) {\hat{\textbf{c}}}_{r, k} = {\hat{c}}^{s}_{t,k} {\hat{\textbf{c}}}_{r, k} \end{aligned},\nonumber \\ \end{aligned}$$

(22a)

$$\begin{aligned} \begin{aligned} {\hat{\textbf{c}}}^{'}_{t,k}(j,1) =&\frac{1}{6} \sum ^{6}_{i=1} {\hat{\textbf{c}}}_{rt,k}(6(i-1)+j,1) (j=1,2,\ldots ,6) \\ =&\frac{1}{6} \sum ^{6}_{i=1} {\hat{\textbf{c}}}_{r,k}(j,1) {\hat{\textbf{c}}}_{t, k} = {\hat{c}}^{s}_{r,k} {\hat{\textbf{c}}}_{t, k} \end{aligned},\nonumber \\ \end{aligned}$$

(22b)

where ${\hat{c}}^s_{t,k} = \frac{1}{6}\sum ^6_{j=1} {\hat{\textbf{c}}}_{t,k}(j,1)$ and ${\hat{c}}^s_{r,k} = \frac{1}{6}\sum ^6_{j=1} {\hat{\textbf{c}}}_{r,k}(j,1)$. It should be emphasized that ${\hat{\textbf{c}}}^{'}_{r,k}$ is the product of the vector ${\hat{\textbf{c}}}_{r, k}$ and the complex number ${\hat{c}}^{s}_{t,k}$, and ${\hat{\textbf{c}}}^{'}_{t,k}$ is the product of the vector ${\hat{\textbf{c}}}_{t, k}$ and the complex number ${\hat{c}}^{s}_{r,k}$. After obtaining the estimated ${\hat{\textbf{c}}}_{r,k}$ and ${\hat{\textbf{c}}}_{t,k}$, the azimuth angle and the polarization parameters can be estimated through ‘Vector Cross-Product’ method in [23]. Let ${\hat{{\textbf{c}}}}^{'}_{r_1,k} \in {\mathbb {C}}^{3 \times 1}$ and ${\hat{{\textbf{c}}}}^{'}_{r_2,k} \in {\mathbb {C}}^{3 \times 1}$ be the first and last three elements of ${\hat{\textbf{c}}}^{'}_{r,k}$, respectively. And let ${\hat{{\textbf{c}}}}^{'}_{t_1,k} \in {\mathbb {C}}^{3 \times 1}$ and ${\hat{{\textbf{c}}}}^{'}_{t_2,k} \in {\mathbb {C}}^{3 \times 1}$ be the first and last three elements of ${\hat{\textbf{c}}}^{'}_{t,k}$, respectively. Utilize (6), we can estimate ${\textbf{v}}_{r,k}$ and ${\textbf{v}}_{t,k}$ via

$$\begin{aligned} {\hat{\textbf{v}}}_{r,k}{} & {} = \frac{{\hat{{\textbf{c}}}}^{'}_{r_1,k}}{ \left\| {\hat{{\textbf{c}}}}^{'}_{r_1,k} \right\| _\textrm{F} } \circledast \frac{{\hat{{\textbf{c}}}}^{'*}_{r_2,k}}{ \left\| {\hat{{\textbf{c}}}}^{'}_{r_2,k} \right\| _\textrm{F} } =\frac{ {\hat{c}}^s_{t,k} {\hat{{\textbf{c}}}}_{r_1,k}}{ \left\| {\hat{c}}^s_{t,k} {\hat{{\textbf{c}}}}_{r_1,k} \right\| _\textrm{F} } \circledast \frac{ {\hat{c}}^{s*}_{t,k}{\hat{{\textbf{c}}}}^{*}_{r_2,k}}{ \left\| {\hat{c}}^s_{t,k} {\hat{{\textbf{c}}}}_{r_2,k} \right\| _\textrm{F} }\nonumber \\{} & {} =\frac{ {\hat{{\textbf{c}}}}_{r_1,k}}{ \left\| {\hat{{\textbf{c}}}}_{r_1,k} \right\| _\textrm{F} } \circledast \frac{ {\hat{{\textbf{c}}}}^{*}_{r_2,k}}{ \left\| {\hat{{\textbf{c}}}}_{r_2,k} \right\| _\textrm{F} }= \begin{bmatrix} \textrm{sin}({\hat{\theta }}_{r,k}) \textrm{cos} ({\hat{\phi }}_{r,k})\\ \textrm{sin}({\hat{\theta }}_{r,k}) \textrm{sin} ({\hat{\phi }}_{r,k})\\ \textrm{cos}({\hat{\theta }}_{r,k}) \end{bmatrix}, \end{aligned}$$

(23)

$$\begin{aligned} {\hat{\textbf{v}}}_{t,k}{} & {} =\frac{{\hat{{\textbf{c}}}}^{'}_{t_1,k}}{ \left\| {\hat{{\textbf{c}}}}^{'}_{t_1,k} \right\| _\textrm{F} } \circledast \frac{{\hat{{\textbf{c}}}}^{'*}_{t_2,k}}{ \left\| {\hat{{\textbf{c}}}}^{'}_{t_2,k} \right\| _\textrm{F} } = \frac{ {\hat{c}}^s_{r,k} {\hat{{\textbf{c}}}}_{t_1,k}}{ \left\| {\hat{c}}^s_{r,k} {\hat{{\textbf{c}}}}_{t_1,k} \right\| _\textrm{F} } \circledast \frac{ {\hat{c}}^{s *}_{r,k} {\hat{{\textbf{c}}}}^{*}_{t_2,k}}{ \left\| {\hat{c}}^s_{r,k} {\hat{{\textbf{c}}}}_{t_2,k} \right\| _\textrm{F} } \nonumber \\{} & {} =\frac{{\hat{{\textbf{c}}}}_{t_1,k}}{ \left\| {\hat{{\textbf{c}}}}_{t_1,k} \right\| _\textrm{F} } \circledast \frac{{\hat{{\textbf{c}}}}^{*}_{t_2,k}}{ \left\| {\hat{{\textbf{c}}}}_{t_2,k} \right\| _\textrm{F} } = \begin{bmatrix} \textrm{sin}({\hat{\theta }}_{t,k}) \textrm{cos} ({\hat{\phi }}_{t,k})\\ \textrm{sin}({\hat{\theta }}_{t,k}) \textrm{sin} ({\hat{\phi }}_{t,k})\\ \textrm{cos}({\hat{\theta }}_{t,k}) \end{bmatrix}, \end{aligned}$$

(24)

where ${\hat{\textbf{c}}}_{r_1,k}$ and ${\hat{\textbf{c}}}_{r_2,k}$ are the first and last three elements of ${\hat{\textbf{c}}}_{r,k}$, respectively. ${\hat{\textbf{c}}}_{t_1,k}$ and ${\hat{\textbf{c}}}_{t_2,k}$ are the first and last three elements of ${\hat{\textbf{c}}}_{t,k}$, respectively. As we can see from Eq. (23), $\hat{c}^{s}_{t,k}$ in ${\hat{\textbf{c}}}^{'}_{r,k}$ and $\hat{c}^{s}_{r,k}$ in ${\hat{\textbf{c}}}^{'}_{t,k}$ can be eliminated by ‘Vector Cross-Product.’ The following receive (transmit) azimuth angle estimation will not be affected by ${\hat{c}}^s_{t,k}$ (${\hat{c}}^s_{r,k}$).

Then, ${\phi }_{r,k}$ and ${\phi }_{t,k}$ can be estimated by

$$\begin{aligned}{} & {} {\hat{\phi }}_{r,k} = \textrm{arctan} \left( \frac{{\hat{\textbf{v}}}_{r,k}(2)}{{\hat{\textbf{v}}}_{r,k}(1)}\right) , \end{aligned}$$

(25a)

$$\begin{aligned}{} & {} {\hat{\phi }}_{t,k} = \textrm{arctan} \left( \frac{{\hat{\textbf{v}}}_{t,k}(2)}{{\hat{\textbf{v}}}_{t,k}(1)}\right) , \end{aligned}$$

(25b)

Once $({\hat{\theta }}_{r,k}, {\hat{\phi }}_{r,k})$ and $({\hat{\theta }}_{t,k}, {\hat{\phi }}_{t,k})$ are obtained, we can construct the transmit and receive polarization steering vector ${\hat{\textbf{F}}}_{r,k}$ and ${\hat{\textbf{F}}}_{t,k}$ according to (3), respectively. Then, ${{\textbf{h}}}_{r,k}$ and ${{\textbf{h}}}_{t,k}$ can be estimated via

$$\begin{aligned} {\hat{\textbf{h}}}_{r,k}= & {} {\hat{\textbf{F}}}^{\dagger }_{r,k} {\hat{\textbf{c}}}^{'}_{r,k} = {\hat{c}}^s_{t,k} \begin{bmatrix} \textrm{sin }\left( {\hat{\gamma }}_{r,k} \right) e^{j {\hat{\eta }}_{r,k}}\\ \textrm{cos}\left( {\hat{\gamma }}_{r,k}\right) \end{bmatrix} , \end{aligned}$$

(26a)

$$\begin{aligned} {\hat{\textbf{h}}}_{t,k}= & {} {\hat{\textbf{F}}}^{\dagger }_{t,k} {\hat{\textbf{c}}}^{'}_{t,k} ={\hat{c}}^s_{r,k} \begin{bmatrix} \textrm{sin }\left( {\hat{\gamma }}_{t,k} \right) e^{j {\hat{\eta }}_{t,k}}\\ \textrm{cos}\left( {\hat{\gamma }}_{t,k}\right) \end{bmatrix} , \end{aligned}$$

(26b)

Finally, $({\gamma }_{r,k}, {\eta }_{r,k})$ and $({\gamma }_{t,k}, {\eta }_{t,k})$ can be estimated via

$$\begin{aligned} \left\{ \begin{aligned}&{\hat{\gamma }}_{r,k} = \textrm{arctan} \left( \left| \frac{ {\hat{\textbf{h}}}_{r,k} (2) }{{\hat{\textbf{h}}}_{r,k}(1) } \right| \right) \\&{\hat{\eta }}_{r,k} = \textrm{angle} \left( \frac{{\hat{\textbf{h}}}_{r,k} (2) }{{\hat{\textbf{h}}}_{r,k}(1) } \right) \end{aligned} \right. , \end{aligned}$$

(27a)

$$\begin{aligned} \left\{ \begin{aligned}&{\hat{\gamma }}_{t,k} = \textrm{arctan} \left( \left| \frac{ {\hat{\textbf{h}}}_{t,k} (2) }{{\hat{\textbf{h}}}_{t,k}(1) } \right| \right) \\&{\hat{\eta }}_{t,k} = \textrm{angle} \left( \frac{{\hat{\textbf{h}}}_{t,k} (2) }{{\hat{\textbf{h}}}_{t,k}(1) } \right) \end{aligned} \right. , \end{aligned}$$

(27b)

From Eq. (27), we can know that when calculating ${\hat{\gamma }}_{r,k}$ and ${\hat{\eta }}_{r,k}$, ${\hat{c}}^s_{t,k}$ in ${\hat{\textbf{h}}}_{r,k}$ can be eliminated by division, and the ${\hat{c}}^s_{r,k}$ in ${\hat{\textbf{h}}}_{t,k}$ also can be eliminated by division when calculating ${\hat{\gamma }}_{t,k}$ and ${\hat{\eta }}_{t,k}$. The receive elevation angle estimate ${\hat{\theta }}_{t,k}(k=1,2,\ldots ,K)$ and the transmit elevation angle estimate ${\hat{\theta }}_{t,k}$ are automatically paired by using joint diagonalization. Other receive and transmit parameters correspond one to one with the receive and transmit elevation angles, so the above algorithm can ensure automatic matching of all parameters. Although the azimuth angle and the polarization parameters are estimated by the ‘Vector Cross-Product’ and LS ideas like that in [23], respectively, we proved that the transmit or receive parameters does not affect the receive or transmit parameters estimation in the proposed approach, which is also not reflected in previous subspace-based algorithms. The main steps of the proposed algorithm are listed in Algorithm 1.

Algorithm 1

The main steps of the proposed algorithm.

4 Performance analysis

Table 1 Computational complexity

4.1 Computational complexity

Here, the proposed parameters estimation approach is applied to the signal subspace obtained by the PM [26], the EVD, and the HOSVD [24]. After that, we marked them as Im PM, ImESPRIT, and ImHOSVD, respectively. The computation complexity of those three methods is mainly concentrated in the signal-subspace acquisition process, as analyzed in [26]. Besides, in the proposed parameters estimation approach, the main complexity of the joint receive–transmit polarization steering vector recovery process is $K[(36)^2NM]$. Table 1 lists the main computational loads of the proposed ImPM algorithm, the proposed ImESPRIT algorithm, the proposed ImHOSVD algorithm, the PM in [26], the HOSVD algorithm in [24], and the ESPRIT algorithm in [23]. It can be seen from Table 4 that the proposed parameter estimation method will not bring excessive calculation amount.

4.2 Cramer–Rao bound (CRB)

Let $\Theta = [\theta _{r,1},\ldots ,\theta _{r,K}, \theta _{t,1}, \ldots , \eta _{t,K}] \in {\mathbb {C}}^{8K \times 1}$ be the parameters needed to be estimated. According to [27], the CRB on $\Theta$ is given by

$$\begin{aligned} \textrm{CRB} = \frac{\sigma ^2}{2L} \left\{ \textrm{Re} \left[ \left( \mathbf{{B}}^{\textrm{H}}_{rt, \Delta } {\varvec{\Pi ^{\perp }_{{\textbf{B}}_{rt}} }} \mathbf{{B}}_{rt,\Delta } \right) \oplus \left( {\textbf{R}}_{{\textbf{S}}^{'}}^{\textrm{T}} \otimes {\textbf{I}}_{8} \right) \right] \right\} ^{-1},\nonumber \\ \end{aligned}$$

(28)

where ${\varvec{\Pi ^{\perp }_{{\textbf{B}}_{rt}}}}={\textbf{I}}_{36NM}-{\textbf{B}}_{rt} ({\textbf{B}}_{rt}^{\textrm{H}} {\textbf{B}}_{rt} )^{-1} {\textbf{B}}_{rt}^{\textrm{H}}$, in which ${\textbf{B}}_{rt}$ is the joint receive–transmit array manifold; $\mathbf{{R}}_{{\textbf{S}}^{'}} = {\textbf{S}}^{'} {\textbf{S}}^{'{\textrm{H}}} / L$, in which L is the number of pulses; $\sigma ^2$ is the noise power; ${\textbf{B}}_{rt, \Delta } = \left[ \frac{\partial {\textbf{B}}_{rt} }{\partial {\theta }_{r,1} }, \ldots , \frac{\partial {\textbf{B}}_{rt} }{\partial {\theta }_{r,K} }, \frac{\partial {\textbf{B}}_{rt} }{\partial {\theta }_{t,1} }, \ldots , \frac{\partial {\textbf{B}}_{rt} }{\partial {\eta }_{t,K} } \right]$. The detailed derivation process of $\textrm{CRB}$ can be referred to [27].

5 Simulation

In this section, 200 Monte Carlo trials are taken to evaluate the performance of the proposed parameter estimation approach. The PM algorithm in [26], the ESPRIT algorithm in [23], the HOSVD algorithm in [24], and the CRB are introduced as comparisons. Except for special instruction, the bistatic EMVS-MIMO radar is equipped with $M=6$ transmit antennas and $N=8$ receive antennas. Both the transmit and receive arrays are ULAs arranged in half-wavelength. The transmit baseband code matrix is $\mathbf{{S}} = (1+j)/{\sqrt{2}} \mathbf{{H}}_{6\,M}$, where $\mathbf{{H}}_{6\,M}$ is composed of the first 6M rows of the $Q\times Q$ Hadamard matrix. Here, Q is set to 512. Suppose there are three uncorrelated far-field point-like targets. The angle information of these targets is ${\varvec{\theta }}_t=[40^{\circ }, 20^{\circ }, 30^{\circ } ]$, ${\varvec{\phi }}_t=[15^{\circ }, 25^{\circ }, 35^{\circ } ]$, ${\varvec{\gamma }}_t=[10^{\circ }, 22^{\circ }, 35^{\circ } ]$, ${\varvec{\eta }}_t=(36^{\circ }, 48^{\circ }, 56^{\circ } )$, ${\varvec{\theta }}_r=[24^{\circ }, 38^{\circ }, 16^{\circ } ]$, ${\varvec{\phi }}_r=[21^{\circ }, 32^{\circ }, 55^{\circ } ]$, ${\varvec{\gamma }}_r=[42^{\circ }, 33^{\circ }, 60^{\circ } ]$, ${\varvec{\eta }}_r=[17^{\circ }, 27^{\circ }, 39^{\circ } ]$. The reflection coefficient of targets obeys the Gaussian distribution. The additive noise is assumed to be a spatial white complex Gaussian noise. The performance of the algorithm is evaluated by root-mean-square errors (RMSE), which is defined as

$$\begin{aligned} \textrm{RMSE}=\frac{1}{K} \sum ^K_{k=1} \sqrt{\frac{1}{M_c} \sum ^{M_c}_{m_c=1} \left( {\hat{\zeta }}_{k,m_c}-\zeta _k\right) ^2}, \end{aligned}$$

(29a)

where K is the number of targets, $M_c$ is the number of Monte Carlo trials, and $\zeta _{k,m_c}$ is the estimate of $\zeta _k$ in the $m_c$-th Monte Carlo trial. As in [24], to simplify the RMSE results, we only display the average RMSE of the direction angle estimation, namely 2D-DOA and 2D-DOD, and the average RMSE of the polarization parameters estimation, namely 2D-TPA and 2D-RPA.

Fig. 2

The performance of different methods versus SNR. a The RMSE of direction angle estimation of different methods versus SNR. b The RMSE of polarization parameters estimation of different methods versus SNR. c The probability of successful detection of different methods versus SNR. d The computational complexity of different methods versus SNR

In the following simulations, the proposed ImPM algorithm, the proposed ImESPRIT algorithm, the proposed ImHOSVD algorithm, the PM algorithm in [26], the ESPRIT algorithm in [23], and the HOSVD algorithm in [24] are tested from three aspects: the RMSE performance, the computational complexity, the probability of successful detection, thus to show that the proposed parameter estimation approach can improve the accuracy of parameter estimation when it is applied to the signal subspace obtained by different methods. Suppose the target can be successfully detected as long as the absolute error of the estimated angle is under $\rho _e$.

Figure 2 depicts the performance of different algorithms versus SNR, where $L=100$ and $\rho _e = 1^{\circ }$. Figure 2a, b shows that the RMSE performance of different algorithms gradually improves as the SNR increases. The probability of successful detection of different methods increase with the increase of SNR. When the proposed parameter method is applied to signal subspaces obtained differently, the parameter estimation accuracy is improved compared with the original corresponding method, as we can see from Fig. 2a–c. The reason may be that the proposed parameter estimation method uses the entire signal subspace to estimate all parameters rather than a part of the signal subspace. Furthermore, it can be seen from Fig. 2d that the proposed method does not bring additional computational effort when applied to signal subspaces obtained in different ways.

Fig. 3

The parameters estimation performance of different methods versus L. a The RMSE of direction angle estimation of different methods versus L. b The RMSE of polarization angle estimation of different methods versus L. c The probability of successful detection of different methods versus L. d The computational complexity of different methods versus L

Fig. 4

The parameters estimation performance of different methods versus N. a The RMSE of direction angle estimation of different methods versus N. b The RMSE of polarization angle estimation of different methods versus N. c The probability of successful detection of different methods versus N. d The computational complexity of different methods versus N

Fig. 5

The parameters estimation performance of different methods versus K. a The RMSE of direction angle estimation of different methods versus K. b The RMSE of polarization angle estimation of different methods versus K. c The probability of successful detection of different methods versus K. d The computational complexity of different methods versus K

Figure 3 depicts the performance of different algorithms versus L, where SNR = 10 dB and $\rho _e = 0.15^{\circ }$. Figure 3a, b shows that the RMSE of different algorithms gradually decrease as the L increases. The probability of the ImPM, the ImESPRIT, the ImHOSVD, the PM, and the HOSVD gradually decrease with the increase of L. The same conclusion as the first test can be drawn from Fig. 3a–c that when the proposed parameters estimation approach is applied to the signal subspace obtained by different methods, the parameters estimation performance is better than the previous old one. The computational complexity gradually increases with the increase in the number of L; still, when the proposed algorithm acts on different signal subspaces, it does not bring too much calculation compared to the original algorithm, as we can see from Fig. 3d.

Figure 4 depicts the performance of different algorithms versus the number of the receive antenna N, where SNR =10 dB, $L = 100$, and $\rho _e = 0.15^{\circ }$. The RMSE of different algorithms degrade gradually as N increases, as shown in Fig. 1a, b. The computational complexity of different algorithms gradually increases as the increase of N. Similarly, when the proposed parameter estimation approach is applied to the signal subspace obtained by different methods, the RMSE of the improved methods is less than the corresponding old method. In the signal subspace obtained by the HOSVD, the probability of successful detection of the proposed approach is also better than that in [24].

Figure 5 displays the performance of different algorithms versus K, where SNR = 10 dB, $L=100$, and $\rho _e = 0.15^{\circ }$. The targets are selected from the front K targets from the following targets: ${\varvec{\theta }}_t=(10^{\circ }, 15^{\circ }, 25^{\circ },30^{\circ }, 35^{\circ },50^{\circ },$ $58^{\circ },67^{\circ } )$, ${\varvec{\phi }}_t=(30^{\circ }, 56^{\circ }, 15^{\circ }, 36^{\circ },65^{\circ },22^{\circ }, 40^{\circ },48^{\circ } )$, ${\varvec{\gamma }}_t=(14^{\circ }, 30^{\circ }, 54^{\circ },62^{\circ },38^{\circ }$ $,46^{\circ },22^{\circ },70^{\circ } )$, ${\varvec{\eta }}_t=(18^{\circ }, 64^{\circ }, 34^{\circ },56^{\circ },48^{\circ },72^{\circ },30^{\circ },40^{\circ } )$, ${\varvec{\theta }}_r=(12^{\circ }, 52^{\circ }, 27^{\circ },$ $37^{\circ },20^{\circ },40^{\circ },46^{\circ },$ $40^{\circ } )$, ${\varvec{\phi }}_r=(62^{\circ },13^{\circ },54^{\circ },28^{\circ }, 38^{\circ },34^{\circ }, 46^{\circ }, 21^{\circ }),$ ${\varvec{\gamma }}_r=(35^{\circ }, 15^{\circ }$ $,25^{\circ },65^{\circ },45^{\circ },55^{\circ }$ $, 5^{\circ }, 75^{\circ })$, ${\varvec{\eta }}_r=(81^{\circ }, 31^{\circ }, 51^{\circ },61^{\circ },45^{\circ },55^{\circ },5^{\circ },75^{\circ })$. As shown in Fig. 5d, the computational complexity of different algorithms hardly increases with the increase in K. Similar to the previous result, the proposed parameter estimation approach has better performance than the previous signal-subspace-based methods when the proposed approach is adopted to the corresponding signal subspace, as we can see from Fig. 5a–c.

6 Conclusion

This paper proposed a more accurate signal-subspace-based parameters estimation approach for joint 2D-DOD, 2D-DOA, and polarization parameters estimation in bistatic EMVS-MIMO radar. When the proposed parameter estimation approach is applied to the signal subspace obtained by performing EVD or HOSVD on the covariance matrix or tensor or by the PM algorithm, the estimation performance can be improved compared with the existing estimation methods since the proposed approach used the whole signal subspace to estimate the parameters. Simulation experiments verified the effectiveness of the proposed algorithm.