1 Introduction

As a tool for approximating the incompressible Navier–Stokes equations (NSE) in turbulent flow simulations, the Lattice Boltzmann method (LBM) has attracted attention in recent years due to its efficiency and parallelization [1], especially in connection with large eddy simulation (LES) [2]. The applicability of LBM for direct numerical simulations(DNS) or LES has been investigated in several studies (see for example [3] and references therein). The application of LBM to the LES methodology provides significant speedup over traditional finite volume methods(FVM) [4, 5]. In a recent study [6], comparing open-source packages for wall-modeled LES of an internal combustion engine demonstrated that LBM (OpenLBM [7]) is on average 32 times faster than FVM (OpenFOAM). On an industrial scale in the order of one billion grid cells, LBM LES could even be the first method allowing for overnight simulations [8].

After the first LBM LES model (based on the standard Smagorinsky eddy viscosity) was proposed [9], the approach has been extended [10, 11] to be consistent in the inertial range and complemented with a dynamic procedure [12] for calculating model constants. Weickert et al. [13] proposed and studied an LBM for the wall adaptive large eddy (WALE) model. Based on a Hermite expansion, Malaspinas et al. [14] introduced consistent subgrid closures for the filtered Bhatnagar–Gross–Krook (BGK) Boltzmann equation. Besides LES models based on eddy viscosity approximations, the approximate deconvolution model (ADM) has been formulated in the framework of LBM [15, 16] and was extended by adaptive filtering [17, 18]. Jacob et al. [19] recently proposed a hybrid approach by combining a recursive regularization technique with hyperviscosity. The simplicity of implementation as well as the vast amount of extension possibilities to other physical flow models promote the necessity of exploring such advanced turbulence models for LBM [20, 21]. Apart from the classical approaches based on spatial filtering, Pruett [22] raised several advantages of time-filtering in the context of LES and introduced a temporal variant of the ADM, called the temporal approximate deconvolution model (TADM). Recently a new temporal LES (TLES) based on temporal direct deconvolution (TDDM) was proposed [23, 24]. A TLES upholding the high parallelizability of LBM due to intrinsic spatial locality, along with the benefits of a turbulence model, is a promising alternative to classical LES [25].

In recent years, researchers have also transformed the original complex iterative calculation or solution process into an image generation problem [7, 26,27,28]. For example, Yang et al proposed a CNN-based pressure solver model to replace the original iterative solution of the pressure in the process of solving the N–S equation. Based on this, they have a good speed-up effect and high accuracy for the solution of N-S equations, but they are not suitable for fully explicit LBM. It solves in the histogram domain instead of the pixel domain and is faster to calculate. In the acceleration of the LBM, the Adaptive Neural Fuzzy Inference System (ANFIS) is used to learn lattice Boltzmann method (LBM) data and predict fluid patterns based on their understanding. Chen et al. [29] replaced the multi-step computation of LBM with LSTM model operations, which are highly accurate and fast [30]. In this paper, the Convolutional Neural Network and Gated Recurrent Unit Neural Network combined with Lattice Boltzmann Method (CG-LBM) is proposed to replace the calculation process in the LBM to improve computational efficiency. By inputting the flow field information with dual dimensions of time and space, the prediction results of the flow field across multiple iterations are obtained using a novel network structure. This model specifically constructs a CNN network to extract the spatial characteristics and a two-layer GRU network to fully learn the temporal characteristics of the fluid data in the pipeline simultaneously. The first layer GRU extracts the timing characteristics and transmits the fluid information matrix of the same format to the second-layer GRU according to the CNN layer’s times 24 fluid particle migration matrix. After the second-layer GRU extracts more timing information, the neuron outputs a vector of fluid information in times 1 format to the fully connected layer in the final step. This model has the advantage of dealing with both the process of non-steady-state and steady-state problems. Meanwhile, the model can have faster calculation speed and better accuracy.

2 LBM method based on CNN–GRU network

2.1 Basic principles and methods of LBM

The calculation process of the complete lattice Boltzmann method can be summarized as follows. According to the characteristics of the research object, the macroscopic physical quantities on all nodes are first determined, and then the equilibrium-state distribution function of each node in each direction is calculated to obtain the initial field. The node characteristics are treated in different boundary formats, and the distribution of physical quantities at each node is calculated according to the rules of macroscopic quantity definition of the lattice Boltzmann model.

In the LBM numerical, the flow field is divided into many grids of equal size, and the particle distribution function f on each grid point is used to describe the state of the flow field, and \(f_i\) is used on the grid point to represent the number of particles moving in the direction of \(e_i\). The D2Q9 model for two-dimensional problems used in this paper discretizes the motion directions of particles into 9 directions including the zero vector, as shown in Fig. 1

Fig. 1
figure 1

Probabilistic model of particle motion

Full size image

Add probabilities to these nine velocity vectors to simulate a continuous Boltzmann distribution as accurately as possible. For a stationary fluid \((u = 0)\), Eq. 1 indicate that 0 must be the most probable velocity. The longer diagonal velocity vectors must be less probable than shorter horizontal and vertical velocity vectors. Velocities of the same magnitude must have the same probability regardless of direction. The optimal probability for velocity 0 is 4/9, 1/9 for the four cardinal directions, and 1/36 for the diagonal. These probabilities (or weights) \({\omega _i}\) can be expressed as follows,

$$\begin{aligned} \left\{ \begin{array}{l} {w_0} = 4/9\\ {w_1} = {w_2} = {w_3} = {w_4} = 1/9\\ {w_5} = {w_6} = {w_7} = {w_8} = 1/36 \end{array} \right. \end{aligned}$$
(1)

These weights have the correct qualitative properties, and they are correctly normalized to add up to 1. But otherwise, they predicted the same average of \({v_x}\),\({v_y}\) and all powers of \({v_x}\),\({v_y}\) up to the fourth power. The Boltzmann equation is derived for the modeling equation of continuous fluid dynamics as follows.

$$\begin{aligned} \frac{{\partial f}}{{\partial t}} + \xi \frac{{\partial f}}{{\partial r}} = - \frac{1}{\tau _C }(f - {f^{\text {eq}}}) \end{aligned}$$
(2)

Since the motion of molecules in a fluid exists at all times, Eq. 2 is infinite-dimensional. Then the BGK operator \({e_i }\) is used to replace \(\xi \). The Boltzmann method changes the infinite-dimensional equation 1 into Eq. 3 with respect to the velocity discretization.

$$\begin{aligned} \frac{{\partial {f_i}}}{{\partial t}} + {e_i}\frac{{\partial {f_i}}}{{\partial r}} = - \frac{1}{{{\tau _C}}}({f_i} - {f_i}^{\text {eq}}) \end{aligned}$$
(3)

The derivatives in time and space are then discretized in the next step to obtain Eq. 4. The overall is a forward differencing process of first-order accuracy. The Lattice Boltzmann equation absorbs the values generated in the first-order accuracy process and continues into the physical viscosity. After the absorption, it changes from first-order accuracy to second-order accuracy. After this method of processing, the numerical dissipation of the Lattice Boltzmann method is smaller than the fourth-order accuracy of the same physical scenario using the CFD method.

$$\begin{aligned}{} & {} \frac{{{f_i}(r,t + {\delta _t}) - {f_i}(r,t)}}{{{\delta _t}}} \nonumber \\{} & {} \qquad + {e_i}\frac{{{f_i}(r + {e_i},t + {\delta _t}) - {f_i}(r,t + {\delta _t})}}{{\Delta r}}\nonumber \\{} & {} \quad = - \frac{1}{{{\tau _C}}}({f_i} - f_i^{\text {eq}}) \end{aligned}$$
(4)

where \(\frac{{{f_i}(r,t + {\delta _t}) - {f_i}(r,t)}}{{{\delta _t}}}\) and \(\frac{{{f_i}(r + {e_i},t + {\delta _t}) - {f_i}(r,t + {\delta _t})}}{{\Delta r}}\) in Eq. 4 are the discrete forms of the temporal and spatial features to be processed in Fig. 2, respectively.

Other physical information about the position can be obtained by using the particle distribution function, such as the macroscopic density \({\rho }\) and the velocity u have the following expression,

$$\begin{aligned} \rho (r,t) = \sum \limits _{t = 0}^8 {{f_i}(r,t),u = \frac{1}{\rho }\sum \limits _{t = 0}^8 {{f_i}{e_i}} } \end{aligned}$$
(5)

where r is the grid position and t is the time. The governing equation of the discrete form of LBM is

$$\begin{aligned} {f_i}(r + {e_i}{\delta _i},t) - {f_i}(r,t) = \Omega ({\tau _C})[{f_i}(r,t) - f_i^{\text {eq}}(r,t)] \end{aligned}$$
(6)

where \({\delta _i}\) is the time step, \({\tau _C}\) is the relaxation factor, and \(\Omega \) is the collision factor calculated from \({\tau _C}\). The governing equations contain descriptions of particle migration and collision. These two parts are calculated separately in the numerical program. The expressions of the two are,

$$\begin{aligned} {f_i}(r,t) = {f_i}(r,t) + \Omega ({\tau _C})[f_i^{\text {eq}}(r,t) - {f_i}(r,t)] \end{aligned}$$
(7)
$$\begin{aligned} {f_i}(r + {e_i}{\delta _t},t + {\delta _t}) = f_i^*(r,t) \end{aligned}$$
(8)

Eq. 7 expresses the collision process of particles and Eq. 8 expresses the migration process of particles.

From the LBM model, the core physical quantity of the whole calculation process was the spatial size of the discrete particle velocity distribution function (x, y). Therefore, it was set as a three-dimensional array of size (x, y, 9) according to the requirements of the model, so that it exactly meets the required specification of gated recurrent neural network input as an array, with the first two dimensions representing the length and width of the space and the last dimension being the number of channels, it corresponds to the number of discrete velocities. Therefore, in the network model of this paper, the original discrete particle velocity distribution function information was extracted and the corresponding calculation was completed.

2.2 CG-LBM model network structure

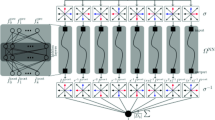
In order to fully learn the multi-featured fluid data, the CG-LBM fluid-state prediction model was further proposed in this paper. The model structure mainly includes CNN, GRU and a fully connected layer. The overall network structure is shown in Fig. 2.

Fig. 2
figure 2

Schematic diagram of CG-LBM calculation flow

Full size image

This model builds a two-layer GRU structure to fully learn the temporal characteristics of fluid state data. Based on the \(U \times 24\) particle migration information matrix output by the CNN layer, the timing characteristics are extracted from the first-layer GRU, and the particle migration matrix in the same format is passed to the second-layer GRU. After the second-layer GRU further extracts timing information, the final one-step neuron outputs a vector of particle motion information in \(U \times 1\) format to the fully connected layer. The mathematical description is shown in Eq. 9.

$$\begin{aligned} \left\{ {\begin{array}{*{20}{c}} {{z_t} = \sigma ({W_{hz}} \cdot [{y_{t - 1}},{x_t}] + {b_z})}\\ {{r_t} = \sigma ({W_{hr}} \cdot [{y_{t - 1}},{x_t}] + {b_r})}\\ {{s_t} = \tanh ({W_{ht}} \cdot [{y_{t - 1}},{x_t}] + {b_g})}\\ {{y_t} = (1 - {z_t}) \cdot {y_{t - 1}} + {z_t} \cdot {s_t}} \end{array}} \right. \end{aligned}$$
(9)

Among them, x is the number multiplication of the matrix, \(\sigma \) is the activation function sigmoid function, tanh is the activation function tanh function, ’\(1-\)’ indicates that the data propagated forward by the link are \(1 - {z_t}\). \({z_t}\) and \({r_t}\) are the update gate and reset gate. \({x_t}\) is the input, \({h_t-1}\) is the output of the previously hidden layer, and \({h_t}\) is the output of the hidden layer.

The fully connected layer containing V neurons further performs a nonlinear mapping of the particle motion in the fluid extracted by the GRU network. Finally, the output layer containing individual neurons outputs the prediction results. The equations for the fully connected layer and the output layer are shown in Eq. 10.

$$\begin{aligned} y = {W_{1 \times V}} \cdot \sigma ({W_{v \times u}} \cdot {h_{U \times 1}} + {b_{V \times 1}}) + {b_{1 \times 1}} \end{aligned}$$
(10)

In the formula, y is the predicted value of representing fluid state information, \({h_{U \times 1}}\) is the vector representing fluid state information output by the GRU network, \({W_{V \times U}}\) and \({b_{V \times 1}}\) are the weight matrix and bias vector of the fully connected layer, \({W_{1 \times V}}\) and \({b_{1 \times 1}}\) are the weight matrix of the output layer and bias.

The combined CNN–GRU model leverages the advantages of convolutional neural networks and recurrent neural networks in spatial and sequence prediction. First, the convolutional neural network is used to extract and simulate the spatial features of the fluid model. Then, sequence data containing spatial features are fed into the GRU network to further extract temporal features. Finally, the fluid state is predicted by a fully connected neural network.

A process can be divided into four steps. First, the input dataset is divided into training, test sets and normalized. Second, the network parameters of the CNN–GRU model are set, and the mean square error and LOSS function are selected as the loss function, respectively. Then the training set is used to train the model and test the training effect. If the model fits the training set as required, it goes to the next step, otherwise, it returns to the previous step and adjusts the network parameters. Finally, the trained model is used to test the test set and the test results are de-weighted to obtain the predicted values of the fluid state.

2.3 CG-LBM loss function with physical information

The loss function is extremely important in deep learning. Based on the physical background of LBM and the loss functions commonly used in neural network training, a loss function named \(\text {LOSS}_{\text {CG} - \text {LBM}}\) is introduced to the CG-LBM model and a loss function named \(\text {LOSS}_{\text {LBM}}\) is introduced to the LBM model.

The distribution function of inputs and outputs in a neural network is the result obtained at the end of each iteration. It is also the result obtained after completing two processes of collision and migration. Therefore, the two output results can be substituted into the collision process. Make it complete the collision and migration process once and get two distribution function results. If the actual value and the predicted value are the same, the error is zero. With this loss function, the physical background information including the velocity input and Reynolds number of the flow field is introduced to make the predicted values match the LBM as closely as possible. The significance of this loss function is to introduce a macroscopic physical quantity to control the model.

Specifically, \(LOS{S_{GRU - \text {LBM}}}\) and \(LOS{S_{\text {LBM}}}\) are represented by Eq. 11 through Eq. 15.

$$\begin{aligned}{} & {} f_i^{\text {true}} = {f_i} + \frac{1}{{{\tau _c}}}(f_i^{\text {eq}} - {f_i}) \end{aligned}$$
(11)
$$\begin{aligned}{} & {} f_{\text {CG} - \text {LBM}\_i}^{\text {pre}} ={f_i} + \frac{1}{{{\tau _c}}}({\mathop {f}\limits ^{\frown }} _{\text {CG} - \text {LBM}\_i}^{\text {eq}} - {{\mathop {f}\limits ^{\frown }} _{\text {CG} - \text {LBM}\_i}}) \end{aligned}$$
(12)
$$\begin{aligned}{} & {} f_{\text {LBM}\_i}^{\text {pre}} = {f_i} + \frac{1}{{{\tau _c}}}({\mathop {f}\limits ^{\frown }}_{\text {LBM}\_i}^{\text {eq}} - {{\mathop {f}\limits ^{\frown }}_{\text {LBM}\_i}}) \end{aligned}$$
(13)
$$\begin{aligned}{} & {} LOS{S_{\text {CG} - \text {LBM}}} =f_{\text {CG} - \text {LBM}}^{\text {pre}} - f_i^{\text {true}} \end{aligned}$$
(14)
$$\begin{aligned}{} & {} LOS{S_{\text {LBM}}} = f_{\text {LBM}\_i}^{\text {pre}} - f_i^{\text {true}} \end{aligned}$$
(15)

Among them, \(f_i^{\text {eq}}\) is the equilibrium distribution function calculated from the experimental value \({f_i}\), and \({\mathop {f}\limits ^{\frown }}_{\text {CG} - \text {LBM}\_i}^{\text {eq}}\) is the equilibrium distribution function calculated from the GRU-LBM predicted value \({\mathop {f}\limits ^{\frown }}_{\text {CG} - \text {LBM}\_i}\), and \({\mathop {f}\limits ^{\frown }}_{\text {LBM}\_i}^{\text {eq}}\) is the equilibrium distribution function calculated from the LBM prediction value \({\mathop {f}\limits ^{\frown }}_{\text {LBM}\_i}\). The significance of the loss function is to introduce a macroscopic physical quantity to control the model. To verify the effect of the loss function LOSS on the model performance, four models were trained using different network structures and training loss functions. They were labelled by MSE LBM, MSE CG-LBM, LOSS CG-LBM, and LOSS LBM. Figure 3 shows these four models. During the training of the different models, the decreasing process of the corresponding function values is recorded.

Fig. 3
figure 3

Loss function value during training

Full size image

In Fig. 3, the final convergence value of the loss function is significantly lower when using the CG-LBM structure. It is proved that the model with this structure has better learning ability and degradation resistance. Compared with the MSE-trained model, the LOSS-trained model converges with the same trend as the MSE-trained model, but the initial state of convergence is different. This indicates that the introduction of LOSS does not affect the prediction results of the model. At the same time, the former converges faster than the latter under the same method. In general, the designed LOSS loss function is more suitable for the network structure of this paper in terms of accuracy and efficiency.

3 Calculation verification and result analysis

To verify the feasibility and prediction accuracy of CG-LBM, eddy current shedding experiments were designed to conduct CG-LBM training and testing. There are three main reasons for choosing the vortex shedding experiment as the CG-LBM validation experiment. First, the initial and boundary conditions of the vortex shedding problem are relatively simple to program. Second, the flow field of this experiment is distinctly characterized, which facilitates comparison between results. Finally, the vortex shedding flow field varies significantly with parameters, and it is easy to test the generalization ability of the model [31].

In this paper, a fluid short-term state prediction model is developed and the performance of the model is tested and evaluated using a test set. Also, the results in terms of training time and prediction accuracy are compared with LBM under the same conditions. The effectiveness of the model was verified. The CG-LBM model is built using the idea presented in Section 2.2, where the number of convolutional kernels U in the convolutional layer, the number of neurons W in each GRU layer, and the number of neurons in the fully connected layer is set to 128, 32 and 32.

3.1 Model environment

The experimental environment in this paper uses AMD Ryzen 7 4800 H processor and NVIDIA GeForce RTX 2060 graphics card. Python3.6 is used as the programming language, the deep learning architecture is based on the Tensorflow 2.0 framework and the Scikit-learn machine learning library. The model parameters of this paper are shown in Table 1.

Table 1 Laminar flow experimental environment
Full size table

Among them, the value range of the relaxation factor \(\tau \) in the control equation of the LBM is [0–1], and its size is only related to the convergence speed of the control equation. The relaxation factor \(\tau \) is firstly taken as 0.2, 0.4, 0.6, and 0.8, respectively. The convergence rate of the governing equation under different relaxation factors \(\tau \), the results are shown in Fig. 4.

Fig. 4
figure 4

Convergence at different viscosity

Full size image
Fig. 5
figure 5

Variation trend of state variables at different Reynolds numbers

Full size image

As shown in Fig. 4, when the control equations take different relaxation factors, they converge significantly after at most 500 calculations. This study focuses on the acceleration and accuracy improvement of CG-LBM to traditional LBM. Therefore, the number of calculations of the model is well over 500 times, and the value of the relaxation factor has little effect on the convergence of the equations. Therefore, the experiments in this paper all take the middle value of the relaxation factor of 0.5.

Table 2 Time-consuming Comparison
Full size table

3.2 Model building and result analysis

Based on the determined parameters, the software was used to perform experiments on the vortex shedding model with Reynolds numbers Re = 1000, 2000 and 4000. The results are shown in Fig. 5. Figure 5 shows the vorticity, velocity and pressure of fluids with different Reynolds numbers after the calculation of 2000. The black dashed line divides Fig. 5 into three groups of Reynolds numbers 1000, 2000 and 4000 according to the different Reynolds numbers. It can be seen that for the same number of calculations when the number of calculations reaches 1000, the fluid with a Reynolds number of 1000 just appears to have laminar flow, while the fluid with a Reynolds number of 2000 already has a stable laminar flow, and the fluid with a Reynolds number of 4000 already has laminar flow fluctuations. When the number of calculations reaches 2000, the fluid with Reynolds numbers 1000 and 2000 has laminar fluctuation, but the fluid with Reynolds number 4000 has already appeared with vortex detachment phenomenon. The vorticity diagram, shows us that as the Reynolds number increases, the stability of the fluid becomes less stable, the fluid state is more likely to change, and the corresponding velocity and pressure change frequency is faster. The velocity diagrams with Reynolds numbers of 2000 and 4000 show us that there is a period of time when the velocity changes from laminar fluctuation to the first vortex detachment are almost without an obvious pattern, and this can seriously affect the prediction accuracy. Predictably, for fluids with Reynolds numbers of 1000 and 2000, when the number of calculations reaches 3000 or more, the vortex shedding phenomenon will also occur, and the velocity and pressure change frequency will also become faster, and both will go through periods of almost irregular changes.

3.3 Error comparison of CG-LBM and LBM

3.3.1 Comparison of operation speed

Table 2 shows the time consumption comparison of four methods, CG-LBM, LSTM-LBM, GRU-LBM and conventional LBM, at different Reynolds numbers, and the time periods are expressed in terms of the number of completed iterations.

Table 2 shows us that the computational efficiency is weakly correlated with both the Reynolds number size and the computational time period, and only with the different models. On the home platform proposed in Sect. 3, the computation time of the serial LBM program model is about 17.2 times higher than that of the CG-LBM model. the CG-LBM model is about 2 times more efficient than the LSTM-LBM model and about 1.16 times more efficient than the GRU-LBM model. It can be seen that the new model proposed in this paper has a significant effect on reducing the consumption of computational resources compared with the traditional LBM model, and the experimental results of this method are in line with expectations.

3.3.2 Comparison of computational accuracy

Error analysis verifies the accuracy of the model on the test set of Re = 1000, 2000, 4000. Figures 6, 7 and 8 show the loss functions of Re=1000, 2000, and 4000. The horizontal axis is the number of CG-LBM calculations corresponding to the iterations of ordinary LBM.

Fig. 6
figure 6

Error(Re=1000)

Full size image
Fig. 7
figure 7

Error(Re=2000)

Full size image
Fig. 8
figure 8

Error(Re=4000)

Full size image

Figures 6, 7 and 8 show the prediction errors of the CG-LBM model and the conventional LBM at different Reynolds numbers for different computation time periods, which are expressed by the number of completed computations. When the Reynolds number is 1000, the average loss function of the conventional LBM model is 0.022, and that of the CG-LBM model is 0.0021, with an accuracy improvement of about 10.47 times. When the Reynolds number is 2000, the average loss function of the conventional LBM model is 0.023 and that of the CG-LBM model is 0.0023, with an improvement in accuracy of about 10 times. When the Reynolds number is 4000, the average loss function of the conventional LBM model is 0.018, and that of the CG-LBM model is 0.0065, with an accuracy improvement of about 2.77 times.

4 Conclusion

To improve the computational efficiency of the LBM, we propose a deep learning-based algorithm to change the computational process of the LBM. A CG-LBM model is built using CNN and GRU networks. It can predict the particle distribution function after multiple time steps. In this paper, the accuracy of the predicted values and the computational efficiency of the model after a series of calculations and parameter adjustments are analyzed for the laminar flow problem as an example. The results show that the CG-LBM has the necessary reliability and can speed up the computation. Based on this study, the following three conclusions can be drawn.

  1. (1)

    Based on the training and testing results of the CG-LBM model, the model can guarantee the necessary accuracy. The study proves that using the physical information loss function can improve the performance of the neural network in the presence of physical background.

  2. (2)

    The computational structure based on the CG-LBM model achieves significant results in guaranteeing prediction accuracy. As a result, a deep learning-based algorithm is successfully constructed and can be used to deal with fluid prediction problems.

  3. (3)

    The computational structure of the CG-LBM model greatly reduces the consumption of computational resources without degrading the accuracy. In the arithmetic example designed in this paper, the computational efficiency of the method on a home testbed is 22.23 times higher than that of the serial LBM program, showing good computational efficiency results and great potential.

Some future development prospects should be proposed for the current model, and improving the prediction accuracy and computational efficiency is the direction of our continuous efforts. The study in this paper shows that the CG-LBM model with high accuracy performs better in the long-term calculation process. However, the computational error of fluids with a Reynolds number higher than 4000 is not studied in this paper, so it is also our work to continue to improve the generalization ability of the model.