1 Introduction

Adaptive filter (AF) algorithms are frequently employed in equalization, active noise control, acoustic echo cancelation, biomedical engineering and many other fields [1]. The step size is a critical parameter in addressing the issue of obtaining either fast convergence rate or low excess mean-square error. Although a large step size responds quickly to plant changes, it may lead to a large MSD and even cause loss of convergence, while a small step size may degrade the tracking speed of the AF algorithm. To address this issue, a relatively large step size can be selected during the initial convergence of an AF algorithm and then a small step size used as the algorithm approaches its steady state. Selection of the step size should balance low steady-state error with a fast convergence rate. So the variable step size method attracts considerable attentions from scholars. There are various methods that can be adopted to get the step size formula. Shin et al. [2] made use of a special function to update step size. Kwong and Johnston [3] proposed a method based on the input data to obtain the step size. Ang [4] presented an approach based on squared instantaneous estimation errors to update the step size. step size parameter was selected in [5] such that the sum of the squares of the measured estimation errors was minimized at the current instant in time. Liu et al. [6] and Benesty et al. [7] utilized the various nonparametric variance estimates and proposed the nonparametric variable step size NLMS algorithms. In [8], Huang and Lee presented a method based on the mean-square error and the estimated system noise power to obtain the step size. Many of these algorithms were developed in a system identification context, and the reference signal is considered as the output of a time-invariant system, usually corrupted by additive noise. However, in practical engineering applications, the system is often non-stationary. Moreover, it makes more sense to minimize the system misalignment, instead of the classical error-based cost function. The approximating optimal step size is selected in [9] such that the MSD was minimized. Lee and Park [10] made use of mean-square deviation to update the step size of the APA algorithm. Zhi et al. [11] proposed the optimal step size of the PAP algorithm. Ciochină et al. [12] proposed an optimized NLMS algorithm which takes advantage of the joint optimization problem with both the normalized step size and regularization parameters. More recently, research has focused on AF algorithms based on high-order error power (HOEP) conditions [13,14,15]. Among HOEP algorithms, the LMAT algorithm can achieve the most robust against the unknown noise of several different probability densities [16]. For example, in [17, 18], impulsive noise is modeled by an \(\alpha \)-stable random process. Besides, some algorithms for impulsive noise environments are introduced. The LMAT algorithm is based on the minimization of the mean of the absolute error value of the third power. The error function is a perfect convex function with respect to filter coefficients, so there is no local minimum for the LMAT algorithm. The feature of unknown system, the characteristics of the additive noise, SNR and the input excitation govern the effectiveness of the LMAT-type algorithm. However, in practical engineering applications, the measurement noise of an unknown system is non-Gaussian, and the system is often non-stationary with low SNR. So on the basis of work presented in [9,10,11,12, 16], the optimal step size rather than approximating optimal step size is selected in this paper such that the MSD at the current in time is minimum. The purpose of the OPLMAT algorithm is to deal with the Gaussian, uniform, Rayleigh and exponential noise distributions, which is different from the literature [17, 18]. The mean convergence and MSD of the OPLMAT algorithm are also derived. The computational complexity of the OPLMAT algorithm is analyzed theoretically. Finally, we have carried out four system identification simulation experiments to illustrate significant superiorities of the OPLMAT algorithm over the LMAT and NLMAT algorithms.

The main contributions of this work are as follows: (a) an OPLMAT algorithm based on minimizing the MSD at the current in time; (b) the step size of the OPLMAT algorithm can achieve minimum steady-state error; (c) the stability of the proposed algorithm is studied; (d) the steady-state errors are derived from both Gaussian and non-Gaussian noises; and (e) the obtained results may also have some potential value in practical applications.

Briefly, this paper is organized as follows. The proposed OPLMAT algorithm is introduced in Sect. 2. The performance of the OPLMAT algorithm is studied in Sect. 3. The numerical simulations are carried out in Sect. 4, and conclusions are presented in Sect. 5.

2 Proposed OPLMAT algorithm

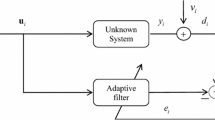
The coefficient vector of the unknown system is defined as \(\mathbf{W}_\mathrm{opt} =[w_0 ,w_1 ,\ldots ,w_{L-1} ]^{\mathrm{T}}\). L is the filter length. \(\mathbf{X}(n)=[x(n),x(n+1),\ldots ,x(n+L-1)]^{\mathrm{T}}\) denotes the input data vector of the unknown system at times instant n, and d(n) denotes the observed output signals, respectively.

$$\begin{aligned} d(n)={\mathbf{W}_\mathrm{opt}}^{\mathrm{T}}{} \mathbf{X}(n)+\xi (n) \end{aligned}$$
(1)

where \(\xi (n)\) is a stationary additive noise with zero mean and variance of \(\sigma _\xi ^2\). In addition, \(\xi (n)\) is assumed to be uncorrelated with any other signal. \(\mathbf{X}(n)\) is also stationary with zero mean, a variance of \(\sigma _{x}^2\), and \(\mathbf{X}(n)\) is Gaussian with a definite positive autocorrelation matrix.

The cost function used for obtaining the OPLMAT algorithm is given by

$$\begin{aligned} \mathbf{W}(n)= & {} \arg \; \min \; J\left( {\mathbf{W}(n)} \right) \nonumber \\= & {} \arg \; \min \;\frac{1}{3}\hbox {E}\left[ {|e(n)|} \right] ^{3} \end{aligned}$$
(2)

where

$$\begin{aligned} e(n)=d(n)-y(n) \end{aligned}$$
(3)

The corresponding filter output is

$$\begin{aligned} y(n)=\mathbf{W}^{\mathrm{T}}(n)\mathbf{X}(n) \end{aligned}$$
(4)

Assuming

$$\begin{aligned} \mathbf{V}(n)=\mathbf{W}_\mathrm{opt} -\mathbf{W}(n) \end{aligned}$$
(5)

So

$$\begin{aligned} e(n)=\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)+\xi (n) \end{aligned}$$
(6)

The updated recursion of coefficients vectors can be derived as Eq. (7):

$$\begin{aligned} \mathbf{W}(n+1)= & {} \mathbf{W}(n)-\mu (n)\frac{\partial J\left( {\mathbf{W}(n)} \right) }{\partial \mathbf{W}(n)} \nonumber \\= & {} \mathbf{W}(n)+\mu (n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) \end{aligned}$$
(7)

In Eq. (7), \(\hbox {sgn}\left( {e(n)} \right) \) denotes the sign function of the variable e(n) [13].

Combine Eqs. (5) and (7),

$$\begin{aligned} \mathbf{V}(n+1)=\mathbf{V}(n)-\mu (n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) \end{aligned}$$
(8)

The following assumptions are used in the subsequent analysis [15, 19].

Assumption A1

\(\mathbf{W}(n)\) is independent of \(\mathbf{X}(n)\).

Assumption A2

the error sequence e(n) conditioned on the weight vector \(\mathbf{V}(n)\) is a zero mean and Gaussian.

Based on Assumption A2, the distribution function of \(Y=e^{2}(n)\) is shown as Eq. (9).

$$\begin{aligned} F\left( {y} \right)= & {} p\left( {e^{2}\left( n \right) \le y} \right) \nonumber \\= & {} \int \limits _{-\sqrt{y}}^{\sqrt{y}} {\frac{1}{\sqrt{2\pi }\sigma _{e|V\left( n \right) } }\exp \left( {-\frac{e^{2}\left( n \right) }{2\sigma _{e|V\left( n \right) }^2 }} \right) \hbox {d }e\left( n \right) } \nonumber \\= & {} erf\left( {\frac{\sqrt{y}}{\sqrt{2}\sigma _{e|V\left( n \right) } }} \right) \end{aligned}$$
(9)

Based on Eq. (9), the probability density function of \(Y=e^{2}(n)\) is shown as Eq. (10).

$$\begin{aligned} p\left( y \right)= & {} \frac{\partial F\left( {y} \right) }{\partial {y}} \nonumber \\= & {} \frac{1}{\sqrt{2\pi }\sigma _{e|V\left( n \right) } e\left( n \right) }\exp \left( {-\frac{e^{2}\left( n \right) }{2\sigma _{e|V\left( n \right) }^2 }} \right) \end{aligned}$$
(10)

So

$$\begin{aligned}&\hbox {E}\left[ {\mathbf{V}(n+1)} \right] \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}(n)} \right] -\mu (n)\hbox {E}\left[ {\mathbf{X}(n)e^{2}\,(n)\hbox {sgn}\left( {e(n)} \right) } \right] \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}(n)} \right] -\mu (n)\hbox {E}\left\{ {\hbox {E}\left[ {\mathbf{X}(n)e^{2}\,(n)\hbox {sgn}\left( {e(n)} \right) |\mathbf{V}(n)} \right] } \right\} \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}(n)} \right] -\mu (n)\hbox {E}\left\{ \hbox {E}\left[ {e^{2}(n)|\mathbf{V}(n)} \right] \right. \nonumber \\&\qquad \left. \times \,\hbox {E}\left[ {\mathbf{X}(n)\hbox {sgn}\left( {e(n)} \right) |\mathbf{V}(n)} \right] \right\} \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}(n)} \right] -2\sqrt{\frac{2}{\pi }}\mu (n)\sigma _e \mathbf{R}_{xx} \hbox { E}\left[ {\mathbf{V}(n)} \right] \end{aligned}$$
(11)

where \(\mathbf{R}_{xx} =\hbox {E}\left[ {\mathbf{X}(n)\mathbf{X}^{\mathrm{T}}(n)} \right] \) and \(\mathbf{R}_{xx} =\sigma _{x}^2 \mathbf{I}\). \(\mathbf{I}\) denotes the identity matrix of proper dimension.

Ultimately, it is easy to show that the mean behavior of the weight vector converge to the optimal weight vector \(\mathbf{W}_\mathrm{opt}\) if \(\mu (n)\) is bounded by:

$$\begin{aligned} 0<\mu (n)<\sqrt{\frac{\pi }{2}}\frac{1}{\lambda _{\mathrm{max}} \sigma _e } \end{aligned}$$
(12)

where \(\lambda _{\mathrm{max}}\) represents the maximum eigenvalue of the regressor covariance matrix \(\mathbf{R}_{xx}\).

As seen from Eq. (11), we will get \(\hbox {E}\left[ {\mathbf{V}(\infty )} \right] \) when \(n\rightarrow \infty \).

$$\begin{aligned} \hbox {E}\left[ {\mathbf{V}(\infty )} \right] =0 \end{aligned}$$
(13)

Now we will derive the optimal \(\mu (n)\).

$$\begin{aligned}&{} \mathbf{V}^{\mathrm{T}}(n+1)\mathbf{V}(n+1) \nonumber \\&\quad =\left[ {\mathbf{V}(n)-\mu (n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) } \right] ^{\mathrm{T}}\nonumber \\&\qquad \times \, \left[ {\mathbf{V}(n)-\mu (n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) } \right] \nonumber \\&\quad =\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)-\mu (n)\mathbf{V}^{T}(n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) \nonumber \\&\qquad -\,\mu (n)\hbox {sgn}\left( {e(n)} \right) e^{2}(n)\mathbf{X}^{\mathrm{T}}(n)\mathbf{V}(n)\nonumber \\&\qquad +\,\mu ^{2}(n)\mathbf{X}^{\mathrm{T}}(n)\mathbf{X}(n)e^{4}\,(n) \end{aligned}$$
(14)

Assuming \(\hbox {tr}\left( {\mathbf{R}_{xx}}\right) \) is the trace of the \(\mathbf{R}_{xx}\) and when \(L\gg 1\), then \(\hbox {tr}\left( {\mathbf{R}_{xx}}\right) =L\sigma _x^2\) [7].

Taking the statistical expectation of both sides with (14), Eq. (15) can be obtained.

$$\begin{aligned}&\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n+1)\mathbf{V}(n+1)} \right] \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] +\mu ^{2}(n)L\sigma _x^2 \hbox {E}\left[ {e^{4}(n)} \right] \nonumber \\&\qquad -2\mu (n)\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) } \right] \end{aligned}$$
(15)

Based on Eqs. (9), (10) and Eqs. (11), (16) can be obtained.

$$\begin{aligned}&\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) } \right] \nonumber \\&\quad =\hbox {E}\left\{ {E\left[ {\mathbf{V}^{T}(n)\mathbf{X}(n)e^{2}(n)\hbox {sgn}\left( {e(n)} \right) |\mathbf{V}(n)} \right] } \right\} \nonumber \\&\quad \approx \hbox {E}\left\{ 2\sigma _e^2 \sqrt{\frac{2}{\pi }}\frac{1}{\sigma _e }\hbox {E}\left[ \left( \mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)\mathbf{X}^{\mathrm{T}}(n)\mathbf{V}(n)\right. \right. \right. \nonumber \\&\qquad \left. \left. \left. +\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)\xi (n) \right) |\mathbf{V}(n) \right] \right\} \nonumber \\&\quad =2\sqrt{\frac{2}{\pi }}\sigma _e \sigma _{x}^2 \hbox { E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \end{aligned}$$
(16)

Based on Eq. (6),

$$\begin{aligned}&\hbox {E}\left[ {e^{4}(n)} \right] \nonumber \\&\quad =\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)+\xi (n)} \right] ^{4}} \right\} \nonumber \\&\quad =\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{4}} \right\} +4\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{3}\xi (n)} \right\} \nonumber \\&\qquad +\,6\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{2}\left[ {\xi (n)} \right] ^{2}} \right\} \nonumber \\&\qquad +\,4\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] \left[ {\xi (n)} \right] ^{3}} \right\} +\hbox {E}\left\{ {\left[ {\xi (n)} \right] ^{4}} \right\} \end{aligned}$$
(17)

Combining Assumption A1–Assumption A2 with Eq. (17), we get Eq. (18).

$$\begin{aligned}&\hbox {E}\left[ {e^{4}(n)} \right] =\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{4}} \right\} \nonumber \\&\quad +\,6\hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{2}} \right\} \sigma _\xi ^2 +\hbox {E}\left\{ {\left[ {\xi (n)} \right] ^{4}} \right\} \end{aligned}$$
(18)

Substituting Eqs. (16) and (18) into Eq. (15), we get Eq. (19).

$$\begin{aligned}&\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n+1)\mathbf{V}(n+1)} \right] \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] -4\sqrt{\frac{2}{\pi }}\mu (n)\sigma _e \sigma _{x}^2 \hbox { E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \nonumber \\&\qquad +\mu ^{2}(n)L\sigma _x^2\hbox { E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{4}} \right\} \nonumber \\&\qquad +\,\mu ^{2}(n)L\sigma _x^2\hbox { E}\left\{ {\left[ {\xi (n)} \right] ^{4}} \right\} \nonumber \\&\qquad +\,6\mu ^{2}(n)L\sigma _x^2 \hbox { E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{2}} \right\} \sigma _\xi ^2 \end{aligned}$$
(19)

Based on Eq. (8) in [16],

$$\begin{aligned} \left\{ {\begin{array}{l} \hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{4}} \right\} =3\sigma _x^4\hbox { E}^{2}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \\ \hbox {E}\left\{ {\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{X}(n)} \right] ^{2}} \right\} =\sigma _x^2\hbox { E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \\ \end{array}} \right. \end{aligned}$$
(20)

Substituting Eq. (20) into Eq. (19), we obtain Eq. (21).

$$\begin{aligned}&\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n+1)\mathbf{V}(n+1)} \right] \nonumber \\&\quad =\hbox {E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] -4\sqrt{\frac{2}{\pi }}\mu (n)\sigma _e \sigma _{x}^2\hbox { E}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \nonumber \\&\qquad +6\mu ^{2}(n)L\sigma _x^4\, E\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \sigma _\xi ^2 \nonumber \\&\qquad +3\mu ^{2}(n)L\sigma _x^6\hbox { E}^{2}\left[ {\mathbf{V}^{\mathrm{T}}(n)\mathbf{V}(n)} \right] \nonumber \\&\qquad +\mu ^{2}(n)L\sigma _x^2\hbox { E}\left\{ {\left[ {\xi (n)} \right] ^{4}} \right\} \end{aligned}$$
(21)

The MSD at times instant n is defined as \(\hbox {MSD}\left( n \right) =\hbox {E}\left[ {\left\| {\mathbf{V}\left( n \right) } \right\| ^{2}} \right] \). So Eq. (21) can be derived as Eq. (22).

$$\begin{aligned}&\hbox {MSD}\left( {n+1} \right) \nonumber \\&\quad =\left[ {1-4\sqrt{\frac{2}{\pi }}\mu (n)\sigma _e \sigma _{x}^2 +6\mu ^{2}(n)L\sigma _x^4 \sigma _\xi ^2 } \right] \hbox {MSD}\left( n \right) \nonumber \\&\qquad +\mu ^{2}(n)L\sigma _x^2\hbox { E}\left[ {\xi ^{4}(n)} \right] +3\mu ^{2}(n)L\sigma _x^6\hbox { MSD}^{2}\left( n \right) \end{aligned}$$
(22)

When the algorithm tends to be stable, \(\hbox {MSD}(n)\) is very small. So, Eq. (22) can be rewritten as Eq. (23) when discarding \(\hbox {MSD}^{2}(n)\).

$$\begin{aligned}&\hbox {MSD}\left( {n+1} \right) \nonumber \\&\quad =f\left( {L,\mu (n),\sigma _x^2 ,\sigma _{e} ,\sigma _\xi ^2 } \right) \hbox {MSD}\left( n \right) \nonumber \\&\qquad +g\left( {L,\mu (n),\sigma _x^2 ,\xi (n)} \right) \end{aligned}$$
(23)

where

$$\begin{aligned}&f\left( {\alpha (n),L,\mu (n),\sigma _x^2 ,\sigma _{e} ,\sigma _\xi ^2 } \right) \nonumber \\&\quad =1-4\sqrt{\frac{2}{\pi }}\mu (n)\sigma _e \sigma _{x}^2 +6\mu ^{2}(n)L\sigma _x^4 \sigma _\xi ^2 \end{aligned}$$
(24)
$$\begin{aligned}&g\left( {L,\mu (n),\sigma _x^2 ,\xi (n)} \right) =L\sigma _x^2 \mu ^{2}(n)\hbox {E}\left[ {\xi ^{4}(n)} \right] \end{aligned}$$
(25)

In the real practical world, \(\sigma _e^2(n)\) and \(\sigma _x^2 (n)\) are unknown; however, we can estimate \(\sigma _e^2(n)\) and \(\sigma _x^2(n)\) by using Eq. (26) [8].

$$\begin{aligned} \left\{ {\begin{array}{l} \sigma _e^2 (n)\hbox {=}\frac{1}{\rho \hbox {+}\sigma _{x}^2 (n)}{} \mathbf{p}^{\mathrm{T}}\,(n)\mathbf{p}(n) \\ \sigma _x^2 (n)=\chi \sigma _x^2 (n-1)+(1-\chi )\mathbf{X}^{\mathrm{T}}\,(n)\mathbf{X}(n) \\ \end{array}} \right. \end{aligned}$$
(26)

where \(\mathbf{p}(n)=\hbox {E}\left[ {e(n)\mathbf{X}(n)} \right] \), \(\rho \) is a small positive number to guarantee that the denominator of Eq. (26) remains finite when \(\sigma _{x}^2 (n)=0\).

Although in Eq. (26), \(\mathbf{p}(n)\) is also unknown, we can estimate this parameter by using Eq. (27).

$$\begin{aligned} \mathbf{p}(n)=\chi \mathbf{p}(n-1)+(1-\chi )e(n)\mathbf{X}(n) \end{aligned}$$
(27)

Based on NPVSS-NLMS algorithm [7], we can get \(( {1-\frac{1}{2L}})\le \chi <1\).

The result from Eq. (23) illustrates a “separation” between the convergence and misadjustment components. Therefore, the term \(f\left( {L,\mu (n),\sigma _x^2 ,\sigma _{e} ,\sigma _\xi ^2 } \right) \) influences the convergence rate of the algorithm. It can be noticed that the fastest convergence mode is obtained when the function of Eq. (24) reaches its minimum.

$$\begin{aligned} \mu (n)=\sqrt{\frac{2}{\pi }}\frac{\sigma _e }{3L\sigma _x^2 \sigma _\xi ^2 } \end{aligned}$$
(28)

The stability condition can be found by imposing \(\left| {f\left( {L,\mu (n),\sigma _x^2 ,\sigma _{e} ,\sigma _\xi ^2 } \right) } \right| <1\) which leads to Eq. (29).

$$\begin{aligned} 0<\mu (n)<\sqrt{\frac{2}{\pi }}\frac{2\sigma _e }{3L\sigma _x^2 \sigma _\xi ^2 } \end{aligned}$$
(29)

There are two important issues to be considered: (1) in the context of system identification, it is reasonable to follow a minimization problem in terms of the system misalignment and (2) we have main parameters \(\mu (n)\) which influences the overall performance of the OPLMAT algorithm.

Thus, based on Eq. (23),

$$\begin{aligned} \frac{\partial \hbox {MSD}(n)}{\partial \mu (n)}=0 \end{aligned}$$
(30)

Substituting Eqs. (23), (24) and (25) into Eq. (30), the optimal step size is then given by

$$\begin{aligned} \mu (n)=\frac{2}{L}\sqrt{\frac{2}{\pi }}\frac{\sigma _{e} \hbox { MSD}\left( n \right) }{6\sigma _x^2 \sigma _\xi ^2\hbox { MSD}\left( n \right) +\hbox {E}\left[ {\xi ^{4}(n)} \right] } \end{aligned}$$
(31)

Using Eq. (31) in Eq. (23), followed by several straight forward computations, it results in

$$\begin{aligned} \hbox {MSD}\left( {n+1} \right)= & {} \hbox {MSD}\left( n \right) \nonumber \\&-\frac{16}{L\pi }\frac{\sigma _e^2 \sigma _{x}^2\hbox { MSD}^{2}\,\left( n \right) }{6\sigma _x^2 \sigma _\xi ^2\hbox { MSD}\left( n \right) +\hbox {E}\left[ {\xi ^{4}(n)} \right] } \nonumber \\&+\frac{8}{L\pi }\frac{\sigma _e^2 \sigma _x^2\hbox { MSD}^{2}\,\left( n \right) \hbox {E}\left[ {\xi ^{4}(n)} \right] }{\left\{ {6\sigma _x^2 \sigma _\xi ^2\hbox { MSD}\left( n \right) +\hbox {E}\left[ {\xi ^{4}(n)} \right] } \right\} ^{2}} \nonumber \\&+\frac{48}{L\pi }\frac{\sigma _e^2 \sigma _x^4 \sigma _\xi ^2\hbox { MSD}^{3}\,\left( n \right) }{\left\{ {6\sigma _x^2 \sigma _\xi ^2\hbox { MSD}\left( n \right) +\hbox {E}\left[ {\xi ^{4}(n)} \right] } \right\} ^{2}}\nonumber \\ \end{aligned}$$
(32)

Denoting \(\lim \limits _{n\rightarrow \infty } \hbox {MSD}\left( n \right) =\hbox {MSD}\left( \infty \right) \) and developing Eq. (32), we obtain Eq. (33).

$$\begin{aligned} \sigma _e^2 \sigma _{x}^2 \left\{ {6\sigma _x^2 \sigma _\xi ^2 \hbox { MSD}\left( \infty \right) +\hbox {E}\left[ {\xi ^{4}(\infty )} \right] } \right\} \hbox {MSD}^{2}\left( \infty \right) =0 \end{aligned}$$
(33)

Based on Eq. (33), we know \(\hbox {MSD}\left( \infty \right) =0\). It means that our aforementioned step size adjusting mechanism can achieve zero steady-state mean-square deviation. For a Gaussian desired signal, \(\hbox {E}\left[ {\xi ^{4}(n)} \right] =3\sigma _\xi ^4\) [15]. For a uniform desired signal, \(\hbox {E}\left[ {\xi ^{4}(n)} \right] ={9\sigma _\xi ^4 }/5\) [15]. For a Rayleigh desired signal, \(\hbox {E}\left[ {\xi ^{4}(n)} \right] =8\sigma _\xi ^4\) [20]. For an exponential desired signal, \(\hbox {E}\left[ {\xi ^{4}(n)} \right] =3\sigma _\xi ^4\) [20].

The excess mean-square error (EMSE) at times instant n is given by Eq. (34).

$$\begin{aligned} \hbox {EMSE}\left( n \right)= & {} \hbox {E}\left[ {e^{2}\left( n \right) } \right] \nonumber \\= & {} \hbox {E}\left\{ \left[ {\mathbf{V}^{\mathrm{T}}\left( n \right) \mathbf{X}\left( n \right) +\xi \left( n \right) } \right] \right. \nonumber \\&\times \left. \left[ {\mathbf{X}^{\mathrm{T}}\left( n \right) \mathbf{V}\left( n \right) +\xi \left( n \right) } \right] \right\} \nonumber \\= & {} \sigma _\xi ^2 +\sigma _{x}^2\hbox { MSD}\left( n \right) \end{aligned}$$
(34)

Finally, the steady-state \(\hbox {EMSE}_{\mathrm{EMSE}\left( \infty \right) }\) is given by using Eqs. (33) and (34).

$$\begin{aligned} \hbox {EMSE}\left( \infty \right) =\sigma _\xi ^2 \end{aligned}$$
(35)

A summary of the procedure for the OPLMAT algorithm based on the analysis presented above is given in Table 1.

Table 1 OPLMAT algorithm summary
Full size table

3 Computational complexity

The updated step size and \(\sigma _{e}\) formulas are added to the OPLMAT algorithm compared to the LMAT algorithm, meaning that the computational complexity of OPLMAT algorithm is greater than that of the LMAT algorithm. Furthermore, unlike the NLMAT algorithm, there is also no recursion required to compute \(\mathbf{X}^{\mathrm{T}}(n)\mathbf{X}(n)\) in OPLMAT algorithm. The computational complexity of the OPLMAT algorithm is slightly greater than that of the LMAT algorithm. However, the computational complexity of the OPLMAT algorithm is less than the complexity of the NLMAT algorithm when L is large. From Table 2, the OPLMAT algorithm has a considerable complexity advantage over NLMAT when \(L > 4\). Besides, the NLMAT algorithm also needs to estimate \(\sigma _{e}\). So compared to the NLMAT algorithm, there is no recursion to compute \(\mathbf{X}^{\mathrm{T}}(n)\mathbf{X}(n)\) and there are no comparisons. For convenience, the computational complexity of the OPLMAT algorithm and that of other existing LMAT-type algorithms are listed in Table 2.

Table 2 Computational complexity of OPLMAT, LMAT and NLMAT algorithms
Full size table

4 Simulation results

This section presents the results of simulations in the context of system identification using various noise distributions of both stationary and non-stationary systems to illustrate the accuracy of the OPLMAT algorithm. The length of the unknown coefficient vector \(\mathbf{W}_\mathrm{opt}\) is L. The input signal x(n) is a Gaussian white noise with zero mean and \(\sigma _{x}^2 =1\). The correlated input signal y(n) is calculated by using \(y(n)=0.5y(n-1)+{x}(n)\). In all of our experiments, the coefficient vectors are initialized as zero vectors. Four different noise distributions (Gaussian, uniform, Rayleigh and exponential) are used in the experiments. \(\hbox {MSD}\left( n \right) =10\log _{10} \left( {\left\| {\mathbf{W}\left( n \right) -\mathbf{W}_\mathrm{opt}} \right\| _2^2 } \right) \) is used to measure the performance of algorithms. In addition, MSD error equals the absolute of simulation values and theory value (Eq. 23). The results are obtained via Monte Carlo simulation using 20 independent run sets and an iteration number of 5000. The values of steady-state error of the three algorithms are recognized in Table 3.

Table 3 MSD values
Full size table

Experiment 1

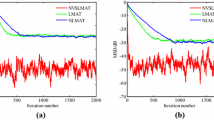
The system noise is Gaussian white noise, and the input signal is x(n) with SNR \(=\) 3 dB. A time-varying system is modeled, and its coefficients are varied from a random walk process defined by \(\mathbf{W}_\mathrm{opt} (n)=\mathbf{W}_\mathrm{opt} +{\varvec{\upsilon }}(n)\), where \({\varvec{\upsilon }}(n)\) is an independent identically distributed (i.i.d.) Gaussian sequence with \(m_v =0\) and \(\sigma _v^2 =0.01\). \(\mathbf{W}_\mathrm{opt} =\left[ {0.8,0.2,0.7,0.2,0.1} \right] ^{\mathrm{T}}\). The MSD curves for the LMAT (\(\mu =0.02\)), NLMAT (\(\mu =0.02\)), and OPLMAT (\(\chi =0.98)\) algorithms with the uncorrelated input signal are shown in Fig. 1. Figure 2 depicts the MSD error curves for the OPLMAT algorithm. In order to make case of the OPLMAT algorithm more persuasive, we provide a plot elucidating the evolution of \(\mu (n)\) as a function of the number of iterations in Fig. 3.

Fig. 1
figure 1

MSD comparisons under this condition of Experiment 1

Full size image
Fig. 2
figure 2

Learning curves of MSD error under this condition of Experiment 1

Full size image
Fig. 3
figure 3

Evolution of \(\mu (n)\) as a function of iteration number under the condition of Experiment 1

Full size image

Experiment 2

The system noise is a uniformly distributed noise over the interval (−3, 3) and the input signal is correlated input signal y(n) with SNR \(=\,-\)5 dB. A time-unvarying system is modeled, and its coefficients vector of the unknown system is \(\mathbf{W}_\mathrm{opt} =\left[ {0.8,0.2,0.7,0.2,0.1} \right] ^{\mathrm{T}}\). The MSD curves for the LMAT (\(\mu =0.05\)), NLMAT (\(\mu =0.05\)), and OPLMAT (\(\chi =0.98)\) algorithms with the uncorrelated input signal are shown in Fig. 4. Figure 5 shows the MSD error curves for the OPLMAT algorithm. In order to make case of the OPLMAT algorithm more persuasive, we provide a plot describing the evolution of \(\mu (n)\) as a function of the number of iterations in Fig. 6.

Fig. 4
figure 4

MSD comparisons under this condition of Experiment 2

Full size image
Fig. 5
figure 5

Learning curves of MSD error under this condition of Experiment 2

Full size image
Fig. 6
figure 6

Evolution of \(\mu (n)\) as a function of iteration number under the condition of Experiment 2

Full size image

Experiment 3

The system noise is a Rayleigh distribution with 3, and the input signal is correlated input signal y(n) with SNR \(=\) 14 dB. A time-varying system is modeled, and its coefficients are varied from a random walk process defined by \(\mathbf{W}_\mathrm{opt} (n)=\mathbf{W}_\mathrm{opt} +{\varvec{\upsilon }}(n)\), where \({\varvec{\upsilon }}(n)\) is an i.i.d. Gaussian sequence with \(m_v =0\) and \(\sigma _v^2 =0.01\). \(\mathbf{W}_\mathrm{opt} =\left[ {0.8,0.2,0.7,0.2,0.1} \right] ^{\mathrm{T}}\). The MSD curves for the LMAT (\(\mu =0.01\)), NLMAT (\(\mu =0.01\)) and OPLMAT (\(\chi =0.98)\) algorithms with the uncorrelated input signal are shown in Fig. 7. Figure 8 plots the MSD error curves for the OPLMAT algorithm. In order to make case of the OPLMAT algorithm more persuasive, we provide a plot showing the evolution of \(\mu (n)\) as a function of the number of iterations in Fig. 9.

Fig. 7
figure 7

MSD comparisons under this condition of Experiment 3

Full size image
Fig. 8
figure 8

Learning curves of MSD error under this condition of Experiment 3

Full size image
Fig. 9
figure 9

Evolution of \(\mu (n)\) as a function of iteration number under the condition of Experiment 3

Full size image

Experiment 4

The system noise is an exponential distribution with 2, and the input signal is correlated input signal y(n) with SNR \(=\) 14 dB. A time-varying system is modeled, and its coefficients are varied from a random walk process defined by \(\mathbf{W}_\mathrm{opt} (n)=\mathbf{W}_\mathrm{opt} +{\varvec{\upsilon }}(n)\), where \({\varvec{\upsilon }}(n)\) is an i.i.d. Gaussian sequence with \(m_v =0\) and \(\sigma _v^2 =0.01\). \(\mathbf{W}_\mathrm{opt} =\left[ {0.8,0.2,0.7,0.2,0.1} \right] ^{\mathrm{T}}\). The MSD curves for the LMAT (\(\mu =0.005\)), NLMAT (\(\mu =0.005\)) and OPLMAT (\(\chi =0.98)\) algorithms with the uncorrelated input signal are shown in Fig. 10. Figure 11 shows the MSD error curves for the OPLMAT algorithm. In order to make case of the OPLMAT algorithm more persuasive, we provide a plot showing the evolution of \(\mu (n)\) as a function of the number of iterations in Fig. 12.

Figures 1, 4, 7 and 10 show the OPLMAT algorithm has a smaller misalignment than the LMAT and NLMAT algorithms in steady-state stage. The reason for this observation is small \(\mu (n)\) in steady-state stage. From Fig. 1 and Table 3, the improvement due to implementation of the LMAT and NLMAT algorithms can nearly approach 14.32 and 10.62 dB, respectively. Thus, compared to the LMAT and NLMAT algorithms, the OPLMAT algorithm can perform better in identifying the unknown coefficients under this condition. From the other experimental results, the same conclusion can be obtained.

Fig. 10
figure 10

MSD comparisons under this condition of Experiment 4

Full size image
Fig. 11
figure 11

Learning curves of MSD error under this condition of Experiment 4

Full size image
Fig. 12
figure 12

Evolution of \(\mu (n)\) as a function of iteration number under the condition of Experiment 4

Full size image

Figures 2, 5, 8 and 11 show the MSD error. We observe an excellent match between predictions provided by our newly designed algorithm and results given by Monte Carlo simulations.

From Figs. 3, 6, 9 and 12, we know that \(\mu (n)\) has a large value in the initial stage, which results in a high convergence rate as expected. After the algorithm converges on the point where a low misalignment is desired, \(\mu (n)\) automatically decreases.

5 Conclusions

In the context of system identification using the LMAT-type algorithm, this paper described a way to derive the optimal variable step size of the LMAT based on mean-square deviation analysis. The OPLMAT algorithm is developed in this paper in order to addresses both stationary and non-stationary unknown systems in the presence of several types of noise under low SNR. The optimal step size leads the proposed algorithm to achieve the lowest steady-state error theoretically. The step size can be updated based on the number of iteration. In addition, the computational complexity of this algorithm is less when \(L>4\). Simulation results showed that the proposed algorithm performed better than the LMAT and NLMAT algorithms. The analytical result corroborated the simulations.