The linear ordering problem with clusters: a new partial ranking

Abstract

The linear ordering problem is among core problems in combinatorial optimization. There is a squared non-negative matrix and the goal is to find the permutation of rows and columns which maximizes the sum of superdiagonal values. In this paper, we consider that columns of the matrix belong to different clusters and that the goal is to order the clusters. We introduce a new approach for the case when exactly one representative is chosen from each cluster. The new problem is called the linear ordering problem with clusters and consists of both choosing a representative for each cluster and a permutation of these representatives, so that the sum of superdiagonal values of the sub-matrix induced by the representatives is maximized. A combinatorial linear model for the linear ordering problem with clusters is given, and eventually, a hybrid metaheuristic is carefully designed and developed. Computational results illustrate the performance of the model as well as the effectiveness of the metaheuristic.

1 Introduction

The linear ordering problem is a well-established combinatorial optimization problem. Given a squared non-negative matrix, the problem consists in finding the permutation of rows and columns that maximizes the sum of superdiagonal values. The linear ordering problem has been studied in many fields including antropology (Glover et al. 1974), machine translation (Tromble and Eisner 2009), and voting theory (Kemeny 1959). It is also related to the single-machine scheduling problem, where the objective is to minimize the total weighted (or average weighted) completion time (Grötschel et al. 1984). Given the broad interest in the problem, different computational strategies either exact or heuristics and metaheuristics have been developed. The book Marti and Reinelt (2011) provides a comprehensive study of the linear ordering problem and a thorough discussion of different solution techniques.

When the goal is to obtain the closest permutation of rows and columns to a given set of permutations and the distance among permutations is measured with the Kendall–Tau distance,¹ then the problem results in the rank aggregation problem (see Andoni et al. 2008; Dwork et al. 2001; Fagin et al. 2003; Yasutake et al. 2012 for a description and evolution of the rank aggregation problem and its applications). These two problems are closely related and it can be proved that the rank aggregation problem reduces to the linear ordering problem under a suitable transformation (García-Nové et al. 2017).

Both of the above problems, the linear ordering problem and the rank aggregation problem give total orders, i.e., do not leave unordered columns. If only a partial order of the columns/rows of a squared matrix is required, the solution would be a bucket order instead of a permutation. A bucket order is an ordered partition of the columns into buckets, so that all the elements (columns/rows) within a bucket are assumed to be tied or incomparable and the order between two elements of different buckets is given by the relative ordering of the buckets which they belong to. The notion of bucket order was formalized by Fagin et al. (2004) as a way to approach the rank aggregation problem with ties. Given a squared matrix with all the entries in [0, 1], the bucket order problem (Fagin et al. 2003, 2004; Feng et al. 2008; Gionis et al. 2006) consists of computing the bucket order that best captures the data. The bucket order problem has been used to discover ordering information among elements in many applications. It is used in the context of seriation problems in scientific disciplines such as Paleontology (Fortelius et al. 2006; Puolamaki et al. 2006), Archaeology (Halekoh and Vach 2004), and Ecology (Miklos et al. 2005), and also to aggregate browsing patterns of visitors to a web portal (Feng et al. 2008). The bucket order problem gives a clustering of columns (rows).

In this paper, we consider that columns of the matrix belong to different clusters and that the goal is to obtain good permutations of the clusters. The goal is to chose a representative column of each cluster and an order of the representative columns, such that the sum of superdiagonal values of the sub-matrix induced by the representatives is maximum. Contrary to the bucket order problem, the column affiliation with clusters is an input instead of an output. If columns represent politicians, clusters could be parties; if columns represent athletes, clusters could be teams, etc. We propose a new approach to choose a representative of each cluster and find the best permutation of these representatives. The new problem is appropriated when scheduling tasks, such that only one task of each cluster is required. Also when a representative of each cluster is required. Some Spanish Universities give a set of rewards, one for each Department, among all the teachers that sign up for the National Teaching Evaluation Program called Docentia (https://programadocentia.umh.es/), and then, the Departments can be sorted according to the scores awarded to their teachers.

The new ranking order introduced in this paper generalizes the linear ordering problem and the rank aggregation problem. In fact, the linear ordering problem and the rank aggregation problem have been proved to be the same in some particular cases. In the case where clusters have one element, the new ranking orders coincide with linear ordering and rank aggregation. Besides, the new ranking orders are alternative partial rankings different from the bucket order problem and useful when the clusters are known and when the belonging of an element to a cluster is not part of the solution but of the data themselves.

Clusters are different to buckets, because clusters are inherent to the population and thus are inputs of the problem, while buckets are induced by the data in entries in the matrix and are outputs of the problem.

A small example is kept throughout the paper which illustrates the different ranking orders as well as the different percentages of voter preferences that can be achieved. In fact, it is the example proposed in Feng et al. (2008) for illustrating the bucket order problem.

The remainder of this paper is organized as follows. In Sect. 2, we give some preliminaries and definitions. In Sect. 3, we model the new ranking problem and we discuss about its integrality and linear gaps as well as about how to adapt valid inequalities from the Linear Ordering Problem. In Sect. 4, we propose a hybrid metaheuristic algorithm for the Linear Ordering Problem with Clusters. This will be followed in Sect. 5 by extensive numerical analysis, showing the performance of the linear ordering problem with clusters model and of the metaheuristic algorithm. Conclusions are drawn in Sect. 6.

2 Preliminaries and notation

In this section, the definition of two known ranking methods is revised, the linear ordering problem and the rank aggregation problem, both consisting of obtaining total rankings.

Let $V=\{ 1,\ldots , n\}$ be a set of indices and let C be a non-negative $n\times n$ matrix. Let R be the set of all the permutations of V. The Linear Ordering Problem (LOP) for matrix C consists of finding the permutation $\pi \in R$, such that

$$\begin{aligned} \sum _{i=1}^{n-1}\sum _{j=i+1}^nc_{\pi (i)\pi (j)} \end{aligned}$$

is maximized.

Let $R'\subseteq R$ be a set of permutations of V, and let $d(r_1,r_2)$ be the Kendall–Tau distance between $r_1$ and $r_2$ for all $r_1,r_2\in R'.$ The Rank Aggregation Problem (RAP) consists of finding the permutation $\pi \in R$, such that:

$$\begin{aligned} \sum _{r\in R'}d(\pi ,r) \end{aligned}$$

is minimized.

Both LOP and RAP are defined for general non-negative squared matrices. Anyway, in practice, general non-negative rankings can be transformed in [0, 1] ranking in several ways.

The following example illustrates the kind of solution of the LOP.

Table 1 Candidate rankings: list of five total orders

Table 2 Matrix C of preferences

Example 1

Let $V=\{a,b,c,d,e,f\}$ be a set of six candidates. Suppose that five voters rank them as Table 1 shows. The table corresponds to an example in Feng et al. (2008). Thus, the square non-negative matrix C in Table 2 represents the preferences: $c_{ij}$ is the fraction of rankings in which candidate i is listed (ranked) before candidate j.

The solution for Linear Ordering Problem (LOP), which maximizes the preferences of the voters on the 6 candidates, is the rank $(a\,|\,c\,|\,d\,|\,b\,|\,f\,|\,e)$ with an optimal value of 11.2. If a consensus permutation with zero disagreements with respect to a database of permutations was to exist, the optimal value of LOP would be 15, the superdiagonal sum of ones; therefore, $74.6\% (=(11.2/15)\times 100)$ is the percentage in which the linear order solution guarantees voter preferences.

3 A new partial ranking

In this section, a new partial ranking is introduced for the case where V is partitioned into disjoint subsets (clusters): $V=V_1\cup V_2 \cdots V_{m}$ and $V_r\cap V_s=\emptyset$ for all $r,s\in \{ 1,\ldots ,m\}$ $r\ne s.$

We define $M=\{ 1,\ldots ,m\} .$

3.1 The linear ordering problem with clusters

The Linear Ordering Problem with Clusters (LOP-C) consists in finding the best linear order for $V_1,\ldots ,V_m$ when only one representative of each cluster is considered to define the order.

For all $i\in V,$ let $z_i$ be a binary variable which takes the value of one, if and only if index i is the representative of its cluster. For all $i,j\in V$ belonging to different clusters, let $x_{ij}$ be a binary variable which takes the value of one if and only if indexes i and j are the representative of theirs clusters and the cluster to which i belongs to goes before the cluster to which j belongs to. The IP formulation of the LOP-C can be stated as follows:

$$\begin{aligned} \text {(LOP-C)} \,\, \max \,\,&\sum _{r,s\in M:r\ne s} \sum _{\begin{array}{c} i\in V_r \\ j\in V_s \end{array}} c_{ij}x_{ij}&\end{aligned}$$

(1)

$$\begin{aligned}&\nonumber \\ \hbox {s.t. }&\sum _{\begin{array}{c} k\in V_t \\ j\in V_s \end{array}} x_{kj} - \sum _{\begin{array}{c} i\in V_r \\ j\in V_s \end{array}} x_{ij} - \sum _{\begin{array}{c} k\in V_t \\ i\in V_r \end{array}} x_{ki}\le 0&\quad r,s,t\in M{:} \text{ pairwise } \text{ disjoint } \end{aligned}$$

(2)

$$\begin{aligned}&\sum _{j\in V_r} (x_{ij}+x_{ji}) - z_i= 0&\quad r\in M, i\notin V_r \end{aligned}$$

(3)

$$\begin{aligned}&\sum _{i\in V_r} z_i = 1&\quad r\in M \end{aligned}$$

(4)

$$\begin{aligned}&x_{ij}\in \{ 0,1\}&\quad i\in V_r,\,j\in V_s,r\ne s\end{aligned}$$

(5)

$$\begin{aligned}&z_{i}\in \{ 0,1\}&\quad i\in V, \end{aligned}$$

(6)

The objective function (1) is the weighted sum of all the x-variables. Even if matrix C has $|V|\times |V|$ elements, only the elements in positions associated with indexes belonging to different clusters are required. Constraints (2) state transitivity in the order of clusters, if cluster t goes before cluster s and cluster s goes before cluster r,  then cluster t must go before cluster r. Constraints (3) state that given i the representative of a cluster and another cluster $V_r,$ there is a variable $x_{ij}$ or a variable $x_{ji}$ with $j\in V_r$ which takes the value of one and $x_{jk}=0$ if $j,k\ne i.$ Constraints (4) entail that only one element from each cluster is selected. Constraints (5) and (6) are the domain constraints.

Any feasible solution of LOP-C induces a permutation of m elements in V, one in each cluster and thus a cluster permutation. The indexes of the variables in LOP-C are in V, while the optimal solution is an order of the elements of M.

Table 3 Voter preferences about selected candidates

Example 1

(cont) Let $V_1=\{ a,b\}, V_2=\{ c,d\}$ and $V_3=\{ e,f\}.$ The optimal solution for the LOP-C is $(c,b,e)\equiv (\mathbf{c},d\,|\,a,\mathbf{b}\,|\,\mathbf{e},f)$ and the optimal value is 2.6. In terms of variables, $z_c=z_b=z_e=1,$ $x_{cb}=x_{ce}=x_{be}=1$ and the rest of variables take the value zero. If the preferences of non-selected candidates are removed, the list of preferences would be the list in Table 3 and a consensus permutation with zero disagreement would give an objective value of 3. Then, the optimal solution (c, b, e) guarantees $86.6\% ((2.6/3)\times 100)$ of voter preferences.

Besides, the LOP solution does not lead to the LOP-C solution. The LOP solution is $(a\,|\,c\,|\,d\,|\,b\,|\,f\,|\,e),$ then the first three elements of different clusters are $(a,c,f)\equiv (\mathbf{a},b\,|\,\mathbf{c},d\,|\,e,\mathbf{f}),$ which is not the LOP-C solution. In fact, the objective value for the solution (a, c, f) in the LOP-C is 2, which only guarantees the $66.6\% ((2/3)\times 100)$ of voter preferences.

The Linear Ordering Problem with Clusters (LOP-C) is NP-hard, since it is the Linear Ordering Problem (LOP) when all the clusters have a single element.

3.2 Integrality gap, linear gap, and valid inequalities

In this section, we show that LOP-C is more difficult than LOP in terms of integrality gap and thus in terms of linear gap. Furthermore, we adapt some well-known families of valid inequalities of the LOP to the LOP-C.

In Boussaid et al. (2013), the authors establish that the LOP is “asymptotically easy”. Under certain mild probability assumptions, the ratio between the best and worst solution is arbitrarily close to 1 with probability tending to 1 if the problem size goes to infinity. If all the elements of the preference matrix follow from a uniform distribution, all the swapped matrices look similar.

In Marti and Reinelt (2011), the authors define the integrality gap of the LOP as the ratio between the optimal value of the relaxation of the problem that allows in-transitivity and the integer optimal value. Note that when the transitivity constraint is removed, the relaxed LOP is trivial and its optimal value is achieved by forcing $x_{rs}=1$ if $m_{rs} > m_{sr}$. Later, in Aparicio et al. (2019), the authors prove that the integrality gap of LOP converges to 4/3 if the preference matrix is in a certain normal form.

LOP-C is more difficult than LOP in the sense that the relaxed LOP-C is not trivial. The following example illustrates this issue.

Remark 3.1

The relaxation of the transitivity constraints in LOP-C does not provide an integer solution.

Example 2

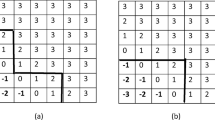
Let $V=\{a,b,c,d,e,f\}$ be a set of six elements in three clusters $V_1=\{ a,b\} , V_2=\{ c,d\}$ and $V_3=\{ e,f\},$ and let the following matrix be the preference matrix.

	a	b	c	d	e	f
a			1	2	2	0
b			3	1	0	1
c	0	2			3	1
d	0	0			1	1
e	0	1	3	2
f	1	2	0	3

The optimal solution of LOP-C is $(e,b,c)\equiv (\mathbf{e},f,|\,a,\mathbf{b}\,|\,\mathbf{c}, d)$ and the optimal value is 7. If the transitivity constraints are relaxed, we obtain the same solution, but if the transitivity constraints are relaxed and the linear relaxation of the problem is considered, then the optimal value is 7.5 with a fractional solution, $z_i=0.5$ $\forall i$, and $x_{14}=x_{23}=x_{15}=x_{62}=x_{53}=x_{64}=0.5$.

The integrality gap is related with the linear gap in the sense that the integrality gap gives an upper bound of the linear gap: if the integrality gap of a LOP is $\alpha ,$ its linear gap is smaller than $\alpha -1.$ Thus, the linear gap for LOP is expected to be small. In fact, in Marti and Reinelt (2011), the authors propose several families of valid inequalities for the LOP and conclude that the linear gap is scarcely reduced when these are added to the problem.

Since the LOP-C is more complex than the LOP gap-wise, valid inequalities for LOP-C could be sensible for reducing its linear gap. For instance, since $x_{ij}+x_{ji}=z_iz_j$ for all i, j, the valid inequalities for the Boolean polytope in Remark 3.2 and the equalities in Remark 3.3 apply.

Remark 3.2

The following inequalities are valid for LOP-C:

$$\begin{aligned} z_i+z_j \le 1 + x_{ij} + x_{ji} \quad i\in V, j\in V. \end{aligned}$$

Remark 3.3

The following equalities are valid for LOP-C:

$$\begin{aligned} \sum _{i\in V} (x_{ij}+x_{ji}) = (m-1)z_j \quad j\in V. \end{aligned}$$

On the other hand, all the valid inequalities for LOP in the shape of $\sum _{(i,j)\in T}x_{ij}\le t$ for $T\subseteq V\times V,$ $t\in {\mathbb {N}}$ can become a valid inequality for LOP-C by replacing variables by sum of variables.

Fig. 1

3-fence graph

By way of example, the LOP 3-fence inequality:

$$\begin{aligned} x_{if}+x_{fj}+x_{fk}+x_{jg}+x_{gi}+x_{gk}+x_{kh} +x_{hi}+x_{hj}\le 7; \end{aligned}$$

f, g, h, i, j, k pairwise disjoint, which represents the 3-fence graph in Figure 1, becomes the inequality in Remark 3.4 for LOP-C.

Remark 3.4

The following 3-fence inequality is a valid inequality for LOP-C:

$$\begin{aligned} \begin{aligned}&\left. \sum _{\begin{array}{c} i\in V_r \\ f\in V_u \end{array}} x_{if} + \sum _{\begin{array}{c} f\in V_u \\ j\in V_s \end{array}} x_{fj} + \sum _{\begin{array}{c} f\in V_u \\ k\in V_t \end{array}} x_{fk} \right. \\&\quad \left. + \sum _{\begin{array}{c} j\in V_s \\ g\in V_v \end{array}} x_{jg} + \sum _{\begin{array}{c} g\in V_v \\ i\in V_r \end{array}} x_{gi} + \sum _{\begin{array}{c} g\in V_v \\ k\in V_t \end{array}} x_{gk}\right. \\&\quad + \sum _{\begin{array}{c} k\in V_t \\ h\in V_w \end{array}} x_{kh} + \sum _{\begin{array}{c} h\in V_w \\ i\in V_r \end{array}} x_{hi} + \sum _{\begin{array}{c} h\in V_w \\ j\in V_s \end{array}} x_{hj} \le 7 \\&\quad r,s,t,f,g,h\in M:\text{ pairwise } \text{ disjoint }. \end{aligned} \end{aligned}$$

4 A hybrid metaheuristic

For the last decades, metaheuristic techniques have been imposed on simple heuristics to give approximate solutions to difficult combinatorial optimization problems. These techniques incorporate procedures that, well designed, are able to escape from local optima to achieve quality solutions. Scatter search (SS) and Genetic Algorithms (GA) are two of the most widely used and can be hybridized to improve their performance, both in terms of speed and effectiveness. SS was first introduced by Glover (1977) who described it as a method that uses a succession of coordinated initializations to generate solutions. The original proposal did not provide certain implementation details and later Glover in (1994) provided such details and expanded the scope of application of the method to nonlinear, binary, and permutation problems. In Glover (1998), Glover gives the scatter search template. The basic idea of the method is to generate a systematically dispersed set of points from a chosen set of reference points to maintain a certain diversity level among the members of this set. Genetic algorithms were first introduced by Holland (1975) and imitate the evolution of species, based on the survival of the fittest principle. These algorithms maintain a population of solutions and apply a set of genetic operators like crossover or mutation to generate new individuals and maintain an appropriate level of diversity. The original proposals of these methods have been later transformed by several authors, incorporating advanced designs and procedures obtaining hybrid algorithms that have been successfully applied to several combinatorial optimization problems. A description of some of these methods and their applications are described in Boussaid et al. (2013) and Laguna and Marti (2003), among others.

In this paper, we propose an algorithm to give approximate solutions for the Linear Ordering Problem with Clusters (LOP-C) which is based on the Scatter Search template but introduces efficient procedures, some of them based on genetic operators, that incorporate problem specific knowledge. This makes the proposed algorithm an efficient hybrid metaheuristic tool to manage this problem. The algorithm starts generating an initial population pool of randomized feasible solutions of a given size. Then, a reference set of solutions with a good level of quality and diversity is selected from the initial population. Later, the evolutive process starts and is repeated until a stopping criterion is satisfied. First, a procedure based on path relinking is applied over two solutions of the RefSet, creating a new solution that can replace one of the originals. Then, a new solution of this set is randomly chosen and undergoes three different operations: mutation, interchange, and insertion. The order in which these operators are applied over the solution depends on the type of mutation, which is selected randomly between two different types: one affects nodes and another modifies clusters. Moreover, each type has two different versions, depending on whether it affects only one or all the nodes/clusters of the solution, and the version to be applied is also chosen randomly. After these operations are carried out, RefSet is updated and the new solution replaces the original one in RefSet if it is better. Once the evolution process is finished, a final improvement procedure is performed to increase the quality of the solutions in RefSet. It consists of applying to every solution in RefSet, the interchange and insertion techniques in a successive way but in a random order. Once more, the modified solution replaces the original one if it has been improved. The result of the algorithm is the best solution of the reference set.

In the next subsections, the main operators and procedures performed by the hybrid metaheuristic are described in detail. In the following, we define the function $\rho : V \longrightarrow M$ which indicates the cluster to which the column belongs: $\rho (i)=r$ iff $i\in V_r$. Abusing of notation, $\rho (\pi )$ shall represent the vector $(\rho (\pi (1)),\ldots ,\rho (\pi (m)))$. Moreover, we shall refer to the objective value in LOP-C of a feasible solution $\pi$ as $v(\pi )$.

Example 1

(cont). Let $V=\{a,b,c,d,e,f\}, V_1=\{a,b\}, V_2=\{c,d\}, V_3=\{e,f\}$. The optimal solution for the LOP-C is a node permutation $\pi ^*=(c,b,e)\equiv (\mathbf{c},d\,|\,a,\mathbf{b}\,|\,\mathbf{e},f)$, associated with a cluster permutation $\rho (\pi ^*)=(2,1,3)$.

4.1 Initial population and reference set

In general, the initial population (IniPob) is a set of feasible solutions that can be obtained either randomly or through a specific algorithm. The first mechanism is faster, but the quality of the solutions is poorer and the second has the advantage of creating good solutions, but requires more computational effort.

In the proposed algorithm, we have employed a pure random mechanism to generate an initial population of feasible solutions, IniPob, sized ${ Pop}\_{ size}$. Each solution is a partial ranking of V given by a permutation $\pi$ of length m. After creating the IniPob, a set of ${ RefSet}\_{ size}$ good and diverse solutions called Reference Set (RefSet) is chosen from IniPob.

The construction of the initial RefSet starts with the selection of the best ${ RefSet}\_{ size}/2$ solutions [best value of the objective function (1)] from the initial population. The remaining ${ RefSet}\_{ size}/2$ solutions are included in the RefSet to increase the level of diversity in it. The distance between two solutions $\pi ^0\in$ RefSet and $\pi ^1\in$ IniPob$\setminus$RefSet is defined as:

$$\begin{aligned} D(\pi ^0,\pi ^1)= \frac{\alpha }{2}\left( \frac{d(\rho ({\pi }^0),\rho ({\pi }^1))}{\frac{m(m-1)}{2}}+\frac{s}{m}\right) + (1-\alpha )\left( \frac{v(\pi ^1)}{v(\pi ^0)}\right) , \end{aligned}$$

(7)

where $\alpha$ is a value in (0, 1), $d(\rho ({\pi }^0), \rho ({\pi }^1))$ is the Kendall–Tau distance, s is the number of clusters with different representatives, and $m(m-1)/2$ is the maximum value of a Kendall–Tau distance between two permutations of size m. Note that the distance function D is bounded by 1 when $\alpha \in (0,1)$.

The minimum distance from each solution in IniPob to the solutions in RefSet is computed. Then, the solution with the maximum of these minimum distances is added to RefSet. This process is repeated ${ RefSet}\_{ size}/2$ times. The resulting reference set has ${ RefSet}\_{ size}/2$ high-quality solutions and ${ RefSet}\_{ size}/2$ diverse solutions.

Example 1

(cont). Let $\pi ^0:=(d\,|\,a\,|\,e) \equiv (c,\mathbf{d}\,|\,\mathbf{a},b\,|\,\mathbf{e},f)$ and $\pi ^1=(f\,|\,a\,|\,c) \equiv (e,\mathbf{f}\,|\,\mathbf{a},b\,|\,\mathbf{c},d)$. The distance between $\pi ^0$ and $\pi ^1$ is:

$$\begin{aligned} D(\pi ^0,\pi ^1)= \frac{\alpha }{2}\left( \frac{3}{\frac{3(3-1)}{2}}+\frac{2}{3}\right) + (1-\alpha )\left( \frac{v(\pi ^1)}{v(\pi ^0)}\right) . \end{aligned}$$

4.2 Adapted path relinking

Path relinking was originally proposed by Glover (1996) as an intensification strategy to explore trajectories connecting elite solutions obtained by tabu search or scatter search (Glover and Laguna 1997; Glover et al. 2000, 2004). The path relinking mechanism produces new solutions combining every pair of solutions in the RefSet. Given one pair of solutions selected to undergo the mechanism, one is used as the origin of the path and the other as the end of the same path. Going from the origin to the end consists of generating a set of intermediate solutions. The resulting solution is the best of the path.

We have designed an adapted path relinking operator which randomly chooses only one pair of solutions of RefSet, among the $RefSet\_size/2$ best solutions. The operator is bi-directional and moves from the origin to the end and then from the end to the origin. The operator evaluates all the neighbour solutions generated in both paths, returning the best as result. This solution replaces the worst of the originals if it is better. Given two solutions form RefSet, $\pi ^0$ and $\pi ^1$, the way of moving from $\pi ^0$ to $\pi ^1$ is depicted in Algorithm 2.

Example 1

(cont). Let $\pi ^0=(a\,|\,d\,|\,e) \equiv (\mathbf{a},b\,|\,c,\mathbf{d}\,|\,\mathbf{e},f)$ and $\pi ^1=(c\,|\,b\,|\,e) \equiv (\mathbf{c},d\,|\,a,\mathbf{b}\,|\,\mathbf{e},f)$. The first neighbour solution is $\pi =(d\,|\,a\,|\,e) \equiv (c,\mathbf{d}\,|\,\mathbf{a},b\,|\,\mathbf{e},f)$, and the second is $\pi =(c\,|\,a\,|\,e) \equiv (\mathbf{c},d\,|\,\mathbf{a},b\,|\,\mathbf{e},f)$, while the third and the last is $\pi =(c\,|\,b\,|\,e) \equiv (\mathbf{c},d\,|\, a,\mathbf{b}\,|\,\mathbf{e},f)$.

4.3 Insertion

Given a solution $\pi$ and two positions $r,s \in M$, we define the insertion of element $\pi (r)$ in position s as a result of adding at position s the element $\pi (r)$ and moving all subsequent elements up one position. Given a solution, the insertion operator evaluates all the possible insertions in that solution checking the objective function for each. The result of the insertion operator is the best of the evaluated solutions. This operator is based on the idea of the “adding” procedure used in the metaheuristic proposed in Alcaraz et al. (2019).

Remark 4.1

Let $\pi ^0$ be a solution of LOP-C and let r, s in M. Let $\pi$ be the result of inserting the element $\pi ^0(r)$ in position s, and then:

$$\begin{aligned} \text {if }\,&r<s&v(\pi )=v(\pi ^0)+\sum _{t=r+1}^{s} (c_{\pi ^0(t) \pi ^0(r)} - c_{\pi ^0(r) \pi ^0(t)} )\\ \text {if }\,&r>s&v(\pi )=v(\pi ^0)+\sum _{t=s}^{r-1} (c_{\pi ^0(r) \pi ^0(t)} - c_{\pi ^0(t) \pi ^0(r)} ).\\ \end{aligned}$$

Remark 4.1 facilitates the evaluation of the new solutions. While the calculation of the objective function by (1) requires $m(m-1)/2$ operations, the calculation by the formula in Remark 4.1 requires between 2 and $2(m-1)$ operations, depending on the positions being considered.

4.4 Mutation

Mutation is used as one of the most important operators in GA, imitating the mutation of genetic material that sometimes occurs in nature, changing the characteristics of an individual. The mutation mechanism permits the introduction of new characteristics that were not present in the population into a solution or characteristics that some individuals had in the past but were lost in the evolution process. This is very important in evolutionary algorithms, to introduce variability and avoid being trapped in local optima, producing a premature convergence of the algorithm. We have designed a mutation strategy that, making use of the problem-knowledge, allows us to introduce diversity into the RefSet in a very appropriate way. Here, we present two different types of mutation, mutation of nodes and mutation of clusters, and for each one, two different versions depending on whether only one or all the nodes/clusters mutate. Given a solution $\pi$ of the RefSet: OneNodeMutation$(\pi )$, AllNodeMutation$(\pi )$, OneClusterMutation$(\pi )$, and AllClusterMutation$(\pi )$ can be applied to it. The first two procedures mutate nodes, while the others produce the mutation of clusters.

Given a solution $\pi$ in RefSet, OneNodeMutation$(\pi )$ chooses a random node $i \in V$, such that i is a node of the solution $\pi$, that is $i=\pi (r)$, and it is replaced by a random node $j \in V_r$ with a probability of mutation, $P_{\mathrm{mut}1}$; AllNodeMutation$(\pi )$ selects every node $i \in V$, such that i is a node of the solution $\pi$, that is $i=\pi (r)$, and it is replaced by a random node $j \in V_r$ with a probability of mutation, $P_{\mathrm{mut}2}$; OneClusterMutation$(\pi )$ chooses two random clusters $r,s \in M$ and inserts the element $\pi (r)$ in the position of cluster s (OneClusterMutation works as in Sect. 4.3) with a given probability $P_{\mathrm{mut}1}$; Finally, AllClusterMutation$(\pi )$ applies OneClusterMutation$(\pi )$ for all $r \in M$, but with probability $P_{\mathrm{mut}2}$ for each cluster. Therefore, the result of this procedure could be the original solution or the mutated one.

Example 1

(cont). Let $\pi ^0=(a\,|\,d\,|\,e) \equiv (\mathbf{a},b\,|\,c,\mathbf{d}\,|\,\mathbf{e},f)$ The output for OneNodeMutation$(\pi ^0)$ with $i=c$ is $=(a\,|\,c\,|\,e) \equiv (\mathbf{a},b\,|\,\mathbf{c},d\,|\,\mathbf{e},f)$. The output for AllNodeMutation$(\pi ^0)$ with random values b, d, e is $(b\,|\,d\,|\,e) \equiv (a,\mathbf{b}\,|\,c,\mathbf{d}\,|\,\mathbf{e},f)$. The output for OneClusterMutation$(\pi ^0)$ with $r=3$ and $s=1$ is $(e\,|\,a\,|\,d) \equiv (\mathbf{e},f,\,|\,\mathbf{a},b\,|\,c,\mathbf{d})$. Eventually, the output for AllClusterMutation$(\pi ^0)$ when the first cluster is selected to move to the third position, the second cluster is selected to move to the third position, and the third cluster is selected to move to the first position is $(e\,|\,d\,|\,a) \equiv (\mathbf{e},f\,|\,c,\mathbf{d},|\,\mathbf{a},b)$.

4.5 Interchange

The interchange method was introduced by Teitz and Bart (1968) and consists of interchanging one solution attribute that is in the solution with one that is not. An extension of this version is the so-called k-interchange, in which k solution attributes are interchanged (Mladenovic et al. 1996).

We use a particular m-interchange previously proposed as operator of a metaheuristic algorithm for a location problem (Alcaraz et al. 2012). Given a solution $\pi$, this operator replaces each element i in $\pi$ for the best element $i^*\in V_{\rho (i)}$. The best element $i^*$ is the one whose interchange leads to the best possible objective value.

To evaluate the objective value for each $j\in V_{\rho (i)}$, it is useful to make the following remark.

Remark 4.2

Let $\pi ^0$ and $\pi$ be two solutions of LOP-C, such that $\rho (\pi ^0(r))=\rho (\pi (r))$, for all $r \in M$, and $\pi ^0(s) \ne \pi (s)$ for exactly one $s \in M$. Then:

$$\begin{aligned} v(\pi )=v(\pi ^0)+\sum _{s=1}^{r-1}(c_{\pi ^0(s) \pi (r)} -c_{\pi ^0(s) \pi ^0(r)}) + \sum _{s=r+1}^{m}(c_{\pi (r) \pi ^0(s)} - c_{\pi ^0(r) \pi ^0(s)} ).\\ \end{aligned}$$

Remark 4.2 also facilitates the evaluation of the new solutions. Again, the calculation of the objective function by (1) requires $m(m-1)/2$ operations, while the calculations by the formula in Remark 4.2 requires $2(m-1).$

The resulting solution of this procedure replaces the original solution in the RefSet only if it a better objective value.

5 Computational study

We have used a set of instances in http://www.optsicom.es/lolib/ for the Linear Ordering. In particular, the set of instances comprises the 25 instances of size 100 in the group of problems called Random instances of type AI which are generated from a [0, 100] uniform distribution and were proposed in Reinelt (1985) and generated in Campos et al. (2001). Each instance of size $n=100$ has been split in $m=4,10,20,50$ clusters of equal size. Thus, we have used 100 different problems that form 4 groups.

All tests were performed on a PC with a 2.33 GHz Intel Xeon dual core processor, 8.5 GB of RAM, and LINUX Debian 4.0 operating system. A CPLEX v.11.0 optimization engine was used for solving the LOP-C model, while MH_LOP-C was implemented in C.

First, we have solved the model LOP-C for all the instances imposing a time limit of 3 h and for each group of instances, $m=4, 10, 20, 50$. After that, we have solved the linear relaxation and calculated the linear Gap of each instance.

Table 4 $m =4,\, 10,\, 20\, y \, 50$ (time limit: CPLEX 3 h)

Table 4 report the results for $m=4,10,20,50$. Headings are as follows. The first column is the instance number. The second, third, fourth, and fifth blocks of columns are the results for the different clusters: $v^*$ shows the objective value of the best solution achieved by CPLEX (if CPLEX finishes before the time limit, it is the optimal solution), $t^*$ shows the CPU time (seconds) needed by CPLEX to reach that solution when solving the LOP-C model and Gap shows the difference between the integer and the linear relaxation problem. From the values in columns, Gap follows that LOP-C is more difficult than LOP. When $m=4,$ the problem has small linear gap, but when m increases, this linear gap also increases. When $m=10,$ the average linear gap is 36.59 which is larger than the common upper bound for the linear gap of LOP, i.e., 0.33 ($=4/3-1$). Anyway, the Gap when $m=20$ and when $m=50$ uses the best integer solution within the time limit.

The addition of valid inequalities in Remark 3.2 as well as the heuristic separation of the 3-fence inequality in Remark 3.4 have failed to reduce the linear gap or the CPU time.

Now, we check the goodness of the metaheuristic proposed and described in Sect. 4 (Algorithm 1). The interest is on the efficiency of the method, that is, the quality of the solutions in a given computation time.

First with the results of Table 4, we have measured the average computation time needed by CPLEX to solve the instances in each group, $t^*_{aver\_m}$. Then, we have run MH_LOP-C three times for each instance, and the time limit imposed in each one of those executions depends on the problem size and it has been calculated by the following expression:

$$\begin{aligned} \min \left\{ t^*_{\mathrm{aver}\_m}, \log \left( \frac{n}{m}\right) ^{m}\right\} . \end{aligned}$$

Preliminary studies have indicated some appropriate values for the parameters of the metaheuristic algorithm, and those are the ones employed in all the executions of MH_LOP-C: ${ Pop}\_{ size}=100, { RefSet}\_{ size}=10, \alpha =0.5, P_{\mathrm{mut}1}=0.1$, and $P_{\mathrm{mut}2}$ depends on m, being $P_{\mathrm{mut}2}=0.05$ for instances with 4 clusters, $P_{\mathrm{mut}2}=0.025$ for the instances with $m=10$, $P_{\mathrm{mut}2}=0.0125$ for instances where the number of clusters is 25 and $P_{\mathrm{mut}2}=0.00625$ for 50 cluster instances.

Tables 5, 6, 7, 8 report the results for $m=4,10,20,50$, respectively. Headings are as follows. The first column is the instance number, $v^*$ shows the objective value of the best solution achieved by CPLEX (if CPLEX finishes before the time limit, it is the optimal solution), and $t^*$ shows the CPU time (seconds) needed by CPLEX to reach that solution when solving the LOP-C model. The third block of columns, called BEST SOLUTION, shows the results of the best among the three executions performed by MH_LOP-C. This block is divided into four columns: $v^*_{\mathrm{BS}}$ shows the best solution achieved, $t^*_{\mathrm{BS}}$ shows the CPUs time (seconds) to find this solution, $\#$iter shows the number of iterations performed by the algorithm, and $\%$diff shows the deviation from the solution reported by CPLEX, namely:

$$\begin{aligned} \%\text{ diff }= 100 \frac{v_{\mathrm{BS}}^* - v^*}{v^*}. \end{aligned}$$

(8)

Column $\#$OPT in Tables 5 and 6 indicates the number of times among the three executions that MH_LOP-C finds the optimum and column $\#$BST in Tables 7 and 8 reports the number of times that the metaheuristic finds, in the time limit considered, a solution which is better than the given by CPLEX. The last block of columns, Average, gives the averages for the three executions: average optimal value ($v_{\mathrm{A}}$), average time ($t_{\mathrm{A}}$), average number of iterations, and average deviation from the solution reported by CPLEX.

Table 5 reports the results for the case $m=4$, in which all the clusters have 25 elements. In this case, the time limit imposed to the metaheuristic is, $t^*_{\mathrm{aver}\_4}$, the average time employed by CPLEX to solve the instances with 4 clusters. The results show that both methods obtain the optimal solution in the 25 instances of this group. The average time employed by CPLEX is 2 s and MH_LOP-C finds the optimum, in the best of the three executions, in 0.03 s, on average. Moreover, in all the instances, the metaheuristic proposed finds the optimal solution in less than one-fourth of a second, on average. Moreover, column $\#$OPT, which reports the number of executions where the optimal solution is achieved by MH_LOP-C, shows that the metaheuristic reaches the optimum in all the three executions performed, which demonstrates its robustness and stability. The average number of iterations carried out by MH_LOP-C is around 90,000, which means that it performs more than 1,000,000 iterations by second.

Table 6 shows the results for the case $m=10$, that is, the instances have ten clusters with ten nodes per cluster in each instance. The average computation time for solving LOP-C with CPLEX is 320.12 s. Therefore, the time limit imposed to the metaheuristic is 10 s, ($\log (n/m)^m)$, per execution. However, MH_LOP-C employs only 2.31 s on average for the instances in this group and, if we consider only the best of the three executions, less than 1 s on average. MH_LOP-C finds the optimal solution in the 25 instances and in 71 of the 75 executions performed. Only in 3 of the 25 instances, it does not achieve the optimal solution in all 3 executions. The average deviation of the solutions found by MH_LOP-C with respect to the optimal solution given by CPLEX is always smaller than 0.53$\%$, employing a cpu time 140 times smaller. It varies from − 1.9 to − 6.53$\%$ in an average computation time which is 2245 times smaller. In this case the algorithm performs, on average, around 80,000 iterations to find the optimum, more than 35,000 iterations per second.

Table 7 summarizes the results for the instances with $m=20.$ In this case, CPLEX cannot find the optimal solution in any of the 25 instances in 3 h and column $v^*$ reports the objective value of the best solutions achieved in that time. The time limit for MH_LOP-C is then 14 s. The metaheuristic needs, on average, 4.81 s to reach the best solution and only 1.43 s on average if only the best execution is considered. Negative values in column $\%$diff indicate that the solution given by the metaheuristic is better than that the given by CPLEX. Moreover, column $\#$BST indicates that MH_LOP-C always finds a solution which is better than the reported by CPLEX, in all the instances and all the executions performed per instance. Although in all cases, MH_LOP-C finds the best solution in less than 4 s, some time averages require nearly 14 s. For instance, the time needed by this algorithm to reach the best solution for instance 22 is of 1.13, 13.98, and 5.89 s, respectively, that leads to an average computation time of 7 s. In this group of instances the ratio iterations by second is of $45{,}874/4.81=9537$.

Finally, Table 8 summarizes the results for the instances with $m=50$ clusters and all the clusters of size 2. As CPLEX cannot find the optimal solution and it employs the 3 h in the solution process, the time limit for MH_LOP-C is then 15 s. The best option of each trio of iterations is always obtained in less than 14 s and in around 8 s on average. As in the previous table, values in column %diff are negative, and column $\#$BST shows that MH_LOP-C finds better solutions than CPLEX in all the instances and all the executions. In the best execution for instance 20, MH_LOP-C outperforms CPLEX by about 23.73$\%.$ In this group of instances, the average differences vary between − 5.68 and − 23.09$\%$ in only 10.66 s, in contrast to the 10,800 s employed by CPLEX. Now, the number of iterations per second has decreased until to 900.

Fig. 2

Comparison of Tables 5, 6, 7, and 8

Results in Tables 5, 6, and 7, 8 illustrate that the difficulty of the problem increases as m increases. With regards to CPLEX, somehow, it is due to the number of binary variables that the model has. If all the clusters are of size n/m,  the LOP-C model has $n^2(m-1)/m+n$ binary variables. In particular, the number of binary variables is 7600, 9100, 9600, and 9900 for $m=$ 4, 10, 20, and 50, respectively. In the case of the metaheuristic, the number of iterations per second decreases from 1 million to less than 1000, which implies that the problem is computationally hardest mainly as the number of clusters increases if the number of nodes remains unaltered. However, although $t_{\mathrm{A}}$ considerably increases with m, $\%$diff decreases from zero to near -12%. Column $\%$diff reports almost zero differences for the cases with 4 and 10 clusters, but these differences become negative values in the hardest instances, where the number of clusters is 20 and 50. Therefore, the difference between both algorithms is larger as the difficulty of the problem increases. Figure 2 depicts the evolution in the average time ($t_{\mathrm{A}}$) and $\%$diff for the different sizes considered in the computational study: computational time goes from 0 to 8 s, while the gap goes from values very close to zero to negatives values. For the easiest instances, with four or ten clusters, both resolution methods are effective, because the optimal solution is reached in all the instances, but MH_LOP-C is much more efficient, because this optimum is reached in a considerably much smaller computation time. When the difficulty of the problem increases, for instances with 20 or 50 clusters, CPLEX takes 3 h to reach solutions which are very far, in terms of quality, from the solutions reached by the metaheuristic in just a few seconds.

6 Conclusions

In this paper, we have presented the problem of linear ordering clusters of elements. The option of considering that only one representative of each cluster is required has been modeled through a binary linear formulation, LOP-C. A metaheuristic algorithm has been developed for approximating optimal solutions of LOP-C when the model itself requires too much computational time. The computational section illustrates the goodness of both the LOP-C model and the metaheuristic. The model allows the solution of problems with 9100 binary variables and the metaheuristic algorithm proposed reaches the optimal solution in the easy instances in most cases and outperforms, in seconds, the solution given by the exact optimizer within a time limit of 3 h in the hardest instances. This demonstrates the robustness and stability of the metaheuristic proposed. The computational section also gives some insights on the complexity that the number of clusters adds to the problem; when the same number of nodes are split in more clusters, the difficulty of the problem in terms of computational time for solving the problem increases.

Table 5 $m =4$ (time limit: CPLEX 3 h, MH_LOP-C 2 s)

Table 6 $m =10$ (time limit: CPLEX 3 h, MH_LOP-C 10 s)

Table 7 $m =20$ (time limit: CPLEX 3 h, MH_LOP-C 14 s)

Table 8 $m =50$ (time limit: CPLEX 3 h, MH_LOP-C 15 s)