1 Background and Motivation

Analysis of rankings and tied rankings as a topic in data analysis is receiving increasing attention, especially in relation to automated decision-making and search. Considered initially as a model for human judgment in psychology, ranking came to the attention of social scientists as a basis for voting and other social decisions. It was next adopted in economics as a model of utility and rational choice. Rankings are currently used in many areas of computational data analysis. Among abundant examples are the following: ordering alternatives in collaborative filtering, document ranking in information retrieval engines, similarity scoring of protein sequences in bioinformatics, and league tables in sports and in higher education. Important sources of such ranked data are social surveys in which respondents are asked to classify alternatives using an ordered set of categories, such as “strongly agree,” “agree,” “neutral,” “disagree,” and “strongly disagree.” This type of scale is widely used for scoring the strength of complex phenomena, such as winds, earthquakes, and sentiment expressions in texts.

The topic of comparing tied rankings was initiated by Charles Spearman (a junior collaborator of the founding fathers of multivariate statistics, Francis Galton and Karl Pearson), who was hired to further pursue the golden dream of Galton, a proof that human talent is inherited from one’s parents and, partly, from even more distant ancestors. Although ranking is non-quantitative, Spearman proposed using ranks as numerical values, so that the Pearson correlation coefficient could be employed (Spearman 1904). This is straightforward when the observations being compared are linearly ordered. However, different observations can sometimes be assigned the same numerical rank value, which led to the introduction of the term “tied observations,” subsequently replaced by “tied ranking.” Formally, a tied ranking can be represented as an ordered partition R = (R1, R2, …, Rp), that is, a partition whose parts are linearly ordered by their indices 1, 2, …, p. We say that an element iprecedes an element j in the tied ranking R if the part containing i precedes the part containing j. A clear-cut case of an ordered partition is given by the rank features in social surveys, as mentioned above. There is a difference between tied rankings and ordered partitions by rank features: as the number of objects grows, the length of a tied ranking will grow accordingly, whereas the number of categories of a feature and, thus, parts in the corresponding ordered partition, remains constant. However, this difference plays no role in the current paper as we do not consider processes in which the numbers of objects grow.

Despite the use of the Pearson correlation coefficient for non-metric judgements having no theoretical foundation, it took another 35 years to develop a more satisfactory approach. In 1938, Maurice Kendall introduced a different representation for rankings by using the relation of precedence between ranks rather than the ranks themselves (Kendall 1938). Given a tied ranking R, we define a square observation-to-observation matrix (the Kendall matrix) in which the (i, j) entry is + 1 if i precedes j in R, 0 if i and j have the same rank, or − 1 if j precedes i. The Kendall rank correlation coefficient between two tied rankings is the Pearson correlation coefficient between the corresponding Kendall matrices, considered as vectors in an N × N-dimensional space, where N is the number of observations. This accords with the non-quantitative nature of tied rankings. The twentieth century saw intense work on the analysis of the relationship between the Kendall and Spearman correlation coefficients; these were proven to be asymptotically equivalent under conventional statistical assumptions (Lehmann and D’Abrera 2006). This is also compatible with the finding that metrics based on the Spearman and Kendall representations are nearly equivalent, that is, their ratio always lies in a fixed finite interval (Diaconis and Graham 1977). Yet, the similarity between them should not be overemphasized: in a more recent investigation, for a model in which a bivariate Gaussian distribution is contaminated with a dose of high variation noise, these two rank correlation coefficients were found to behave differently (Xu et al. 2013).

In the 1950s, John Kemeny approached the issue of comparing rankings from a social consensus perspective. Given a set of ordered partitions, a consensus ordered partition should represent the major tendency in the set. A conventional approach, the majority rule, may fail when determined by voting on pairs of alternatives. Specifically, the so-called Condorcet paradox holds: if there are three parties at a meeting, each supporting one of three cyclically related linear orderings of three alternatives, say, (a) [i, j, k], (b) [j, k, i], and (c) [k, i, j], respectively, then the majority rule would lead to a cycle in the precedence relation: i would precede j because this is so for the majority, (a) and (c); similarly, j would precede k, and k would precede i. This contradicts the requirement that the precedence relation corresponding to the majority consensus ranking should be transitive. This paradox is a basis of the celebrated “social choice impossibility theorem” by Kenneth Arrow (see, for example, Aleskerov and Monjardet 2002).

John Kemeny proposed a different definition for consensus ranking using a distance measure between tied rankings. Rather than defining any specific distance measure ab initio, he formulated four axioms that should hold for any admissible distance measure. These axioms led Kemeny to derive the unique distance measure satisfying them. The Kemeny distance turned out to be the L_1-distance between the Kendall matrices (see Kemeny and Snell 1962 and Heiser and D’Ambrosio 2013).

In the monograph (Mirkin 1979), a joint geometric space of ordered and unordered partitions was considered using the corresponding weak order and equivalence relations on the set of observations. The distance was introduced as the mismatch, or symmetric difference, distance between the binary relations as subsets of the Cartesian product of the set of objects with itself. This distance can also be expressed as the L1-distance, or Hamming distance, between the 0 and 0-1 matrices of the relations. Unfortunately, the differences between the mathematical structures of rankings and the corresponding binary relations were glossed over in (Mirkin 1979). The ordered partitions were only considered via the corresponding binary relations. On the one hand, this was useful because of the greater flexibility of binary relations (being just subsets of ordered pairs) over tied rankings (being ordered sets of subsets). For example, the binary relation perspective allowed a reinterpretation of Arrow’s impossibility theorem by using the fact that the set-theoretic union of transitive binary relations is not necessarily transitive. On the other hand, the suppression of the ranking aspects led to ignoring the ways international developments were proceeding. For example, the fact that the mismatch and Kemeny distances were equal, although well known to the author (see Mirkin and Cherny 1972), was never proven, nor even formulated, in the book. This perhaps resulted in the distance between preference relations being excluded from the current ranking research discourse. The binary relations related to rankings play a more or less hidden role and are just used as auxiliary constructions in the derivations; (Fagin et al. 2006) it can be considered a representative example of this.

This paper is aimed at bringing the distance between binary relations back onto the scene. Therefore, we formulate the Kemeny approach in terms of binary preference relations, the so-called weak orders, and derive some properties of the Kemeny consensus (or median) that so far have not appeared in the international literature. These include, in particular, the following:

  1. (i)

    A proof that the Kemeny distance between rankings is, in fact, the mismatch distance between the corresponding weak-order binary relations. The importance of this result stems from the fact that the former involves Kendall object-to-object matrices with three possible values for the entries: 1 for preceding, − 1 for following, and 0 for a tie; whereas the latter involves only two: 1 for the presence and 0 for the absence of a pair in the binary relation. This makes the result rather counter-intuitive.

  2. (ii)

    Explicit statements of some of the properties of the distance, especially those regarding the relationship between weak orders and their induced equivalence relations, using the ternary relation “between” on the set of binary relations and the notion of “refinement” on the set of tied rankings.

  3. (iii)

    An explicit reformulation of the Kemeny consensus criterion in terms of the relational summary matrix, analogous to the so-called consensus matrix in the problem of consensus clustering (see, for example, Mirkin 2012). In contrast to the analysis of consensus clustering, however, the (i, j) entry in this consensus matrix is not simply the number of partitions for which elements i and j belong to the same part, but also includes the number of rankings for which i precedes j. The problem, which involves the subtraction of a threshold, is equivalent to maximizing the sum of the consensus matrix entries minus the number of pairs in the corresponding equivalence relation (sometimes referred to as the partition concentration index), weighted with a penalty defined by the threshold. The subtracted part plays the role of a naturally emerged regularizer. Of course, the regularizer does not affect the solution if it is restricted to a class of ranked partitions for which the partition concentration index is constant, like, for example, the class of linear rankings with no ties.

  4. (iv)

    The sensitivity of the Kemeny median concept is tested by extending the so-called Muchnik test from the case of unordered partitions (Mirkin 2012) to the case of ordered partitions. Specifically, we apply the concept of median to the Likert scales popular in Psychology (Likert 1932). Given an ordered partition R = (R1, R2, …, Rp), the Likert scale replaces R by the set of binary ordered partitions St (t = 1, 2, …, p-1) that separate the union of the first t parts of R from the rest. The question then arises as to whether R is a median for the set of binary rankings St (t = 1, 2, …, p-1), as one might expect, or not. Perhaps surprisingly, it turns out that it is one of the “coarse” binary rankings St that is a median, rather than R itself.

The remainder of the paper is structured as follows. In Section 2, we describe the mathematical structures of tied rankings (ordered partitions) and the corresponding weak orders. This includes the operation of intersection and a ternary relation “between.” In Section 3, we analyze distances between rankings and between weak orders, including a proof that the Kemeny distance between rankings and the mismatch distance between weak orders are equal. Various expressions for the distance in terms of the elements of the contingency table are reviewed, and its representation as the sum of the “ordered” and “unordered” components is precisely formulated. In Section 4, we describe the Kemeny median consensus rankings in terms of a related “triangulation” problem, with a specific emphasis on the penalty coefficient and its effect on the distribution of the median ordered partition. We also demonstrate that the median is rather insensitive to the granularity of ties in the raw rankings. To this end, we utilize the Muchnik test from the theory of consensus clustering (Mirkin 2012) and apply it to the median-ordered partition. Specifically, we analyze what median would emerge as a consensus for dichotomous versions of the Likert scale: unfortunately, as mentioned above, this is nothing more granular than one of the central binary rankings. Section 5 concludes the paper.

2 Ordered Partitions and Preference Relations

2.1 Characterization of the Preference Relation for an Ordered Partition

Given a finite set A of N elements, a collection of its subsets R = {R1, R2, …, Rp} is referred to as a partition if the subsets Rs are all non-empty, non-overlapping, and cover the entire set A, so that each i ∈ A belongs to a unique subset Rs, 1 ≤ s ≤ p. The subsets are called the parts of the partition R. A partition is said to be ordered if there is a linear order relation of precedence between its parts, Rs < Rt, that is transitive, anti-reflexive, and complete. If the order coincides with the natural order between indices 1, 2, …, p, we use parentheses to denote this, viz. R = (R1, R2, …, Rp). In Decision Theory, an ordered partition is referred to as a tied ranking. In Computer Science, the terms “partial ranking” and “bucket partition” have sometimes been used (Fagin et al. 2006). We consider that the term “partial ranking” should apply according to usage in the mathematical theory of partial orders: when the precedence relation between parts is not complete, so that for some distinct s and t, the precedence between Rs and Rt is not defined. We do not consider here this type of partial ranking.

Each ordered partition R = (R1, R2, …, Rp) generates a binary preference relation

$$ \uprho =\left\{\left(i,j\right):i\in {R}_s,j\in {R}_t,\mathrm{and}\ s\le t\right\}. $$
(1)

Usually, two non-overlapping binary relations are defined with respect to a tied ranking R = (R1, R2, …, Rp): the strict preference relation P = {(i, j): i∈Rs, j∈Rt, and s < t} and the indifference relation E = {(i, j): i, j∈Rs for some s}. The indifference relation E here is transitive, reflexive, and symmetric, thus E is the equivalence relation corresponding to the unordered partition Ř having the same parts as R. Obviously, ρ = P ∪ E, that is, ρ in (1) is a non-strict preference relation in which the strict preference and indifference relations are merged together. Usually, researchers try to avoid such a “mix;” but we will see later that there is no problem with this merger. The next part of this section is a brief reminder of some conventional concepts and facts about preference relations (see, for example, Steele and Stefánsson 2015).

If ρ is a binary relation, its inverse ρ−1 is defined as ρ−1 = {(i, j): (j, i)∈ ρ}. If ρ is the preference relation corresponding to a tied ranking R = (R1, R2, …, Rp), then its inverse ρ−1 corresponds to the reverse tied ranking R−1 = (Rp, …, R2, R1). It is easy to see that the indifference relation E corresponding to any tied ranking R satisfies E = ρ ∩ ρ−1. Thus, the strict preference relation is the difference P = ρ - E = ρ - ρ−1.

It is clear that ρ in (1) is

  • Reflexive, that is, (i, i) ∈ ρ for any i ∈ A,

  • Transitive, that is, if (i, j) ∈ ρ and (j, k) ∈ ρ, then (i, k) ∈ ρ for any i, j, k ∈ A, and

  • Complete, that is, (i, j) ∈ ρ or (j, i) ∈ ρ, or both, for any i, j ∈ A.

Of course, reflexivity can be considered as the special case of completeness for which i = j. A binary relation satisfying these properties is usually referred to as a weak order (Steele and Stefánsson 2015). In fact, a converse statement also holds:

Theorem 1

A preference relation ρ corresponds to an ordered partition R if and only if it is a weak order.

Proof

Let ρ be a binary relation on the set A that is reflexive, transitive, and complete. Consider any i ∈ A and define the subset ρ(i) = {j∈ A: (i, j) ∈ ρ}. Then, for any pair i, k ∈ A, if (i, k) ∈ ρ then ρ(k) ⊆ ρ(i). This holds because whenever j ∈ ρ(k), i.e., (k, j) ∈ ρ, then (i, j)∈ ρ also, because ρ is transitive. Therefore, since ρ is complete, for any pair i, k ∈ A, either ρ(k) ⊆ ρ(i) or ρ(i) ⊆ ρ(k), or both. It follows that the collection of sets ρ(i) is linearly ordered by set-theoretic inclusion, so they can be ordered as a sequence of sets St for t = 1, 2, …, p, where S1 ⊃ S2 ⊃ … ⊃ Sp. Then the subsets Rt = St − St + 1, t = 1, 2, …, p-1, and Rp = Sp,, form an ordered partition R = (R1, R2, …, Rp). It is quite easy to check that its corresponding preference relation (1) coincides with the given relation ρ. The reverse implication, that the relation (1) corresponding to an ordered partition is reflexive, transitive, and complete, has already been established above. This completes the proof.

Corollary 1

The subsets Rt = St − St + 1 in the proof each satisfy Rt = ρ(i)∩ρ−1(i) for some i ∈ A.

Corollary 2

A binary relation ρ is a weak order if and only if its strict part P is anti-reflexive and transitive, its indifference part E is an equivalence relation, and P, P−1, E form a partition of the Cartesian product A × A.

2.2 Refinement and Betweenness

A tied ranking R' is a refinement of a tied ranking R if it is obtained from the latter by subdividing some of its parts into smaller ones, and some ordering is defined between the smaller parts of each subdivided part of R. The corresponding preference relations, ρ’ and ρ, are related by set-theoretic inclusion:

Theorem 2

A tied ranking R′ is a refinement of a tied ranking R if and only if ρ' ⊂ ρ.

Proof

Indeed, if R’ is a refinement of a tied ranking R then, for some pairs i, j of elements of A such that both (i, j) ∈ ρ and (j, i)∈ ρ, only one of these holds for ρ’. Conversely, suppose that ρ and ρ′ correspond to tied rankings R and R’, respectively, and that ρ’ ⊂ ρ. Then ρ’(i) ⊆ ρ(i) for any i ∈ A, and, moreover, the inclusion is proper for some i ∈ A. Consider any such i.

Let {i1, i2, …, ik} be a maximal subset of A such that ρ(i) ⊃ ρ’(i1) ⊃ ρ’(i2) ⊃ … ⊃ ρ’(ik). Then, by Corollary 1, every equivalence class R′tu = ρ’(iu)∩ρ’−1(iu) will be part of the equivalence class Rt = ρ(i)∩ρ−1(i), which completes the proof.

We say that ρ is coarser than ρ′, if ρ′ is a refinement of ρ.

A binary relation τ on A is said to be between binary relations ρ and ρ’ if and only if ρ∩ρ’ ⊆ τ ⊆ ρ∪ρ′ (Mirkin 1979). A tied ranking T is said to be between tied rankings R and R if, for any i, j ∈ A, the ordering between them in T is compatible with their ordering in both R and R′: that is, (i) if i precedes j in both R and R′ then i precedes j in T; (ii) if i precedes j in one of R and R′, and i and j are indifferent in the other, then i either precedes j or is indifferent to j in T; (iii) if i and j are indifferent in both R and R′, then i and j are indifferent in T; lastly, (iv) if i precedes j in R but j precedes i in R′, then anything can be true of the ordering between i and j in T: i may precede j, or j may precede i, or i and j may be indifferent in T (Kemeny and Snell 1962). It follows that T is between R and R′ if and only if the same is true for their weak orders, as stated in the following theorem.

Theorem 3

A preference relation τ on A, corresponding to the tied ranking T, is between preference relations ρ and ρ′, corresponding to tied rankings R and R′, if and only if T is between R and R′.

For preference relations ρ and ρ′ corresponding to tied rankings R and R′, usually neither ρ∩ρ′ nor ρ∪ρ′ corresponds to a tied ranking. There is a class of situations, however, for which the intersection does correspond to a tied ranking. We say that R and R’ are concordant if there exists a linear ordering that is a refinement of both R and R′; so the parts of both are just intervals of the underlying linear ordering. In this case, ρ∩ρ′ does correspond to a tied ranking and the equivalence classes corresponding to ρ∩ρ’ are formed by the non-empty intersections of these intervals of the linear ordering.

In the general case of two arbitrary tied rankings R and R′, the relation ρ∩ρ′ is a partial preference relation because there can be i, j ϵ A such that i strictly precedes j in R, whereas j strictly precedes i in R′, so that neither (i, j) nor (j, i) belongs to ρ∩ρ′. Such a case, which is not uncommon, is exemplified by a proverbial question: “What is better: being poor but healthy or being rich but ill?” (with a proverbial answer that to be both rich and healthy is better indeed.)

What is appealing about ρ∩ρ’ is that its indifference relation is always an equivalence relation, thus corresponding to the partition that is just the intersection of the unordered partitions Ř and Ř’ that correspond to the ordered partitions R and R′, respectively. The intersection Ř∩Ř′ is the partition of A in which the parts are the intersections Rs∩Rt’ of some part Rs of R and some part Rt’ of R’ for which Rs and Rt’ are not disjoint.

Both ordered and unordered intersections can be visualized as a block matrix in which the blocks are formed by the subsets of rows and columns corresponding to the parts of the ordered partitions R′ and R, respectively (see Table 1). Of course, the blocks of the intersections are only partially ordered so that, for example, blocks R2’∩R3 and R3’∩R2 are not comparable. However, a linear order can be imposed naturally by ordering the blocks first by rows and then by columns, so that any block of the first row precedes the blocks in all other rows. This is the so-called lexicographic product R′ × R introduced in (Mirkin 1979). Similarly, an alternative lexicographic product R × R′ is defined by ordering blocks first by columns and then by rows. Curiously, in the ordered series R′, R′ × R, R × R′, and R, the middle term of each triplet is between the other two (Mirkin 1979). A similar statement holds for the corresponding relations ρ′, ρ′ × ρ, ρ × ρ′, and ρ.

Table 1 The intersection of two tied rankings R’∩R, where R’ relates to rows and R to columns. It is assumed that the rows and columns are permuted according to the rankings R’ and R, respectively
Full size table

3 Matrix Representation of Preference Relations and Distance Between Them

3.1 Correlation by Spearman and Kendall

Consider the Spearman rank correlation, that is, the Pearson correlation coefficient between ranks taken as numerical values. To deal with the case of tied rankings, each element of an equivalence class of indifference is assigned with the average within-class rank. The average rank of the elements in part Rs of the tied ranking R = (R1, R2, …, Rp) is L + (|Rs| + 1)/2, where L is the cardinality of R1∪R2∪ … ∪Rs-1, and |·| denotes the number of elements in a set. The Kendall rank correlation is based on the representation of tied rankings on A by N × N matrices. Given a tied ranking R and the corresponding preference relation ρ = P ∪ E, we now define a skew-symmetric matrix K = (kij), for i, j ∈ A, such that kij = 1 if (i, j) ∈ P, kij = 0 if (i, j) ∈ E, and kij = − 1, if (j, i) ∈ P. The Kendall rank correlation coefficient between R and R′ is the correlation coefficient between their Kendall matrices, K and K′, considered as vectors in an N2-dimensional space. This is compatible with the non-quantitative nature of tied rankings, especially since the mean of a skew-symmetric matrix is always 0.

It should be noted that, soon after the Kendall matrix was defined, a somewhat similar skew-symmetric representation for quantitative features was proposed by Daniels (1944), who proved that, given a quantitative feature x on A, the matrix X = (xij), where xij = xi − xj, can be used to represent the feature in statistical computations. For example, the inner product of the matrices X and X′ corresponding to features x and x′ is proportional to the inner product of x and x′ after they have been centered by subtracting their means, viz. <X, X′ > = 2N < x − m(x), x′ − m(x′)>, where m(x) is the mean of x. This implies that the correlation coefficient between X and X′ is equal to the correlation coefficient between x and x′. Therefore, the Spearman rank correlation coefficient can also be defined as the Pearson correlation coefficient between the corresponding matrices of rank differences (rij), where rij = ri − rj. The Kendall matrix is then just the matrix of signs in the Daniels matrix X = (xij), where xij = xi − xj. The past century saw intense work on the analysis of the relationship between the Kendall and Spearman correlations; these were proven to be asymptotically equivalent under conventional statistical assumptions (see, for example, Lehmann and D’Abrera 2006).

3.2 Kemeny Distance

Rather than defining an ad hoc distance measure, Kemeny formulated four axioms that should hold for any acceptable distance measure d(R, R′) between rankings R and R′. These axioms require that the acceptable distance measures should:

  • A1. Be a mathematical metric, that is, have the following properties:

    1. (a)

      Symmetry: d(R, R′) = d(R′, R);

    2. (b)

      Non-negativity and definiteness: d(R, R’) ≥ 0 and d(R, R′) = 0 if and only if R = R′;

    3. (c)

      Strict triangle inequality: for any rankings R, R’ and R”, d(R, R”) ≤ d(R, R’) + (R′, R′′); moreover, equality holds if and only if R′ is between R and R′′.

  • A2. If R′ is obtained from R by a permutation of the set A and S’ from S by the same permutation, then d(R′, S′) = d(R, S).

To formulate the next axiom, let us say that a subset B ⊂ A is a segment of a tied ranking R if its complement A − B ≠ ∅ and each element i ∈ A − B either precedes all the elements of B or is situated after all the elements of B. The tied ranking R restricted to a segment B will be denoted by RB.

  • A3. If R and R′ coincide on A − B and B is a segment of both R and R′, then d(R, R′) = d(RB, RB′).

  • A4. Unit of scale: The minimum positive distance is equal to 1.

Kemeny proved that the only distance satisfying all four axioms is the L1-metric between the corresponding skew-symmetric Kendall matrices divided by 2 (Kemeny 1959), namely:

$$ kd\left(\boldsymbol{R},{\boldsymbol{R}}^{\prime}\right)=\frac{1}{2}{\sum}_{i,j\in A}\mid {k}_{ij}-{k}_{ij}^{\hbox{'}}\mid $$
(2)

We see from (2) that the pairs of elements (i, j) in A can be divided into three subsets:

  1. (a)

    those contributing 1 to kd(R, R′): pairs (i, j) such that i precedes j in either R or R′ while j precedes i in the other;

  2. (b)

    those contributing ½ to kd(R, R′): pairs (i, j) such that i and j are indifferent in either R or R′ while one precedes the other in the other ranking;

  3. (c)

    those contributing 0 to kd(R, R′): pairs (i, j), that are similarly related in both rankings—either i precedes j, or j precedes i, or i and j are indifferent.

In Fagin et al. (2006), the family of so-called Kendall metrics is defined using the rules (a), (b), and (c), modified by replacing the contribution ½ in rule (b) by some constant α, ½ ≤ α ≤ 1. Therefore, the Kemeny distance between rankings is just the Kendall metric for α = ½.

3.3 The Mismatch Distance Between Binary Relations and the Corresponding Binary Matrices

Binary relations considered as subsets of the Cartesian product A × A may be compared using any of the many measures of dissimilarity between subsets that have been introduced over the years (Baulieu 1989; Snijders et al. 1990; Morlini and Zani 2012). One particularly simple measure is the number of pairs for which they differ, the so-called mismatch distance, i.e., the number of pairs in their symmetric difference:

$$ d\left(\uprho, {\uprho}^{\prime}\right)=\kern0.5em \mid \left(\uprho -{\uprho}^{\prime}\right)\cup \left({\uprho}^{\prime }-\uprho \right)\mid $$
(3)

The geometric spaces of ordered and unordered partitions with respect to this distance have been described at length in Mirkin (1979). The mismatch distance between unordered partitions was described in earlier publications by B. Mirkin in Russian from 1969 onwards (see, for example, Mirkin and Cherny 1972); it is sometimes referred to as Mirkin’s distance (Meilă 2007).

We note that d(ρ, ρ′) is a metric on the space of all binary relations on A and satisfies Axiom A1, including the strict triangle inequality, even for binary relations that do not correspond to tied rankings.

The mismatch distance can easily be translated into a distance between N × N matrices. Given a binary relation ρ ∈ A × A, we define its binary matrix r = (rij) by:

$$ {r}_{ij}=\left\{\begin{array}{c}\ 1\ \mathrm{if}\ \left(i,j\right)\in \kern0.5em \rho \\ {}\ 0\ \mathrm{if}\ \left(i,j\right)\notin \kern0.5em \rho \end{array}\right. $$

Then the mismatch distance between R and R’ is the mismatch (Hamming) distance between the corresponding binary relations ρ and ρ’, and is thus given by:

$$ d\left(\boldsymbol{R},{\boldsymbol{R}}^{\prime}\right)=d\left(\uprho, {\uprho}^{\prime}\right)=\mid \left(\uprho -{\uprho}^{\prime}\right)\cup \left({\uprho}^{\prime }-\uprho \right)\mid ={\sum}_{i,j\in A}\mid {r}_{ij}-{r}_{ij}^{\prime}\mid ={\sum}_{i,j\in A}{\left({r}_{ij}-{r}_{ij}^{\prime}\right)}^2 $$
(4)

The right-hand equality allows the original L_1-distance to be transformed into the square of the more conventional, Euclidean or L_2-distance because the absolute differences are either 1 or 0.

Obviously, the mismatch distance (4) is much simpler than the Kemeny distance (2) because the only possible non-zero contribution to d(R, R′) by an ordered pair (i, j) is 1, and this only occurs when j precedes i in one of the tied rankings but not in the other ranking. This happens when rij = 0 and rii′ = 1 or, vice versa, rij′ = 0 and rij = 1. It may therefore be somewhat of a surprise that these two distance measures are, in fact, equal.

Theorem 4

The Kemeny distance (2) is equal to the mismatch distance (4).

Proof

We first analyze the contributions of pairs of elements i, j ∈ A to the Kemeny distance between R and R′ depending on their relative positions in the rankings R and R′; the various cases are shown in Table 2. We note that the contribution of the pair (j, i) is exactly the same as that of the pair (i, j).

Table 2 The contribution of a pair (i, j) ∈ A × A to the Kemeny distance (2) between R and R’
Full size table

Now, we need to take into account a subtle difference between the concepts of ranking and preference relation. The Kemeny distance is between two rankings—it records disagreements in the relative positions between a pair of elements in the two rankings; the symmetry between i and j accounts for the factor ½ in the expression (2) for the Kemeny distance.

In contrast, the mismatch distance is between binary relations and counts the disagreements between the relations in respect of ordered pairs of elements. We, therefore, must distinguish between the ordered pair (i, j) and the inverse pair (j, i), relative to the corresponding relation, ρ or ρ’. The various cases of the contributions to the mismatch distance are shown in Tables 3 and 4, respectively.

Table 3 The contribution of the ordered pair (i, j) ∈ A × A to the mismatch distance (4) between R and R’
Full size table
Table 4 The contribution of the ordered pair (j, i) ∈ A × A to the mismatch distance (4) between R and R’
Full size table

Returning to the analysis of the interrelation between two elements i, j ∈ A, we need to combine Tables 3 and 4 by adding them, which produces Table 5.

Table 5 Summary contribution of the ordered pairs (i, j) and (j, i) to the mismatch distance (4)
Full size table

If we double the values in Table 2 to account for both ordered pairs (i, j) and (j, i), we observe that the resulting entries are identical to those in Table 5, which completes the proof.

Consider a simple example where A consists of three elements, 1, 2, and 3 that are linearly ordered in R and all tied in R′, so that R = ({1}, {2}, {3}) and R’ = ({1, 2, 3}). Their respective Kendall matrices are

$$ k={\displaystyle \begin{array}{lll}0& 1& 1\\ {}-1& 0& 1\\ {}-1& -1& 0\end{array}}\kern0.5em \mathrm{and}\kern0.5em {k}^{\prime }={\displaystyle \begin{array}{lll}0& 0& 0\\ {}0& 0& 0\\ {}0& 0& 0\end{array}},\kern0.5em \mathrm{so}\ \mathrm{that}\ \mathrm{the}\ \mathrm{Kemeny}\ \mathrm{distance}\ kd\left(\boldsymbol{R},{\boldsymbol{R}}^{\prime}\right)=6/2=3. $$

On the other hand, their respective weak order matrices are

$$ r={\displaystyle \begin{array}{lll}1& 1& 1\\ {}0& 1& 1\\ {}0& 0& 1\end{array}}\kern0.5em \mathrm{and}\kern0.5em {r}^{\prime }={\displaystyle \begin{array}{lll}1& 1& 1\\ {}1& 1& 1\\ {}1& 1& 1\end{array}},\kern0.5em \mathrm{so}\ \mathrm{that}\ \mathrm{the}\ \mathrm{mismatch}\ \mathrm{distance}\ d\left(R,{R}^{\prime}\right)=3\ \mathrm{as}\ \mathrm{well}. $$

3.4 The Mismatch Distance Expressed in Terms of the Contingency Table

Although the following results can be established directly, we now rely on Axiom A1(c), which states that d(R, R′) = d(R, R′′) + d(R′′, R′) if and only if R′′ is between R and R′, that is ρ∩ρ’ ⊆ ρ” ⊆ ρ∪ρ’ for the corresponding preference relations. By virtue of (4), we may use d(R, R′) and d(ρ, ρ’) interchangeably.

Let us first consider a tied ranking R and its reverse R−1. Obviously, ρ∩ρ−1 = E, where E is the indifference relation of R, which is an equivalence relation, stripped of all ranking information. Similarly, ρ∪ρ−1 = U, the universal relation U = A × A, which contains all possible ordered pairs of elements of A. Both E and U are, therefore, between ρ and ρ−1 for any weak order ρ.

Let Ns be the number of elements in part Rs of the tied ranking R = (R1, R2, …, Rp). Then the mismatch distance between U and E is easily seen to be

$$ d\left(E,U\right)={N}^2-{\Sigma}_s{N_s}^2, $$
(5)

since the first term on the right is the number of ones in the binary matrix of U and the second term is the number of ones in the binary matrix of E.

Curiously, the mismatch distance between U and R itself is exactly half the distance in (5).

Theorem 5 The mismatch distance between a tied ranking R and the universal relation U is given by

$$ d\left(\boldsymbol{R},U\right)=1/2\ \left({N}^2-{\Sigma}_s{N_s}^2\right). $$
(6)

Proof

We first notice that d(R, U) = d(R−1, U) and d(R, E) = d(R−1, E). Indeed, neither U nor E depend on the ranking information in R, and, moreover, the number of pairs in ρ and ρ−1, which is the number of ones in their respective matrices r and r−1, is the same. Since both U and E are between R and R−1, we have:

$$ d\left(\boldsymbol{R},{\boldsymbol{R}}^{-1}\right)=d\left(\boldsymbol{R},U\right)+\mathrm{d}\left(U,{\boldsymbol{R}}^{-1}\right)=2d\left(\boldsymbol{R},U\right)\ \mathrm{and}\ d\left(\boldsymbol{R},{\boldsymbol{R}}^{-1}\right)=d\left(\boldsymbol{R},E\right)+d\left(E,{\boldsymbol{R}}^{-1}\right)=2d\left(\boldsymbol{R},E\right). $$

This implies that d(R, U) = d(R, E). So, since R is between E and U, d(E, U) = d(E, R) + d(R, U) = 2d(R, U). Equation (6) now follows from this and (5), which completes the proof.

Corollary 1

The distance d(R, R−1) is equal to d(E, U) given by (5), whereas the distance d(R, E) is equal to d(R, U), given by (6).

Proof

These results are included in the proof of Theorem 5.

Now, we are in a position to prove a formula for the mismatch distance between a tied ranking R and its arbitrary refinement R′. Like the previous results in this subsection, this does not depend on the ranking information.

Theorem 6

The mismatch distance between a tied ranking R = (R1, R2, …, Rp) and an arbitrary refinement R′ = (R1′, R2′, …, Rq′) of R, where q > p, is given by

$$ d\left(\boldsymbol{R},{\boldsymbol{R}}^{'}\right)=\frac{1}{2}\ \left({\Sigma}_s{N_s}^2-{\Sigma}_t{{N^{'}}_t}^2\ \right), $$
(7)

where Ns and N’t are the numbers of elements in the parts Rs of R and Rt’ of R’, respectively.

Proof

Indeed, since R is between R′ and U, we have d(R′, U) = d(R′, R) + d(R, U), so d(R′, R) = d(R′, U) - d(R, U). Both distances d(R′, U) and d(R, U) are determined by Eq. (6), adjusted for the corresponding parts of R’ and R, respectively. This immediately yields (7), completing the proof.

Consider now two ordered partitions, R and R′, and their lexicographic products R * R′ and R′ * R. We shall show that the entire ranking component contributing to the distance between R and R′ is accounted for by the distance between R * R′ and R′ * R. First, consider the intersection R∩R′, as presented in Table 1. Letting Nst = |Rs∩R’t|, for s = 1, 2, …, p and t = 1, 2, …, q, denote the numbers of elements in the parts of the intersection, we can present these cardinalities as the so-called contingency table, or cross-classification, between R and R′ – a popular concept in statistics (see, for example, Mirkin 1979, 2012).

The distance between R * R′ and R′ * R is equal to half of the total of the products of the cardinalities of those parts in the intersection R∩R’ for which the orderings in R and R’ are contradictory:

$$ d\left({\boldsymbol{R}}^{\ast }{\boldsymbol{R}}^{\prime },{\boldsymbol{R}}^{\prime \ast}\boldsymbol{R}\right)=\frac{1}{2}{\sum}_{s>s\prime }{\sum}_{t<t\prime }{\mathrm{N}}_{st}{\mathrm{N}}_{s\prime t\prime } $$
(8)

Considering the rankings R and R’ as unordered partitions, denoted above by Ř and Ř’, respectively, the mismatch distance between the corresponding equivalence relations, E and E’, can be expressed as

$$ d\left(E,{E}^{\prime}\right)={\sum}_s{N}_s^2+{\sum}_tN{\prime}_t^2-2{\sum}_{s,t}{N}_{st}^2 $$
(9)

where Ns, N’t, and Nst are, as above, the numbers of elements in parts Rs of R, R′t of R′ and Rs∩R′t of R∩R′, respectively.

  • Theorem 7. The mismatch distance between tied rankings R and R’ can be decomposed into ranking and equivalence parts as follows:

    $$ d\left(\boldsymbol{R},{\boldsymbol{R}}^{\prime}\right)=\kern0.5em \frac{1}{2}\ d\left(E,{E}^{\prime}\right)+\mathrm{d}\left(\boldsymbol{R}\times {\boldsymbol{R}}^{\prime },{\boldsymbol{R}}^{\prime}\times \boldsymbol{R}\right). $$
    (10)

Proof

Consider the corresponding binary relations ρ, ρ′, and ρ∩ρ′. Since the intersection ρ∩ρ’ is between ρ and ρ′, d(ρ, ρ′) = d(ρ, ρ∩ρ′) + d(ρ∩ρ′, ρ′). On the other hand, ρ × ρ′ is between ρ∩ρ′ and ρ, and ρ′ × ρ is between ρ∩ρ′ and ρ′, so d(ρ, ρ∩ρ′) = d(ρ, ρ × ρ′) + d(ρ × ρ′, ρ∩ρ′), and d(ρ∩ρ′, ρ′) = d(ρ∩ρ′, ρ′ × ρ) + d(ρ′ × ρ, ρ′). But ρ∩ρ′ is between ρ × ρ′ and ρ′ × ρ, so d(ρ × ρ′, ρ′ × ρ) = d(ρ × ρ′, ρ∩ρ′) + d(ρ∩ρ′, ρ′ × ρ). Substituting these in the equation d(ρ, ρ′) = d(ρ, ρ∩ρ′) + d(ρ∩ρ′, ρ′), we obtain

$$ d\left(\uprho, {\uprho}^{\prime}\right)=d\left(\uprho, \uprho \times {\uprho}^{\prime}\right)+d\left(\uprho \times {\uprho}^{\prime },{\uprho}^{\prime}\times \uprho \right)+d\left(\uprho \times {\uprho}^{\prime },{\uprho}^{\prime}\right). $$
(11)

Since ρ × ρ′ is a refinement of ρ, and ρ′ × ρ is a refinement of ρ′, d(ρ, ρ × ρ′) = ½(ΣsNs2 - Σs,tNst2) and d(ρ′ × ρ, ρ′) = ½(ΣtN’t2 - Σs,tNst2) by Theorem 6. This implies, by (9), that d(ρ, ρ × ρ′) + d(ρ′ × ρ, ρ′) = ½d(E, E′). Together with (11), this completes the proof.

4 Consensus Among Tied Rankings

4.1 Consensus Matrix

Let us consider the concept of consensus ranking formulated by John Kemeny as follows. Given a set of tied rankings R1, R2, …, Rn, find a ranking R, referred to by Kemeny as a median, that minimizes the summary distance D(R) = Σmkd(R, Rm). Such a problem, for unordered partitions, has been widely accepted as a consensus rule in the literature on data analysis and machine learning (see, for example, Guénoche 2011).

Given a set of tied rankings R1, R2, …, Rn, let us define a ranking consensus matrix C = (cij) as follows: for any pair (i, j), cij is the number of those rankings Rm, 1 ≤ m ≤ n, in which i either precedes j or is indifferent to j. This means that C = Σmrm, where rm is the binary matrix of the binary relation ρm corresponding to Rm, for 1 ≤ m ≤ n.

This matrix can be used to obtain an explicit criterion for the concept of median.

Theorem 8

A ranking R = (R1, R2, …, Rp) is a median of the set of tied rankings R1, R2, …, Rn if and only if it maximizes

$$ F\left(\boldsymbol{R}\right)={\sum}_{i,j\in A}\left({c}_{ij}-\frac{\mathrm{n}}{2}\right){\mathrm{r}}_{ij}={\sum}_{s=1}^p{\sum}_{t\ge s}{\sum}_{i\in {R}_s}{\sum}_{j\in {R}_t}\left({c}_{ij}-\frac{n}{2}\right) $$
(12)

with respect to a pre-specified set of admissible rankings R.

Proof

By Theorem 4, we may use the mismatch distance in the definition of median, and thus D(R) = Σmd(R, Rm). Substituting the right-most expression in (4) for d(∙, ∙), we get

\( D\left(\boldsymbol{R}\right)={\sum}_{m=1}^n{\sum}_{i,j\in A}{\left({\mathrm{r}}_{ij}-{\mathrm{r}}_{ij}^m\right)}^2={\sum}_{i,j\in A}{\sum}_{m=1}^n\left({\mathrm{r}}_{ij}-{\mathrm{r}}_{ij}^m-2{\mathrm{r}}_{ij}{\mathrm{r}}_{ij}^m\right)={\sum}_{i,j\in A}\left({\mathrm{nr}}_{ij}+{\mathrm{c}}_{ij}-2{\mathrm{r}}_{ij}{\mathrm{c}}_{ij}\right), \)

since squaring does not change the binary 0/1 values. The last expression follows by the definition of the consensus matrix C. Rearranging this, we obtain D(R) = \( \sum \limits_{i,j\in A}{c}_{ij}-2\sum \limits_{i,j\in A}\left({c}_{ij}-\frac{n}{2}\right){\mathrm{r}}_{ij} \), which is equal to a constant minus 2F(R). Therefore, to minimize D(R), we need to maximize F(R), which completes the proof.

We note that the subtracted value n/2 can be moved out of the summation in (12), so that the expression for F(R) becomes

$$ F\left(\boldsymbol{R}\right)={\sum}_{s=1}^{\mathrm{p}}{\sum}_{t\ge s}{\sum}_{i\in {R}_s}{\sum}_{j\in {R}_t}{c}_{ij}-\frac{n}{4}\left({N}^2+{\sum}_{s=1}^p{N}_s^2\right), $$
(13)

where Ns is the cardinality of Rs, 1 ≤ s ≤ p. This follows because \( \sum \limits_{i,j\in A}{\mathrm{r}}_{ij} \)is the number of pairs (i, j)∈ρ, that is, the cardinality of the binary relation ρ corresponding to R, which is given by

$$ \mid \uprho \mid =\frac{1}{2}\left({N}^2+{\sum}_{s=1}^p{N}_s^2\right). $$
(14)

To prove this, we recall from the previous section that ρ∩ρ−1 = E and ρ∪ρ−1 = U. Since |ρ| = |ρ−1|, using the fact that |ρ∪ρ−1| = |ρ| + |ρ−1| - |ρ∩ρ−1|, it follows that |ρ| = \( \frac{1}{2} \)(|U| + |E|). Equation (14) now follows immediately from the remark following Eq. (5).

Since nN2/4 is a constant, maximization of F(R) in (13) is equivalent to the modified criterion of maximizing

$$ G\left(\boldsymbol{R},\boldsymbol{a}\right)={\sum}_{s=1}^p{\sum}_{t\ge s}{\sum}_{i\in {R}_s}{\sum}_{j\in R}{c}_{ij}-a{\sum}_{s=1}^p{N}_s^2, $$
(15)

where a = n/4.

The criterion (12), or equivalently (15), is an extension of the following criterion of linear ordering, sometimes referred to as the triangulation of a square matrix, which was popular a few decades ago: find a simultaneous permutation of the rows and columns that maximizes the sum of the above-diagonal entries in the matrix (see, for example, Grötschel et al. 1983; Charon and Hudry 2007). Obviously, for a linear ordering all parts Rs are singletons and p = N in (15), and thus the right-most term in (15) is a constant. In this case, the solution does not depend on the value n/2 that is subtracted from all the entries in (12).

Curiously, the subtracted term on the right in (15) does not depend on the ordering information. It depends just on the indifference relation E or, more precisely, the distribution of elements over tied parts of the median ranking.

The expression \( \sum \limits_{s=1}^p{N}_s^2 \) for the cardinality of ∣E∣ is not unusual in statistics of categorical variables. To explain its meaning, consider the relative frequency fs = Ns/N of part Rs, and the entire frequency profile f(R) = (f1, f2, …, fp) of an arbitrary p-part partition R. The inner product, c(R) = <f(R), f(R) > = Σsfs2, may be referred to as the concentration index. Its maximum value 1 is attained for the profile in which all the frequencies are 0, except one that is equal to unity. Its minimum value 1/p is attained for the uniform profile in which all the frequencies are equal, so fs = 1/p for all s, 1 ≤ s ≤ p. Obviously, |E| = N2c(R). A precise meaning of c(R) can be given in terms of the so-called proportional prediction rule. The proportional prediction rule is a classifier defined according to profile f(R). A classifier assigns a category s, 1 ≤ s ≤ p, to any object randomly supplied, according to the distribution f(R). The proportional prediction classifier assigns the categories randomly, each category s with probability fs. It is easy to see that the average accuracy of this classifier is c(R). Its complement to unity, δ = 1 - c(R), is well known in social economics as the Gini index, a measure of inequality of social groups in which fs is the proportion of the sth income group in the population.

Since the concentration part in (15) is subtracted, we can safely claim that criterion (15), other things being equal, leads to a more uniform median ranking than it would have had nothing been subtracted from cij in (12). In fact, it can be proved that, when the weight a of the subtracted value in (15) is increased above n/4, the concentration of a ranking R that maximizes the expression corresponding to (15) can only decrease. Indeed, the following stronger statement holds.

Theorem 9 If R and R’ are maximizers of G(R, a) in (15) for a = a1 and a = a2, respectively, and a2 > a1 then c(R’) ≤ c(R).

Proof

From (15), G(R, a) = G(R, 0) - aN2c(R) for any R and a. Since R maximizes G(R, a1) and R’ maximizes G(R, a2), we have G(R’, a1) ≤ G(R, a1) and G(R, a2) ≤ G(R’, a2). Therefore, G(R’, 0) - a1N2c(R’) ≤ G(R, 0) - a1N2c(R) and G(R, 0) - a2N2c(R) ≤ G(R’, 0) - a2N2c(R’).

Combining these two inequalities, we obtain

a1N2c(R) - a1N2c(R’) ≤ G(R, 0) - G(R’, 0) ≤ a2N2c(R) - a2N2c(R’), so (a2 - a1) N2c(R’) ≤ (a2 - a1) N2c(R). Since a2 > a1, it follows that c(R’) ≤ c(R), which completes the proof.

This result supports the view that the second term in (15) is a regularizer of the distribution of elements in the parts of the sought ordered partition R: the greater the weight a, the greater the number of (non-empty) parts and the more uniform the distribution of elements among the parts.

4.2 The Muchnik Test Over Likert Scales

Ranking practitioners have noticed that the concept of median is not that sensitive to their interest in a few leaders rather than an entire consensus ranking (Cook 2006). We focus here upon an even less desirable property: insufficient sensitivity to the differences in similar opinions.

Let us consider a test example, akin to the so-called Muchnik test in consensus clustering (Mirkin 2012), in the context of the so-called Likert scale (Likert 1932; Allen and Seaman 2007). This scale is applied when an individual cannot reproduce an entire ranking. A psychologist then specifies a number of attributes, each of which splits the ordering in question into two complementary fragments—the beginning and the end. For each object or observation, the psychologist asks the individual, in respect of a specific attribute, whether the object falls within the beginning or end part of the scale. Mathematically, the situation can be described as follows.

There is a ranking with p tied parts, R = (R1, R2, …, Rp). This ranking is used to produce p-1 binary rankings S1, S2, …, Sp-1. Each binary ranking St consists of just two parts, so St = (Ut, Vt) for t = 1, 2, …, p-1. The first part Ut is the set-theoretic union of the first t parts of R, so \( {U}_t=\bigcup \limits_{m=1}^t{R}_m, \) and the second part Vt is the union of the remaining parts of R, so Vt = A − Ut. These binary rankings completely determine the underlying ranking R. Therefore, we may pose the problem of finding a consensus ranking or median S for the set of binary rankings S1, S2, …, Sp-1. In particular, will the underlying ordered partition R be a solution to this problem?

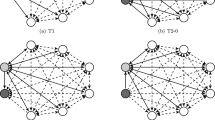
Figure 1 shows two cases representing the ranking consensus matrix for the set of binary rankings corresponding to a ranking with p = 7 tied parts, with the value (p-1)/2 = 3 subtracted from each of the entries. Rather than showing individual elements of A, we show just the block structure of the matrix, where the (s, t)-th block, 1 ≤ s, t ≤ p, corresponds to the pairs (i, j)∈ Rs × Rt, with each entry having the constant value cij − (p-1)/2. There are only six negative blocks in the matrix. Of course, the number of negative entries (i, j) clearly depends on the sizes of the corresponding parts of R. Let us consider, for the sake of simplicity, a case in which each part R1, R2, …, Rp of R contains the same number of elements. To maximize the criterion (12), we just need to minimize the sum of the entries below the diagonal. It is almost evident that the parts of R cannot be split in an optimal ranking S—this, of course, can be proven formally. Therefore, a median S can be obtained by merging some parts of R, that is, R should be a refinement of S. The best option would, if it were possible, be to merge the parts in such a way that these negative blocks of entries, and only they, should be excluded from the upper part of the matrix in Fig. 1. However, this is not possible, because, however, the parts are aggregated, some positive entries must be present below the diagonal—more precisely, below a borderline delineating the aggregated parts. This is shown in Fig. 1a for the case in which the candidate ranking has three parts obtained by merging (i) R1 and R2; (ii) R3, R4, and R5; and (iii) R6 and R7. The borderline between the entries included in and excluded from the sum in (12) is shown in bold. We can see there are six positive entries below the borderline, which almost cancel out the negative values. In this sense, the binary ranking S4 that merges R1, R2, R3, and R4 into the first part of S, and R5, R6, and R7 into the second part of S, as shown in Fig. 1b, is better as it excludes all the negative entries and only three positive entries. It is not difficult to prove that this ranking is optimal, and that another optimal ranking is the binary ranking S3. Similarly, in the general case with a different number of equal-size parts in the underlying ranking R, a binary ranking that splits R into two equal-size parts (or as equal as possible) is an optimal ranking.

Fig. 1
figure 1

Values cij − (p-1)/2 for the blocks of the consensus matrix for the Likert scale consensus problem when p = 7. The bold line represents the boundary separating entries summed in criterion (12), i.e., those above and to the right of it, from the rest. a shows the case in which the seven parts are merged into three aggregated parts: (i) the first two parts, (ii) the next three parts, and (iii) the last two parts. b shows the case in which the seven parts are merged into two aggregated parts: (i) the first four parts and (ii) the last three parts

Full size image

As we can see, the median rule for the Likert scale cannot reproduce the original ranking R when p > 2. The median S in this case is just a coarser binary version of R, which is a very rough model of the original.

5 Conclusion

Human intuition handles summation of positive numbers rather well. An issue emerges when some of the numbers are negative. This paper can be looked at as an attempt to find some structure in the − 1 entries in the Kendall matrices occurring in the formula for the Kemeny distance between tied rankings. These entries appear whenever a pair of elements, i and j, are inversely related so that j precedes i in a ranking. First, we showed in Theorem 4 that the Kemeny distance can be expressed in terms of the mismatch distance between the preference relations (weak orders) corresponding to the tied rankings, in which no negative entries appear. The mismatch distance is defined in terms of the 0–1 matrices of weak orders, rather than the Kendall matrices of the rankings, containing entries 1, 0, and − 1. Our next claim is that, in the problem of finding a consensus between tied rankings, all the negative items relate to the subtracted regularizer term in (15), an expression depending only on the distribution of the sizes of the parts in the consensus ranking, not on the precedence relation between them (see Theorems 8 and 9). The structure of the subtracted term relates the problem of finding a consensus tied ranking to the well-known linear ordering problem. Moreover, when applied to the issue of consensus ranking in the Likert scale case, the concept of Kemeny median, or consensus ranking, appears to be less sensitive than one would have hoped, resulting in a solution being one of the central Likert binary rankings rather than the hidden multi-part ranking.

Following this line of narrative, we have explicitly formulated properties of the Kemeny distance, especially those related to its decomposition into “ordered” and “unordered” parts (see Theorem 7) and its computation via the contingency table, popular in statistics (see (8), (9), and (10)).

Among possible directions for further research, two are quite straightforward. First, to try to solve numerically the problem of consensus ranking. For example, the additive structure in (15) suggests that one might first find an optimal linear ordering and then aggregate some of its parts to form a tied ranking. Second, the failure of the Muchnik test on Likert scales suggests some ways for formulating more sensitive criteria for consensus.

There are other approaches as well (see, for example, Amor and Martel 2014, Barthélemy, Leclerc and Monjardet 1986, Critchlow 1980/2012, Dwork et al. 2001, Emond and Mason 2002, Monjardet 1978, Nandi, Fa and Abu-Jamous 2015).