1 Introduction

Most facility location problems are multi-objective in nature and several objectives should be considered simultaneously. The maximal covering location problem (MCLP) is a well-known location problem where a fixed number of facilities are located to maximize the demand covered. In the classical MCLP, a demand node is defined as being covered if it is within a critical distance from at least one of the facilities, and not covered if it is outside the critical distance. Since the introduction by Church and ReVelle (1974), various extensions of MCLP have been developed in the literature (see Schilling et al. 1993; Berman et al. 2010 for reviews). The MCLP has many applications in public and private sectors, especially in locating emergency facilities (see Goldberg 2004 for a review).

The definition of coverage was extended to model situations where coverage (i.e., the level of service provided by the facility) does not change in a crisp way from “fully covered” to “not covered” at the critical distance. Karasakal and Karasakal (2004) introduced the partial coverage concept in a maximal covering location model. They assumed that the demand node was partially covered up to a maximum critical distance and fully covered within the minimum critical distance. Berman et al. (2003) modeled a covering location problem using a gradual concept. The coverage provided by the facility is assumed to decrease gradually after a certain distance.

A number of researchers have developed coverage models with more than one objective (see Farahani et al. 2010 for a review). Some of them considered backup coverage besides the first coverage (Hogan and Revelle 1986; Storbeck and Vohra 1988). Church et al. (1991) developed a bi-objective maximal covering location model. In addition to the coverage objective, an objective that minimizes the sum of the weighted distance between uncovered demand and the nearest facility is formulated. Badri et al. (1998) proposed a goal programming model for locating fire stations, which considers objectives related to cost, demand, certain system requirements, technical and political strategies. Araz et al. (2007) developed a multi-objective coverage-based model. The maximization of the first coverage of demands, maximization of backup coverage and minimization of the total travel distance between uncovered demands and opened facilities are defined as objectives.

In MCLPs, full or partial coverage of all demand nodes may not always be possible due to limited number of facilities. However, in real life, especially emergency facilities such as ambulance, police, and fire stations should give service to all demand nodes including those that are not within the coverage distance of a facility. Another example may be in the location of Wi-Fi access points at large areas such as airports. People outside the coverage areas should go to the nearest access points. To take into account the quality of service to uncovered demand nodes, the maximum distance between uncovered demands and its nearest facilities (i.e., p-center objective) should also be minimized.

To the best of our knowledge, there are no studies that use the p-center objective to handle the uncovered demands in MCLPs. We present a bi-objective facility location model that considers both partial coverage and service to uncovered demand nodes. We assume that demand nodes within the predefined distance of opened facilities are fully covered and after that the distance coverage level decreases linearly. We also assume that an uncovered demand can be served by its nearest facility when it is needed. Therefore, we define the second objective as the minimization of the maximum distance between any uncovered demand node and its nearest facility.

The MCLP is NP-hard (Megiddo et al. 1983). Thus, bi-objective MCLP addressed in the paper is also NP-hard. Many heuristic and metaheuristic methods have been developed to solve large-size MCLPs since it is cumbersome to solve large-size problems using exact methods (e.g., Karasakal and Karasakal 2004; Fazel Zarandi et al. 2011; ReVelle et al. 2008). In this paper, we develop a new multi-objective genetic algorithm (MOGA) to solve the bi-objective MCLP.

We develop a new multi-objective genetic algorithm (MOGA) called modified SPEA-II (mSPEA-II). We modify the fitness function of SPEA-II and use the crowding distance of NSGA-II. The performance of mSPEA-II is tested on randomly generated problems of different sizes. Results are compared with the solutions of NSGA-II and SPEA-II, since they are the representatives of the state-of-the-art MOGAs (Coello Coello et al. 2007, p. 274; Zhou et al. 2011; Durillo et al. 2009; Pohl and Lamonth 2008). Although there are many variations of these state-of-the-art algorithms, original versions are used in comparative studies of the newly developed MOGAs (Coello Coello et al. 2007, p. 98; Konak et al. 2006).

The organization of the paper is as follows. In the next section, we provide a brief review on the application of MOGAs to multi-objective facility location problems. In Sect. 3, we present the mathematical model. We develop the approach in Sect. 4. We report our computational experiments in Sect. 5 and present concluding remarks in the last section.

2 Literature review

MOGAs are developed to search for nondominated solutions in multi-objective optimization problems (see Ishibuchi et al. 2008 for a review). Deb (2001) categorizes MOGAs into two groups: non-elitist MOGAs and elitist MOGAs. Non-Dominated Sorting Genetic Algorithm (NSGA-II) (Deb et al. 2002) and Strength Pareto Evolutionary Algorithm (SPEA-II) (Zitzler et al. 2001) are the best known elitist MOGAs in literature.

MOGAs are one of the most suitable approaches for multi-optimization problems (Alberto and Mateo 2011), because they generate population of solutions and find entire set of Pareto optimal solutions in a single run (Ghosh and Dehuri 2004).

Li et al. (2011) stated that in emergency facility location models, GAs are one of the most widely used techniques for solving problems. Aytug et al. (2003) listed the production and operation management problems that used GAs and evaluated the state of GA applications in these areas. Jaramillo et al. (2002) demonstrated that performance of GAs are more robust than Lagrangian heuristic in solving location problems.

There are several studies that use GAs to solve coverage problems. Yigit et al. (2006) formulated uncapacitated facility location problem and used simulated annealing for local search and evolutionary approach for global search to obtain the desired solutions. Mahdavie et al. (2012) proposed a multi-facility location problem. They tried to find the optimal locations of new facilities by minimizing the total weighted expected traveled rectilinear distances from the new facilities to those existing. They used genetic algorithm for large-size problems. Gutjahr et al. (2009) presented a multi-objective model for the public facilities. The objectives are based on weighted average of minimum and maximum coverage, minimizing the risk of tsunami for alternative locations and minimizing the cost, respectively. They used NSGA-II to solve the problem. Bhattacharya and Bandyopadhyay (2010) modeled a bi-objective facility location problem and solved the model by NSGA-II. Li and Yeh (2004) integrated the genetic algorithm with geographical information systems to solve a location problem whose objectives are the maximization of population coverage, the minimization of total transportation costs and the minimization of the proximity to roads. Villegas et al. (2006) modeled a bi-objective uncapacitated facility location problem whose objectives are the minimization of the total cost of assigning facilities to related demand nodes and fixed facility opening costs, and the maximization of coverage. They applied multi-objective evolutionary algorithms and an algorithm based on mathematical programming. Yang et al. (2007) proposed a model based on fuzzy multi-objective programming and a genetic algorithm. The achievement levels for fuzzy objectives were defined. The fuzzy multi-objective optimization model was converted into a single unified goal and a genetic algorithm was applied to the problem. Medaglia et al. (2009) formulated a bi-objective model to design a hospital waste management network. They integrated NSGA-II into mixed integer for the solution of the bi-objective problem.

3 Formulation of the problem

We formulate a bi-objective model that maximizes total coverage of the facilities and minimizes the maximum distance between uncovered demand nodes and the nearest facilities.

In Fig. 1, there are four alternative facilities which are numbered from one to four and one of them will be opened. Demand nodes are denoted by points and assumed to have equal weights. The circles around the facilities show the coverage areas of the facilities. If the maximum distance between the demand nodes and their nearest facilities is minimized, facility 3 is selected. The maximum distance to uncovered demand nodes is \(d_{1}\) and the number of uncovered demand nodes is 6. On the other hand if full and partial coverage is minimized, facility 4 is opened and the number of uncovered demand nodes is 3, but the maximum distance is \(d_{2}\) which is greater than \(d_{1}\). These objectives generally conflict with each other in most of the real-life location problems.

Fig. 1
figure 1

An example

Full size image

Notation used in the model is as follows:

I :

set of demand nodes,

J :

set of potential facility sites,

\(a_i\) :

demand at node i,

p :

number of facilities to be sited,

\(d_{ij}\) :

shortest travel distance separating node i from node j,

T :

maximum partial coverage distance,

S :

maximum full coverage distance,

\(\alpha \) :

maximum distance between an uncovered demand node and its nearest facility.

$$\begin{aligned} M_i= & {} \left\{ {j\left| {d_{ij} \le T} \right. } \right\} \\ c_{ij}= & {} \left\{ {\begin{array}{l@{\quad }l} 1 &{}\hbox {if }d_{ij} \le S, \\ f(d_{ij} )&{} \hbox {if }S\le d_{ij} \le T,\quad (0<f(d_{ij} )<1), \\ 0 &{} \hbox {otherwise,} \\ \end{array}} \right. \\ x_{ij}= & {} \left\{ {\begin{array}{l@{\quad }l} 1 &{} \hbox {if uncovered demand node } i \hbox { is assigned to facility } j, \\ 0 &{} \hbox {otherwise,} \\ \end{array}} \right. \\ y_i= & {} \left\{ {\begin{array}{l@{\quad }l} 1 &{} \hbox {if demand node } i \hbox { is not within } T \hbox { of any facility,} \\ 0 &{} \hbox {otherwise,} \\ \end{array}} \right. \\ f_j= & {} \left\{ {\begin{array}{l@{\quad }l} 1 &{} \hbox {if a facility is sited at node } j, \\ 0 &{} \hbox {otherwise,} \\ \end{array}} \right. \\ s_{ij}= & {} \left\{ {\begin{array}{l@{\quad }l} 1 &{} \hbox {if demand at point } i \hbox { is either partially or fully covered by facility}~j, \\ 0 &{} \hbox {otherwise.} \\ \end{array}} \right. \\ \end{aligned}$$

The formulation of the bi-objective MCLP is as follows:

$$\begin{aligned} \hbox {Min}&Z_1 =\alpha \nonumber \\ \hbox {Max}&Z_2 =\sum _{i\in I} {\sum _{j\notin M_i } {c_{ij} a_i s_{ij}}} \nonumber \\ \hbox {s.t.}&\nonumber \\&\sum _{j\in M_i } {f_j } +y_i \ge 1 \quad \forall i\in I, \end{aligned}$$
(1)
$$\begin{aligned}&\sum _{j\notin M_i } {x_{ij}} -y_i =0 \quad \forall i\in I, \end{aligned}$$
(2)
$$\begin{aligned}&f_j -x_{ij} \ge 0 \quad \forall i\in I,\quad j\notin M_i , \end{aligned}$$
(3)
$$\begin{aligned}&\sum _{j\in J} {f_j } =p, \end{aligned}$$
(4)
$$\begin{aligned}&\sum _{j\notin M_i } {x_{ij}\cdot d_{ij}} \le \alpha \quad \forall i\in I, \end{aligned}$$
(5)
$$\begin{aligned}&s_{ij} -f_j \le 0 \quad \forall i\in I,\quad j\notin M_i , \end{aligned}$$
(6)
$$\begin{aligned}&\sum _{j\in M_i } {s_{ij}} \le 1 \quad \forall i\in I, \\&x_{ij, } s_{ij} \in \left\{ {0,1} \right\} \quad \forall i\in I, \quad j\in J,\nonumber \\&y_i \in \left\{ {0,1} \right\} \quad \forall i\in I,\nonumber \\&f_j \in \left\{ {0,1} \right\} \quad \forall j\in J.\nonumber \end{aligned}$$
(7)

The first objective minimizes the maximum distance between uncovered demand nodes and the nearest facilities. The second objective maximizes the total coverage including both partial and full coverage.

Constraint set (1) ensures that if there is not any opened facility within the distance T for a demand node, then that demand node is an uncovered demand node and the variable y is forced to be 1. Constraint set (2) is formulated to assign the uncovered demand to an opened facility, because if the distance between an opened facility and demand node i is less than T, then that demand node is covered and \(y_{i}\) is 0, so all the \(x_{ij}\) values are forced to be 0 for that demand node. However, if a demand node is not covered, then \(y_{i}\) is 1 and constraint set (2) requires the demand node be assigned to a facility. The constraint set (3) ensures that an uncovered demand node be assigned to a facility only if a facility is located at node j. Thus, if \(f_{j}\) is 0, this means that a facility is not opened at node j, so all the corresponding \(x_{ij}\) values are 0. If \(f_{j}\) is 1, then uncovered demand may be assigned to this facility, so some \(x_{ij}\) values may be 1. Constraint (4) restricts the number of opened facilities. Constraint set (5) calculates the maximum of the distances between uncovered demand nodes and their nearest facilities. The constraint sets (6) and (7) are peculiar to the partial coverage concept. If the jth facility is not opened, then all its \(s_{ij}\) values are forced to be 0 and the demand nodes will not be assigned to that facility, but if the jth facility is opened than the values \(s_{ij}\) may be 0 or 1 and may get a facility assigned to it or not. This will be determined together with the constraint set (7), because constraint set (7) allows any demand point to be covered by at most one of the facilities sited. If there is more than one facility covering a demand node, then the second objective determines which of them will provide service.

4 A new multi-objective genetic algorithm (mSPEA-II)

NSGA-II proposed by Deb et al. (2002) incorporates elitism by allowing the best solutions from the parent and offspring pools of chromosomes to be retained. NSGA-II uses nondominated sorting instead of a fitness function to classify the entire population, and calculates crowding distance to maintain a good spread of solutions in the solution set. Nondominated sorting gives the same priority to all members in the same front. This may cause problems in converging the true Pareto front in cases where some members are dominated by many members of the other front, and others are dominated by a few members. A simple bi-objective problem where objectives are to be minimized is depicted in Fig. 2. There are two fronts. Solutions 7 and 9 are in the second front. Solution 7 is dominated only by solution 1. Solution 9 is dominated by three solutions, 3, 4 and 5. Since they are boundary solutions in the second front, their crowding distances are the same and very large, meaning that they have the same priority for selection. However, solution 7 should have more priority than solution 9, because solution 7 should be kept in the population to generate solutions having larger \(Z_{2}\) values and smaller \(Z_{1}\) values than that of solution 1 and converge the true Pareto-optimal front quickly.

Fig. 2
figure 2

A sample population

Full size image

The Strength Pareto Evolutionary Algorithm (SPEA-II) proposed by Zitzler et al. (2001) uses a regular population and an archive (external) set. New generated offsprings are stored in a regular set, whereas nondominated solutions are stored in an archive set. Fitness assignment, based on the domination concept and density estimation, is done for the union of these sets. The fitness of a solution is the sum of raw fitness and density fitness values. The strength of each member in the archive and regular populations is calculated. The greater strength means that it dominates more members in the population. The raw fitness of a solution is calculated by summing up the strength of all the solutions that dominate the given solution. Also, for each member in the union set, the distances to all other solutions are calculated and sorted in increasing order, and density fitness value is calculated to differentiate those solutions which have the same raw fitness values. Density fitness values are used in a truncation operation when the actual archive is greater than the fixed archive size. Calculating the density fitness values and using the truncation operation increase the complexity of the SPEA-II algorithm. Experiments demonstrate that the computational complexity of SPEA-II is considerably greater than that of NSGA-II (Eskandari et al. 2007).

To decrease the computational complexity of SPEA-II and keep good solutions to maintain the diversity and convergence to the true Pareto front, we propose a genetic algorithm based on SPEA-II (mSPEA-II). In mSPEA-II, instead of density fitness, D(i), the objective fitness values, \(\min O(i)\), are calculated. For each minimization objective, the solutions are sorted in ascending order.\(\min O(i)\) is set to the minimum rank among all objectives. For instance, the objective function values of the bi-objective minimization problem depicted in Fig. 2 are given in Table 1.

Table 1 Objective function values of solutions
Full size table

These solutions are sorted according to both objectives as shown in Table 2.

Table 2 Solutions sorted according to each objective
Full size table

As seen in Table 2, \(\min O(7)\) is 2, because it is in the second rank with respect to the first objective, \(Z_{1}\), and in the ninth rank with respect to the second objective, \(Z_{2}\), so the minimum is 2.

A fitness value for each solution is determined as follows:

$$\begin{aligned} F_1 (i)=R(i)+\frac{\mathrm{min} O(i)}{\hbox {no. of solutions}+1}, \end{aligned}$$
(8)

where R(i) is the raw fitness value of a solution, calculated as in SPEA-II. Objective fitness value is divided by “total number of solutions \(+\) 1” to obtain a value \({<}1\). All nondominated solutions have fitness values \({<}1\). Two solutions that have the same raw fitness values are differentiated by their objective fitness values. Thus, more importance is given to boundary solutions. For some objectives, a solution may have worse objective values, but if it has a better objective value for at least one objective, then its objective fitness will be small and that solution can be kept. This method also decreases the run time of the algorithm.

SPEA-II has an archive of fixed size. If the nondominated solutions of the regular and archive populations are less than this fixed size, then dominated solutions are used to fill up the archive population. The dominated solutions are selected according to fitness values that are greater than 1. In this selection, if two solutions have the same raw fitness values, then the objective fitness values determine the selection. However, if the nondominated solutions are greater than the fixed archive size, then some members have to be discarded. In SPEA-II, this truncation is done according to density fitness values. In mSPEA-II, we calculate the objective fitness values instead of density fitness values to decrease the run time. However, using objective fitness values for truncation may not be suitable when all the solutions in the archive set are nondominated. An illustrative example problem is shown in Fig. 3.

Fig. 3
figure 3

An illustrative example when all solutions are nondominated

Full size image

In Fig. 3, all eight solutions are nondominated. \(\min O(7)\) and \(\min O(2)\) are 2. However, solution 2 is responsible for a big region to maintain convergence. Therefore, discarding solutions according to \(\min O(i)\) could avoid the convergence to the true Pareto front. If the algorithm is in a truncation operation, a niching strategy based on the crowding distances can be used to select solutions from less crowded regions. Crowding distance that is the average distance between two solutions on two sides of solution i along each objective is calculated for each solution as in NSGA-II. For all objectives, crowding distance values of boundary solutions are set to infinity. For intermediate solutions, the crowding distance values for each objective are calculated as follows (Deb et al. 2002):

$$\begin{aligned} d_{I_i^m} =\frac{\left( f_m^{I_{i+1}^m }-fm^{I_{i-1}^m }\right) }{\left( f_m^{\max }-f_m^{\min }\right) }, \end{aligned}$$
(9)

where \(I_{i}\) denotes the solution index of the ith member in the list that is obtained by sorting the values of objective m in ascending order, and \(f_m^{I_{i+1}^m}\) and \(f_m^{I_{i-1}^m}\) are the neighbors of the ith member according to the mth objective. \(f_m^{\max }\) and \(f_m^{\min }\) are the maximum and minimum values for the mth objective.

The crowding distance value of one member in a front is measured as follows:

$$\begin{aligned} C(i)=\sum _m {d_{I_i^m}}. \end{aligned}$$

The new fitness value is calculated based on raw fitness and crowding fitness

$$\begin{aligned} F_2 (i)=R(i)+\frac{1}{C(i)+1}, \end{aligned}$$
(10)

where C(i) is the crowding distance value of i.

To summarize, when filling up the mating pool, fitness values that are calculated based on raw and objective fitness are used for binary tournament if the archive size is less than the predefined fixed archive size. If the archive size is greater than the fixed archive size, then fitness values that are calculated based on raw and crowding fitness are used for binary tournament.

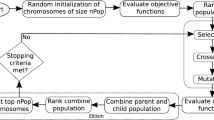
The Algorithm

  1. Step 1:

    Initialization: Generate an initial population \(P_{0}\) and create the empty archive set \(Q_{0}= \{\}\). Set \(t = 0\).

  2. Step 2:

    Selection: Put all nondominated individuals in \(P_{t}\) and \(Q_{t}\) into \(Q_{t+1}\).

  3. Step 3:

    If the size of \(Q_{t+1}\) exceeds a fixed archive size, N, then calculate \(F_{2}\) fitness value of each member and reduce \(Q_{t+1 }\) using the truncation operator. Otherwise, calculate \(F_{1}\) fitness value of each solution and fill \(Q_{t+1}\) with dominated individuals in \(P_{t}\) and \(Q_{t}\).

  4. Step 4:

    Termination: If t \(>\) T or another stopping criterion is satisfied, then set the nondominated individuals in \(Q_{t+1}\) as the resulting set. Stop.

  5. Step 5:

    Fill the mating pool by performing binary tournament selection on \(Q_{t+1}\).

  6. Step 6:

    Variation: Perform crossover and mutation to the mating pool and set offspring population as the new population \(P_{t+1}\). Set \(t =t + 1\) and go to Step 2.

5 Computational experiments

We first test the performance of mSPEA-II on six problem sets. Each problem set consists of nine problems and each problem consists of ten randomly generated problem instances. We run each problem instance five times with different seeds. The problem set properties are given in Table 3. To analyze the effect of the number of facility nodes and number of facilities to be sited on the performance of the algorithms, we define three values for both facility nodes and facilities to be sited in each problem set. For example, for problem set 1, the number of facility nodes is determined as 10, 25 and 50, and number of facilities to be sited is determined as three, five and seven. For each combination of these values, a problem is defined. For ten facility nodes and three, five and seven facilities to be sited, problems 1A, 1B and 1C are defined, respectively. Similarly in problems 1D, 1E and 1F, the number of facility nodes is 25 and numbers of facilities to be sited are three, five and seven, respectively. For 50 facility nodes, problems 1G, 1H and 1I have three, five and seven facilities to be sited, respectively.

Table 3 Problem set characteristics
Full size table

The number of demand nodes changes among problem sets. The region length shows the side length of the plane where facility and demand nodes are generated. For instance, \(x-y\) coordinates are generated from a uniform distribution between 0 and 200 in the first four problem sets. The demand amounts are generated from a uniform distribution in interval [0, 500] for all problem sets. Full coverage and partial coverage distance are taken as 5 and 10 % of the region size, respectively.

To analyze the effect of the number of iterations on the performance of the algorithms, we also change the number of iterations for problem set 4 with 100 facility nodes and five facilities to be sited. We define the number of iterations as 100, 200, 500, 1000 and 2000 while keeping other parameters the same.

We also analyze the effect of computation time on the performance of the algorithms. For problem set 6 with 200 facility nodes and five facilities to be sited, we define computation times as 30, 40, 50 and 60 s. We run the three algorithms and stop them after the same computation time.

5.1 Parameter settings

In the literature, different encodings have been used for the solutions (see Mladenovic et al. 2007 for a review). In binary encoding, the number of potential facilities determines the size of the string and each binary gene represents whether the potential facility is to be sited or not (Hosage and Goodchild 1986). In this encoding, the number of opened facilities is penalized to avoid infeasibility. Computational results show that binary encoding does not result in good results even for small-size problems. In real parameter encoding, the number of facilities to be sited determines the size of the string and each gene represents the index of the opened facility (Alcaraz et al. 2012). We used real parameter encoding, since it is simpler, efficient and never leads to infeasibility. Figure 4 shows an example string where string size is 3 and facilities 5, 9 and 7 are to be opened. The Euclidean distances are considered between the solutions. For SPEA-II, distances between members in the objective space are calculated for the density estimation. In NSGA-II and mSPEA-II, crowding distances are also calculated for the niching mechanism. Since the range of objectives is different, the objective function values are normalized using the estimated maximum possible values in the Pareto front.

Fig. 4
figure 4

Representation of a solution

Full size image

We use uniform crossover with fixed pattern (Villegas et al. 2006; Michalewicz 1996, p.90). In the crossover mechanism, pattern \(\{1,2,1,2,{\ldots }\}\) is used. For example, pattern \(\{1,2,1,2\}\) shows that the first and third genes of the first member, and the second and fourth genes of the second member are taken. However, after crossover, we may need to repair the mechanism. If we have same numbers in the string (solution), this means that a facility is opened twice which is not allowed, and one of these genes should be replaced randomly by another number. We choose archive size as 50 for each problem and MOGA.

As mutation mechanism, single point mutation is used (Mingjun et al. 2004; Iris and Asan 2012). A gene is randomly selected and it is mutated with a probability. After each mutation, the member is again checked for repair. After some preliminary experiments, we determine the mutation probability as 0.3 and the number of iterations as given in Table 3.

5.2 Performance metrics

To compare the performance of the algorithms, three performance metrics are used. These metrics are the hypervolume ratio (HVR), inverted generational distance (IGD) and percentage of found solutions. For the fifth and sixth problem sets, one additional metric, set coverage metric, \(\hbox {C}(A,B)\), is also used. Since we do not know the true Pareto front in these sets, this measure is used to compare the algorithms’ Pareto optimal sets with each other.

HVR is the extension of the hypervolume metric (Zitzler and Thiele 1998). Hypervolume metric calculates the total objective space dominated by a given set of nondominated solutions with respect to a predefined reference point. This metric evaluates both closeness and diversity of the results. The reference point can be determined as the nadir point or worse.

$$\begin{aligned} \hbox {HV}=\hbox {volume}\left( {\bigcup _{i\in A} {v_i }} \right) , \end{aligned}$$
(11)

where A is the nondominated front and \(v_{i}\) is the objective space dominated by solution i with respect to a reference point. HVR measures the ratio of the region enclosed by the nondominated set and the region enclosed by the true Pareto front.

The inverted generational distance (Bosman and Thiernes 2003) is the average Euclidean distance between nondominated solutions and their closest true nondominated front member. Hence, an algorithm with a small IGD is better. IGD is calculated as follows:

$$\begin{aligned} \hbox {IGD}=\frac{1}{\left| A \right| }\sum _{i\in A} {\left( {\mathop {\min }\limits _{j\in \hbox {PF}} \left\| {Z^{i}-Z^{j}} \right\| _2 } \right) }, \end{aligned}$$
(12)

where A denotes the nondominated set generated by MOGA, PF denotes the true Pareto front set and \(\Vert {Z^{i}-Z^{j}}\Vert _2\) represents the Euclidean distance between \(Z^{i}\) and \(Z^{j}\).

The third metric is the percentage of solutions generated by a MOGA in the true Pareto front. Since for the last three problem sets we do not know the true Pareto front, the estimated Pareto front is generated by combining the nondominated solutions of all algorithms. Thus, for the last three problem sets, this metric gives us the contribution of that algorithm when generating the estimated Pareto front.

Set coverage metric \(\hbox {C}(A, B)\) (Zitzler and Thiele 1998) calculates the fraction of B dominated by A.

$$\begin{aligned} \hbox {C}(A,B)=\frac{\left| {\left\{ {b\in B} \right\} \left| {\exists a\in A:a\succ b} \right. } \right| }{\left| B \right| }, \end{aligned}$$
(13)

where A denotes the Pareto front generated by algorithm A and B denotes the Pareto front generated by algorithm B. \(\hbox {C}(A, B) =1\) means that all members in B are dominated by A. \(\hbox {C}(A,B) =0\) represents the situation in which no individual in B is dominated by A. The domination operator is not a symmetric operator. Thus, C(A, B) is not necessarily equal to \(1- \hbox {C}(A, B)\).

5.3 Computational results

Problem sets 1, 2 and 3 are solved by the \(\varepsilon \)-constraint method (Haimes et al. 1971) with GAMS 2.25 Cplex solver (Brooke et al. 1992) on a computer Intel Pentium IV with 1.8 GHz and 512 MB RAM. The true Pareto optimal front is found for these problem sets. However, problem sets 4, 5 and 6 cannot be solved by the \(\varepsilon \)-constraint method within 24 h. For these problems, all run results for the three MOGAs are combined and an estimated Pareto front is generated by combining the nondominated results of the three MOGAs.

For each problem instance, NSGA-II, SPEA-II and mSPEA-II are run five times using different seeds. For each run, the HVR, IGD and percentage of found solutions metrics are calculated. The average metric values and standard deviations of problems are given in Table 4. The values in the parenthesis in the second column of Table 4 correspond to the number of facility nodes and number of facilities to be sited.

Table 4 Computational results
Full size table

A point a little worse than the nadir point is selected as the reference point for HVR measure. The range of HVR values is approximately between 0.90 and 1. For all problem sets, the average HVR values of mSPEA-II are greater than those of the other algorithms. Also, the standard deviations of the HVR values of mSPEA-II are very small and less than or equal to those of the other algorithms in 47 out of 54 problems. These results show that mSPEA-II approximates the true Pareto front better than the others and the HVR values of mSPEA-II are more consistent than those of the other algorithms.

The IGD results are normalized values. Objective function values are scaled since their ranges are different. The IGD average values of mSPEA-II are better than those of the others. This shows that the generated nondominated solutions of mSPEA-II are closer to the true Pareto front than those of the other algorithms.

If the algorithms are compared based on the percentage of found solutions, mSPEA-II generates more nondominated solutions than the other algorithms. For small-size problems, such as in problem set 1 with ten facility nodes, the values are close to each other for all algorithms. However, for the other problems, mSPEA-II outperforms the other algorithms significantly. In problem sets 1–3, mSPEA-II finds 61.67 %, SPEA-II finds 46.95 % and NSGA-II finds 44.77 % of true Pareto front solutions on average. For problem sets 4–6, this metric gives the contribution of the algorithm to the estimated Pareto front, since the true Pareto fronts are unknown for these problem sets. In these problem sets, mSPEA-II finds 61.48 %, SPEA-II finds 36.91 % and NSGA-II finds 18.48 % of estimated Pareto front solutions on average.

We evaluate the effect of the parameters, namely the number of facility nodes and number of facilities to be sited on the performance of MOGAs in Table 4.

In each problem set for a given number of facility nodes, as the number of facilities to be sited increases, the number of efficient solutions increases and as a result the performance of all three MOGAs decreases. However, decrease in the performance of mSPEA-II is less compared to other MOGAs and mSPEA-II outperforms the other algorithms. For instance, in problems 3G and 3I, the number of facility nodes is 100 and the number of facilities to be sited are five and nine. Increasing the number of facilities to be sited from 5 (problem 3G) to 9 (problem 3I) decreases HVR values from 0.958 to 0.934 in NSGA-II, 0.966 to 0.944 in SPEA-II and 0.978 to 0.974 in mSPEA-II. The IGD values increase from 0.006 to 0.014 in NSGA-II, 0.004 to 0.010 in SPEA-II and remain the same (0.004) in mSPEA-II. In terms of percentage of found solutions, mSPEA-II results are significantly better than NSGA-II and SPEA-II when we increase the number of facilities to be sited. For the above problems, the percentage of found solutions decreases from 38.8 to 18.8 % in NSGA-II, 41.1 to 22.1 % in SPEA-II and 54.2 to 48.8 % in mSPEA-II.

When we analyze the effect of the number of facilities to be sited in large-size problems, we again observe that mSPEA-II performs better than NSGA-II and SPEA-II with respect to all performance measures. For example, in problem set 6 for problems with 150 facility nodes, if the number of facilities to be sited is changed from five (problem set 6A) to nine (problem set 6C), the percentage of found solutions decreases from 22.4 to 17.8 % in NSGA-II, 53.2 to 39.6 % in SPEA-II and 69.8 to 68.2 % in mSPEA-II.

We also analyze the effect of the number of facility nodes on the performance of MOGAs. I For any problem set with a given number of facilities to be sited, increase in the number of facility nodes decreases the performance of all MOGAs. For instance, for problem set 1 with three facilities to be sited, increasing the number of facility nodes from 10 to 50 (problems 1A and 1G) decreases the percentage of found solutions from 94.4 to 44.2 % in NSGA-II, 93.3 to 47.6 % in SPEA-II and 95.5 to 62.4 % in mSPEA-II. The amount of decrease is less for mSPEA-II compared to those of other MOGAs. The performance of mSPEA-II is also better in large-size problems. For instance, in problem set 6, with five facilities to be sited, increasing the number of facility nodes from 150 to 250 (problems 6A, 6G) decreases the percentage of found solutions from 22.4 to 11.2 % in NSGA-II, 53.2 to 33.2 % in SPEA-II and 69.8 to 62.2 % in mSPEA-II.

Problem 4D is solved with a different number of iterations. The estimated Pareto fronts of the problems are obtained by combining the results of all solutions generated by solving different MOGAs with different number of iterations, since the true Pareto front of problem set 4 is unknown. The results of the performance metrics are presented in Table 5.

Table 5 Results of problem 4D with different numbers of iterations
Full size table

In all problems, mSPEA-II outperforms NSGA-II and SPEA-II. With 100 iterations, NSGA-II outperforms SPEA-II. In the rest of the problem sets, SPEA-II outperforms NSGA-II with respect to HVR and the percentage of found solutions. The results show that when the number of iterations is increased from 100 to 2000, the performances of MOGAs improve on all metrics as expected. However, the amount of improvement decreases as the number of iterations increases.

To evaluate the performance of mSPEA-II with constant computation time, we run the three MOGAs for problem 6D at a predetermined time. The computation times are set as 30, 40, 50 and 60 s. Table 6 shows the results of each MOGA with different computation times. Since the true Pareto front is unknown for problem set 6, we combine all generated nondominated solutions and estimate the true Pareto front. The performance metric values are computed with respect to the estimated Pareto fronts. For each computation time, mSPEA-II outperforms both NSGA-II and SPEA-II with respect to all performance metrics. For instance, when computation time is set as 30 s, mSPEA-II finds 25.08 % of the estimated Pareto front; however, SPEA-II and NSGA-II generate 10.80 and 12.05 % of it, respectively. The results show that for 30 and 40 s, NSGA-II performs better than SPEA-II; for the rest, SPEA-II performs better than NSGA-II. As the computation time increases, the performance of MOGAs increases as expected.

Table 6 Results of problem 6D with different computation times
Full size table

An illustration of nondominated solutions found by the MOGAs and the generated true Pareto front in problem 3D is given in Fig. 5. The nondominated fronts are the first run results of MOGAs. Some solutions of the true Pareto front cannot be generated by any of the MOGAs.

Fig. 5
figure 5

Nondominated fronts generated by NSGA-II, SPEA-II and mSPEA-II in problem set 3D

Full size image

The set coverage values for problem sets 5 and 6 are presented in Table 7. In the \(\hbox {C}(A,B)\) metric, A corresponds to a row of the table and B corresponds to a column of the table. This metric compares two algorithms.

Table 7 Average set coverage metric values for problem sets 5 and 6
Full size table

In problems sets 5 and 6, solutions found by NSGA-II dominates at most 5 % of solutions generated by SPEA-II and mSPEA-II. This shows that most of the solutions of NSGA-II have worse objective function values than those of SPEA-II and mSPEA-II. On the other hand, SPEA-II solutions dominate NSGA-II solutions between 15 % at the minimum and 64 % at the maximum in problem set 5. The same measure changes between 23 and 75 % in problem set 6. mSPEA-II’s performance is better than that of SPEA-II, and the set coverage metric values for mSPEA-II against NSGA-II changes between 31 and 70 % in problem set 5 and between 28 and 85 % in problem set 6. When we compare SPEA-II and mSPEA-II, SPEA-II solutions dominate mSPEA-II solutions, 1 % at the minimum and 14 % at the maximum for problem sets 5 and 6. However, the set coverage metric values for mSPEA-II against SPEA-II changes between 16 and 34 % in problem set 5 and between 10 and 35 % in problem set 6. Computational experiments show that mSPEA-II outperforms the other algorithms and the second best-performing algorithm is SPEA-II.

Also in any problem set with a given number of facility nodes, as the number of facilities to be sited increases, the average set coverage metric values of mSPAE-II against SPEA-II improve in all problems, and against NSGA-II improve in all problems except problem sets 6B and 6C. This shows that as the string size increases, the performance of the mSPEA-II improves.

Figure 6 shows the estimated true Pareto front of a problem in problem 4E. There are 14 nondominated solutions in the estimated true Pareto front. This front is created by combining all run results of the three MOGAs. mSPEA-II generates all of them, while SPEA-II generates ten of them and NSGA-II only four.

Fig. 6
figure 6

Estimated Pareto front of a sample problem in problem set 4E

Full size image

To check whether a significant difference exists between mSPEA-II and the other two algorithms, we test the following hypothesis at 99 % significance level. In a statistical test, only the HVR is used. The Wilcoxon non-parametric statistical test is performed, and p values are calculated to determine the better-performing algorithm as given in Tables 8 and 9.

$$\begin{aligned}&H_0 :\mu _{\mathrm{hvr}}^{\mathrm{mSPEA-II}} =\mu _{\mathrm{hvr}}^O \\&H_1 :\mu _{\mathrm{hvr}}^{\mathrm{mSPEA-II}} \ne \mu _{\mathrm{hvr}}^O, \end{aligned}$$

where \(\mu _{\mathrm{hvr}}^{\mathrm{mSPEA-II}} \) is the mean of mSPEA-II and \(\mu _{\mathrm{hvr}}^O\) is the mean of NSGA-II or SPEA-II.

Table 8 Wilcoxon test results of the HVR metric between NSGA-II and mSPEA-II
Full size table
Table 9 Wilcoxon test results of the HVR metric between SPEA-II and mSPEA-II
Full size table

There is not a statistically significant difference in problem sets 1A, 1B, 1C, 1D, 2A, 2B, 2C between NSGA-II and mSPEA-II at 99 % significance level. Actually, the size of these problems is very small and the results of all the algorithms are close to each other. Except for these seven problems, mSPEA-II performs significantly better than NSGA-II. Similarly, mSPEA-II outperforms SPEA-II significantly in all problems except these seven problems and problem 4C. However, for problem 4C, there is significant difference between SPEA-II and mSPEA-II at 95 % significance level.

Table 10 reports the average number of solutions in the true Pareto front for problem sets 1, 2 and 3 and run times of the algorithms for all problem sets. For each problem, mSPEA-II and NSGA-II run times are fairly close to each other. SPEA-II run times are greater than those of the other two algorithms for all problems.

Table 10 Average run times of algorithms (s)
Full size table

We choose archive size as 50 for each problem and for each MOGA. In all problem sets, the generated nondominated solutions are less than 50 for each MOGA. Thus in SPEA-II, the truncation operation according to density fitness value is not used in these problems. Thus, the computational complexity of SPEA-II is not significantly higher than that of NSGA-II and mSPEA-II as expected. Only the distance calculation of each solution increases the SPEA-II run times as compared to NSGA-II and mSPEA-II.

6 Conclusion

In this study, we formulate a bi-objective model that maximizes total coverage and minimizes the maximum distance between uncovered demands and their nearest facilities. The model is especially useful for emergency service location problems where all demand nodes are not covered by facilities.

We developed a MOGA, called mSPEA-II, to solve our model. In this algorithm, we modify the fitness assignment of SPEA-II and use the crowding distance of NSGA-II to eliminate the drawbacks of NSGA-II and SPEA-II in reaching the true Pareto front. We tested the performance of mSPEA-II on randomly generated problems and compared the results with those of NSGA-II and SPEA-II. Our experimental results show that the mSPEA-II algorithm performs better than the others. For small problems, the results of these MOGAs are close to each other, but on average mSPEA-II performs better. As the number of facilities to be sited or the number of facility nodes increases, the computational complexity of the problems increases. This affects the performance of all MOGAs. However, decrease in the performance of mSPEA-II is less compared to those of NSGA-II and SPEA-II. Also, the run time performance of mSPEA-II is better than that of SPEA-II, and approximately the same as that of NSGA-II.

An area for future research direction may be to develop a preference-based MOGA to find the best solution for the DM. We may also apply mSPEA-II to other combinatorial optimization problems. Another research direction may be to extend the bi-objective model to handle capacity restrictions on the facilities.