Why Clusters and Other Patterns Can Seem to be Found in Analyses of High-Dimensional Data

Abstract

Recent papers by Cardini et al. (Evolutionary Biology 46:307–316, 2019) and Bookstein (Evolutionary Biology 46:271–302, 2019) show that, when there are many variables and when sample sizes are small, scatterplots made using the between-groups principal components analysis method can appear to indicate clear group differences with little or no overlap between samples even though the samples are all drawn from a single multivariate normally distributed population. The corresponding scatterplots made after a canonical variates analysis (CVA) show an even more extreme separation of groups even though the usual test statistics yield the correct uniform distribution of probabilities. Users of CVA are usually concerned about the problems of small sample sizes and correlated variables but the problems discussed here are present even for large samples and uncorrelated variables. Some less-appreciated properties of sampling from high-dimensional spaces and the “curse of dimensionality” are reviewed to find a simple explanation for these problems. The ratio of variables to sample size is a useful index to predict when false clusters and these other problems may arise. While dependent upon the same variables, this index is not based on Marchenko and Pastur (Mathematics of the USSR–Sbornik 1:457–483, 1967) as discussed by Bookstein (Evolutionary Biology 44:522–541, 2017). It is also shown that multiple regression analysis can have related problems when there are large numbers of independent variables. The explanation for these problems is an incompatibility of showing both points separated by their full p-dimensional distances and low-dimensional projections of points in the same plot. Some implications for geometric morphometric and other multivariate analyses in biology are also discussed.

Introduction

The papers by Cardini et al. (2019) and Bookstein (2019) well-document a problem in interpreting scatterplots made after using the between-groups Principal Components analysis (bgPCA) method. When sample sizes are small relative to the number of variables used in a study repeated samples taken from the same population can appear distinct and may not even overlap. The papers cited above and Fig. 1 shows examples for samples from a standard multivariate normally distributed data randomly divided into equal-sized groups. The scatterplots seem to suggest that the samples were taken from populations with quite different means even though the samples were all drawn from the same standard multivariate normal distribution. The problem is quite general as the “groups” could correspond to different species that one would like to distinguish, treatment and control groups, specimens from different habitats, males and females, etc. With the availability of newer technologies, investigators are now able to obtain data on many variables and that can give rise to the problems discussed in this paper— especially when measurements cannot be collected from comparably large numbers of specimens. For example, in many applications using geometric morphometric based on 3-dimensional landmarks and semilandmarks the number of shape variables can easily be much larger that the number of available specimens. It can also be a problem in ecology when, for example, many environmental variables are used to predict the abundance of a species or in genetic studies using many genetic markers.

Fig. 1

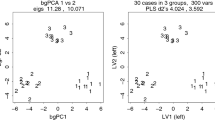
Examples of the results of applying bgPCA to random data, with n_i = 8 and p = 15 variables. The four plots are the first four set of samples obtained in a sampling experiment. Convex hulls are shown to indicate group membership and the numbered red points show the locations of the group means. See Cardini et al. (2019) and Bookstein (2019) for more extreme examples

The purpose of the present note is not to propose a solution for the problem but rather to provide an explanation for why there is this problem with statistical analyses of multivariate data. While it is easiest to find examples of the problem when using high-dimensional data, Figs. 1 and 3 show that examples can also be found using relatively few variables when sample sizes are small relative to the number of variables. Some properties are related to what is often called the “curse of dimensionality” (Bellman 1957). The problem is more general than the comparison of groups using the bgPCA method. It needs to be taken into consideration in evolutionary biology and other fields especially when many variables are used. It is particularly a problem when sample sizes are not large relative to the number of variables used. Cardini and Polly (2020) recently proposed a cross-validated form of bgPCA, XbgPCA. This procedure reduces the apparent magnitude of the false distinctiveness of the groups being compared. Some properties of the bgPCA, CVA, and XbgPCA methods are described below followed by a description of some perhaps counter-intuitive properties of high-dimensional spaces. Finally, these properties are used to explain when groups (even artificial ones) sampled from the same population are expected to seem very distinct when analyzing high-dimensional data. Related effects of high dimensions on multiple regression analysis are also discussed.

Note all of the sampling experiments described below used random samples of size n_i from a single p or q-dimensional standard multivariate normal (multivariate Gaussian) distribution with mean μ=0 (a vector of p zeros) and covariance matrix ∑ = I, where I is a p × p identity matrix. For the bgPCA, CVA, and XbgPCA analyses g samples of size n_i were used. Only the equal sample size case is considered here so the total sample size is n = gn_i. Using unequal sample sizes introduces some interesting additional complexities that may further mislead an investigator (Bookstein 2019). For example, means from smaller samples will tend be shown as more distinct from groups that are based on larger sample sizes (because means with smaller sample sizes have larger standard errors) and thus randomly deviate further from the true mean. The multivariate normal distribution was used for the sampling experiments not because it was realistic for biological data but because it corresponds to simple multidimensional cloud of points with no patterns or dependencies among variables, and no structure other than having a higher density of points near its mean. In an actual study the variables should be carefully selected to capture the variation that was interest and would usually be expected to be correlated, have unequal variances, and other complexities which, for simplicity, are ignored in the present paper.

Between-Groups PCA (bgPCA)

This method was originally proposed by Yendle and MacFie (1989) as an alternative to Canonical Variate Analysis (CVA, see below) to produce a plot showing variation within and among groups when the numbers of variables is too large to allow the use of CVA (CVA is undefined when $p > \sum {n_{i} - g}$). Even with adequate sample sizes, there are often practical problems in the application of CVA because biological variables are usually correlated (often highly correlated). The bgPCA method can still be used in such cases.

One of the attractions of the bgPCA method is that the computations are simple and seem easy to understand.

• (1) Compute the among-group covariance matrix, ${\mathbf{A}} = \frac{1}{v}\sum\limits_{i}^{g} {n_{i} (\overline{{\mathbf{x}}}_{i} } - \bar{\bar{{\mathbf{x}}}} )^{t} \,(\overline{{\mathbf{x}}}_{i} - \bar{\bar{{\mathbf{x}}}} )$, where $v = \sum {n_{i} } - g$, (the number of degrees of freedom), $\overline{{\mathbf{x}}}_{i}$ is the row vector for the mean of the ith group, and $\bar{\bar{{\mathbf{x}}}}$ is the grand mean, again as a row vector. The superscript “t” indicates matrix transpose. While this equation weights the mean for each group by its sample size, that may not be appropriate for all applications, see Bookstein (2019).

• (2) Compute the eigenvectors, E, of A (just the first g-1 eigenvectors because there can be at most g-1 eigenvalues greater than 0). Thus, all of the variation among the g means is perfectly captured by the g-1 dimensions.

• (3) Project the group means and the original samples onto these vectors and construct a scatterplot of these projections.

As documented by Cardini et al. (2019) and Bookstein (2019), the scatterplots produced by this method often show distinct differences between groups (often with little or no overlap between groups) for data divided at random into groups. The examples in Fig. 1 show the groups looking much more distinct than what would expect intuitively for samples with no true differences among the means. Note that relatively few variables and sample sizes are used in these examples to show that it is not just a problem when exceptionally large numbers of variables are used as perhaps implied by Cardini et al. (2019) and Bookstein (2019). The number of variables was also kept small in these examples so that the same data could also be used as examples for the CVA method. The reason for the false distinctiveness of groups was attributed by Cardini et al. (2019) as mostly due to the fact that while the magnitudes of the differences among the means of the g groups can be shown perfectly in g-1 dimensions, only a fraction of the variation in the min (p, n−g) dimensions of within-groups variation can be shown in just g-1 dimensions. If the within-group variation is underrepresented, then the relative amount of among-group variation will seem much larger than it should be. While true, a more fundamental reason will be described below. The method proposed by Dhillon et al. (2002) should have a similar problem because their projections are also only based on the observed differences among the observed means.

In order to further investigate the patterns of distinctiveness of groups for various combinations of p and n_i, it is convenient to construct coefficients that measures the degree of overlap between pairs of samples. Two coefficients are considered here. Because the concern here is only with the special case where ∑ = I, a simple choice is the $\overline{O}_{ij}$ coefficient used by Cardini et al. (2019). It gives the average proportion of points in one group that are actually closer to the mean of a second group than they are to the mean of their own group. With broad overlap a point is about equally likely to be closest to either mean so the maximum value is 0.5. Another convenient coefficient, $\overline{H}_{ij}$, is the average proportion of points in a group that are also within the convex hull of a second group. The maximum value of this coefficient is 1.0 because with complete overlap all points in one group would also be within the convex hull of the other group. In both cases low values imply less overlap and hence more distinct appearing groups. Both plots in Fig. 2 show the same sharp reduction in overlap of groups as p increases and n_i decreases.

Fig. 2

Reduction of overlap between groups as a function of sample size within each group and the number of variables. a Proportion, $\overline{O}_{ij}$, of points in one sample that are closer to the mean of another sample. Regions where the height of the surface is near zero correspond to cases where groups have little or no overlap. The maximum $\overline{O}_{ij}$ is 0.5 for the case where the sample means are essentially identical so that points are almost equally likely to be closest to either mean. b Proportion of points in a sample that also belong to the convex hull of another sample. The maximum possible $\overline{H}_{ij}$ is 1.0 corresponding to the case in which all the points in one group are also within the convex hull of the other group. Plots based on 50 replications for each combination of n_i and p

Canonical Variates Analysis (CVA)

This method was originally proposed by Rao (1948) and is sometimes called multiple-group discriminant analysis or multi-class linear discriminant analysis. It is a standard multivariate method that has often been used in evolutionary biology. For example, Klingenberg and Monteiro (2005), Cardini (2003), Mitteroecker and Bookstein (2011), Rohlf et al. (1996), and many others. It can be viewed as a generalization of the method of linear discriminant functions (Fisher 1936). While the computations are usually defined as a single main operation using the eigenvectors of the AW^-1 matrix (where W is the average within-groups covariance matrix and A is the among groups covariance matrix is used by the bgPCA method). It is helpful here to note that the results can also be described as a 2-step process: a standardization of the data using inversely weighted eigenvectors of the pooled within-group covariance matrix followed by applying bgPCA to this transformed data as follows:

• 1. Standardize the data by multiplying the data matrices, X_i, for each group by the matrix ${\mathbf{E\Lambda }}^{ - {1/2}}$, where ${{\varvec{\Lambda}}}$ is the matrix of eigenvalues and E is the matrix of eigenvectors of the pooled within-group covariance matrix, W. Note that using this step requires that none of the eigenvalues are equal to or even just very close to zero. The standardized data will have an average within-group covariance matrix equal to an identity matrix.

• 2. Perform a bgPCA using this transformed data.

Campbell and Atchley (1981) and Klingenberg and Monteiro (2005) for a description of this approach. What the multiplication by ${\mathbf{E\Lambda }}^{ - {1/2}}$ does is to uniformly stretch the space in directions in which there is less variation within groups and to compress the space in directions in which there is more variation within groups so that the average within-group variances will all be equal to 1. In the present example the true amount of variation is the same in all directions but by chance there will be differences in the amount of variation in different variables. The standardization step removes those differences. It also rotates the space so that the variables are on average uncorrelated within groups. The usual concern about the practical application of this method is that it tends to overfit when the variables are too highly correlated or have small variances within groups and thus some of the eigenvalues will be very small. There has been much work on practical methods to solve this problem. See, for example, Nørgaard et al. (2006). Domingos (2012) discuss this in the context of machine learning where there are large numbers of variables. He relates this to the “curse of dimensionality” (Bellman 1961b). He also suggests that there is a “blessing of non-uniformity” meaning that due to correlations the space is effectively not as high dimensional as it seems (however, this means that the covariance matrix will tend to be singular and require special methods so it is, perhaps, not really a “blessing”). Many, see for example, Campbell (1979), have proposed alternatives to the standard procedures such as using generalized inverses and resampling methods.. However, that is not the problem of interest here where we are only considering samples from a single standard multivariate normal distribution. However, Bookstein (2017) shows that even for such data the theorem by Marchenko and Pastur (1967) predicts that as p and n increase to infinity (but with their ratio y = p/n fixed at some constant value), the ratio, $\lambda_{1} /\lambda_{p}$ , of the largest to the smallest eigenvalues of the covariance matrix is expected to approach ${{\left( {1 + \sqrt y } \right)} \mathord{\left/ {\vphantom {{\left( {1 + \sqrt y } \right)} {\left( {1 - \sqrt y } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \sqrt y } \right)}}$. The ${{\lambda_{1} } \mathord{\left/ {\vphantom {{\lambda_{1} } {\lambda_{p} }}} \right. \kern-\nulldelimiterspace} {\lambda_{p} }}$ ratio is called the condition number for a matrix and large values indicate that a matrix will be difficult to invert accurately. Thus, problems are expected when using large numbers of variables even when analyzing such ideal independent multivariate normally distributed data.

Figure 3 shows examples of CVA scatterplots using the same data used in Fig. 1. The apparent clustering of points around their group means is more extreme than found for the bgPCA method for the same data. If one were to use these CV axes as variables to ascertain group membership for new samples in a taxonomic study, then one would discover that one could not predict group membership nearly as accurately as implied by the scatterplot. It seems that correcting for chance differences in variation in different directions exaggerates the problem found using the bgPCA method. Surfaces for the overlap statistics, such as shown in Fig. 2 for the bgPCA method, would decline even faster as p increased and n_i decreased (but with the constraint that n-g > p). One should not be surprised by this increased separation as CVA is designed to provide a projection of the multivariate space that maximizes any observed differences (even those just due to chance) among the means relative to the variation within the groups.

Fig. 3

Examples of CVA applied to the same data (with n_i = 8 and p = 15 variables) as in Fig. 1

More extensive sampling experiments with the same sample sizes and numbers of variables show, see Fig. 4, that the distributions of probabilities for several standard test criteria are consistent with the expected uniform distributions. Thus, despite how unusually distinct the groups look in Fig. 3, they are consistent with what one should expect by chance when there are no true differences among the sample means. It is our visual expectation of that is wrong. Note: these probabilities were computed using the full p-dimensional space not its projection into the g-1-dimensional space of the among group variation. Doing so would greatly mislead and would not yield the expected uniform distribution of probabilities.

Fig. 4

Histograms of probability, P, values using four standard MANOVA test criteria. Based on sampling experiments such as shown in Fig. 1 but replicated 10,000 times. This shows that results such as shown in Fig. 3 are not unexpected

As Kovarovic et al. (2011) noticed, artificially adding random variables to a study using discriminant analysis can seem to improve the separation of groups. They found (p. 3012) that: “increasing the number of predictors may increase … group separation in scatterplots of non-cross-validated DFAs, even if those predictors are random numbers which do not add any relevant information on group differences”. This is expected because having some “real variables” in a study does not alter the fact that using just large numbers of random variables can, as shown in Fig. 3, give the impression that even randomly defined groups are distinct.

Cross-Validated bgPCA (XbgPCA)

Cardini and Polly (2020) suggest using a leave-one-out cross validated bgPCA as a way to correct for the false impression of group differences such as illustrated in Fig. 1. This method is performed by separately determining the coordinates of each point in the scatterplot by projecting each observation onto bgPCA axes that were computed using group means that ignored that observation. This increases the computational effort but that is not a problem these days. Several examples are shown in Fig. 5. This procedure adds some noise to the location of each point and greatly reduces the apparent distinctiveness of the groups. While, compared to Fig. 1, the distinctness of the groups is greatly reduced in the scatterplots, an effect can still be detected for some combinations of n_i and p. Figure 6 shows plots of overlap statistics used in Fig. 2 for this method. The range of sample sizes considered was reduced from that of Fig. 2 to better show the reduced overlap for smaller sample sizes. Figure 7 shows several examples of scatterplots using smaller sample sizes that Fig. 6 shows will tend to result in less overlap between groups especially for the $\overline{H}_{ij}$ criterion. Note: as discussed later, this criticism is not entirely fair because, even in the original full p-dimensional space, samples of smaller size will tend to overlap less (see Figs. S1 and S2 in the supplement).

Fig. 5

Examples of the use of an XbgPCA using samples of data such as used in Fig. 1. The false distinctiveness of groups is much reduced and look about as one might expect for three samples from the same population

Fig. 6

Average degree of overlap between samples as a function of sample size within each group and the number of variables as in Fig. 2 but using a leave-one-out cross-validated bgPCA, XbgPCA, as in Cardini and Polly (2020). a Proportion of points in one sample that are closer to the mean of another sample. The maximum expected is 0.5 for the case where the sample means are essentially identical so that points are almost equally likely to be closest to either mean. b Proportion of points in a sample that also below to the convex hull of another sample. The convex hull is computed in the g-1-dimensional space constructed by the bgPCA method. The maximum possible value is 1.0 corresponding to the situation in which the two convex hulls coincide so that all points are within both convex hulls. Based on 50 replications for each combination of n_i and p

Fig. 7

Examples of scatterplots using the leave-one-out cross validated bgPCA suggested by Cardini and Polly (2020). Convex hulls are shown to enclose the range of variation in each sample and the numbered filled dots show the locations of the group means. A sample size of n_i = 5 and p = 15 dimensions were used because Fig. 6 suggested there would be less overlap for this combination of n_i and p. While there is overlap as in Fig. 5, the groups sometimes overlap little or not at all. However, the XbgPCA scatterplots seem much less misleading than those produced by bgPCA

Multiple Regression Analysis

Testing for differences among group means using anova or MANOVA is just a special case of multiple regression or multivariate multiple regression. That suggests that multiple regressions with large numbers, k, of independent variables relative to the sample size may also have related problems. Let ${\mathbf{Y}}$ be an n × p matrix (or vector if p = 1) of n observations on p dependent variables and ${\mathbf{X}}$ an n × (q + 1) matrix of q independent variables plus a dummy variable with all values equal to 1 so as to include the mean or intercept in the regression model. It is convenient to write the regression equations in terms of a “hat” matrix, ${\mathbf{H}} = {\mathbf{X}}\left( {{\mathbf{X}}^{t} {\mathbf{X}}} \right)^{ - 1} {\mathbf{X}}^{t}$ so that the predicted values, ${\hat{\mathbf{Y}}}$, of the dependent variables can be computed as ${\hat{\mathbf{Y}}} = {\mathbf{HY}}$(it puts a “hat” on the matrix ${\mathbf{Y}}$, and thus its name). This equation shows that the predicted values, like the scores along the PC axes in a PCA or the canonical axes in a CVA, can be visualized as a projection from a higher to a lower dimensional space (from q + 1 dimensions down to p dimensions). In this case from a space of q independent variables to a space of p dependent variables. An important difference is that the ${\mathbf{H}}$ matrix will not usually be an orthogonal matrix as it is in a PCA. Figure 8a shows a typical histogram from a sampling experiment using n = 600 samples of q = 450 independent variables (just normally distributed random numbers) and a single dummy dependent variable with half the values set to -1 and the other half set to 1 (as if one wished to predict which of two groups an observation belongs). Plotting a histogram of the ${\hat{\mathbf{Y}}}$ values (see Fig. 8a) suggests that one can make good predictions as there is only a small area of overlap between the ${\hat{\mathbf{Y}}}$ values for the two groups. Figure 8b shows the expected uniform distribution of P-values from tests for each of the 10,000 replications of this sampling experiment. Again, a plot of the projections can be very misleading even though the usual tests yield the correct distribution of probabilities. The degree of overlap is a function of q, n, and p. However, the sample size cannot be less than q in order to be able to invert the ${\mathbf{X}}^{t} {\mathbf{X}}$ matrix.

Fig. 8

Results of a sampling experiment using regression to predict membership in one of two groups. a Example of a histogram of $\hat{Y}$ values from a regression of a dummy variable consisting of 300 “−1” values followed by 300 “1” values. The matrix of independent variables was a 600 × 450 matrix of normally distributed random numbers. The degree of separation of the two “groups” is typical of the results. b Histogram of probability, P, values for tests of the regression coefficient in 10,000 replications of the sampling experiment described in (a). As expected, the distribution is close to uniform

One can also perform a similar experiment for 3 groups by using two dependent variables with values corresponding to codes for differences among three groups (e.g., such as 1,1,−2 and 1,−1,0). Scatterplots of the ${\hat{\mathbf{Y}}}$ values for two sampling experiments are given in Fig. 9 for two sample sizes. The scatterplots resemble those shown earlier for the bgPCA method.

Fig. 9

Results of sampling experiments with two dependent variables that encode three groups. Filled dots show the locations of the means. One dependent variable used values (1, 1,−2) and the other used (1, −1, 0).The matrix, X, of independent variables consisted of 450 normally distributed random variables (a). Scatterplot of ${\hat{\mathbf{y}}}_{1}$ vs ${\hat{\mathbf{y}}}_{2}$ based on a sample size of 600. b Scatterplot based on a sample size of 500. Note that the groups appear more distinct than in a which was based on a larger sample size

There can also be problems for the more usual case of predicting a continuous dependent variable using a suite of continuous independent variables. Figure 10 shows the results of a sampling experiment predicting a dependent variable that is just the sequential observation number. The prediction would appear to be even better if smaller sample sizes were used. One intuitive explanation for this phenomenon is that if you use enough random variables then by chance some may happen to correlate with any given dependent variable. The likelihood of this is increased by the fact a multiple regression analysis is a powerful technique that is able to consider all possible linear combinations of the independent variables and thus it may be able to find combinations of variables that appear to be predictive – at least in the given sample though they are not expected to be predictive in new samples.

Fig. 10

Regression of y on X where y is a vector with the ith element equal to i and X is a matrix of independent variables and consists of 600 samples of 450 normally distributed random numbers. a An example plot of y vs.${\hat{\mathbf{y}}}$. b Distribution of probability, P, values from tests for each if the 10,000 replicates of the sampling experiment. As expected, the distribution is close to uniform

Some Properties of High-Dimensional Spaces

While the use of resampling suggested by Cardini and Polly (2020) seems to mostly solve the problem of the bgPCA method showing false distinctness of random groups (at least for larger sample sizes), there is a need to better understand why the bgPCA method shows such false distinctiveness of random groups. The explanation lies in some mathematical and statistical properties of high-dimensional spaces. Some well-established but less well-known (at least among biologists) properties of high dimensional spaces are described below. The term “curse of dimensionality” (Bellman 1961a) is often used to refer to those properties that make computations more difficult and harder to interpret in higher dimensions. Many properties may seem surprising at first.

Volumes of Hyperspheres

First, consider the volume of a unit p-ball (a p-dimensional hypersphere of radius, r = 1) in a space of p dimensions (also called an n-ball). In one dimension it would degenerate to a line from -1 to 1 with a length of 2. In two dimensions it is a circle with area $V_{2} = \pi r^{2}$, which is just $\pi$ for a unit circle because r = 1. The volume of a unit sphere is $V_{3} = \tfrac{4}{3}\pi$. For higher dimensions, the volume of a unit p-ball is.

$V_{p} = \frac{{\pi^{{{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-\nulldelimiterspace} 2}}} }}{{\left( {{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-\nulldelimiterspace} 2}} \right)!}}$ for p even and $V_{p} = \frac{{2\left( {\tfrac{p - 1}{2}} \right)!\left( {4\pi } \right)^{{\tfrac{p - 1}{2}}} }}{p!}$ for p odd.

Figure 11a is a plot of the p-volume as a function of p ranging from 1 to 20. The volume increases at first but then, surprisingly, it reaches a maximum at p = 5 and then rapidly decreases. The volume of a p-ball is important here because this quantity is needed below to compute the expected volume of a convex hull for a sample of n points from a p-dimensional multivariate normal distribution.

Fig. 11

a Volume of a unit hypersphere as a function of dimensionality. Maximum is at p = 5. b The expected volume of a convex hull for a sample of size n from a p-dimensional standard multivariate normal distribution. For a given sample size, the volume increases and then decreases as the number of dimensions increase. It uniformally increases as n_i is increased. Note that the axes are rotated relative to earlier surface plots. Note also that the convex hull is computed in the g-1 dimensional space of differences among means and not the full p-dimensional space which would require n_i > p

In contrast to the unit p-ball, the volume of a unit p-cube (each side of length 1) stays the same because 1^p = 1. However, a p-cube with each side ranging from -1 to 1 is more relevant here as it just encloses a unit p-ball centered on the origin. Its volume, $2^{p}$, increases without bound. Thus, while one can visualize the unit p-ball just fitting within the cube ranging from -1 to 1 along each side, the p-ball would take up a rapidly decreasing proportion of the volume of the p-cube. However, the p-ball is not “shrinking” as p increases because its radius is still 1 and it still touches the center of the faces of the p-cube it is embedded in. Some, for example Lamb (2016), have suggested that one should think of the p-ball as becoming increasingly “spiky” because while the p-ball touches the faces of the p-cube as its volume shrinks. The corners take up a higher and higher proportion of the volume of the p-cube as p increases. Thus, the p-ball extends less and less into the corners.

Expected Volumes of Convex Hulls and Confidence Ellipsoids

Convex hulls are often used to show the outer bounds of a sample of points. They can be useful in two or three dimensions as a graphic technique to simplify scatterplots showing many samples when they overlap broadly. Figures 1, 3, 5, and 7 above, Cardini et al. (2019), and many others provide examples. The volume of a convex hull is also one way to compare the overall range of observed variation of samples. Of course, an adjustment has to be made if the sample sizes are not equal because, as shown below, the volume of a convex hull is expected to increase with sample size because points further from the mean will usually be observed in larger samples.

An approximation to the expected volume, $VH_{p,n}$, of the convex hull of a sample of size n from a p-dimensional multivariate normal distribution was given by Affentranger (1991) as:

$$VH_{p,n} = V_{p} \left( {\log n} \right)^{{\tfrac{p}{2}}} \left( {1 + o\left( 1 \right)} \right)$$

where $V_{p}$ is the volume of the unit p-ball as given earlier and $o\left( 1 \right)$ indicates additional first-order terms are need for the approximation. The need for additional $o\left( 1 \right)$ terms implies that the approximation may not be very accurate, and in fact it considerably underestimates the volume. However, except for small sample sizes, the rate of increase with increasing sample sizes is only slightly underestimated and approximation is good enough to understand how its volume changes with increasing p and n. Because the volume of a p-ball at first increases and then rapidly drops to near zero as p increases, the volume of the convex hull must also increase and then decrease. The dimension with maximum volume depends on the sample size because more deviant observations are expected in larger samples. Figure 11b shows a plot of an approximation to the expected volume as a function of p and n_i.

Another way to measure the amount of volume taken up by a sample of points in different dimensions is to compute the volume of a confidence ellipsoid (also called and an equal frequency ellipsoid) that is expected to enclose the sample $100\left( {1 - \alpha } \right)\%$ percent of the time. Anderson (2004) gives the following formula for the volume, $VC_{p,\alpha }$, of this ellipsoid:

$$VC_{p,\alpha } = \frac{{C\left( p \right)\left[ {\chi_{p,\alpha }^{2} } \right]^{{\tfrac{p}{2}}} }}{p}\left| {{\varvec{\Sigma}}} \right|^{{ - \tfrac{1}{2}}}$$

where $C\left( p \right) = {{2\pi^{{\tfrac{p}{2}}} } \mathord{\left/ {\vphantom {{2\pi^{{\tfrac{p}{2}}} } {\Gamma \left( {\tfrac{p}{2}} \right)}}} \right. \kern-\nulldelimiterspace} {\Gamma \left( {\tfrac{p}{2}} \right)}}$ and $\Gamma ( )$ is the gamma function (a generalization of the factorial function for non-integer values). For the case considered here, $\left| {{\varvec{\Sigma}}} \right| = 1$ because ${{\varvec{\Sigma}}} = {\mathbf{I}}$. Unlike the volume of a p-ball or a convex hull for a sample from a multivariate normal distribution, the volume of the ellipsoid steadily increases with p. However, as in the case of a p-ball, it occupies a steadily decreasing fraction of the volume, $\left( {2\sqrt {\chi_{p,\alpha }^{2} } } \right)^{p}$, of a p-cube that would just enclose it. The fraction quickly becomes close to zero (less than 1% for p > 9).

The pattern is the same, multivariate samples of points will occupy only a tiny fraction of the multivariate sample space when p is not small. This rejection would seem to reduce the degree that independent samples from the same population would overlap as p becomes large because samples with small volumes are less likely to intersect by chance than those that would occupy a large fraction of the space. This property and some properties of distances in high-dimensional spaces are explored in the next section.

Distribution of Squared Euclidean Distances to the Mean

The squared distances, $d_{i}^{2}$, between points from a multivariate normal distribution and their sample mean is distributed as proportional to $\chi_{p}^{2}$(Anderson 2004). The mean of a $\chi_{p}^{2}$ distribution is equal to its degrees of freedom and its variance it twice that, p and 2p in the present case for sampling from the p-dimensional standard multivariate normal distribution. This means that as p increases, the distribution of squared distances becomes concentrated away from zero. Figure 12a shows histograms of squared distances for various numbers of dimensions. Thus, as the number of dimensions get large, only a small fraction of the points will be close to their mean even though that is where the density of the distribution is highest. In terms of distances, one should visualize a sample from a high-dimensional multivariate normal distribution not as a hyper-spherical cloud of points with most points near the mean but rather as like the surface of a ball with radius $\sqrt p$ from the center (Vershynin 2018). This is because while the density is highest close to that region that accounts for only a small fraction of the space occupied by the sample. The space between, for example, radii of 2 and 3 from the center includes a much larger portion of the space than that between radii of 1 and 2 from the center. From Fig. 12a one can also see that the distribution of distances is also skewed to the right. For very large p the distribution of points from the centroid is expected to be close to $\sqrt p$ and thus the distribution of points will be close to that of a uniform distribution on the surface of a sphere of radius $\sqrt p$ as discussed in Exercise 3.3.6 of Vershynin (2018).

Fig. 12

Histograms from sampling experiments. a Histograms of the squared distance, d², between random points and their sample mean for various numbers of dimensions, p. b Histograms of distances between random pairs of points for spaces of different numbers of dimensions, p. c Histogram of projections of points on a vector between a pair of means (each mean based on 100 points). d Histogram of 200 points projected onto a vector connecting two randomly selected points (their positions in the histogram are identified by the numbers “1” and “2” at the extreme tails of the distribution. The number of dimensions used for C and D was p = 1000. Note the scale of variation is very different in C and D. This is because the average squared distance between points is $2p$ whereas for means it is just ${{2p} \mathord{\left/ {\vphantom {{2p} {n_{i} }}} \right. \kern-\nulldelimiterspace} {n_{i} }}$

Distances Between Random Points

The distribution of squared distances between random pairs of points is also of relevant here. Squared distances between random pairs of points from a multivariate standard normal distribution are distributed as $2\chi_{p}^{2}$ (Anderson 2004), where the degrees of freedom are, again, equal to the number of dimensions. This means that in high dimensions there will be relatively few points that are close neighbors. The average squared distance between points, $\overline{{d_{ij}^{2} }}$, is 2p. Said in another way, if one visualizes randomly selected points as endpoints of vectors from the origin then pairs of such vectors will tend to be almost orthogonal in high dimensional spaces (Vershynin 2018). Another interesting property is that the ratio ${{\left( {\max d^{2} - \min d^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {\max d^{2} - \min d^{2} } \right)} {\min d^{2} }}} \right. \kern-\nulldelimiterspace} {\min d^{2} }}$ goes to zero as p increases, see Beyer et al. (1999) and Houle et al. (2010). This implies that for high dimensional spaces it will become less useful to perform cluster analyses that search for sets of close points. However, Houle et al. (2010) suggest that ranking of distances is still useful and suggest using nearest neighbor network relationships. The distribution of squared distances between sample means is similar because a point is just a mean with a sample size of 1. Thus the squared distance between two sample means is distributed as $\tfrac{2}{{n_{i} }}\chi_{p}^{2}$ (Anderson 2004). These imply that when using very large numbers of dimensions it will become more difficult to distinguish close means from more distant ones.

Sampling experiments were performed generating two samples of points from the same population for various numbers of dimensions. The resulting data (both points and means) were then projected onto a vector through the means of the two samples (Fig. 12c shows an example). The variance of the projection for points within the same group was close to 1. This may be surprising because the average squared distance to the mean is p in the original p-dimensional space. As in bgPCA, the squared difference between the projections of the sample means of the two groups grows steadily larger as the number of dimensions increases. It also increased when the sample size was reduced. Figure 13 shows a plot for n_i = 10 (upper solid dots) and 40 (middle solid dots). The average standard deviation for these samples is shown as open triangles. The average $d^{2}$ between means is ${{2p} \mathord{\left/ {\vphantom {{2p} {n_{i} }}} \right. \kern-\nulldelimiterspace} {n_{i} }}$ as one would expect for the full p-dimensional space. The solid and dashed lines on Fig. 13 are based on this theoretical relationship and clearly fit the observed points well. The dotted line is just for a variance of 1.0 for all p. This vector through the two means is, of course, the first bgPCA axis when there are just two groups.

Fig. 13

Plot of the square root of the average squared distance between two means as a function of p for sample sizes, n_i, of 10 (upper solid dots) and 40 (lower solid dots). Based on sampling experiments using 100 replications. The average standard deviation for these sampling experiments is also shown (open triangles). The upper two curves plot the expected relationship $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{d} = \sqrt {{{2p} \mathord{\left/ {\vphantom {{2p} {n_{i} }}} \right. \kern-\nulldelimiterspace} {n_{i} }}}$, which appears to fit the observed results perfectly. The lower, dotted, line shows the expected $\sigma = 1$ for all values of p

The above experiment was repeated using a vector between a random pair of points rather than means. Histograms of these projections, for example, Fig. 12d shows that the projections (ignoring the projections of the two reference points) are consistent with a standard normal distribution. This might seem counter-intuitive but Fig. 3.9 of Vershynin (2018) shows that the projection of a uniform distribution on the surface of a sphere of radius $\sqrt p$ onto a line converges to the standard univariate normal as $p \to \infty$. However, the two reference points are shown as extreme outliers located at each end of the distribution. Note that the distance between the reference points (the two means or the pair of random points) is much larger in Fig. 12d than the distance between means in Fig. 12c. This is because the variance of points is 1 but for means it is only ${1 \mathord{\left/ {\vphantom {1 {n_{i} }}} \right. \kern-\nulldelimiterspace} {n_{i} }}$. Perhaps surprisingly, while one can visualize the multivariate cloud of points as a hyper-spherical normal distribution with a variance of 1.0 in any direction and thus its projection onto any vector a univariate standard normal distribution, the average squared distance between any pair of points, 2p, becomes very large as p increases. In a sense, the distances between selected data points or means are on a different scale than the projections of the within-group scatter. Thus, the distribution of projections and the difference between means should not be shown in the same plot without some adjustment (see the Supplement). This is the key property that explains why samples appear so different when using bgPCA with many variables.

Discussion

Some of the properties and relationships between volumes and distances in high-dimensional spaces may seem counter-intuitive because our intuition is based on our everyday experiences with at most three dimensions. In my early training I was told that while going from spaces of one to two and then three dimensions had some different properties, but beyond three it was satisfactory to visualize the space as just extensions of the properties of 3-dimensional spaces. The “curse of dimensionality” seemed then to be just a complexity of computation and not important for the usual interpretation of statistical analyses of biological data. It seems I was misled!

The results reported above have several important implications for analyses using large numbers of variables not only in morphometrics but other field which now have access to large numbers of variables such as in genetics.

The Key Insight

Figure 12 illustrates what seems to be the key insight that explains much of the results of the sampling experiments performed in this study. In a high dimensional space, Projecting all of the data points onto a vector constructed to go exactly through the sample means of two groups (any two groups whether meaningful or randomly defined will usually result in a plot like Fig. 12c with the distance between the means equal to their distance in the full p-dimensional space but the distribution of the individual data point consistent with a sample from a univariate normal distribution. If instead, one projects the points onto a vector that goes exactly through two sample points then the result will be that those two points (separated by their actual distance in the p-dimensional space) will be shown as outliers as in Fig. 12d but with the other points still appearing consistent with a sample from a univariate normal distribution. On the other hand, projecting points onto a random vector should usually produce a distribution of projections just as expected for a sample from a single univariate normal distribution (Bickel et al. 2018). Of course, there is some chance that a randomly constructed vector might go sufficiently close to some points or means to yield distributions as in Fig. 12c, d but that becomes increasingly unlikely as the number of dimensions increases. The necessary degree of closeness was not investigated here except to observe that cases like those shown in Fig. 12c, d were not found among a large number of sampling experiments using random vectors. Single outliers did appear occasionally indicating that a random vector must have passed close to one of the data points. None were observed as extreme as shown in Fig. 12d. One can, of course, generalize these remarks to projections onto a $g - 1$-dimensional space that passes exactly contains the g means in a bgPCA.

The fact that groups in a bgPCA analysis become more and more distinct as more random variables are added beyond n-1 might seem puzzling because the distances among n points can always be captured exactly in n-1 dimensions and thus adding more variables beyond that does not increase the actual number of dimensions occupied by a data set. If a principal components analysis (PCA) were performed on the entire dataset then all eigenvalues past n-1 will be zero because there would be no variation in the highest dimensions. Thus, a sample actually occupies at most $\min \left( {p,n - 1} \right)$ dimensions no matter how large p becomes. However, adding additional variables past n-1 does in fact cause the groups to appear to be more and more distinct. The separation between groups such as shown in Fig. 12b, c will become greater and greater as p increases beyond n-1. The discussion above about the distribution of distances between points reveals why. It is because the distances between points (whether individual observations or means) increases as p increases because a squared distance is the sum of p squared differences. If a projection captures the actual distance between means then the groups will look more distinct relative to the projection of the within-group variation which does not get inflated as p increases.

Bookstein (2002), page 144, makes a related point for landmark data. If, for example, one has recorded k, 2-dimensional landmarks for $n = 2k - 3$ specimens then for any partitioning of the sample into two groups it is possible to find a dimension in the space that will completely separate the groups and have zero variation within the arbitrary groups along that dimension. This is because k landmarks correspond to a shape space of $2k - 4$ dimensions. Having a sample size one larger than that ($n = 2k - 3$) makes it possible to define an additional dimension that contrasts any arbitrary pair of groups that one might construct. In terms of variables rather than landmarks, with groups of size n₁ and n₂, the first group fills at most n₁-1 dimensions and the second n₂-1 dimensions. This means that together that maximally require $\left( {n_{1} - 1} \right) + \left( {n_{2} - 1} \right) = n - 2$ dimensions to represent the two samples. One can add one more dimension by adding a dummy variable that encodes the group membership. For example, it could have values of 1 for members of one group 1 and -1 for members of the group 2. This dummy variable would provide a dimension that perfectly distinguish the two groups. There would be no variation within groups for this variable. What a method like pgPCA does is to directly find such dimensions using the group means (see Fig. 9).

Inferences About Clusters and Other Patterns

Projection pursuit (Friedman and Tukey 1974) is a well-known method for searching high-dimensional data to find “interesting” projections that reveal insights into the structure of s high-dimensional data set. Interesting is usually defined as projections that are maximally different from a normal distribution, for example strongly bimodal indicating the presence of clusters. Hou and Wentzell (2011) suggested doing this by searching for projections that minimize kurtosis because that would indicate bimodality. Unfortunately, the search can be trivialized in very high-dimensional spaces by selecting vectors that go through the means of any arbitrary pair of groups as projections onto such vectors will show bimodality with perfect separation of the groups.

van der Maaten and Hinton (2008) suggested that If one expected the relationships to be nonlinear, rather than simple round or elliptical clusters methods such as t-SNE (t-Distributed Stochastic Neighbor Embedding) would be useful visualization at different scales in very high-dimensional data. This is because nearest-neighbor relationships may still be useful for clustering even though distances become relatively more concentrated around the mean distance in very high-dimensional data. Aggarwal et al. (2001) proposed the use of fractional distances (such as $d^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}}$) to spread out the distances to reduce the problem in clustering high-dimensional data.

As described earlier, ordination methods such as bgPCA will necessarily give distorted views because the ordination plots are constructed to try to show both the p-dimensional distances between the means and the projections of the within-group variation of the a priori defined clusters. As shown earlier, the CVA method (when the number of variables is not too large) has the same problem as bgPCA. When there are large numbers of variables a PCA is first performed to reduce the number of dimensions and a CVA performed on the reduced data. If the number of dimensions is sufficiently reduced and sample sizes large enough then this may avoid some of the problems. It would of course reduce the ability of CVA to detect subtle differences that may only be reflected in a few variables. These approaches were not investigated here.

Suggestions for Applications Using Large Numbers of Variables

Ordination plots produced using methods such as PCA and PCOORD (Principle coordinates analysis, Gower (1966)), or MDSCAL (non-metric multidimensional scaling, (Kruskal 1964)) of the entire dataset do not exaggerate the distinctness of any groups because the plots they produce are just low-dimensional approximations of the relationships among all of the points. While an eigenvector could happen to go exactly through two data points or group means and cause the problems described above, it is unlikely for high dimensional data. A very conservative approach would be to just use an ordination method to display a low-dimensional view of the total variation. If the groups are very distinct (and the differences are in dimensions that account for a large proportion of the overall variance then group differences should be visible in a 2 or 3-dimensional PCA ordination. This approach is conservative because it will not reveal differences if they were more subtle and just involved as few variables with smaller variances and thus would only be visible in higher dimensions. If finding such differences is important then larger sample sizes are needed. One may wish to at least first try using a method like PCA to see if differences between the expected groups are large. Unfortunately, specimens often differ greatly in size so that the effects of allometric variation may dominate and hide group difference. In that case one could try to restrict sampling to avoid specimens that differ greatly in size or one could try some method of size adjustment. However, a PCA may still not show group differences unless the differences account for a large proportion of the total variance.

Figures 1, 2, 3, 4, 5, 6, 7 show that the number of variables does not have to be exceptionally large in order to encounter the problems described here if sample sizes are not large. It is unclear just how large samples sizes need to be to avoid the problems described above. As noted by Cardini et al. (2019), Bookstein (2017, 2019), the ${p \mathord{\left/ {\vphantom {p n}} \right. \kern-\nulldelimiterspace} n}$ ratio is important rather than the absolute magnitude of n or p (or q in the case of multiple regression analysis). Investigators are usually encouraged to plot their data as a guide to checking and interpreting the numerical results from a statistical analysis. Unfortunately, as shown above, in studies using high-dimensional data it is the low dimensional plots themselves that can be misleading, and more trust should be placed on proper numerical results – especially results using cross-validation methods.

In many morphometric studies very large numbers of landmarks and semilandmarks are now used in morphometric studies because they have become easier to obtain. But having so many variables makes the studies somewhat exploratory in nature and that needs to be taken into account in the statistical analyses. See recent discussions about these methods in Cardini (2020) and Goswami et al. (2020). The high density of points makes the visualizations impressive and realistic looking compared to those using just a few landmark points. Large numbers of variables should increase the chances of capturing whatever differences there may be between groups. It will, of course, provide a more realistic depictions of the organisms. The problem is that unless sample sizes are very large the problems illustrated above are almost certain to arise. The present results showed that clear differences can be found between arbitrary groups when using high dimensional data unless sample sizes are large compared to the number of variables. The separation of groups may seem perfect even though there are no true differences among the means.

When the p/n ratio is large it is not useful to just report that one is able to find some combination of variables that shows a clear separation between groups as such differences can be found even for random partitions of data.

What one should do next in a practical application is to study the results and try to discover whether the apparent differences found using high-dimensional data can be described in terms of functional or developmental differences that can be described in terms of relatively few variables that are biologically meaningful to the study. The apparent result should then be confirmed checked using new samples of specimens. Unfortunately, obtaining new independent data is unrealistic in many types of applications so at least cross validation methods must be used to obtain some confidence in the results.