Introduction

Over-dispersed count data are common in ecological research. Similarly, the occurrence of forest fires is characterized by over-dispersion and a high frequency of zeros. These features of fire occurrence data present challenges for better understanding the ecological processes of forest fires and effectively modeling the future scenarios of forest fires using climate variables. Therefore, selecting an appropriate model or models to address both over-dispersion and excessive zeros is crucial for developing realistic prediction systems of forest fires in order to provide reliable information for fire prevention, land-use planning, and decision-making in natural resources management in China (Guo et al. 2010a; Xu 2014).

In past decades, forest researchers devoted considerable time and effort to model the ignition and occurrence of forest fires. In the literature, logistic regression models have been used to estimate the ignition probability of forest fires, while Poisson regression models have been applied to predict numbers of fire occurrences (Martell et al. 1987; Chou et al. 1993; Poulin-Costello 1993; Vega-Garcia et al. 1995; Mandallaz and Ye 1997; García Diez et al. 1999; Preisler et al. 2004; Griffith and Haining 2006; Liu and Cela 2008; Podur et al. 2009). However, the Poisson model is criticized for its restrictive assumption of equality between the sample mean and variance. It has been noted in various applications that the observed dispersion of count data is commonly underestimated by Poisson models. As an alternative, negative binomial (NB) models have been adopted for count data when the sample variance exceeds the sample mean (i.e., over-dispersion) (Cameron and Trivedi 1998).

In reality, forest fire occurrence data not only exhibit over-dispersion, but also include excessive numbers of zero counts. Zero-inflated models (Lambert 1992) and hurdle models (Mullahy 1986) have been utilized to address these situations. Both zero-inflated and hurdle models assume that count data are a mixture of two separate data generation processes: one generates only zeros, and the other is either a Poisson or an NB data-generating process. However, these two types of models are distinct in their interpretation and analysis of zero counts. Zero-inflated models allow for two separate processes. Conceptually, the first step is to model the structural zeros using a logistic regression and the second step is to model the Poisson distribution conditional on the structural zeros; i.e., a Poisson or NB model is used for the sampling zeros and positive counts. In contrast, hurdle models are interpreted as two-part models, in which a logistic regression model governs the binary outcome of whether a count variable has a zero or a positive realization. If the realization is positive, “the hurdle” is crossed, and the conditional distribution of the positive counts is then determined by a truncated-at-zero Poisson or NB model (Cameron and Trivedi 1998; Rose et al. 2006). In summary, Zero-inflated models assume that zero counts have two different origins-structure and sampling, whereas Hurdle models assume that all zero counts are from one structural source (Erdman et al. 2008; Hu et al. 2011).

The applications of Zero-inflated and hurdle models can be found in different study fields (e.g., Yau and Lee 2001; Ridout et al. 2001; Affleck 2006; Lee et al. 2011), but only few have been related to the prediction of forest fire occurrence (e.g., Krawchuk et al. 2009). Most studies that assessed the relationship between forest fire occurrence and meteorological conditions either emphasized the prediction function of the models or focused on the selection of independent variables in order to improve model performance. Only a few studies undertook comprehensive analysis of the process of model selection based on the principles of statistics (Mandallaz and Ye 1997; Guo et al. 2010b).

In this study, we used six generalized linear models, viz. Poisson, NB, zero-inflated Poisson (ZIP), zero-inflated negative binomial (ZINB), Poisson hurdle (PH), and negative binomial hurdle (NBH) models, to fit the occurrence of lightning-induced fires (count data) to examine the relationship between forest fires and corresponding meteorological factors in the northern Daxing’an Mountains, China. The objective of this study was to provide comparative assessment for researchers to deal with the challenges of analyzing and modeling forest fire occurrence (count data) with over-dispersion and excessive zeros.

Materials and methods

Study site description

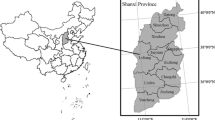
The study site is located in high-latitude boreal forest regions of the Daxing’an Mountains (50°10′–53°33′N, 121°12–127°00′E) with a total area of 8.46 × 106 ha in northeast China (Fig. 1). The Daxing’an Mountains support the largest natural forests in China. Dominant tree species include Daurian larch (Larix gmelinii Rupr.), White birch (Betula platyphylla Suk.), Mongolian pine (Pinus sylvestris L. var. mongolica Litv.), and Mongolian oak (Quercus mongolica Fischer ex Ledebour) (Xu 1998). Mean annual temperature is −2 to 4 °C, with extremes ranging from –52.3 to 39.0 °C. Total annual precipitation is 350–500 mm and most is received in winter and early spring as snow. Elevation ranges from 300 to 1400 m. The Daxing’an Mountains consist of seven sub-administrative regions (Xu 1998). Our study area was located in the northern Daxing’an Mountains, and included three sub-administrative regions (namely Mohe, Huzhong, and Tahe), covering an area of about 42 × 105 ha (Fig. 1).

Fig. 1
figure 1

Map of the study area (shaded) within the Daxing’an Mountains in northeast China

Full size image

Fire frequency data

The Daxing’an Mountains have an extremely high fire risk and the highest average area burned annually in China. The fire occurrence data used in this study were collected from 1980 to 2005. According to the records, there were over 1000 forest fires and nearly 1.3 × 105 ha burned area during this 26-year time period. Our fire data, including location, ignition dates and total burned area, were provided by the Fire Prevention Office of Heilongjiang Province (FPOHP). We chose to focus on the Mohe, Huzhong, and Tahe sub-administrative regions in the Northern Daxing’an Mountains because the records of fire occurrence were relatively complete compared to the other sub-administrative regions. We addressed only lightning-induced fires in this study due to the completeness of the data records and the significant relationship between lightning fires and meteorological factors (Yu et al. 2007; Guo et al. 2010a, b; Chang et al. 2013). The fire frequency or count was calculated on a monthly scale from January to December of each year. Hence, the dependent variable was the monthly occurrence (count) of lightning-induced fires over the 26-year time period (1980–2005).

Meteorological variables

We focused on five meteorological variables, viz. average monthly wind speed (AMWS), average monthly temperature (AMT), average monthly precipitation (AMP), average monthly relative humidity (AMRH), and average monthly evaporation (AME). These variables significantly impact forest fire occurrence in the Daxing’an Mountains (Yu et al. 2007; Guo et al. 2010a, b; Chang et al. 2013). The meteorological data were provided by the China Meteorological Data and Sharing Network (http://cdc.cma.gov.cn/), which included more than seven hundred national meteorological stations across China. Three national meteorological stations were located in our study area, one in each sub-administrative region (Mohe, Huzhong, and Tahe).

The descriptive statistics for the fire occurrence counts and meteorological variables are listed in Table 1. The average monthly fire occurrence was 0.23, while the variance was 0.80. The ratio of the variance to the mean was 3.45, showing over-dispersion in the fire occurrence data. Figure 2 shows the frequency distribution of the observed counts of the lightning-induced fires, illustrating a large proportion of zero counts. The zero records contain some “structural (or true) zeros” due to absence of lightning strikes during non-fire seasons and some “sampling zeros” recorded during fire seasons when fire was not recorded due to the combined effects of meteorological factors but lightning strikes actually occurred.

Table 1 Descriptive statistics for the occurrence of lightning-induced forest fires (dependent variable) and meteorological factors (independent or predictor variables)
Full size table
Fig. 2
figure 2

Frequency distribution of the monthly occurrence of lightning-induced forest fires over the study period (1980–2005). X-axis represents the category of monthly fire occurrence number. Y-axis represents frequency of the category over the study period. The total number of counts (frequency) used was 704 for model fitting

Full size image

Statistical models

Poisson model

The Poisson model is used to model counts of events during a time period as a function of predictor variables and is based on the assumption that the conditional mean equals the conditional variance. The probability density function (pdf) of the Poisson model is:

$$ P\left( Y \right) = \frac{{e^{ - \mu } \cdot \mu_{{}}^{Y} }}{Y!} = \frac{{e^{ - \mu } \cdot \mu_{{}}^{Y} }}{{\varGamma \left( {Y + 1} \right)}} $$
(1)

where \( P\left( Y \right) \) is the probability that the number of events (Y) occurs during a time period, and µ is the parameter representing the expected value of Y; i.e., \( E\left( Y \right) = \mu \) and \( {\text{Var}}\left( Y \right) = \mu \), and Γ() is gamma function. The set of predictor variables X impacts the mean of the response variable µ via a link function such that \( \eta = g\left( \mu \right) = \ln \left( {X\beta } \right) \), and the inverse link function (mean function) is

$$ \mu = g^{ - 1} \left( \eta \right) = e^{X\beta } \,{\text{or}}\,\ln \left( \mu \right) = X\beta \, $$
(2)

where β is the model coefficient to be estimated from data. Thus, Eq. 2 is a regression model relating the natural logarithm of the response mean or expected number of events to the explanatory or predictor variables (Cameron and Trivedi 1998; Osgood 2000).

Negative binomial (NB) model

The NB distribution can be used for count data with over-dispersion, i.e., when the sample variance exceeds the sample mean. The NB model addresses over-dispersion by including a dispersion parameter to accommodate unobserved heterogeneity in count data. The NB model used in this study has the following pdf:

$$ P\left( Y \right) = \frac{{\varGamma \left( {Y + \frac{1}{\kappa }} \right)}}{{\varGamma \left( {Y + 1} \right)\varGamma \left( {\frac{1}{\kappa }} \right)}}\left( {\frac{1}{1 + \kappa \mu }} \right)^{1/\kappa } \left( {\frac{\kappa \mu }{1 + \kappa \mu }} \right)^{Y} $$
(3)

The mean of \( Y \) is \( E\,\left( Y \right)\, = \,\mu \) and the variance of \( Y \) is \( V\,\left( Y \right)\, = \,\mu \, + \,k\mu^{2} \), where \( \kappa \ge 0 \) which is usually referred to as the dispersion parameter. Equation 3 allows the variance to exceed the mean. Consequently, the Poisson model can be regarded as a limiting model of NB model as the dispersion parameter κ approaches 0 (Miaou 1994). Given a set of predictor variables X, the link function of the NB model is also \( \eta = g\left( \mu \right) = \ln \left( {X\beta } \right) \)

Zero-inflated models: ZIP and ZINB

Observed count data are frequently characterized by over-dispersion and many zero counts. Zero-inflated models are powerful in these situations. Zero-inflated models generate two models as follows: a logistic model is first generated for the “certain zero” in order to predict whether a case would happen. Then, a Poisson or NB model is generated to predict the counts for the case (≥0). In other words, Zero-inflated models consider two sources of zero observations: “structural or true zeros” which cannot score anything other than “0”, and “sampling zeros” which are part of the underlying sampling distribution (either a Poisson model (ZIP) or an NB model (ZINB)). Zero-inflated Poisson model can be expressed as (Numna 2009):

$$ P\left( Y \right) = \left\{ {\begin{array}{*{20}c} {\omega + \left( {1 - \omega } \right)e^{ - \mu } } & {Y = 0} \\ {\left( {1 - \omega } \right)\,\frac{{e^{ - \mu } \mu^{Y} }}{Y!}} & {Y \ge 1\quad 0 \le \omega \le 1} \\ \end{array} } \right. $$
(4)

The mean and variance of the ZIP model are, respectively, \( E\,\left( Y \right) = \,\left( {1 - \omega } \right)\mu \) and \( V\,\left( Y \right)\, = \,\left( {1 - \omega } \right) \) \( \left( {\mu + \omega \mu^{2} } \right) \), where \( \omega \) denotes the probability of being an individual having zero count and µ denotes the mean of the underlying distribution. Equation 4 shows that the marginal distribution of \( Y \) exhibits over-dispersion if \( \omega \, < \,0 \), and it reduces to the standard Poisson model when \( \omega \, = \,0 \)

The alternative is that \( Y \) has the Zero-inflated NB distribution, specifically:

$$ P\,\left( Y \right)\, = \,\left\{ {\begin{array}{ll} {\omega + \left( {1 - \omega } \right)\left( {\frac{1}{1 + \kappa \mu }} \right)^{1/\kappa } } & {if\quad Y = 0} \\ {\left( {1 - \omega } \right)\frac{{\varGamma \left( {Y + \frac{1}{\kappa }} \right)}}{{\varGamma \left( {Y + 1} \right)\varGamma \left( {\frac{1}{\kappa }} \right)}}\left( {\frac{1}{1 + \kappa \mu }} \right)^{1/\kappa } \left( {\frac{\kappa \mu }{1 + \kappa \mu }} \right)^{Y} } & {if\quad Y \ge 1} \\ \end{array} } \right. $$
(5)

where \( \kappa \ge 0 \) is a dispersion parameter that is assumed independent of covariates. The mean and the variance of the distribution are E(Y) = \( \left( {1 - \omega } \right) \) μ and V(Y) = \( \left( {1 - \omega } \right) \) \( \left[ {\mu \left( {1 + \mu \kappa } \right) + \omega \mu^{2} } \right] \), respectively. The ZINB model reduces to the ZIP model in the limit \( \kappa \to 0 \)

Hurdle models: PH and NBH

Hurdle models, first discussed by Mullahy (1986), are popular for modeling count data with many zeros. In contrast to Zero-inflated models, Hurdle models can be interpreted as two-part models: a logistic model is used to predict the binary outcome whether a count variable has a zero or a positive realization. If the realization is positive (i.e., the hurdle is crossed), a truncated-at-zero Poisson or NB model is used to predict the conditional distribution of the positive counts (≥1) (Cameron and Trivedi 1998). The Hurdle model can be expressed as:

$$ P\,\left( Y \right)\, = \,\left\{ {\begin{array}{ll} \omega & {Y = 0} \\ {\left( {1 - \omega } \right)\frac{{f\left( {Y = y} \right)}}{{1 - f\left( {Y = 0} \right)}}} & {Y \ge 1\quad 0 \le \omega \le 1} \\ \end{array} } \right. $$
(6)

where \( \omega \) is the probability of a zero count and \( \left( {1 - \omega } \right) \) is the probability of overcoming the hurdle. We can define two Hurdle models by specifying \( f\left( Y \right) \) as a Poisson or an NB distribution. If we substitute Eq. 1 into Eq. 6 we obtain the Poisson Hurdle model (PH) as follows:

$$ P\,\left( Y \right)\, = \,\left\{ {\begin{array}{ll} \omega & {if\;Y = 0} \\ {\left[ {1 - \omega } \right]\frac{{e^{ - \mu } \mu^{Y} }}{{\left( {1 - e^{ - \mu } } \right) \cdot \varGamma \left( {Y + 1} \right)}}} & {if\;Y \ge 1} \\ \end{array} } \right. $$
(7)

Alternatively, if we substitute Eq. 3 into Eq. 6 for \( f\left( Y \right) \) we generate a NBH model as follows:

$$ P\left( Y \right)\, = \,\left\{ {\begin{array}{*{20}c} \omega & {if\;Y = 0} \\ {\left[ {1 - \omega } \right]\frac{{\varGamma \left( {Y + \frac{1}{\kappa }} \right)}}{{\left[ {1 - \left( {\frac{1}{1 + \kappa \mu }} \right)^{1/\kappa } } \right]\varGamma \left( {Y + 1} \right)\varGamma \left( {\frac{1}{\kappa }} \right)}}\left( {\frac{1}{1 + \kappa \mu }} \right)^{1/\kappa } \left( {\frac{\kappa \mu }{1 + \kappa \mu }} \right)^{Y} } & {if\;Y \ge 1} \\ \end{array} } \right. $$
(8)

Model fitting and selection

In this study, the total number of dependent variable observations was expected to be 936 (12 months × 3 regions × 26 years). However, there were some missing fire records, resulting in 834 observations. A random sample of 704 observations (84.4 % of the fire occurrence data) was selected for model development (model calibration), and the remaining 130 observations (15.6 %) were reserved for independently testing the model’s predictive capability (model validation). Five weather variables were used as the predictor variables, viz. AMWS, AMT, AMP, AMRH, and AME. The statistical software R (R Development Core Team, 2005) was used for data analyses and modeling.

The multicollinearity among the 5 predictor variables was diagnosed by a variance inflation factor (VIF), with VIF > 10 as the threshold or red-flag for multicollinearity (O’Brien 2007). In addition, we used a stepwise approach to select significant meteorological factors at the significance level of α = 0.05 through the Poisson model. The theory underlying this approach was that nested models can be obtained by restricting a parameter to zero in a more complex model. Because the other five models were all based on the Poisson model, we were able to use this model to select significant meteorological factors.

Model assessment and evaluation

(1) The Akaike information criterion was used to evaluate the goodness of fit of the six models and is defined as follows:

$$ AIC = - 2\log L + 2p $$
(9)

where logL is the maximum of the likelihood function for a fitted model and p is the number of parameters in the fitted model. The preferred model is the one with the minimum AIC value (Burnham and Anderson 2004).

(2) While AIC enables comparison of models for goodness-of-fit, it does not reveal anything about how well a model fits the data in an absolute sense (Burnham and Anderson 2004). Thus, we also computed the sum of squared errors (SSE) to assess the general goodness-of-fit of each model as follows:

$$ SSE = \sum\limits_{i = 1}^{N} {(Y_{i} - \hat{Y}_{i} } )^{2} $$
(10)

where \( Y_{i} \) is the observed count and \( \hat{Y}_{i} \) is the predicted count from the models.

(3) A likelihood ratio test (LRT) was used to compare nested models (i.e., NB vs. Poisson, ZINB vs. ZIP, and NBH vs. PH) in order to test whether the over-dispersion parameter would be necessary. In LRT, the null hypothesis is for the restricted or constrained model (null model) with the log-likelihood logLR and degrees of freedom dfR, and the alternative hypothesis is for the unrestricted or unconstrained model (alternative model) with log-likelihood logLU and degrees of freedom dfU. Then, LRT follows a \( \chi^{2} \) distribution such that

$$ D = - 2\log \left( {\frac{{L_{R} }}{{L_{U} }}} \right) = - 2\left( {\log L_{R} - \log L_{U} } \right)\,\sim\,\chi^{2} ,{\text{with df}}\,{ = }\,{\text{df}}_{\text{U}} \, - \,{\text{df}}_{\text{R}} $$
(11)

(4) The Vuong test is a likelihood ratio based test for model selection using the Kullback–Leibler information criterion (Vuong 1989). This statistic makes probabilistic statements about two models. It tests the null hypothesis that two models equally approximate the actual model against the alternative hypothesis that one model more accurately represents the actual model (i.e., is preferred). It cannot make the decision that the “more accurate” model is the true model. Suppose we attempt to test between a model \( f\left( {Y|X;\hat{\theta }} \right) \) (e.g., ZIP) against a model \( g\left( {Y|Z;\hat{\gamma }} \right) \) (e.g., Poisson) Under the null hypothesis that these two models are indistinguishable, and the test statistic is asymptotically distributed standard normal, the formula is:

$$ V = \frac{1}{\sqrt n }\frac{{\log Lf\left( {Y|X;\hat{\theta }} \right) - \log Lg\left( {Y|Z;\hat{\gamma }} \right)}}{\varpi }\,\sim\,{\text{N}}\,\left( {0,1} \right) $$
(12)

where \( \varpi^{2} = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left[ {\log \frac{{f\left( {Y|X;\hat{\theta }} \right)}}{{g\left( {Y|Z;\hat{\gamma }} \right)}}} \right]}^{2} - \left[ {\frac{1}{n}\sum\limits_{i = 1}^{n} {\log \frac{{f\left( {Y|X;\hat{\theta }} \right)}}{{g\left( {Y|Z;\hat{\gamma }} \right)}}} } \right]^{2} \); If V > 1.648, reject the null hypothesis and conclude that \( f\left( {Y|X;\hat{\theta }} \right) \) is better than \( g\left( {Y|Z;\hat{\gamma }} \right) \); if V < −1.648, reject the null hypothesis and conclude that \( g\left( {Y|Z;\hat{\gamma }} \right) \) is better than \( f\left( {Y|X;\hat{\theta }} \right) \); and if |V| ≤ 1.648, we cannot reject the null hypothesis and conclude that the two models are the same (Vuong 1989). Thus, the Vuong test can be used to test between pairs of non-nested models (i.e., ZIP vs. Poisson, ZINB vs. NB, PH vs. Poisson, NBH vs. NB, ZIP vs. PH, and ZINB vs. NBH). Using the Vuong test for ZIP versus Poisson and ZINB versus NB pairings also enables testing whether the over-dispersion in count data is attributable to high frequencies of zero counts.

Results

Using the recorded fire occurrence data, the Poisson model was used as a benchmark model for screening the predictor variables, with the result that AMWS was not significant at α = 0.05, while four other meteorological factors (AMT, AMP, AMRH, and AME) were statistically significant. In addition, the VIF values of the four predictor factors were all less than 10, indicating that there was no serious multicollinearity among these predictor variables. Thus, we fitted the other five models (i.e., NB, ZIP, ZINB, PH and NBH) using these four meteorological factors. The model fitting results are listed in Tables 2, 3, 4. According to the AIC and SSE of the six models, the zero-inflated models fitted the fire occurrence data better than other models. The ZINB model had the smallest AIC, and the Poisson model had the largest AIC. The rank order of the model AICs was ZINB < NBH < ZIP < NB < PH < Poisson (Tables 2, 3, 4)

Table 2 Parameter estimates, standard errors (S.E.), and model goodness of fit statistics for Poisson and negative binomial (NB) models
Full size table
Table 3 Parameter estimates, standard errors (S.E.) and model goodness of fit statistics for the zero-inflated Poisson (ZIP) and zero-inflated negative binomial (ZINB) models
Full size table
Table 4 Parameter estimates, standard errors (S.E.) and model goodness of fit statistics for the Poisson hurdle (PH) and negative binomial hurdle (NBH) models
Full size table

The LRT was used to compare nested models (i.e., NB vs. Poisson, ZINB vs. ZIP, and NBH vs. PH) and to test if the over-dispersion parameter in the NB-type models was necessary. All LRT tests were highly significant (p < 0.01) for differences in the three pairs (Table 5). It was evident that the NB-type models (i.e., NB, ZINB, and NBH) were more suitable than Poisson-type models (i.e., Poisson, ZIP, and PH) to handle the over-dispersion of the fire occurrence data in this study (Table 5).

Table 5 The likelihood ratio test (LRT) and Vuong test among the six models, Poisson, negative binomial (NB), zero-inflated Poisson (ZIP), zero-inflated negative binomial (ZINB), Poisson hurdle (PH) and negative binomial hurdle (NBH) models
Full size table

The Vuong test was used to test between the pairs of non-nested models. In this study, we compared ZIP versus Poisson, ZINB versus NB, PH versus Poisson, and NBH versus NB to test if the over-dispersion in the fire occurrence data was attributable to high frequencies of zero counts (excessive zeros). We also compared ZIP versus PH and ZINB versus NBH to investigate if the excessive zeros were due to two sources (structure and sampling) or only one source (structure). The ZIP model was preferred over the Poisson model, and the ZINB model was preferred over the NB model, indicating that the Zero-inflated models were effective to handle the excessive zero counts. Similarly, the PH model was preferred over the Poisson model, and the NBH model was preferred over the NB model, meaning that the Hurdle models were also better than the Poisson and NB models at handling excessive zero counts. There was no difference between ZIP and PH models, indicating both Zero-inflated Poisson and hurdle Poisson handled the excessive zeros equally well, without accounting for over-dispersion. In contrast, the ZINB model was definitely preferred over the NBH model, meaning that when the over-dispersion was accounted for by the NB-type models, the ZINB model was a better choice than the NBH model (Table 5).

Furthermore, the four meteorological factors in the six models showed some differences (Tables 2, 3, 4). For the Poisson and NB models, the estimated parameters of four meteorological factors (AMP, AMT, AMRH, and AME) were all statistically significant (p < 0.05) (Table 2). In these two models, AMP (precipitation) and AMRH (relative humidity) were negatively related to lightning-induced fire occurrence, while AMT (temperature) and AME (evaporation) were positively related to fire occurrence. In contrast, the four meteorological factors behaved differently between Zero-inflated and hurdle models, as well as between the two components (i.e., logistic models and count models) of these models. For example, AMP, AMRH and AME were statistically significant (p < 0.05) for the count portion of the ZIP model, while only AMT and AMRH were significant (p value < 0.05) for the logistic model (Table 3).

In order to assess the predictive capacity of the six models, the independent validation data (130 observations) were used to compare the observed fire counts against the predictions from the six models. The prediction error was defined as the difference between observed count and predicted count. We computed the mean prediction errors (MPE) for predicting the zero counts and for predicting the positive counts (≥1) for each of the six models (Table 6). We found that: (1) all models over-predicted (MPE < 0) zero counts and the ZINB model was the best (smallest MPE), followed by the Poisson, ZIP, NB, NBH models, and the PH model was the worst (largest MPE); and (2) all models under-predicted positive counts (MPE > 0) and the ZINB model was still the best (smallest MPE), followed by the NBH, PH, ZIP, Poisson models, and the NB model was the worst (largest MPE). Figure 3 illustrates the observed frequency of fire occurrence in the 130 validation data points (bar chart) and predicted frequencies of fire occurrence from each of the six models. It was clear that the ZINB model yielded better predictions for both zero counts and positive counts than did the other five models.

Table 6 The mean prediction error (MPE) of the six models using the model validation data (130 observations)
Full size table
Fig. 3
figure 3

The observed and predicted frequencies of fire occurrence for Poisson, Negative Binomial (NB), Zero-inflated Poisson (ZIP), Zero-inflated NB (ZINB), Poisson hurdle (PH), NB hurdle (NBH) models using the 130 validation data

Full size image

Discussion

The fire season of Daxing’an Mountains usually runs from April to October every year, and can be extended or shortened due to the specific meteorological conditions of the year, as well as the specific geographical areas. In contrast, forest fire is rare during winter months (e.g., November to March), resulting in many zero counts when we calculated the number of lightning-induced fires for each month in every annual fire cycle. To avoid dealing with the zero counts during non-fire seasons, some studies limited their fire data to active fire seasons (e.g., Mandallaz and Ye 1997; Martell et al. 1987). In this study, we analyzed fire occurrence over the full year rather than during the fire season only, because the fire seasons in the study area had various lengths from year to year. We anticipated that analysis of fire occurrence data for the entire year would be beneficial to capturing the impacts of meteorological factors on forest fire occurrence.

As described in Methods, the zero-inflated models treat the zero counts from two sources: the structural zeros that cannot score anything other than zero, and the sampling zeros that are a part of the underlying sampling distribution (Poisson or NB). In this study, we considered that all zero records contained some structural zeros due to no lightning strikes during non-fire seasons, and some sampling zeros because zero fire was recorded due to the combined effects of meteorological factors when lightning strikes actually occurred during active fire seasons. The zero-inflated models assume that some lightning strikes may not cause a forest fire due to unfavorable weather conditions, while the Hurdle models presume that each lightning strike would cause a measurable forest fire. Consequently, the zero-inflated models performed better than the Hurdle models in this study.

The ZINB model proved to be the most suitable model for fitting the monthly occurrence of lightning-induced forest fire in the Northern Daxing’an Mountains. However, rather than propose a new approach to forest fire prediction, we attempted to provide comparative assessment and evaluation so that researchers can effectively deal with the challenges of analyzing and modeling count data characterized by over-dispersion and excessive zero counts. Generally speaking, to some extent the data structure decides the model application. Hence, the most suitable model can differ if the data structure of fire occurrence changes. In this study, for example, if we collected fire occurrence data based on a daily scale instead of monthly. As a result, the fire occurrence data were more over-dispersed and zero-inflated. Had we increased the time scale to a yearly basis, the fire occurrence data would likely be less over-dispersed and have fewer zero counts. In addition, more appropriate explanation variables may also affect the modeling of fire occurrence data. Beside the meteorological factors used in this study, other factors such as topography and fuel types and conditions might also be important. Thus, other useful explanation variables and various time scales should be taken into account when forest fire managers and researchers use our results to predict forest fire occurrence in the future.

Conclusions

Our results showed that, based on the model AIC, the ZINB model best fitted the fire occurrence data, followed by (in an order of declining AIC) NBH, ZIP, NB, PH, and Poisson models. It was possible that excessive zeros impacted model fitting more than over-dispersion, because the improvement of model fitting for Poisson vs. ZIP was more than that for Poisson vs. NB (Tables 2, 3). The ZINB model proved best for fitting the fire occurrence data and for predicting either zero counts or positive counts (≥1). The two Hurdle models (PH and NBH) were better than ZIP, Poisson and NB models for predicting positive counts, but worse than these three models for predicting zero counts. The performance of the ZINB model in this study implied that the excessive zero counts arose from both structural and sampling sources, i.e., some lightning strikes occurred, but other environment factors prevented the fire ignition from developing into a measurable forest fire.