Phase Equilibria in Low-Temperature Regions of Phase Diagrams

Abstract

This article considers the features and fundamental difficulties of studying low-temperature phase equilibria associated with an exponential increase in the required duration of syntheses with a decrease in temperature. Methods for accelerating the achievement of equilibrium, including the use of salt solvents, are also considered. The results of phase equilibria studies in the SrF₂–LaF₃ system using sodium nitrate and in the ZrO₂–Sc₂O₃ system using sodium sulfate as fluxes are presented. The methods of extrapolation of phase diagrams to absolute zero temperature in accordance with the third law of thermodynamics are considered. Phase diagrams of the Au–Cu, Cu–Pd, Ni–Pt, and ZrO₂–Y₂O₃ systems are presented. Phase equilibria with plagioclase ordering are considered separately, and the phase diagram of the albite–anorthite (NaAlSi₃O₈–CaAl₂Si₂O₈) system is presented. As the temperature approaches absolute zero, the homogeneity region of labradorite shrinks to the compound NaCaAl₃Si₅O₁₆.

1 Introduction

The title topic is important both in fundamental and applied respects because low temperatures are, as a rule, the performance range of materials, and materials design is based on the corresponding phase diagrams.^1,2,3

In this paper, we intend to review our contribution to studies of the phase diagrams of some binary systems at low temperatures, including experimental studies that used a liquid catalytic phase and those studies that employed a corollary of the third law of thermodynamics to extrapolate phase equilibria to absolute zero temperature. References to other researches will be given whenever appropriate.

2 The Time Necessary to Acquire Equilibrium

First of all, the time required for samples to achieve equilibrium upon annealing (τ) increases exponentially as temperature T decreases. This follows from the diffusion laws and is dictated by the temperature dependence of the diffusion coefficients of atoms (ions). From a logτ ~ 1/T plot (Fig. 1), one can estimate the activation energy of the sintering process involved in solid-phase synthesis.^4,5,6

Fig. 1

Temperature-dependent annealing time required for the batch to acquire equilibrium.^4,5 Reprinted with permission from Pleiades Publishing, Ltd

Accordingly, the amount of time required for equilibrium to be achieved goes quickly beyond the limits of experimental capabilities when temperature decreases. Even most tough researchers usually limit anneals to at most 6–8 months,^7,8,9,10,11 while historical, geological, or even astronomical times would have been required to achieve the desired result. Relevant calculations can be found in, e.g., (Ref 12). It is especially difficult to carry out long-term experiments when the research is funded through grants.

We will refer to the boundary of the low-temperature region as Tc, the critical temperature at which the equilibration time is one year. This temperature is strongly differentiated from one system to another. For zirconium dioxide systems with lanthanide oxides, it is about 1300 °C.⁶

An important thesis may be formulated: for each system there is a critical temperature below which an experimental study of phase equilibria is impossible.⁵

3 How to Speed up Equilibration

The primary and major strategy in the study of low-temperature equilibria is to use techniques that would help in expanding the capabilities of the experiment.

There are techniques that allow determination of the boundaries of phase fields without achieving complete equilibrium. In two-phase regions, equilibrium is acquired more quickly. As a rule (but not always), solid solutions retain the composition dependences of their unit cell parameters upon quenching, from whatever temperature. Thus, one can elucidate these dependences at high temperatures, and then deal with the unit cell parameters of two-phase samples that were annealed at lower temperatures. Figure 2 illustrates a similar procedure.

Fig. 2

Unit cell parameters of Pb_1-xNd_xF_2+x fluorite solid solution in the PbF₂–NdF₃ system.¹³ The quenched after annealing at 740 °C: (1) 8 hours and (2) 24 hours

Igami et al.¹⁴ used an interesting method to achieve mullite–sillimanite phase equilibria in the Al₂O₃–SiO₂ system.

There are various ways to speed up equilibration and, accordingly, to shift critical temperature T_c toward lower temperatures. The most common and popular method is to intermittently grind intermediates, interrupting continuous annealing.

Some activation of the materials to be sintered is also useful. The mechanochemical activation of batch components is widely applied.^15,16 Batch components can be compounds produced by the thermal decomposition of adducts with the evolution of gas constituents. An example is barium fluoride produced by the thermolysis of barium hydrofluoride BaF₂·HF.^5,17 The thus-produced barium fluoride powder is comprised of micrometer-sized particles that do retain the precursor shapes but are fractured, thus having greater surface areas (Fig. 3).

Fig. 3

Micrograph of a barium fluoride powder produced by the thermolysis of barium hydrofluoride BaF₂·HF

A particular case is where the sintering temperature is close to the phase-transition temperature of a component (in addition to temperature oscillations, which itself speed up the process).

A universal strategy is to reduce particle sizes, and accordingly, to shorten the diffusion paths of atoms during the synthesis. Particle sizes can be reduced to nanosized particles (e.g., in the Ni–Pt system¹¹) and even to amorphous precursors, which is systematically done in studies of zirconia systems comprising rare earths (ZrO₂–R₂O₃).^7,8,9,10

A very important way is to introduce a liquid phase into the synthesis process.¹⁸ The appearance of a liquid seriously accelerates the chemical reactions accompanying the acquisition of equilibrium. It is very important in this case that only a negligible amount of solvent enter the reaction products; if so, we might speak about the role of the liquid as a sintering catalyst.

The most important and common solvent is water. A good example is the sodium sulfate–potassium sulfate system (Fig. 4). The Na₂SO₄–K₂SO₄–H₂O ternary system was well studied using cold, hot, and boiling water to recognize the evolution of the glaserite homogeneity area, and these results agree well with the data at higher temperatures in the anhydrous system Na₂SO₄–K₂SO₄.¹⁹ However, this version of the phase diagram does not take into account the formation of low-temperature compounds.²⁰

Fig. 4

Phase diagram of the system Na₂SO₄-K₂SO₄ system according to Eysel.¹⁹ The following symbols are used: H = high-K₂SO₄ structure type, L = low-K₂SO₄ structure type, G = glaserite type, III = Na₂SO₄(III) type and V = Na₂SO₄(V). Reprinted with the permission from Mineralogical Society of America

Even a trace of water can have a very strong effect on the synthesis of refractory substances. When water is added to the albite–anorthite (NaAlSi₃O₈–CaAl₂Si₂O₈) silicate system, for example, the constituent cations have their diffusion coefficients increasing by three orders of magnitude during sintering.²¹

A natural extension of this approach is hydrothermal synthesis.^22,23 However, water is a dangerous substance. A striking example is that of lanthanide oxides. Residual water stabilizes the cubic C phases of lanthanide oxides (bixbyite type, space group Ia $\overline{3 }$) in the cerium group due to the formation of hydrates like Nd₂O₃xH₂O,^{24,25,26,27,28} and thereby grossly distorts the picture of polymorphism and morphotropism in the series of lanthanide sesquioxides (Fig. 5).

Fig. 5

(a) Incorrect^24,25,26 and (b) correct^27,28 polymorphism and morphotropism schemes in the lanthanide oxides series

The widespread use of the hydrothermal protocol for the low-temperature syntheses of inorganic fluorides carries the danger of partial hydrolysis with an isomorphic replacement of fluoride ions by hydroxyl ions. This danger is usually ignored.

Salt melts are an attractive alternative for studying phase equilibria at relatively low temperatures.^29,30,31 Our systematic studies of nitrate and sulfate melts are underway as applied to the investigation of phase equilibria in fluoride and oxide systems.

Figure 6 shows a summary phase diagram of the SrF₂–LaF₃ system.¹² Sobolev and Seiranian³² in their detailed studies of high-temperature phase equilibria by differential thermal analysis (DTA) and the anneal-and-quench method discovered extensive solid solutions with maxima on their melting curves. Unusually, the composition boundary of the fluorite solid solution is almost independent of temperature in the range 1400–750 °C. Yoshimura et al.’s studies of hydrothermal synthesis^22,33 traced this trend to 500 °C. We used sodium nitrate melts to elucidate phase equilibria in the range 500°–300 °C and to trace the solvus line.¹² The extent of the solid solution sharply narrows below 350 °C. The solvus line features an inflection with a near-horizontal segment. This anomalous behavior is explained by a diffuse phase transition that occurs in compounds with a fluorite structure, accompanied by disordering of the anion sublattice.^34,35,36 The fact is that lanthanide fluorides are soluble only in the high-temperature disordered phases of fluorite compounds.

Fig. 6

Copyright^© 2024 The American Ceramic Society, all rights reserved.

Phase diagram of the SrF₂–LaF₃ system plotted according to Sobolev and Seiranian,³² Yoshimura et al.,^23,33 and our data.¹² Notations: (ο) SrF₂ss = Sr_1-xR_xF_2+x solid solution and (·) LaF₃ss = La_1-ySr_yF_3-y solid solution. Half-shaded circles refer to two-phase samples. Reprinted with permission from Pavel P. Fedorov, Alexander A. Alexandrov, Valery V. Voronov, et al., Low‐temperature phase formation in the SrF₂–LaF₃ system, Journal of the American Ceramic Society, John Wiley and Sons.

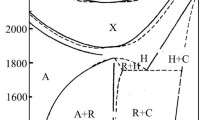
Figure 7 shows a summary phase diagram of the ZrO₂–Sc₂O₃ system. The high-temperature portion of the phase diagram is constructed based on detailed experimental data.^{37,38,39,40,41,42,43} For 1200 °C, Spiridonov et al.’s data⁷ were taken into account, too. In order to construct the 1000 °C isotherm, we annealed the precursors coprecipitated from aqueous solutions in a sodium sulfate melt for one week.

Fig. 7

Summary phase diagram of the ZrO₂-Sc₂O₃ system according to Sekiya et al.,³⁷ Spiridonov et al.,¹² Shevchenko et al.,^38,39,40,41 Fujimori et al.,^42,43 and our data. Notations: dots refer to DTA data, empty circles to single-phase samples, and half-shaded circles to two-phase samples

The ZrO₂–Sc₂O₃ system forms extensive solid solutions based on scandium oxide (bixbyite type, phase C) and the high-temperature cubic zirconia phase: Zr_1-xSc_xO_2-0.5x (phase F). The melting curves of the fluorite solid solution feature a maximum. As temperature decreases, the fluorite solid solution (phase F) transforms into separate ordered phases, to which the notations β, γ, and δ were assigned, with the respective compositions Zr₇Sc₂O₁₇, Zr₅Sc₂O₁₅, and Zr₃Sc₄O₁₂ (the cubic solid solution, i.e. phase F, was referred to as phase α). The composition of phase β was determined more exactly as Zr₅₀Sc₁₂O₁₁₈ due to structural studies.⁴⁴ The β, γ, and δ low-temperature phases have their fluorite lattices trigonally distorted because of an ordered arrangement of anionic vacancies. The differentiation of cations over crystallographic positions, although favorable in energy,⁴⁵ almost does not occur because of frozen diffusion.⁴⁶

4 Extrapolation to Low Temperatures

The third law of thermodynamics provides a reliable base for the design of phase equilibria at low temperatures, where direct experiments are not possible.^47,48 In Planck’s formulation, phases in equilibrium at T = 0 K should have zero entropies. This means the following: as temperature tends to absolute zero, all phases of variable composition, which have an excess configurational entropy, should either decompose or transform into strictly ordered stoichiometric compounds in a quasi-equilibrium process.^2,3,5

The above-considered phase diagrams illustrate these scenarios, namely, the decomposition of solid solutions into components (in the SrF₂–LaF₃ system; Fig. 6) and the transformation of solid solutions into separate ordered phases having narrow homogeneity ranges (in the ZrO₂–Sc₂O₃ system; Fig. 7). Another striking example of the manifestation of the third law of thermodynamics is the aluminum oxide–magnesium oxide system,⁴⁹ where an intermediate spinel phase is formed with a large homogeneity range at high temperatures, but shrinks to the MgAlO₄ stoichiometry below 1400 °C. In the Na₂SO₄–K₂SO₄ system, a continuous solid solution between the high-temperature sodium sulfate and potassium sulfate phases transforms into a separate nonstoichiometric phase with a large homogeneity range (ca. 25–70 mol% K₂SO₄), which shrinks to stoichiometric composition, K₃Na(SO₄)₂ (glaserite), as temperature decreases to ca. 0 °C (Fig. 4)¹⁹).

The third law offers a powerful tool to extrapolate phase equilibria and to design phase diagrams at temperatures to absolute zero. However, reliable results can be gained thereby only when reliable experimental data are used, corresponding to an equilibrium state of the system at the temperatures studied. First of all, before extrapolation one has to understand in which temperature range equilibrium is acquired.

A significant addition to such an extrapolation is the condition for the presence of vertical tangents to the solvus curves at T → 0 K.⁵⁰ This pertains both to terminal solid solutions and to intermediate phases.

We have demonstrated the effectiveness of this approach for a number of systems.

4.1 The Au–Cu System

In this system (Fig. 8), the Au_1-xCu_x continuous solid solution having an fcc structure (space group Fm $\overline{3 }$ m) crystallizes from melt. As temperature decreases, the solid solution experiences ordering, noticed as long ago as by Kurnakov et al.,⁵³ to separate three intermetallic phases. Two of these phases have structures of the Cu₃Au type (cubic crystals system, sub-space group Pm $\overline{3 }$ m) and one of the AuCu type (tetragonal crystal system, sub-space group P4/mmm). Their ideal compositions, which correspond to the full differentiation of metal atoms over crystallographic positions, are formulated as Cu₃Au, AuCu, and CuAu₃. It is to these compositions that the homogeneity ranges of the three phases of variable composition shrink when temperature tends to absolute zero. The increasing temperature decreases the degree of ordering and gives rise to the appearance of homogeneity ranges in these phases. The phase diagram also features phases that correspond to intermediate ordering stages of the solid solution (AuCuII and Cu₃AuII phases). Noteworthy, Fedorov and Volkov in their low-temperature extrapolation of phase fields⁵² almost needed not to correct Okamoto et al.’s diagram.⁵¹

Fig. 8

Phase diagram of the Au–Cu system. Solid lines refer to Okamoto et al.⁵¹ and dashed lines refer to Fedorov and Volkov’s low-temperature extrapolation.⁵² Reprinted with permission from Pleiades Publishing, Ltd

4.2 The Cu–Pd System

The copper–palladium system (Fig. 9) is similar to the preceding one. At high temperatures, a continuous fcc solid solution (phase α) is formed. Detailed experiments by Popov et al.⁵⁴ detected low-temperature ordering. As a result of our extrapolation, the phase fields naturally shrink to two phases (γ and β), whose ideal compositions are Cu₃Pd and CuPd, respectively⁵⁵ (Fig. 9). However, the near-palladium course of the curve along which solid solution α limit decreases and does not allow for extrapolation with the observance of a vertical tangent to the solvus curve at T → 0. Likely, a third intermetallic with the ideal composition CuPd₃ (phase ε) is formed in this system, but its stability field lies below 200 °C. A suggested phase diagram appears in Fig. 9b. This diagram is a good complement to the summary diagram in Ref 56.

Fig. 9

Phase diagram of the Cu–Pd system extrapolated to 0 K: (a) our previous data from (Ref 55) and (b) data of this work. Notations: (1) α phase (fcc copper–palladium solid solution), (2) CuPd-based β phase, (3) Cu₃Pd-based γ phase, (4) δ phase of idealized composition Cu₂₁Pd₇, (5) α + β two-phase area, and (6) δ + β two-phase area. Reprinted with permission from Pleiades Publishing, Ltd

4.3 The Ni–Pt System

In long-term experiments, three intermetallics were found to exist at 400–550 °C in the nickel–platinum system because of ordering of the high-temperature fcc solid solution. Experimental data^11,56,57 can naturally be extrapolated to absolute zero temperature (Fig. 10a). The misfit between the extrapolation and experiment is in the following: the diagram features Ni_1-xPt_x + Ni₃Pt and Ni_1-xPt_x + NiPt₃ two-phase areas at 400 °C as shown in Fig. 9(a), while anneals yielded disordered single-phase samples. Apparently, the transition from the disordered solid solution to two-phase areas requires that the solid solution decays by the nucleation scheme to overcome the potential barrier, and long anneals at this low temperature are needed. It is pertinent to mention here that the annealing times Popov et al.¹¹ used were as close to the longest possible times for a laboratory experiment.

Fig. 10

(a) Correct and (b) incorrect extrapolation of phase equilibria to absolute zero temperature in the Ni–Pt system.⁵⁸ Notations: (1) disordered Ni_1–xPt_x solid solution, (2) intermetallic compound Ni₃Pt, (3) intermetallic compound NiPt, (4) two-phase region NiPt + NiPt₃, (5) two-phase region NiPt + Ni_1–xPt_x, (6) intermetallic compound NiPt₃, (7) boundaries of single-phase regions according to X-ray powder diffraction data, (8) NiPt₃ disordering temperature,⁵⁷ and (9) single-phase NiPt₃ sample.⁵⁷ [Ni] is the Ni_1–xPt_x solid solution enriched in nickel, [Pt] is the Ni_1–xPt_x solid solution enriched in platinum. Asterisks mark tricritical points. Reprinted with permission from Pleiades Publishing, Ltd

Our suggested phase diagram variant is in reasonable agreement with Lu et al.’s thermodynamic simulation.⁵⁹ In contrast, the bizarre model phase diagram Dahmani et al.⁶⁰ calculated for this system based on mean field theory grossly contradicts the third law of thermodynamics and, accordingly, is incorrect.

Figure 10(b) illustrates a second option for extrapolating experimental data to zero temperature. It involves an assumption that the single-phase Ni_1-xPt_x solid solution prepared at 400 °C is in an equilibrium state. The Ni_1-xPt_x + Ni₃Pt and Ni_1-xPt_x + NiPt₃ two-phase areas are degenerate to segments of curves. This means that the ordering to form Ni₃Pt and NiPt₃ phases occurs through the second-order phase transition mechanism. In the phase diagram, there appear what is called tricritical points; a tricritical point is the point where the character of phase transition changes from a second-order to first-order one, to generate two-phase areas.^61,62,63,64 Such a point is well known for the helium ³He–⁴He isotope system at low temperatures.^65,66 The phase diagrams of the CaCO₃–MgCO₃⁶⁷ and NaNO₃–KNO₃⁶⁸ systems also feature tricritical points in a solid state. However, this interpretation of phase equilibria in the Ni–Pt system is incorrect, because the thermodynamics forbids ordering of an fcc solid solution to separate phases of the Cu₃Au type by the second-order transition scheme.⁶⁹

4.4 The ZrO₂-Y₂O₃ System

This is a classic and a model system. It was studied by various research teams.⁷⁰ The most detailed studies of solid-state phase equilibria in this system are those by Pascual and Duran⁸ and by Stubican et al.,⁹ where anneals lasted up to eight months. The results of the two works are in good agreement with each other. The low-temperature extrapolation (Fig. 11a) is based on Pascual and Duran’s data.⁸ Pascual and Duran annealed samples for 3 hours at 2000 °C, 10 hours at 1800 °C, and up to 8 month at 1500 °C, which looks acceptable for their results to be taken as corresponding to equilibrium.⁶ Obviously, however, their 8-month anneals at 800 °C were yet insufficient. A revised equilibrium phase diagram is shown in Fig. 11(b). The phase compositions of the samples annealed and quenched by Pascual and Duran are shown in Fig. 11(b) (half-shaded symbols refer to two-phase samples).

Fig. 11

(a) Phase diagram of the ZrO₂–Y₂O₃ system according to Pascual and Duran⁸ and (b) its revision subject to the third law of thermodynamics. Reprinted from Ref 70 with permission from Condensed Matter and Interphases

Extensive heterovalent solid solutions based on the high-temperature fluorite ZrO₂ phase (phase F, space group Fm $\overline{3 }$ m) and the low-temperature cubic Y₂O₃ phase (phase C, bixbyite type, space group Ia $\overline{3 }$) are formed in the system. Although the bixbyite structure is a derivative from the fluorite type with an ordered vacancy arrangement,⁷¹ the F + C two-phase field of the phase diagram was reliably identified as long ago as by Duwes et al.⁷²

The dissolution of yttrium oxide in the high-temperature ZrO₂ phase stabilizes the fluorite structure, and the liquidus curve shows a maximum. The maximum on the melting curve of the solid solution is an invariant point, and this is the point where the liquidus and solidus curves coincide with a common horizontal tangent. When drawing the liquidus in this region of the phase diagram, Pascual and Duran made an unfortunate mistake, which is corrected in Fig. 11(b). The solid solutions based on phase F and phase C become ordered as temperature decreases as separate ordered phases: Y₄Zr₃O₁₂ and Y₆ZrO₁₁ (idealized compositions), respectively. Pascual and Duran’s⁸ and Stubican et al.’s⁹ data on the F ↔ Y₄Zr₃O₁₂ phase-transition temperature are in excellent agreement (± 10 °C). The corrections we made in the region of high yttrium oxide compositions are: an appreciably narrowed homogeneity range of the ordered phase, which should shrink to the ideal composition Y₆ZrO₁₁ as temperature decreases; and a revised position of the decreasing solubility curve for the yttrium oxide-base cubic solid solution, which should come to the pure component point at T → 0 K.

Apparently, the observation of an extensive area of the “Y₆ZrO₁₁” ordered phase in the absence of a two-phase field shared with phase C is due to the following: in Pascual and Duran’s experiments,⁸ the ordering in this system occurred according to a diffusionless, nonequilibrium mechanism, which did not require overcoming the potential barrier to the nucleation of a new phase in the bulk of the old one. Our analysis shows that the same occurred during low-temperature ordering in the Ni–Pt system⁵⁸ (see above) and in the HfO₂–R₂O₃ systems (fluorite–pyrochlore transitions).⁷⁰

The low yttrium oxide composition region (where the tetragonal phase, i.e., the solid solution based on medium-temperature ZrO₂ phase, decomposes) in Fig. 11(b) was corrected by analogy with Yashima et al.’s data,⁷³ who annealed samples for 48 hours at 1690 °C and for 8 months at 1315 °C when they studied equilibria in a similar system (ZrO₂–Er₂O₃). In our corrected version, the eutectoid decomposition temperature of the tetragonal phase is several hundred degrees higher than that in the documented variant phase diagrams^8,9).

The dashed line in Fig. 11(b) refers to a metastable extension of the limiting composition curve of the solid solution (the solvus curve of phase F). This curve should come to the origin, in addition to having there a vertical tangent. This condition can be fulfilled if there is an inflection on the solvus curve (in the case at hand, on the metastable portion of this curve). Importantly, the eutectoid corresponding to the decomposition of the fluorite phase should lie above the metastable solvus curve. Accordingly, the eutectoid decomposition temperature of the cubic solid solution is provisionally drawn at 600 ± 100 °C. This is a much higher temperature than reported in all works (both in experimental and computational ones) that deal with phase equilibria in this system.

4.5 The NaAlSi₃O₈–CaAl₂Si₂O₈ System

The albite–anorthite (NaAlSi₃O₈–CaAl₂Si₂O₈) system, which reflects phase transformations in sodium–calcium feldspars (plagioclases), in particular, their ordering is very important from the geological point of view. Feldspar minerals with medium cation contents are referred to as labradorites.

The albite–anorthite system is a classical example of conjugate heterovalent cationic isomorphism with the maintenance of the number of ions in the unit cell described by the reaction Na⁺  + Si⁴⁺ ⇔ Ca²⁺ + Al³⁺. The general formula of the solid solution is written as Na_1-xCa_xAl_1+xSi_3-xO_8.

The main difficulty one encounters in constructing a phase diagram lies in the extremely slow rates of ordering and decomposition of solid solutions at low temperatures; as a result, reaching equilibrium at temperatures below ca. 400–600 °C is impossible even over geological time, even in the presence of water promoting phase reactions.²² However, variants of phase transformations are proposed primarily based on studies of natural minerals by both X-ray diffraction analysis and high-resolution electron microscopy and electron diffraction.^{74,75,76,77,78,79}

A second-order phase transition is reliably identified to occur between the high- and low-temperature albites: C-1(high) and C-1(low). The line of this phase transition in the binary system ends with a tricritical point to generate a C-1(high) + C-1(low) miscibility gap, which appears mineralogically as a lamellar structure (peristerite). The line of the second-order phase transition between C-1(high) and the anorthite-base solid solution (phase I-1) is also reliably identified. In addition, two modulated intermediate phases with incommensurate ordering were isolated in this system, namely, phase e₁ and phase e₂. In addition to peristerite, two more fields with lamellar structures occur at higher anorthite content: Bøggild and Huttenlocher gaps.

Various versions of solid-solution ordering were proposed.^{74,75,76,78,79} We took Jin and Xu’s data^78,79 (Fig.12a) as the base for our low-temperature extrapolation.

Fig. 12

(a) Phase equilibria in the albite–anorthite system according to Jin et al.⁷⁹ and (b) our extrapolation to 0 K. Triangular symbols denote tricritical points

Our scheme of phase equilibria appears in Fig. 12(b). The images of possible spinodals are omitted from the figure. A small correction for the three-phase horizontal was needed to interpret the relationships among phases C-1(high), I-1, and e₁. It is pertinent to mention that there was almost no need to correct the lines in the diagram of Fig. 12(a) in order to extend phase fields to 0 K. The homogeneity range of phase e₁ naturally shrinks to the 1:1 composition, namely, to the compound NaCaAl₃Si₅O₁₆. The condition for the presence of vertical tangents at T → 0 is fulfilled. The same pertains to the boundaries of the terminal solid solutions.

Thus, the diagram should be in its final form. However, it is very unusual. The diagram features:

• One horizontal segment at ca. 700 °C, corresponding to peritectoid equilibrium of three phases: C-1(high), I-1, and e₁;

• Six second-order phase transitions (or “continuous phase transitions”), which occur without two-phase fields in the binary T–x phase diagram, represented by curvilinear segments between single-phase fields in the diagram;

• Horizontals in two-phase fields, which do not correspond to three-phase equilibria but refer to second-order phase transitions in one of the coexisting phases (there are five of them);

• Two classical tricritical points, where the phase transitions change their character from second-order to first-order phase transitions, to generate miscibility gaps (shown by triangular symbols in Fig. 12(b)); and

• An unusual quaternary point,^1,80 where e₁, e₂, and C-1 phase fields meet.

Overall, this system is a tasty morsel for theorists.

A specific feature of this phase diagram variant is the formation of fully ordered labradorite, namely, a 1:1 compound described by the formula NaCaAl₃Si₅O₁₆. The fundamental distinction of the Bøggild lamellar structure from the peristerite and Huttenlocher structures becomes obvious. While the latter two correspond to the morphology of the spinodal decay of solid solutions⁸¹ (C-1_low + e and e + I-1, respectively), the Bøggild gap ocorresponds to the modulation of the solid solution, which ultimately should give rise to the appearance of albite and anorthite nanolayers of equal thicknesses in the ordered labradorite structure.

5 Conclusions

To conclude the paper, we will make some general comments and, among other things, outline some issues that require further research.

• 1. As shown above, the third law of thermodynamics offers a powerful and very efficacious tool to gain new information about phase equilibria in that region of temperatures where experiment is impossible practically, and even theoretically. However, the universality and, thus, the scope of applicability of the third law of thermodynamics is not entirely clear. Some questions arise, for example, with the system of helium isotopes ³He–⁴He, where one of the components certainly has its homogeneity region reaching absolute zero temperature as temperature decreases.^65,66 It also remains unclear whether the third law is applicable to systems comprised of various isotopes of one element. Metals, as well as oxides and halides (ionic compounds), however, apparently obey this law, as the above analysis of a number of examples showed.

• 2. Interesting is the seeming disobedience to the third law of thermodynamics in the case of series of homologous compounds and, in particular, modulated phases, which, upon experimental study, at first glance look like phases of variable composition. In this case, the composition area of existence for an infinite number of stoichiometric phases can apparently reach absolute zero temperature. The Sb–Te system⁸² and Vernier phases in lanthanide oxyfluorides^5,83 can serve as examples. However, the presence of a modulated phase does not necessarily mean that a series of modulated phases covering the entire composition range would reach absolute zero temperature. Examples are the above-considered plagioclase system and the Al₂O₃–SiO₂ system, in which high-temperature modulated mullite converts to stoichiometric sillimanite.^14,84,85,86

• 3. In view of the great complexity of research into phase equilibria at relatively low temperatures, it looks quite natural that so-called "glued-together" phase diagrams appear, including in reference literature, in which the high-temperature part of the diagram shows equilibrium phase fields and the low-temperature part shows nonequilibrium or partial equilibrium fields. In many cases, the "glued-together" word could also apply to the phase diagrams with martensitic phase transformations described in the literature.⁸⁷ Therefore, special attention should be paid to the choice of phase equilibria to be used for the design of thermodynamic models.

• 4. The laws governing the course of spinodals are completely unclear. Experimental methods for determining the spinodal position are few, and they are efficacious only when the kinetics of phase transitions is relatively fast.⁹⁰ Eliseev et al.’s work⁹¹ is also worth mentioning. In the regular solution model, the spinodal coincides at its maximum with the binodal curve. At T → 0 K, the spinodal curve comes to the terminal component points, but as opposed to the binodal, at these points it has no ordinate axes as vertical tangents (Fig. 13). We noted a mistake in Fig. 16 in Prigogin and Defay’s monograph.⁸⁸ In systems with continuous solid solutions, the spinodals have fundamentally the same course in case the system deviates from regularity,⁸⁹ but more complex cases with limited solid solutions are not so obvious. For example, how does the spinodal behave with the decomposition of Sr_1-xR_xF_2+x solid solution (Fig. 5)? However, qualitative considerations imply that fluorite solid solutions, both fluoride M_1-xR_xF_2+x (M = Ca, Sr, or Ba) and oxide Zr_1-xR_xO_2-0.5x (R = lanthanides) ones, are in a labile state at ambient temperature and pressure, but their spinodal decomposition is very retarded. The same pertains to functional materials comprising them: the technological stability of those materials is far higher than their thermodynamic stability.⁹²

• 5. In the analysis of low-temperature phase equilibria, a first- principles calculations can be of significant help. There may be situations when calculations show that a phase that is stable at elevated temperatures loses stability when the temperature decreases. Or vice versa, the phase, which, according to the calculation, is stable at T = 0, is absent in the studied temperature range of the phase diagram. In such cases, it should be assumed that there is a non-invariant three-phase equilibrium on the phase diagram, which will have the character of eutectoid decomposition in the first case (Fig. 14a), or peritectoid equilibrium in the second (Fig. 14b). The temperatures of the corresponding αβγ equilibria remain very uncertain.

Fig. 13

Binodal and spinodal (dashed) lines for the decomposition of solid solutions in terms of the regular solutions model

Fig. 14

Low-temperature regions of binary phase diagrams in cases where the gamma phase loses stability with a decrease (a) or an increase in temperature (b)