1 Introduction

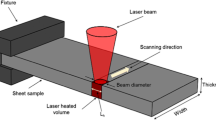
During the last two decades laser forming process has been considered as a new and suitable technique to manufacture the contoured parts, without external forces, from the sheet materials. It allows automation of manufacturing processes in the aerospace, automobile, and shipbuilding industries (Ref 1,2,3). The technique offers various engineering advantages compared to common forming processes. The known advantages consist of design flexibility, manufacture of complex shapes, and possibility of rapid prototyping (Ref 4,5,6,7,8). In this process, external forces and dies are not necessary, and various shapes can be produced (Ref 9,10,11). When the sheet material is subjected to the laser irradiation, because of the absorption of laser energy, the temperature in the sheet is increased leading to the generation of thermal stress in the sheet. So laser irradiation has a thermo-mechanical coupling effects that can be used in laser processing applications (Ref 12,13,14).

To control the deformation of a metallic sheet during the laser forming, the dominant mechanism of deformation should be detected. The mechanism is identified by the temperature field in the sheet which is affecting by the dimensions of the sheet, as well as, the laser parameters such as the laser spot diameter, scanning velocity, scanning path, and the laser power (Ref 15,16,17,18,19). The three main mechanisms of deformation proposed so far are the temperature gradient mechanism (TGM), buckling mechanism (BM), and upsetting mechanism (UM) (Ref 20,21,22,23). These mechanisms are illustrated in Fig. 1. As it is seen there is a temperature gradient in the sheet thickness in the TGM while in the other two mechanisms the temperature through the thickness is nearly constant. Hence, in order to identify the deformation mechanism, the temperature field should be evaluated. This has generally been carried out by the thermal analysis computer software based on the finite element method or the simplified theoretical formulae (Ref 21, 24, 25). Therefore, from the results of temperature analysis, if there is a temperature gradient along the thickness, one can be sure that TGM is the dominant mechanism but if no temperature gradient exists, the temperature analysis is not sufficient to distinguish which of the other two mechanisms (UM and BM) shall be dominant. The dominant mechanism depends on many factors such as sheet thickness, sheet material, scanning velocity, power of laser, etc. In the conditions with similar process parameters, the sheet is thinner in BM than in UM. However, the TGM is dominant in the different process parameters and the thickness of the sheet in this process cannot be compared with the two other mechanisms. In UM, the geometry of the sheet inhibits the buckling due to the increased moment of inertia and the metal sheet is mainly reduced in width and increased in thickness inducing plane strain deformation in the sheet (Ref 21, 26). Moreover, in UM, a negligible bending deformation takes place while in BM there is a considerable bending deformation (Ref 27). In some industrial cases only the plane strain deformation needs to be carried out, so in these cases the UM must be dominant. On the other hand, in many industrial applications, the aim of laser forming is to achieve a bending deformation. In such cases either the BM or TGM must be applied because as mentioned earlier, in UM the bending deformation is negligible. However, as in thin sheets, the temperature through the thickness direction is nearly constant, thus, the TGM should not occur. Here this question arises that in laser forming of thin sheet which of the remaining mechanisms (UM or BM) is likely to occur? On the other words, in laser forming of thin sheet, detecting the dominant mechanism between the probable two mechanisms (UM and BM) is necessary to control the deformation of the sheet during the laser forming. In order to answer to that question, in some published works it has been expressed that if the width of the heated area by the laser beam is much larger than the plate thickness, the BM is dominant (Ref 28,29,30). However, it will be shown for the first time, by a new analytical and numerical analyses carried out in present work, that there are other factors such as the dimensions, thermal, and mechanical properties of the sheet and the laser beam diameter, power, and scanning velocity which can affect the dominant deformation mechanism. Therefore, the aim of this research is to predict the dominant deformation mechanism in laser forming of thin sheet and to predict the effects of process parameters on the position of the boundary between BM and UM. To verify the analytical model, the predicted results are compared with the published experimental data, as well as, the results achieved from a finite element analysis based on the ABAQUS software.

Fig. 1
figure 1

The schematics of the laser forming mechanisms

Full size image

2 Modeling

2.1 Analytical Model

In order to establish the analytical model, the following assumptions were made:

1) The initial sheet is stress-free, thin, and isotropic flat with thickness h, width 2b, and length 2L; lying in the x-y plane (x along the length and z through the thickness direction).

2) The sheet is a thin sheet with length to width ratio greater than 5.

3) At the boundaries, at \(y=\pm b\), no torque and force is applied.

4) The thermal strains in the y and z directions were neglected.

5) The sheet is suddenly heated and the variation of temperature due to laser scanning, in the longitudinal direction of the sheet, is ignored.

6) The plate width is much larger than the laser beam diameter.

It should be mentioned that the thin sheet usually refers to a sheet with a thickness smaller than 1 mm. It has been reported by Shen et al. (Ref 4) that the dependence of the laser parameters and material properties on the average temperature change in the heated area is:

$$\Delta {\text{T}} = \frac{{4{\text{PAK}}\left( {1 - {\text{exp}}\left( { - \frac{1}{2}\frac{{\rho {\text{Cu}}_{{\text{s}}} {\text{h}}}}{{\text{K}}}} \right)} \right)}}{{\rho^{2} {\text{C}}^{2} {\text{u}}_{{\text{s}}}^{2} {\text{h}}^{2} {\text{d}}}}$$
(1)

where K, ρ, and C are the coefficient of thermal conductivity, density, and heat capacity of the sheet material, us the laser scanning velocity, and A is the absorption coefficient of the sheet material. P and d are the laser power and laser beam diameter, respectively.

In our work, the laser beam was assumed to be a Gaussian beam. Therefore, it was reasonable to define the thermal strain imposing to the sheet due to laser beam irradiation as:

$${\overline{\varepsilon }}_{x}^{th}=\alpha \cdot\Delta T\cdot \text{exp}\left(-8\cdot \frac{{y}^{2}}{{d}^{2}}\right)$$
(2)

where \(\alpha\) is the thermal expansion coefficient, y is the -y direction in the cartesian coordinate system, and \(\Delta T\) is the average temperature change which can be represented by Eq 1. For a given sheet geometry, by controlling the laser parameters, the magnitude of imposed average temperature change can be increased. By increasing the average temperature change, the strain energy in the sheet is enhanced and the plate is stretched along its length. This stretching is continued until the stored strain energy in the sheet becomes enough for the occurrence of buckling. Using the Hook’s law, the elastic energy per unit volume (U) is equal to (Ref 31):

$$U=\frac{E}{2\cdot (1-{\nu }^{2})}\cdot {\int }_{V}\left({{\overline{\varepsilon }}_{x}^{e}}^{2}+{{\overline{\varepsilon }}_{y}^{e}}^{2}+2\cdot \nu \cdot {\overline{\varepsilon }}_{x}^{e}\cdot {\overline{\varepsilon }}_{y}^{e}+2{{\cdot (1-\nu )\cdot \overline{\varepsilon }}_{xy}^{e}}^{2}\right)dx\cdot dy\cdot dz$$
(3)

where E is the young modulus, ν the Poisson ratio, \({\overline{\varepsilon }}_{x}^{e}\) and \({\overline{\varepsilon }}_{y}^{e}\) the normal elastic strains in the x and y directions, respectively, and \({\overline{\varepsilon }}_{xy}^{e}\) the elastic shear strain. The total strain component is equal to the sum of elastic and thermal strain components. Hence:

$${\overline{\varepsilon }}_{x}={\overline{\varepsilon }}_{x}^{e}+{\overline{\varepsilon }}_{x}^{th}, {\overline{\varepsilon }}_{y}={\overline{\varepsilon }}_{y}^{e}+{\overline{\varepsilon }}_{y}^{th}, {\overline{\varepsilon }}_{xy}={\overline{\varepsilon }}_{xy}^{e}+{\overline{\varepsilon }}_{xy}^{th}$$
(4)

Using the Kirchhoff assumptions (Ref 31), it is easy to show that:

$${\overline{\varepsilon }}_{x}={\varepsilon }_{x}+z\cdot {k}_{x}, {\overline{\varepsilon }}_{y}={\varepsilon }_{y}+z\cdot {k}_{y}, {\overline{\varepsilon }}_{xy}={\varepsilon }_{xy}+z\cdot {k}_{xy}$$
(5)

where k and ε notations represent the middle plane strains and curvatures, defined by Eq 6 and 7, respectively.

$${k}_{x}=-\frac{{\partial }^{2}w}{\partial {x}^{2}}{, k}_{y}=-\frac{{\partial }^{2}w}{\partial {y}^{2}}, {k}_{xy}=-\frac{{\partial }^{2}w}{\partial x\partial y}$$
(6)

and

$$\varepsilon _{x} = \frac{{\partial u}}{{\partial x}} + \frac{1}{2} \cdot \left( {\frac{{\partial w}}{{\partial x}}} \right)^{2} ,\varepsilon _{y} = \frac{{\partial v}}{{\partial y}} + \frac{1}{2} \cdot \left( {\frac{{\partial w}}{{\partial y}}} \right)^{2} ,\varepsilon _{{xy}} = \frac{1}{2} \cdot \left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} + \frac{{\partial w}}{{\partial x}} \cdot \frac{{\partial w}}{{\partial y}}} \right)$$
(7)

where u and v are the in-plane displacement components in the x and y directions, respectively and w is the displacement in the z direction (lateral displacement). These components belong to the middle plane of the sheet. The internal forces per unit length (N) and moments per unit length (M) acting on the edges of an element \(dx\cdot dy\) are related to the internal stresses using the following relations (Ref 32):

$${N}_{x}={\int }_{-h/2}^{h/2}{\sigma }_{x}dz, {N}_{y}={\int }_{-h/2}^{h/2}{\sigma }_{y}dz, {N}_{xy}={\int }_{-h/2}^{h/2}{\sigma }_{xy}dz$$
(8)

and

$${M}_{x}={\int }_{-h/2}^{h/2}{\sigma }_{x}\cdot z\cdot dz, {M}_{y}={\int }_{-\frac{h}{2}}^\frac{h}{2}{\sigma }_{y}\cdot z\cdot dz, {M}_{xy}={\int }_{-h/2}^{h/2}{\sigma }_{xy}\cdot z\cdot dz$$
(9)

Taking the first variation of the elastic energy functional, Eq 3, setting it to zero, and using Eq 5 to 7, the following relations are achieved:

$$\frac{\partial {\text{N}}_{\text{x}}}{\partial \text{x}}+\frac{\partial {\text{N}}_{\text{xy}}}{\partial \text{y}}=0$$
(10)
$$\frac{\partial {\text{N}}_{\text{xy}}}{\partial \text{x}}+\frac{\partial {\text{N}}_{\text{y}}}{\partial \text{y}}=0$$
(11)
$$D\cdot \left(\frac{{\partial }^{4}w}{\partial {x}^{4}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}+2\cdot \frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}\right)+\left({k}_{x}\cdot {N}_{x}+2\cdot {k}_{xy}\cdot {N}_{xy}+{k}_{y}\cdot {N}_{y}\right)=-{M}^{th}$$
(12)

where D, the bending stiffness, is equal to:

$$D=\frac{E\cdot {h}^{3}}{12\cdot (1-{\nu }^{2})}$$
(13)

and Mth is a function relating to the thermal strains components as:

$$M^{{th}} = \frac{{\text{E}}}{{1 - \nu ^{2} }} \cdot \smallint _{{ - h/2}}^{{h/2}} \left( {\frac{{\partial ^{2} \bar{\varepsilon }_{x}^{{th}} }}{{\partial x^{2} }} + \nu \cdot \frac{{\partial ^{2} \bar{\varepsilon }_{x}^{{th}} }}{{\partial y^{2} }} + \frac{{\partial ^{2} \bar{\varepsilon }_{y}^{{th}} }}{{\partial y^{2} }} + \nu \cdot \frac{{\partial ^{2} \bar{\varepsilon }_{y}^{{th}} }}{{\partial x^{2} }} + (1 - \nu ) \cdot \frac{{\partial ^{2} \bar{\varepsilon }_{{xy}}^{{th}} }}{{\partial x\partial y}}) \cdot zdz} \right)$$
(14)

Considering the Airy stress function, Φ, the internal forces per unit length are:

$${N}_{x}=\frac{{\partial }^{2}\Phi }{\partial {y}^{2}}, {N}_{y}=\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}, {N}_{xy}=-\frac{{\partial }^{2}\Phi }{\partial x\partial y}$$
(15)

Equation 15 satisfies the equilibrium Eq 10 and 11. Then, Eq 12 becomes:

$$D\cdot \left(\frac{{\partial }^{4}w}{\partial {x}^{4}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}+2\cdot \frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}\right)-\left(\frac{{\partial }^{2}\text{w}}{\partial {x}^{2}}\cdot \frac{{\partial }^{2}\Phi }{\partial {y}^{2}}+\frac{{\partial }^{2}\text{w}}{\partial {y}^{2}}\cdot \frac{{\partial }^{2}\Phi }{\partial {x}^{2}}-2\cdot \frac{{\partial }^{2}w}{\partial x\partial y}\cdot \frac{{\partial }^{2}\Phi }{\partial x\partial y}\right)=-{M}^{th}$$
(16)

The compatibility equation can be expressed as (Ref 32):

$$\frac{{\partial }^{2}}{\partial {\text{y}}^{2}}\left(\frac{\partial \text{u}}{\partial \text{x}}\right)+\frac{{\partial }^{2}}{\partial {\text{x}}^{2}}\left(\frac{\partial \text{v}}{\partial \text{y}}\right)-\frac{{\partial }^{2}}{\partial \text{x}\partial \text{y}}\left(\frac{\partial \text{u}}{\partial \text{y}}+\frac{\partial \text{v}}{\partial \text{x}}\right)=0$$
(17)

Using the Eq 4 to 7, the integration in z direction from the both sides of Eq 17 leads to:

$$\left(\frac{{\partial }^{4}\Phi }{\partial {x}^{4}}+\frac{{\partial }^{4}\Phi }{\partial {y}^{4}}+2\cdot \frac{{\partial }^{4}\Phi }{\partial {x}^{2}\partial {y}^{2}}\right)+E\cdot h\cdot \left(\frac{{\partial }^{2}\text{w}}{\partial {x}^{2}}\cdot \frac{{\partial }^{2}\text{w}}{\partial {y}^{2}}-{(\frac{{\partial }^{2}\text{w}}{\partial x\partial y})}^{2}\right)=-{N}^{th}$$
(18)

where Nth is a function relating to the thermal strain components as:

$${N}^{th}=E\cdot {\int }_{-h/2}^{h/2}\left(\frac{{\partial }^{2}{\overline{\upvarepsilon }}_{\text{x}}^{\text{th}}}{\partial {y}^{2}}+\frac{{\partial }^{2}{\overline{\upvarepsilon }}_{\text{y}}^{\text{th}}}{\partial {x}^{2}}-2\frac{{\partial }^{2}{\overline{\upvarepsilon }}_{\text{xy}}^{\text{th}}}{\partial x\partial y}\right)dz$$
(19)

For a thin sheet with length to width ratio greater than 5, it is reasonable to assume that the sheet length is infinite along its length (the x direction) (Ref 33). Since the edges of the sheet at \(y=\pm b\) are free, the \({N}_{xy}\) and \({N}_{y}\) at \(y=\pm b\) are zero. Moreover, as the sheet length is much larger than its width, the variation of the internal forces in the y direction may be ignored. This means:

$$\frac{\partial {N}_{y}}{\partial y}=\frac{\partial {N}_{xy}}{\partial y}=0$$
(20)

Referring to Eq 10, 11, and 20 one can conclude that:

$$\frac{\partial {N}_{x}}{\partial x}=\frac{\partial {N}_{xy}}{\partial x}=0$$
(21)

According to Eq 21, \(\frac{\partial {N}_{x}}{\partial x}=0\). Thus, Nx depends only on y direction. Since \(\frac{\partial {N}_{xy}}{\partial x}=\frac{\partial {N}_{xy}}{\partial y}=0\), so, Nxy must be constant and as Nxy at the boundary is zero, it is deduced that at any point in the sheet, Nxy is zero. Similarly, according to Eq 20, Ny only depends on x direction. Further, at \(y=\pm b\), Ny must be zero for all the x values. Therefore, Ny does not depend on the x direction. Hence, at any point in the sheet Ny is equal to zero and in term of the Airy stress function one can write:

$$\frac{{\partial }^{2}\Phi }{\partial {x}^{2}}=\frac{{\partial }^{2}\Phi }{\partial x\partial y}=0$$
(22)

As in the boundaries, at \(y=\pm b\), no torque and force is applied, the boundary conditions can be defined as (Ref 34):

$$\left(\frac{{\partial }^{2}\text{w}}{\partial {y}^{2}}+\nu \cdot \frac{{\partial }^{2}\text{w}}{\partial {x}^{2}}\right)=\left(\frac{{\partial }^{3}\text{w}}{\partial {y}^{3}}+(2-\nu )\cdot \frac{{\partial }^{3}\text{w}}{\partial {x}^{2}\partial y}\right)=0, aty=\pm b$$
(23)

It is assumed that \({\alpha }_{y}={\alpha }_{xy}=0\) and \({\alpha }_{x}\ne 0\), where, \({\alpha }_{x}\), \({\alpha }_{y}\) and \({\alpha }_{xy}\) are the thermal expansion coefficients. It was shown in section 3 that this assumption produces a negligible error. With regard to this assumption:

$${\overline{\varepsilon }}_{y}^{th}={\overline{\varepsilon }}_{xy}^{th}=0$$
(24)

Since the sheet is thin, therefore, there is no temperature gradient in the z direction. The laser beam is assumed to be a Gaussian beam with a heat flux density expressed by (Ref 28):

$$q=\frac{8\cdot A\cdot P}{\pi \cdot {d}^{2}}\cdot \text{exp}(-8\cdot \frac{{x}^{2}+{y}^{2}}{{d}^{2}})$$
(25)

where q is the heat flux density, A the absorption coefficient, P the laser power, and d the laser beam diameter. For simplification, it is assumed that the sheet is suddenly heated. Thus, the variation of the physical quantities in the x direction is ignored. Therefore, it is reasonable to define the thermal strain in the x direction as Eq 2.

The term \(\frac{{\partial }^{2}\text{w}}{\partial x\partial y}\) at boundaries is zero and in the other areas it is small compared with the other curvatures. Thus, its squared can be ignored and Eq 16 and 18 are converted to Eq 26 and 27, respectively.

$$D\cdot \left(\frac{{\partial }^{4}w}{\partial {x}^{4}}+\frac{{\partial }^{4}w}{\partial {y}^{4}}+2\cdot \frac{{\partial }^{4}w}{\partial {x}^{2}\partial {y}^{2}}\right)-\left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\frac{{\partial }^{2}\Phi }{\partial {y}^{2}}\right)=0$$
(26)
$$\frac{{\partial }^{4}\Phi }{\partial {y}^{4}}+E\cdot h\cdot \left(\frac{{\partial }^{2}w}{\partial {x}^{2}}\cdot \frac{{\partial }^{2}w}{\partial {y}^{2}}+\frac{{\partial }^{2}{\overline{\varepsilon }}_{x}^{th}}{\partial {y}^{2}}\right)=0$$
(27)

Because of the fact that the length to width ratio of the sheet is large, the variation of the curvatures in the x direction is small, so:

$$\frac{\partial {k}_{x}}{\partial x}=\frac{\partial {k}_{y}}{\partial x}=\frac{\partial {k}_{xy}}{\partial x}=0$$
(28)

Further one can show that (Ref 35):

$$\frac{\partial {k}_{x}}{\partial y}=\frac{\partial {k}_{xy}}{\partial x}$$
(29)
$$\frac{\partial {k}_{y}}{\partial x}=\frac{\partial {k}_{xy}}{\partial y}$$
(30)

Eq 28 to 30 infer that kx and kxy are constant. Hence, the z displacement of the middle plane is defined as:

$$w=-\frac{1}{2}\cdot {k}_{x}\cdot {x}^{2}-{k}_{xy}\cdot x\cdot y+F(y)$$
(31)

The magnitude of kxy is small; therefore, Eq 31 can be rewritten as:

$$w=-\frac{1}{2}\cdot {k}_{x}\cdot {x}^{2}+F(y)$$
(32)

Substituting Eq 32 in Eq 27, and considering the fact that at the early stages of buckling, kx and \(\frac{{\partial }^{2}F}{\partial {y}^{2}}\) are small, their product can be ignored and Eq 27 is converted to Eq 33.

$$\frac{{\partial }^{4}\Phi }{\partial {y}^{4}}+E\cdot h\cdot \frac{{\partial }^{2}{\overline{\varepsilon }}_{x}^{th}}{\partial {y}^{2}}=0$$
(33)

Where \({\overline{\varepsilon }}_{x}^{th}\) is determined by Eq 2. Solving Eq 33 by considering that \({\int }_{-b}^{b}\frac{{\partial }^{2}\Phi }{\partial {y}^{2}}dy=0\) (no external forces are acting on the edges), yields:

$$\frac{{\partial^{2} \Phi }}{{\partial y^{2} }} = - E \cdot h \cdot \alpha \cdot \Delta T \cdot e^{{ - 8 \cdot \frac{{y^{2} }}{{d^{2} }}}} + \frac{{\sqrt {2\pi } }}{8} \cdot \frac{E \cdot h \cdot \alpha \cdot \Delta T \cdot d}{b} \cdot {\text{erf}}\left( {2\sqrt 2 \frac{b}{d}} \right)$$
(34)

Substitution of Eq (32) and (34) into Eq (26) leads to:

$$D \cdot \frac{{\partial^{4} F}}{{\partial y^{4} }} + k_{x} \cdot \left( { - E \cdot h \cdot \alpha \cdot \Delta T \cdot e^{{ - 8 \cdot \frac{{y^{2} }}{{d^{2} }}}} + \frac{{\sqrt {2\pi } }}{8} \cdot \frac{E \cdot h \cdot \alpha \cdot \Delta T \cdot d}{b} \cdot {\text{erf}}\left( {2\sqrt 2 \frac{b}{d}} \right)} \right) = 0$$
(35)

To solve the above equation, according to Eq (23) and (32), the boundary conditions are:

$$\left(\frac{{\partial }^{2}\text{F}}{\partial {\text{y}}^{2}}-\upnu {\cdot \text{k}}_{\text{x}}\right)=\frac{{\partial }^{3}\text{F}}{\partial {\text{y}}^{3}}=0,\text{ at y}=\pm \text{b}$$
(36)

Assuming \({\int }_{-b}^{b}F\left(y\right)dy=0\) (for simplification), the solution of Eq (35) with these boundary conditions is:

$$\begin{aligned} F\left( y \right) & = \frac{{\left( {1 - \nu^{2} } \right)\alpha {\Delta }Tk_{x} d}}{{64h^{2} }} \cdot \left( {d\left( {d^{2} - 16y^{2} } \right)e^{{ - 8 \cdot \frac{{y^{2} }}{{d^{2} }}}} - \frac{{4\sqrt {2\pi } }}{b}y^{2} {\text{erf}}\left( {\frac{2\sqrt 2 b}{d}} \right)\left( {6b^{2} + y^{2} } \right)} \right. \\ \left. { + \sqrt {2\pi } y{\text{erf}}\left( {\frac{2\sqrt 2 y}{d}} \right)\left( {3d^{2} + 16y^{2} } \right)} \right) - \frac{{k_{x} \left( {1 - \nu^{2} } \right)\alpha {\Delta }Td}}{{61440bh^{2} }} \\ \cdot \left( {\sqrt {2\pi } {\text{erf}}\left( {\frac{2\sqrt 2 b}{d}} \right)\left( {1440b^{2} d^{2} - 4608b^{4} + 45d^{4} } \right) + bd\left( {600d^{2} - 5760b^{2} } \right)e^{{ - 8 \cdot \frac{{y^{2} }}{{d^{2} }}}} } \right) + k_{x} \nu \left( {\frac{{y^{2} }}{2} - \frac{{b^{2} }}{6}} \right) \\ \end{aligned}$$
(37)

After deformation, the internal moment cannot be calculated by Eq (9) and this equation should be modified to Eq (38) as below:

$${M}_{x}={\int }_{-h/2}^{h/2}{\sigma }_{x}\left(z+w\right)dz$$
(38)

Using the Hook’s law and regarding the Kirchhoff’s assumptions, Eq (38) is converted to Eq (39) (Ref 31).

$${M}_{x}=D\left({k}_{x}+\nu {k}_{y}\right)+{N}_{x}w$$
(39)

Since there is no external moment, so:

$${\int }_{-b}^{b}{M}_{x}dy=0$$
(40)

Substituting Eq (15) and (32) in Eq (39) yield to:

$${\text{M}}_{{\text{x}}} = {\text{D}} \cdot \left( {{\text{k}}_{{\text{x}}} - \nu \frac{{\partial ^{2} F}}{{\partial {\text{x}}^{2} }}} \right) + \frac{{\partial ^{2} \Phi }}{{\partial {\text{y}}^{2} }} \cdot \left( {{\text{F}}\left( {\text{y}} \right) - \frac{1}{2}{\text{k}}_{{\text{x}}} {\text{x}}^{2} } \right)$$
(41)

According to Eq (41), the integration of Mx in the y direction can be expressed as:

$${\int }_{-b}^{b}({\text{M}}_{\text{x}}) dy={\int }_{-b}^{b}(\text{D}\cdot ({\text{k}}_{\text{x}}-\upnu \frac{{\partial }^{2}\text{F}}{\partial {\text{x}}^{2}})+\frac{{\partial }^{2}\Phi }{\partial {\text{y}}^{2}}\cdot (\text{F}\left(\text{y}\right)-\frac{1}{2}{\text{k}}_{\text{x}}{\text{x}}^{2}))dy$$
(42)

But as no external forces are acting on the edges of the sheet:

$$\smallint _{{ - b}}^{b} \frac{{\partial ^{2} \Phi }}{{\partial y^{2} }} \cdot \left( { - \frac{1}{2}k_{x} \cdot x^{2} } \right)dy = \left( { - \frac{1}{2}k_{x} \cdot x^{2} } \right) \cdot \smallint _{{ - b}}^{b} \frac{{\partial ^{2} \Phi }}{{\partial y^{2} }}dy = 0$$
(43)

Substituting Eq (43) in Eq (42) yields to:

$${\int }_{-b}^{b}({\text{M}}_{\text{x}}) dy={\int }_{-b}^{b}(\text{D}\cdot ({\text{k}}_{\text{x}}-\upnu \frac{{\partial }^{2}\text{F}}{\partial {\text{x}}^{2}})+\frac{{\partial }^{2}\Phi }{\partial {\text{y}}^{2}}\cdot \text{F}\left(\text{y}\right)) dy$$
(44)

Substituting Eq (34) and (37) in Eq (44) and getting the integration yields to:

$$\begin{aligned} \int_{{ - b}}^{b} {M_{x} dyM_{x} dy} & = \frac{{\sqrt {2\pi } \nu }}{{61440}}\left( {Ek_{x} h\Delta T\alpha d\left( {5120b^{2} - 960d^{2} } \right)} \right){\text{erf}}\left( {\frac{{2\sqrt 2 b}}{d}} \right) \\ + \frac{\nu }{8}\left( {Ek_{x} hb\Delta T\alpha d^{2} } \right)e^{{ - 8\frac{{b^{2} }}{{d^{2} }}}} \\ + \frac{{\left( {1 - \nu ^{2} } \right)\pi }}{{61440bh}}\left( {Ek_{x} \alpha ^{2} \Delta T^{2} d^{2} \left( {45d^{4} - 2304b^{4} + 1440b^{2} d^{2} } \right)} \right){\text{erf}}\left( {\frac{{2\sqrt 2 b}}{d}} \right)^{2} \\ + \frac{{\sqrt {2\pi } \left( {1 - \nu ^{2} } \right)}}{{61440h}}\left( {Ek_{x} \alpha ^{2} \Delta T^{2} d^{3} \left( {1020d^{2} - 2880b^{2} } \right)} \right){\text{erf}}\left( {\frac{{2\sqrt 2 b}}{d}} \right)e^{{ - 8\frac{{b^{2} }}{{d^{2} }}}} \\ - \frac{{\left( {1 - \nu ^{2} } \right)}}{{32h}}\left( {Ek_{x} b\alpha ^{2} \Delta T^{2} d^{4} } \right)e^{{ - 16\frac{{b^{2} }}{{d^{2} }}}} \\ - \frac{{\sqrt \pi \left( {1 - \nu ^{2} } \right)}}{{64h}}\left( {Ek_{x} \alpha ^{2} \Delta T^{2} d^{5} } \right){\text{erf}}\left( {\frac{{4b}}{d}} \right) + \frac{{Ek_{x} h^{3} b}}{6} \\ \end{aligned}$$
(45)

Assuming that b > d it can be inferred that:

$${e}^{-8\cdot \frac{{b}^{2}}{{d}^{2}}}\simeq 0$$
(46)
$$\text{erf}\left(2\sqrt{2}\frac{b}{d}\right)\simeq 1$$
(47)

Substituting Eq (46) and (47) in Eq (45) yields to:

$${\int }_{-b}^{b}{M}_{x}dy=\frac{\sqrt{2\pi }\nu }{61440}\left(E{k}_{x}h\Delta T\alpha d(5120{b}^{2}-960{d}^{2})\right)+\frac{(1-{\nu }^{2})\pi }{61440bh}\left(E{k}_{x}{\alpha }^{2}{\Delta T}^{2}{d}^{2}(45{d}^{4}- 2304{b}^{4}+1440{b}^{2}{d}^{2})\right)-\frac{\sqrt{\pi }(1-{\nu }^{2})}{64h}\left(E{k}_{x}{\alpha }^{2}{\Delta T}^{2}{d}^{5}\right)+\frac{E{k}_{x}{h}^{3}b}{6}$$
(48)

As there is no external moment, so, \({\int }_{-b}^{b}{M}_{x} dy=0\). Hence from Eq (48) it can be inferred that:

$$\frac{\sqrt{2\pi }\nu }{61440}\left(E{k}_{x}h\Delta T\alpha d(5120{b}^{2}-960{d}^{2})\right)+\frac{(1-{\nu }^{2})\pi }{61440bh}\left(E{k}_{x}{\alpha }^{2}{\Delta T}^{2}{d}^{2}(45{d}^{4}-2304{b}^{4}+ 1440{b}^{2}{d}^{2})\right)-\frac{\sqrt{\pi }(1-{\nu }^{2})}{64h}\left(E{k}_{x}{\alpha }^{2}{\Delta T}^{2}{d}^{5}\right)+\frac{E{k}_{x}{h}^{3}b}{6}=0$$
(49)

Equation (49) is a quadratic equation in terms of the temperature change at the start of buckling, which we call it as the critical temperature change, \({\Delta T}_{cr}\). Thus, solving this equation in term of \(\Delta T\) and extracting the positive root of \(\Delta T\), the critical temperature change, Eq (50), is achieved:

$${\Delta T}_{cr}=\frac{2.344{h}^{2}}{\alpha bd}\cdot \frac{56.4{(d/b)}^{2}-300.795-\sqrt{Q}}{47.124{(d/b)}^{4}-567.185{(d/b)}^{3}+1507.964{(d/b)}^{2}-2412.743}$$
(50)

where

$$Q=-28981.192{(d/b)}^{4}+3.871{\cdot 10}^{5}{(d/b)}^{3}-1.063{\cdot 10}^{6}\cdot {(d/b)}^{2}+1.737{\cdot 10}^{6}$$
(51)

To solve Eq (40), the poison ratio was taken as 0.3 and the sheet width was assumed to be much larger than the laser beam diameter. As \({\Delta T}_{cr}\) in Eq (50) is the temperature change at the start of buckling, it indicates the dominant deformation mechanism in the laser forming of thin sheet. Indeed, if it is considered that the UM and BM are separated by a boundary, the amount of \({\Delta T}_{cr}\) can represent such boundary, i.e. if the temperature change due to the laser beam (ΔT) exceeds \({\Delta T}_{cr}\), the BM is dominant. On the other words, if the temperature change is lower than this value, the UM will be dominant. However, If UM is dominant the bending angle of the sheet is zero but if the BM is dominant the final bending angle, \(\theta\)(in radian), is determined as (Ref 36):

$$\theta =\sqrt[3]{\frac{36\alpha {\sigma }_{0}AP}{\rho CE{u}_{s}{h}^{2}}}$$
(52)

where E, \({\sigma }_{0}\) and P are the young modulus, the flow stress of the heated region and the laser power, respectively.

It should be noted that Eq (50) has been derived based on elastic deformation, but the deformation condition in laser forming process is elastic-plastic. Regarding the three following reasons the elastic assumption assumed in this work leads to reasonable results in detecting the dominant deformation mechanism in the laser forming of thin sheet. The first reason is based on the fact that the heated region is small, so, if yielding takes place, it occurs in a very narrow region and thus it has a little effect on the critical temperature change. Moreover, the assumption of elastic deformation presents an upper bound for the critical temperature change compared with the elastic-plastic deformation, so, for \(\Delta T > \Delta T_{cr}\) one can be sure that the BM is dominant. Further, in some cases, when the temperature change reaches the critical value, all the points of the sheet are still in elastic region. Therefore, regarding these three reasons, Eq (50) may also be applied with a good approximation for the localized elastic-plastic deformation of the sheet occurring in the laser forming process. These reasons are verified in section 3.

It should be mentioned that although we ignored the variation of temperature in the longitudinal direction of the sheet in the calculation of the buckling critical temperature change \((\Delta T_{cr} )\) but we considered it indirectly by calculating the average temperature change \((\Delta T)\) using Eq (1). For example, laser scanning velocity is an important parameter that affects the variation of temperature in the longitudinal direction of the sheet. By comparing Eq (1) and (50), it appears that the laser scanning velocity is not presented in Eq (50) but it exists in Eq (1). It means that however laser scanning velocity is not presented in the buckling critical temperature change expression, but using Eq (1), laser scanning velocity is considered as an important parameter for determination of laser deformation dominant mechanism. Therefore, by increasing the laser scanning velocity, the average temperature change decreased, and bucking occurrence was postponed. In section 3 of the paper, it is shown that the assumptions made to establish the analytical model are reasonable and produce small errors.

2.2 Finite Element Model

To verify the analytical model predictions, a finite element analysis was also performed using the ABAQUS software. The linear perturbation method was employed to study the buckling modes. A temperature field according to Eq (2) was applied to the sheet as a predefined field and after the buckling analysis; the first positive Eigen value was extracted as the buckling critical temperature change. The ABAQUS software was used to perform the finite element analysis. The material was considered as an isotropic material and in addition to the x direction, a thermal expansion was also considered in other directions.

In the analyses, a 3D rectangular deformable shell was employed. The sheet was laid in the x-y plane while the x coordinate was along the length and the z coordinate in the thickness direction of the sheet. In order to apply the condition of an infinite sheet along the x direction, the length to width ratio equal to 5 was chosen in the analyses. The S4R element being a standard, linear, and quad element for the shell family was used to conduct the analyses. To reduce the total CPU time needed for the analyses, small meshes in the heat affected zone and large meshes in other regions were employed. In general, small meshes were used to achieve more accurate predictions.

In the analyses any boundary condition eliminating the rigid body motion is suitable. Due to the fact that at the beginning stages of buckling, there are symmetries about the x and y axes, so all displacements and rotations of the central node is zero. This boundary condition eliminated any rigid body motion in the analyses. In such condition, the central node coincides with the origin of coordinate axes.

Post buckling analysis was also performed to prove the elastic deformation assumption is applicable to the elastic-plastic deformation of the sheet. By conducting the post buckling analysis, we could predict the stress distribution in the specimen. In view of stress distribution in the sheet, we could show that three reasons expressed in the last paragraph of section 2.1 were reasonable. For the geometrically nonlinear static problems involving buckling or collapse behavior, the static Riks method is a convenient method to study the buckling behavior of the specimen. In order to employ the modified Riks method in the ABAQUS software, we introduced an imperfection and performed the post buckling analysis. The first positive Eigen mode resulting from linear perturbation method was taken as the dominant mode. Half of the sheet thickness was used as its associated scale factor (Ref 37). The results of the post-buckling analysis are presented in section 3.

3 Model Verification

In order to verify the finite element analysis, the FEM results were compared with the experimental results derived from (Ref 38). The derivation procedure is described in Appendix A. Two types of sheets were considered; the first type is made of carbon steel with \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\), \(K=45 (\frac{W}{m\cdot K})\),\(C=481 (\frac{J}{kg\cdot K})\) and the second type of a stainless steel with \(\alpha =17.1\cdot {10}^{-6}(\frac{1}{K}\)),\(K=18 \left(\frac{W}{m\cdot K}\right)\) and \(C=481 (\frac{J}{kg\cdot K})\). The sheet width was 2b = 100 mm and the width to length ratio equals 2. Experimental results relating to the 7 different cases presented in Table 1 were chosen for comparison with the FEM results.

Table 1 The laser parameters and sheet thickness used for the studied cases
Full size table

Figure 2 shows the occurrence of buckling for different values of temperature change and laser scanning velocity for the carbon steel sheet. The filled points represent the experimental situations that buckling occurs and the non-filled points show the conditions that it is not prevailed. The lines being parallel with the scanning velocity axis depicts the buckling critical temperature change (predicted by the FEM) for the cases presented in Table 1. According to the Finite element analysis, it can be inferred that if a point stays above the appropriate critical temperature change, buckling should occur and if that point locates below the respective critical temperature, buckling should not occur. Referring to Fig. 2, at the points shown by A, B and C notations, the FEM predictions are not valid. As it is seen the positions of point B and C are close to their respective critical temperatures change; hence, the lack of correct predictions for these points may be attributed to the assumption of independency of material properties on temperature change in the FEM analysis. Since for point A, the temperature change is high; therefore, the assumption makes a significant error.

Fig. 2
figure 2

Comparison of the experimental and FEM results representing the occurrence of buckling for the carbon steel sheet. The experimental results were extracted from (Ref 38)

Full size image

In Fig. 3 the occurrence of buckling predicted by the FEM is compared with the experimental results for the stainless steel sheet. As it is seen, in point D, the FEM prediction is not true. Similar to the carbon steel sheet, the lack of correct prediction for this point can be attributed to the assumption of independency of material properties to the temperature change in the FEM. According to Fig. 2 and 3, if the temperature change is not close to the critical temperature change, the Finite element analysis is suitable for prediction of the critical temperature change at which the buckling is occurred.

Fig. 3
figure 3

Comparison of the experimental and FEM results representing the occurrence of buckling for the stainless steel sheet. The experimental results were extracted from (Ref 38)

Full size image

Now it should be exhibited that the elastic deformation assumption used for the prediction of the critical temperature change is justified. To achieve this purpose, we should define effective stress first. The von Mises effective stress is a critical parameter used to assess whether an isotropic and ductile material will yield or deform permanently under complex loading conditions. The von Mises effective stress can be expressed as (Ref 39):

$${\sigma }_{v}^{2}=\frac{1}{2}[{\left({\sigma }_{11}-{\sigma }_{22}\right)}^{2}+{\left({\sigma }_{22}-{\sigma }_{33}\right)}^{2}+{\left({\sigma }_{11}-{\sigma }_{33}\right)}^{2}+6({\sigma }_{12}^{2}+{\sigma }_{13}^{2}+{\sigma }_{23}^{2})]$$
(53)

where \({\sigma }_{v}\) is the von Mises effective stress, and \({\sigma }_{11}\), \({\sigma }_{22}\), \({\sigma }_{33}\), \({\sigma }_{12}\), \({\sigma }_{13}\), \({\sigma }_{23}\) are components of the stress tensor.

Figure 4 shows the effective stress (von Mises stress) versus the displacement of a point (x = 0.2 m, y = 0, z = 0) resulting from the post buckling analysis produced by applying a gradually increasing predefined temperature field. The position of the point in the sheet, point B, is shown in Fig. 5. The selected point is in the region of the maximum Mises stress. The predefined temperature field is related to a laser process using a laser beam diameter of 5 mm. The sheet material was assumed as an isotropic carbon steel material with Young modulus of E = 200 GPa and thermal expansion coefficient of \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\). The sheet dimensions were; 2b = 90 mm in width, 2L = 450 mm in length, and h = 0.6 mm in thickness. Referring to the figure, at early stages, the increase in lateral displacement is low but after point A, it increases suddenly. It means that this point coincides with the start of the buckling phenomenon. If a material has a high yielding stress, for example higher than 450 (MPa), from Fig. 4 it can be inferred that buckling starts in the elastic region and so the elastic deformation assumption is valid in our analysis.

Fig. 4
figure 4

Effective stress versus lateral displacement at the point (x = 0.2m, y = 0, z = 0)

Full size image
Fig. 5
figure 5

The plot of effective stress (Mises stress) contour for a long sheet subjected to a predefined temperature field. Point B shows the position of the selected node

Full size image

Figure 5 shows a post buckling Mises stress contour of the deformed sheet at the start of buckling (point A in Fig. 4). It is observed that only in a narrow region the stress is high enough for plastic deformation to occur. Therefore, according to the results in Fig. 4 and 5, the three reasons expressed in section 2 are acceptable and the elastic deformation assumption made in the analytical model is justified.

4 Discussion

Referring to Eq (1) and (50), the parameters such as the specimen size, material properties and laser forming process parameters can affect the occurrence of buckling in laser sheet forming process. In the following sections, the effects of these parameters on the boundary separating UM from BM are discussed.

4.1 Effect of Specimen Size

The length, width, and thickness of the sheet can affect the critical temperature change at which the buckling deformation is started. Figure 6 shows the dependence of critical temperature change on the thickness of a sheet with dimensions of b = 30 mm, d = 5 mm, L = 150 mm, and thermal expansion coefficient of \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\). It is noted that the critical temperatures change predicted by the FEM model are the same as those predicted by Eq (50). The figure indicates that with increasing the thickness of the sheet, the critical temperature change for starting the buckling is increased. This is because with increasing the thickness, the moment of inertia is increased and thus the occurrence of buckling in the sheet is prevented.

Fig. 6
figure 6

Critical temperature change versus thickness for d = 5 mm, b = 30 mm, L = 150 mm, and \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\)

Full size image

Figure 7 depicts the effect of sheet width on the critical temperature change. Again the FEM and analytical results are coincided completely. It is observed that with the increase in the sheet width, the critical temperature change is decreased. The reason to this behavior is that with the increase in sheet width, more constraints are applied to the heated region enhancing the occurrence of buckling. The agreement between the FEM predictions and the analytical results indicates that the assumptions made to develop the analytical model are reasonable.

Fig. 7
figure 7

Effect of sheet width on the critical temperature change for h = 0.6 mm, d = 5 mm, and \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\)

Full size image

In the analytical model, it was assumed that the sheet length is much larger than its width. Figure 8 shows the effect of length to width ratio on the prediction of critical temperature change by the analytical model. For a sheet with length to width ratio greater than 5, the sheet may be assumed as an infinite sheet. Referring to the figure, by increasing this ratio, the analytical predictions exhibit a better agreement with the FEM predictions. Therefore, the analytical model is applicable to the length to width ratio greater than 5.

Fig. 8
figure 8

The effect of changing the sheet length to width ratio on the critical temperature change predicted by the analytical model and FEM analysis. The values of other parameters are h = 0.6 mm, b = 30 mm, d = 5 mm, and \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\)

Full size image

4.2 Effect of Material Properties

Regarding Eq (50) the only material property affecting the critical temperature change is the thermal expansion coefficient. So, the other material properties such as the thermal conductivity, heat capacity, and density of the sheet material do not change the critical temperature change. However, according to Eq (1), they affect ΔT and in turn the occurrence of the buckling phenomenon. Figure 9 shows the effect of thermal expansion coefficient on the critical temperature change. As it is observed the critical temperature change decreases with increase in thermal expansion coefficient. This is due to the increase in the imposed thermal strain by increasing the thermal expansion coefficient. It is noted that the critical temperature change is in agreement with the prediction of FEM analyses.

Fig. 9
figure 9

Dependence of critical temperature change on thermal expansion coefficient, d = 5 mm, b = 30 mm, L = 150 mm and h = 0.6 mm

Full size image

Figure 10 indicates the shift of the interface separating BM from UM to the left by decrease in thermal expansion coefficient. On the other word with decrease in thermal expansion coefficient, the possibility of buckling is reduced.

Fig. 10
figure 10

The shift of the position of interface separating BM and UM to the left, arising from the decrease in thermal expansion coefficient

Full size image

Figure 11 shows the shift of the boundary separating the BM from UM to the left because of the increase in specific heat capacity. According to this figure, the region at which BM is a dominant deformation mechanism is reduced with increase in specific heat capacity because with increase in heat capacity, the thermal diffusivity of material is decreased, therefore, the temperature change imposing to the specimen is reduced.

Fig. 11
figure 11

The shift of position of the boundary separating BM from UM to the left due to increase in specific heat capacity of sheet material

Full size image

Figure 12 demonstrates the effect of thermal conductivity on the boundary separating BM from UM. It is observed that with increase in thermal conductivity, because of increase in thermal diffusivity, the imposed temperature change to the specimen is increased, so, the possibility of buckling occurrence is enhanced.

Fig. 12
figure 12

Dependence of the boundary separating BM from UM on thermal conductivity

Full size image

4.3 Effects of Laser Forming Process Parameters

Laser beam diameter has a direct effect on critical temperature change but the parameters such as the laser power, scan velocity, and laser beam diameter affect ΔT and consequently the occurrence of buckling. With increase in laser power and/or decrease in laser scan velocity, more heat is imposed to the specimen causing ΔT to increase which in turn promote the occurrence of buckling.

Figure 13 exhibits the effect of laser beam diameter on the critical temperature change. With increasing the beam diameter, the heat affected zone becomes wider and so a more internal force is produced. This leads to a decrease in critical temperature change. But according to Eq (1), with increase in the beam diameter, ΔT is reduced, so, the occurrence of buckling is postponed. Thus, the effect of laser beam diameter on both ΔTcr and ΔT must be considered simultaneously. Referring to Fig. 14, it is observed that the position of the boundary separating BM from UM does not change with variation of laser beam diameter. This means that decrease in both ΔTcr and ΔT compensates the effect of each other, so, the boundary does not move.

Fig. 13
figure 13

Effect of laser beam diameter on critical temperature change, h = 0.6 mm, b = 30 mm, d = 5 mm, and \(\alpha =11.6\cdot {10}^{-6}(\frac{1}{K})\)

Full size image
Fig. 14
figure 14

Effect of laser beam diameter on the position of the boundary

Full size image

Figure 15 exhibits the effect of laser power on the position of the boundary. Increase in the laser power result in enhancement of heat input to the specimen, so, the area at which the BM is dominant is increased.

Fig. 15
figure 15

Effect of laser power on the position of the boundary

Full size image

Figure 16 demonstrates the effect of change in laser scanning velocity on the boundary separating BM from UM. From this figure it can be inferred that with increase in scanning velocity, the possibility of buckling is decreased. This is due to the decrease in heat input to the specimen arising from the increase in scanning velocity.

Fig. 16
figure 16

The effect of scanning velocity on the position of the boundary separating BM from UM

Full size image

5 Conclusions

In this research, a new analytical model was developed to predict the position of the boundary separating the buckling and upsetting mechanisms in laser forming of thin sheet. To verify the analytical model, its results were compared with the results of a finite element model. It is shown that although the analytical model is based on the assumption of elastic deformation, also it is applicable to the elastic-plastic deformation occurring in the laser forming process. The effects of several factors such as the sheet dimensions, laser power, laser beam diameter, laser scanning velocity, the material properties including thermal expansion coefficient, thermal conductivity, and the heat capacity of material on the dominant mechanism were also assessed. The following conclusions can be made from the results:

1. By increase in thermal conductivity and/or decrease in heat capacity, the heat input to the specimen is increased and the possibility of the buckling phenomenon in the sheet is increased.

2. Increase in laser power and/or decrease in laser scanning velocity, leads to the increase in the heat input to the sheet, so, the occurrence of buckling is promoted.

3. By increase in the sheet width, a lower critical temperature change is predicted due to the increase of surrounded materials. Also increase in the sheet thickness raises the critical temperature change because of raising the moment of inertia of the sheet.

4. With increase in thermal expansion coefficient, a higher thermal strain is imposed to the specimen; therefore, the possibility of buckling phenomenon is increased.

5. The analytical model predicts more reasonably the effects of the mentioned parameters when the length to width ratio of the sheet is greater than 5.