1 Introduction

In recent years, finite element analysis (FEA) has been a popular method to numerically understand the deformation response of metals and alloys under specified conditions. The approach finds utility in simulating a variety of physical phenomena, including ballistic impact (Ref 1, 2), high-speed cutting (Ref 3, 4), hot forming (Ref 5, 6), and hot deformation (Ref 7, 8) processes. Integral to an FEA are the constitutive equations that govern the stress–strain relationship of materials, which serve as critical input parameters, thus significantly influencing the accuracy of FEA simulation outcomes. Consequently, the development of a reliable and accurate constitutive equation is of prime importance in attaining realistic FEA simulations.

Constitutive models typically encompass both physically based and phenomenological approaches. Physically based models excel at accurately describing material deformation across various temperatures and strain rates; however, their development necessitates extensive experimental data (Ref 9, 10). In contrast, phenomenological models can be developed with limited experimental data and involve fewer material constants compared to their physically based counterparts, thus making them the preferred approach (Ref 11). Among the phenomenological models, Johnson-Cook and Arrhenius-type constitutive models are widely used. The Johnson-Cook constitutive model finds extensive application in simulating material deformation response under high strain rate loading conditions, including machining, impact, and explosion processes. This model incorporates strain rate hardening, strain hardening, and thermal softening effects into the flow behaviors of metals and alloys (Ref 12, 13).

Notably, the Johnson-Cook model assumes that the effects of the strain rate, strain, and temperature are independent of each other, yet interactions between these factors have been observed in the flow behavior of many types of materials (Ref 5, 7, 8, 11). For instance, Li et al. (Ref 7) reported the coupled influence of temperature on strain hardening and strain rate hardening effects in the flow behavior of T24 steel during hot compression tests. Similarly, Tan et al. (Ref 11) observed the combined effects of strain and strain rate in the flow stress–strain response of 7050-T7451 aluminum alloy at high strain rates. He et al. (Ref 8) revealed that the effects of strain, strain rate, and temperature interacted in the flow behavior of 10%Cr steel during hot deformation. Consequently, the conventional Johnson-Cook model may prove insufficient for accurately predicting the mechanical behavior of metals and alloys. Therefore, appropriate modifications to the Johnson-Cook model are necessary to capture the combined effects of strain rate, strain, and temperature on flow stress–strain relationships. For example, Li et al. (Ref 7) and Tan et al. (Ref 11) successfully modified the Johnson-Cook model by incorporating functions of strain and strain rate into a thermal softening term and strain rate hardening coefficient, respectively. These modifications result in accurate predictions of the flow behavior of materials, as demonstrated in the case of T24 steel (Ref 7) and 7050-T7451 aluminum alloy (Ref 11). However, it is worth noting that modifying the Johnson-Cook model is material-specific. There is no general formula, as specific modifications are made for different types of materials.

The Arrhenius-type model is typically employed to forecast the flow behavior of materials at elevated temperatures and strain rates, such as hot compression tests (Ref 14,15,16,17). This model establishes a relationship between the strain rate, temperature, and flow stress, while the effect of strain on the flow stress is ignored (Ref 15,16,17). However, the flow stress of materials is indeed influenced by strain, promoting the proposal of the multiple linear regression Arrhenius-type model (Ref 15,16,17). This model considers strain effect, yet its implementation involves complex high-order polynomial functions, e.g., sixth-order polynomial functions for Pb–Mg–10Al–0.5B alloy (Ref 17) and eighth-order polynomial functions for 60 Mg–30Pb–9.2Al–0.8B magnesium alloy (Ref 15), resulting in numerous materials constants. Furthermore, it is reported that the multiple linear regression Arrhenius-type model exhibited lower predictability to predict the flow stress of the DED-Arc built precipitation-strengthened ATI 718Plus alloy at high strain rates and different temperatures than the modified Johnson-Cook model (Ref 18).

Maraging steels, characterized by their 18 wt. % nickel (18% Ni) content and being iron-Ni-based ultrahigh-strength steels, distinguish themselves from conventional high-carbon martensitic high-strength steels owing to their possession of both ultrahigh strength and exceptional toughness (Ref 19, 20). These two distinctive properties are attributed to their microstructure, which is characterized by a lath martensite matrix with exceptionally low carbon content, thus rendering 18% Ni steels relatively ductile, with a significant number of intermetallic strengthening precipitates (Ref 19, 20). Their excellent mechanical properties mean that they are extensively used in high-tech fields, such as the aerospace, aircraft, and automotive industries as well as in the military (Ref 21,22,23,24,25,26,27).

The high strain rate compressive deformation behavior of 18% Ni maraging steels, which is of paramount importance in their applications, has recently gained attention from researchers (Ref 28,29,30,31,32). Song et al. (Ref 32) investigated the influence of the strain rate on the dynamic compressive deformation response of C250 maraging steel at room temperature and observed a 10% enhancement in the flow stress of the C250 alloy when the strain rate was increased from 1000 to 3000 s-1. Fu et al. (Ref 30) carried out compression tests on 18% Ni maraging steel, which involved a range of strain rates from 0.0001 s-1 to 104 s-1 and deformation temperatures from 25 °C to 1200 °C. Their findings revealed the presence of strain rate hardening across all deformation temperatures and dynamic recrystallization at 600 °C, thus resulting in strain softening. However, to the best of the knowledge of the authors, few studies have been conducted to investigate the high strain rate compressive deformation behavior of C250 maraging steel in the literature. There is still the absence of a fundamental understanding of the influences of strain rate, strain, and temperature on the high strain rate compressive deformation response of C250 maraging steel, and an appropriate constitutive model for predicting this behavior has yet to be proposed. Hence, the objective of this study is to explore the high strain rate compressive deformation behavior of C250 maraging steel at different strain rates and temperatures, and subsequently develop a modified Johnson-Cook constitutive model based on the experimental data.

2 Experimental Materials and Methods

The material used in this investigation is a commercially available rod of wrought C250 maraging steel. The chemical composition of the C250 maraging steel is provided in Table 1. Cylindrical samples with a diameter of 8 mm and height of 8 mm were machined from the rod of wrought C250. Subsequently, the samples were subjected to a solution treatment at 1088 K for 1 hour, followed by air cooling (Ref 33). These heat-treated samples were further aged at 753 K for 3 hours and cooled in air (Ref 33).

Table 1 Chemical composition of C250 maraging steel (wt. %)
Full size table

In order to evaluate the mechanical compression properties of the samples, compression tests were conducted under quasi-static and high strain rate loading conditions. The quasi-static compressive behavior of the samples was investigated by using an MTS 880 servo-hydraulic universal test machine. During the testing, the samples were compressed until they reached a true strain of 0.7 at a strain rate of 0.1 s-1 at room temperature. The uniaxial compression tests were repeated three times to ensure the reliability and consistency of the results.

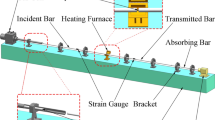
To explore the dynamic compressive behavior of C250 maraging steel, the direct impact Hopkinson pressure bar (DIHPB) technique was used, as illustrated in Fig. 1. The equipment to conduct the DIHPB method includes a firing chamber, gun barrel, timer, steel box (which serves as the impact site), furnace, projectile and transmitter bars, strain gauges, and a data acquisition system. Both the projectile and transmitter bars are made of AISI 4340 steel. The ends of the projectile and transmitter bars that face the samples during the impact tests were subjected to surface heat treatment to enhance their hardness to 59 HRC. A custom-made furnace is connected to the DIHPB apparatus adjacent to the steel box (impact site) to conduct dynamic compression tests at elevated temperatures. The strain gauges are adhered to the transmitter bar. During the dynamic compression tests, elastic waves were generated as the projectile bar impacted the specimen. These elastic waves were propagated through the transmitter bar and detected by the strain gauges. Then, the elastic wave signals were recorded by the data acquisition system and used to construct the dynamic true stress–strain curves. The true strain \({\varepsilon }_{t}\) is calculated by using (Ref 34):

Fig. 1
figure 1

Schematic of DIHPB equipment and data acquisition system

Full size image
$${\varepsilon }_{t}=\text{ln}(\frac{l\left(t\right)}{{l}_{o}})$$
(1)

where \({l}_{o}\) and \(l(t)\) denote the initial and the instantaneous lengths of the samples, respectively. The \(l(t)\) can be obtained by using (35):

$$l(t)={l}_{o}-{v}_{o}t+\frac{2}{ZA}{\int }_{0}^{t}f({t}{\prime})d{t}{\prime}$$
(2)

where \({\upsilon }_{o}\) denotes the impact velocity, \(t\) is the impact time, \(f({t}{\prime})\) is the force history of the impact on the sample, and \(Z\) and \(A\) denote the acoustic impedance of the projectile bar and the cross-section area of the projectile bar, respectively. The equivalent true stress \({\sigma }_{t}\) is calculated by using (Ref 36):

$${\sigma }_{t}=\frac{F(t)}{A(t)}-\frac{3\rho }{8}{(\frac{{r}_{o}{v}_{o}}{{l}_{o}})}^{2}\frac{1}{{(1-{\varepsilon }_{e}\left(t\right))}^{3}}$$
(3)

where \(F(t)\) is the load pulse that corresponds to the impact time \(t\), and \({\varepsilon }_{e}(t)\) is the engineering strain. \({r}_{o}\) and \(\rho\) denote the initial radius of the sample and density of the projectile bar, respectively.

Dynamic compression tests were performed on the C250 maraging steel specimens at different impact momentums (15 kg m/s, 21 kg m/s, and 29 kg m/s) over a range of deformation temperatures (from 298 K to 823 K). Prior to each dynamic compression test, the surface of the projectile and transmitter bars was polished and lubricated to reduce the friction between the specimens and bars during the tests. For the impact tests at elevated temperatures, the samples were preheated at the prescribed deformation temperature for 10 minutes. After that, the samples were promptly taken out of the furnace and subjected to dynamic compression tests immediately. The tests for each condition were repeated three times. The impact momentums of 15 kg m/s, 21 kg m/s, and 29 kg m/s yielded average strain rates of 726 s-1, 1139 s-1, and 1644 s-1, respectively. As such, the approximate strain rates of 700 s-1, 1200 s-1, and 1700 s-1 represent the impact tests carried out under the impact momentums of 15 kg m/s, 21 kg m/s, and 29 kg m/s in this study, respectively.

3 Results and Discussion

3.1 Compressive Behavior of C250 Maraging Steel

Figure 2 shows the flow stress–plastic strain relationships for the C250 maraging steel samples tested at different strain rates and deformation temperatures. The flow stress corresponds to the true stress of samples at the plastic deformation regime during the deformation process. The plots indicate the apparent influence of strain rate, temperature, and strain on the flow stress of C250 maraging steel. Under quasi-static loading, as shown in Fig. 2a, the flow stress initially increases to 1753 ± 19 MPa and subsequently declines with increasing strain. Notably, when the strain rate is increased to 700 s-1 at room temperature, a considerable increase in the maximum flow stress to 2034 ± 9 MPa is observed, thus indicating a significant strain rate hardening effect. However, Fig. 3a reveals that under high strain rates that range from 700s-1 to 1700 s-1 at room temperature, the maximum flow stresses of C250 maraging steel are similar, which shows limited strain rate hardening effects at high strain rates. At elevated deformation temperatures, the influence of the strain rate on the maximum flow stress of C250 maraging steel exhibits distinctive characteristics. At 623 K, the maximum flow stress obtained at 700 s-1 (1704 ± 3 MPa) is similar to that obtained at 1200 s-1 (1686 ± 29 MPa). However, with a further increase in strain rate to 1700 s-1, a substantial and rapid reduction in the maximum flow stress is observed, which results in a value of 1506 ± 23 MPa. Similar influences of the strain rate on the maximum flow stress are also observed at 723 K, as shown in Fig. 3a. In contrast, the maximum flow stress is gradually enhanced from 1162 ± 31 MPa to 1339 ± 1 MPa at a deformation temperature of 823 K, when the strain rate is increased from 700 s-1 to 1700 s-1. These findings present that the effect of strain rate on the flow stress of C250 maraging steel varies at different temperatures, demonstrating the coupled effects of strain rate and temperature. In addition, a pronounced thermal softening effect can be observed in the C250 maraging steel at elevated temperatures, as shown in Fig. 3b. For instance, in the dynamic compression tests conducted at a strain rate of 1200 s-1, there is a substantial reduction in the maximum flow stress, as the deformation temperature is increased from 298 K to 823 K, thus resulting in a remarkable decline from 2089 ± 48 MPa to 1252 ± 33 MPa.

Fig. 2
figure 2

Flow stress–strain plots of C250 maraging steel tested at different strain rates and deformation temperatures: (a) 0.1 s-1 at 298 K; (b) 700 s-1; (c) 1200 s-1; and (d) 1700 s-1

Full size image
Fig. 3
figure 3

Effects of strain rate and deformation temperature on the maximum flow stress of C250 maraging steel: (a) strain rate and (b) deformation temperature

Full size image

Furthermore, it is worth noting that the trend of the flow stress of C250 maraging steel at different strain rates differs in response to the plastic strain across all deformation temperatures. For instance, Fig. 2b shows that the flow stress gradually increases to 1704 ± 3 MPa, and then keeps constant during the compression test at a strain rate of 700 s-1 and temperature of 623 K. When the strain rate is increased to 1200 s-1 at 623 K, the flow stress rapidly increases until unloading during the impact tests; see Fig. 2c. However, with a further increase to 1700 s-1 at 623 K, the flow stress remains constant throughout the dynamic compression tests; see Fig. 2d. These findings reveal that the effect of strain on the flow stress of C250 maraging steel is dependent on strain rate at a high deformation temperature, indicating the interaction between the influences of strain rate and strain. The interactions among the strain rate, temperature, and strain are not only limited to the flow behavior of C250 maraging steel, but observed in the flow behavior of many other metals and alloys, such as Aermet 100; a high-strength alloy steel with the chemical composition of 0.450C-0.280Si-0.960Cr-0.630Mn-0.190Mo-0.016P-0.012S-0.014Cu-(bal.)Fe; 30Cr2Ni4MoV rotor steel; 10%Cr steel; 7050-T7451 aluminum alloy; Al-Cu-Mg alloy; and Alloy 800H (Ref 5, 8, 11, 37,38,39).

3.2 Original Johnson-Cook Model

The obtained flow stress–strain plots of the C250 maraging steel are used to develop the constitutive models in this study. The original Johnson-Cook model was used to predict the flow behavior of C250 maraging steel across different strain rates and deformation temperatures, which includes the effects of strain rate hardening, strain hardening, and thermal softening (Ref 12, 13). In the original Johnson-Cook model, the flow stress is expressed as (Ref 40):

$$\sigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\cdot \text{ln}({\dot{\varepsilon }}^{*})\right)(1-{{T}^{*}}^{m})$$
(4)

where σ denotes the von Mises flow stress, namely the equivalent flow stress; ε is the equivalent plastic strain; A is the yield stress obtained at the reference temperature and reference strain rate; B denotes the strain hardening coefficient; n represents the strain hardening exponent; C is the strain rate hardening coefficient; m is the thermal softening exponent; \(\dot{{\varepsilon }^{*}}=\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\) is the dimensionless strain rate with strain rate \(\dot{\varepsilon }\) and reference strain rate \(\dot{{\varepsilon }_{0}}\); and T* is the homologous temperature, \({T}^{*}=\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}\), in which T is the deformation temperature, K, Tr is the reference temperature, K, and Tm is the melting point, K.

In order to derive the material constants of the original Johnson-Cook constitutive model, experimental data points were extracted from the flow stress–strain plots in Fig. 2 in the plastic strain interval of 0.005. In this study, 298 K and 0.1 s-1 are used as the reference temperature and reference strain rate, respectively. Under this reference experimental condition, Equation (4) can be rewritten as follows:

$$\sigma =A+B{\varepsilon }^{n}$$
(5)

The experimental data points where the flow stresses are higher than the yield stress are used to determine the material constants B and n. Taking the natural logarithm of both sides of Equation (5) yields:

$$\text{ln}\left(\sigma -A\right)=\text{ln}\left(B\right)+n\text{ln}(\varepsilon )$$
(6)

The yield stress of C250 maraging steel under the reference experimental condition, A, is 1685 MPa. The data points that have higher flow stress than the yield stress were selected for the fitting analysis. The relationship between \(\text{ln}(\sigma -A)\) and \(\text{ln}(\varepsilon )\) is presented in Fig. 4. The values of B and n are calculated as 1.0961 MPa and − 0.91, respectively, from the intercept and slope of the linear fitting plot.

Fig. 4
figure 4

Relationship between \(\text{ln}\left(\sigma -A\right)\) and \(\text{ln}\left(\varepsilon \right)\)

Full size image

At reference temperature, the original Johnson-Cook model does not consider the thermal softening effect, so Equation (4) is modified as follows:

$$\sigma =\left(A+B{\varepsilon }^{n}\right)\left(1+C\cdot \text{ln}{(\dot{\varepsilon }}^{*})\right)$$
(7)

Equation (7) can be further transformed into Equation (8) to establish a relationship between \(\frac{\sigma }{A+B{\varepsilon }^{n}}\) and \(\text{ln}(\dot{{\varepsilon }^{*}})\), as shown in Fig. 5. The slope of the fitted line in the plotted \(\frac{\sigma }{A+B{\varepsilon }^{n}}\)-ln \((\dot{{\varepsilon }^{*}})\), which is denoted as C, is determined to be 0.0198.

Fig. 5
figure 5

Relationship between \(\frac{\sigma }{A+B\bullet {\varepsilon }^{n}}\) and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\)

Full size image

\(\frac{\sigma }{A+B{\varepsilon }^{n}}=1+C\times \text{ln}(\dot{{\varepsilon }^{*}})\) (8)

When the strain rate is kept constant, Equation (4) can be transformed into Equation (9). The experimental data obtained from the tests at a strain rate of 700 s-1 and temperature that ranges from 623 K to 823 K are used for a fitting analysis of Equation (9). The melting point of C250 maraging steel falls within the range of 1708 K to 1778 K (Ref 41), so an average temperature of 1743 K is used as the representative melting point in this study. The relationship between \(\text{ln}\left(1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)\left(1+C\times \text{ln}\dot{{(\varepsilon }^{*})}\right)}\right)\) and \(\text{ln}({T}^{*})\) is shown in Fig. 6. The thermal softening exponent, denoted as m, was determined from the slope of the fitting line and found to be 0.9958.

Fig. 6
figure 6

\(\text{ln}\left(1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)\left(1+C\times \text{ln}\dot{({\varepsilon }^{*})}\right)}\right)\) and \(\text{ln}({T}^{*})\) at 700 s-1 and temperature range of 623 K to 823 K

Full size image
$$\text{ln}\left(1-\frac{\sigma }{\left(A+B{\varepsilon }^{n}\right)\left(1+C\times \text{ln}\dot{{(\varepsilon }^{*})}\right)}\right)=m\text{ln}({T}^{*})$$
(9)

Therefore, the original Johnson-Cook model for C250 maraging steel is shown as Equation (10). The measured and predicted flow stresses at different high strain rates and deformation temperatures are plotted in Fig. 7. It is evident that the predictions of the original Johnson-Cook model show significant deviations from the experimental data under the most dynamic compression test conditions. This disparity arises from the initial assumption of the model that the influences of the strain, strain rate, and temperature on the flow stress–strain behavior of C250 maraging steel are mutually independent. Nonetheless, this study demonstrates that the strain rate significantly impacts the effects of strain hardening and thermal softening in the compressive mechanical response of C250 maraging steel, as shown in Figs. 2 and 3. Consequently, modifications need to be made to the Johnson-Cook model to capture the coupled effects of strain, strain rate, and temperature in the flow behavior of C250 alloy.

Fig. 7
figure 7

Comparison of measured and predicted flow stresses with original Johnson-Cook model at strain rates of: (a) 700 s-1; (b) 1200 s-1; and (c) 1700 s-1

Full size image
$$\sigma =\left(1685+1.0961{\varepsilon }^{-0.91}\right)(1+0.0198\times \text{ln}(\dot{{\varepsilon }^{*}}))(1-{{T}^{*}}^{0.9958})$$
(10)

3.3 Modified Johnson-Cook Models

To effectively capture the coupled effects of strain rate and strain, as well as the strain rate and temperature on the flow behavior of C250 maraging steel, modified Johnson-Cook models were proposed at reference temperature and above reference temperature in this study as follows (see Equations (11)-(14)), respectively. Equation (11) shows the modified Johnson-Cook model at the reference temperature, in which a polynomial function is introduced to replace the strain hardening item of the original Johnson-Cook model to better capture the deformation behavior of C250 maraging steel at the reference temperature and reference strain rate. Equations (12)-(14) represent the modified Johnson-Cook model above the reference temperature. In addition to the same modification as Equation (11), two more modifications were made to the Johnson-Cook model based on the flow stress–strain plots of C250 maraging steel at high deformation temperatures. Firstly, two new functions consisting of the strain rate are inserted into the thermal softening item to show the coupled effects of strain rate and temperature on the dynamic deformation behavior of C250 maraging steel at high temperatures (see Equation (12)). Secondly, a new function consisting of strain rate and strain is introduced into the modified Johnson-Cook model to indicate their combined effects at high temperatures (see Equations (12)-(14)).

The modified Johnson-Cook model at T = 298 K is:

$$\sigma =\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\times \text{ln}({\dot{\varepsilon }}^{*})\right)$$
(11)

The modified Johnson-Cook model above 298 K is:

$$\sigma =\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\times \text{ln}\left({\dot{\varepsilon }}^{*}\right)\right)(1-\text{exp}(\left({k}_{1}\times \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{k}_{2}\right)\times \text{ln}({T}^{*})+\left({b}_{1}\times \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{b}_{2}\right)))(d\times \varepsilon +f)$$
(12)
$$d={d}_{1}+{d}_{2}\text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{{d}_{3}(\text{ln}\left(\dot{{\varepsilon }^{*}}\right))}^{2}$$
(13)
$$f={f}_{1}+{f}_{2}\text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{{f}_{3}(\text{ln}\left(\dot{{\varepsilon }^{*}}\right))}^{2}$$
(14)

where σ is the von Mises flow stress, namely the equivalent flow stress; ε is the equivalent plastic strain; C is the strain rate hardening coefficient; \(\dot{{\varepsilon }^{*}}=\frac{\dot{\varepsilon }}{\dot{{\varepsilon }_{0}}}\) is the dimensionless strain rate with strain rate \(\dot{\varepsilon }\) and reference strain rate \(\dot{{\varepsilon }_{0}}\); and T* is the homologous temperature, \({T}^{*}=\frac{T-{T}_{r}}{{T}_{m}-{T}_{r}}\), in which T is the deformation temperature, K, Tr is the reference temperature, K, and Tm is the melting point, K. A, B1, B2, k1, k2, b1, b2, d, d1, d2, d3, f, f1, f2, and f3 are material constants.

Similarly, experimental data were extracted from the flow stress- strain plots of C250 maraging steel in the plastic strain interval of 0.005 to determine the material constants of the modified Johnson-Cook models; see Fig. 2. The reference temperature and reference strain rate are 298 K and 0.1 s-1, respectively. Under this reference condition, Equation (11) can be expressed as Equation (15). The relationship between σ and ε is plotted in Fig. 8. After the fitting analysis, the values of A, B1, B2 are determined to be 1733.34 MPa, − 482.87 MPa, and − 186.20 MPa, respectively.

Fig. 8
figure 8

Plotted relationship between σ and ε

Full size image
$$\sigma =A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}$$
(15)

At the reference temperature, Equation (11) can be rewritten as:

$$\frac{\sigma }{A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}}=1+C\times \text{ln}({\dot{\varepsilon }}^{*})$$
(16)

The relationship between \(\frac{\sigma }{A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}}\) and ln \((\dot{{\varepsilon }^{*}})\) is established by substituting the flow stress–strain data obtained at various strain rates at 298 K, as shown in Fig. 9. The parameter C is determined as the slope of the fitted line in the \(\frac{\sigma }{A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}}\)-\(\text{ln}(\dot{{\varepsilon }^{*}})\) plot, which is 0.0208.

Fig. 9
figure 9

Relationship between \(\frac{\sigma }{A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}}\) and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\)

Full size image

For temperatures above 298 K, two new parameters \(k={k}_{1}\times \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{k}_{2}\) and \(b={b}_{1}\times \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{b}_{2}\) are introduced into the thermal softening effect term of the modified Johnson-Cook model above reference temperature. These parameters are functions of the strain rate. Assuming \(d\times \varepsilon +f=1\), Equation (12) can be rewritten as:

\(\text{ln}(1-\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\bullet \text{ln}{(\dot{\varepsilon }}^{*})\right)})=k\times \text{ln}({T}^{*})+b\) (17). Figure 10 shows the relationship between \(\text{ln}(1-\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\cdot \text{ln}\dot{{\varepsilon }^{*}}\right)})\) and \(\text{ln}({T}^{*})\). It is important to note that the \(\text{ln}(1-\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\cdot \text{ln}(\dot{{\varepsilon }^{*})}\right)})\)-\(\text{ln}({T}^{*})\) relationship varies at different strain rates, thus indicating the combined influences of the strain rate and temperature. Different k and b values are determined from the slope and intercept of the fitted lines in the relationship between \(\text{ln}(1-\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\cdot \text{ln}{(\dot{\varepsilon }}^{*})\right)})\) and \(\text{ln}({T}^{*})\) at different strain rates. The obtained values of k and b are listed in Table 2. Then, the relationships among the material constants, k and b, and \(\text{ln}(\dot{{\varepsilon }^{*}})\) are plotted in Fig. 11. The values of k1 and k2, obtained from the slope and intercept of the fitted line in the relationship between k and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\) in Fig. 11a, are − 1.4833 and 15.0994, respectively. Similarly, b1 and b2 are calculated to be − 1.7138 and 16.3861, respectively, from the slope and intercept of the relationship between b and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\) in Fig. 11b.

Fig. 10
figure 10

Relationship between \(\text{ln}(1-\frac{\sigma }{\left(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2}\right)\left(1+C\text{ln}(\dot{{\varepsilon }^{*}})\right)})\) and \(\text{ln}({T}^{*})\) at different strain rates: (a) 700 s-1; (b) 1200 s-1; and (c) 1700 s-1

Full size image
Table 2 Material constants k and b obtained at different strain rates
Full size table
Fig. 11
figure 11

Relationships among k and b, and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\): (a) k vs. \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\), and (b) b vs. \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\)

Full size image

The different effects of the strain hardening are evident in the flow stress–strain plots of C250 maraging steels under different strain rates at high deformation temperatures; see Fig. 2. This highlights the significant impact of the strain rate on strain hardening. To effectively explain this influence, a novel parameter λ is introduced and expressed in Equation (18). The relationship between λ and ε is simplified as a linear relationship for all the impact testing conditions, as shown in Fig. 12. The values of the material constants d and f are determined from the slope and intercept of the linear fitted line for each impact testing condition, and all of the corresponding values are listed in Table 3. Based on the results, the relationships among d and f, and \(\text{ln}(\dot{{\varepsilon }^{*}})\) are established in Fig. 13, respectively. Polynomial fitting is used to determine the material constants, which shows that d1, d2, and d3 are − 257.8390, 57.1302, and − 3.1469, respectively, as plotted in Fig. 13a, respectively. Similarly, f1, f2, and f3 are calculated to be 18.5280, − 3.8316, and 0.2084, respectively, as shown in Fig. 13b.

Fig. 12
figure 12

Relationship between λ and ε at strain rates of: (a) 700 s-1; (b) 1200 s-1; and (c) 1700 s-1

Full size image
Table 3 Material constants d and f from impact tests at high temperatures
Full size table
Fig. 13
figure 13

Relationships among d and f, and \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\): (a) d vs. \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\); (b) f vs. \(\text{ln}\left(\dot{{\varepsilon }^{*}}\right)\)

Full size image
$$\lambda =\frac{\sigma }{(A+{B}_{1}\varepsilon +{B}_{2}{\varepsilon }^{2})(1+C\cdot \text{ln}(\dot{{\varepsilon }^{*})})(1-\text{exp}(\left({k}_{1}\cdot \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{k}_{2}\right)\cdot \text{ln}{T}^{*}+\left({b}_{1}\cdot \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+{b}_{2}\right)))}=d\times \varepsilon +f$$
(18)

Therefore, the proposed modified Johnson-Cook models are defined as follows. The measured and predicted flow stresses are plotted with the modified Johnson-Cook model under different high strain rates and deformation temperatures in Fig. 14. It can be observed that the predicted flow stress values show excellent agreement with the experimental data. This demonstrates the enhanced accuracy and compatibility of the modified Johnson-Cook models with the experimental data, compared to the original model. The improved performance of the modified Johnson-Cook models are because the models wholly consider the integrated effects of the strain rate and strain, as well as strain rate and temperature in their equations.

Fig. 14
figure 14

Comparison of measured and predicted flow stresses with modified Johnson-Cook model at strain rates of: (a) 700 s-1; (b) 1200 s-1; and (c) 1700 s-1

Full size image

At T = 298 K,

$$\sigma =\left(1733.34-482.87\varepsilon -186.20{\varepsilon }^{2}\right)\left(1+0.0208\times \text{ln}({\dot{\varepsilon }}^{*})\right)$$
(19)

For T > 298 K,

$$\sigma =\left(1733.34-482.87\varepsilon -186.20{\varepsilon }^{2}\right)\left(1+0.0208\times \text{ln}\left({\dot{\varepsilon }}^{*}\right)\right)(1-\text{exp}(\left(-1.4833\text{ln}\left(\dot{{\varepsilon }^{*}}\right)+15.0994\right)\times \text{ln}({T}^{*})+\left(-1.7138\times \text{ln}\left(\dot{{\varepsilon }^{*}}\right)+16.3861\right)) (d\times \varepsilon +f)$$
(20)
$$d=-257.839+57.1302\text{ln}\left(\dot{{\varepsilon }^{*}}\right)-3.1469({\text{ln}\left(\dot{{\varepsilon }^{*}}\right))}^{2}$$
(21)
$$f\,=\,18.528-3.8316\text{ln}\left(\dot{{\varepsilon }^{*}}\right)+0.2084({\text{ln}\left(\dot{{\varepsilon }^{*}}\right))}^{2}$$
(22)

3.4 Validation of Constitutive Models

To quantitatively evaluate the accuracy of both the original and modified Johnson-Cook constitutive models, statistical analysis parameters, including the correlation coefficient (R) and the absolute average relative error (AARE), are calculated, and defined as follows (Ref 42):

$$R=\frac{\sum_{i=1}^{N}({E}_{i}-\overline{E })({P}_{i}-\overline{P })}{\sqrt{\sum_{i=1}^{N}{({E}_{i}-\overline{E })}^{2}\sum_{i=1}^{N}{({P}_{i}-\overline{P })}^{2}}}$$
(20)
$$AARE=\frac{1}{N}\sum_{i-1}^{N}\left|\frac{{E}_{i}-{P}_{i}}{{E}_{i}}\right|\times 100\%$$
(21)

where Ei represents the measured data, and Pi corresponds to the predicted data. \(\overline{E }\) and \(\overline{P }\) are the mean values of the measured and predicted data, respectively. N stands for the total number of measured or predicted values used in this study. The correlation coefficient, R, quantifies the strength of the linear relationship between the measured and predicted data (Ref 43). A correlation coefficient closer to 1 indicates higher model accuracy. Unlike the correlation coefficient, AARE is an unbiased statistical parameter for assessing model accuracy (Ref 44), where a lower AARE value shows improved predictive capability.

Figure 15 plots the correlation between the measured and predicted flow stresses with the two models. It is evident that only a limited number of experimental data points fall on the 45-degree line of the original Johnson-Cook model, which yields a corresponding correlation coefficient of just 0.9422. On the other hand, a large number of the experimental data points are on or near the 45-degree line of the modified model, which results in a significantly higher correlation coefficient of 0.9870, and thus excels the original model with enhanced correlation between the measured and predicted data. Furthermore, the AARE values for the original and modified Johnson-Cook models are calculated to be 6.67% and 2.21%, respectively. The AARE for the modified Johnson-Cook models are 66.87% lower than that of the original model, thus further confirming its superior accuracy in predicting the flow stress values of C250 maraging steel. Therefore, the modified Johnson-Cook models have a higher degree of accuracy than the original model.

Fig. 15
figure 15

Correlation between measured and predicted flow stresses: (a) original Johnson-Cook and (b) modified Johnson-Cook models

Full size image

Furthermore, additional dynamic compression tests were conducted under three distinct conditions (913 s-1 and 673 K, 1307 s-1 and 473 K, as well as 1868 s-1 and 298 K) on the C250 maraging steel to further corroborate the predictive capability of the modified Johnson-Cook models. A comparison between the measured and predicted flow stress–strain plots based on these dynamic compression tests is presented in Fig. 16. It is obvious that the plotted flow stress–strain predicted by the proposed modified Johnson-Cook models are in good agreement with the corresponding experimental data. Consequently, this confirms that the modified Johnson-Cook models are a viable tool for predicting the compressive flow stress of C250 maraging steel at different strain rates and deformation temperatures.

Fig. 16
figure 16

Validation of the modified Johnson-Cook model

Full size image

4 Conclusion

Constitutive models provide critical input in FEA simulations to understand and predict the behavior of a material during deformation. To develop an appropriate constitutive model for C250 maraging steel, its quasi-static and dynamic compressive behaviors at various strain rates and deformation temperatures are investigated in this study by using a servo-hydraulic universal test machine and the DIHPB technique. The experimental results present that the effect of strain rate on the flow stress of C250 maraging steel varies at different temperatures. Furthermore, the effect of strain on the flow stress of C250 maraging steel is dependent on the strain rate at a high deformation temperature. Based on the coupled effects between the strain rate and temperature, as well as the strain rate and strain on the flow behavior of C250 maraging steel, modified Johnson-Cook models are proposed in this study. The modified Johnson-Cook models consider the combined influences of strain rate and strain, as well as strain rate and temperature. The predicted results show excellent agreement with the observed flow behavior. Moreover, validation is done under new dynamic compression conditions which further confirms the ability of the modified Johnson-Cook models to reliably predict the flow behavior of C250 maraging steel under various conditions.