1 Introduction

GCr15 steel (Chinese GB/T-standard), also known as American Iron and Steel Institute (AISI) 52,100 steel, is a typical high-carbon chromium bearing steel that is widely used in industrial applications. Its high hardness, wear resistance, and fatigue strength make it an ideal material for producing various bearing rings and rolling elements, which are critical components in many mechanical systems, including automobiles, airplanes, and industrial machinery (Ref 1,2,3). Given its excellent mechanical properties and widespread industrial applications, GCr15 steel is an essential material in modern engineering and manufacturing. Ongoing research into the properties and performance of this material remains a crucial area of study for materials scientists and engineers. The working environment of bearings typically involves high temperature, high speed, and heavy load, which places strict demands on the mechanical properties of the bearing steel. Therefore, an in-depth study of the hot deformation behavior of GCr15 steel under dynamic loading and the establishment of a suitable constitutive model are essential for practical applications (Ref 4, 5). Yin et al. (Ref 6) conducted a study on the effects of grain size and plastic strain on the microstructure of GCr15 steel using experiments and finite element simulations. They developed constitutive models for flow stress, austenite grain growth, and dynamic recrystallization of GCr15 steel to predict the microstructure evolution of the material during the hot deformation process and subsequently validated the accuracy of the model. Huo et al. (Ref 7) investigated the dynamic recrystallization behavior of GCr15 steel at varying deformation temperatures and strain rates. They found that reducing the strain rate and increasing the deformation temperature can promote dynamic recrystallization in the material. Additionally, they developed a viscoplastic constitutive model for GCr15 steel.

With the advancement of numerical simulation methods, the finite element method (FEM) has become a widely adopted approach to simulate the hot deformation of metal materials (Ref 8, 9). To employ FEM for simulating the elastoplastic deformation process of materials, a material constitutive model needs to be determined beforehand. Constitutive model is a crucial tool for describing the mechanical behavior of materials, and its accuracy significantly influences the accuracy of numerical simulation (Ref 10). Therefore, it is imperative to establish a high-precision constitutive model. However, from the existing literature, it is evident that the research on the constitutive model of GCr15 steel at high strain rate is considerably limited, and further studies are necessary.

Currently, the constitutive models used to describe the flow behavior of metal materials can be classified into three types: empirical models (Ref 11,12,13,14), phenomenological models (Ref 15,16,17), and physical models (Ref 18,19,20,21,22,23,24). Empirical models are proposed based on empirical observations, and due to their simplicity, high precision, and practicality, they often find widespread application in commercial finite element software. One of the most commonly used empirical models is the Johnson–Cook (JC) model (Ref 11). Samantaray et al. (Ref 12) investigated the high-temperature flow behavior of 9Cr-1Mo steel across a widely temperature range using the JC constitutive model. Zhao et al. (Ref 13) found that the laser additive manufacturing FeCr alloy has strain rate softening effect. Based on this finding, they proposed a modified Johnson–Cook (MJC) model that takes into account the coupling effect of strain rate and temperature to describe the dynamic behavior of FeCr alloy. Taking into account that dynamic recovery (DRV) is the primary softening mechanism during hot deformation of A356 aluminum alloy, Chen et al. (Ref 14) introduced a stress-dislocation relationship and proposed a MJC model. The phenomenological model analyzes the factors that affect the flow stress of metal materials at the macro level, such as the Arrhenius-type constitutive model. This model proposes a temperature compensation factor to express the relationship between strain rate and temperature, which enables predicting the flow stress under high-temperature deformation conditions. Li et al. (Ref 15) investigated the high-temperature flow behavior of SnSbCu alloy using the Arrhenius-type constitutive model. Jain et al. (Ref 16) studied the hot deformation behavior of CoFeMnNiTi Eutectic High-Entropy Alloy with Arrhenius-type constitutive model and artificial neural network (ANN) model. He et al. (Ref 17) incorporated strain-related parameters into the Arrhenius-type model to predict the high-temperature flow behavior of 316LN stainless steel. The physical model is based on the microscopic deformation mechanism and is characterized by a relatively complex constitutive model with many parameters. Physically based models, such as the Mechanical Threshold Stress (MTS) model and Zerilli–Armstrong model, propose that plastic deformation behavior is closely associated with the motion and accumulation of material microstructure dislocations (Ref 18,19,20). Banerjee (Ref 21) established the MTS model of AISI 4340 steel at different tempering temperatures. Prasad et al. (Ref 22) proposed a modified MTS model to study the flow behavior of austenitic stainless steels, which incorporates athermal and dynamic strain aging components that are variable. Rudra et al. (Ref 23, 24) employed the modified Zerilli–Armstrong model, which accounts for the combined effect of thermal softening, strain rate hardening, isothermal hardening, temperature, strain rate, and strain, to forecast the hot deformation behavior of two materials: Aluminum 5083 + 10 Wt Pct SiCp Composite and Al-5083 + SiC Composite.

In this study, the split Hopkinson pressure bar (SHPB) apparatus is employed to investigate the dynamic compression deformation behavior of GCr15 steel. Four models, namely the JC model, MJC model, MTS model, and modified Arrhenius-type constitutive model, are employed to predict the flow behavior of GCr15 steel. Grey Wolf Optimizer (GWO) is employed to optimize the constitutive model parameters, while the average absolute relative error (AARE) is used to evaluate the model's applicability. The predicted curves of the four constitutive models are compared with the fundamental experimental data to verify the model's reliability. Finally, the micromorphology of the GCr15 steel specimens after impact is observed by scanning electron microscope (SEM).

2 Experiment Details and Optimization Methods

2.1 Experimental Materials and Procedure

The material used in the experiment is GCr15 bearing steel, extracted from cylindrical roller bearings. The chemical composition of GCr15 steel is presented in Table 1. The material is machined into several cylindrical specimens with a diameter of 5 mm and length of 4 mm. All specimens are machined using a wire electrical discharge machine (EDM) and polished on both sides to minimize the radial friction at both ends of the specimen. The SHPB apparatus used in this study is depicted in Fig. 1. During the experiment, high-pressure nitrogen in the gas gun propels the striker bar, which then impacts the incident bar. The cylindrical specimen is placed between the incident and transmitted bars and is subjected to axial loading. The stress–strain relationship of the specimen is obtained by measuring the strain caused by the stress wave generated by the high impact pressure. Using the SHPB apparatus, dynamic compression experiments are conducted on the specimens at impact pressures of 0.3–0.6 MPa and temperatures of 298, 473, 673, and 873 K.

Table 1 GCr15 steel chemical components used in this study, wt.% (Ref 25)
Full size table
Fig. 1
figure 1

Schematic diagram of SHPB apparatus

Full size image

2.2 Experimental Results

At least two repeated experiments are conducted under each loading condition to obtain the stress–strain relationship of the specimen, as shown in Fig. 2. It should be noted that the effective rise time of the strain of the specimen is lower than the rise time required for the stress balance in the specimen, which may lead to errors in the stress–strain data (Ref 2). To avoid the influence of initial wave reverberation, a safety strain of 3.5% is taken as the starting point of the stress–strain curve. In this study, the constitutive models all use a strain of 0.035 as the starting point for prediction. Figure 3 shows the stress peaks of GCr15 steel at different temperatures and strain rates. It can be clearly seen that GCr15 steel exhibits both strain rate strengthening and temperature softening effects. At 298 K, the peak stress of GCr15 steel increased from 2636 to 3068 MPa under dynamic impact testing with a strain rate ranging from 460 to 1370 s−1, representing an increase of 432 MPa. However, at the high temperature of 873 K, and with a wider strain rate range of 1680–3940 s−1, the peak stress of GCr15 steel increased from 1520 to 1661 MPa, indicating only an increase of 141 MPa. These results suggest that the strain rate sensitivity of GCr15 steel is dependent on temperature, with the strain rate sensitivity decreasing as the temperature increases.

Fig. 2
figure 2

The results of dynamic compression experiments: (a) 0.3 MPa, (b) 0.4 MPa, (c) 0.5 MPa, (d) 0.6 MPa

Full size image
Fig. 3
figure 3

Stress peaks at different strain rates and temperatures

Full size image

2.3 Evaluation Method of Constitutive Models

The accuracy of the model can be verified by means of the AARE, the correlation coefficient (Rr) and relative error. The AARE represents the relationship between a single stress point and the average stress under different strains, and it accurately reflects the prediction error. The Rr provides information on the strength of the linear relationship between the experimental stress points and the predicted stress points. Relative errors reflect the accuracy of calculation relative to the true or expected value. They can be expressed as:

$$AARE = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\frac{{E_{i} - P{}_{i}}}{{E_{i} }}} \right|} \times 100$$
(1)
$$R_{r} = \frac{{\sum\limits_{i = 1}^{N} {\left( {E_{i} - \overline{E}} \right)} \left( {P_{i} - \overline{P}} \right)}}{{\sqrt {\sum\limits_{i = 1}^{N} {\left( {E_{i} - \overline{E}} \right)^{2} } \sum\limits_{i = 1}^{N} {\left( {P_{i} - \overline{P}} \right)^{2} } } }}$$
(2)
$${\text{Relative error percentage}} = \frac{{E_{i} - P{}_{i}}}{{E_{i} }} \times 100{\text{\% }}$$
(3)

where N is the total number of flow stress points, Ei is the experimental flow stress point, Pi is the flow stress point predicted by the constitutive model, \(\overline{E}\) is the average of the experimental stress points, and \(\overline{P}\) is the average of the predicted stress points.

2.4 Grey Wolf Optimizer (GWO)

GWO is a group intelligence optimization algorithm that is used to solve the optimal value problem (Ref 26,27,28). The optimization algorithm is implemented by simulating the hierarchical structure of gray wolves in their population and their predation mechanism. The algorithm defines the hierarchy of gray wolves into four different grades, namely α wolf, β wolf, δ wolf, and ω wolves based on their status, as shown in Fig. 4. The hunting method of the gray wolf group in the algorithm includes three steps: searching for prey, surrounding prey, and attacking prey. During the hunting process, the positions of all gray wolves of level ω are updated based on the positions of gray wolves of level α, β, and δ. The specific steps of the GWO algorithm used in this paper are described as follows:

Fig. 4
figure 4

Hierarchy of grey wolves in GWO

Full size image
  1. (1)

    Initialization of gray wolf population position.

In this step, the number of gray wolves is set to 50, and the maximum number of iterations is set to 1000 as the stopping condition for the gray wolves to stop hunting. An initial population of gray wolves is then randomly generated within the given range of constitutive parameters.

  1. (2)

    Gray wolf population social hierarchy.

The AARE serves as the fitness evaluation index to establish a social hierarchy model for gray wolves. The three wolves with the smallest fitness of constitutive parameters are marked as α, β, and δ wolves, respectively, and they are considered the top-class of the wolf pack and issue instructions to the rest of the pack. The remaining wolves are designated as ω wolves and are responsible for hunting to find the optimal solution of the constitutive parameters.

  1. (3)

    Encircling prey.

The ω wolves will encircle the optimal solution of the constitutive parameters based on the commands of the α wolf, β wolf, and δ wolf. The encircling process can be represented by the following mathematical model (Ref 29):

$${\mathbf{X}}^{(k + 1)} = {\mathbf{X}}_{p}^{(k)} - {\mathbf{A}}^{(k)} \cdot {\mathbf{D}}^{(k)}$$
(4)
$${\mathbf{A}}^{(k)} = 2{\mathbf{a}}^{(k)} \cdot {\mathbf{r}}_{1}^{(k)} - {\mathbf{a}}^{(k)}$$
(5)
$${\mathbf{D}}^{(k)} = \left| {{\mathbf{C}}^{(k)} \cdot {\mathbf{X}}_{p}^{(k)} - {\mathbf{X}}^{(k)} } \right| = \left| {2{\mathbf{r}}_{2}^{(k)} \cdot {\mathbf{X}}_{p}^{(k)} - {\mathbf{X}}^{(k)} } \right|$$
(6)

where k represents the iteration number, X represents the position vector of a gray wolf, and Xp represents the position vector of the prey, which is the best constitutive parameter. A is a coefficient vector. When \(\left| {\mathbf{A}} \right|\)> 1, the wolf pack performs a global search, and when \(\left| {\mathbf{A}} \right|\)< 1, the wolf pack narrows down and performs a local search. The position of the prey determines the value of the D vector, C is the coefficient vector, a vector is linearly reduced from 2 to 0 in the iteration, and r1, r2 are random vectors with values between 0 and 1.

  1. (4)

    Hunting the prey.

Under the guidance of α wolf, β wolf, and δ wolf, the wolves first locate the prey, surround it, and eventually attack it. In the first iteration, the wolves do not know the position of the prey, and thus, the range of the best constitutive parameters cannot be determined. It is assumed that α wolf, β wolf, and δ wolf have a strong sense of smell that helps them locate the position of the constitutive parameters. After each iteration, the three wolves with the smallest fitness, as measured by AARE, become the new α wolf, β wolf, and δ wolf. The other wolves update their positions by following the positions of the three wolves and then search and surround the prey for the attack. Once the maximum number of iterations is reached, the hunting stops. At this point, the position of the α wolf with the best fitness represents the optimal solution, which is the optimized constitutive parameter. The following expression is used to update the position of the gray wolf (Ref 29):

$${\mathbf{D}}_{\alpha }^{(k)} = \left| {{\mathbf{C}}_{1}^{(k)} \cdot {\mathbf{X}}_{\alpha }^{(k)} - {\mathbf{X}}^{(k)} } \right|,{\mathbf{D}}_{\beta }^{(k)} = \left| {{\mathbf{C}}_{2}^{(k)} \cdot {\mathbf{X}}_{\beta }^{(k)} - {\mathbf{X}}^{(k)} } \right|,{\mathbf{D}}_{\delta }^{(k)} = \left| {{\mathbf{C}}_{3}^{(k)} \cdot {\mathbf{X}}_{\delta }^{(k)} - {\mathbf{X}}^{(k)} } \right|$$
(7)
$${\mathbf{X}}_{1}^{(k)} = {\mathbf{X}}_{\alpha }^{(k)} - {\mathbf{A}}_{1}^{(k)} \cdot {\mathbf{D}}_{\alpha }^{(k)} ,{\mathbf{X}}_{2}^{(k)} = {\mathbf{X}}_{\beta }^{(k)} - {\mathbf{A}}_{2}^{(k)} \cdot {\mathbf{D}}_{\beta }^{(k)} ,{\mathbf{X}}_{3}^{(k)} = {\mathbf{X}}_{\delta }^{(k)} - {\mathbf{A}}_{3}^{(k)} \cdot {\mathbf{D}}_{\delta }^{(k)}$$
(8)
$${\mathbf{X}}^{(k + 1)} = \frac{{{\mathbf{X}}_{1}^{(k)} + {\mathbf{X}}_{2}^{(k)} + {\mathbf{X}}_{3}^{(k)} }}{3}$$
(9)

where the values of Dα, Dβ and Dδ are determined by the α, β, and δ wolves, respectively, X1, X2 and X3 represent the positions of α, β, and δ wolves, respectively, X(k+1) denotes the search range position of the wolf in the next iteration.

3 Results

In the context of dynamic loading conditions, the deformation of metal materials leads to a rise in temperature, which is regarded as an adiabatic process. Accordingly, this study employs the following equation to express the temperature (Ref 19):

$$T = T_{0} + \frac{\eta }{{\rho C_{p} }}\int \sigma d\varepsilon_{p}$$
(10)

where T0 represents the initial temperature, η denotes the ratio of plastic work converted to heat, which is set to 0.9 in this study. The plastic strain εp is calculated using the equation εp = ε − σ/E, where ε is the true strain, σ is the flow stress, and E is Young's modulus. Additionally, ρ and Cp represent the density and specific heat capacity of GCr15 steel, respectively, and their values are presented in Table 2.

Table 2 The properties of GCr15 steel
Full size table

3.1 Johnson–Cook (JC) Model

The JC model was proposed by Johnson and Cook in 1983 (Ref 11). Among various empirical constitutive models, it has gained wide acceptance in commercial finite element software due to its straightforward form, fewer parameters, and practicality (Ref 30). This model is appropriate for predicting the behavior of materials under dynamic loading conditions. The expression is as follows:

$$\sigma = (A + B\varepsilon_{p}^{n} )(1 + C\ln \dot{\varepsilon }^{ * } )(1 - T^{ * m} )$$
(11)

where the constitutive model comprises three main parts (Ref 31). The first part is the strain hardening term \((A + B\varepsilon_{p}^{n} )\), where A is the yield stress at the reference temperature and reference strain rate, B is a factor associated with strain hardening, and n is the strain hardening index. The second part is the strain rate sensitivity term \((1 + C\ln \dot{\varepsilon }^{ * } )\), where \(\dot{\varepsilon }^{ * } = \dot{\varepsilon }/\dot{\varepsilon }_{ref}\) is the dimensionless strain rate, \(\dot{\varepsilon }\) is the strain rate, the reference strain rate \(\dot{\varepsilon }_{ref}\) is considered as 0.01 s−1, C is the strain rate related factor. The third part is the temperature softening term (1 − T*m), where T* = (T − Tref)/(Tm − Tref) is the dimensionless temperature, T is the current absolute temperature, the reference temperature Tref is considered as 298 K, Tm is the melting point temperature of the material, and m is the temperature softening index.

The least square method is commonly used to linearly fit the parameters of the constitutive model for determining the parameters in the JC model. However, this method is prone to errors in data point selection and the accuracy of the experimental curve, particularly when a small number of data points are used to represent the entire plastic stage or when the experimental curve is far from the reference temperature and strain rate. Consequently, the fitting parameters obtained may not accurately reflect the stress–strain relationship under various loading conditions.

GWO is utilized for parameter optimization. 16 stress–strain curves obtained at different temperatures (298, 473, 673, and 873 K) under the loading condition of 0.3–0.6 MPa are input into the algorithm, and the constitutive model parameters are optimized by using the AARE as the fitness evaluation metric. After reaching the maximum number of iterations, GWO can determine the optimal parameters within the specified parameter range. The optimized JC model parameters are presented in Table 3.

Table 3 JC model parameters for GCr15 steel
Full size table

The JC model, with the parameters listed in Table 3, can predict the flow stress of GCr15 steel during dynamic loading. Figure 5 displays a comparison between the experimental data and the prediction data of the JC model under different loading conditions. Figure 6 illustrates the AARE of the JC model parameters obtained during each iteration of the GWO iteration process, which gradually converges to 3.7192%. The results suggest that the JC model is able to accurately capture the flow behavior of GCr15 steel at high strain rates.

Fig. 5
figure 5

Comparison of experimental flow stress (solid line) and JC model (dotted line) under different loading conditions: (a) 0.3 MPa, (b) 0.4 MPa, (c) 0.5 MPa, (d) 0.6 MPa

Full size image
Fig. 6
figure 6

The convergence curve of AARE of JC model in GWO

Full size image

3.2 Modified Johnson–Cook (MJC) model

It can be observed that the JC model employs fewer parameters to forecast the flow stress of the material during dynamic loading, and it does not take into account the combined effects of strain hardening, strain rate sensitivity, and temperature softening (Ref 32). In reality, the cumulative effect of strain, temperature, and strain rate should not be ignored.

In the JC model, the strain hardening term \((A + B\varepsilon_{p}^{n} )\) plays a dominant role in predicting the flow stress of the material, while the strain rate strengthening term \((1 + C\ln \dot{\varepsilon }^{ * } )\) and temperature softening term (1 − T*m) play an adjusting role in the calculation. The strain rate related factor C and the temperature softening index m control the amplitude of adjustment. However, stress peak experimental data in Fig. 3 reveals a coupling effect between temperature and strain rate in GCr15 steel. It can be seen that the strain rate sensitivity of GCr15 decreases as the temperature increases. Therefore, the strain rate related factor C should be modeled as a function of both temperature and strain. Additionally, relying on only one temperature softening index m may not be sufficient to precisely control the temperature softening range. Thus, a temperature-sensitive proportional factor D has been introduced in this study. As a result, the MJC model for GCr15 steel has been established, as shown in Eq. 12:

$$\left\{ {\begin{array}{*{20}c} {\sigma = (A_{1} + B_{1} \varepsilon_{p}^{{n_{1} }} )(1 + f(T,\varepsilon_{p} )\ln \dot{\varepsilon }^{ * } )(1 - DT^{{ * m_{1} }} )} \\ {f(T,\varepsilon_{p} ) = k_{0} + k_{1} T^{ * } + k_{2} T^{ * 2} + k_{3} \varepsilon_{p} + k_{4} \varepsilon_{p}^{2} \,\,\,\,\,\,\,\,\,\,\,\,} \\ \end{array} } \right.$$
(12)

where A1, B1, D, k0, k1, k2, k3, k4, m1, n1 are material parameters, and f(T,εp) is a polynomial function with respect to temperature and plastic strain, where 298 K is used as the reference temperature and 0.001 s−1 is used as the reference strain rate to predict the material constant. GWO is employed to optimize all parameters. Finally, the parameters of the MJC model are shown in Table 4.

Table 4 MJC model parameters for GCr15 steel
Full size table

The flow stress of GCr15 steel during dynamic loading can be predicted using the MJC model parameters in Table 4. Figure 7 presents a comparison between the MJC model's predicted data and the experimental data obtained from the SHPB apparatus under different loading conditions of temperature and strain rate. The AARE of the optimized parameters of the MJC model obtained during each iteration of the GWO iteration process, gradually converges to 2.6501%, as shown in Fig. 8. It is evident that the MJC model yields better prediction results compared to the original JC model.

Fig. 7
figure 7

Comparison of experimental flow stress (solid line) and MJC model (dotted line) under different loading conditions: (a) 0.3 MPa, (b) 0.4 MPa, (c) 0.5 MPa, (d) 0.6 MPa

Full size image
Fig. 8
figure 8

The convergence curve of AARE of MJC model in GWO

Full size image

3.3 Mechanical Threshold Stress (MTS) model

MTS model believes that the plastic deformation behavior is closely related to the movement and accumulation of material microstructure dislocations (Ref 20). In the MTS model, the flow stress is considered as a function of a reference stress (mechanical threshold stress), which is the flow stress at 0 K or the flow stress without any resistance. And it can be divided into athermal component and thermal component, as shown in Eq. 13 (Ref 19, 20, 33):

$$\hat{\sigma }_{y} = \hat{\sigma }_{a} + \hat{\sigma }_{t}$$
(13)

where \(\hat{\sigma }_{a}\) is the athermal component of the mechanical threshold stress. It describes the irrelevant interactions related to the short-range barrier rate of dislocations within the metal. This component changes with variations in the internal grain size of the metal, dislocation density, and other factors. \(\hat{\sigma }_{t}\) is the thermal component of the mechanical threshold stress, which describes the interactions related to the short-range barrier rate of dislocations within the metal. In a short time, thermal activation will cause the flow stress of the latter to decrease, while the former remains unchanged (Ref 20). Therefore, the relationship between flow stress and mechanical threshold stress can be expressed as (Ref 19, 20):

$$\sigma_{y} = \sigma_{a} + \sigma_{t} = \hat{\sigma }_{a} + S(\dot{\varepsilon }_{p} ,T)\hat{\sigma }_{t} \frac{\mu (T)}{{\mu_{0} }}$$
(14)

where the athermal component \(\sigma_{a} \equiv \hat{\sigma }_{a}\) (Ref 34), \(S(\dot{\varepsilon }_{p} ,T)\) represents the scale factor related to strain rate and temperature, μ is the shear modulus, μ0 is the shear modulus at 0 K, and the stress \(\hat{\sigma }_{t}\) of the thermal component is divided into two parts, one part \(\hat{\sigma }_{i}\) is the flow stress related to the rate caused by the inherent thermally activated dislocation movement obstacle inside, and the other part \(\hat{\sigma }_{e}\) is the flow stress with a strain hardening component. Therefore, the constitutive can be rewritten as the following (Ref 19, 20, 35):

$$\sigma_{y} = \sigma_{a} + S_{i} (\dot{\varepsilon }_{p} ,T)\hat{\sigma }_{i} \frac{\mu (T)}{{\mu_{0} }} + S_{e} (\dot{\varepsilon }_{p} ,T)\hat{\sigma }_{e} \frac{\mu (T)}{{\mu_{0} }}$$
(15)

where Si and Se, respectively, represent the scaling factors of these two parts, they can be derived from the Arrhenius law, which relates the strain rate, activation energy, and temperature. In the thermally activated sliding zone, the dynamics of the short-range barrier interaction are described as follows:

$$\dot{\varepsilon }_{p} = \dot{\varepsilon }_{0} \exp (\frac{ - \Delta G}{{k_{b} T}})$$
(16)

where \(\dot{\varepsilon }_{0}\) is the reference strain rate, which is a constant, kb is Boltzmann constant, the free energy ΔG is a function of stress and can be expressed as follows in the phenomenological relational expression (16) (Ref 19, 20):

$$\Delta G = g_{0} \mu b^{3} \left[ {1 - \left( {\frac{{\sigma_{t} /\mu }}{{\hat{\sigma }_{t} /\mu_{0} }}} \right)^{p} } \right]^{q}$$
(17)

where g0 is the normalized activation energy, and b is the Burgers vector. p and q represent empirical constants that describe the distribution of sliding resistance in the high activation energy region and the low activation energy region, respectively. The relationship between μ and μ0 is as follows (Ref 19, 20):

$$\mu = \mu_{0} - \frac{{D_{r} }}{{\exp (T_{r} /T) - 1}}$$
(18)

where Dr, Tr is the modified parameters. After combining Equation. 15-16, the scale factor (Si, Se) has a modified Arrhenius law, as follows (Ref 21):

$$S_{i} (\dot{\varepsilon }_{p} ,T) = \left[ {1 - \left( {\frac{{k_{b} T}}{{g_{0i} b^{3} \mu (T)}}\ln \frac{{\dot{\varepsilon }_{0i} }}{{\dot{\varepsilon }_{p} }}} \right)^{{1/q_{i} }} } \right]^{{1/p_{i} }}$$
(19)
$$S_{e} (\dot{\varepsilon }_{p} ,T) = \left[ {1 - \left( {\frac{{k{}_{b}T}}{{g_{0e} b^{3} \mu (T)}}\ln \frac{{\dot{\varepsilon }_{0e} }}{{\dot{\varepsilon }_{p} }}} \right)^{{1/q_{e} }} } \right]^{{1/p_{e} }}$$
(20)

Therefore, the MTS constitutive model can finally be expressed as the following:

$$\begin{gathered} \sigma _{y} = \sigma _{a} + S_{i} (\dot{\varepsilon }_{p} ,T)\hat{\sigma }_{i} \frac{{\mu (T)}}{{\mu _{0} }} + S_{e} (\dot{\varepsilon }_{p} ,T)\hat{\sigma }_{e} \frac{{\mu (T)}}{{\mu _{0} }} \hfill \\ \quad \quad = \sigma _{a} + \left[ {1 - \left( {\frac{{k_{b} T}}{{g_{{0i}} b^{3} \mu (T)}}\ln \frac{{\dot{\varepsilon }_{{0i}} }}{{\dot{\varepsilon }_{p} }}} \right)^{{1/q_{i} }} } \right]^{{1/p_{i} }} \hat{\sigma }_{i} \frac{{\mu (T)}}{{\mu _{0} }} \hfill \\ \quad \quad \quad + \left[ {1 - \left( {\frac{{k_{b} T}}{{g_{{0e}} b^{3} \mu (T)}}\ln \frac{{\dot{\varepsilon }_{{0e}} }}{{\dot{\varepsilon }_{p} }}} \right)^{{1/q_{e} }} } \right]^{{1/p_{e} }} \hat{\sigma }_{e} \frac{{\mu (T)}}{{\mu _{0} }} \hfill \\ \end{gathered}$$
(21)

where the strain hardening component \(\hat{\sigma }_{e}\) of the mechanical threshold stress is obtained by a modified Voce law, as follows:

$$\theta (\hat{\sigma }_{e} ) = \frac{{d\hat{\sigma }_{e} }}{{d\varepsilon_{p} }}$$
(22)

where

$$\theta (\hat{\sigma }_{e} ) = \theta_{0} \left[ {1 - F(\hat{\sigma }_{e} )} \right] + \theta_{1} F(\hat{\sigma }_{e} )$$
(23)
$$\theta_{0} = c_{00} + c_{10} \ln \dot{\varepsilon } + c_{20} \sqrt {\dot{\varepsilon }} + c_{30} T$$
(24)

where θ0 is the strain hardening rate caused by dislocation accumulation (Ref 33), \(F(\hat{\sigma }_{e} )\) is empirically derived the dynamic recovery rate, θ1 is the saturation strain hardening rate caused by dislocation accumulation, its value is 0 (Ref 21, 34), and c00, c10, c20, c30 are parameters. The influence of temperature on hardening rate is greater than that of strain rate. Therefore, the impact of strain rate on hardening rate can be disregarded in Eq. 24, and the equation can be rewritten as follows (Ref 21, 22):

$$\theta_{0} = c_{00} + c_{30} T$$
(25)

When the strain rate is more than 500 s−1, it is assumed that the material is an adiabatic deformation process, and the resulting temperature change must satisfy Eq. 10 (Ref 19, 21). The specific expression of \(F(\hat{\sigma }_{e} )\) is as follows:

$$F(\hat{\sigma }_{e} ) = \frac{{\tanh \left( {\gamma \frac{{\hat{\sigma }_{e} }}{{\hat{\sigma }_{es} }}} \right)}}{\tanh \left( \gamma \right)}$$
(26)

where γ represents the linear change of strain hardening rate with stress. The saturation threshold stress \(\hat{\sigma }_{es}\) is a function of temperature and strain rate, and its expression is as follows (Ref 19, 21):

$$\ln \left( {\frac{{\hat{\sigma }_{es} }}{{\hat{\sigma }_{0es} }}} \right) = \frac{{k_{b} T}}{{g_{0es} b^{3} \mu (T)}}\ln \left( {\frac{{\dot{\varepsilon }_{p} }}{{\dot{\varepsilon }_{0es} }}} \right)$$
(27)

where \(\hat{\sigma }_{0es}\), \(g_{0es}\) are the saturation threshold stress and normalized activation energy at 0 K. \(\dot{\varepsilon }_{0es}\) is the reference maximum strain rate. The reference maximum strain rate of the constitutive is usually limited to approximately 107 s−1 (Ref 21).

The reference strain rate \(\dot{\varepsilon }_{0i}\) = 108 s−1 is commonly used in the literature. The values of pi, pe, and qi, qe are in the range of 0–1 and 1–2, respectively (Ref 20). Empirical guidance shows that pi and qi are equal to 0.5 and 1.5, respectively (Ref 19). And in the strain hardening component pe, qe, \(\dot{\varepsilon }_{0e}\),\(\dot{\varepsilon }_{0es}\) and the normalized activation energy g0e are assigned their values as 2/3, 1, 107, 107 s−1 and 1.6 (Ref 34). The value of the linear change of strain hardening rate with stress (γ) is set to 1 (Ref 35). The value of the Boltzmann constant (kb) is 1.38 × 10–23 J/K, and the magnitude of the Burgers vector (b) is assumed to be 2.48 × 10–10 m. Under the condition of neglecting the slight fluctuations in Poisson's ratio at high temperature, the data in Table 5 can be substituted into Eq. 28 to obtain the shear modulus at different temperatures. Subsequently, the obtained values can be substituted into Eq. 18 to fit the parameters Dr = 40,064.8, Tr = 738.0.

$$\mu = \frac{E}{2(1 + \nu )}$$
(28)

where E is Young's modulus, ν is Poisson's ratio. The shear modulus of GCr15 steel at 0 K (μ0) is 77.537 GPa. Other parameters σa, \(\hat{\sigma }_{i}\), g0i, \(\hat{\sigma }_{oes}\), g0es, c00, c30 can be optimized by GWO. Finally, all parameters of MTS model are shown in Table 6.

Table 5 Test data of Young's modulus of GCr15 steel at different temperatures (Ref 1)
Full size table
Table 6 Parameters of MTS model of GCr15 steel
Full size table

Using the MTS model presented in Table 6, the flow stress of GCr15 steel under various loading conditions can be predicted. Figure 9 presents a comparison between the experimental data and the MTS model prediction data under different loading conditions. The AARE of the optimized parameters obtained in each iteration of the GWO iteration process is depicted in Fig. 10, and it gradually converges to 3.2152%. It is observed that MTS model can also predict the flow behavior of GCr15 steel at high strain rates.

Fig. 9
figure 9

Comparison of experimental flow stress (solid line) and MTS model (dotted line) under different loading conditions: (a) 0.3 MPa, (b) 0.4 MPa, (c) 0.5 MPa, (d) 0.6 MPa

Full size image
Fig. 10
figure 10

The convergence curve of AARE of MTS model in GWO

Full size image

3.4 Modified Arrhenius-type Constitutive Model

The Arrhenius-type model, which is widely used to describe the relationship between strain rate, temperature, and flow stress during high temperature material deformation, is expressed under the hyperbolic law. To characterize the impact of strain rate and deformation temperature on the material's deformation behavior, a Zener–Hollomon parameter is introduced (Ref 36). The Arrhenius-type model can be expressed as the following (Ref 37):

$$Z = \dot{\varepsilon }\exp (\frac{Q}{RT})$$
(29)
$$\dot{\varepsilon } = \left\{ {\begin{array}{*{20}c} {S_{1} \sigma^{{\overline{n}_{1} }} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \sigma < 0.8} \\ {S_{2} \exp (\beta \sigma )\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\alpha \sigma > 1.2} \\ {\overline{A}\left[ {\sinh (\alpha \sigma )} \right]^{{\overline{n}}} \exp ( - \frac{Q}{RT})\;\;\;\;\;{\text{for all }}\sigma } \\ \end{array} } \right.$$
(30)

where Eq. 30 indicate that at a certain deformation temperature, the relationship between flow stress and strain rate can be expressed by a power exponent (low stress levels), an exponent (high stress levels), and hyperbolic sine functions (all stress levels), respectively. σ is the flow stress at a given true strain. \(\dot{\varepsilon }\) is the strain rate, Q is the effective activation energy of hot deformation, R is the universal gas constant, which has a value of 8.31 J mol−1 K−1. T is the current absolute temperature. Further, S1, \(\overline{n}_{1}\), S2, β, \(\overline{A}\), α, \(\overline{n}\) are independent of the temperature of the material parameters determined from experimental data (Ref 38). Among them, the relationship between the three material parameters of \(\overline{n}_{1}\), β, and α is \(\alpha = \beta /\overline{n}_{1}\).

Combining Eq. 29 and 30, according to the definition of hyperbolic law, the Arrhenius-type constitutive model that uses the Zener–Hollomon parameter to describe the explicit form can be obtained comprehensively (Ref 39):

$$\sigma_{m} = \frac{1}{\alpha }\ln \left\{ {\left( {\frac{Z}{{\overline{A}}}} \right)^{{\frac{1}{{\overline{n}}}}} + \left[ {\left( {\frac{Z}{{\overline{A}}}} \right)^{{\frac{2}{{\overline{n}}}}} + 1} \right]^{\frac{1}{2}} } \right\}$$
(31)

He et al. (Ref 18) developed a modified Arrhenius-type constitutive model for 316LN stainless steel based on the impact of strain on flow stress, using the original Arrhenius-type constitutive model as a foundation. Due to the substantial variation in GCr15 steel's sensitivity to strain rate at different temperatures, the Arrhenius constitutive equation model may not accurately reflect the temperature softening effect. Therefore, in view of the above problem, a modified Arrhenius-type constitutive equation model is proposed:

$$\begin{gathered} \sigma = \left[ {1 - \left( {\frac{{T - T_{ref} }}{c}} \right)^{d} } \right]\sigma_{m} \hfill \\ \;\; = \frac{{\left[ {1 - \left( {\frac{{T - T_{ref} }}{c}} \right)^{d} } \right]}}{\alpha }\ln \left\{ {\left( {\frac{Z}{{\overline{A}}}} \right)^{{\frac{1}{{\overline{n}}}}} + \left[ {\left( {\frac{Z}{{\overline{A}}}} \right)^{{\frac{2}{{\overline{n}}}}} + 1} \right]^{\frac{1}{2}} } \right\} \hfill \\ \;\; = \frac{{\left[ {1 - \left( {\frac{{T - T_{ref} }}{c}} \right)^{d} } \right]}}{\alpha }\ln \left\{ {\left( {\frac{{\dot{\varepsilon }\exp (\frac{Q}{RT})}}{{\overline{A}}}} \right)^{{\frac{1}{{\overline{n}}}}} + \left[ {\left( {\frac{{\dot{\varepsilon }\exp (\frac{Q}{RT})}}{{\overline{A}}}} \right)^{{\frac{2}{{\overline{n}}}}} + 1} \right]^{\frac{1}{2}} } \right\} \hfill \\ \end{gathered}$$
(32)

where Tref is the reference temperature, which has a value of 298 K. c and d are the temperature softening coefficients about the true strain. Since the values of each constant changes greatly with the strain variation, \(\overline{n}\), α, Q, \(\ln \overline{A}\), c, and d can be expressed by the fifth-order polynomial of the true strain, as shown in Equations. (33-38).

$$\overline{n} = \overline{n}_{0} + \overline{n}{}_{1}\varepsilon + \overline{n}{}_{2}\varepsilon^{2} + \overline{n}{}_{3}\varepsilon^{3} + \overline{n}{}_{4}\varepsilon^{4} + \overline{n}{}_{5}\varepsilon^{5}$$
(33)
$$\alpha = \alpha_{0} + \alpha {}_{1}\varepsilon + \alpha {}_{2}\varepsilon^{2} + \alpha {}_{3}\varepsilon^{3} + \alpha {}_{4}\varepsilon^{4} + \alpha {}_{5}\varepsilon^{5}$$
(34)
$$Q = Q_{0} + Q{}_{1}\varepsilon + Q{}_{2}\varepsilon^{2} + Q{}_{3}\varepsilon^{3} + Q{}_{4}\varepsilon^{4} + Q{}_{5}\varepsilon^{5}$$
(35)
$$\ln \overline{A} = \overline{A}_{0} + \overline{A}{}_{1}\varepsilon + \overline{A}{}_{2}\varepsilon^{2} + \overline{A}{}_{3}\varepsilon^{3} + \overline{A}{}_{4}\varepsilon^{4} + \overline{A}{}_{5}\varepsilon^{5}$$
(36)
$$c = c_{0} + c{}_{1}\varepsilon + c{}_{2}\varepsilon^{2} + c{}_{3}\varepsilon^{3} + c{}_{4}\varepsilon^{4} + c{}_{5}\varepsilon^{5}$$
(37)
$$d = d_{0} + d{}_{1}\varepsilon + d{}_{2}\varepsilon^{2} + d{}_{3}\varepsilon^{3} + d{}_{4}\varepsilon^{4} + d{}_{5}\varepsilon^{5}$$
(38)

For the determination of GCr15 steel parameters, in this study, 18 different true strains (0.035, 0.04, 0.05, 0.06, 0.07, 0.08, 0.09, 0.10, 0.11, 0.12, 0.13, 0.14, 0.15, 0.16, 0.17, 0.19, 0.20 and 0.21) are selected. Taking the experimental data with a true strain of 0.07 as an example, the process of determining material parameters can be introduced. By taking natural logarithms on both sides of Eq. 30 at a certain deformation temperature, the following equations can be obtained, respectively.

$$\ln \dot{\varepsilon } = \ln S_{1} + \overline{n}_{1} \ln \sigma$$
(39)
$$\ln \dot{\varepsilon } = \ln S_{2} + \beta \sigma$$
(40)
$$\ln \dot{\varepsilon } = \ln \overline{A} - \frac{Q}{RT} + \overline{n}\ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]$$
(41)

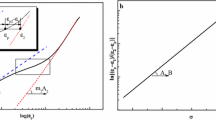
As shown in Fig. 11, at a certain temperature, the flow stress and corresponding strain rate at a strain of 0.07 are used to substitute into Eq. 39-41. The values of \(\overline{n}_{1}\) and β can be obtained from the average slope of several straight lines in Fig. 11(a) of \(\ln \dot{\varepsilon } - \ln \sigma\) and Fig. 11(b) of \(\ln \dot{\varepsilon } - \sigma\).The value of α can be obtained based on the relationship \(\alpha = \beta /\overline{n}_{1}\). Furthermore, by linear fitting in Fig. 11(c) of \(\ln \dot{\varepsilon } - \ln \sinh (\alpha \sigma )\), the value of \(\overline{n}\) can also be obtained. Finally, the effective activation energy (Q) is calculated by determining the slope of the line fitting in Fig. 11(d) of \(1000/T - \ln \sinh (\alpha \sigma )\) at a certain strain rate, as shown in Eq. 42 (Ref 18).

$$Q = R\left\{ {\frac{{\partial \ln \dot{\varepsilon }}}{{\partial \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]}}} \right\}_{T} \left\{ {\frac{{\partial \ln \left[ {\sinh \left( {\alpha \sigma } \right)} \right]}}{\partial (1000/T)}} \right\}_{{\dot{\varepsilon }}}$$
(42)

where the second term is the value of \(\overline{n}\), and the value of \(\ln \overline{A}\) can be obtained by the intercept of Eq. 41. When \(\ln \overline{A}\), α, \(\overline{n}\), Q material parameters are determined, the remaining parameters c, d in Eq. 37-38 can be optimized according to AARE. Finally, the material parameters of GCr15 steel at 0.07 true strain are shown in Table 7.

Fig. 11
figure 11

Relationships between (a) \(\ln \dot{\varepsilon } - \ln \sigma\), (b) \(\ln \dot{\varepsilon } - \sigma\), (c) \(\ln \dot{\varepsilon } - \ln \sinh (\alpha \sigma )\), (d) \(1000/T - \ln \sinh (\alpha \sigma )\) at the true strain of 0.07

Full size image
Table 7 The material constant of GCr15 steel at 0.07 strain
Full size table

To further determine the values of α, \(\overline{n}\), Q, \(\ln \overline{A}\), c, d of GCr15 steel under different true strains, the relationship between the value of each material constant and the strain can be fitted with a fifth-order polynomial to obtain a good correlation, as shown in Fig. 12.

Fig. 12
figure 12

Fifth-order polynomial fit of variations of (a) α, (b) \(\ln \overline{A}\), (c) \(\overline{n}\), (d) Q, (e) c and (f) d with true strain

Full size image

The results indicate that the material parameters can be effectively described by fifth-order polynomials. The regression coefficients of the fifth-order polynomial for the modified Arrhenius-type constitutive model parameters of GCr15 steel are presented in Table 8.

Table 8 Coefficients of the polynomial for \(\ln \overline{A}\), α, \(\overline{n}\), Q, c, and d of GCr15 steel
Full size table

Using the obtained material parameters, Eq. 32 is used to predict the flow stress under different strains. The comparison between the predicted data of the modified Arrhenius-type constitutive model and the experimental data under different temperature and strain rate loading conditions is shown in Fig. 13. It is observed that the modified Arrhenius-type model can effectively predict the flow behavior of GCr15 steel at high strain rates.

Fig. 13
figure 13

Comparison of experimental flow stress (solid line) and modified Arrhenius-type constitutive model (dotted line) under different loading conditions: (a) 0.3 MPa, (b) 0.4 MPa, (c) 0.5 MPa, (d) 0.6 MPa

Full size image

4 Discussion

4.1 Analysis of Constitutive Equation Accuracy

The JC model assumes that the effects of strain rate and temperature on flow stress are independent of each other, and the model may not be appropriate for experimental conditions that are far from the reference temperature and reference strain rate. However, this study employs the GWO, which uses all experimental data to optimize the material parameters. Therefore, the JC constitutive model with optimized parameters can accurately predict the dynamic compression behavior of GCr15 steel not only at the reference strain rate or reference temperature but also at high temperature and high strain rate. As depicted in Fig. 5, the predicted stress–strain curves at different strain rates and temperatures exhibit good agreement with the experimental data. Additionally, the AARE and Rr of the JC model are 3.7193% and 0.9542, respectively, as illustrated in Fig. 6 and 14(a). Figure 15 is a graph of the relative error percentages for the four models, with the same data points as those used to calculate Rr, and the numbers above the column indicate the number of samples within a specific range of relative error. It can be seen form Fig. 15(a) that the relative error of the JC model ranges from − 9.272 to 13.609%, and the mean relative error is 1.695%. Further calculations show that 76% of the predicted values fall within the relative error range of ± 5%. In conclusion, the JC model is a suitable model to predict the flow behavior of GCr15 steel at high strain rate.

Fig. 14
figure 14

Correlation between experimental data and predicted data over the entire range of strains (0.035–0.210 in steps of 0.015) using (a) JC model, (b) MJC model, (c) MTS model, (d) modified Arrhenius-type model

Full size image
Fig. 15
figure 15

Results of relative error analysis by means of (a) JC model, (b) MJC model, (c) MTS model, (d) modified Arrhenius-type model

Full size image

The JC model does not consider the coupling effect among strain, strain rate, and temperature. Based on the stress peaks observed under various experimental conditions in Fig. 3, it is evident that the influence of flow stress on strain rate is dependent on temperature. Therefore, this study proposes an MJC model that considers the coupling effects of strain rate and temperature to predict the flow behavior of GCr15 steel at high temperatures and high strain rates. Figure 7 illustrates the stress–strain prediction curves and experimental curves of GCr15 steel at different strain rates and temperatures. It can be observed that the MJC model has a better prediction performance compared to the original JC model. As shown in Fig. 8 and 14(b), the AARE and Rr of the MJC model are 2.6501% and 0.9711, respectively. The relative error calculation results are shown in Fig. 15(b), where the relative error range of the MJC model is − 13.576 to 6.101%, the mean relative error is − 0.2899, and 94% of the predicted values are within the relative error range of ± 5%. These results show a significant improvement in accuracy compared to the JC model.

The MTS model attributes the strain rate behavior to the microstructure of the material, and suggests that plastic deformation is caused by the accumulation and movement of dislocations within the metal. The model introduces the concept of mechanical threshold stress and is appropriate for describing the dynamic mechanical behavior of materials with a strain rate within 107 s−1. Moreover, the MTS constitutive model fully considers the influence of temperature, strain, and crystal dislocation. Comparing Fig. 5 and 9, it can be observed that with the increase of strain, the temperature softening phenomenon of the JC model is more apparent, while the proportion of strain hardening in the MTS constitutive model is larger, which is most prominent at low temperatures and low strain rates. Figure 9 presents the prediction curve and experimental curve of the MTS model. The AARE and the Rr of the MTS model are 3.2152% and 0.9686, respectively, as depicted in Fig. 10 and 14(c). Furthermore, the relative error range is − 10.123 to 13.183%, the mean relative error is 0.697%, and 76% of the predicted values are within the relative error range of ± 5%, as shown in Fig. 15(c).

The Arrhenius-type model introduces Zener–Hollomon parameters to characterize the effects of strain rate and temperature on hot deformation behavior. Based on the flow stress of different strains, the model can more accurately track the deformation behavior of materials. The modified Arrhenius-type constitutive model analyzes the factors influencing the flow behavior of metal materials from a macro perspective. Its prediction performance is more accurate than that of the JC and MTS models. However, its disadvantage is that the calculation time is longer and there are numerous parameters involved. The figures depict that the model has an AARE of 2.8480% and an Rr of 0.9702, with a relative error range of − 15.374 to 8.443%. The mean relative error is 0.376%, and 84% of the predicted values fall within the relative error range of ± 5%, as shown in Fig. 14(d) and 15(d).

The four constitutive models have demonstrated the ability to accurately reflect the flow behavior of GCr15 steel under high strain rates. Among them, both the MJC model and the modified Arrhenius-type model exhibit higher prediction accuracy than the other two models. However, the modified Arrhenius-type model is associated with a longer calculation time and a greater number of material parameters. The MJC model demonstrated a higher prediction accuracy, which can be attributed to its ability to consider the coupling effect of temperature, strain rate, and strain by incorporating the strain rate related factor f(T,εp). The inclusion of two quadratic terms for strain and temperature enables the model to accurately reflect the relationship between strain hardening and strain rate, as well as the effect of temperature and strain rate on the material behavior. In contrast, the JC model assumes constant strain hardening throughout the deformation process, which may not accurately capture the behavior of some materials and does not consider the coupled effects of temperature, strain rate, and strain. While the MTS model considers the dislocation movement of the material microstructure, it exhibits weak sensitivity of strain hardening to strain rate, as the strain hardening rate θ0 is only related to temperature and not to strain rate. In reality, strain hardening is known to exhibit a clear strain rate correlation. The modified Arrhenius-type constitutive model considers only the coupling effect of strain rate and temperature, which limits its predictive ability. These factors may explain why the MJC model exhibits strong predictive capabilities. In contrast, the MJC model boasts a simpler model structure and fewer material parameters, which make it more appropriate for numerical simulation in describing the flow behavior of GCr15 steel at high strain rates.

4.2 Scanning Electron Microscope (SEM) Observation

Microstructure plays a critical role in determining the properties and behavior of materials. The exceptional mechanical properties of GCr15 steel are due to its microstructure, which includes a fine network of carbides embedded in a tempered martensitic matrix. This unique microstructure enables the steel to withstand high loads and resist wear and tear, even under harsh working conditions.

After conducting the SHPB experiment, the cylindrical sample is uniformly divided into two parts along the axial direction. The cross-section is then ground, polished, and etched with a 4% nitric acid solution for 15 s, followed by metallographic analysis using SEM. The SEM images of the microstructure of the original specimen and the specimens after the SHPB experiment are presented in Fig. 16 and 17, respectively. Figure 16 illustrates that the original structure of GCr15 steel is primarily comprised of acicular martensite and carbide particles. The carbides are distributed in the martensite matrix and are mainly of two types: spherical and rod-shaped. The presence of carbides contributes to the material's high hardness and wear resistance. Acting as hard particles, the carbides resist deformation and impede the dislocation movement in the matrix. The finer and more uniformly distributed the carbides, the longer the bearing service life. Figure 17 depicts the SEM images of the specimen after the experiment conducted at temperatures of 298, 473, and 873 K, and impact pressures of 0.3 and 0.6 MPa. The number of carbides increases with the impact pressure at the same temperature, especially at 298 K. This may be due to the strong plastic deformation caused by the enhanced strain rate, which intensifies the precipitation of granular carbides in the martensitic matrix. With increasing temperature, the martensite decomposes, leading to the disappearance of the coherent relationship between the carbide and the matrix, which is believed to be the cause of the thermal softening of GCr15 steel. Additionally, there are no shear bands or cracks in the material, meaning that the material is undamaged. The stress–strain curve obtained from the Hopkins compression bar test confirms this. It should be noted that in some locations of the specimen, excessive corrosion of the nitric acid solution results in dark areas. As presented in Fig. 17, a cluster of elongated grains (indicated by red arrows) and a group of small globular grains (indicated by red circles) can be observed in the SEM image.

Fig. 16
figure 16

SEM micrograph of original structure of GCr15 steel

Full size image
Fig. 17
figure 17

SEM micrograph of GCr15 steel after SHPB experiment

Full size image

5 Conclusion

Establishing an accurate material constitutive model is critical for achieving more precise numerical simulations. This study conducted SHPB experiments on GCr15 steel at a temperature range of 298–873 K and a strain rate of 470–3940 s−1. The material parameters are optimized through experimental data and GWO. The flow behavior of GCr15 steel at high strain rates is described using four constitutive models, including the JC model, MJC model, MTS model, and modified Arrhenius-type constitutive model, and their prediction results are compared with experimental data. Based on this study, the following conclusions are obtained:

  1. (1)

    Under dynamic impact loading, GCr15 steel exhibits both strain rate strengthening and temperature softening effects, and it is noteworthy that the strain rate sensitivity of GCr15 decreases as temperature increases.

  2. (2)

    The parameters optimized by GWO can more accurately reflect the material's constitutive model, especially the model with multiple parameters. GWO is capable of optimizing multiple parameters simultaneously and demonstrates excellent convergence and convergence speed.

  3. (3)

    The original structure of GCr15 steel, as observed by SEM, is primarily composed of acicular martensite and carbide particles. In the SEM image of the specimen after the SHPB experiment, the number of carbides increases with increasing impact pressure at the same temperature, and the number of carbides decreases with increasing temperature at the same impact pressure.

  4. (4)

    After a comparative study based on experimental and predicted data, taking into account the actual conditions, the MJC model is more suitable for numerical simulation to describe the flow behavior of GCr15 steel at high strain rate. The AARE values for the JC model, MJC model, MTS model, and modified Arrhenius-type constitutive model are 3.7193, 2.6501, 3.2152, and 2.8480%, respectively. The Rr values are 0.9542, 0.9711, 0.9686, and 0.9702, respectively, and the mean relative error values are 1.695, − 0.2899, 0.697, and 0.376%, respectively. The predicted curves of the four models show good agreement with the experimental curves.