Experimental Determination and Theoretical Prediction of Limiting Strains for ASS 316L at Hot Forming Conditions

Abstract

In the present work, the austenitic stainless steel 316L is used for determining the forming limit diagrams (FLDs) at hot forming conditions. Firstly, the theoretical prediction of flow stress was done using Johnson-Cook and modified Zerilli-Armstrong (m-ZA) constitutive equations at three test temperatures (750, 825 and 900 °C). It was found that the m-ZA model displayed better predictability of flow stress. Additionally, Hill 1948 and Barlat 1989 yielding functions have been formulated, and it was found that Barlat 1989 displays better-yielding behavior predictability at all considered temperatures. Further, the Nakazima test has been used to find the experimental FLD. The limiting strains of the material displayed an improvement of approximately 57% with an increase in temperature from 750 °C to 900 °C. The Marciniak-Kuczynski (M-K) model has been used for theoretical prediction of FLD and it was found that the combination of Barlat 1989 function with m-ZA model displayed the best FLD prediction ability at all the considered temperatures with an error of approximately 5%. Further, the limiting dome height, surface strain and thickness distribution have been found at all the testing temperatures. The fractographic study revealed a ductile type of failure for all the specimens at all the temperatures.

Introduction

Materials having extraordinary mechanical properties, easy availability and low cost have been extensively used in manufacturing industries. Austenitic stainless steel (ASS) 316L is one such grade of steel. It is used especially in the nuclear industries which involve various critical applications having high temperatures and pressure working conditions (Ref 1). It is extensively used in nuclear reactors for fuel rod cladding. The nuclear reactors involve generation and exchange of high amounts of heat under high-pressure conditions, and liquid sodium which is quite compatible with ASS is used to keep them cool (Ref 2).

The flow stress behavior of various grades of high-strength steel is very much complex in hot working conditions (Ref 3, 4). The softening and hardening mechanism is often influenced by parameters, namely working temperature and deformation rate. The experimental determination of flow stress requires rigorous experimentation and testing facility. Hence, the theoretical method for the determination of flow stress can be predicted using various constitutive models (Ref 5, 6). Constitutive models are modeled to record the response of material at several deformation rate, temperatures and loading conditions (Ref 7,8,10). Further, it is very much important to evaluate the predicting capability of flow stress for each considered model when compared with the experimental results. Constitutive modeling being a wide field is segregated into the physical- and phenomenological-based model. Cabrera et al. (Ref 11) developed a constitutive equation for predicting the flow stress of Ti steel within the temperature range of 1123 to 1423 K for different strain rates. The predicted flow stress displayed a ± 5% error which is well within the acceptance limit. Cingara et al. (Ref 12) worked on ASS 317, 304 and 301 for higher temperature and found constitutive relation having coupled effect of temperature, deformation rate and also considered peak stress found using hyperbolic sinusoidal equations which in turn helped in increasing the accuracy of flow stress prediction. Maheshwari et al. (Ref 13) worked over Al-2024 alloy and developed equations using a modified Johnson-Cook (JC) constitutive model for determining its hot deformation behavior. Regression analysis is the basis of finding the constants of such empirical relations. Gupta et al. (Ref 14) applied modified Arrhenius (Arr.), modified Zerilli-Armstrong (ZA) and JC constitutive relations for predicting the flow stress behavior of ASS 316 within the range of 323 K to 623 K and four different deformation rates. On comparing the experimental and predicted results, they found that modified ZA has the best prediction ability followed by modified Arr. and JC models for material properties and deformation behavior of ASS 316 alloy.

The bulk manufacturing of several complex components used in various industrial applications can be easily done using different metal forming process such as bending, stretching and deep drawing (Ref 6, 15,16,17,18). Several metals have limited formability at room temperature condition; hence, in order to increase the formability, warm/hot forming is used as an alternative in industries (Ref 19, 20). The forming limit diagram (FLD) can be used as a tool to know the forming limits of the material to successfully form complex components without any fracture (Ref 21, 22). Hussaini et al. (Ref 23) did stretch forming of ASS 316 using hemispherical punch for a temperature range from room temperature (RT) to 400 °C and plotted experimental FLD. They also predicted theoretical FLD using Marciniak-Kuczynski (M-K) (Ref 24) model. They found predominance of major strain in FLD and concluded that onset of dynamic strain aging (DSA) plays a major role in deciding the formability of metal. Talyan et al. (Ref 25) worked over the formability of some ASS and ferritic stainless steel (FSS) grades and found that martensite transformation takes place in ASS at RT. When the temperature becomes more dominant, the suppression of martensitic transformation takes place and hence the forming limits of FSS and ASS become almost similar. In the biaxial (tension) region of FLD, the FLD is higher at a low rate of deformation. This increased formability in this region mainly corresponds to very fast martensitic transformations.

ASS is one of the most common, cheap and easily available material. Several researchers have put extensive efforts in determining the deformation behavior under different loading conditions. However, very limited comprehensive studies are available at hot forming conditions for ASS 316L. The present work focuses on systematic thorough investigations of material models and hot forming behavior of ASS 316L. Further, this study also covers the theoretical prediction of FLDs and detailed fractographic analysis at different forming temperatures.

Experimental Details

Tensile Testing

All the experimental work has been done on a 1-mm ASS 316L sheet. The chemical composition of as-received ASS 316L consists majorly of Cr (16.56%), Ni (10.85%), Mo (2.02%), Mn (2%) and Fe (~ 70%) by weight percent. The tensile test specimens for determining various mechanical properties were designed as per the sub-size ASTM E8/E8M − 11 standard. The testing was done at three different temperatures, viz. 750 °C, 825 °C and 900 °C with sheet orientations in 0°, 45° and 90° with respect to the rolling direction of the sheet at 0.001 s⁻¹ deformation rate. Table 1 represents the calibrated mechanical properties at different testing conditions.

Table 1 Average mechanical properties for ASS 316L

The anisotropy of material is defined by the variation in material properties with different directions because of varying atomic spacing in different crystallographic planes. Various parameters which help in defining the anisotropic behavior of material are anisotropic index (δ), in-plane anisotropy (A_IP), planar anisotropy (ΔR), normal anisotropy $(\bar{R})$ and Lankford coefficient (R). These are calculated according to Eq 1 to 5.

$${\text{Lankford}}\;{\text{Coefficient}},\;R = \frac{{ \in_{w} }}{{ \in_{t} }}$$

(1)

$${\text{Normal}}\;{\text{Anisotropy}},\;\bar{R} = \frac{{R^{0} + 2R^{45} + R^{90} }}{4}$$

(2)

$${\text{Planar}}\;{\text{Anisotropy}},\;\Delta R = \frac{{R^{0} - 2R^{45} + R^{90} }}{4}$$

(3)

$${\text{In{-}plane}}\;{\text{Anisotropy}},\;A_{\text{IP}} = \frac{{2\sigma_{\text{ys}}^{0} - \sigma_{\text{ys}}^{90} - \sigma_{\text{ys}}^{45} }}{{2\sigma_{\text{ys}}^{0} }}$$

(4)

$${\text{Anisotropic}}\;{\text{index}},\;\delta = \frac{{\left( {\% {\text{El}}} \right)^{0} - \left( {\% {\text{El}}} \right)^{90} }}{{\left( {\% {\text{El}}} \right)^{0} + \left( {\% {\text{El}}} \right)^{90} }}$$

(5)

where $\in_{t}$ and $\in_{w}$ are the plastic strains along thickness and width, respectively. (%El)⁹⁰ and (%El)⁰ are the elongations along 90° and 0° directions, respectively. $\sigma_{\text{ys}}^{90}$, $\sigma_{\text{ys}}^{45}$ and $\sigma_{\text{ys}}^{0}$ are the yield stress along 90°, 45° and 0° directions, respectively. R⁹⁰, R⁴⁵ and R⁰ are the Lankford coefficient along 90°, 45° and 0° directions, respectively.

Anisotropic properties at different temperatures for ASS 316L are reported in Table 2. The formability of the sheet is affected by parameter $\bar{R}$. Minimization in thickness variation during operation such as deep drawing and stretching is observed when a material with higher $\bar{R}$ is used. $\bar{R}$ is found to be directly proportional to defects such as earing, wrinkling and tearing at the time of deep drawing of the sheet. The anisotropic nature of the material is identified by its A_IP value. Very small $\delta$ values were observed which show minimization of elongation anisotropy at elevated temperature for ASS 316L (Ref 26).

Table 2 Anisotropic parameters for ASS 316L

Hemispherical Dome Test for Stretch Forming (Nakazima Test)

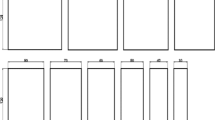
The stretching operation of ASS 316L material was performed over a 20-ton hydraulic press. It has a 2-zone split furnace with ± 3% accuracy as well as a temperature controller to accurately control it. The punch used is in hemispherical dome shape having 50 mm diameter. The groove bead is present in the blank holder plate to restrict the flow of material into the cavity. Hasek specimens with different widths were used in the present study. The schematic representation of the stretching setup used in the present study is shown in Fig. 1. Laser etching was done over blanks to mark circular grids of 2.5 mm diameter before the experiment to measure strains after performing the stretching operation using traveling electron microscope. The test was performed at 3 different temperatures (750 °C, 825 °C and 900 °C), fixed blank holding pressure of 25 bar and punch speed as 5 mm/min. Six different types of specimens shown in Fig. 1(a)-(f) were used for plotting the FLD in present study.

Fig. 1

Schematic representation of stretching setup and six different types of specimen design for plotting FLD

Material Modeling

Constitutive Modeling

Johnson-Cook (JC) Model

Johnson-Cook (Ref 27, 28) proposed a constitutive relation on the basis of phenomenological theory. It is one of the most popular constitutive models because of its simplicity and requires the determination of very few material constants for finding flow stress. It can be used for finding the flow stress at various deformation rates and temperatures for different materials. However, it was found by some researchers that at high deformation speeds the prediction capability of the JC model is reduced. Equation 6 represents the relation proposed in the JC model for flow stress prediction. JC model does not consider the coupled effect of process parameters such as the rate of deformation and testing temperature.

$$\sigma = \left( {A + B\varepsilon^{n} } \right)(1 + Cln\acute{\epsilon})\left( {1 + \left( {T^{*} } \right)^{m} } \right)$$

(6)

$$T^{*} = \frac{{T - T_{r} }}{{T_{m} - T_{r} }}$$

(7)

where A, B, C, n and m are constants calculated as per method followed by Kotkunde et al. (Ref 29) and Samantaray et al. (Ref 30). T^* is homologous temperature. T_r is the reference temperature and is considered to be 750 °C. The calculated constants for JC model are shown in Table 3.

Table 3 Constants considered for JC model

Modified Zerilli-Armstrong (m-ZA) Model

Constitutive equation suggested in ZA model is on the basis of dislocation by thermal activation. The proposed relation for m-ZA model is shown by Eq 8. This model considers the combined effect of various process parameters such as temperature, deformation rate and the deformation shown by material. Hence, m-ZA is always considered to be better than the JC model.

$$\sigma = \left( {C_{1} + C_{2} \varepsilon^{n} } \right){ \exp }\{ \left( { - C_{3} + C_{4} \varepsilon } \right)\left( {T - T_{ref} } \right) + [C_{5} + C_{6} \left( {T - T_{ref} } \right)\ln \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{ref} }}} \right)$$

(8)

where C₆, C₅, C₄, C₃, C₂, C₁ and n are constants of m-ZA model and are calculated as per method suggested by Samantaray et al. (Ref 31). $\varepsilon$ is the plastic strain, $\dot{\varepsilon }$ is the deformation rate, T is the working temperature, and T_ref (750 °C) is the reference temperature. The material constants for ASS 316L are displayed in Table 4.

Table 4 Constants considered for m-ZA model

The plots for predicted flow stress at 0.001 s⁻¹ strain rate for JC and m-ZA models are shown in Fig. 2(a) and (b), respectively. The original Johnson-Cook model requires fewer material constants and also few experiments to evaluate these constants. It assumes that thermal softening, strain rate hardening, and strain hardening are three independent phenomena and can be isolated from each other. So, the original Johnson-Cook model cannot adequately represent the high-temperature flow behavior of the studied ASS 316L steel (Ref 32). Further, various statistical measures shown in Table 5 were used to evaluate the predictability of flow stress, and it was found that the best results were predicted by the m-ZA model.

Fig. 2

True stress-strain plots at 0.001/s deformation rate for (a) JC and (b) m-ZA models

Table 5 Statistical parameters calibrated for different constitutive models

Yield Criteria

The yielding behavior for ASS 316L has been calibrated using Barlat 1989 and Hill 1948 yield criteria (Ref 33) in the present study. These yield criteria help in defining the end limit of elastic deformation and the start of permanent plastic deformation under different loading conditions.

Hill 1948 Yield Criterion

Hill (Ref 34) modified the von Mises yield criteria by incorporating the effect of sheet anisotropy in it. The r-value approach has been used in the present work for evaluating the yielding behavior of material. Equation 9 shows the extended version of yield function proposed by Hill.

$$f\left( \sigma \right) = \tilde{\sigma }^{2} = F\sigma_{22}^{2} + \, G\sigma_{11}^{2} + H\left( {\sigma_{11} - \sigma_{22} } \right)^{2} + 2N\sigma_{12}^{2}$$

(9)

where N, H, G and F are the anisotropic material coefficients which were calibrated using method followed by Pandre et al. (Ref 35). These constants are shown in Table 6.

Table 6 Calibrated yielding function constants for Hill 1948 criterion

Barlat 1989 Yield Criterion

Barlat (Ref 36) proposed a yielding function influenced by the planar stresses developed during deformation for the prediction of yield loci. The Barlat 1989 yielding function is shown by Eq 10.

$$2\tilde{\sigma }^{m} = a\left| {k_{1} + k_{2} } \right|^{m} + a\left| {k_{1} - k_{2} } \right|^{m} + c\left| {2k_{2} } \right|^{m} = \phi$$

(10)

where k₂ and k₁ are the parameter calibrated using Eq 11 and 12.

$$k_{1} = \frac{{\sigma_{1} - h\sigma_{2} }}{2}$$

(11)

$$k_{2} = \sqrt {\left( {\frac{{\sigma_{1} - h\sigma_{2} }}{2}} \right)^{2} - p^{2} \tau_{12}^{2} }$$

(12)

The terms a, c and h consisting of anisotropic ratios can be evaluated using Eq 13-15.

$$a = 2\left( {1 - \sqrt {\frac{{r_{0} r_{90} }}{{\left( {1 + r_{0} } \right)\left( {1 + r_{90} } \right)}}} } \right)$$

(13)

$$h = \sqrt {\frac{{r_{0} \left( {1 + r_{90} } \right)}}{{r_{90} \left( {1 + r_{0} } \right)}}}$$

(14)

$$c = \, \left( {2 \, - a} \right)$$

(15)

The iterative computation method has been used for the evaluation of p value used in Eq 12 by using function shown in Eq 17.

$$R = \frac{{2m\sigma_{0}^{m} }}{{\sigma_{\theta } \left( {\frac{\partial \phi }{{\partial \sigma_{11} }} + \frac{\partial \phi }{{\partial \sigma_{22} }}} \right)}} - 1$$

(16)

The parameter m used in Eq 10 and 16 is known as yield function exponent, and its value is considered to be 8 in the present case. Its value is highly dependent upon the crystallographic structure of the material. The Barlat 1989 calibrated constants are shown in Table 7.

Table 7 Calibrated yielding function constants for Barlat 1989 criterion

The final yield loci for the considered yielding functions at different test temperatures are compared in Fig. 3(a) and (b). Barlat 1989 criterion seems to be closely covering all the experimentally calibrated points, but Hill 1948 criterion shows inability in capturing the whole yielding behavior of ASS 316L. Thus, Barlat 1989 criterion better predicts the yielding behavior of ASS 316L at all the considered temperatures.

Fig. 3

Yielding behavior of ASS 316L using (a) Hill 1948 and (b) Barlat 1989 criteria

Stretch Forming

Forming Limit Diagram (FLD)

The experimental FLD with true major and minor strains at three different temperatures is shown in Fig. 4(a)-(c). For easy identification of the safe, necked and failed regions, different types of symbols were used for the representation. The safe forming limit of the material is defined using a solid black color line, also known as the forming limit curve for separating the safe and failure regions of the FLD. The whole FLD is analyzed in three different regions, namely tension--tension (T-T), plane strain and tension--compression (T-C). At 750 °C, the slope of strain paths varied from − 0.485 in the T-C region to 0.794 in the T-T region. With the increase in processing temperature, the slope strain paths increased in the T-C region, while it decreased in the T-T region and at 900 °C, it varied from − 0.231 in the T-C region to 0.431 in the T-T region. Figure 4(d) shows the comparison of experimental FLD at three different testing temperatures. Substantial necking before the final failure has also been observed, especially for the specimens lying in the T-C and plane strain regions at all the testing temperatures. At 900 °C, except D-1 all the specimens displayed necking before failure. The forming limiting strains displayed an effective improvement of approximately 57% as the temperature increased from 750 °C to 900 °C. The forming temperature plays a major role in deciding the limiting strains of the material. With the increase in the forming temperature, the material becomes soft and hence the formability of material increases.

Fig. 4

FLD at (a) 750 °C, (b) 825 °C, (c) 900 °C and (d) comparison of the limiting strains at all the testing temperatures

In the present work, a sub-sized punch of hemispherical shape (diameter = 50 mm) has been used for the stretch forming analysis instead of punch having a diameter of 101.4 mm as proposed in ASTM E2218-15 standard. Thus, the effect of bending strain on the outer curved convex-shaped surface of stretch formed specimens in the region around the surrounding of sub-sized hemispherical punch needs to be considered. It has a very significant effect over the stretching limits of the material. The procedure mentioned by Prasad et al. (Ref 37) has been followed step by step for calculating the corrected FLD by considering the bending strains induced due to the use of sub-sized punch. Especially, the limiting strain of material depends directly upon the curvature of punch (1/R) by considering no variation in the sheet thickness. The corrected FLD is shown in Fig. 5. It is drawn after reducing the bending correction strain from the calculated true strains. The forming limit curve shifted downward on the major strain axis by approximately 4.5-6% in all the regions of FLD at all the forming temperatures.

Fig. 5

Corrected FLD after considering the effect of bending strains

Surface Strain

The true strain distribution at different temperatures for the specimens lying in the T-T, plane strain and T-C regions is shown in Fig. 6(a)-(c). The strain was measured along the representative profile at a fixed curvilinear distance 3 mm from the pole as shown in Fig. 6(d). For the D-1 specimen which is lying in the T-T region of FLD, the fracture approximately occurred at a curvilinear distance of 15-18 mm from the pole. The highest major and minor true strains were observed at place from where the fracture occurred. Further, with the increase in temperature, the surface strains of specimens also increased. For the specimen lying in the region of plane strain (D-4), the highest major strain was observed approximately 10-15 mm from the pole of the specimen. The true minor strain of the specimen varied between T-C and T-T regions of the FLD; hence, it shows both the positive and negative values. For D-6 specimen, the major strain seems to be lying in the positive zone, while the minor true strain seems to be lying in the negative zone which confirms that this design underwent tension--compression type of deformation. The major true strain increased, while the minor true strain decreased with the increase in temperature from 750 °C to 900 °C. Further, highest major strain and minimum minor strain have been observed at a curvilinear distance of 10-15 mm from the pole which is also the region of fracture over the D-6 specimen.

Fig. 6

Surface strain variation for (a) D-1, (b) D-4, (c) D-6 mm specimen and (d) representative diagram for strain measurement

Thickness Distribution and Limiting Dome Height (LDH)

The representative normalized thickness variation for D-1 and D-6 specimen is shown in Fig. 7(a) and (b). The thickness was measured along a representative curvilinear profile shown in Fig. 6(d). At 750 °C and 825 °C testing temperatures, the minimum thickness has been observed at a distance of approximately 15 and 12 mm, respectively. However, at 900 °C, the minimum thickness has been observed at a distance of 18 and 15 mm for D-1 and D-6 specimen, respectively, from the pole of specimen. The thickness of the hemispherical specimen did not vary much near pole of the specimens. Further, the minimum thickness was observed near a place of fracture of the specimen. The thickness then increased gradually up to the flange portion of the specimen. Thickness of 1 mm was observed near the flange portion of the specimen which is almost equal to the thickness of as-received sheet. Plots with similar nature of thickness variation have been observed at all the test temperatures in the present work. As the testing temperature increases, the minimum thickness of the formed specimens also decreased because of the thermal softening phenomenon which in turn increases the formability of material.

Fig. 7

Representative plot for thickness distribution for (a) 25-mm- and (b) 50-mm-width samples

Limiting dome height (LDH) is an important parameter which is helpful in knowing the drawability of different specimens at different temperature. LDH is the height of specimen considered just before occurring of fracture. The variation of average LDH with temperature is shown in Fig. 8. LDH was found to be increasing with the increase in test temperature because of the thermal softening of material.

Fig. 8

Variation of LDH

Theoretical Prediction of Forming Limit Diagram

Marciniak-Kuczynski (M-K) (Ref 24) model is an analytical tool for the prediction of forming limits. The prediction of limiting strains depends upon some fundamental assumptions such as initial inhomogeneity factor (f₀). Maximum principle stresses are always considered to be perpendicular each other. It is assumed that on sheet surface before the occurrence of deformation, there must be a linear groove. The groove is named as zone B and outside region is zone A as shown in Fig. 9.

Fig. 9

Geometric imperfection in M-K model

Rolling direction of sheet is to be aligned with x-axis and transverse direction along y-axis. Thickness ratio defining the initial imperfection is defined by Eq 17 in which h_B and h_A are thickness defined for zone B and A, respectively. The sheet boundary often underwent monotonically proportional strain which is always parallel to considered geometric axes.

$$f_{0} = \frac{{h_{A} }}{{h_{B} }} < 1$$

(17)

$$\rho^{A} = \frac{{ \in_{y}^{A} }}{{ \in_{x}^{A} }}$$

(18)

where ∈_y and ∈_x are considered to be the strain components along corresponding geometric axes. Strain component along x-axis is considered to be major strain, and along y-axis, it is considered to be minor strain. On the basis of variation in f₀ value, it can be if FLD is in good relation with experimental value for $\rho$ = 0 (plane strain condition). On increasing the deformation, zone A thickness reduces at relatively slower rate as compared to zone B. Hence, the initialization of necking can be marked when zone B is deformed more than A. The failure can be marked using Eq 19.

$$\frac{{d\overline{{ \in_{A} }} }}{{d\overline{{ \in_{B} }} }} < N$$

(19)

where $d\overline{{ \in_{B} }}$ and $d\overline{{ \in_{A} }}$ are equivalent strains in their zones, respectively. N is a number which should be considered small enough so as to confirm that sufficient deformation (necking) took place in region B as compared to that of A. For the present study of ASS 316L, N value is considered to be 0.15. For formulation of M-K model, the ratio of strains and stresses is defined according to Eq 20. RD is considered to be along x-axis and TD along y-axis. Equation 21 gives effective strain and stress for M-K model.

$$\alpha = \frac{{\sigma_{y} }}{{\sigma_{x} }}\;\& \;\rho = \frac{{ \in_{y} }}{{ \in_{x} }} = \frac{{d \in_{y} }}{{d \in_{x} }}$$

(20)

$$\overline{\sigma \in } = \left( {\sigma \in } \right)_{x} + \left( {\sigma \in } \right)_{y} = \left( {\sigma \in } \right)_{x} (1 + \alpha \rho )$$

(21)

Equation 22 defines the associative flow law. Using this flow law and isochoric condition mentioned in Eq 22, compatibility condition is also incorporated in M-K model and is shown in Eq 24.

$$d \in_{ij} = d\lambda \frac{{\partial \bar{\sigma }}}{{\partial \sigma_{ij} }}$$

(22)

$$d \in_{x} + d \in_{y} + d \in_{z} = 0$$

(23)

$$d \in_{y}^{A} = d \in_{y}^{B}$$

(24)

Further, the balancing of force is done in Eq 25 to show that equilibrium is achieved by deformed sheet metal.

$$\varphi_{A} C\left( {\varepsilon = \overline{{ \in^{A} }} + \overline{{d \in^{A} }} , \dot{\varepsilon } = d \in^{A} } \right) = f\varphi_{B} C\left( {\varepsilon = \overline{{ \in^{B} }} + \overline{{d \in^{B} }} , \dot{\varepsilon } = d \in^{B} } \right)$$

(25)

where f = $\frac{{t_{A} }}{{t_{B} }}$, $\varphi = \frac{{\sigma_{x} }}{{\bar{\sigma }}}$ and constitutive model required is represented by C. Ratio f can further be written as shown in Eq 26.

$$f = f_{0} { \exp }\left( { \in_{z}^{A} - \in_{z}^{B} } \right)$$

(26)

Ratios $\rho$ and f₀ are assumed initially for start of calculation. Small increase in strains ($d \in_{x}^{B}$) are given in groove zone. Further the assumption of $d \in_{x}^{A}$ is done and by iterative computation the values of $d \in^{B}$, $d\sigma^{A}$, $d \in_{x}^{B}$ and $d \in_{x}^{A}$ are determined and equality in equation of force balance is checked. Value of $\frac{{d \in^{A} }}{{d \in^{B} }}$ is found if equality in equation of force balance is satisfied. Necking condition occurs if the value of ratio is smaller than 0.15 and zone A strain state has a fixed point marked on FLD. But if equality in equation of force balance does not satisfy, then that point is marked below FLD in safe zone. To impose necking condition, the value of $d \in_{x}^{B}$ is increased by a calculated amount and the above-mentioned process is repeated again. This process is repeated till the start of necking for a $\rho$ value. This whole above-mentioned procedure is repeated for obtaining full FLD plot with different $\rho$ values. Figure 10 represents theoretical FLD prediction algorithm followed in the present work.

Fig. 10

Algorithm for plotting theoretical FLD

Thickness inhomogeneity is the fundamental hypothesis of M-K theory. This thickness inhomogeneity causes localized instability (Ref 38). On the basis of thorough literature review, it was found that the FLD is majorly affected by thickness ratio (inhomogeneity term (f₀)). Further f₀ shows dependency upon factors, viz. material properties, grain size, texture and thickness of sheet (Ref 33). Usually, f₀ is a factor which can be adjusted to get accurate predicted results in theoretical FLDs. Parameter f₀ varies with different constitutive models and yield criteria. Further, it was also observed from previous research done by Kotkunde et al. (Ref 39) that FLD moves downward with decrease in f₀ value. Parameter f₀ represents the ratio of thickness for thinner groove region to that of sheet. As the parameter f₀ decreases, deformation rate increases in thin groove as compared to its thicker counterpart, and as a result, necking starts and ultimately fracture occurs. On the basis of comparing theoretical plots obtained at different f₀ values and comparing it with experimental results, for Hill 1948 criteria, f₀ is 0.99 for JC and 0.96 for m-ZA, while for Barlat 1989 criteria, f₀ is 0.995 for JC and 0.97 for m-ZA in the present study on ASS 316L.

Figure 11(a)-(c) represents the comparison of various theoretical FLDs with the experimentally obtained FLD. The theoretical FLDs were obtained using M-K model. The combination of various constitutive models and yield criteria considered in the present study has been incorporated in the M-K model for prediction with high accuracy. The mean absolute error (MAE) of the predicted FLD with respect to the experimental one at all the temperatures is shown in Fig. 11(d). At all the test temperatures, the predicted FLD using the combination of Barlat 1989 yielding function and m-ZA constitutive equation displays the best least MAE. At 750 °C and 825 °C, the Hill 1948 yielding function in combination with the m-ZA constitutive equation displays worst prediction and hence should be least preferred. At 900 °C, Hill 1948 coupled with JC model seems to have the highest MAE and hence should not be used to predict the FLD.

Fig. 11

Comparison of experimental and predicted FLD at (a) 750 °C, (b) 825 °C, (c) 900 °C and (d) MAE (%)

Microstructure Analysis

The macro-images of the fracture specimen are shown in Fig. 12. Some circumferential cracks with no localized necking have been observed in the nearby regions of the crack propagating area at all temperatures. Interestingly, the crack initiation and propagation at 825 °C for D-4 and D-1 specimens slightly differed when compared with other specimens. The localized necking has appeared at multiple locations along the circumferential direction causing the mismatch in the crack propagation. This localized necking restricts the drawability of material and fracture initiates from this point.

Fig. 12

Macro-images of fracture specimens of ASS 316L at various temperatures and widths (a) 750 °C, D-6, (b) 825 °C, D-4, (c) 825 °C, D-1 and (d) 900 °C, D-4

The fractographic examination of the deformed specimens using scanning electron microscope of various temperatures is presented in Fig. 13(a)-(f). It clearly reveals the presence of dimple structures as a predominating feature of the fracture surfaces at 750 °C, 825 °C and 900 °C indicating a ductile fracture irrespective of the orientation and width. The void nucleation and growth being the primary cause of dimple formation indicate a ductile fracture. From Fig. 13(a)-(c), for a given temperature and orientation, it can be observed that with the increase in the width, the flowability has increased which can be attributed to more number of dimples and the flow regions as evident from the fracture surface. Also, along the thickness direction, the depth of crack has increased for D-1 specimen as observed from Fig. 13(c) and (e) which could be the reason for increase in deformation where D-1 specimen has the highest displacement except at 750 °C, 0° orientations and 900 °C, 90° orientations. Comparatively, from Fig. 13(b) and (d), the amount of deformation seems to be similar for 45 ° and 90 ° orientations due to the availability of more grains boundary surface area and as evident from the table where higher n values are observed.

Fig. 13

Fracture surfaces of ASS 316L at various temperatures and specimen widths and its orientations. (a) 750 °C, 45 °, D-6, (b) 750 °C, 45 °, D-4, (c) 750 °C, 45 °, D-1, (d) 750 °C, 90 °, D-4, (e) 825 °C, 45 °, D-1 and (f) 900 ° °C, 45 °, D-6

As the temperature is increasing, the ductility has increased as evident from the presence of more flow lines and dimple concentration. Deeper and large size dimples indicate the increase in the amount of plastic deformation before fracture. This might have been the cause for the increase in the forming limits by approximately 57% with temperature increasing from 750 °C to 900 °C. On the contrary, the strength decreased which could be due to the material becoming weak with increase in the amount of voids with the temperature as observed from Fig. 13(d)-(f).

Conclusions

The present work over ASS 316L includes determination of the experimental and theoretical forming limits at different forming temperatures. Some of the important conclusions based upon the present study are listed below:

• Johnson-Cook (JC) and modified Zerilli-Armstrong (m-ZA) constitutive models were developed based on the flow stress data. The flow stress prediction capability of m-ZA model was found to be more superior than the JC model. The JC model consider factors such as thermal softening, strain rate hardening and strain hardening as three independent phenomena and do not consider their combined effect over the deformation of metal, and hence, it should be less preferred for the prediction of flow stress behavior at elevated temperature condition. From the yield loci plotted at different temperatures using Hill 1948 and Barlat 1989 criteria, it has been concluded that the Barlat 1989 follows the experimental results accurately in all the testing conditions.

• The experimental FLD at three different forming temperatures (750 °C, 825 °C and 900 °C) has been plotted using Nakazima test. It has been found that the forming limits of the material improved by approximately 57% with the increase in forming temperature from 750 ° °C to 900°C. The surface strain and the thickness of specimen have been found to be maximum and minimum, respectively, in the region near to the fracture. Bending correction due to the use of sub-sized punch has also been included in present study, and hence, the overall forming limits of the material decreased by approximately 4.5-6%.

• Theoretical FLD was plotted with the help of M-K model by incorporating Hill 1948 and Barlat 1989 yielding functions with JC and m-ZA constitutive equations. Barlat 1989 criteria along with m-ZA model are found to have the best prediction ability of theoretical FLD for ASS 316L at all the temperatures.

• The flow lines and dimple concentration increased with the increase in temperature, which clearly indicates the increase in ductility of material because of the thermal softening phenomenon. The ductile type of failure occurred as all the specimens underwent proper substantial necking before the final fracture of specimen.