Introduction

In the field of sheet metal forming, the forming limit diagram (FLD) is widely used for characterizing the extent to which metal sheets can be deformed without localized necking. However, since more and more materials with high strength but less ductility, especially the high-strength steel (HSS) even the ultra-high-strength steel (UHSS), have been employed in the field of industrial production, ductile fracture becomes more and more common in sheet metal forming process. The FLD can be determined by corresponding plastic instability theory based on the onset of through-thickness necking of sheet. Because the fracture of AHSS often occurs without obvious necking phenomenon, the conventional plastic instability theories are no longer suitable for the failure prediction (Ref 1). Therefore, the prediction of ductile fracture for sheet metals becomes more important.

Ductile fracture models have gained a lot of attention in the past decades. Many ductile fracture models have been proposed and extensively investigated in the mechanics community. These ductile fracture models are classified into three groups: physics-based models, phenomenological models and empirical models by Bai and Wierzbicki (Ref 2). The physics models include McClintock model (Ref 3), Rice-Tracey model (Ref 4), Gurson’s model (Ref 5) and GNT models (Ref 6) and shear-modified Gurson’s model (Ref 7, 8). These fracture models are widely known as the so-called coupled damage model, in which the elastic and plastic behavior is assumed to be affected by the evolution of damage. The Lemaitre model (Ref 9), as a typical example of continuum damage mechanics (CDM) models, which considers the formation of macroscopic cracks as the result of accumulation of damage, also belongs to this group. The phenomenological models include maximum shear stress, Cockcroft-Latham model (Ref 10), pressure-modified maximum shear stress and modified Mohr-Coulomb criterion (Ref 11). This kind of model is generally established based on the understandings and assumptions of ductile fracture mechanism learned from experimental phenomenon. The selected empirical models are Johnson-Cook (Ref 12), Bao-Wierzbicki (Ref 13), Xue-Wierzbicki (Ref 14), Wilkins (Ref 15), CrashFEM (Ref 16) and fracture forming limit diagram (FFLD). These models are most in the form of empirical formulas, which are obtained through the experimental data fitting. The last two kinds of models can be considered as uncoupled damage models. The elastic and plastic behavior of material is not affected by the fracture models, which only define a fracture surface to predict the onset of the fracture. However, most of these models are established in the stress space and that makes it difficult for engineering applications, because stress is more difficult to measure than strain in experiments. Moreover, all these models are proposed for isotropic materials in the first place.

Sheet metals generally exhibit a significant anisotropy of mechanical properties due to their crystallographic structure and the characteristics of the rolling process. As an example, it is found that the equivalent strains to fracture of specimens with the same shape, which means that the specimens undergo the same stress state during the deformation process, are different when the specimens are pulled at 0°, 45°, and 90° to the rolling direction for aluminum alloy 6061-T6 (Ref 17). Zhao et al. (Ref 18) studied the anisotropic damage evolution in warm stamping process of magnesium alloy sheets. It is found that both the damage evolution and failure locations in the AZ31Mg alloy sheets during warm stamping process at different temperatures can be predicted accurately if the anisotropic damage model is adopted. Therefore, the effect of material plastic anisotropy needs to be considered in the ductile fracture model for sheet metals. Recently, some studies on modeling anisotropic ductile fracture were proposed. A Gurson-like model incorporating the direction-dependent void growth was developed by Steglich et al. (Ref 19). Khan and Liu (Ref 20) proposed an uncoupled stress-based criterion, which was extended from an isotropic one based on the magnitude of stress vector with a modified Hill anisotropic function. Luo et al. (Ref 21) developed an anisotropic damage indicator model to predict the ductile fracture of the extruded sheets of 6260-T6 aluminum alloy. Gu et al. (Ref 22) proposed an anisotropic extension of the Hosford-Coulomb fracture model. The material anisotropy is introduced into the originally isotropic formulation by the linear transformation of the stress tensor. These anisotropic fracture models can predict the onset of ductile fracture under the three-dimensional stress state. However, the application of these models is relatively difficult, especially for the finite element technology. In the field of sheet metal forming, the plane stress assumption is usually adopted, which means that the stress state is two-dimensional. Therefore, the fracture model should have a more simplified form for the sake of convenient application.

The present work proposes a simple expression of anisotropic ductile fracture model for sheet metals under the assumption of proportional loading and plane stress state. The expression is established in the strain space for the convenient application. Material plastic anisotropy is described by Hill 1948 yield criterion (Ref 23). Ductile fracture in the stress space is described by Mohr-Coulomb model. Furthermore, experimental method is presented to obtain the material parameters in the expression proposed in this study. Four different types of specimens, prepared with their longitudinal axis inclined with the angle of 0°, 45°, and 90° to the rolling direction, are stretched to fracture. The displacement field is captured by using a 3D DIC system, and the strain tensor is obtained by the DIC software ARAMIS. The fracture locus predicted by the proposed model and the experimental data are compared.

Ductile Fracture Model in the Stress Space

The Mohr-Coulomb (M-C) fracture criterion, which considers the effects of hydrostatic pressure and the Lode angle parameter, has been widely used for predicting the fracture of brittle materials. These two factors have been proven to be critical for controlling ductile fracture by many researchers (Ref 11). Therefore, the M-C model has been extended to the spherical coordinate system, where the axes are the equivalent strain to fracture \(\overline{{\varepsilon_{\text{f}} }}\), the stress triaxiality η and the normalized Lode angle parameter \(\overline{\theta }\) by Bai and Wierzbicki (Ref 11) to predict the ductile fracture, which is well known as the MMC criterion. In this paper, the M-C model is chosen as the fracture criterion in the stress space as well.

According to the M-C fracture criterion, fracture occurs when the combination of normal stress and shear stress at an arbitrary cutting plane reaches a critical value, which can be expressed as:

$$(\tau + c_{1} \sigma_{n} )_{\text{f}} = c_{2} \text{ }$$
(1)

where c 1 and c 2 are material constants.

This expression should be transformed to the space of principal stress σ 1, σ 2 and σ 3 for the purpose of convenient application. The M-C criterion expressed by the principal stress, which is in the form of Eq 2, can be obtained through the transformation and solution of the maximum value problem. The detailed deducing can be found in the research of Bai and Wierzbicki (Ref 11).

$$(\sqrt {1 + c_{1}^{2} } + c_{1} )\sigma_{1} - (\sqrt {1 + c_{1}^{2} } - c_{1} )\sigma_{3} = 2c_{2}$$
(2)

Equation 2 is the expression of M-C criterion in the three-dimensional stress state. It can be seen from the formula that fracture is only affected by the maximum and minimum principal stress in M-C model. However, in the plane stress state, the principal stress in the thickness direction is supposed to be zero. That is to say that one of the three principal stresses σ 1, σ 2 and σ 3 will be zero. In Eq 2, the three principal stresses are constrained by σ 1 ≥ σ 2 ≥ σ 3, which means that σ 1 is the maximum principal stress and σ 3 is the minimum principal stress. Therefore, in the plane stress situation, the principal stress in the thickness direction, which is zero, should be either σ 2 or σ 3 in Eq 2. In this study, another way of expression is used. Assuming that σ 1 and σ 2 are the principal stress in plane, Eq 2 should be expressed in two parts according to positive or negative sign of the minor stress σ 2, which can be expressed as follows:

$$\left\{ {\begin{array}{*{20}l} {a\sigma_{1} - \frac{1}{a}\,\;\sigma_{2} = b} \hfill & {{\text{for}}\;\sigma_{2} \le 0} \hfill \\ {a\sigma_{1} = b} \hfill & {{\text{for}}\;\sigma_{2} > 0} \hfill \\ \end{array} } \right.$$
(3)

where \(a = \sqrt {1 + c_{1}^{2} } + c_{1}\), b = 2c 2 for the purpose of simplification. Apparently, a and b are also material constants. Equation 3 is the expression of M-C criterion in the plane stress assumption.

In the MMC model, the 3D fracture locus can be represented in the space of (\(\overline{{\varepsilon_{f} }}\), η, \(\overline{\theta }\)), where \(\overline{{\varepsilon_{f} }}\) denotes the equivalent strain at fracture and η; \(\overline{\theta }\) denotes the stress triaxiality and Lode angle parameter defined, respectively, by

$$\eta = \frac{ - p}{q} = \frac{{\sigma_{m} }}{{\overline{\sigma } }}$$
(4)
$$\overline{\theta } = 1 - \frac{2}{\pi }\arccos \left( {\frac{r}{q}} \right)^{3}$$
(5)

where σ m and \(\overline{\sigma }\) are the hydrostatic pressure and equivalent stress. p, q, r are the three invariants of a stress tensor [σ] defined, respectively, by

$$p = - \sigma_{m} = - \frac{1}{3}tr\left( {\left[ \sigma \right]} \right) = - \frac{1}{3}\left( {\sigma_{1} + \sigma_{2} + \sigma_{3} } \right)$$
(6)
$$q = \overline{\sigma } = \sqrt {\frac{1}{2}\left[ {\left( {\sigma_{1} - \sigma_{2} } \right)^{2} + \left( {\sigma_{2} - \sigma_{3} } \right)^{2} + \left( {\sigma_{3} - \sigma_{1} } \right)^{2} } \right]}$$
(7)
$$r = \left[ {\frac{27}{2}\left( {\sigma_{1} - \sigma_{m} } \right)\left( {\sigma_{2} - \sigma_{m} } \right)\left( {\sigma_{3} - \sigma_{m} } \right)} \right]^{1/3}$$
(8)

In plane stress, the fracture locus can be established in the space of (\(\overline{{\varepsilon_{f} }}\), η), since only one parameter η can be used to characterize the loading path.

In order to facilitate the derivation, plane stress ratio β is employed with the form of

$$\beta = \frac{{\sigma_{2} }}{{\sigma_{1} }} .$$
(9)

Since the assumption σ 1 ≥ σ 2, the range of β is β ≤ 1. η and β have the relation of

$$\eta = \frac{1 + \beta }{{3\sqrt {1 - \beta + \beta^{2} } }}.$$
(10)

So the fracture locus can be established in the space of (\(\overline{{\varepsilon_{f} }}\), β), which is employed in this research.

Given that the Mohr-Coulomb criterion is an isotropic function, the fracture criterion in the stress space remains isotropic in this study. For example, the material will fail at the same stress for uniaxial tension along the RD and TD directions. However, it will fail at different strains. This is not due to the anisotropy in the fracture criterion but due to the anisotropy of the plasticity model. The objective of this work is to investigate the influence of material plastic anisotropy on the ductile fracture in the strain space.

Modeling of Material Anisotropic Plasticity

In this research, the plastic behavior of the material is modeled using a standard plasticity featuring: (Ref 2) the anisotropic Hill 1948 yield function, (Ref 3) an associated flow rule and (Ref 4) an isotropic hardening law.

In the process of material preparation of sheet metals, such as aluminum alloy (Ref 24) and high-strength steels (Ref 25), the development of the microstructure and texture is significantly affected by the rolling process. These facts make sheet metals generally exhibit a significant anisotropy of mechanical properties. In fact, the rolling process makes the sheet orthotropic, which means that the material can be characterized by the symmetry of the mechanical properties with respect to three orthogonal planes. And the intersection lines of the symmetry planes are the orthotropy axes. In the case of the rolled sheet metals, their orientation is usually defined as follows: rolling direction (RD), transverse direction (TD), normal direction (ND), shown in Fig. 1 (Ref 26).

Fig. 1
figure 1

Orthotropy axes of the rolled sheet metals: RD, rolling direction; TD, transversal direction; ND, normal direction (Ref 26)

Full size image

The variation of their plastic behavior with direction can be assessed by a parameter called Lankford parameter or anisotropy coefficient r. Experimental results show that r depends on the in-plane direction. If the tensile specimen is cut having its longitudinal axis inclined with the angle θ to the rolling direction, the coefficient r θ is obtained, shown in Fig. 2. The subscript specifies the angle between the axis of the specimen and the rolling direction (Ref 26). In Hill 1948s yield model, r 0, r 45 and r 90 are usually used to describe the material plastic anisotropy.

Fig. 2
figure 2

Tensile specimen cut at the angle θ (measured from the rolling direction) (Ref 26)

Full size image

The Hill 1948 expression for the equivalent stress is expressed as

$$\overline{\sigma }^{2} = F(\sigma_{22} - \sigma_{33} )^{2} + G(\sigma_{33} - \sigma_{11} )^{2} + H(\sigma_{11} - \sigma_{22} )^{2} + 2L\sigma_{23}^{2} + 2M\sigma_{31}^{2} + 2N\sigma_{12}^{2}.$$
(11)

The parameters F, G, H, L and M can be determined by Lankford’s coefficients.

$$\begin{aligned} & F = \frac{{r_{0} }}{{r_{90} (r_{0} + 1)}},\quad G = \frac{1}{{r_{0} + 1}},\quad H = \frac{{r_{0} }}{{r_{0} + 1}}, \\ & M = L = N = \frac{{(r_{0} + r_{90} )(1 + 2r_{45} )}}{{2r_{90} (r_{0} + 1)}} \\ \end{aligned}$$
(12)

In the case of plane stress (σ 33 = σ 23 = σ 31 = 0), the Hill 1948 expression for the equivalent stress is of the form:

$$\overline{\sigma }^{2} = \sigma_{11}^{2} - \frac{{2r_{0} }}{{r_{0} + 1}}\sigma_{11} \sigma_{22} + \frac{{r_{0} (1 + r_{90} )}}{{r_{90} (r_{0} + 1)}}\sigma_{22}^{2} + \frac{{(r_{0} + r_{90} )(1 + 2r_{45} )}}{{r_{90} (r_{0} + 1)}}\sigma_{12}^{2}$$
(13)

When the Lankford parameters have the relationship of r 0 = r 45 = r 90 = r, the sheet only exhibits through-thickness anisotropy. The corresponding expressions for the yield function and the equivalent stress become:

$$\overline{\sigma }^{2} = \sigma_{1}^{2} - \frac{2r}{r + 1}\sigma_{1} \sigma_{2} + \sigma_{2}^{2}$$
(14)

A simple power law representation of the hardening rule will be used in this paper:

$$\overline{\sigma } = A\overline{\varepsilon }^{n}$$
(15)

where A is a material constant; n is the strain-hardening exponent. The present model is based on the assumption of isotropic hardening, which means that the initial yield function depends on material direction, but the hardening rule is not affected by the material anisotropy.

Influence of Plastic Anisotropy on Ductile Fracture in the Strain Space

Planar Isotropy (Through-Thickness Anisotropy)

In the situation of planar isotropy, the sheet only exhibits through-thickness anisotropy, which means that the Lankford parameters have the relationship of r 0 = r 45 = r 90 = r. The material behavior will be the same if the load is along different direction in the plate plane. In this situation, Eq 14 is used to describe the yield function.

Substituting Eq 3, 9, and 15 into Eq 14, the Mohr-Coulomb fracture criterion can be transformed from the stress-based form into the space of (\(\overline{{\varepsilon_{f} }}\), β).

$$\left\{ {\begin{array}{*{20}l} {\overline{{\varepsilon_{f} }} = \left\{ {\frac{{a^{2} b^{2} (1 + r - 2r\beta + \beta^{2} + r\beta^{2} )}}{{A^{2} (a^{4} - 2a^{2} \beta + \beta^{2} + ra^{4} - 2ra^{2} \beta + r\beta^{2} )}}} \right\}^{{\frac{1}{2n}}} } \hfill & {{\text{for}}\;\beta \le 0} \hfill \\ {\overline{{\varepsilon_{f} }} = \left\{ {\frac{{(b^{2} (1 + r - 2r\beta + \beta^{2} + \beta^{2} r)}}{{A^{2} a^{2} (1 + r)}}} \right\}^{{\frac{1}{2n}}} } \hfill & {{\text{for}}\;0 < \beta \le 1} \hfill \\ \end{array} } \right.$$
(16)

The results show that the equivalent strain to fracture \(\overline{{\varepsilon_{f} }}\) is a nonlinear function of stress ratio β and the Lankford parameter r. The expression of Eq 16 can be geometrically represented in the 3D space of (\(\overline{{\varepsilon_{f} }}\), β, r), see Fig. 3. Here, parameters of 2024-T351 aluminum alloy, reference to Bai and Wierzbicki’s work (Ref 11), are used: A = 740 MPa, n = 0.15, c 1 = 0.0345, c 2 = 338.6 MPa, that is a = 1.035 and b = 677.2 MPa.

Fig. 3
figure 3

3D geometry representation of the propose expression for planar isotropy (A = 740 MPa, n = 0.15, c 1 = 0.0345, c 2 = 338.6 MPa, that is a = 1.035 and b = 677.2 MPa)

Full size image

It can be concluded that the equivalent strain at fracture is determined by not only the loading path, the stress ratio β, but also the material anisotropy, the Lankford parameter r. If the Lankford parameter r in Eq 16 is fixed at some certain value, the expression reduces to a nonlinear function of stress ratio β. An example plot is shown in Fig. 4. It can be concluded from the figure that the fracture locus in the space of (\(\overline{{\varepsilon_{\text{f}} }}\), β) is similar to the locus in the space of (\(\overline{{\varepsilon_{\text{f}} }}\), η) predicted by the MMC model when the Lankford parameter r is not considered. They are both an “S”-shaped curve. But the material anisotropy parameter r will affect the shape of this locus curve. The results also show that the influence of material anisotropy on ductile fracture is reverse on the two side of the “S”-shaped curve. The demarcation point is the point of β = 0, the stress state of uniaxial tension. If β is in the range of [−1 0], the equivalent strain at fracture \(\overline{{\varepsilon_{\text{f}} }}\) increases with the Lankford parameter r. Conversely, if β is in the range of [0 1], the equivalent strain at fracture \(\overline{{\varepsilon_{\text{f}} }}\) decreases with the increase in Lankford parameter r. For the HSS, the parameter r is usually less than 1, and the stress ratio β of the material during the forming process is basically in the range of [0 1]. These facts make the fracture failure more serious for HSS during the forming process based on the results of this research.

Fig. 4
figure 4

Influence of plastic anisotropy on ductile fracture for planar isotropy in the space of (\(\overline{{\varepsilon_{\text{f}} }}\), β) for planar isotropy situation (assuming r = 0.7, 1, 1.2 and 1.5)

Full size image

Orthotropy

If the Lankford parameters r 0, r 45 and r 90 are not equal to one another, the sheet exhibits planar anisotropy, which is called orthotropy for rolled sheet metal. The material behavior will be different if the load is along different direction in the plate plane. Equation 13 is used to describe the yield function in this situation. Assuming that the principal stress direction is not consistent with the material orthotropy axes, the stress components in Eq 13 can be expressed as:

$$\left\{ {\begin{array}{*{20}c} { \sigma_{11} = \sigma_{1} \cos^{2} \theta + \sigma_{2} \sin^{2} \theta } \\ {\sigma_{22} = \sigma_{2} \cos^{2} \theta + \sigma_{1} \sin^{2} \theta } \\ {\sigma_{12} = (\sigma_{1} - \sigma_{2} )\cos \theta \sin \theta } \\ \end{array} } \right.$$
(17)

where the parameter θ is the angle of the direction of major principal stress σ 1 and the rolling direction.

Substituting Eq 3, 9, 15, and 17 into Eq 13, the Mohr-Coulomb fracture criterion is transformed from the stress-based form into the space of (\(\overline{{\varepsilon_{\text{f}} }}\), β, θ).

$$\left\{ {\begin{array}{*{20}l} {\overline{{\varepsilon_{f} }} = \left\{ {\frac{1}{{A^{2} r_{90} (a^{4} - 2a^{2} \beta + \beta^{2} + r_{0} a^{4} - 2r_{0} a^{2} \beta + r_{0} \beta^{2} )}}(a^{2} b^{2} (B + C\beta + D\beta^{2} )} \right\}^{{\frac{1}{2n}}} } \hfill & {{\text{for}}\;\beta \le 0} \hfill \\ {\overline{{\varepsilon_{f} }} = \left\{ {\frac{1}{{A^{2} a^{2} r_{90} (1 + r_{0} )}}(b^{2} (B + C\beta + D\beta^{2} )} \right\}^{{\frac{1}{2n}}} } \hfill & {{\text{for}}\;0 < \beta \le 1} \hfill \\ \end{array} } \right.$$
(18)

where

$$\begin{aligned} B & = r_{90} + r_{90} r_{0} + 4r_{90} r_{0} \sin^{4} \theta - 4r_{90} r_{0} \sin^{2} \theta + 2\sin^{2} \theta r_{0} r_{45} + 2\sin^{2} \theta r_{90} r_{45} - 2\sin^{4} \theta r_{90} r_{45} - 2\sin^{4} \theta r_{0} r_{45} + \sin^{2} \theta r_{0} - \sin^{2} \theta r_{90} \\ C & = - 2r_{90} r_{0} - 8r_{90} r_{0} \sin^{4} \theta + 8r_{90} r_{0} \sin^{2} \theta - 4\sin^{2} \theta r_{0} r_{45} - 4\sin^{2} \theta r_{90} r_{45} + 4\sin^{4} \theta r_{0} r_{45} + 4\sin^{4} \theta r_{90} r_{45} \\ D & = r_{0} + r_{90} r_{0} - \sin^{2} \theta r_{0} + \sin^{2} \theta r_{90} + 4r_{90} \sin^{4} \theta r_{0} - 4r_{90} r_{0} \sin^{2} \theta + 2\sin^{2} \theta r_{0} r_{45} + 2\sin^{2} \theta r_{90} r_{45} - 2\sin^{4} \theta r_{90} r_{45} - 2\sin^{4} \theta r_{0} r_{45} \\ \end{aligned}$$
(19)

It can be found that if r 0 = r 45 = r 90 = r in Eq 18, the expression will reduce to Eq 16. This is another way to explain that the material behavior will be the same if the load is along different direction in the plate plane for the planar isotropy situation.

The expression of Eq 18 can be also geometrically represented in the 3D space of (\(\overline{{\varepsilon_{\text{f}} }}\), β, θ), see Fig. 5. Here, an example group of parameters for DP590, which are obtained by experiments in this research, is used: A = 970 MPa, n = 0.196, r 0 = 0.6, r 45 = 0.95, r 90 = 0.83, a = 1.265 and b = 1179 MPa (c 1 = 0.24, c 2 = 589.5 MPa).

Fig. 5
figure 5

3D geometry representation of the proposed expression for plane stress state (A = 970 MPa, n = 0.196, r 0 = 0.6, r 45 = 0.95, r 90 = 0.83, a = 1.265 and b = 1179 MPa)

Full size image

If the angle θ in Eq 18 is fixed at some certain value, for example θ = 0, θ = π/4 and θ = π/2, the equation reduces to a nonlinear function of stress ratio β. An example plot is shown in Fig. 6.

Fig. 6
figure 6

Influence of plastic anisotropy on ductile fracture in the space of (\(\overline{{\varepsilon_{\text{f}} }}\), β) for orthotropy situation (assuming θ = 0, θ = π/4 and θ = π/2)

Full size image

Obviously, in the situation of orthotropy, the equivalent strain at fracture is affected by not only the stress ratio but also the loading direction, which can be indicated by the angle of the direction of major principal stress and the rolling direction.

The expression of Eq 18 is more important for application. The fracture parameters a and b can be obtained by experiments through fracture tests in only one direction, for example the rolling direction. Then, the equivalent strain at fracture in other directions can be calculated through this equation. The fracture locus of DP590, which will be discussed below, is obtained by this method in this study.

Verification of the Proposed Expression

In order to verify the accuracy of the proposed expression, the fracture data of 2024-T351 aluminum alloy in Ref. 11 are used to verify whether this model can reduce to the MMC fracture model when the material is considered to be isotropic. The material parameters of 2024-T351 aluminum alloy acquired from the reference are shown in Table 1. In order to obtain the fracture locus of proposed expression, the Lankford parameters r 0, r 45, r 90 are set to 1 and θ is set to zero in Eq 18. The horizontal axis is transformed to η through Eq 10. The fracture locus of MMC model is captured by getting the data points on the curve in the reference, shown in Fig. 7(a) (the blue full line), by using image processing software. Data points, η range of −1/3 to 2/3, are used for the verification. Figure 7(b) shows the comparison of these two fracture loci. The results show that the proposed expression will reduce to the MMC model if the material is considered to be isotropic. That is to say that the derivation process and the expression are correct.

Table 1 Material parameters of 2024-T351 aluminum alloy
Full size table
Fig. 7
figure 7

(a) The fracture locus of MMC model in Ref. 11. (b) The comparison of the locus of the proposed fracture model and MMC model

Full size image

Fracture Locus of DP590

In this section, experimental method is presented to obtain the fracture locus predicted by the expression proposed in this study. The material used in this paper is dual-phase steel DP590 with thickness of 1.2 mm, which is already widely used in the manufacture of car body. A total of seven parameters (A, n, a, b, r 0, r 45, r 90) need to be found in Eq 18. Experimental method of parameters calibration is explained in details in this section.

Hardening Rule (Calibration of Parameters A and n)

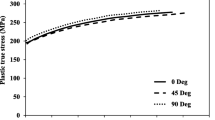
The strain-hardening behavior of DP590 is determined from uniaxial tensile tests on samples cut from the sheets. The engineering stress-strain curves of all specimens prepared from three directions are shown in Fig. 8(a). Tests in the same direction are presented three times, and the results are very repeatable. The true stress-strain curve is given in Fig. 8(b). It is clear from Fig. 8(a) that the engineering stress-strain curves are almost the same in 0° and 45° direction up to the point of necking. Meanwhile, the curves are a little higher in the 90° direction. This result demonstrates that the material anisotropy for DP590 is relatively significant.

Fig. 8
figure 8

(a) Engineering stress-strain curves measured in uniaxial dog-bone specimens. (b) True stress vs. plastic strain calculated up to necking

Full size image

Equation 15 is used to represent the hardening rule, and the parameters A and n are obtained by fitting the experimental data. The results are shown in Table 2. The average value is calculated by the following equation:

$$X_{\text{Average}} = \frac{{X_{0} + 2X_{45} + X_{90} }}{4}$$
(20)

where X represents the parameters A and n.

Table 2 Measured values of A and n for DP590
Full size table

Quantification of Plastic Anisotropy (Calibration of Parameters r 0, r 45, r 90)

The Lankford parameter r is defined by

$$r = \frac{{\varepsilon_{22} }}{{\varepsilon_{33} }}$$
(21)

where ɛ 22 and ɛ 33 are the strains in the width and thickness directions of specimen in the uniaxial tensile test, respectively. Taking into account the condition of volume constancy ɛ 11 + ɛ 22 + ɛ 33 = 0, ɛ 11 is the strain in the loading direction; the following form of Eq 21 is obtained.

$$r = - \frac{{\varepsilon_{22} }}{{\varepsilon_{11} + \varepsilon_{22} }}$$
(22)

Since the strain tensor can be calculated from the displacement field by the DIC software ARAMIS, the Lankford parameter in three directions can be obtained accurately. ARAMIS uses the digital image correlation theory to utilize a series of digital images for optical measurements. The strain tensor is calculated by the displacement change between the pixels. The 3D DIC system used in this study is shown in Fig. 9. Virtual two-point extensometers were used to determine the histories of both the major strain and the minor strain, as shown in Fig. 10(a). The results of the r measurements are summarized in Fig. 10(b), which shows the relation between the major and minor strains for tensile specimens, cut at 0°, 45°, and 90°. The results in the same direction are very repeatable, and the calculated values of the Lankford parameters are given in Table 3. The values of all the parameters of anisotropy calculated from the measured strain ratios are given in Table 3 as well.

Fig. 9
figure 9

The 3D DIC system used in this study

Full size image
Fig. 10
figure 10

(a) Virtual extensometers in ARAMIS at their initial position. (b) Major strain vs. minor strain for uniaxial tension

Full size image
Table 3 Measured values of the Lankford parameters and parameters of the Hill 1948 model for DP590
Full size table

Four Types of Fracture Tests (Calibration of Parameters a and b)

In order to prepare the database for calibration of the fracture locus, a series of specimens, described in Table 4, including classical dog-bone specimens, flat specimens with cutouts and center holes and pure shear specimens (Fig. 11), are performed to fracture. Every specimen is prepared with their longitudinal axis inclined with the angle of 0°, 45°, or 90° to the rolling direction. All tensile tests are performed on a 50-kN mechanical loading frame. The equivalent strains to fracture \(\overline{{\varepsilon_{\text{f}} }}\) of all these specimens are calculated by the strain tensor measured by the DIC system. The gauge section of each of the specimens is painted completely with a thin layer of white paint, and then, black speckles are spray painted on the white layer, providing a pattern for the DIC program to follow. Two digital cameras are used to take pictures through each experiment, so that the 3D strain components can be calculated by the DIC software ARAMIS. The optical measurement system is set up to take 10 pictures per second. After each test is completed, ARAMIS was used to analyze the resulting pictures.

Table 4 List of the four types of fracture tests
Full size table
Fig. 11
figure 11

Geometry of specimens (a) dog bone, (b) flat with a center hole, (c) flat with cutout, (d) pure shear

Full size image

The strain history can be calculated accurately by ARAMIS. Therefore, the stress ratio β is determined from the strain ratio α in this paper. The postulate of plastic incompressibility imposes the following restrictions on the strain rate ratio:

$$d\varepsilon_{1} {:}d\varepsilon_{2}{:}d\varepsilon_{3} = 1{:}\alpha {:}- (1 + \alpha )$$
(23)

where α = dɛ 1/dɛ 2. Under the hypothesis of proportional loading, the strain rate ratio is equal to the stain ratio. From the associated flow rule, the stress ratio, β = σ 1/σ 2, can be calculated by the equation:

$$\beta = \frac{\alpha + H}{F + (1 + \alpha )H}$$
(24)

Figure 12 shows the strain paths of these four types of fracture tests. The strain history of the fracture points is measured. The definition of the fracture point and the directions of the major and minor strain are explained below, shown in Fig. 14. Average strain ratio α is determined for each case. Then, the stress ratio β can be obtained by Eq 24. The results are summarized in Table 4.

Fig. 12
figure 12

Strain paths of these four types of fracture tests

Full size image

The DIC technique employed in this study is a 3D DIC method with two cameras. Therefore, the strain components calculated from the displacement field are accurate when applying to the material that necks before fracture. The Hill 1948 expression for the equivalent strain in the case of plane stress (σ 13 = σ 23 = σ 33 = 0) is of the form:

$$\overline{\varepsilon } = \sqrt {\frac{1}{\gamma }[(F + H)\varepsilon_{11}^{2} + (H + G)\varepsilon_{22}^{2} + 2H\varepsilon_{11} \varepsilon_{22} ] + \frac{2}{N}\varepsilon_{12}^{2} }$$
(25)

where γ = FH + HG + FG. The in-plane components of the plastic strain tensor ɛ 11, ɛ 22 and ɛ 12 can be calculated by the major and minor principal strain ɛ 1 and ɛ 2 measured by DIC system through the following equations.

$$\left\{ {\begin{array}{*{20}c} { \varepsilon_{11} = \varepsilon_{1} \cos^{2} \theta + \varepsilon_{2} \sin^{2} \theta } \\ {\varepsilon_{22} = \varepsilon_{2} \cos^{2} \theta + \varepsilon_{1} \sin^{2} \theta } \\ {\varepsilon_{12} = (\varepsilon_{1} - \varepsilon_{2} )\cos \theta \sin \theta } \\ \end{array} } \right.$$
(26)

For the tensile test of flat specimen with center hole, the onset of fracture can be captured very specifically by the DIC technique. The first visible crack in the paint layer on the specimen surface is very clear, as shown in Fig. 13. However, for the tests of dog-bone specimens and flat specimens with cutout, the specimens rupture in a very short time that the DIC system cannot capture the onset of first visible crack under the photofrequency of 10 Hz. So the stage that right before the rupture is defined as the onset of fracture. The DIC-measured strain field of the stage of fracture for all the four types of specimens is shown in Fig. 14. ɛ 1 and ɛ 2 are the major strain and minor strain, respectively. The point with the maximum strain value is defined as the fracture point, where the strain is measured. Figure 15 shows the force-displacement curves of all the four types of specimens.

Fig. 13
figure 13

The first visible crack in the paint layer on the specimen surface of flat with a center hole

Full size image
Fig. 14
figure 14

The DIC-measured strain field of the stage that right before the rupture (a) dog bone, (b) flat with center hole, (c) flat with cutout, (d) pure shear

Full size image
Fig. 15
figure 15

Force-displacement curves of all the four types of specimens (a) dog bone, (b) flat with center hole, (c) flat with cutout, (d) pure shear

Full size image

The values of the equivalent strains to fracture measured according to Eq 25 and 26 for all specimens are shown in Table 5, 6, 7 and 8. In Table 5, 6, 7 and 8, there are two different columns, specimen orientation and θ. Specimen orientation means the loading direction, which is the angle between the loading direction and the rolling direction. θ means the angle between the direction of the maximum principal stress and the rolling direction. These two angles are the same for these three specimens, dog-bone specimens, flat specimens with cutouts and center holes. The loading direction and the direction of the maximum principal stress are the same for these three specimens, which are shown in Fig. 14(a)-(c). So in Table 5, 6, 7, these two columns are the same. However, for the specimen of pure shear, these two angles are not the same, shown in Fig. 14(d), so these two columns in Table 8 are different.

Table 5 Strain measured using the DIC method for specimens of dog bone
Full size table
Table 6 Strain measured using the DIC method for specimens of flat with center hole
Full size table
Table 7 Strain measured using the DIC method for specimens of flat with cutout
Full size table
Table 8 Strain measured using the DIC method for specimens of pure shear
Full size table

The results of dog bone prepared with their longitudinal axis inclined with the angle of 0 to the rolling direction and pure shear specimens with their longitudinal axis inclined with the angle of 45° to the rolling direction are used to calibrate the two basic material constants a and b in Eq 18. The direction of major stress for the dog-bone specimens is parallel with the tensile direction, and the direction of major stress for the pure shear specimens is inclined with the angle of 45° to the tensile direction, shown in Fig. 14. So that the parameter θ equals to zero for these two kinds of specimens. Substituting the experimental data (β, \(\overline{{\varepsilon_{f} }}\)) into Eq 18, a set of two nonlinear algebraic equations for a and b are obtained. The solution of this system yields a = 1.266 and b = 1179 MPa. Substituting these results into Eq 7, the M-C fracture criterion parameters c 1 and c 2 are obtained (c 1 = 0.238, c 2 = 589.544 MPa).

Now all seven parameters in Eq 18 have been determined, which are summarized in Table 9. The plot of the resulting fracture locus is shown in Fig. 16. Average values of test nos. 1, 2 and 24, 25, 26, used for calibration, are displayed as diamonds. The “S”-shaped curve passes exactly through those two points. Points corresponding to the remaining tests are denoted by crosses. They are approximate to the fracture locus predicted by the proposed expression, except for point corresponding to pure shear test of 0° from rolling direction. This is mainly because the equivalent strain to fracture for the stress state of pure shear is difficult to measure by DIC system. The displacement field of the onset of fracture stage is hard to be obtained because the pixels are difficult to distinguish due to the large deformation in the very small region. Otherwise, the accuracy of the model is acceptable. Particularly, the orders of the equivalent strain to fracture for different specimen orientation under certain stress ratios are predicted accurately by the proposed model. In the stress state of β = 0.05 (dog bone) and β = 0.14 (flat with center hole), the equivalent strain to fracture of the specimen with orientation of 45° is the largest and that of specimen with orientation of 90° is the smallest. Meanwhile, in the stress state of β = 0.35 (flat with cutout), the equivalent strain to fracture of the specimen with orientation of 0 is the largest and that of specimen with orientation of 90° is the smallest. The proposed model predicts these results accurately.

Table 9 Material constants for DP590
Full size table
Fig. 16
figure 16

Fracture locus for DP590

Full size image

The proposed model can be conveniently applied in engineering practice. For a specific metal material, the fracture tests for only one direction, for example the rolling direction, are needed to be carried out for parameter identification. The fracture loci for the other direction can be obtained by the proposed model directly and can be used to predict the ductile fracture behavior of the material more accurately.

Conclusion

In this paper, the effect of plastic anisotropy on ductile fracture in the strain space is investigated for sheet metals under the assumption of plane stress. The plastic behavior of the material is modeled using a standard plasticity featuring: (Ref 2) the anisotropic Hill 1948 yield function, (Ref 3) an associated flow rule and (Ref 4) an isotropic hardening law. The Hill 1948 yield function can describe the differences of the material performance in different directions with good accuracy. Besides, the anisotropy parameters, r 0, r 45 and r 90, which are proved to have a significant effect on ductile fracture in the strain space in this study, can be easily obtained by experiments. The Mohr-Coulomb fracture model is employed to describe ductile fracture in the stress space. The form of the M-C criterion is transformed to the coordinate system, where the axes are the equivalent strain to fracture \(\overline{{\varepsilon_{\text{f}} }}\) and the stress ratio β. Material anisotropy, characterized by the Lankford parameter r, is introduced into the expression of the fracture locus function. The main conclusions of this work are:

  1. 1.

    The fracture criterion in the stress space remains isotropic in this study. However, the anisotropy of the plasticity model leads to different fracture strains when the material undergoes the same load path but different load directions.

  2. 2.

    Explicit mathematical expression is presented. The effect of material anisotropy on ductile fracture in the strain space is revealed and quantitatively analyzed.

  3. 3.

    Experimental method is presented to obtain the fracture locus predicted by the expression proposed in this study. Material constants and fracture locus of DP590 are obtained. It is shown that the proposed model is able to predict the material direction dependency of the fracture strain with good accuracy.