The Effect of High-Pressure Devitrification and Densification on Ballistic-Penetration Resistance of Fused Silica

Abstract

Recent experimental and molecular-level computational analyses have indicated that fused silica, when subjected to pressures of several tens of GPa, can experience irreversible devitrification and densification. Such changes in the fused-silica molecular-level structure are associated with absorption and/or dissipation of the strain energy acquired by fused silica during high-pressure compression. This finding may have important practical consequences in applications for fused silica such as windshields and windows of military vehicles, portholes in ships, ground vehicles, spacecraft, etc. In the present work, our prior molecular-level computational results pertaining to the response of fused silica to high pressures (and shear stresses) are used to enrich a continuum-type constitutive model (that is, the so-called Johnson-Holmquist-2, JH2, model) for this material. Since the aforementioned devitrification and permanent densification processes modify the response of fused silica to the pressure as well as to the deviatoric part of the stress, changes had to be made in both the JH2 equation of state and the strength model. To assess the potential improvements in respect to the ballistic-penetration resistance of this material brought about by the fused-silica devitrification and permanent densification processes, a series of transient non-linear dynamics finite-element analyses of the transverse impact of a fused-silica test plate with a solid right-circular cylindrical steel projectile were conducted. The results obtained revealed that, provided the projectile incident velocity and, hence, the attendant pressure, is sufficiently high, fused silica can undergo impact-induced devitrification, which improves its ballistic-penetration resistance.

Introduction

The present work deals with computational modeling and simulations of the devitrification/crystallization and permanent densification of fused silica (a transparent-armor material) under ballistic-impact conditions, and the associated increase in the fused-silica ballistic limit. Hence, the main aspects of the present work include (a) current reputation and standing of ceramic glasses like fused-silica as transparent-armor materials; (b) microstructure of fused-silica, main SiO₂ crystalline polymorphs, and glass devitrification/crystallization under high imposed pressures; (c) prior experimental; and (d) prior computational efforts dealing with the analysis of fused-silica devitrification under high pressures. A brief overview of these aspects of the problem at hand is presented in the remainder of this section.

Ceramic Glasses as Transparent-Armor Materials

Currently, a number of materials and design strategies are employed in transparent, ballistic-impact-resistant vehicle structures (e.g., windshields, door windows, viewports, etc.). Among the most recently introduced transparent materials and technologies, the following have received the most attention: (a) transparent crystalline ceramics [e.g., aluminum-oxynitride spinel, AlON, sapphire (Ref 1)]; (b) new transparent polymer materials [e.g., transparent nylon (Ref 2)]; (c) new interlayer technologies [e.g., polyurethane bonding layers (Ref 3)]; and (d) new laminate structure designs [e.g., (Ref 4)]. Despite the clear benefits offered by these materials and technologies (e.g., transparent ceramics offer a very attractive combination of high stiffness and high hardness levels, highly ductile transparent polymers provide superior fragment containing capabilities, etc.), ballistic ceramic glass like fused-silica remains an important constituent material in a majority of transparent impact-resistant structures used today. Among the main reasons for the wide-scale use of glass, the following three are most frequently cited: (1) glass-structure fabrication technologies enable the production of curved, large surface-area, transparent structures with thickness approaching several inches; (2) relatively low material and manufacturing costs; and (3) compositional modifications, chemical strengthening, and controlled crystallization have been demonstrated to be capable of significantly improving the ballistic properties of glass ( e.g., Ref 2).

Fused-Silica, SiO₂ Polymorphs, and High-Pressure Devitrification

Ceramic glasses are amorphous materials. The molecular-level microstructure of these materials involves entities such as a random network of covalently bonded atoms, atomic free volumes, network-forming atoms (e.g., Si), bridging and non-bridging oxygen atoms, cations of glass-modifier species, etc. However, despite the absence of a crystalline structure, the microstructure of ceramic glasses is not completely random. Rather, it involves different extents of short- and intermediate-range order spanning over a range of length scales (from the quantum-mechanical to the continuum-level). To describe the structure of ceramic glasses as determined using various experimental techniques (e.g., neutron-diffraction, nuclear magnetic resonance, small angle x-ray scattering (SAXS), etc.), the so-called random network model (Ref 5) is typically employed. Such a model represents an amorphous material as a three-dimensional linked network of polyhedra. The character (number of facets) of the polyhedra is controlled by the species-specific coordination of the central (glass-forming) atom (cation). In fused silica, the polyhedron-center atoms are all silicon and each silicon atom is surrounded by four oxygen atoms (while each oxygen atom is connected to or bridges two silicon atoms, i.e., all oxygen atoms are of a bridging type), forming a network of SiO₄ ⁴⁻ tetrahedra. Other silicate-based glasses contain network modifiers (alkali or alkaline earth oxides) which compromise the continuity of the network and introduce non-bridging oxygen anions.

Within the random network model, the microstructure of glass is described using several network-state parameters. A detailed description of these parameters, as well as the experimental/computational procedures which are commonly employed to determine these parameters, can be found in our prior work (Ref 6). Previous investigations (e.g., Ref 6-15) established that under high-rate (shockwave or ballistic) loading conditions, fused-silica targets can, at least in the vicinity of the impact region, experience transformation of the amorphous structure into a crystalline one. To help rationalize potential transformations of fused silica into various (crystalline) polymorphs of SiO₂, the corresponding temperature-pressure phase diagram and the SiO₂ polymorphs were analyzed in our prior work (Ref 16). The analysis established that under ballistic-impact loading conditions and the accompanying adiabatic temperatures, the following three polymorphs have the highest probability of forming during the impact-induced devitrification process:

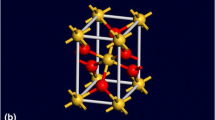
• (1) α-Quartz-structure: trigonal; space group: P3₂21 (No. 154); Lattice parameters: a = b = 4.9137 Å, c = 5.4047 Å, α = β = 90.0°, γ = 120.0°, Z = 3 (where Z is the number of SiO₂ units within the unit cell); mass density: 2.66 g/cm³. The atomic arrangement within the non-primitive unit cell of α-quartz is depicted in Fig. 1(a).

  Fig. 1

  

  The atomic arrangements within the non-primitive unit cells of: (a) α-quartz; (b) stishovite; and (c) coesite

• (2) Coesite—structure monoclinic; space group: C2/c; Lattice parameters: a = 7.1356 Å, b = 12.3692 Å, c = 7.1736 Å; α = 90.0°, β = 120.34°, γ = 90.0°, Z = 16; mass density: 2.92 g/cm³. The atomic arrangement within the non-primitive unit cell of coesite is depicted in Fig. 1(b).

• (3) Stishovite-structure tetragonal (ditetragonal dipyramidal); Space group: P 4₂/mnm (No. 136) P4₂/mnm {P4₂/m 2₁/n 2/m}; Lattice parameters: a = b = 4.179 Å, c = 2.6649 Å, Z = 2; mass density: 4.29 g/cm³. The atomic arrangement within the non-primitive unit cell of stishovite is depicted in Fig. 1(c).

Prior Experimental Work

A detailed overview of the public-domain literature carried out as part of the present work revealed a number of experimental investigations dealing with the mechanical response of fused silica to dynamic loading. Some of these studies revealed the formation of shear bands within otherwise amorphous glass, others established the formation of crystalline phases (α-quartz and stishovite, but not coesite), while still others demonstrated increased hardness of the material surrounding the impact region without establishing the microstructural cause for this property change.

Chakraborty et al. (Ref 17) carried out a series of nano-indentation tests and showed that, as the loading rate increases, the extent of shear band formation in the region surrounding the indentation decreases, while the hardness value increases. No crystal-structure analysis was carried out to determine potential formation of any of the crystalline phases as a result of loading or to provide a rationale for the observed effect of the loading rate.

Tschauner et al. (Ref 18) investigated formation of stishovite in soda-lime glass during 57 GPa shock loading experiments and the reversion of this phase during subsequent release/unloading. They demonstrated that upon loading, high-density non-fully crystallized SiO₂ phase was present in the “shocked” fused-silica. Upon static loading to only 13 GPa, this phase was fully converted into the crystalline stishovite, suggesting that the shock loading was able to devitrify fused silica and form crystalline stishovite.

Salleo et al. (Ref 19) demonstrated the formation of a defective form of stishovite in the surface region of fused-silica wafers through irradiation with a high-powered laser. The formation of such a phase and its continuous growth has been found to be the main cause of failure in optics used for high-power photonics.

Prior Computational Work

A detailed overview of the public-domain literature carried out as part of the present work also revealed three computational investigations dealing with the mechanical response of fused silica to dynamic loading.

Mantisi et al. (Ref 20) carried out a comprehensive atomic-scale simulation of fused silica under combined pressure/shear loading conditions. The results obtained established permanent/irreversible densification of the fused-silica test sample and the change of the silicon and oxygen coordination relative to that present in the as-received fused silica. However, these microstructural changes could not be considered to be the result of glass devitrification/crystallization processes, i.e., the glass remained amorphous. One of the potential reasons for this observation was inadequacy of the interatomic potentials used in the simulation of the fused-silica mechanical behavior.

Kubota et al. (Ref 21) used molecular dynamics simulations to infer the atomic-scale structural changes in fused silica induced by shock-compression loading. The results obtained revealed that shock-compressive loading involving stress levels exceeding the Hugoniot elastic limit gives rise to dramatic changes in the structure and topology of the fused-silica network and densifications in excess of 20%. Coordination analysis of the as-shocked fused silica revealed the formation of under- and over-coordinated Si atoms. While under-coordinated Si atom regions could be interpreted as shock-induced fused-silica flaws, over-coordinated Si atom regions showed some resemblance to the crystalline stishovite. In addition to the coordination changes just described, changes in glass topology (such as increases in the number of the threefold, fourfold, sevenfold, and larger rings) were observed.

Grujicic et al. (Ref 16) carried out an all-atom molecular-level computation of the dynamic response and material microstructure/topology changes of fused silica subjected to ballistic impact by a hard projectile. The results obtained clearly revealed the formation of stishovite (and perhaps α-quartz) within fused silica during ballistic impact. To rationalize the findings obtained, the all-atom molecular-level computational analysis was complemented by a series of quantum-mechanics density functional theory (DFT) computations. The latter computations enabled determination of the relative potential energies of the fused silica, α-quartz, and stishovite under ambient pressure (i.e., under their natural densities) as well as under imposed (as high as 50 GPa) pressures (i.e., under higher densities) and shear strains. In addition, the transition states associated with various fused-silica devitrification processes were identified.

Main Objective

The main objective of the present work is to utilize the atomic-scale and quantum-mechanical-scale results obtained in our recent work (Ref 16) regarding the devitrification of fused silica under ballistic-impact conditions in order to enrich and upgrade a continuum-level material model for the same material. Once such material model enrichment/upgrading is completed and the model is implemented into a material user subroutine and linked with a finite-element solver, it is used, within a transient non-linear dynamics finite-element analysis, to investigate the response of a fused-silica target plate to a normal (i.e., zero obliquity angle) impact by an armor-piercing bullet. By turning off and on the glass devitrification process, such analysis will enable quantification of the ballistic-impact improvement brought about by the formation of high-density crystalline polymorphs of SiO₂ from fused silica during a ballistic impact.

Paper Organization

A summary of the molecular- and quantum-mechanics-level computational results (the results used in the present work) regarding the response of fused silica to high-pressure/-shear loading is presented in section 2. A brief overview of the original JH2 material model and its proposed modifications is given in section 3. Details regarding the transient non-linear dynamics finite-element analysis of impact of a fused-silica target plate by an armor-piercing bullet, the results obtained, and interpretation of the results are all presented in section 4. A summary of the main findings and conclusions is provided in section 5.

Summary of Main Results from Ref 16

Since the present work utilizes many of the (atomic-scale and quantum-mechanics) results reported in our recent work (Ref 16), a brief summary of these results is given in this section. For improved clarity, this summary is divided into several subsections.

Validation of the Fused-Silica Atomic-Scale Material Model

To validate the atomic-scale model for fused silica, a number of model predictions are compared with either their experimental or with their more accurate quantum-mechanical computational counterparts. The material characteristics used in this validation procedure include room-temperature and ambient pressure: (a) mass density; (b) partial radial distribution functions for the three (Si-Si, Si-O, and O-O) atomic pairs; and (c) distributions of the Si atom and O-atom coordination numbers. The level of agreement obtained indicated that the computational unit cell used to represent the amorphous structure of fused silica, and the force-field potentials used to quantify various bonding and non-bonding interactions within the computational cell account quite well for the natural state of densification, for the short-range order, and for the coordination environment within fused silica.

Ballistic-Impact-Induced Fused-Silica Devitrification

In Ref 16, atomic-scale simulations were carried out of the impact of a fused-silica target plate by a diamond solid right-circular cylindrical projectile. Examples of such results as a function of the post-initial-contact time are depicted in Fig. 2(a)-(d). In these figures, for improved clarity, the symbols for the target plate atoms are made smaller. Examination of the results displayed in Fig. 2(a)-(d) reveals that the target plate material in the close vicinity of the projectile experiences major changes. Detailed examination of the regions of the target experiencing such changes revealed

Fig. 2

Temporal evolution of the computational domain at four times: (a) 0.5 ps; (b) 1.5 ps; (c) 2.5 ps; and (d) 3.5 ps, following the initial contact between the diamond solid right-circular cylindrical projectile moving at a high velocity and the fused-silica target plate

• (a) the presence of numerous six-folded Si and three-folded O atoms (the Si and O coordinations characteristic of stishovite and not of fused silica). Local stishovite-like microstructure showing two six-folded Si and two three-folded O atoms is shown in Fig. 3(a). For clarity, a larger sphere radius is assigned to the atoms involved. In addition, six-folded Si atoms and three-folded O atoms are tagged with circular symbols. Since the initial state of fused-silica only contained four-folded Si and two-folded O atoms, this result suggested that ballistic impact can lead, at least locally, to the conversion of amorphous SiO₂ into the crystalline (but highly deformed) stishovite structure;

  Fig. 3

  

  Results indicating devitrification of fused silica in the target region adjacent to the penetration hole: (a) Local stishovite-like microstructure showing two six-folded Si and two three-folded O atoms. (b) Size distribution function for the smallest Si-O rings in the fused-silica initial and as-impacted states; (c) and (d) Si-Si, O-O, and Si-O partial radial distribution functions in (c) the as-received/initial state of silica; and (d) the silica region adjacent to the penetration hole

• (b) changes in the size distribution of the smallest/primitive Si-O rings (i.e., the rings which cannot be described as combinations of smaller rings). That is, while five-membered rings are found in the as-impacted fused silica, only larger rings were present in the initial state of this material. An example of the results pertaining to the size distribution function for the smallest Si-O rings in the fused-silica initial and as-impacted states is shown in Fig. 3(b);

• (c) changes in the Si-O ring topology. That is, while in the initial state of fused silica these rings resemble the corresponding rings found in cristobalite (another SiO₂ polymorph), in the as-impacted fused silica, the topology of the six-membered rings was found to resemble more that found in α-quartz and stishovite;

• (d) changes in the Si-Si, O-O, and Si-O partial pair correlation functions from those characteristics of amorphous materials found in the initial state of fused silica, Fig. 3(c), to those found in the silica region adjacent to the penetration hole, Fig. 3(d); and

• (e) changes in the Si atomic coordination from 4 in the as-received fused silica to approximately 6 in the fused-silica region affected by the ballistic impact, as well as changes in the O atomic coordination from 2 in the as-received fused silica to approximately 3 in the same fused-silica region.

Quantum-Mechanical Analysis of Fused-Silica Devitrification

To help rationalize the aforementioned changes in the microstructure of fused silica in the region adjacent to the penetration hole, a series of quantum-mechanical calculations are carried out in Ref 16. The main objective of these calculations was determination of the relative stability of fused silica, α-quartz, and stishovite, as well as of the energy barriers associated with the fused-silica → α-quartz and fused-silica → stishovite transition states. The main results obtained revealed:

• (a) At the ambient conditions, the thermodynamic stability of the three states of SiO₂ decreases in the order α-quartz, fused silica and stishovite. When the pressure is increased to 50 GPa, fused silica becomes more stable than α-quartz, while the thermodynamic stability of stishovite (still the lowest) becomes more comparable to those of the other two states;

• (b) In the presence of 5% shear, the order of thermodynamic stability of the three states under ambient conditions does not change, although their values become more comparable to each other. On the other hand, at an applied pressure of 50 GPa and in the presence of 5% shear, stishovite becomes the most thermodynamically stable state, followed by α-quartz and then fused silica; and

• (c) In the absence of applied shear, the energy associated with the fused-silica → stishovite transition state is higher than that for the fused-silica → α-quartz transition state. However, when 5% shear is applied, the energy associated with the fused-silica → stishovite transition state becomes substantially lower than that for the fused-silica → α-quartz transition state. These findings suggest that, in the presence of shear, and at pressures as high as 50 GPa, fused silica is more likely to convert to stishovite than α-quartz.

JH2 Continuum-Material Model

The results presented and discussed in the previous section were obtained using the atomic-scale and quantum-mechanical-scale computational tools. At these length scales, glass is modeled as an assembly of discrete interacting particles. On the other hand, when one is concerned with the ballistic limit of a ceramic glass, the employed computational methods treat glass as a continuum and, hence, a high-fidelity constitutive model is needed for this material. One of the frequently used continuum-level material models for ceramic glasses is the Johnson-Holmquist-2 (JH2) material model (Ref 22). This model is adopted in the present work and is briefly reviewed in the remainder of this section. Additionally, in the last portion of this section, details are presented regarding modification of the JH-2 model made in the present work in order to enable the incorporation of the ballistic-impact-induced devitrification and permanent densification effects on the constitutive behavior of fused silica.

General Structure of a Continuum-Level Material Model

To completely define a continuum-level material constitutive model, the relationships among the flow variables (pressure, effective stress, mass density, energy density, temperature, etc.) must be specified. These relations typically involve (a) an equation of state (EOS); (b) a strength model; (c) a failure model; and (d) an erosion equation. These equations arise from the fact that, in general, the total stress tensor can be decomposed into a sum of a hydrostatic stress (negative pressure) tensor (which causes a change in the volume/density of the material) and a deviatoric stress tensor (which is responsible for the shape change of the material).

Equation of state An EOS is used to define the corresponding functional relationship between pressure, mass density (degree of compression), and internal energy density (temperature).

Strength model As far as the strength model is concerned, the number and the type of equations needed to describe material-shape change induced by the deviatoric component of stress are dependent on the absence/presence of the inelastic components of the deformation tensor. That is, when the response is elastic, the changes in the corresponding deviatoric stress at a given level of deviatoric strain quantities all scale with the shear modulus of the material. Conversely, in the presence of the inelastic strains (e.g., plasticity, micro-cracking, etc.), the strength material model requires specification of the “yield criterion,” “flow rule,” and “constitutive relation.” The yield criterion defines the (typically stress-based) condition which must be met for the onset and continuation of inelastic material response. The flow rule relates the components of the inelastic deformation increment to the applied deviatoric stress. The constitutive relation defines the appropriate equivalent inelastic strain, equivalent inelastic strain rate, and temperature dependencies of the material yield strength (or, more precisely, the material inelastic deformation resistance).

Failure model A failure model generally consists of a failure criterion, i.e., an equation describing the hydrostatic or deviatoric stress and/or strain condition(s) which, when attained, cause the material to fracture and lose its ability to support tensile normal and shear stresses.

Erosion equation The erosion equation defines one or more stress-/strain-based erosion conditions which, when met, will cause removal of the concerned material region from the computational model. This equation is generally intended for eliminating numerical difficulties arising either from highly distorted Lagrangian elements (within a finite-element framework) or from the cells containing highly degraded material. Since material removal, as modeled by the erosion equation, is a non-physical process, the extent of such removal must be limited to preserve physical fidelity of the computational model.

To summarize, the EOS along with the strength and failure models enables assessment of the evolution of the complete stress tensor during a transient non-linear dynamics analysis (like the one dealing with the transverse impact of a high-speed projectile onto a fused-silica target plate). Such an assessment is needed in order to solve the governing (mass, momentum, and energy) conservation equations. It is important to note that separate treatments of the pressure and the deviatoric stress enable inclusion of the non-linear effects in the EOS. Generally these effects are shock-related but, in the present work, they will be, at least partly, attributed to the high-pressure-/ballistic-impact-induced devitrification and permanent densification in fused-silica.

Original JH2 Material Model

The JH2 model is a phenomenological model which postulates the existence of two terminal glass states: (a) an intact material and (b) a failed material. The two material states are weighted by a single scalar variable called damage, D, the evolution of which is governed by an inelastic (plasticity-like) deformation model. In the remainder of this section, details are presented regarding the JH2 model components, i.e., EOS, the strength model, the failure model, and the erosion equation.

Equation of State The JH2 model utilizes a polynomial EOS, which, for a damage-free material, takes on the following form:

$$P = K_{1} \mu + K_{2} \mu^{2} + K_{3} \mu^{3} ,\quad \mu > 0\quad ({\text{hydrostatic}}\;{\text{compression}})$$

(1)

and

$$P = K_{1} \mu ,\quad \mu < 0\quad ({\text{hydrostatic}}\;{\text{tension}}),$$

(2)

where the degree of compression is μ = ρ/ρρ ₀·ρ ₀ − 1, ρ and ρ ₀ are the current and reference mass-densities, and K ₁ (the bulk modulus), K ₂, and K ₃ are material-specific constants.

After glass has begun to accumulate damage (i.e., when the extent of damage is no longer zero, D > 0), Eq 1 has to be upgraded to include the effect of bulking. Bulking is a phenomenon associated with the fact that fragments of fractured materials are not generally fully conformable, and consequently, fractured material is associated with a larger volume (a lower density at a constant pressure) than the damage-free material. Thus, to reach the same degree of compression μ, an additional pressure ΔP must be applied to the damaged material. The bulking-modified polynomial EOS is then given by Ref 23:

$$P = K_{1} \mu + K_{2} \mu^{2} + K_{3} \mu^{3} + \Delta P,\quad \mu > 0,$$

(3)

where the bulking-induced pressure increment, ΔP, is determined from energy considerations and varies from zero at D = 0 to ΔP _max at D = 1.0. Assuming that a fraction 0 < β < 1 of the deviatoric strain energy decrease ΔU (due to the damage-induced decrease in deviatoric stresses, or more precisely in the material damage resistance) is converted to an increase in hydrostatic internal energy, the bulking-induced pressure increment ΔP at a time t + Δt can be represented in terms of ΔP at the time t as

$$\Delta P(t + \Delta t) = - K\mu (t + \Delta t) + \sqrt {(K_{1} \mu (t + \Delta t) + \Delta P(t))^{2} + 2\beta K_{1} \Delta U} ,\quad \mu (t + \Delta t),$$

(4)

where ΔU is the decrease in deviatoric strain energy due to damage-induced damage resistance reduction, and is given by

$$\Delta U = U_{t} - U_{t + \Delta t} = \frac{{\sigma_{t}^{2} - \sigma_{t + \Delta t}^{2} }}{6G},$$

(5)

where σ denotes the actual (i.e., not a normalized) damage resistance, and G the (damage-invariant) shear modulus.

Schematics of the JH2 EOS functional relationships for intact, fractured, and damaged materials are shown in Fig. 4(a). Examination of Eq 1 to 5 reveals that the JH2 EOS model includes the following parameters: ρ ₀, K ₁, K ₂, K ₃, and β.

Fig. 4

Schematics pertaining to the JH2 model: (a) equation of state; (b) strength model; and (c) failure model

Strength Model The JH2 strength model (Ref 23, 24) utilizes (a) the von Mises yield criterion; (b) normality flow rule; and (c) a pressure and strain rate-hardening constitutive relation. Since the von Mises yield criterion and the normality flow rule are well established and frequently used, details regarding their governing equations will not be presented here. However, the JH2 constitutive relation is fairly unique and will be overviewed in the remainder of this section.

For convenience, the JH2 constitutive relations utilize normalized quantities denoted by an asterisk. For example, the normalized damage resistance (also referred to as the yield strength hereafter) σ* is a ratio of the yield strength to the deviatoric part, σ _HEL, of the Hugoniot Elastic Limit, HEL. In other words, σ _HEL is the deviator-based effective stress component of the (total) uniaxial-strain yield strength, HEL. Next, σ* is defined as the following rule of mixtures of its intact and damaged counterparts:

$$\sigma^{ * } = \sigma_{i}^{ * } - D(\sigma_{i}^{ * } - \sigma_{f}^{ * } ),$$

(6)

where subscripts i and f are used to denote intact and fractured material states. The normalized (pressure- and strain rate-dependent, ideal-plastic) yield strengths of the damage-free material, σ _i *, and the fractured material, σ _f *, are respectively given by

$$\sigma_{i}^{ * } = A(P^{ * } + T^{ * } )^{N} (1 + C\,\ln \,\dot{\varepsilon }^{ * } )$$

(7)

$$\sigma_{f}^{ * } = B(P^{ * } )^{M} (1 + C\,\ln \,\dot{\varepsilon }^{ * } ),$$

(8)

where A, B, C, M, and N appearing in Eq 7, 8 are all material-specific constants, while P ^* and T ^* are, respectively, defined as

$$P^{ * } = \frac{P}{{P_{\text{HEL}} }}$$

(9)

and

$$T{}^{ * } = \frac{T}{{P_{\text{HEL}} }},$$

(10)

where P and T are the actual pressure and the maximum hydrostatic tensile pressure (defined as a positive quantity) that the fused-silica material can withstand, respectively, and P _HEL is the pressure at the Hugoniot Elastic Limit.

As shown in Ref 23, P _HEL and σ _HEL are related to the (uni-directional shockwave-based) uniaxial-strain compressive-yield strength, HEL, as

$${\text{HEL}} = P_{\text{HEL}} + \tfrac{2}{3}\sigma_{\text{HEL}} = K_{1} \mu_{\text{HEL}} + K_{2} \mu_{\text{HEL}}^{2} + K_{3} \mu_{\text{HEL}}^{3} + \tfrac{2}{3}\tfrac{{2G\mu_{\text{HEL}} }}{{1 + \mu_{\text{HEL}} }}$$

(11)

Equation (11) shows that both P _HEL and σ _HEL can be determined from the known HEL and μ _HEL (degree of compression at the elastic limit). Finally, the dimensionless material strain rate, $\dot{\varepsilon }^{*}$, appearing in Eq 7 and 8 is defined as

$$\dot{\varepsilon }^{ * } = \frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }},$$

(12)

where $\dot{\varepsilon }$ is the actual equivalent strain rate and $\dot{\varepsilon }_{0}$ is the reference strain rate (typically set to 1.0 s⁻¹).

Schematics of the JH2 strength model in the normalized yield strength versus normalized pressure plane for intact, fractured, and damaged materials are shown in Fig. 4(b). Examination of Eq 6 to 12 reveals that the JH2 strength model includes the following parameters: A, B, C, M, N, σ _HEL, and P _HEL.

Failure Model The JH2 failure model (Ref 23, 24) is of a progressive character and the evolution/accumulation of damage in this model is defined as

$$D_{t + \Delta t} = D_{t} + \frac{{\Delta \varepsilon_{p,t + \Delta t} }}{{\varepsilon_{p,t + \Delta t}^{f} }},$$

(13)

where Δɛ _p is the increment in equivalent inelastic strain with an increment in loading and the failure strain ɛ ^f _p is a pressure-dependent equivalent fracture strain which is defined as

$$\varepsilon_{p}^{f} = D_{1} (P^{ * } + T^{ * } )^{{D_{2} }},$$

(14)

where D ₁ and D ₂ are material-specific constants.

Within the JH2 failure model, fracture occurs either when damage reaches a critical value of 1.0 or when negative pressure reaches a value of T. Fractured material has no ability to support any negative pressure, while its ability to support shear is defined by Eq 8.

A schematic of the JH2 failure model showing the effect of the pressure on the equivalent fracture strain is given in Fig. 4(c). Examination of Eq 13 and 14 reveals that the JH2 failure model includes the following parameters: D ₁ and D ₂.

Erosion Equation The JH2 failure model discussed above revealed that the “failed” elements do not completely lose their load-bearing capacity (at least with respect to the compression and shear). However, the resistance to deformation in such elements may be so low that they can readily acquire a large amount of deformation and significantly distort the associated finite elements. Excessively distorted elements may cause numerical problems, and are often removed from the model when a condition for the maximum allowable total equivalent strain is met. Since element removal is an unphysical process, care must be taken to ensure that the mass and the momentum of the removed elements is preserved at the instant of their removal. As will be discussed in greater detail in the next section, this is done in the present work by converting the continuum elements into particles. The erosion model contains only one parameter, ɛ _rem, the maximum allowable total equivalent strain.

Model Parameterization for Fused Silica Table 1 summarizes the parameterization for fused silica of the original JH2 model, i.e., the model which does not account for potential devitrification under high pressure and shear conditions encountered during a ballistic-impact event.

Table 1 Original Johnson-Holmquist-2 material model parameters for fused silica

Inclusion of High-Pressure-Induced Devitrification into the JH2 Material Model

Before the JH2 model can be modified to include the effects of devitrification, additional atomic-scale simulations, using the same methods and tools as those employed in Ref 16, had to be conducted. Two types of such simulations were conducted: (1) simulations of hydrostatic-pressure-loading/unloading; and (2) simulations of simple-shear-loading of the hydrostatic-pressure-preloaded fused silica. A brief description of these simulations is presented in the remainder of this subsection.

Hydrostatic Loading/Unloading Simulations

Within these simulations, the computational cell for fused silica [given in Fig. 3(a) of Ref 16] is subjected to a series of hydrostatic-compression loading-unloading cycles, where each subsequent loading cycle was associated with a somewhat higher peak pressure. These simulations resulted in two sets of results: (a) peak pressure versus degree of compression (under loading); and (b) peak pressure versus degree of irreversible compression (after unloading). Examples of these results are given in Fig. 5(a) and (b), respectively.

Fig. 5

(a) Pressure vs. degree of compression relationship associated with monotonic loading; and (b) peak pressure vs. degree of irreversible compression (after unloading)

Examination of the results depicted in Fig. 5(a) shows that

• (a) as the degree of compression initially increases, the pressure grows at an increasing rate up to a value of approximately 8.76 GPa;

• (b) as the compression increases beyond this point, the pressure first goes through an inflexion point, beyond which it grows at a decreasing rate, and then through another inflexion point, beyond which it again grows at an increasing rate; and

• (c) the pressure continues to grow at an increasing rate as compression increases.

The behavior of fused silica revealed in Fig. 5(a) suggests the occurrence of some kind of phase transition, which is initiated at the pressure of 8.76 GPa [point A in Fig. 5(a)], and appears to terminate at the pressure of 17.2 GPa [point B in Fig. 5(a)]. Examination of the molecular-level microstructure of fused silica after its exposure to very high pressures revealed the presence of stishovite-like topology. Thus, the phase transition in question appears to be devitrification of fused silica into a stishovite-like structure.

Examination of the results depicted in Fig. 5(b) and its comparison with the results depicted in Fig. 5(a) revealed that

• (a) once the pressure versus degree of compression begins to deviate from its initial behavior, unloading starts to produce residual compression. In other words, subjecting the material to pressure levels P > P _A  = 8.76 GPa produces permanent changes in the fused-silica microstructure;

• (b) as the applied pressure increases, the degree of residual compression also increases, first at a progressively higher rate, and subsequently at a progressively lower rate; and

• (c) once the pressure exceeds a value P > P _B  = 17.2 GPa, increase in the degree of residual compression ceases. This finding suggests that in this regime of loading, fused silica does not transform any further and the (transformed/devitrified) material is also stable and does not undergo any additional permanent changes.

Simple-Shear-Loading Simulations

Molecular-level simple-shear tests were carried out in order to assess the effect of the irreversible changes in the fused-silica microstructure and the residual degree of compression, observed in Fig. 5(b), on the material (shear) strength. Towards that end, once the unit cell is subjected to a sufficiently high level of pressure, and made to acquire the maximum level of residual compression, it is subjected to simple shear in small increments followed by energy minimization with respect to the atomic positions. To help prevent the computational crystal from settling into a nearby metastable higher-energy configuration, a 10,000-step 300 K NVT (N—number of particles, V—computational cell volume, T—temperature, all fixed) molecular dynamics (equilibration) run was introduced between the cell shearing and the energy minimization steps. This procedure yielded a plot of the potential energy increase (relative to that in the initial optimized computational cell) versus the shear angle of the computational cell. The shear angle gradient of the potential energy increase divided by the constant unit cell volume is then used to define the material shear strength. This procedure revealed that the shear strength of (partially) devitrified fused silica is higher by a factor of ca. 1.87 relative to the strength of fused silica in the initial state.

Modification of the JH2 Model

To account for the devitrification and permanent densification effects revealed by the results depicted in Fig. 5(a), (b), both the JH2 equation of state and the associated strength model are modified. Details of these modifications are presented in the remainder of this subsection.

EOS model Modification of the EOS entailed a number of steps including

(a) Functional representation of the P versus μ relationship depicted in Fig. 5(a). This was done by decomposing the P versus μ curve in Fig. 5(a) into the following three segments:

• (1) OA segment, within which the P versus μ functional relationship is represented by that for the initial fused silica, Eq 1, as

$$P_{OA} = K_{1}^{FS} \mu + K_{2}^{FS} \mu^{2} + K_{3}^{FS} \mu^{3} ,\,\,\,\,\mu > 0\,\,\,\,\,\,$$

(15)

where superscript FS is used to denote the fact that the EOS parameters refer to the original fused silica.

• (2) AB segment, within which the P versus μ segment shown in Fig. 5(a) is represented as a cubic-spline function; and

• (3) BC segment, which is assumed to correspond to the state of pure (highly deformed) stishovite, in which the following P versus μ functional relationship is used:

$$P_{BC} = K_{1}^{ST} \left( {\mu - \mu_{\text{irr}}^{\hbox{max} } } \right) + K_{2}^{ST} \left( {\mu - \mu_{\text{irr}}^{\hbox{max} } } \right)^{2} + K_{3}^{ST} \left( {\mu - \mu_{\text{irr}}^{\hbox{max} } } \right)^{3} ,\quad \left( {\mu - \mu_{\text{irr}}^{\hbox{max} } } \right) > 0,$$

(16)

where superscript ST is used to denote the fact that the EOS parameters refer to stishovite, and μ ^max_irr is the maximum degree of compression (which corresponds to complete devitrification of fused silica into stishovite); and

(b) Calculation of the pressure P _t+Δt corresponding to the value of the degree of compression at the end of a given time step, μ _t+Δt  = μ _t  + Δμ, is then done accordingly depending on which of the three (OA, AB or BC) segments μ _t+Δt lies, whether the μ _t+Δt is larger than the degree of compression ever experienced by the material point in question and whether the material point is under a state of (compressive) loading, unloading, or reloading as:

• (1) when μ _t+Δt is associated with OA and BC segments, then loading, unloading, and reloading are all defined using Eq 15 and 16, respectively; and

• (2) when μ _t+Δt is associated with AB segment, the way in which P _t+Δt is calculated is dependent on whether μ _t+Δt is larger than the maximum degree of compression, μ _max, ever experienced by the material point in question (loading) or not (unloading/reloading). In the case of loading, P _t+Δt is obtained from μ _t+Δt using the aforementioned P versus μ spline function representation for AB segment. On the other hand, in the case of unloading or elastic-reloading, P _t+Δt is given by the following relationship:

$$P_{t + \Delta t} = K_{1}^{AB} \left( {\mu - \mu_{\text{irr}} \left( {P_{\hbox{max} } } \right)} \right) + K_{2}^{AB} \left( {\mu - \mu_{\text{irr}} \left( {P_{\hbox{max} } } \right)} \right)^{2} + K_{3}^{AB} \left( {\mu - \mu_{\text{irr}} \left( {P_{\hbox{max} } } \right)} \right)^{3} ,\quad \mu - \mu_{\text{irr}} \left( {P_{\hbox{max} } } \right) > 0,$$

(17)

where superscript AB is used to denote the fact that the EOS parameters refer to the partially devitrified condition of fused silica associated with AB segment, and μ _irr(P _max) is given by tabulating the results depicted in Fig. 5(b). The EOS parameters appearing in Eq 17 are assumed to be given by the rule of mixtures of the corresponding parameters for the fused silica and stishovite as

$$K_{i}^{AB} \left( {P_{\hbox{max} } } \right) = \left( {1 - f_{\text{ST}}^{{}} \left( {P_{\hbox{max} } } \right)} \right)K_{i}^{\text{FS}} + f_{\text{ST}}^{{}} \left( {P_{\hbox{max} } } \right)K_{i}^{\text{ST}} ,\quad i = 1 - 3,$$

(18)

where the volume fraction of stishovite, which is controlled by the maximum pressure ever experienced by the material point in question, is given as

$$f_{\text{ST}}^{{}} \left( {P_{\hbox{max} } } \right) = \frac{{\mu_{\text{irr}}^{{}} \left( {P_{\hbox{max} } } \right)}}{{\mu_{\text{irr}}^{\hbox{max} } }}$$

(19)

The procedure outlined above ensures that, during loading, the pressure traces the P versus μ relationship depicted in Fig. 5(a), while during unloading and reloading, P versus μ is given by the non-linear elastic relationship of the polynomial type.

Strength model As indicated by the molecular-level simple-shear loading results described earlier, devitrification strengthens the material, and the intrinsic strength of devitrified glass is higher by a factor α ≈ 1.87 than that of the initial fused silica. To account for this finding, the JH2 strength model given by Eq 6 is modified by multiplying the right-hand side of this equation by a factor 1 − (α − 1)f _ST.

Implementation The modified JH2 model is next implemented in the material user subroutine, VUMAT, of the commercial finite-element program ABAQUS/explicit (Ref 25). This subroutine is compiled and linked with the finite-element solver and enables ABAQUS/explicit to obtain the needed information regarding the state of the material and the material mechanical response during each time step, for each integration point of each element. The essential features of the coupling between the ABAQUS/explicit finite-element solver and the VUMAT material user subroutine at each time increment at each integration point of each element can be summarized as follows:

• (a) The corresponding previous time increment stresses and material state variables as well as the current time-step deformation gradient are provided by the ABAQUS/explicit finite-element solver to the material subroutine. In the present work, the components of the strain tensor, damage variable D, a variable characterizing the extent of fused-silica → stishovite conversion, the maximum pressure ever experienced by the material point in question during loading, and one variable pertaining to the deletion status of the finite element are used as the state variables; and

• (b) Using the information provided in (a), and the functional relationships constituting the modified JH2 material model presented in the previous section, the material stress state as well as values of the material state variables at the end of the time increment is determined within the VUMAT and returned to the ABAQUS/explicit finite-element solver. In addition, the changes in the total internal and the inelastic energies (where appropriate) are computed and returned to the solver.

Fused-Silica Devitrification and Ballistic Limit

In the previous section, the JH2 model was modified to include the effects of high-pressure-/high-shear-induced devitrification on the (dynamic) mechanical response of fused silica. In this section, a simple transverse impact of a monolithic fused-silica target plate by an armor-piercing bullet is analyzed computationally in order to assess if the aforementioned modifications in the JH2 model have any significant effect on the temporal evolution and spatial distribution of damage within the fused-silica plate during impact and on the overall fused-silica-plate penetration resistance.

Computational Analysis

The transverse impact of the fused-silica target plate by the armor-piercing bullet is investigated using a Lagrangian, transient, non-linear dynamics finite-element analysis (FEA). Within such an analysis, the following should be specified: (a) geometrical model; (b) meshed model; (c) computational algorithm; (d) initial conditions; (e) boundary/loading conditions; (f) contact interactions; (g) material models; (h) computational tool; and (i) computational accuracy, stability, and cost. These items are briefly overviewed in the remainder of this subsection.

Geometrical Model

The geometrical model consists of (a) a circular-disk-shaped fused-silica target plate with dimensions R × H = 90 mm × 22 mm; and (b) an M855 armor-piercing bullet, having a diameter of 5.56 mm and a mass of ~4.0 g, consisting of a steel tip, a lead core, and a 0.5-mm-thick copper jacket. Due to the fact that only a normal (i.e., zero obliquity angle) impact is considered, the geometrical model possesses two vertical planes of symmetry and, hence, only one-quarter of the model, Fig. 6(a), needs to be analyzed explicitly.

Fig. 6

(a) Geometrical; and (b) meshed models for the transient non-linear finite-element analyses of the impact of a full-jacketed metal bullet onto a fused-silica target plate. Due to inherent symmetry of the problem, only one-quarter of the model is analyzed

Meshed Model

The fused-silica target plate is discretized using 70,720 six-node triangular-prism first-order continuum elements, while the bullet is meshed using 1955 four-node tetrahedron first-order continuum elements. A close-up of the finite-element mesh is depicted in Fig. 6(b). It is seen that, in order to improve the resolution of the deformation, damage, and devitrification fields, smaller finite elements are used in (a) the cylindrical portion of the target plate which will be affected by the advancing armor-piercing bullet; and (b) the surface sections of the bullet.

Computational Algorithm

To ensure robustness of the computational analysis, all the calculations carried out in the present work utilized a transient, displacement-based, purely Lagrangian, conditionally stable, dynamic explicit finite-element algorithm.

Initial Conditions

The target plate is assumed to be initially stress-free and stationary. While the bullet is also assumed to be stress-free, it is assigned a uniform downward (i.e., in the −z-direction) initial velocity.

Boundary/Loading Conditions

Due to the fact that only one-quarter of the model was analyzed explicitly, the symmetry boundary condition had to be applied over the faces of the quarter-model coinciding with the symmetry planes. In addition, to simulate simple all-around simple-supporting conditions, the rim nodes on the bottom face of the target plate are fixed in the z-direction, and left unconstrained in the in-plane x- and y-directions. Also, to properly simulate the propagation of the impact-induced shock waves in a fused-silica structure larger than the target plate, transmit boundary conditions are prescribed over the outer transverse faces of the target plate.

Material Models

The three metallic materials (steel, lead and copper) present in the bullet are modeled using a linear equation of state, the Johnson-Cook strength model, the Johnson-Cook failure model, and an erosion algorithm based on the maximum allowable instantaneous geometrical strain. Considering the fact that these material models were reviewed in our recent work (Ref 26-31), they will not be discussed any further here. As far as the fused-silica material model is concerned, the modified JH2 model (developed in the previous section) is employed. In a few of the analyses, the original JH2 material model for fused silica was also used. This model is generally parameterized at pressures which are not high enough to induce fused-silica devitrification. Here, the original JH2 model is used in the pressure range in which fused-silica devitrification takes place. By comparing the results obtained using this model and the modified JH2 model, it was possible to assess the effect of fused-silica devitrification on the ballistic-penetration resistance of this material.

Contact Interactions

At the beginning of the simulation, only contact interactions between the bullet and the target plate exist. However, as the fused-silica plate begins to experience damage and fragments are created, additional contacts involving these fragments must be taken into account.

Normal interactions are modeled using a “penalty” contact method, within which the interpenetration of the surfaces is resisted by linear spring forces/contact pressures with values proportional to the depth of penetration. These forces, hence, tend to pull the surfaces into the (no-penetration) equilibrium position. Contact pressures are not transmitted between the interacting bodies unless the nodes on the (node-defined) “slave surface” of one body contact the (element-defined) “master surface” of the other body. There is no limit to the magnitude of the contact pressure that could be transmitted when the surfaces are in contact. Transmission of shear stresses across the contact interfaces is defined in terms of a static and a kinetic friction coefficient as well as an upper-bound shear stress limit (a maximum value of shear stress which can be transmitted before the contacting surfaces begin to slide).

Computational Tool

All the calculations carried out in the present work were done using ABAQUS/explicit, a general purpose finite-element program (Ref 25). Within this tool, the problem at hand (formulated in terms of a set of mass, momentum, and energy conservation differential equations along with the material constitutive relations, initial boundary and contact/interaction conditions) is solved numerically using the aforementioned finite-element algorithm.

Computational Accuracy, Stability, and Cost

A standard mesh sensitivity analysis was carried out (the results not shown for brevity) in order to ensure that the results obtained are accurate, i.e., insensitive to the size of the elements used.

Due to the conditionally stable nature of the explicit finite-element analysis used, the maximum time increment during each computational step had to be lower than the attendant stable time increment. To keep the computational cost reasonable while ensuring accuracy and stability of the computational procedure, a mass-scaling algorithm is used. This algorithm adaptively adjusts material density in the critical stable-time-increment-controlling finite elements without significantly affecting the computational analysis results. A typical transient non-linear dynamics analysis of a VMT required 15 min to 2 h of (wall-clock) time on a 12-core, 3.0 GHz machine with 12 GB of memory.

Results and Discussion

In this section, the main results pertaining to the transverse-normal impact of the M855 armor-piercing projectile onto the fused-silica target plate are presented and discussed. Since fused-silica devitrification takes place only at sufficiently high pressures and the peak pressure of the fused-silica target plate impacted by the projectile scales directly with the projectile incident velocity, the results at one representative low projectile incident velocity (the condition which does not result in fused-silica devitrification) and the results at one representative high projectile incident velocity (the condition which results in fused-silica devitrification) are presented and discussed. In each case, two sets of results are presented (unless they are practically indistinguishable), one for the original and the other for the modified JH2 fused-silica material models. This approach enabled quantification of the effect of fused-silica devitrification on its ballistic-penetration resistance.

Projectile Incident Velocity 1000 m/s

The temporal evolution and spatial distribution of the hydrostatic pressure within the fused-silica target plate for the case of the projectile incident velocity of 1000 m/s and the original JH2 fused-silica material model is displayed in the right half of Fig. 7(a) to (d). The corresponding (mirrored across the symmetry plane) results for the case of the modified JH2 material model are presented in the left half of Fig. 7(a) to (d). It is seen that the corresponding results obtained using the two JH2 models are essentially identical. This finding suggests that at this projectile incident velocity, the attendant pressures are too low to initiate fused-silica devitrification.

Fig. 7

Temporal evolution and spatial distribution of the hydrostatic pressure within the fused-silica target plate for the case of the projectile incident velocity of 1000 m/s at post-impact times of: (a) 8 μs; (b) 22 μs; (c) 36 μs; and (d) 50 μs. In each part, the results shown on the left and the right halves correspond to the cases of the modified and the original JH2 material models, respectively

It should be noted that in Fig. 7(a) to (d), for improved clarity, the projectile is not shown. Also, the finite elements within the impacted region of the fused-silica target plate and the surrounding region are adaptively (i.e., when their distortion reaches a critical level) converted into the smoothed particle hydrodynamics (SPH) particles. Traditionally, to avoid numerical problems caused by highly distorted elements, such elements are removed from the analysis (an unphysical process which compromises the accuracy of the results). The conversion of such elements into SPH (interpolation pseudo-)particles is a significant improvement since these particles continue to provide the material they represent with structural and inertial deformation resistance. Within the ABAQUS viewer, SPH particles are shown as circles regardless of the orientation of the computational model.

Examination of the results displayed in Fig. 7(a) to (d) reveals the following:

• (a) for all the simulation times covered in these figures, the highest pressures are found in the region of the fused-silica target plate surrounding, laterally, the penetration hole; (b) at the shortest simulation time, Fig. 7(a), a high-pressure region is also found underneath the advancing projectile. However, by the next simulation time, Fig. 7(b), the compressive pressure wave emitted from the projectile tip arrives to, and reflects as a tensile pressure wave from, the target plate back face;

• (b) as the wider cylindrical portion of the projectile enters the penetration hole, it pushes the fused-silica material outward, causing the development of an increased high-pressure region in the top portion of the target plate, Fig. 7(b) to (d); and

• (c) as the projectile begins to leave the penetration hole, high-pressure regions surrounding the hole begin to relax, Fig. 7(c) and (d).

The temporal evolution of the projectile (back face) velocity for the cases of the original and the modified JH2 material models, and the projectile incident velocity of 1000 m/s are depicted in Fig. 8. Examination of the results depicted in Fig. 8 reveals that, as expected, the two sets of results are effectively identical.

Fig. 8

Temporal evolution of the projectile (back face) velocity for the case of the original and modified JH2 material models, with projectile incident velocity of 1000 m/s

Projectile Incident Velocity 2000 m/s

The temporal evolution and spatial distribution of the stishovite volume fraction and hydrostatic pressure within the fused-silica target plate for the case of the projectile incident velocity of 2000 m/s and the original JH2 fused-silica material model is displayed in the left and right halves of Fig. 9(a) to (d), respectively. The corresponding results, but for the case of the fused-silica represented using the modified JH2 model, are given in Fig. 10(a) to (d). At this projectile incident velocity, the attendant pressures are sufficiently high to initiate fused-silica devitrification. Again, the finite elements are adaptively converted into the SPH particles.

Fig. 9

Temporal evolution and spatial distribution of the stishovite volume fraction (left half) and hydrostatic pressure (right half) within the fused-silica target plate for the case of the projectile incident velocity of 2000 m/s and stable fused-silica target plate, at post-impact times of (a) 4 μs; (b) 11 μs; (c) 18 μs; and (d) 25 μs

Fig. 10

Temporal evolution and spatial distribution of the stishovite volume fraction (left half) and hydrostatic pressure (right half) within the fused-silica target plate for the case of the projectile incident velocity of 2000 m/s and devitrified fused-silica target plate, at post-impact times of (a) 4 μs; (b) 11 μs; (c) 18 μs; and (d) 25 μs

Examination of the results displayed in Fig. 9(a) to (d) reveals the following:

• (a) since the original JH2 model used does not allow fused-silica devitrification, the volume fraction of stishovite formed, as shown in Fig. 9(a) to (d), is zero;

• (b) for all the simulation times covered in these figures, the highest pressures are found in the region of the fused-silica target plate surrounding, laterally, the penetration hole;

• (c) at the shortest simulation time, Fig. 9(a), a high-pressure region is also found underneath the advancing projectile. However, by the next simulation time, Fig. 9(b), the compressive pressure wave emitted from the projectile tip arrives to, and reflects as a tensile pressure wave from, the target plate back face; and

• (d) as the wider cylindrical portion of the projectile enters the penetration hole, it pushes the fused-silica material outward, causing the development of an increased high-pressure region in the top portion of the target plate, Fig. 9(b) to (d).

Comparison of the results displayed in Fig. 9(a) to (d) and Fig. 7(a) to (d) reveals the effect of the incident projectile velocity on the structural and the failure response of fused silica in the case when devitrification of this material is not permitted. It is seen that

• (a) higher projectile incident velocities increase the size of the damage region, as represented by the number of target plate continuum elements converted to SPH particles;

• (b) the pressures in the target plate region surrounding the penetration hole are generally higher for the case of the higher projectile incident velocity; and

• (c) at the lower projectile incident velocity, the projectile causes both penetration and elastic bending of the target plate. Consequently, once the projectile has left the penetration hole, the target plate springs back, Fig. 7(c) and (d). In the case of the higher projectile incident velocity, on the other hand, the projectile mainly penetrates the target plate and very little target plate spring-back is observed, Fig. 9(c) and (d).

Examination of the results displayed in Fig. 10(a) to (d) reveals

• (a) formation of stishovite in the target plate region surrounding the penetration hole, Fig. 10(a) to (d) (left half); and

• (b) points (b)-(d) made for the results shown in Fig. 9(a) to (d) are still valid here.

Comparison of the results displayed in Fig. 9(a) to (d) and 10(a) to (d) reveals the effect of fused-silica devitrification on its structural and failure response during impact by the same type of projectile with the same (2000 m/s) incident velocity. It is seen that

• (a) the extent of damage surrounding the penetration hole is reduced in the case of fused-silica undergoing devitrification, e.g., Fig. 9(b) versus 10(b). This finding is expected since devitrification competes with the fused-silica deformation/fracture processes; and

• (b) high-pressure regions are more closely localized to the walls of the penetration hole in the case of the fused-silica undergoing devitrification, e.g., Fig. 9(c) versus 10(c). This finding is also expected since, as shown in Fig. 5(a), once the devitrification process begins, the accompanying pressure levels are lower (compared to the case of fused-silica).

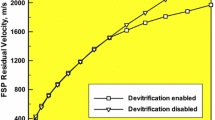
The temporal evolution of the projectile (back face) velocity for the case of the original and modified JH2 material models, and the projectile incident velocity of 2000 m/s, is depicted in Fig. 11. Examination of the results depicted in Fig. 11 reveals that fused-silica devitrification enables more extraction of the kinetic energy from the projectile. This results in lowering residual velocity of the projectile from 1971 to 1963 m/s. On the absolute scale, the effect is quite small (8 m/s). On the other hand, in relative terms, the effect is significant ($\frac{1971 - 1963}{2000 - 1971} \times 100 = 27.6\%$).

Fig. 11

Temporal evolution of the projectile (back face) velocity for the case of the original and modified JH2 material models, with projectile incident velocity of 2000 m/s

Brief Discussion

The results presented in the previous subsection clearly revealed that, if the projectile velocity, and thus, the pressure in the target plate region surrounding the penetration hole, is sufficiently high, fused-silica devitrification can lead to measurable improvements in the glass ballistic-resistance. It should be noted that this effect is an outcome of the competition between two opposing phenomena: (a) since devitrification results in a reduction of pressure, at a given level of compression, and the strength of the JH2-intact-phase of the fused-silica is affected by the pressure level, devitrification tends to promote inelastic deformation (and thus fracture) of fused-silica; and (b) since the result of fused-silica devitrification is stishovite, which possesses substantially higher shear strength than fused-silica, devitrification also contributes to an increase in the strength of the JH2-intact-phase of the fused-silica, and thus reduces the tendency for fused-silica inelastic deformation/fracture. The fact that improvements in the fused-silica ballistic-penetration resistance are observed as a result of its devitrification then suggests that the contribution of the second phenomenon to the material strength overrides the contribution of the first phenomenon.

Another way to analyze the outcome of the projectile/target plate interaction in the case of the non-devitrified and devitrified fused-silica is to consider partitioning of the energy transferred from the projectile to the target plate during impact. In the case of stable fused-silica, the target plate acquires three nonzero components of its energy: (a) kinetic energy; (b) strain energy; and (c) friction-induced dissipated energy. In the case of the devitrified fused-silica, on the other hand, the target plate acquires an additional component of its energy, that is, the zero-stress internal energy. This energy is associated with the transformation of the amorphous SiO₂ into a crystalline high-energy form of SiO₂. Furthermore, zero-stress internal energy may become a significant fraction (approximately 20%, in the present case) of the total energy acquired by the target plate. Since zero-stress internal energy is associated with fused-silica devitrification and, hence, is not present in the case of stable fused silica, one would expect an increase in the target plate penetration resistance in the case of fused silica undergoing devitrification.

Summary and Conclusions

Based on the results obtained in the present work, the following main conclusions can be made:

• (1) Molecular-level simulations revealed that fused-silica, when subjected to high pressures, can undergo devitrification which results in the formation of high-density stishovite. This process is facilitated by the application of shear stresses which help lower the energy barrier associated with the fused-silica → stishovite transition state.

• (2) To include the aforementioned devitrification effects into the fused-silica constitutive response, the classical Johnson-Holmquist-2 (JH2) model was appropriately modified. This was done by using the molecular-level computational results to infer the nature and extent of the devitrification process, as a function of the applied pressure, as well as the effect of the formed stishovite on the material (shear) strength.

• (3) The modified JH2 model was used within a transient, non-linear dynamics finite-element analysis of a fused-silica target plate normal impact by an armor-piercing bullet, in order to assess the potential devitrification-induced improvements in the fused-silica ballistic limit. To help with this assessment, a parallel set of computational analyses was carried out in which the original JH2 fused-silica material model was used, the model which does not account for the pressure-induced devitrification and strengthening.

• (4) The results obtained revealed that only when the bullet incident velocity and, thus, the impact-generated pressures within the fused-silica target plate are sufficiently high, can the fused-silica devitrification process improve ballistic-penetration resistance of fused-silica. Furthermore, when the degree of devitrification is high, as observed at the highest bullet incident velocities, the effects of devitrification on the ballistic-penetration resistance are considerable.