Introduction

Prediction of mechanical properties such as hardness after heat treatment of alloys can help engineers in determination and designing of quenching systems by which the desired properties are to be obtained. There are several methods in dealing with prediction of mechanical properties such as strength in heat-treated alloys. One of the methods has been developed for prediction of strength in quenched-tempered aluminum alloys. The technique is based on the value of average cooling rate at the critical temperature range (between 400 and 290 °C for aluminum alloys) (Ref 1). The average cooling rate is determined by dividing the 200 °F (93 °C) temperature difference by the corresponding time difference, in seconds. It is known the strength of the alloys is increased when an increase in average cooling rate is occurred (Ref 1).

Another important method in dealing with the effect of cooling rate on mechanical properties such as hardness in quenched-tempered aluminum alloys and quenched steel parts is quench factor analysis (QFA). The method was first developed by Evancho and Staley (Ref 2) in order to predict the mechanical properties of quenched-tempered aluminum alloys. By combining the cooling curves at each point and Time-Temperature-Property (TTP) curve, desired property is calculated. In addition to aluminum alloys, QFA has been successfully applied to predict the hardness of some quenched steel parts (Ref 3-7). For plain carbon steels such as 1045 steel, it was shown that the accuracy of the method for accurate prediction of hardness is reduced with reducing hardness (Ref 7). Also Kianezhad and Sajjadi (Ref 8) developed a modified method from QFA and improved the hardness prediction of a quenched steel part.

Another method for the prediction of mechanical properties of heat-treated alloys is artificial neural networks (ANNs). Implementing ANNs has introduced a new methodology in several applications of engineering materials including prediction of mechanical properties of metals and alloys. Prediction of fatigue crack growth rates (Ref 9), hardness in metal matrix composites (Ref 10), tensile behavior of carbon steels (Ref 11), and formability analysis (Ref 12) are some of the applications of neural computations.

In this paper, the accuracy of QFA in the prediction of hardness at different points of quenched CK60 steel parts was evaluated. Moreover, based on the average cooling rate at the critical temperature range and using the ANNs, the hardness related to each cooling rate was calculated. At the end, accuracy of the two methods was compared.

Experimental Procedure

In the current study, samples of CK60 steel with various shapes and thicknesses were used. The chemical composition of the alloy used in this research was determined by optical emission spectroscopy (OES).

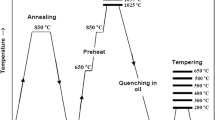
Longitudinal holes were drilled in the samples with different shapes at different points of the samples, and K-type thermocouples were placed in the holes to measure the temperature variations of the points during quenching. Figure 1 shows a schematic illustration of a cylindrical sample and the K-type thermocouples inserted at different points of the sample. In order to prevent the water penetration into the holes, the holes were filled with fireproof gypsum. The samples were austenitized at 830 °C for 50 min and then quenched in different environments, such as water and oil with different temperatures, soapy water, etc. Cooling curve for each point of the samples was determined using a data acquisition set (Advantech-USB4718) capable of recording ten different temperatures per second. In order to ensure the accuracy of the results, each experiment was repeated three times. The hardness of each point was measured on Vickers scale (HV30) using the hardness tester set model Avery-Dennison. To study the relation of microstructure to hardness, the samples were ground, polished, and then etched by Nital 2% etchant. Finally, the microstructure of each point of the quenched samples was studied using optical microscopy.

Fig. 1
figure 1

Schematic of round samples and K-type thermocouples at different points of the sample

Full size image

Results and Discussion

Quench Factor Analysis (QFA)

The chemical composition of the steel used in this study, as determined by OES, is C = 0.64, Si = 0.27, Mn = 0.9, P = 0.015, S = 0.011, and Fe = 98.16 wt.%. As mentioned before, QFA was first developed by Evancho and Staley (Ref 2) in the early 1970s to predict the effect of continuous cooling rate on the yield strength and corrosion resistance of wrought aluminum alloys. The technique provides a single value that correlates the cooling rate and cooling curve to the transformation rate of a particular alloy being quenched (Ref 13).

The basic theory for QFA is referred to the Johnson-Mehl-Avrami-Kolmogorov (JMAK) equation as shown in Eq 1 (Ref 14):

$$ X = 1 - \exp \left( { - kt} \right)^{n} , $$
(1)

where X is the transformed volume fraction, n is Avrami exponent (constant), and k is a temperature-dependent constant. For isothermal precipitation kinetics for aluminum alloys, Evancho and Staley (Ref 2) showed this equation can be re-written as below:

$$ X = 1 - \exp \left( {\frac{ - t}{k}} \right), $$
(2)

where t is time (second), and the value of k is estimated from the following equation developed by Evancho and Staley (Ref 2):

$$ k = \frac{{C_{T} }}{{k_{1} }} = - k_{2} { \exp }\left( {\frac{{k_{3} }}{{RT\left( {k_{4} - T} \right)^{2} }}} \right){ \exp }\left( {\frac{{k_{5} }}{RT}} \right), $$
(3)

where C T is the critical time required to form a constant amount of diffusion phases (ferrite or pearlite) (s), k 1 is a constant which equals to the natural logarithm of the untransformed fraction (1—the fraction defined by the C-curve) or equals to −0.00501, k 2 is a constant related to the reciprocal of the number of nucleation sites (s), k 3 is a constant related to the energy required to form a nucleus (J/mol), k 4 is a constant related to the solvus temperature (for steels equal to Ar3 temperature line versus K), k 5 is a constant related to the activation energy for diffusion (J/mol), T is temperature (K), and R = 8.3143 (J/mol K) (Ref 2, 15, 16).

The values from k 2 to k 5 define a C-curve showing TTP relationship similar to the TTT curve for steels (Ref 3, 17). All of the constants are calculated using iteration method. By fitting cooling curve of each point of specimen on the C-curve, the corresponding hardness of the point is obtained. In order to use this technique, first the incremental quench factor (q) is calculated for each time interval in the cooling process according to Eq 4 (Ref 17):

$$ q = \frac{\Delta t}{{C_{T} }} $$
(4)

The incremental quench factor represents the ratio of holding time of steel at a particular temperature to the time required for 0.5% transformation at that temperature (Ref 3). The value of cumulative quench factor is then calculated by summation of the q i over the critical temperature range (between Ar3 and M s for steels) according to Eq 5 (Ref 3):

$$ Q = \sum {q_{i} = \sum\limits_{{M_{s} }}^{{{\text{Ar}}_{3} }} {\frac{\Delta t}{{C_{\text{Ti}} }}} } $$
(5)

Figure 2 schematically shows the calculation of Q value. The quench factor can be related to the hardness of as-quenched steel according to Eq 6 (Ref 3):

$$ P = P_{ \hbox{min} } + \left( {P_{\hbox{max} } - P_{\hbox{min} } } \right)\exp \left( {k_{1} Q} \right), $$
(6)

where P min, and P max. are the minimum and maximum hardness of steel, as measured after cooling in furnace and cold brine, respectively, k 1 is ln(0.995) = −0.00501, and Q is quench factor.

Fig. 2
figure 2

Calculation of the Q value

Full size image

Table 1 represents k 2 to k 5 constants related to CK60 steel. Also, Fig. 3 shows the C-curve for this steel which was obtained by placing different temperatures between AC3 and M s at C T equation. As can be seen from the figure, the critical temperature range (which the sensitivity of the alloy to create the diffusional phases such as pearlite is maximum) for the CK60 steel is between 450 and 650 °C.

Table 1 CK60 steel C(T) curve coefficients
Full size table
Fig. 3
figure 3

Schematic diagram of TTP curve for CK60 steel

Full size image

Figure 4 shows some cooling rate curves related to the samples cooled in different environments. The accuracy of the model has been evaluated in Fig. 5, where the experimental results are illustrated versus the model prediction. The deviation from continues line, which represents the accuracy of the model, increases when the hardness declines. Thus, the model works much precisely at higher values of hardness. Figure 6 shows microstructures of different points with different hardness values. The white areas in the figure represent the martensitic phases, while the black areas represent the pearlitic structure. Depending on the cooling rate, the amount of the phases formed in the samples is different. The amount of each phase was determined using image analyzer and is summarized in Table 2. It can be seen from the Table that there are different phases in quenched steel parts. The results showed that the accuracy of the method in accurate prediction of the hardness is limited to the dominant structure. The dominant phase in the steel is martensite. Thus, the method is proper for prediction of accurate hardness in steels at specific ranges of the hardness.

Fig. 4
figure 4

Cooling rates curves related to different environments

Full size image
Fig. 5
figure 5

Variation of actual hardness versus predicted hardness of different points determined by QFA

Full size image
Fig. 6
figure 6

The microstructures related to the different points with different hardness values

Full size image
Table 2 The amount of each phase produced in different points and the related harness values
Full size table

Artificial Neural Networks (ANNs)

ANN method is considered as a useful soft computational tool, which is used to simulate a wide range of different engineering cases with high prediction accuracy. Neural network has inspired by human nervous mechanism and has the power of learning directly by examples without any predefined relation. In addition, ANNs can perform the non-linear computations when an exact analytical solution is very complicated to achieve (Ref 18). A neural network is a system consisting of many linked units called neurons or nodes. Each neuron in neural network receives input from several others. The neural system generally consists of three parts connected to each other: input layer, hidden layer, and output layer. The input layer includes the primary data. The primary information is entered to the input layer. No processing operation happens on this layer. In the hidden layers, training and testing actions take place. It is so-called because its outputs are invisible. The number of neurons should be determined according to the necessities of the problem in the layer of the neural networks. Finally, the processed data present in the output layer.

In this study, the feed-forward back-propagation type of ANNs is used. Back-propagation algorithm has an outstanding capability of training networks in order to find logical relation between inputs and outputs. The tangent sigmoid transfer function (tansig) for the hidden layers and linear transfer function (purelin) for the output layer were utilized. Different structural combinations for hidden layers were examined, and finally, the architecture of two hidden layers with eight and three neurons was chosen. Multi-Layer Perceptron neural network uses a gradient descent algorithm to minimize the mean square error between the computed outputs and the targets (Ref 19). The input data were normalized before training, and at last for representing the actual hardness and calculating accurate errors, denormalization was carried on. Normalization action means putting the datasets in a specific range so that it can give off maximum sensitivity and performance in training, regarding the training function of neural computation.

First step of the calculation before using the two mentioned approaches is to standardize all the input data to values in special range, and the last step is the de-standardization of outputs. The first action is done to assure having sensitivity and accuracy for network, and the purpose of the second one is to calculate the actual desired values and achieving real errors. In this study, standardization was carried out using the below formulation which puts data in a range with mean and standard deviation of 0 and 1 (Eq 7), respectively.

$$ X({\text{normal}}) = \frac{{X({\text{actual}}) - X({\text{mean}})}}{{X({\text{STD}} - {\text{DEV}})}}, $$
(7)

where X (actual) is the actual parameter, and X (mean) and X (STD-DEV) are the mean values of all data and standard deviation of actual parameters, respectively, which produce X (normal) or final standardized parameter as an input to the ANN structure.

In order to predict the hardness for each point of the heat-treated samples, the average cooling rate in the critical temperature range at each point of the samples was used. For steels, the critical temperature ranges from Ac3 to M s. There are two categories of data: one for the network learning called training data, and the other for evaluating the network called testing data. First, the network was trained by a fraction of experimental values (60 numbers) and then, as a result of neural computation, an assessment between experimental and calculated hardness was done. Figure 7 shows the neural network results and the actual trends of the hardness as a result of changing the average cooling rate at a specific range with an acceptable fitting between data. Following this step, a regression plot of harness values was drawn. The regression plot showed the high degree of accuracy of neural network in predicting the experimental results in all ranges of cooling rates (Fig. 8). It should be mentioned that the regression is R 2 = 0.9907 for the curves.

Fig. 7
figure 7

The predicted and experimental trends of hardness versus cooling rate obtained using neural network analysis

Full size image
Fig. 8
figure 8

Regression analysis between the neural networks and target results

Full size image

The results show that the accurate prediction of the hardness in whole range of the hardness and different structures can be achieved using ANNs. Also, unlike the QFA in which the accurate prediction of the hardness is limited to the dominant phase (martensite) formed at the steel, the ANNs are able to predict properties at different phases formed in quenched steel parts.

Conclusions

In this research, the accuracy of two different methods for prediction of hardness of as-quenched CK60 is evaluated. It was shown that

  1. (1)

    The accuracy of the QFA method in prediction of the hardness at quenched CK60 steel parts is limited, and accuracy of the method is reduced by reducing the hardness.

  2. (2)

    Based on the C-curve related to CK60 steel, the critical temperature range for the CK60 steel is between 450 and 650 °C.

  3. (3)

    The ANNs are a prominent method for accurate prediction of hardness in steel parts.

  4. (4)

    Unlike QFA, the ANN method can predict the accurate hardness in whole range of hardness and different phases which formed in quenched steel parts.