Soft-Sensing Model for Submerged Arc Furnace Electrode Current Based on Machine Learning

Abstract

Electrode current plays a significant role in control of submerged arc furnaces. However, it is difficult to measure the values directly. Recent studies have expanded the available information on current distribution of submerged arc furnaces, thus enabling the soft-sensing model for submerged arc furnace electrode current to be constructed. The present study aimed to establish a soft-sensing model for submerged arc furnace electrode current. The study consisted of the establishment of the mechanism model, identification of the mechanism model parameters, compensation of the mechanism model errors, and update of the soft-sensing model. The main conditions considered in the mechanism model include operating resistance, short network resistance and inductance, and electrode depth. The innovation of this study is that a dual particle swarm optimization algorithm with information exchange is proposed to ensure the speed and accuracy of mechanism model parameter identification. The experimental results demonstrate that the soft-sensing model can predict the electrode current with high accuracy. Compared with the traditional method using the transformation ratio of the transformer and the primary current, the prediction accuracy of the electrode current is improved by about 12 pct. The model update strategy can improve the adaptability of the model.

Introduction

Submerged arc furnace is the key metallurgical equipment for ferroalloy smelting. The ferroalloy produced by submerged arc furnace is more than 80 pct of the total.^[1] During the smelting process, the electrical energy is delivered into the furnace through the electrode. The ore is melted and reduced by arc heat of the end of the electrode and resistance heat between the material or slag.^[2] The operator adjusts the power delivered into the furnace and the temperature distribution of the molten pool by raising and lowering the electrode to change the value of the operating resistance. Therefore, the depth of the electrode inserted into the charge directly affects the power consumption and the melting temperature distribution of the furnace.^[3] Uniform distribution of melting temperature is helpful in keeping the melting rate of the charge consistent in the furnace. At the same time, it is useful in reducing the collapse of the furnace charge, the furnace gas detonation, and the electric energy consumption.^[4]

However, most of the key information about the smelting process cannot be measured directly due to the high temperature in the furnace. For example, the depth of the electrode inserted into the charge.^[5] The operator has to raise and lower the electrodes based on their experiences and electrode current.^[6] However, it is difficult to directly measure the electrode current because the electrode current of the submerged arc furnace is as high as tens of thousands of amperes. The operator has to estimate the electrode current based on the transformation ratio.^[7] Affected by many reasons, the electrode current estimation method based on transformation ratio cannot satisfy the accuracy, such as the voltage of each phase is not equal, the furnace body is asymmetric, the ore composition is not uniform, and the electrodes interact. Being in an unbalanced state for a long time will cause the temperature of one of the molten pools to be too high, and the deoxidized metal will be lost due to overheating. The temperature of the other phase molten pool is too low to reach the temperature for ore oxidized, and too much molten ore is converted into slag. Although Pan^[8] has successfully measured the secondary side current of electrical furnace transformers using the Rogowski coils. But in his research, Rogowski coil is installed at the copper tube on the secondary side of the transformer. The experimental measurement shows that the current measured by the Rogowski coil is basically the same as the estimation using the primary side current and the transformation ratio when it is installed at the copper tube of the secondary side of the transformer.^[9] In this type of installation, the current measured by the Rogowski coil is not the actual electrode current, because there is energy transfer between short network, and the compensation capacitor will affect the electrode current. When the Rogowski coil is installed near the electrode at the end of the short network, the harsh environment (such as high temperature, dust, short-term flashing, etc.) may easily cause damage to the Rogowski coil. This will limit the application of Rogowski coils in electrode current measurement of submerged arc furnaces. Furthermore, companies usually use multiple submerged arc furnaces of the same model to produce metals with the same raw materials. Therefore, it is meaningful to guide the production of other same model submerged arc furnaces that produce the same raw materials, if only need to install Rogowski coil on a certain submerged arc furnace and use the measured current data to establish a soft-sensing model for electrode current.

Due to the influence of many causes, it is difficult to model the electrode current of the submerged arc furnace.^[10] For example, the electrode currents are coupled to each other. Therefore, there is a relatively small body of literature that is concerned with the measurement or prediction of electrode current in submerged arc furnaces. However, we have noticed that there are some results published on current distribution of submerged arc furnaces using computational fluid dynamics and finite element methods. Diahnaut^[11] is an earlier researcher who used computational fluid dynamics to compute the current distribution in submerged arc furnaces. Diahnaut's research focused on the effect of contact resistance on current distribution in submerged arc furnaces. Evidence suggests that contact resistance is among the important factors for affecting current distribution in submerged arc furnaces. Then Darmana et al.^[12] presented a model method for submerged arc furnaces using computational fluid dynamics which is considering various physical phenomena. This is helpful to enhance understanding of critical process parameters in the smelting process. On the basis of this method, some research has been carried out on the effect of other parameters on the current distribution, such as electrode shape, pitch circle diameter of electrodes, frequency of the power supply system, side arcs, and carbide configuration in the charge.^{[13,14,15,16,17]} Although these results cannot offer value information of electrode current, it is fundamental to develop a soft-sensing model for predicting electrode current. Therefore, the aim of this thesis is to establish a soft-sensing model for submerged arc furnace electrode current, based on these previous works.

However, interference from the industrial field will bring about a mismatch of model parameters and affect the prediction accuracy of the soft-sensing model. Thus, it is necessary to update the parameters of the soft-sensing model online. Some studies have shown that it is an appropriate method to update the model parameters online by representing the estimation of model parameters as an optimization problem.^[18] Ahmed^[19] applied this method to update the parameter of the NO_x emission prediction model. When all the historical data are used to update the model parameters, the parameter update speed will decrease. Therefore, Wang^[20] only used the historical transient fault samples to train the early transient frequency prediction model for the power system. And Lv^[21] used the strategy to enhance the speed of mechanism model parameters updated, which is dividing process variations into irreversible and reversible variations. In addition to reducing the sample size of training data participating in model updating, the optimization algorithm with low time complexity also has the potential to improve the model updating speed. Therefore, this study provides a model update strategy for the soft-sensing model based on the relative error between the soft-sensing model prediction value and the measured value.

The overall structure of the study takes the form of six sections. The first section of this paper will give a brief overview of the previous studies of submerged arc furnace electrode current. Section II will propose a mechanism model for describing the electrode current variation. Since the mechanical model can’t achieve the expected accuracy, an integrated prediction model framework will be proposed in the Section III. In the integrated prediction model, an error compensation model based on Elman dynamic neural network is used to compensate for the errors of the mechanism model. In addition, in order to ensure the speed and accuracy of mechanism model parameter identification, a new cooperative dual particle swarms optimization algorithm (CDPSO) will be proposed. Section IV is concerned with the model update strategy for the soft-sensing model. In the fifth section, we successfully applied the proposed method to predict the electrode current of 12.5MV. A silicon manganese alloy submerged arc furnace. The final section will give some conclusions of the modeling method and identify areas for further research.

The novelties and contributions of this paper are listed as follows.

• 1) An integrated prediction model of electrode current is established.

• 2) A dual particle swarm optimization algorithm is proposed, to obtain the optimal parameter of the mechanism model.

Electrical System Analysis and Mechanism Model

Electrical System for Submerged Arc Furnace

Different from the electrical arc furnace, in the smelting of submerged arc furnace, the electrode is deeply inserted into the charge. The charge is continuously or intermittently fed into the furnace by the charging system. So, the deoxidize reaction of the ore is mainly concentrated around the electrode. During the smelting process, workers can move electrodes up and down to control the temperature in the furnace. As shown in Figure 1, it is the submerged arc furnace electrical system. The electrical system mainly includes four parts: electrical transformer, short network, self-baking electrode, and load. The secondary circuit between the furnace transformer and the electrodes are called short network. To ensure the mobility of the electrode, the short network and the electrode need to be connected by a flexible copper cable. The flexible copper cable and the transformer are connected by the copper tube and the copper bar. There is cooling water in the copper tube to control the temperature of the copper tube. The power factor of the submerged arc furnace is usually low, because the resistance of the molten pool is small, and the reactance of the short network is large. In order to compensate for the power factor, a capacitor needs to be added to the electrical system for power compensation.

Fig. 1

Submerged arc furnace electrical system

The principle of the electrical system is as follows. The electrical transformer converts the high voltage on the bus bar into the low voltage and high current needed for smelting. The converted electrical energy is conducted to the self-baking electrode through the short network and then delivered into the furnace by the electrode. Using the heat generated by the arc at the end of the electrode and the resistance between the charge to provide the high temperature for the deoxidize reaction. Usually, the transformers are arranged around the electrical furnace in a regular triangle form. The primary side of the transformer is connected in a delta form. The secondary side completes the delta connection on the electrode through the short network.

Mechanism Model

After proper transformation, the three-phase submerged arc furnace electrical system can be transformed into the form shown in Figure 2.

Fig. 2

Circuit diagram of submerged arc furnace electrical system

In Figure 2, $R_{Ti}$(i=1, 2, 3) and $L_{Ti}$(i=1, 2, 3) are the resistance and inductance of three single-phase transformers, which can be calculated from the transformer parameters. $R_{Bi}$(i=1, 2, 3) and $L_{Bi}$(i=1, 2, 3) are the resistance and inductance of the short network, which are determined by the structural parameters of the short network. $R_{A}$, $R_{B}$ , and $R_{C}$ are operating resistances, which are determined by the depth of the electrode inserted into the furnace and the resistivity of the material. $M_{ab} ,\;M_{bc} {\text{and}} M_{ac}$ are the mutual inductance between short networks. $O$ is the neutral point of the transformer, and $O^{\prime}$ is the neutral point of the molten pool.

Set $R_{a} = R_{T1} + R_{B1} + R_{A}$, $R_{b} = R_{T2} + R_{B2} + R_{B}$, $R_{c} = R_{T3} + R_{B3} + R_{C}$,$L_{a} = L_{T1} + L_{B1}$, $L_{b} = L_{T2} + L_{B2}$, $L_{c} = L_{T3} + L_{B3}$

According to Kirchhoff's voltage law (KVL), the voltage of each phase electrode relative to the neutral point of the transformer is given as follows:

$$ \begin{array}{*{20}c} \begin{gathered} U_{A} = I_{A} R_{a} + I_{A} j\omega L_{a} + I_{B} j\omega M_{ab} + I_{C} j\omega M_{ac} + u_{0} \hfill \\ \hfill \\ \end{gathered} \\ \begin{gathered} U_{B} = I_{B} R_{b} + I_{B} j\omega L_{b} + I_{A} j\omega M_{ab} + I_{C} j\omega M_{bc} + u_{0} \hfill \\ \hfill \\ \end{gathered} \\ {U_{C} = I_{C} R_{c} + I_{C} j\omega L_{c} + I_{A} j\omega M_{ac} + I_{B} j\omega M_{bc} + u_{0} } \\ \end{array} $$

(1)

According to Kirchhoff's current theorem (KLC), the current equation at the neutral point $O^{\prime}$ is given as follows:

$$ I_{A} + I_{B} + I_{C} = 0 $$

(2)

If the power supply is symmetrical, then

$$ U_{B} = \left( { - 0.5 - j\frac{\sqrt 3 }{2}} \right)U_{A} ,\;U_{C} = \left( { - 0.5 + j\frac{\sqrt 3 }{2}} \right)U_{A} $$

(3)

From Eqs. [1], [2], and [3], we can get the A-phase electrode current as Eq. [4]:

$$ I_{A} = U_{A} \frac{{a_{r} + ja_{x} }}{A + jB} = U_{A} \left( {\frac{{Aa_{r} + Ba_{x} }}{{A^{2} + B^{2} }} + {\text{j}}\frac{{Aa_{x} + Ba_{r} }}{{A^{2} + B^{2} }}} \right) $$

(4)

In Eq. [4], where

$$ \left\{ {\begin{array}{*{20}l} {A = {\text{R}}_{a} {\text{R}}_{b} + {\text{R}}_{a} {\text{R}}_{c} + {\text{R}}_{b} {\text{R}}_{c} - {\text{X}}_{1} {\text{X}}_{3} + {\text{X}}_{2}^{2} } \hfill \\ {B = {\text{X}}_{1} \left( {{\text{R}}_{b} + {\text{R}}_{{\text{c}}} } \right) + {\text{X}}_{3} \left( {{\text{R}}_{a} + {\text{R}}_{{\text{c}}} } \right) - 2{\text{X}}_{2} {\text{R}}_{{\text{c}}} } \hfill \\ \end{array} } \right. $$

(5)

$$ \left\{ {\begin{array}{*{20}l} {a_{r} = 1.5\left( {{\text{R}}_{b} + {\text{R}}_{{\text{c}}} } \right) - \sqrt 3 \left( {{\text{X}}_{2} - 0.5{\text{X}}_{3} } \right)} \hfill \\ {a_{x} = 1.5{\text{X}}_{3} - \sqrt 3 \left( {{0}{\text{.5R}}_{b} - 0.5{\text{R}}_{{\text{c}}} } \right)} \hfill \\ \end{array} } \right. $$

(6)

$$ \left\{ {\begin{array}{*{20}l} {{\text{X}}_{1} = {\upomega }\left( {{\text{L}}_{a} + {\text{L}}_{c} - 2{\text{M}}_{ac} } \right)} \hfill \\ {{\text{X}}_{2} = {\upomega }\left( {{\text{L}}_{c} + {\text{M}}_{ab} - {\text{M}}_{ac} - {\text{M}}_{bc} } \right)} \hfill \\ {{\text{X}}_{3} = {\upomega }\left( {{\text{L}}_{b} + {\text{L}}_{c} - 2{\text{M}}_{bc} } \right)} \hfill \\ \end{array} } \right. $$

(7)

In the same way, the two-phase electrode currents of B and C can be written using the following equation:

$$ I_{B} = U_{B} \frac{{b_{r} + jb_{x} }}{A + jB} = U_{B} \left( {\frac{{Ab_{r} + Bb_{x} }}{{A^{2} + B^{2} }} + {\text{j}}\frac{{Ab_{x} + Bb_{r} }}{{A^{2} + B^{2} }}} \right) $$

(8)

$$ I_{C} = U_{C} \frac{{c_{r} + jc_{x} }}{A + jB} = U_{C} \left( {\frac{{Ac_{r} + Bc_{x} }}{{A^{2} + B^{2} }} + {\text{j}}\frac{{Ac_{x} + Bc_{r} }}{{A^{2} + B^{2} }}} \right) $$

(9)

where

$$ b_{r} = 1.5\left( {{\text{R}}_{a} + {\text{R}}_{{\text{c}}} } \right) - \sqrt 3 \left( {{0}{\text{.5X}}_{1} - {\text{X}}_{2} } \right), $$

$$ b_{x} = 1.5X_{1} - \sqrt 3 \left( {0.5R_{c} - 0.5R_{a} } \right). $$

$$ c_{r} = 1.5\left( {{\text{R}}_{a} + {\text{R}}_{{\text{b}}} } \right) - \sqrt 3 \left( {{0}{\text{.5X}}_{3} - 0.5{\text{X}}_{1} } \right), $$

$$ c_{x} = 1.5\left( {{\text{X}}_{1} + {\text{X}}_{3} - 2{\text{X}}_{2} } \right) - \sqrt 3 \left( {{0}{\text{.5R}}_{a} - 0.5{\text{R}}_{{\text{b}}} } \right). $$

In Eqs. [4], [8], and [9], the resistance and inductance of each circuit in the mechanism model are unknown. Therefore, we take the A-phase circuit as a case to study the calculation method of unknown parameters in the model.

Operating Resistance

Operating resistance is an important electrical parameter of submerged arc furnace. It reflects the external impedance characteristics of the submerged arc furnace load. The size of the operating resistance is affected by multiple variables, such as electrode size, electrode insertion depth, charge properties, furnace structure parameters, and smelting conditions. Researchers have explored the calculation method of operating resistance based on different assumptions.^[22] Based on the hemispherical grounding device resistance calculation method, Downing^[23] proposed two different forms of operating resistance estimation formulas. According to the relationship between the operating resistance and the electrode size, the position of the electrode working end, the nature of the charge and other parameters, the experimental calculation formula of the operating resistance is given.

$$ R_{A} = \frac{{1.275\gamma_{a} h_{a0} (h_{a0} + 2h_{a} )}}{{d^{2} [h_{a0} (k_{a2} - k_{a1} )^{2} + k_{a1}^{2} (h_{a0} + 2h_{a} )]}} \times 10^{ - 4} $$

(10)

where $\gamma_{a}$ is the average resistivity of ore in the furnace of the A-phase electrode, $h_{a}$ is the electrode insertion depth, $h_{a0}$ is the distance from the electrode end to the molten pool bottom, d is the electrode diameter, $k_{1}$ and $k_{2}$ are electrode equivalent section coefficient.

Set $h_{a} = 1.5m$,$h_{a0} = 1.2m$, $d = 1.4m$, $k_{1} = 1.75\left( {h_{0} /0.8d} \right)^{0.4}$,$k_{2} = 1.67\left( {\left( {h_{a} + h_{a0} } \right)/0.884d} \right)^{0.75}$.

In Eq. [10] $\gamma_{a}$ is a parameter that need to be identified, and its values will vary with the smelting conditions and the properties of the material.

Short Network Resistance and Inductance

The short network resistance includes copper bar resistance and self-baking electrode resistance. Considering the skin effect and proximity effect of the conductor, the equivalent resistance of the short network can be expressed as following equation^[23]:

$$ R_{B1} = \frac{1}{n}\left[ {\rho_{20} (1 + \alpha_{a} \Delta t)\frac{l}{s}K_{a} } \right] + \frac{{\rho_{a} l_{h} }}{{\pi r_{0}^{2} }} $$

(11)

where $K_{a}$ is coefficient of short network resistance related to skinning effect and proximity effect, which needs to be identified. $\rho_{20}$ is the resistivity of copper at 20 °C, $\alpha_{a}$ is the temperature coefficient of short network resistance, $\Delta t$ is the temperature rise of the short network, $l$ is the short network length, $s$ is the copper tube cross sectional area, and n is the number of short network copper tubes. $\rho_{a}$ is resistivity of self-baking electrode, which needs to be identified. $l_{h}$ is the length from the copper tile to the self-baking electrode end, $r_{0}$ is diameter of electrode.

Set $\rho_{20} = 1.75 \, \times 10^{ - 8} \Omega \cdot m$, α = 0.0043 $\Omega$ °C, $\Delta t = 55$ °C, $l = 13m$, $s = 1.65 \times 10^{ - 3} m^{2}$, $n = 4$, $l_{h} = 4.5m$, $r_{0} = 1.2m$.

According to the self-inductance formula of a hollow tube, the self-inductance of the short network can be written using the following equation:

$$ L_{B1} = \eta_{a} \times \frac{{\mu_{0} l}}{2\pi }\left( {\ln \frac{2l}{r} + \varepsilon - 1} \right) $$

(12)

where $\eta_{a}$ is the correction coefficient of the short network self-induction of the A-phase electrode, which needs to be identified. l is the short network length, r is the outer radius of copper tube,$\mu_{0}$ is the vacuum permeability, and $\varepsilon$ is the structural parameter of short network, which is related to the ratio of the outer diameter to the inner diameter of the tube. Set $l = 13m$, $\varepsilon = 0.188$,$r = 0.05m$, and $\mu_{0} = 2\pi \times 10^{ - 7} H/m$.

When the submerged arc furnace is powered by three single-phase transformers, and the transformers are arranged in a triangle around the furnace, the mutual induction between the short networks can be estimated by the following formula.

$$ M_{ab} = \delta_{a} \times \frac{{\mu_{0} l_{h} }}{2\pi }(\ln \frac{{2l_{h} }}{{g_{m} }} - 1) $$

(13)

where $\delta_{a}$ is the correction coefficient of the short network mutual induction, which needs to be identified. $l_{h}$ is the length from the copper tile to the self-baking electrode end, $\mu_{0}$ is the vacuum permeability, and $g_{m}$ is the mutual geometric mean distance. Set $l_{h} = 4.5m$, $\mu_{0} = 2\pi \times 10^{ - 7} H/m$, $g_{m} = 2.45m$.

Transformer Resistance and Inductance

Transformer energy loss includes no-load loss and short-circuit loss. The no-load loss includes hysteresis loss and eddy current loss. Hysteresis loss is the energy loss caused by hysteresis during the magnetization of the iron core. Eddy current loss is the energy loss caused by the swirling current in the transformer core. The transformer short-circuit loss is the energy loss caused by the transformer coil resistance. It is related to the size of the current through the coil and the temperature of the transformer. Transformer resistance and inductance can be calculated according to the transformer nameplate parameters. The transformer parameters are shown in Table I.

Table I Transformer Parameters

Substitute operating resistance, short network resistance, short network inductance, transformer resistance, and transformer inductance into Eqs. [4], [8], and [9], we can obtain a simplified form of the electrode current mechanism model as follows:

$$ \hat{y} = x\theta^{T} $$

(14)

where $\hat{y}$ is the output vector, $\theta = [\gamma_{a} ,K_{a} ,\rho_{a} ,\eta_{a} ,$ $\delta_{a} ,\gamma_{b} ,K_{b} ,\rho_{b} ,\eta_{b} ,\delta_{b} ,\gamma_{c} ,K_{c} ,\rho_{c} ,\eta_{c} ,\delta_{c} ]$ are the parameters that need to be identified in the model.

Soft-Sensing Model of Submerged Arc Furnace Electrode Current

Framework Design of the Soft-Sensing Model

Because certain conditions are assumed and simplified in the mechanical model, the mechanical model cannot achieve the expected accuracy. With the development of basic automation in the industry, massive production data are available by using sensors. If the production data are exploited appropriately, it is helpful to describe the nature of the actual process. The data-driven model established with production data has been successfully applied in many industrial processes. However, when using data-driven models to deal with uncertain or heterogeneously distributed data, unexplainable results are often obtained. The reason is that the data-driven model ignores the basic mechanism of industrial processes. Therefore, the integrated predictive model is more suitable for modeling complex industrial processes.^[24] It can take advantage of both the mechanism model and the data-driven model. Using error compensation models to modify mechanical models is a more promising modeling method for complex industrial processes.

The framework of the submerged arc furnace electrode current soft-sensing model is presented in Figure 3. It mainly includes the mechanism model, error compensation model, parameter identification method, and model update strategy. The parameter identification method based on CDPSO algorithm can find suitable parameters for the mechanism model. The model update strategy based on current accuracy analysis can modify the integrated prediction model by retraining the Elman neural network error compensation model or the calibration mechanism model parameters.

Fig. 3

Framework of the soft-sensing model

In Figure 3, w₁ is the input vector of the mechanism model, w₂ is the input vector of the error compensation model, $y^{\prime}$ is the prediction value by the mechanism model, y is the measured value of electrode current by the Rogowski coils, E is the prediction error of the mechanism model, e is the output of the error compensation model, $\theta$ is the parameter of the mechanism model.

Model Parameter Identification Algorithm

For model parameter identification, it can be regarded as an optimization problem. The parameter identification fitness function of the submerged arc furnace electrode current mechanism model is given as Eq. [15]:

$$ f(\theta ) = 1/\left( {\sum\limits_{i = 1}^{N} {\left[ {(I_{ai} - \hat{I}_{ai} )^{2} + (I_{bi} - \hat{I}_{bi} )^{2} + (I_{ci} - \hat{I}_{ci} )^{2} } \right]} } \right) $$

(15)

The objective of parameter identification is to maximize the fitness function. In Eq. [15] $I_{ai}$, $I_{bi}$, and $I_{ci}$ are the measured values of the ith test sample, $\hat{I}_{ai}$, $\hat{I}_{bi}$, and $\hat{I}_{ci}$ are the predicted values of the mechanism model of the ith test sample as described in Eqs. [4], [8], and [9], N is the number of samples.

$\theta = [\gamma_{a} ,K_{a} ,\rho_{a} ,\eta_{a} ,$ $\delta_{a} ,\gamma_{b} ,K_{b} ,\rho_{b} ,\eta_{b} ,\delta_{b} ,\gamma_{c} ,K_{c} ,\rho_{c} ,\eta_{c} ,\delta_{c} ]$ are the decision variables. The boundaries of decision variables are shown in Table II.

Table II Boundaries of Decision Variables

Particle swarm optimization (PSO) algorithm, as a global optimization algorithm, has been successfully applied in parameter identification.^[25] Its excellent solution speed has been recognized by researchers. It should be noted that although the global search ability of genetic algorithm is powerful, its local search ability needs to be further enhanced. The parameter setting of the ant colony algorithm has been criticized. Thus, the PSO algorithm is adopted to identify model parameters in this paper.

By updating the moving velocity and position of the particles, the particles move to the best particles in the group, to obtain the optimal solution of the problem.^[26] Obviously, the update method of particle velocity and position directly affects the performance of the algorithm. Based on the standard PSO algorithm, Shi and Eberhart introduced inertial weights to balance global and local search.^[27] The velocity and position of the particle are updated as Eqs. [16] and [17].

$$ \begin{gathered} v_{i} (k + 1) = \omega v_{i} (k) + c_{1} rand()(pbest_{i} - x_{i} (k)) \\ + c_{2} rand()(gbest - x_{i} (k)) \\ \end{gathered} $$

(16)

$$ x_{i} (k + 1) = x_{i} (k) + v_{i} (k + 1) $$

(17)

where i is the number of particles, v_i(k) is the ith particle's velocity in the kth iteration, x_i(k) is the position of the ith particle in the kth iteration, p_best is the historical personal best position, g_best is the historical global best position, ω is the inertial weight,c₁ and c₂ are positive accelerating constants, and rand() is a random functions with the range [0,1].

Shi^[25] pointed out that the inertia weight is very important to the performance of the algorithm. A larger inertia weight is conducive to the global search, and a smaller inertia weight can improve the local optimization ability. Compared with fixed inertial weights, dynamic inertial weights can obtain better optimization results. However, PSO is easily trapped into the local optima when applied to complex multimodal problems. To balance the global search and local search capabilities of the algorithm, researchers have made some beneficial improvements.^[27] Among them, the improved scheme using multiple groups of particles has attracted researcher's attention. Mohammed proposed a discrete cooperative particle swarm optimization algorithm for the routing of integrated circuits. Although two groups of particles are used to search, there is no information interaction between the two groups of particles.^[28] He used damping factor and cooperation mechanism to improve the performance of particle swarm optimization algorithm.^[29] Hajer proposed a modified scheme that uses two groups of particles to search. In his proposal, the first one performs exploration, while the second one is responsible for exploitation.^[30] This is beneficial to restrain the premature convergence of the algorithm. Based on these previous works, we proposed a CDPSO algorithm in this paper.

The detailed description of the CDPSO algorithm strategy is as follows:

In searching process, we use two groups of particles with different inertia weights to search at the same time. The first group particles are designed for global search by setting a larger inertia weight. And the second group particles are designed for accurately searching by setting a smaller inertia weight. A selection pool with a capacity of L is set up. In searching process, the position, velocity, and inertial weight of the second group with better fitness function values are stored in the selection pool. If the best fitness function value of the first group particles is better than the second group particles, replace the position, velocity, and inertial weight of the second group particle with the first group particle. It means that the second group particles fly to the optimal position of the first group for accurate searches. The position, velocity, and inertial weight of the first group particles are selected from the selection pool using roulette selection mechanism. The two groups of particles update the position, velocity, and inertia weights under the above method, and continue to search until one of the final conditions is met. In the iterative process, if the optimal position of the two groups of particles exceeds the edge of the feasible region, the boundary value is taken. Through the leap between the two groups of particles and the roulette selection mechanism, the algorithm can avoid premature convergence and improve the search precision.

The selection pool of the algorithm is a queue structure. When the elements in the selection pool exceed the capacity of the selection pool, the element that enters the selection pool first is deleted. The position, velocity, and inertial weight of the first group of particles can be generated by the following selection methods:

Let the ith element in the selection pool be E_i. So, f(E_i) is the fitness function value of the ith element, then the selection probability of the ith element in the selection pool can be represented by Eq. [18]:

$$ p_{i} = {{f(E_{i} )} \mathord{\left/ {\vphantom {{f(E_{i} )} {\sum\limits_{j = 1}^{L} {f(E_{j} )} }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{j = 1}^{L} {f(E_{j} )} }} $$

(18)

The cumulative probability of the ith element is written as Eq. [19]:

$$ q_{i} = \sum\limits_{j = 1}^{i} {p_{j} } $$

(19)

Use the function rand( ) to generate a uniformly distributed pseudo-random number r in the interval [0,1]; If r<q₁, select element 1, otherwise, select individual k such that: q_k−1<r ≤ q_k holds.

Since a larger inertia weight can improve the global search ability, the inertia weight update strategy of the first group can be set to the following equation.

$$ \omega_{1} = \omega_{\max } - \left( {\omega_{\max } - \omega_{\min } } \right)\frac{{k^{2} }}{{T^{2} }} $$

(20)

where $\omega_{1}$ denote the inertial weight in the first group; $\omega_{\max }$ and $\omega_{\min }$ are the maximum and minimum values of the inertial weight; k is the current iteration number; T is the maximum iteration. In Eq. [20], the inertia weight is a quadratic function of iteration number. The inertia weights change slowly during the initial iteration, which is useful for global search. Near the maximum number of iterations, the inertia weights vary similarly to the linear decreasing strategy, which is conducive to convergence to the global optimum.

The second group is designed for accurate search. Thus, the inertia weight of the second group is described as Eq. [21].

$$ \omega_{2} = \omega_{\min } + (\omega_{\max } - \omega_{\min } )\left[ {1 - logsig(\frac{\alpha k}{T} - \beta )} \right] $$

(21)

where $\omega_{2}$ denote the inertial weight in the second group. $logsig(\;)$ is sigmoid function. $\alpha$ and $\beta$ are the feature parameters.

The variations of inertia weights with iterations for different $\alpha$ and $\beta$ is shown in the Figure 4. Where, $\omega_{\max }$=0.9, $\omega_{\min }$=0.4, T=200.

Fig. 4

Variations of inertia weights with iterations for different $\alpha$ and $\beta$

From Figure 4, we know that the values of $\alpha$ and $\beta$ determine the changing trend of the inertia weights. When $\alpha$ and $\beta$ are set to larger values, the inertia weight can decrease at a slower speed in the beginning and the end. When the values of $\alpha$ and $\beta$ are small, the decreasing speed of the inertial weight will increase. When $\alpha$ is twice $\beta$, the inertia weight is centrosymmetric. In order to keep the inertia weight of the second group of particles at a larger value during the initial iteration, and keep a smaller value when the iteration is halfway through, we set $\alpha = 12$ and $\beta = 6$.

The particle's maximum velocity V_max determines the accuracy between the particle search position and the best position,^[31] so the maximum velocity V_max need to be limited. To make the two groups of particles search according to different trajectories in space, the maximum velocity of the first group particles is set to 1 and used for global search. The maximum velocity of the second group particles decreases linearly with the number of iterations, used for accurately search, as shown in Eq. [22].

$$ v_{\max } = \max (v_{\max } ) + [\min (v_{\max } ) - \max (v_{\max } )]\frac{k}{T} $$

(22)

The steps of the CDPSO algorithm applied to parameter identification are as follows:

Step 1.:

Set the initial population number, initial velocity, and position of the two groups of particles. Initialize selection pool, including the selection pool capacity, the fitness function value of each element, the position and velocity of particles, the inertia weight. Set the termination conditions.

Step 2.:

For each group, calculate the fitness value according to (15), save the historical personal best position, the historical global best position.

Step 3.:

Calculate the inertia weights of the two groups of particles according to (20) and (21).

Step 4.:

Update the positions and velocities of the two groups of particles according to (16) and (17).

Step 5.:

Recalculate the particle fitness function value according to the updated particle position, and update the historical global best position and historical individual best position.

Step 6.:

Compare the best fitness function value of the two groups. If the first group's best fitness function value better than that of the second group, replace the second group particle's position, velocity, and inertial weight with that of the first group. Save the position, velocity, and inertial weight of the second group in the selection pool.

Step 7.:

Use the selection mechanism of roulette to select positions, velocity, and inertial weight from the selection pool for the first group.

Step 8.:

If the termination conditions are met, stop the search, and output the optimization result, otherwise go to step 2. The termination condition is that the number of iterations exceeds allowed iterations or the reduction of the objective function is less than the allowed accuracy.

Elman Dynamic Neural Network Error Compensation Model

Affected by a variety of reasons, the mechanism model cannot achieve the required prediction accuracy. Firstly, the information taken into the mechanism model is limited. A significant case is the capacitance compensation system. To meet the power factor requirements of the power system, there is a capacitance compensation system in the power supply system. Undoubtedly, the capacitance compensation system will affect the electrode current. However, in the mechanism model, the influence of the capacitance compensation system is ignored. Secondly, some parameters in the mechanism model are difficult to directly measure. It has to be calculated based on the measurable parameters. As a result, the accuracy of some parameters in the mechanism model is insufficient. The most important factor is the voltage on the secondary side of the transformer. In addition, several assumed conditions are introduced when discussing and establishing the mechanism model. In the actual smelting process, these assumptions will cause model to mismatch.

The data-driven model can reflect the influence of capacitance compensation system, transformer voltage error, model assumptions, etc. on electrode current. Therefore, the transformer primary side voltage, primary side current, primary side power, primary side power factor, secondary side voltage, secondary side capacitance compensation current and electrode insertion depth are used as the input of the error compensation model of the Elman neural network. The error between the predicted value and the measured value of the electrode current mechanism model after parameter identification is used as a training sample. The error compensation model is described as:

$$ e = f_{Elman} (X_{n} ) $$

(23)

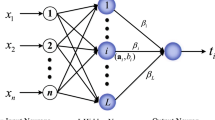
where $X_{n}$ is the input of the Elman neural network and e is the output of the error compensation model.

For industrial applications, a shorter model training time is beneficial. Although a larger learning rate can accelerate the learning process in the early stage of training. But a larger learning rate will cause larger fluctuations in the later stage of training. Therefore, the learning rate of Elman neural network is taken as the exponential gradient decay, as shown in Eq. [24].

$$ \eta = \eta_{init} \times S_{d} \wedge {\text{int}} \left( {\frac{ST}{{ST_{d} }}} \right) $$

(24)

where $\eta$ is the current learning rate, $\eta_{{{\text{init}}}}$ is the initial value of the learning rate, $ST$ is the current iteration steps, $ST_{d}$ is the decay step length, means how many rounds to adjust the learning rate, $S_{d}$ is the exponential decay coefficient, and ${\text{int}} (\;)$ is the rounding function. Set $\eta_{{{\text{init}}}} = 0.1$,$ST_{d} = 200$,$S_{d} = 0.8$.

The error between the measured value and the predicted value of the mechanism model is used as the input of the error compensation model. Then, the errors in the mechanism model are predicted and compensated online. Therefore, the electrode current integrated prediction model is established by combining the mechanism model and the error compensation model. The integrated prediction model is described as Eq. [25].

$$ Y = \hat{y} + e = f_{1} (\hat{y}|w1) + f_{Elman} (e|w2) $$

(25)

where Y is the comprehensive predicted output of the electrode current, $f_{1} (\hat{y}|w1)$ represents the mechanism model with $w1$ as the input vector and $\hat{y}$ as the output, $f_{Elman} (e|w2)$ is the error compensation model with $w2$ as the input vector and e as the output error compensation model. $w1$ and $w2$ are the voltage on the secondary side of the transformer and the electrode insertion depth.

Model Updating Strategy

Model Updating Strategy

In industrial applications, the prediction accuracy of the integrated prediction model may decrease with changes in production conditions or time. To improve the adaptability of the prediction model, it is necessary to update the model online. According to production requirements, when the relative error between the integrated model prediction value and measured value is within 1 pct, the accuracy of the model is acceptable. Therefore, the model update strategy of the integrated model is determined as follows.

• (1) In a smelting cycle (the smelting cycle of silico manganese alloy is 200 minutes), if the relative error is between 1 and 1.5 pct, and the duration exceeds 5 minutes, we believe that the parameters of the mechanism model are correct. The error is caused by insufficient accuracy of the error compensation model. Therefore, the Elman neural network error compensation model is retrained by using new historical error data.

• (2) In a smelting cycle, if the relative error is greater than 1.5 pct and the duration exceeds 10 minutes, we believe that the mechanism model parameters are not matched. The parameters of the mechanism model need to be calibrated. If the model still cannot achieve the required prediction accuracy after parameter calibration, it needs to use the parameter identification method proposed in Section III–B.

• (3) In a smelting cycle, if the relative error is between 1 and 1.5 pct, and the duration does not exceed 5 minutes, we believe that this is an error caused by accidental factors or interference. It is not necessary to update the integrated prediction model.

Parameters Calibration of Mechanism Model

With the environment changes, the integrated prediction model will fail to meet expected accuracy due to the mismatch of mechanism model parameters. Therefore, it is necessary to recognize changes in the system and environment in real time, and automatically modify the model parameters accordingly. In the mechanism model shown as Eq. [16], the estimation of the parameters that need to be calibrated can be expressed in the following form.

$$ Y_{n} = \left[ {\begin{array}{*{20}c} {\hat{y}_{1} } \\ \vdots \\ {\hat{y}_{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\phi_{1}^{T} } \\ \vdots \\ {\phi_{n}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\theta_{1} } \\ \vdots \\ {\theta_{n} } \\ \end{array} } \right] = \Phi_{n} \Theta_{n} $$

(26)

where n is the number of groups of observed data.

According to the recursive least square’s estimation method, the parameters can be updated in the following form.

$$ \begin{gathered} \hat{\Theta }_{n + 1} = \hat{\Theta }_{n} + K_{n} \varepsilon_{n} \hfill \\ K_{n} = P_{n} \phi_{n} \hfill \\ \varepsilon_{n} = y_{n} - \phi_{n}^{T} \hat{\Theta }_{n - 1} \hfill \\ P_{n} = P_{n - 1} - \frac{{P_{n - 1} \phi_{n} \phi_{n}^{T} P_{n - 1} }}{{1 + \phi_{n}^{T} P_{n - 1} \phi_{n} }} \hfill \\ \end{gathered} $$

(27)

An Industrial Application Case

To evaluate the prediction accuracy of the established integrated model, we will give an industrial application case in a silico manganese alloy smelting plant. We installed Rogowski coil near the electrode at the end of the short network to measure the electrode current. With a sampling interval of 1 minute, the industrial data of the #6 submerged arc furnace in Ningxia from July 8 to July 31 was continuously collected.

There are totally 12236 valid samples, which constructs the dataset in this experiment. The dataset was split into training dataset, validation dataset and test dataset by the ratios 60, 20, and 20 pct, respectively. The training dataset was used to train the model, the validation dataset was used to select the hyperparameters, and the test dataset was used to evaluate the model performance.^[32,33] In the training process, the early stop was selected to avoid overfitting.^[34] In addition to the methods we used, the researchers also provided some other ideas.^[35] Meanwhile, in the proposed model, the number of hidden neurons is the key hyperparameter. Therefore, the trial-and-error method was used to select the optimal hyperparameter on the validation dataset. When the number of hidden neurons equals to 13, the validation loss archives the minimum. Therefore, the optimal number of hidden neurons is 13. Although we choose the trial-and-error method to find the parameters of the model, it is a good choice to find the optimal values of network hyper parameters by solving a multi-objective optimization problem.^[36] To validate the effectiveness of the proposed correction model, we have compared it with the ARIMA and wavelet model. The results are shown in Table III. As can be seen, the proposed model has less maximum absolute error (MAE), average relative error (MRE), and root mean square error (RMSE) than the ARIMA and Wavelet models. This shows that the proposed model has better accuracy than others.

Table III Performance Comparison of Different Correction Models

Linear decreasing particle swarm optimization algorithm (LDPSO) and CDPSO algorithm are used to identify mechanism model parameters. The two algorithms are set with the same parameters. The population sizes of both groups of the particles are 50, c1 and c2 are 1.49445, ω_max=1.0, ω_min= 0.1, and max(V_max)=1. The maximum iteration number is 800. Since PSO is a stochastic algorithm, we have tested the PSO algorithms randomly by 100 times. The average of the fitness function value (AFV), the variance of the fitness function value (VFV), and the average number of iterations required to obtain the optimal solution (AI) are used as the evaluation index of the algorithm performance, and the results are shown in Table IV.

Table IV The Comparison of Two Identification Algorithm

From Table IV, it is concluded that the AFV of the CDPSO algorithm is smaller than the LDPSO algorithm, and the VFV is smaller than the LDPSO algorithm. Therefore, the CDPSO algorithm has better stability in the identification of mechanism model parameters than the LDPSO algorithm. And, the AI of the CDPSO algorithm is less than that of the LDPSO algorithm. In summary, the CDPSO algorithm is more suitable than the LDPSO algorithm in the identification of mechanism model parameters. The results of parameter identification are shown in Table V.

Table V Identification Result of the Model Parameters

Set the transformer primary side voltage, primary side current, primary side power, primary side power factor, secondary side voltage, secondary side capacitance compensation current, and electrode insertion depth as the input vectors of the error compensation model. The error data between the mechanism model prediction value and the measured value are used as the target value. The number of neurons in the Elman neural network is 120, the hidden sizes is 4, the layer delays is 1, the maximum number of iterations is 5000, and the error tolerance is 1e-5. The weights are updated by Eq. [24]. The simulation results of the mechanism model and the integrated model are shown in Figure 5. The MAE, MRE, and RMSE of the mechanism model and the integrated model are shown in Table VI.

Fig. 5

(A) The integrated model and mechanism model prediction of the A-phase electrode current. (B) The integrated model and mechanism model prediction of the B-phase electrode current. (C) The integrated model and mechanism model prediction of the C-phase electrode current

Table VI Performance Comparison of Prediction Results

From Figure 5, the mechanism model reflects the changing trend of the current. However, the accuracy of the mechanism model is insufficient. There is a large error between the predicted value and the measured value. The performance of the integrated model is significantly better than the mechanism model. Especially when the current has a large change, such as the 1 to 7 sample points in Figure 5, the predicted value of the integrated model matches well with the measured value. From Table VI, the MRE, RMSE, and MAE of the A-phase electrode current integration model decreased from 1.3 pct, 1761, and 5387 of the mechanism models to 0.51 pct, 627, and 454. The MRE, RMSE, and MAE of the B-phase electrode current integration model decreased to 0.39 pct, 1460, and 526. The MRE, RMSE, and MAE of the C-phase electrode current integration model decreased to 0.69 pct, 1382, and 776. Therefore, the integrated model has higher prediction accuracy than the mechanism model.

The integrated model is applied to the practical production for predicting the electrode current without model updating strategy. The application results of the integrated model are shown in Figure 6, using the data from 11:30 to 14:50 on July 20. As shown in Figure 6(A), the predicted value of the A-phase electrode current can match well the measured value. But in the 31th to 40th and the 160th to 167th sample points in Figure 6(A), the panel 123th to 131th and the 190th to 198th sample points in Figure 6(C), the relative error is between 1 and 1.5 pct, and the duration exceeded 5 minutes. Therefore, the Elman neural network error compensation model must be retrained. It should be noted that in Figure 6(B), although the relative error of the 123th to 127th sample points exceeded 1 pct, the duration did not exceed 5 minutes. It can be considered that it is caused by accidental factors or interference. The predicted value after updating the model is shown in Figure 7. In Figure 7, the prediction errors are reduced.

Fig. 6

(A) Results without model updating strategy of the A-phase electrode current. (B) Results without model updating strategy of the B-phase electrode current. (C) Results without model updating strategy of the C-phase electrode current

Fig. 7

(A) The B-phase electrode current predicted value after updating the model. (B) The C-phase electrode current predicted value after updating the model

Shown in Figure 8 is the application results of the integrated model, using the data from 17:25 to 20:45 on July 29. The relative error of the three-phase electrode current exceeds 1.5 pct and the duration exceeds 10 minutes. Therefore, the mechanism model parameters need to be calibrated according to the model update strategy. On the other hand, the precision of the integrated model has decreased slightly over time. The main reason is the fluctuation of raw materials and uncertain interference. However, using the model update strategy can effectively reduce the error of the predicted value and improve the stability of the integrated model. Most of all, industrial application results prove that the proposed integrated prediction model can predict electrode current with high accuracy and reliability.

Fig. 8

The A-phase electrode current predicted value from 17:25 to 20:45 on July 29

Conclusion

In this paper, an integrated prediction model of electrode current is proposed and verified. Based on the analysis of the main circuit of the submerged arc furnace, the mechanism model of the electrode current of the submerged arc furnace is established. A cooperative dual particle swarms optimization algorithm was developed to identify the mechanism model parameters. To improve the prediction accuracy of the mechanism model, an error compensation model was established using the Elman dynamic neural network. An integrated prediction model of electrode current is established, by combining the mechanism model with error compensation. To improve the reliability of the integrated prediction model, an online update strategy of the model was developed. Industrial verification shows that the integrated model can effectively predict the electrode current. Compared with the traditional method using the transformation ratio of the transformer and the primary current, the prediction accuracy of the electrode current is improved by about 12 pct. So it is helpful to realize automatic control of submerged arc furnace. In the following research, we will focus on the control strategy of the electrode regulation system based on the integrated prediction model of electrode current established in this paper.