Introduction

Viscosity of heterogeneous silicate melts (containing solid crystals) has long been investigated to support the understanding of natural processes, e.g. volcano eruption[1,2] and control the industrial production, e.g. iron and steelmaking.[3] Enormous efforts have been made to develop a mathematic model allowing viscosity estimation without the costly and time-consuming experimental measurement. The most widely used viscosity equation for suspension system is the Einstein-Roscoe (ER)[4] equation. Kondratiev and Jak[5] validated the applicability of the ER equation with a large experimental data set in the Al2O3-CaO-“FeO”-SiO2 slag with solid fraction up to 30 vol pct. They underlined the effect of solid fraction and liquid viscosity, however, the effect of particle shape and shear rate were neglected. Wright et al.[6,7] observed the shear rate-dependent behavior in the calcium ferrite slags and calcium alumino-silicate slags containing spinel particles, but no model was proposed to calculate the non-Newtonian behavior. Later work by Wu et al.,[8] Xu et al.[9] and Zhen et al.[10] all employed the ER equation in calculating solid-bearing slag viscosity by fitting the parameters in this equation to the measured data. Consequently, the values of the parameters varied at lot. One of the main reasons is that they neglected the influence of particle shape (Xu et al.,[9] Wu et al.[8]) or approximated the non-spherical particles as spheres (Zhen et al.[10]). In reality, however, the heterogeneous silicate melt systems contain solid particles of different sizes and shapes. And it has been experimentally observed that solid particles’ shape can influence the viscosity of melts significantly.[6,7] Furthermore, although non-Newtonian behavior has been observed in solid-containing slags and it is found the Newtonian assumption is only valid at dilute limit, i.e., solid fraction <2 vol pct,[11] most of the existing work still treat the heterogeneous slag as Newtonian system in terms of modeling. As a consequence, the calculated viscosities are inevitably erroneous and incomparable between different reports.

To correctly evaluate viscosity of heterogeneous silicate melts, in this work, a non-Newtonian viscosity model incorporating solid fraction, solid shape, and shear rate is proposed by re-examining the currently published viscosity data with respect to solid-bearing silicate systems. Reliability of the model is subsequently assessed by comparing the calculated results with measured data.

Examination of Measured Data

There have been multiple experimental studies on viscosity of the solid-bearing silicate melt, including magmatic system, metallurgical slag, and coal ash slag. The limited data reported in metallurgical were reviewed firstly. Most of the published data, however, do not include all of the relevant measurement parameters, with respect to solid fraction and shape, temperature, and shear rate. For example, Wright et al.[6,7] studied the viscosity of calcium ferrite slags and calcium alumino-silicate slags containing spinel particles. However, the particle shape was not quantified and its effect was neglected. In Wu’s study[8] on Al2O3-CaO-MgO-SiO2 system, the irregular MgO particles were not further characterized and the shear rate applied was not reported. Xu et al.[9] investigated the CaO-MgO (-Al2O3) -SiO2 system without quantifying the particle shape. Additionally, the volume fraction of solids was calculated through weight fraction and estimated densities, leading to large uncertainty. Zhen et al.[10] measured the viscosity of CaO-MgO-Al2O3-SiO2-(TiN) system with TiN as particles, which were approximated as spheres. The rotating speed was given instead of shear rate and the dimensions of spindle and crucible were not specified, thus the shear rate is not accessible. Therefore, it is not possible to apply these data for modeling in this study. Alternatively, it is found that the recent work on magmas are well-documented with the detailed structural information (silicate system, crystal type, volume fraction of solid and solid shape) and clearly defined experimental conditions (temperature, shear rate and shear rate ramp), which are necessary information for the purpose of viscosity modeling. Therefore, they are summarized in Table I and critically reviewed afterwards.

Table I Summary of Experimental Data of Heterogeneous Silicate Melts in Literature
Full size table

In order to ensure a reliable dataset for viscosity modeling, the crucial parameters, i.e., volume fraction of solid, solid shape, melt viscosity, shear rate, and shear rate ramp, which determine the viscosity of solid-bearing silicates are examined.

Volume fraction of crystals is the key parameter affecting viscosity of silicate melts. To determine the volume fraction, the SEM (scanning electron microscopy) or OM (optical microscopy) images of the quenched silicates are analyzed via image processing software, e.g., Corel Draw,[14] Image J,[15] Adobe Photoshop,[16] and SCION.[12] The area fraction is used as a measure of the volume fraction, provided that the particles are randomly distributed in the matrix and sufficient area of the sample is analyzed.[17] However, an error of this technique is inevitable due to the poor resolution of the image, the limited observation area, the inhomogeneously distributed crystals etc. Analysis of different locations of the same sample demonstrates a standard deviation of 1.44 to 2.5 pct by Vona et al.[14] and 1 pct by Cherverl et al.[15] in terms of volume fraction of crystals. Instead of the direct measurement with the SEM/OM images, Ishibashi[13] calculated the weight percentage of each mineral phase using a generalized mixing model (a thermodynamic model used for calculating equilibrium content of each phase). And the volume fraction is then obtained with the known density of each phase. These data are also included in the present study considering that the generalized mixing model is widely used in magmatic systems.

The second parameter, which should receive particular attention, is the crystal shape. Due to characterization difficulty of irregular shapes, an approximation of ellipsoidal shape is commonly applied. The aspect ratio (r p), which is expressed as the ratio between the axis length of rotational symmetry and the maximum axis length orthogonal to the rotational axis,[11] is used for characterizing particle shape. The aspect ratio is obtained by digitally analyzing the SEM/OM images using image processing software as mentioned above. It is difficult to assess the error level of this technique due to the irregular shape and connected crystals in silicate melts. However, as no better approach is available, the aspect ratio analyzed by this image processing is used for the interpretation of present results. According to Table I, the aspect ratio of solid crystals varies between 1.32 and 11.6, covering most of the cases in heterogeneous silicate melts.

The viscosity of pure liquid also influences the viscosity of overall solid-bearing system. Due to the fact that melt composition is changing with crystallization, the direct measurement of residual melt viscosity is complex, time-consuming, and costly.[16] In general, it can be calculated using the existing viscosity models, provided that the compositions of residual liquid at different temperatures are known. In the articles listed in Table I, the compositions of residual liquid are all obtained by analyzing the quenched samples at different temperatures using electron microprobe (WDS or EDS), ensuring the accuracy of liquid chemistry. In this way, the effect of temperature on the melt chemistry is taken into account. A number of viscosity models with good precision for liquid silicate melt are available in literature, such as the GRD equation[18] used by Ishibashi and Sato,[12] Vona et al.,[14] Chevrel et al.[15] and Campagnola et al.[16] Ishibashi[13] calculated the residual melt viscosity with Shaw’s equation.[19] In order to keep consistency with other data and ensure the reliability of viscosity data, the melt viscosity in Ishibashi’s study is re-calculated in the present work using the GRD equation, which is based on more recently published viscosity data.

Another important parameter in viscosity study is the shear rate, which is often omitted from discussion. However, it critically influences the measured result. With increasing solid fraction, the viscosity tends to be shear rate-dependent, i.e., non-Newtonian. A heterogeneous silicate melt may exhibit evident non-Newtonian behavior at very low solid concentration, e.g., 6 vol pct in Ishibashi and Sato’s work.[12] Therefore, it is of great importance to take into account the shear rate in viscosity modeling. As shown in Table I, the selected five studies present detailed shear rate/rotating speed information. For comparison, the rotating speed in the work of Ishibashi and Sato[12] is converted to shear rate using the following equation based on the geometry of spindle and crucible in their study.

$$ \dot{\gamma } = \frac{{2\omega R_{\text{o}}^{2} }}{{(R_{\text{o}}^{2} - R_{\text{i}}^{2} )}} $$
(1)

where R o, R i are the radius of the crucible and the spindle, respectively, m; \( \omega \) is the rotating speed, rad/s.

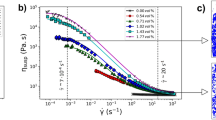
It is also noted in Table I that the viscosity is measured at shear rate decreasing ramp (down ramp) except for the work of Campagnola et al., who conducted the measurement on both decreasing ramp and increasing ramp (up ramp) of shear rate. According to Campagnola et al.’s observation, the viscosity variations in the two processes are asymmetrical. For the up-ramp condition, the progressive alignment of crystals and/or the disruption of aggregates lead to a decrease in viscosity with increasing shear rate, exhibiting a pronounced non-Newtonian behavior. However, under the down-ramp condition, the viscosity is only slightly increased.[16] This is probably due to that the randomly orientated crystals or the solid network cannot be completely recovered during shear rate decreasing, once disrupted by high shear rate at the beginning of rotating. For a shear-thinning silicate system, the viscosity shows an abrupt decrease with increasing shear rate, due to the rearrangement of solid particles. At a shear rate above a critical value \( \dot{\gamma }_{\text{c}} \) (determined by the intersection of two tangent lines, as shown in Figure 1), the particles are well aligned and change only slightly with further increased shear rate (provided no shear-induced clusters occur). We therefore define silicate melts as less-sheared (a system with randomly orientated crystals) and well-sheared system (the crystals are well aligned) depending on the viscosity changing profile with increasing shear rate, shown in Figure 1. The critical shear rate may vary with solid fraction and particle shape and the typical range of \( \dot{\gamma }_{\text{c}} \) is between 102 and 103 s−1.[20]

Fig. 1
figure 1

Different flow behaviors at different shear rate ranges

Full size image

Five datasets are selected for the viscosity modeling of a solid-bearing silicate melt in this paper. The details of these five datasets are summarized in Table I, providing information of each study with respect to the specified volume fraction of crystals, crystal’s aspect ratio and shear rate, which are of significant importance for the subsequent viscosity modeling.

Viscosity Modeling of the Solid-Bearing Silicate Melts

Numerous equations have been formulated to account for the viscosity of solid-liquid systems. Rutgers reviewed over 250 viscosity equations in 1962.[21] Many other review articles are also available.[22,23,24] However, most of the equations gradually fade into oblivion due to the limited application range or the phenomenological nature, except for a few equations, such as the well-known formula (Eq. [2]) derived by Einstein in 1906.[25]

$$ \eta_{r} = \frac{{\eta_{S} }}{{\eta_{L} }} = 1 + 2.5\varPhi $$
(2)

where η r is the relative viscosity; η S the viscosity of a suspension and η L the viscosity of the liquid; \( \varPhi \) the volume fraction of solids; 2.5 is termed as the Einstein coefficient or the intrinsic viscosity, which is a non-unit parameter characterizing the behavior of non-interacting particles in a dilute system.

Although the Einstein equation enables viscosity calculation of suspensions at dilute regime, i.e. 2 vol pct,[26] it fails with increasing solid fraction or particle’s shape diversity, as it does not account for the particle-particle interaction (e.g., collision). In concentrated suspensions, however, the flow field around a particle is “felt” by other particles and the collisions between particles lead to the formation of aggregates[27] or even a solid network.[28,29] The complicated structure leads to non-Newtonian behavior which has been observed in a number of silicate systems.[12,13,15] Most of the existing viscosity models only deal with the dilute and Newtonian regime, which are far from some practical applications. The present work aims to develop a viscosity model of solid-bearing silicate melts by taking into account non-Newtonian behaviors.

Power-Law Equation

In order to quantify the non-Newtonian behavior of solid-bearing silicate melts, the power-law equation is employed, as it is the most commonly used constitutive equation which allows characterizing both shear thinning and shear-thickening behaviors. The power-law model is expressed as

$$ \tau = m\dot{\gamma }^{n} $$
(3)

or

$$ \eta = \frac{\tau }{{\dot{\gamma }}} = m\dot{\gamma }^{n - 1} $$
(4)

where \( \tau \) is the shear stress, \( \dot{\gamma } \) the shear rate, m the flow consistency, n the flow index. The equation encapsulates various types of fluid, i.e., n = 1 for a Newtonian fluid; n < 1 for a shear-thinning fluid; n > 1 for a shear-thickening fluid. A shear-thinning liquid has a decreasing viscosity with increasing shear rate, whereas a shear-thickening liquid has an increasing viscosity with that, as illustrated in Figure 2.

Fig. 2
figure 2

Behavior of Newtonian, shear thinning, and thickening systems. (a) Correlation between shear stress and shear rate for different systems; (b) correlation between viscosity and shear rate for different systems

Full size image

In order to correlate the constitutive equation with system properties, e.g., solid particle fraction and particle shape, the power-law equation is divided by the viscosity of residual liquid (η L):

$$ \eta_{\text{r}} = \frac{m}{{\eta_{\text{L}} }}\dot{\gamma }^{n - 1} { = }m_{\text{r}} \dot{\gamma }^{n - 1} $$
(5)

where m r is defined as the relative flow consistency, which is equivalent to the relative viscosity for Newtonian fluid or the non-Newtonian fluid at shear rate of 1 s−1, using the consistent unit system. Physically, the relative flow consistency reflects the structure (i.e., spatial distribution and orientation of crystals) of solid-bearing silicate melts at unit shear rate. The flow index n is the parameter characterizing the influence of shear rate on structure, therefore on viscosity. According to Eq. [5], m r and n can be obtained by fitting this equation to measured data. Employing the viscosity data from the articles reviewed in Table I, the relative flow consistency and flow index are obtained by the best fit, as shown in Table II.

Table II The Relative Flow Consistency m r and the Flow Index n Obtained by the Best Fit to the Measured Viscosity at Different Shear Rates
Full size table

Considering the physical meaning of the flow consistency and flow index, it is reasonable to conclude that these two parameters are dependent on the structure of silicate melts, e.g., crystal fraction (\( \varPhi \)) and shape (r p). In this work, the efforts will be attempted to express m r and n as functions of the structure parameters (\( \varPhi \) and r p) of a solid-bearing silicate melt.

Relative Flow Consistency

A number of formulas have been derived to correlate the relative viscosity with solid concentration. Amongst these equations, Krieger–Dougherty (KD) equation[30] has been widely applied in silicate melts. This KD equation is considered by Wildemuth and Williams as the most successful viscosity model due to the most rigorous derivation process.[31] The KD equation is therefore employed in the present work to relate the relative flow consistency with the solid fraction (Eq. [6]).

$$ m_{\text{r}} = \left( {1 - \frac{\varPhi }{{\varPhi_{\text{m}} }}} \right)^{{ - [\eta ]\varPhi_{\text{m}} }} $$
(6)

where [η] is the intrinsic viscosity,[32] which is considered to be 2.5 for suspensions containing spherical particles,[33,34,35] but it varies with particle shapes;[36] \( \varPhi_{\text{m}} \) is geometrically defined as the upper limit of the volume fraction, beyond which there is no space to accommodate more particles.[11]

The obtained relative flow consistency in Section III–A is plotted against the volume fraction of solids and Eq. [6] is applied to fit to the data, as shown in Figure 3. The obtained parameters are demonstrated in Table III together with the crystals’ aspect ratio.

Fig. 3
figure 3

Fitting of the Krieger–Dougherty model (Eq. [6]) to the selected viscosity data

Full size image
Table III Parameters Obtained by the Best Fit to the Measured Data and the Crystal’s Aspect Ratio
Full size table

As shown in Table III, the determination coefficients (adjusted R 2) are close to unity, indicating an excellent fitting, except for that of Ishibashi and Chevrel et al.’ data. The poor fitting to these two datasets is mainly because of the large analytical error of the samples with low solid fractions (both of the systems studied have solid fraction <25 vol pct) as discussed in Section II. The fitting confirms that the correlation between m r and \( \varPhi \) can be expressed via the KD equation. Secondly, it is noted that with a change in the aspect ratio r p, the obtained maximum packing fraction \( \varPhi_{\text{m}} \) varies from 0.33 to 0.57 and the intrinsic viscosity [η] increases from 0.92 to 5.16. This suggests that not only the relative flow consistency is connected to the solid fraction and solid shape, but also the extent of the crystal’s effect at a given solid fraction on the viscosity is dependent on its morphology. This influence extent, represented by \( \varPhi_{\text{m}} \) and [η], of the solid crystal morphology is further discussed below.

The maximum packing fraction \( \varPhi_{\text{m}} \), at which the relative viscosity approaches infinity, is proved to be 63.66 ± 0.05 pct[37] for randomly packed monodisperse spheres. For non-spherical particles, a number of equations are found in literature attempting to correlate \( \varPhi_{\text{m}} \) with the particle’s aspect ratio, r p, as summarized in Table IV. The comparison between calculated \( \varPhi_{\text{m}} \) from different equations is demonstrated in Figure 4.

Table IV Summary of the Expressions for the Maximum Packing Fraction of Particle
Full size table
Fig. 4
figure 4

Comparison of the proposed correlations between \( \varPhi_{\text{m}} \) and \( r_{\text{p}} \). Parameters used in Mueller et al.’s[44] equation: \( \varPhi_{{{\text{m}}1}} \) = 0.66, α = 1.08

Full size image

It is clear that (1) Rahli et al. and Evans and Gibson’s equations predict \( \varPhi_{\text{m}} \) > 1 at low aspect ratio, while Parkhouse and Kelly’s equation predict \( \varPhi_{\text{m}} \) ≤ 0 at aspect ratio ≤1, no one of which has physical meaning; (2) Kitano et al., Pabst et al. and Mueller et al.’s equations are merely valid in a certain range of aspect ratios; (3) Mueller et al.’s equation can calculate \( \varPhi_{\text{m}} \) in all the r p ranges by assuming the asymmetrical effect of the prolate (rod-like, r p > 1) and oblate (plate-like, r p < 1) particles on the viscosity. This assumption is reasonable based on the author’s experimental data[44] and is therefore adopted in the present study. The parameters \( \varPhi_{{{\text{m}}1}} \) and α in this equation are optimized by fitting to the experimental data in Table I (see Figure 5) and the fitted equation is expressed as Eq. [7].

Fig. 5
figure 5

Fitting of the Mueller et al.’s equation to the measured silicate melt data (\( \varPhi_{\text{m}} \)–\( r_{\text{p}} \)) in literature. The data from analogy experiment (silicone oil containing particles of biotite and polyacrylic glitter (oblate), glass beads (spherical), glass, and carbon fibers (prolate)) at room temperature[44] are also shown for comparison

Full size image
$$ \varPhi_{\text{m}} = 0.52\exp \left[ { - \frac{{\left( {\log r_{\text{p}} } \right)^{2} }}{{2 \times 1.48^{2} }}} \right] $$
(7)

Although the experimental data points show scatter in Figure 5, Eq. [7] is acceptable considering the large error in viscosity measurement (25 pct according to Mills et al.[45]), and the error and distribution in the determination of the particle’s aspect ratio. This result reveals: (1) \( \varPhi_{{{\text{m}}1}} \), the maximum packing fraction for particles in the silicate melt at r p = 1 is approximately 0.52, which is lower than that for the system of randomly packed monodisperse spheres (0.63 according to Scott et al.[37]). We find this to be due to the characterization imperfection of crystal shape using r p (for example, the r p non-spherical particles such as cubes can also be 1); (2) the maximum packing fraction, \( \varPhi_{\text{m}} \), decreases with increasing particle’s aspect ratio in the range of r p > 1, suggesting the strong exclusion-volume effect[46] in the orientationally disordered packings; (3) the fitted curve based on silicate data is consistent with the data obtained from analogy experiment at room temperature, as seen from the room temperature data in Figure 5; (4) more experimental work is needed to validate the Eq. [7] for plate-like crystals, i.e. particle’s aspect ratio smaller than 1 (r p < 1).

The other parameter, the intrinsic viscosity [η] in Eq. [6], reflects the hydrodynamic interaction between particles and the suspending liquid, which is linked with the particle shape. As proved by Einstein, the intrinsic viscosity is 2.5 for the rigid spherical particle. A number of empirical equations, which correlates [η] with the particle shape r p, are summarized in Table V.

Table V Summary of Expressions for the Intrinsic Viscosity
Full size table

It can be seen that the application ranges of the existing formulas deviate far from the aspect ratio of 1. In the selected systems, however, crystals with 1.52 ≤ r p ≤ 6 are present (see Table III). Considering the fact that (1) the intrinsic viscosity is 2.5 at r p = 1 and (2) the intrinsic viscosity increases with increasing r p (this is confirmed by experimental observation[38,44]), Eq. [8] is proposed herein to link [η] with the particle shape parameter r p.

$$ \left[ \eta \right] = \frac{1}{{0.4 - k(r_{\text{p}} - 1)}} $$
(8)

where k is a fitting parameter and \( r_{\text{p}} \, < \,1 + 0.4k^{ - 1} \).

To obtain a reasonable [η]–r p relations/curves with enough data points, the viscosity data of polymer melts containing inorganic particles (glass fiber, etc.),[38] are also considered as this system is similar with a heterogeneous silicate melt. Figure 6 shows the [η]–r p relations/curves by fitting Eq. [8] to the above mentioned polymer melt containing inorganic particles. The fitted parameters k of Eq. [8] and the determination coefficient (the adjusted R 2) for these data are 0.012 (k) and 0.85 (adj. R2), respectively.

Fig. 6
figure 6

Fitting of Eq. [8] to the measured data (\( \left[ \eta \right] \)–\( r_{\text{p}} \)) in literature (Data from Kitano et al. are reproduced from Mueller et al.[43])

Full size image

It is evident that: (a) the intrinsic viscosity increases with increasing particle’s aspect ratio due to the larger solid-liquid interaction for more anisotropic particles; (b) the Eq. [8] can be applied to the particles with 1 ≤ \( r_{\text{p}} \, < \,1 + 0.4k^{ - 1} \), i.e., spherical and rod-like crystals; (c) [η] is 2.5 at r p = 1, which is in agreement with the well-known Einstein’s equation; (d) the measured data from the silicate systems are scattered, resulting in poor fitting. More experimental data, (specifically, data in the range of r p < 1, plate-like crystal) are required to further identify/evaluate the reliability of Eq. [8].

By inserting Eqs. [7] and [8] into Eq. [6], the relative flow consistency m r in the power-law equation (Eq. [5]) can therefore be calculated as a function of \( \varPhi \) and r p. In this way, influences of the system properties (e.g. solid fraction and particle shape) are incorporated in the viscosity calculation of solid-bearing silicate melts at unit shear rate. The effect of shear rate on viscosity will then be discussed in the following section.

Flow Index

The other determinant in the power-law equation (Eq. [5]) is the flow index, n, which quantifies the effect of shear rate on the viscosity. Shear-thickening behavior (i.e. viscosity increases with shear rate) is constantly observed in colloidal systems and densely packed suspensions.[49] However, it is rarely observed in silicate melt whereas shear-thinning behavior (i.e., viscosity decreases with shear rate) has been experimentally identified in a number of silicate melts. Many efforts have been attempted to reveal the underlying physical process and a number of mechanisms have been proposed to account for the origin of the shear-thinning behavior, including flow-induced reorientation of solids,[12,13,15] migration of solids,[34,50] formation, and break up of aggregates,[16,51] decrease of solid phase contiguity (the fraction of the solid’s internal surface area shared with other solids[52]), viscous heating,[53,54] amongst which the flow-induced reorientation of particles is commonly believed to be one of the main causes of shear thinning. Before applying shear to a solid-bearing silicate melt, the solids orientate randomly, however, the solids tend to align parallel to the flow direction when subjected to a shear stress in a rotational viscometer.[11,13,55,56] The decrease in the dispersion of solid orientation alleviates the solid-solid interaction, minimizes the viscous dissipation,[43,57] and also increases the maximum packing fraction,[12] leading to the viscosity decrease. Moreover, in melts with a high solids fraction, less space intensifies the solid-solid collision, resulting in the formation of aggregates[16] or even the construction of a solid framework.[29] The weak connection between the solid crystals is likely to be disrupted when subjected to a sufficient shear stress, separating individual crystals.[16] Consequently, the obstruction exerted on the rotation of the spindle decreases, resulting in a shear-thinning behavior.[51] The key parameters controlling the motion of an ellipsoidal particle and therefore the particle orientation and interaction are the particle concentration[11,43] and the aspect ratio.[11,57,58] It is deduced that the flow index is a function of both solid concentration and aspect ratio.[59] In order to figure out the correlation between flow index and its influencing factors, the recently published experimental data in Table I except the data from Chervel et al. are employed for the discussion. In Chervel et al.’s study, an abrupt flow index decrease with increasing solid fraction is found, which is unexplainable and therefore are excluded in this discussion. As shown in Figure 7, it is clear that the experimental data from Campagnola et al. (up ramp) deviate from the other data.

Fig. 7
figure 7

Flow index dependence on the solid fraction for both well-sheared and less-sheared systems

Full size image

As has been reviewed and re-analyzed in Section II, there are two types of shear history conditions in the work summarized in Table I for viscosity measurement. Those are (1) the less-sheared one, e.g., the studies of Campagnola et al. (up ramp), where the melt is in the state with random orientated crystals or clusters/framework prior to viscosity measurement, and (2) the well-sheared condition, e.g., the other work in Table I, where the silicate melt has been subjected to a sufficient shear (enable to align the crystals and/or breakdown the solid network) prior to viscosity measurement. Therefore, a lower flow index, i.e., more pronounced shear-thinning behavior, is expected for the less-sheared system, resulting in the deviation of Campagnola et al. (up ramp)’s experimental data. In order to correlate the flow index with the solid fraction and shape, a formula is proposed in the present work, as shown in Eq. [9].

$$ n = 1 - \alpha \left( {\frac{\varPhi }{{\varPhi_{m} }}} \right) $$
(9)

where α is a fitting parameter. The effect of particle shape on the flow index is reflected by the maximum packing fraction, which is a function of particle’s aspect ratio.

Due to the fact that shear history condition can significantly affect the rheological behavior, flow index in Table II as a function of normalized solid fraction (\( \varPhi /\varPhi_{m} \)) under the two shear history conditions are fitted separately with Eq. [9]. According to fitting results, formulas to calculate the flow index of silicate melts are obtained as Eqs. [10] and [11], respectively for the well-sheared and the less-sheared conditions. It is clear that the fitting is excellent (a value nearly unity for the adjusted R 2) and at a given normalized solid fraction, the flow index of the less-sheared system is smaller than that of the well-sheared system. This arises from (1) the structure with randomly orientated and inter-connected crystals in the less-sheared system is gradually broken up with increasing shear rate, leading to significant viscosity decreases; (2) in the system with isolated and well-aligned crystals in the initial state, the viscosity increases marginally as the decreasing in shear rate only changes the structure to a limited extend, yielding little shear-thinning behavior. The distinct formula is therefore necessary for evaluation of the flow index to develop a reliable viscosity model of heterogeneous silicate melts.

Well-sheared system:

$$ n = 1 - 0.098\left( {\frac{\varPhi }{{\varPhi_{\text{m}} }}} \right),\quad {\text{Adj}} . { }R^{2} = \, 0.999 $$
(10)

Less-sheared system:

$$ n = 1 - 0.50\left( {\frac{\varPhi }{{\varPhi_{\text{m}} }}} \right),\quad {\text{Adj}} . { }R^{2} = \, 0.997 $$
(11)

Validation of Present Viscosity Model

By using the above calculation method, viscosities of the silicate systems listed in Table I are calculated and compared with the measured values (in Figure 8).

Fig. 8
figure 8

Comparison between the calculated and measured relative viscosity

Full size image

Reliability of the present calculation has been evaluated using the error factor \( \Delta \) proposed by Mills et al.[45]:

$$ \Delta = \frac{1}{N}\sum\limits_{{}}^{N} {\left| {\frac{{\eta_{\text{calc}} - \eta_{\exp } }}{{\eta_{\exp } }}} \right|} $$
(12)

where N is the number of data points; \( \eta_{\text{calc}} \) and \( \eta_{\exp } \) are the calculated and the experimentally measured viscosities, respectively.

The error factor \( \Delta \) of the present viscosity calculation is 32 pct with respective to approximately 200 experimental data points of silicate melts. This is fairly acceptable considering the fact that there is a 25 pct[45] error in viscosity measurement of the fully liquid silicates and a higher measuring error is expected for the solid-bearing silicate due to the non-uniformly distributed crystals. That a reasonable reliability has been achieved in the present method is the result of (1) the three significant viscosity determinants of solid-containing systems, \( \varPhi_{\text{m}} \), [η] and n are correctly evaluated as functions of the crystal shape and volume fraction, presenting a complete picture of the effect of crystal characteristics on viscosity; (2) the non-Newtonian behavior of the solid-bearing silicates has been considered in the calculation, which reflects the real measurement conditions; and (3) the shear history of the measurement has been taken into account in the viscosity calculation, giving a deeper insight into the complex structural influence on the viscosity. It should also be underlined that the proposed/fitted equations (Eqs. [7] to [11]) are only validated for crystal fraction up to 34 vol pct due to the limited reliable viscosity database at high solid fractions. This is mainly due to the fact that the spatial distribution of crystals in melt is much more inhomogeneous than in the case of dilute suspensions. And the measured data differ a lot among researchers and are not reproducible. Secondly, this model is proposed based on the assumption of a power-law fluid. This means it is not able to predict the yield strength. At last, the particle size is not included herein as its influence on viscosity is too complicated, particularly for crystals with a large size and shape dispersion. More work is needed in the future.

Algorithm of Viscosity Calculation

According to the aforementioned analysis, three equations are formulated to calculate the maximum packing fraction \( \varPhi_{\text{m}} \), the intrinsic viscosity [η] and flow index n. Combining Eqs. [5] to [8], [10] and [11], viscosity of the solid-bearing silicate melts can be calculated for a given shear rate, using data of the crystal shape and its fraction of the measured samples. Figure 9 proposes a flow chart for viscosity calculation. This includes the following steps: (i) measure the volume fraction (\( \varPhi \)) and the shape (r p) of solid crystals; (ii) calculate the maximum packing fraction \( \varPhi_{m} \) and the intrinsic viscosity [η] using Eqs. [7] and [8], respectively; (iii) calculate the relative flow consistency m r with the obtained \( \varPhi_{m} \) and [η] using the Krieger-Dougherty equation; (iv) examine the measurement condition, if the silicate melt is well-sheared (the critical shear rate is between 102 and 103 s−1 and in-between the two values, both two equations, i.e., Eqs. [10] and [11], can be used) prior to the measurement, apply Eq. [10] to calculate the flow index n, if not, use Eq. [11]; (v) calculate the liquid melt viscosity η L with the existing models in literature and calculate the shear rate \( \dot{\gamma } \) applied to the silicate system during measurement; (vi) calculate the viscosity of the solid-bearing silicate melt η with the power-law equation (Eq. [5]) by plugging the obtained relative flow consistency m r and flow index n as well as the liquid melt viscosity η L and shear rate \( \dot{\gamma } \).

Fig. 9
figure 9

The algorithm of viscosity calculation for solid-bearing silicate melts (power-law fluid)

Full size image

Conclusions

In most of the existing work, the ER or KD equation is employed to account for the effect of solid fraction on viscosity and the influence of particle shape and shear rate are constantly neglected. This leads to big deviation in the values of parameters in ER/KD equation as they are functions of particle shape and/or shear rate. Therefore, the significance of particle shape and shear rate is stressed herein and incorporated in the developed model, presenting a more complete picture of the particle’s influence on viscosity. In this work, the measured viscosity data of the solid-bearing silicate melts from recent years are firstly assessed and a viscosity dataset with specified crystal fraction, crystal shape, and shear rate/rotating speed is established for the purpose of viscosity calculation. On the basis of the power-law and Krieger–Dougherty equation, a non-Newtonian viscosity calculation method is proposed. The following conclusions are obtained:

  1. 1.

    Two new empirical equations are proposed to calculate respectively the intrinsic viscosity in the Krieger–Dougherty viscosity model and the flow index in the power-law equation as functions of the particle’s aspect ratio.

  2. 2.

    The shear history (with or without sufficient shear to align the crystal’s orientation or breakdown the clusters/solid framework prior to viscosity measurement) is found to significantly influence the flow index. Distinct equations have been proposed to evaluate the flow indexes for the well-sheared and less-sheared measurement condition respectively. In this way, shear history has been for the first time considered in viscosity calculation.

  3. 3.

    An algorithm is presented to give a step-by-step method for calculating the viscosity of the crystal-bearing silicates at a given shear rate by using the measured crystal shape and fraction. The relative error between the calculated and measured viscosity is evaluated to be 32 pct with respect to approximately 200 measured viscosity data points with solid fraction up to 34 vol pct. This is fairly acceptable considering the current level of viscosity studies on solid-containing silicates at high temperature.